|
Transcriber’s note:
|
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version.
Links to other EB articles: Links to articles residing in other EB volumes will
be made available when the respective volumes are introduced online.
|
THE ENCYCLOPÆDIA BRITANNICA
A DICTIONARY OF ARTS, SCIENCES, LITERATURE AND GENERAL INFORMATION
ELEVENTH EDITION
VOLUME XIV SLICE II
Hydromechanics to Ichnography
Articles in This Slice
115
HYDROMECHANICS (ὑδρομηχανικά), the science of the
mechanics of water and fluids in general, including hydrostatics
or the mathematical theory of fluids in equilibrium, and hydromechanics,
the theory of fluids in motion. The practical application
of hydromechanics forms the province of hydraulics (q.v.).
Historical.—The fundamental principles of hydrostatics were first
given by Archimedes in his work Περὶ τῶν ὀχουμένων, or De iis quae
vehuntur in humido, about 250 B.C., and were afterwards applied
to experiments by Marino Ghetaldi (1566-1627) in his Promotus
Archimedes (1603). Archimedes maintained that each particle of
a fluid mass, when in equilibrium, is equally pressed in every direction;
and he inquired into the conditions according to which a solid
body floating in a fluid should assume and preserve a position of
equilibrium.
In the Greek school at Alexandria, which flourished under the
auspices of the Ptolemies, the first attempts were made at the
construction of hydraulic machinery, and about 120 B.C. the fountain
of compression, the siphon, and the forcing-pump were invented by
Ctesibius and Hero. The siphon is a simple instrument; but the
forcing-pump is a complicated invention, which could scarcely
have been expected in the infancy of hydraulics. It was probably
suggested to Ctesibius by the Egyptian Wheel or Noria, which was
common at that time, and which was a kind of chain pump, consisting
of a number of earthen pots carried round by a wheel. In
some of these machines the pots have a valve in the bottom which
enables them to descend without much resistance, and diminishes
greatly the load upon the wheel; and, if we suppose that this valve
was introduced so early as the time of Ctesibius, it is not difficult
to perceive how such a machine might have led to the invention of
the forcing-pump.
Notwithstanding these inventions of the Alexandrian school, its
attention does not seem to have been directed to the motion of
fluids; and the first attempt to investigate this subject was made
by Sextus Julius Frontinus, inspector of the public fountains at
Rome in the reigns of Nerva and Trajan. In his work De aquaeductibus
urbis Romae commentarius, he considers the methods
which were at that time employed for ascertaining the quantity of
water discharged from ajutages, and the mode of distributing the
waters of an aqueduct or a fountain. He remarked that the flow of
water from an orifice depends not only on the magnitude of the orifice
itself, but also on the height of the water in the reservoir; and that
a pipe employed to carry off a portion of water from an aqueduct
should, as circumstances required, have a position more or less
inclined to the original direction of the current. But as he was
unacquainted with the law of the velocities of running water as
depending upon the depth of the orifice, the want of precision which
appears in his results is not surprising.
Benedetto Castelli (1577-1644), and Evangelista Torricelli (1608-1647),
two of the disciples of Galileo, applied the discoveries of their
master to the science of hydrodynamics. In 1628 Castelli published
a small work, Della misura dell’ acque correnti, in which he satisfactorily
explained several phenomena in the motion of fluids in
rivers and canals; but he committed a great paralogism in supposing
the velocity of the water proportional to the depth of the
orifice below the surface of the vessel. Torricelli, observing that in
a jet where the water rushed through a small ajutage it rose to nearly
the same height with the reservoir from which it was supplied,
imagined that it ought to move with the same velocity as if it had
fallen through that height by the force of gravity, and hence he
deduced the proposition that the velocities of liquids are as the
square root of the head, apart from the resistance of the air and the
friction of the orifice. This theorem was published in 1643, at the
end of his treatise De motu gravium projectorum, and it was confirmed
by the experiments of Raffaello Magiotti on the quantities
of water discharged from different ajutages under different pressures
(1648).
In the hands of Blaise Pascal (1623-1662) hydrostatics assumed
the dignity of a science, and in a treatise on the equilibrium of
liquids (Sur l’équilibre des liqueurs), found among his manuscripts
after his death and published in 1663, the laws of the equilibrium
of liquids were demonstrated in the most simple manner, and amply
confirmed by experiments.
The theorem of Torricelli was employed by many succeeding
writers, but particularly by Edmé Mariotte (1620-1684), whose
Traité du mouvement des eaux, published after his death in the year
1686, is founded on a great variety of well-conducted experiments
on the motion of fluids, performed at Versailles and Chantilly. In
the discussion of some points he committed considerable mistakes.
Others he treated very superficially, and in none of his experiments
apparently did he attend to the diminution of efflux arising from the
contraction of the liquid vein, when the orifice is merely a perforation
in a thin plate; but he appears to have been the first who attempted
to ascribe the discrepancy between theory and experiment to the
retardation of the water’s velocity through friction. His contemporary
Domenico Guglielmini (1655-1710), who was inspector of
the rivers and canals at Bologna, had ascribed this diminution of
velocity in rivers to transverse motions arising from inequalities in
their bottom. But as Mariotte observed similar obstructions even
in glass pipes where no transverse currents could exist, the cause
assigned by Guglielmini seemed destitute of foundation. The
French philosopher, therefore, regarded these obstructions as the
effects of friction. He supposed that the filaments of water which
graze along the sides of the pipe lose a portion of their velocity;
that the contiguous filaments, having on this account a greater
velocity, rub upon the former, and suffer a diminution of their
celerity; and that the other filaments are affected with similar
retardations proportional to their distance from the axis of the pipe.
In this way the medium velocity of the current may be diminished,
and consequently the quantity of water discharged in a given time
must, from the effects of friction, be considerably less than that
which is computed from theory.
The effects of friction and viscosity in diminishing the velocity of
running water were noticed in the Principia of Sir Isaac Newton,
who threw much light upon several branches of hydromechanics.
At a time when the Cartesian system of vortices universally prevailed,
he found it necessary to investigate that hypothesis, and in
the course of his investigations he showed that the velocity of any
stratum of the vortex is an arithmetical mean between the velocities
of the strata which enclose it; and from this it evidently follows
that the velocity of a filament of water moving in a pipe is an arithmetical
mean between the velocities of the filaments which surround
it. Taking advantage of these results, Henri Pitot (1695-1771)
afterwards showed that the retardations arising from friction are
inversely as the diameters of the pipes in which the fluid moves.
The attention of Newton was also directed to the discharge of water
from orifices in the bottom of vessels. He supposed a cylindrical
vessel full of water to be perforated in its bottom with a small hole
by which the water escaped, and the vessel to be supplied with
water in such a manner that it always remained full at the same
height. He then supposed this cylindrical column of water to be
divided into two parts,—the first, which he called the “cataract,”
being an hyperboloid generated by the revolution of an hyperbola
of the fifth degree around the axis of the cylinder which should pass
through the orifice, and the second the remainder of the water in
the cylindrical vessel. He considered the horizontal strata of this
hyperboloid as always in motion, while the remainder of the water
was in a state of rest, and imagined that there was a kind of cataract
in the middle of the fluid. When the results of this theory were
compared with the quantity of water actually discharged, Newton
concluded that the velocity with which the water issued from the
orifice was equal to that which a falling body would receive by
descending through half the height of water in the reservoir. This
conclusion, however, is absolutely irreconcilable with the known
fact that jets of water rise nearly to the same height as their reservoirs,
and Newton seems to have been aware of this objection. Accordingly,
in the second edition of his Principia, which appeared in 1713,
he reconsidered his theory. He had discovered a contraction in the
vein of fluid (vena contracta) which issued from the orifice, and found
that, at the distance of about a diameter of the aperture, the section
of the vein was contracted in the subduplicate ratio of two to one.
He regarded, therefore, the section of the contracted vein as the
true orifice from which the discharge of water ought to be deduced,
and the velocity of the effluent water as due to the whole height of
water in the reservoir; and by this means his theory became more
conformable to the results of experience, though still open to
serious objections. Newton was also the first to investigate the
difficult subject of the motion of waves (q.v.).
In 1738 Daniel Bernoulli (1700-1782) published his Hydrodynamica
seu de viribus et motibus fluidorum commentarii. His theory of
the motion of fluids, the germ of which was first published in his
memoir entitled Theoria nova de motu aquarum per canales quocunque
fluentes, communicated to the Academy of St Petersburg as
early as 1726, was founded on two suppositions, which appeared to
him conformable to experience. He supposed that the surface of
the fluid, contained in a vessel which is emptying itself by an orifice,
remains always horizontal; and, if the fluid mass is conceived to be
divided into an infinite number of horizontal strata of the same
bulk, that these strata remain contiguous to each other, and that
all their points descend vertically, with velocities inversely proportional
to their breadth, or to the horizontal sections of the
reservoir. In order to determine the motion of each stratum, he
employed the principle of the conservatio virium vivarum, and
obtained very elegant solutions. But in the absence of a general
demonstration of that principle, his results did not command the
confidence which they would otherwise have deserved, and it
became desirable to have a theory more certain, and depending solely
on the fundamental laws of mechanics. Colin Maclaurin (1698-1746)
and John Bernoulli (1667-1748), who were of this opinion,
resolved the problem by more direct methods, the one in his Fluxions,
published in 1742, and the other in his Hydraulica nunc primum
detecta, et demonstrata directe ex fundamentis pure mechanicis, which
forms the fourth volume of his works. The method employed by
Maclaurin has been thought not sufficiently rigorous; and that of
John Bernoulli is, in the opinion of Lagrange, defective in clearness
and precision. The theory of Daniel Bernoulli was opposed also by
Jean le Rond d’Alembert. When generalizing the theory of pendulums
of Jacob Bernoulli (1654-1705) he discovered a principle of
dynamics so simple and general that it reduced the laws of the
motions of bodies to that of their equilibrium. He applied this
116
principle to the motion of fluids, and gave a specimen of its application
at the end of his Dynamics in 1743. It was more fully developed
in his Traité des fluides, published in 1744, in which he gave simple
and elegant solutions of problems relating to the equilibrium and
motion of fluids. He made use of the same suppositions as Daniel
Bernoulli, though his calculus was established in a very different
manner. He considered, at every instant, the actual motion of a
stratum as composed of a motion which it had in the preceding
instant and of a motion which it had lost; and the laws of equilibrium
between the motions lost furnished him with equations representing
the motion of the fluid. It remained a desideratum to
express by equations the motion of a particle of the fluid in any
assigned direction. These equations were found by d’Alembert from
two principles—that a rectangular canal, taken in a mass of fluid in
equilibrium, is itself in equilibrium, and that a portion of the fluid,
in passing from one place to another, preserves the same volume
when the fluid is incompressible, or dilates itself according to a
given law when the fluid is elastic. His ingenious method, published
in 1752, in his Essai sur la résistance des fluides, was brought to perfection
in his Opuscules mathématiques, and was adopted by Leonhard
Euler.
The resolution of the questions concerning the motion of fluids
was effected by means of Euler’s partial differential coefficients.
This calculus was first applied to the motion of water by d’Alembert,
and enabled both him and Euler to represent the theory of fluids
in formulae restricted by no particular hypothesis.
One of the most successful labourers in the science of hydrodynamics
at this period was Pierre Louis Georges Dubuat (1734-1809).
Following in the steps of the Abbé Charles Bossut (Nouvelles
Experiences sur la résistance des fluides, 1777), he published, in 1786,
a revised edition of his Principes d’hydraulique, which contains a
satisfactory theory of the motion of fluids, founded solely upon
experiments. Dubuat considered that if water were a perfect
fluid, and the channels in which it flowed infinitely smooth, its
motion would be continually accelerated, like that of bodies descending
in an inclined plane. But as the motion of rivers is not continually
accelerated, and soon arrives at a state of uniformity, it is evident that
the viscosity of the water, and the friction of the channel in which
it descends, must equal the accelerating force. Dubuat, therefore,
assumed it as a proposition of fundamental importance that, when
water flows in any channel or bed, the accelerating force which obliges
it to move is equal to the sum of all the resistances which it meets
with, whether they arise from its own viscosity or from the friction
of its bed. This principle was employed by him in the first edition
of his work, which appeared in 1779. The theory contained in that
edition was founded on the experiments of others, but he soon saw
that a theory so new, and leading to results so different from the
ordinary theory, should be founded on new experiments more direct
than the former, and he was employed in the performance of these
from 1780 to 1783. The experiments of Bossut were made only on
pipes of a moderate declivity, but Dubuat used declivities of every
kind, and made his experiments upon channels of various sizes.
The theory of running water was greatly advanced by the researches
of Gaspard Riche de Prony (1755-1839). From a collection
of the best experiments by previous workers he selected eighty-two
(fifty-one on the velocity of water in conduit pipes, and thirty-one
on its velocity in open canals); and, discussing these on physical
and mechanical principles, he succeeded in drawing up general
formulae, which afforded a simple expression for the velocity of
running water.
J. A. Eytelwein (1764-1848) of Berlin, who published in 1801 a
valuable compendium of hydraulics entitled Handbuch der Mechanik
und der Hydraulik, investigated the subject of the discharge of water
by compound pipes, the motions of jets and their impulses against
plane and oblique surfaces; and he showed theoretically that a water-wheel
will have its maximum effect when its circumference moves
with half the velocity of the stream.
J. N. P. Hachette (1769-1834) in 1816-1817 published memoirs
containing the results of experiments on the spouting of fluids and the
discharge of vessels. His object was to measure the contracted part
of a fluid vein, to examine the phenomena attendant on additional
tubes, and to investigate the form of the fluid vein and the results
obtained when different forms of orifices are employed. Extensive
experiments on the discharge of water from orifices (Expériences
hydrauliques, Paris, 1832) were conducted under the direction of the
French government by J. V. Poncelet (1788-1867) and J. A. Lesbros
(1790-1860). P. P. Boileau (1811-1891) discussed their results and
added experiments of his own (Traité de la mésure des eaux courantes,
Paris, 1854). K. R. Bornemann re-examined all these results with
great care, and gave formulae expressing the variation of the coefficients
of discharge in different conditions (Civil Ingénieur, 1880).
Julius Weisbach (1806-1871) also made many experimental investigations
on the discharge of fluids. The experiments of J. B.
Francis (Lowell Hydraulic Experiments, Boston, Mass., 1855) led him
to propose variations in the accepted formulae for the discharge over
weirs, and a generation later a very complete investigation of this
subject was carried out by H. Bazin. An elaborate inquiry on the
flow of water in pipes and channels was conducted by H. G. P.
Darcy (1803-1858) and continued by H. Bazin, at the expense of the
French government (Recherches hydrauliques, Paris, 1866). German
engineers have also devoted special attention to the measurement
of the flow in rivers; the Beiträge zur Hydrographie des Königreiches
Böhmen (Prague, 1872-1875) of A. R. Harlacher (1842-1890)
contained valuable measurements of this kind, together with a comparison
of the experimental results with the formulae of flow that had
been proposed up to the date of its publication, and important data
were yielded by the gaugings of the Mississippi made for the United
States government by A. A. Humphreys and H. L. Abbot, by Robert
Gordon’s gaugings of the Irrawaddy, and by Allen J. C. Cunningham’s
experiments on the Ganges canal. The friction of water, investigated
for slow speeds by Coulomb, was measured for higher speeds by
William Froude (1810-1879), whose work is of great value in the
theory of ship resistance (Brit. Assoc. Report., 1869), and stream line
motion was studied by Professor Osborne Reynolds and by Professor
H. S. Hele Shaw.
(X.)
Hydrostatics
Hydrostatics is a science which grew originally out of a number
of isolated practical problems; but it satisfies the requirement
of perfect accuracy in its application to phenomena, the largest
and smallest, of the behaviour of a fluid. At the same time,
it delights the pure theorist by the simplicity of the logic with
which the fundamental theorems may be established, and by the
elegance of its mathematical operations, insomuch that hydrostatics
may be considered as the Euclidean pure geometry of
mechanical science.
1. The Different States of a Substance or Matter.—All substance
in nature falls into one of the two classes, solid and fluid; a
solid substance, the land, for instance, as contrasted with a
fluid, like water, being a substance which does not flow of itself.
A fluid, as the name implies, is a substance which flows, or
is capable of flowing; water and air are the two fluids distributed
most universally over the surface of the earth.
Fluids again are divided into two classes, termed a liquid
and a gas, of which water and air are the chief examples.
A liquid is a fluid which is incompressible or practically so,
i.e. it does not change in volume sensibly with change of pressure.
A gas is a compressible fluid, and the change in volume is
considerable with moderate variation of pressure.
Liquids, again, can be poured from one open vessel into another,
and can be kept in an uncovered vessel, but a gas tends to diffuse
itself indefinitely and must be preserved in a closed reservoir.
The distinguishing characteristics of the three kinds of substance
or states of matter, the solid, liquid and gas, are summarized
thus in O. Lodge’s Mechanics:—
A solid has both size and shape.
A liquid has size but not shape.
A gas has neither size nor shape.
|
2. The Change of State of Matter.—By a change of temperature
and pressure combined, a substance can in general be made to
pass from one state into another; thus by gradually increasing
the temperature a solid piece of ice can be melted into the liquid
state of water, and the water again can be boiled off into the
gaseous state as steam. Again, by raising the temperature,
a metal in the solid state can be melted and liquefied, and poured
into a mould to assume any form desired, which is retained when
the metal cools and solidifies again; the gaseous state of a metal
is revealed by the spectroscope. Conversely, a combination
of increased pressure and lowering of temperature will, if carried
far enough, reduce a gas to a liquid, and afterwards to the solid
state; and nearly every gaseous substance has now undergone
this operation.
A certain critical temperature is observed in a gas, above which
the liquefaction is impossible; so that the gaseous state has two
subdivisions into (i.) a true gas, which cannot be liquefied, because
its temperature is above the critical temperature, (ii.) a vapour,
where the temperature is below the critical, and which can
ultimately be liquefied by further lowering of temperature or
increase of pressure.
3. Plasticity and Viscosity.—Every solid substance is found to
be plastic more or less, as exemplified by punching, shearing
and cutting; but the plastic solid is distinguished from the
viscous fluid in that a plastic solid requires a certain magnitude
of stress to be exceeded to make it flow, whereas the viscous
liquid will yield to the slightest stress, but requires a certain
length of time for the effect to be appreciable.
117
According to Maxwell (Theory of Heat) “When a continuous
alteration of form is produced only by a stress exceeding a certain
value, the substance is called a solid, however soft and plastic
it may be. But when the smallest stress, if only continued long
enough, will cause a perceptible and increasing change of form,
the substance must be regarded as a viscous fluid, however hard
it may be.” Maxwell illustrates the difference between a soft
solid and a hard liquid by a jelly and a block of pitch; also by
the experiment of supporting a candle and a stick of sealing-wax;
after a considerable time the sealing-wax will be found
bent and so is a fluid, but the candle remains straight as a solid.
4. Definition of a Fluid.—A fluid is a substance which yields
continually to the slightest tangential stress in its interior;
that is, it can be divided very easily along any plane (given plenty
of time if the fluid is viscous). It follows that when the fluid has
come to rest, the tangential stress in any plane in its interior
must vanish, and the stress must be entirely normal to the plane.
This mechanical axiom of the normality of fluid pressure is the
foundation of the mathematical theory of hydrostatics.
The theorems of hydrostatics are thus true for all stationary
fluids, however viscous they may be; it is only when we come
to hydrodynamics, the science of the motion of a fluid, that
viscosity will make itself felt and modify the theory; unless we
begin by postulating the perfect fluid, devoid of viscosity, so
that the principle of the normality of fluid pressure is taken to
hold when the fluid is in movement.
5. The Measurement of Fluid Pressure.—The pressure at any point
of a plane in the interior of a fluid is the intensity of the normal
thrust estimated per unit area of the plane.
Thus, if a thrust of P ℔ is distributed uniformly over a plane
area of A sq. ft., as on the horizontal bottom of the sea or any
reservoir, the pressure at any point of the plane is P/A ℔ per sq. ft.,
or P/144A ℔ per sq. in. (℔/ft.2 and ℔/in.2, in the Hospitalier notation,
to be employed in the sequel). If the distribution of the thrust is
not uniform, as, for instance, on a vertical or inclined face or wall of a
reservoir, then P/A represents the average pressure over the area; and
the actual pressure at any point is the average pressure over a small
area enclosing the point. Thus, if a thrust ΔP ℔ acts on a small plane
area ΔA ft.2 enclosing a point B, the pressure p at B is the limit of
ΔP/ΔA; and
p = lt (ΔP/ΔA) = dP/dA,
(1)
in the notation of the differential calculus.
6. The Equality of Fluid Pressure in all Directions.—This fundamental
principle of hydrostatics follows at once from the principle of
the normality of fluid pressure implied in the definition of a fluid in
§ 4. Take any two arbitrary directions in the plane of the paper, and
draw a small isosceles triangle abc, whose sides are perpendicular
to the two directions, and consider the equilibrium of a small triangular
prism of fluid, of which the triangle is the cross section. Let P, Q
denote the normal thrust across the sides bc, ca, and R the normal
thrust across the base ab. Then, since these three forces maintain
equilibrium, and R makes equal angles with P and Q, therefore
P and Q must be equal. But the faces bc, ca, over which P and Q
act, are also equal, so that the pressure on each face is equal. A
scalene triangle abc might also be employed, or a
tetrahedron.
 |
| Fig. 1a. |
It follows that the pressure of a fluid requires
to be calculated in one direction only, chosen as
the simplest direction for convenience.
7. The Transmissibility of Fluid Pressure.—Any
additional pressure applied to the fluid will be
transmitted equally to every point in the case of
a liquid; this principle of the transmissibility of
pressure was enunciated by Pascal, 1653, and
applied by him to the invention of the hydraulic
press.
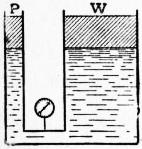
This machine consists essentially of two communicating cylinders
(fig. 1a), filled with liquid and closed by pistons. If a thrust P ℔ is
applied to one piston of area A ft.2, it will be balanced by a thrust
W ℔ applied to the other piston of area B ft.2, where
p = P/A = W/B,
(1)
the pressure p of the liquid being supposed uniform; and, by
making the ratio B/A sufficiently large, the mechanical advantage
can be increased to any desired amount, and in the simplest manner
possible, without the intervention of levers and machinery.
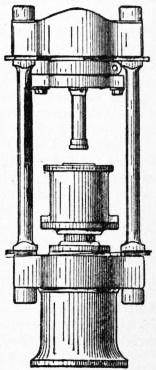
Fig. 1b shows also a modern form of the hydraulic press, applied
to the operation of covering an electric cable with a lead coating.
8. Theorem.—In a fluid at rest under gravity the pressure is the
same at any two points in the same horizontal plane; in other
words, a surface of equal pressure is a horizontal plane.
This is proved by taking any two points A and B at the same
level, and considering the equilibrium of a thin prism of liquid AB,
bounded by planes at A and B perpendicular to AB. As gravity
and the fluid pressure on the sides of the prism act at right angles
to AB, the equilibrium requires the equality of thrust on the ends
A and B; and as the areas are equal, the pressure must be equal at
A and B; and so the pressure is the same at all points in the same
horizontal plane. If the fluid is a liquid, it
can have a free surface without diffusing
itself, as a gas would; and this free surface,
being a surface of zero pressure, or more
generally of uniform atmospheric pressure,
will also be a surface of equal pressure, and
therefore a horizontal plane.
 |
| Fig. 1b. |
Hence the theorem.—The free surface of
a liquid at rest under gravity is a horizontal
plane. This is the characteristic distinguishing
between a solid and a liquid; as, for instance,
between land and water. The land
has hills and valleys, but the surface of
water at rest is a horizontal plane; and if
disturbed the surface moves in waves.
9. Theorem.—In a homogeneous liquid at
rest under gravity the pressure increases
uniformly with the depth.
This is proved by taking the two points
A and B in the same vertical line, and
considering the equilibrium of the prism by
resolving vertically. In this case the thrust
at the lower end B must exceed the thrust
at A, the upper end, by the weight of the
prism of liquid; so that, denoting the cross
section of the prism by α ft.2, the pressure at A and By by p0 and
p ℔/ft.2, and by w the density of the liquid estimated in ℔/ft.3,
pα − p0α = wα·AB,
(1)
p = w·AB + p0.
(2)
Thus in water, where w = 62.4℔/ft.3, the pressure increases
62.4 ℔/ft.2, or 62.4 ÷ 144 = 0.433 ℔/in.2 for every additional foot of
depth.
10. Theorem.—If two liquids of different density are resting in
vessels in communication, the height of the free surface of such liquid
above the surface of separation is inversely as the density.
For if the liquid of density σ rises to the height h and of density ρ
to the height k, and p0 denotes the atmospheric pressure, the pressure
in the liquid at the level of the surface of separation will be σh + p0
and ρk + p0, and these being equal we have
σh = ρk.
(1)
The principle is illustrated in the article Barometer, where a
column of mercury of density σ and height h, rising in the tube to the
Torricellian vacuum, is balanced by a column of air of density ρ,
which may be supposed to rise as a homogeneous fluid to a height k,
called the height of the homogeneous atmosphere. Thus water being
about 800 times denser than air and mercury 13.6 times denser
than water,
k/h = σ/ρ = 800 × 13.6 = 10,880;
(2)
and with an average barometer height of 30 in. this makes k 27,200
ft., about 8300 metres.
11. The Head of Water or a Liquid.—The pressure σh at a depth
h ft. in liquid of density σ is called the pressure due to a head of h ft.
of the liquid. The atmospheric pressure is thus due to an average
head of 30 in. of mercury, or 30 × 13.6 ÷ 12 = 34 ft. of water, or
27,200 ft. of air. The pressure of the air is a convenient unit to
employ in practical work, where it is called an “atmosphere”; it is
made the equivalent of a pressure of one kg/cm2; and one ton/inch2,
employed as the unit with high pressure as in artillery, may be taken
as 150 atmospheres.
12. Theorem.—A body immersed in a fluid is buoyed up by a force
equal to the weight of the liquid displaced, acting vertically upward
through the centre of gravity of the displaced liquid.
For if the body is removed, and replaced by the fluid as at first,
this fluid is in equilibrium under its own weight and the thrust of the
surrounding fluid, which must be equal and opposite, and the surrounding
fluid acts in the same manner when the body replaces the
displaced fluid again; so that the resultant thrust of the fluid acts
vertically upward through the centre of gravity of the fluid displaced,
and is equal to the weight.
When the body is floating freely like a ship, the equilibrium of
this liquid thrust with the weight of the ship requires that the weight
of water displaced is equal to the weight of the ship and the two
centres of gravity are in the same vertical line. So also a balloon
begins to rise when the weight of air displaced is greater than the
weight of the balloon, and it is in equilibrium when the weights are
equal. This theorem is called generally the principle of Archimedes.
It is used to determine the density of a body experimentally;
for if W is the weight of a body weighed in a balance in air (strictly
in vacuo), and if W′ is the weight required to balance when the
body is suspended in water, then the upward thrust of the liquid
118
or weight of liquid displaced is W − W′, so that the specific gravity
(S.G.), defined as the ratio of the weight of a body to the weight
of an equal volume of water, is W/(W − W′).
As stated first by Archimedes, the principle asserts the obvious
fact that a body displaces its own volume of water; and he utilized it
in the problem of the determination of the adulteration of the crown
of Hiero. He weighed out a lump of gold and of silver of the same
weight as the crown; and, immersing the three in succession in
water, he found they spilt over measures of water in the ratio
1⁄14 : 4⁄77 : 2⁄21 or 33 : 24 : 44; thence it follows that the gold : silver alloy
of the crown was as 11 : 9 by weight.
13. Theorem.—The resultant vertical thrust on any portion of a
curved surface exposed to the pressure of a fluid at rest under
gravity is the weight of fluid cut out by vertical lines drawn round
the boundary of the curved surface.
Theorem.—The resultant horizontal thrust in any direction is
obtained by drawing parallel horizontal lines round the boundary,
and intersecting a plane perpendicular to their direction in a plane
curve; and then investigating the thrust on this plane area, which
will be the same as on the curved surface.
The proof of these theorems proceeds as before, employing the
normality principle; they are required, for instance, in the determination
of the liquid thrust on any portion of the bottom of a ship.
In casting a thin hollow object like a bell, it will be seen that the
resultant upward thrust on the mould may be many times greater
than the weight of metal; many a curious experiment has been
devised to illustrate this property and classed as a hydrostatic
paradox (Boyle, Hydrostatical Paradoxes, 1666).
 |
| Fig. 2. |
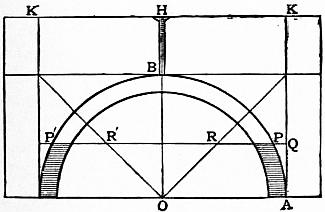
Consider, for instance, the operation of casting a hemispherical
bell, in fig. 2. As the molten metal is run in, the upward thrust on
the outside mould, when
the level has reached
PP′, is the weight of
metal in the volume generated
by the revolution
of APQ; and this, by a
theorem of Archimedes,
has the same volume as
the cone ORR′, or 1⁄3πy3,
where y is the depth of
metal, the horizontal
sections being equal so
long as y is less than the
radius of the outside
hemisphere. Afterwards,
when the metal has risen
above B, to the level KK′, the additional thrust is the weight of
the cylinder of diameter KK′ and height BH. The upward thrust
is the same, however thin the metal may be in the interspace
between the outer mould and the core inside; and this was formerly
considered paradoxical.
Analytical Equations of Equilibrium of a Fluid at rest under any
System of Force.
14. Referred to three fixed coordinate axes, a fluid, in which
the pressure is p, the density ρ, and X, Y, Z the components of
impressed force per unit mass, requires for the equilibrium of the part
filling a fixed surface S, on resolving parallel to Ox,
∫ ∫ lpdS = ∫ ∫ ∫ρX dx dy dz,
(1)
where l, m, n denote the direction cosines of the normal drawn
outward of the surface S.
But by Green’s transformation
| ∫ ∫ lp dS = ∫ ∫ ∫ | dp |
dx dy dz, |
| dx |
(2)
thus leading to the differential relation at every point
| dp |
= ρX, | dp |
= ρY, | dp |
= ρZ. |
| dx | dy |
dz |
(3)
The three equations of equilibrium obtained by taking moments
round the axes are then found to be satisfied identically.
Hence the space variation of the pressure in any direction, or the
pressure-gradient, is the resolved force per unit volume in that
direction. The resultant force is therefore in the direction of the
steepest pressure-gradient, and this is normal to the surface of equal
pressure; for equilibrium to exist in a fluid the lines of force must
therefore be capable of being cut orthogonally by a system of
surfaces, which will be surfaces of equal pressure.
Ignoring temperature effect, and taking the density as a function
of the pressure, surfaces of equal pressure are also of equal density,
and the fluid is stratified by surfaces orthogonal to the lines of force;
| 1 |
| dp |
, | 1 |
| dp |
, | 1 |
| dp |
, or X, Y, Z |
| ρ | dx |
ρ | dy |
ρ | dz |
(4)
are the partial differential coefficients of some function P, = ∫ dp/ρ,
of x, y, z; so that X, Y, Z must be the partial differential coefficients
of a potential −V, such that the force in any direction is the downward
gradient of V; and then
| dP |
+ | dV |
= 0, or P + V = constant, |
| dx | dx |
(5)
in which P may be called the hydrostatic head and V the head of
potential.
With variation of temperature, the surfaces of equal pressure and
density need not coincide; but, taking the pressure, density and
temperature as connected by some relation, such as the gas-equation,
the surfaces of equal density and temperature must intersect in lines
lying on a surface of equal pressure.
15. As an example of the general equations, take the simplest
case of a uniform field of gravity, with Oz directed vertically downward;
employing the gravitation unit of force,
| 1 |
| dp |
= 0, | 1 |
| dp |
= 0, | 1 |
| dp |
= 1, |
| ρ | dx |
ρ | dy |
ρ | dz |
(1)
P = ∫ dp/ρ = z + a constant.
(2)
When the density ρ is uniform, this becomes, as before in (2) § 9
p = ρz + p0.
(3)
Suppose the density ρ varies as some nth power of the depth
below O, then
dp/dz = ρ = μzn
(4)
| p = μ | zn+1 |
= | ρz |
= | ρ |
( | ρ |
) | 1/n |
, |
| n + 1 | n + 1 |
n + 1 | μ |
|
(5)
supposing p and ρ to vanish together.
These equations can be made to represent the state of convective
equilibrium of the atmosphere, depending on the gas-equation
p = ρk = R ρθ,
(6)
where θ denotes the absolute temperature; and then
| R | dθ |
= | d |
( | p |
) = | 1 |
, |
| dz | dz |
ρ | n + 1 |
(7)
so that the temperature-gradient dθ/dz is constant, as in convective
equilibrium in (11).
From the gas-equation in general, in the atmosphere
| 1 |
| dp |
= | 1 |
| dp |
− | 1 |
| dθ |
= | ρ |
− | 1 |
| dθ |
= | 1 |
− | 1 |
| dθ |
, |
| ρ | dz |
p | dz |
θ | dz |
p | θ |
dz | k |
θ | dz |
(8)
which is positive, and the density ρ diminishes with the ascent,
provided the temperature-gradient dθ/dz does not exceed θ/k.
With uniform temperature, taking k constant in the gas-equation,
dp/dz = ρ = p/k, p = p0ez/k,
(9)
so that in ascending in the atmosphere of thermal equilibrium the
pressure and density diminish at compound discount, and for
pressures p1 and p2 at heights z1 and z2
(z1 − z2)/k = loge (p2/p1) = 2.3 log10 (p2/p1).
(10)
In the convective equilibrium of the atmosphere, the air is supposed
to change in density and pressure without exchange of heat by
conduction; and then
ρ/ρ0 = (θ/θ0)n, p/p0 = (θ/θ0)n + 1,
(11)
| dz |
= | 1 |
| dp |
= (n + 1) | p |
= (n + 1) R, γ = 1 + | 1 |
, |
| dθ | ρ |
dθ | ρθ |
n |
where γ is the ratio of the specific heat at constant pressure and
constant volume.
In the more general case of the convective equilibrium of a spherical
atmosphere surrounding the earth, of radius a,
| dp |
= (n + 1) | p0 |
| dθ |
= − | a2 |
dr, |
| ρ | ρ0 |
θ0 | r2 |
(12)
gravity varying inversely as the square of the distance r from the
centre; so that, k = p0/ρ0, denoting the height of the homogeneous
atmosphere at the surface, θ is given by
(n + 1) k (1 − θ/θ0) = a(1 − a/r),
(13)
or if c denotes the distance where θ = 0,
| θ |
= | a |
· | c − r |
. |
| θ0 | r |
c − a |
(14)
When the compressibility of water is taken into account in a
deep ocean, an experimental law must be employed, such as
p − p0 = k (ρ − ρ0), or ρ/ρ0 = 1 + (p − p0)/λ, λ = kρ0,
(15)
so that λ is the pressure due to a head k of the liquid at density ρ0
under atmospheric pressure p0; and it is the gauge pressure required
on this law to double the density. Then
dp/dz = kdρ/dz = ρ, ρ = ρ0ez/k, p − p0 = kρ0 (ez/k − 1);
(16)
and if the liquid was incompressible, the depth at pressure p would
be (p − p0)/p0, so that the lowering of the surface due to compression is
kez/k − k − z = ½z2/k, when k is large.
(17)
For sea water, λ is about 25,000 atmospheres, and k is then 25,000
times the height of the water barometer, about 250,000 metres, so
that in an ocean 10 kilometres deep the level is lowered about 200
metres by the compressibility of the water; and the density at the
bottom is increased 4%.
On another physical assumption of constant cubical elasticity λ,
dp = λdρ/ρ, (p − p0)/λ = log (ρ/ρ0),
(18)
| dp |
= | λ |
| dρ |
= ρ, λ ( | 1 |
− | 1 |
) = z, 1 − | ρ0 |
= | z |
, λ = kρ0, |
| zd | ρ |
dz | ρ0 |
ρ | ρ |
k |
(19)
119
and the lowering of the surface is
| p − p0 |
− z = k log | ρ |
− z = −k log ( 1 − | z |
) − z ≈ | z2 |
| ρ0 | ρ0 |
k | 2k |
(20)
as before in (17).
16. Centre of Pressure.—A plane area exposed to fluid pressure
on one side experiences a single resultant thrust, the integrated
pressure over the area, acting through a definite point called
the centre of pressure (C.P.) of the area.
Thus if the plane is normal to Oz, the resultant thrust
R = ∫ ∫ p dx dy,
(1)
and the coordinates x, y of the C.P. are given by
xR = ∫ ∫ xp dx dy, yR = ∫ ∫ yp dx dy.
(2)
The C·P. is thus the C·G. of a plane lamina bounded by the area,
in which the surface density is p.
If p is uniform, the C·P. and C·G. of the area coincide.
For a homogeneous liquid at rest under gravity, p is proportional
to the depth below the surface, i.e. to the perpendicular distance
from the line of intersection of the plane of the area with the free
surface of the liquid.
If the equation of this line, referred to new coordinate axes in the
plane area, is written
x cos α + y sin α − h = 0,
(3)
R = ∫ ∫ ρ (h − x cos α − y sin α) dx dy,
(4)
xR = ∫ ∫ ρx (h − x cos α − y sin α) dx dy,
(5)
yR = ∫ ∫ ρy (h − x cos α − y sin α) dx dy.
Placing the new origin at the C.G. of the area A,
∫ ∫ xd x dy = 0, ∫ ∫ y dx dy = 0,
(6)
R = ρhA,
(7)
xhA = −cos α ∫ ∫ x2 dA − sin α ∫ ∫ xy dA,
(8)
yhA = −cos α ∫ ∫ xy dA − sin α ∫ ∫ y2 dA.
(9)
Turning the axes to make them coincide with the principal axes
of the area A, thus making ∫∫ xy dA = 0,
xh = −a2 cos α, yh = −b2 sin α,
(10)
where
∫ ∫ x2dA = Aa2, ∫ ∫ y2dA = Ab2,
(11)
a and b denoting the semi-axes of the momental ellipse of the area.
This shows that the C.P. is the antipole of the line of intersection of
its plane with the free surface with respect to the momental ellipse at
the C.G. of the area.
Thus the C.P. of a rectangle or parallelogram with a side in the
surface is at 2⁄3 of the depth of the lower side; of a triangle with a
vertex in the surface and base horizontal is ¾ of the depth of the base;
but if the base is in the surface, the C·P. is at half the depth of the
vertex; as on the faces of a tetrahedron, with one edge in the
surface.
The core of an area is the name given to the limited area round
its C.G. within which the C·P. must lie when the area is immersed
completely; the boundary of the core is therefore the locus of the
antipodes with respect to the momental ellipse of water lines which
touch the boundary of the area. Thus the core of a circle or an
ellipse is a concentric circle or ellipse of one quarter the size.
The C.P. of water lines passing through a fixed point lies on a
straight line, the antipolar of the point; and thus the core of a triangle
is a similar triangle of one quarter the size, and the core of a
parallelogram is another parallelogram, the diagonals of which are
the middle third of the median lines.
In the design of a structure such as a tall reservoir dam it is
important that the line of thrust in the material should pass inside
the core of a section, so that the material should not be in a state
of tension anywhere and so liable to open and admit the water.
 |
| Fig. 3. |
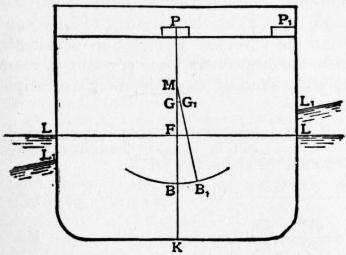
17. Equilibrium and Stability of a Ship or Floating Body.
The Metacentre.—The principle of Archimedes in § 12 leads
immediately to the
conditions of equilibrium
of a body supported
freely in fluid,
like a fish in water or
a balloon in the air,
or like a ship (fig. 3)
floating partly immersed
in water and
the rest in air. The
body is in equilibrium
under two
forces:—(i.) its
weight W acting
vertically downward
through G, the C.G. of the body, and (ii.) the buoyancy of the
fluid, equal to the weight of the displaced fluid, and acting
vertically upward through B, the C.G. of the displaced fluid;
for equilibrium these two forces must be equal and opposite in
the same line.
The conditions of equilibrium of a body, floating like a ship
on the surface of a liquid, are therefore:—
(i.) the weight of the body must be less than the weight of the
total volume of liquid it can displace; or else the body will sink
to the bottom of the liquid; the difference of the weights is
called the “reserve of buoyancy.”
(ii.) the weight of liquid which the body displaces in the
position of equilibrium is equal to the weight W of the body; and
(iii.) the C.G., B, of the liquid displaced and G of the body,
must lie in the same vertical line GB.
18. In addition to satisfying these conditions of equilibrium,
a ship must fulfil the further condition of stability, so as to keep
upright; if displaced slightly from this position, the forces
called into play must be such as to restore the ship to the upright
again. The stability of a ship is investigated practically by
inclining it; a weight is moved across the deck and the angle is
observed of the heel produced.
Suppose P tons is moved c ft. across the deck of a ship of W tons
displacement; the C.G. will move from G to G1 the reduced distance
G1G2 = c(P/W); and if B, called the centre of buoyancy, moves
to B1, along the curve of buoyancy BB1, the normal of this curve at
B1 will be the new vertical B1G1, meeting the old vertical in a point
M, the centre of curvature of BB1, called the metacentre.
If the ship heels through an angle θ or a slope of 1 in m,
GM = GG1 cot θ = mc (P/W),
(1)
and GM is called the metacentric height; and the ship must be
ballasted, so that G lies below M. If G was above M, the tangent
drawn from G to the evolute of B, and normal to the curve of buoyancy,
would give the vertical in a new position of equilibrium. Thus in
H.M.S. “Achilles” of 9000 tons displacement it was found that
moving 20 tons across the deck, a distance of 42 ft., caused the bob
of a pendulum 20 ft. long to move through 10 in., so that
| GM = | 240 |
× 42 × | 20 |
2.24 ft. |
| 10 | 9000 |
(2)
also
cot θ = 24, θ = 2°24′.
(3)
In a diagram it is conducive to clearness to draw the ship in one
position, and to incline the water-line; and the page can be turned
if it is desired to bring the new water-line horizontal.
Suppose the ship turns about an axis through F in the water-line
area, perpendicular to the plane of the paper; denoting by y the
distance of an element dA if the water-line area from the axis of
rotation, the change of displacement is ΣydA tanθ, so that there is
no change of displacement if ΣydA = 0, that is, if the axis passes
through the C.G. of the water-line area, which we denote by F
and call the centre of flotation.
The righting couple of the wedges of immersion and emersion
will be
Σwy dA tan θ·y = w tan θ Σ y2 dA = w tan θ·Ak2 ft. tons,
(4)
w denoting the density of water in tons/ft.3, and W = wV, for a
displacement of V ft.3
This couple, combined with the original buoyancy W through B,
is equivalent to the new buoyancy through B, so that
W.BB1 = wAk2 tan θ,
(5)
BM = BB1 cot θ = Ak2/V,
(6)
giving the radius of curvature BM of the curve of buoyancy B, in
terms of the displacement V, and Ak2 the moment of inertia of the
water-line area about an axis through F, perpendicular to the plane
of displacement.
An inclining couple due to moving a weight about in a ship will heel
the ship about an axis perpendicular to the plane of the couple, only
when this axis is a principal axis at F of the momental ellipse of
the water-line area A. For if the ship turns through a small angle θ
about the line FF′, then b1, b2, the C·G. of the wedge of immersion
and emersion, will be the C·P. with respect to FF′ of the two parts of
the water-line area, so that b1b2 will be conjugate to FF′ with respect
to the momental ellipse at F.
The naval architect distinguishes between the stability of form,
represented by the righting couple W.BM, and the stability of ballasting,
represented by W.BG. Ballasted with G at B, the righting
couple when the ship is heeled through θ is given by W.BM. tanθ; but
if weights inside the ship are raised to bring G above B, the righting
couple is diminished by W·BG.tanθ, so that the resultant righting
couple is W·GM·tanθ. Provided the ship is designed to float
upright at the smallest draft with no load on board, the stability
at any other draft of water can be arranged by the stowage of the
weight, high or low.
19. Proceeding as in § 16 for the determination of the C.P. of an
area, the same argument will show that an inclining couple due to
120
the movement of a weight P through a distance c will cause the ship
to heel through an angle θ about an axis FF′ through F, which is
conjugate to the direction of the movement of P with respect to an
ellipse, not the momental ellipse of the water-line area A, but a
confocal to it, of squared semi-axes
a2 − hV/A, b2 − hV/A,
(1)
h denoting the vertical height BG between C.G. and centre of
buoyancy. The varying direction of the inclining couple Pc may be
realized by swinging the weight P from a crane on the ship, in a circle of
radius c. But if the weight P was lowered on the ship from a crane
on shore, the vessel would sink bodily a distance P/wA if P was
deposited over F; but deposited anywhere else, say over Q on the
water-line area, the ship would turn about a line the antipolar of Q
with respect to the confocal ellipse, parallel to FF′, at a distance FK
from F
FK = (k2 − hV/A)/FQ sin QFF′
(2)
through an angle θ or a slope of one in m, given by
| sin θ = | 1 |
= | P |
= | P |
· | V |
FQ sin QFF′ |
| m | wA·FK |
W | Ak2 − hV |
(3)
where k denotes the radius of gyration about FF′ of the water-line
area. Burning the coal on a voyage has the reverse effect on a
steamer.
Hydrodynamics
20. In considering the motion of a fluid we shall suppose it
non-viscous, so that whatever the state of motion the stress
across any section is normal, and the principle of the normality
and thence of the equality of fluid pressure can be employed, as
in hydrostatics. The practical problems of fluid motion, which
are amenable to mathematical analysis when viscosity is taken
into account, are excluded from treatment here, as constituting
a separate branch called “hydraulics” (q.v.). Two methods are
employed in hydrodynamics, called the Eulerian and Lagrangian,
although both are due originally to Leonhard Euler. In the
Eulerian method the attention is fixed on a particular point of
space, and the change is observed there of pressure, density
and velocity, which takes place during the motion; but in the
Lagrangian method we follow up a particle of fluid and observe
how it changes. The first may be called the statistical method,
and the second the historical, according to J. C. Maxwell. The
Lagrangian method being employed rarely, we shall confine
ourselves to the Eulerian treatment.
The Eulerian Form of the Equations of Motion.
21. The first equation to be established is the equation of
continuity, which expresses the fact that the increase of matter
within a fixed surface is due to the flow of fluid across the surface
into its interior.
In a straight uniform current of fluid of density ρ, flowing with
velocity q, the flow in units of mass per second across a plane area A,
placed in the current with the normal of the plane making an angle θ
with the velocity, is ρAq cos θ, the product of the density ρ, the area
A, and q cos θ the component velocity normal to the plane.
Generally if S denotes any closed surface, fixed in the fluid, M the
mass of the fluid inside it at any time t, and θ the angle which the
outward-drawn normal makes with the velocity q at that point,
dM/dt = rate of increase of fluid inside the surface,
= flux across the surface into the interior
= − ∫∫ ρq cos θ dS,
|
(1)
the integral equation of continuity.
In the Eulerian notation u, v, w denote the components of the
velocity q parallel to the coordinate axes at any point (x, y, z) at the
time t; u, v, w are functions of x, y, z, t, the independent variables;
and d is used here to denote partial differentiation with respect to
any one of these four independent variables, all capable of varying
one at a time.
To transfer the integral equation into the differential equation of
continuity, Green’s transformation is required again, namely,
| ∫∫∫ ( | dξ |
+ | dη |
+ | dζ |
) dx dy dz = ∫∫ (lξ + mη + nζ) dS, |
| dx | dy |
dz |
(2)
or individually
| ∫∫∫ | dξ |
dx dy dz = ∫∫ lξ dS, ..., |
| dx |
(3)
where the integrations extend throughout the volume and over the
surface of a closed space S; l, m, n denoting the direction cosines
of the outward-drawn normal at the surface element dS, and ξ, η, ζ
any continuous functions of x, y, z.
The integral equation of continuity (1) may now be written
| ∫∫∫ | dρ |
dx dy dz = ∫∫ (lρu + mρv + nρw) dS = 0, |
| dt |
(4)
which becomes by Green’s transformation
| ∫∫∫ ( | dρ |
+ | d(ρu) |
+ | d(ρv) |
+ | d(ρw) |
) dx dy dz = 0, |
| dt | dx |
dy | dz |
(5)
leading to the differential equation of continuity when the integration
is removed.
22. The equations of motion can be established in a similar
way by considering the rate of increase of momentum in a fixed
direction of the fluid inside the surface, and equating it to the
momentum generated by the force acting throughout the space
S, and by the pressure acting over the surface S.
Taking the fixed direction parallel to the axis of x, the time-rate
of increase of momentum, due to the fluid which crosses the surface, is
− ∫∫ ρuq cos θ dS = − ∫∫ (lρu2 + mρuv + nρuw) dS,
(1)
which by Green’s transformation is
| − ∫∫∫ ( | d(ρu2) |
+ | d(ρuv) |
+ | d(ρuw) |
) dx dy dz. |
| dx | dy |
dz |
(2)
The rate of generation of momentum in the interior of S by the
component of force, X per unit mass, is
∫∫∫ ρX dx dy dz,
(3)
and by the pressure at the surface S is
| − ∫∫ lp dS = − ∫∫∫ | dp |
dx dy dz, |
| dx |
(4)
by Green’s transformation.
The time rate of increase of momentum of the fluid inside S is
(5)
and (5) is the sum of (1), (2), (3), (4), so that
| ∫∫∫ ( | dρu |
+ | dρu2 |
+ | dρuv |
+ | dρuw |
− ρX + | dp |
) dx dy dz = 0, |
| dt | dx |
dy | dz |
dx |
(6)
leading to the differential equation of motion
| dρu |
+ | dρu2 |
+ | dρuv |
+ | dρuw |
= ρX − | dp |
, |
| dt | dx |
dy | dz |
dx |
(7)
with two similar equations.
The absolute unit of force is employed here, and not the gravitation
unit of hydrostatics; in a numerical application it is assumed that
C.G.S. units are intended.
These equations may be simplified slightly, using the equation of
continuity (5) § 21; for
| dρu |
+ | dρu2 |
+ | dρuv |
+ | dρuw |
| dt | dx |
dy | dz |
| = ρ ( | du |
+ u | du |
+ v | du |
+ w | du |
) |
| dt | dx |
dy | dz |
| + u ( | dρ |
+ | dρu |
+ | dρv |
+ | dρw |
), |
| dt | dx |
dy | dz |
(8)
reducing to the first line, the second line vanishing in consequence of
the equation of continuity; and so the equation of motion may be
written in the more usual form
| du |
+ u | du |
+ v | du |
+ w | du |
= X − | 1 |
| dp |
, |
| dt | dx |
dy | dz |
ρ | dx |
(9)
with the two others
| dv |
+ u | dv |
+ v | dv |
+ w | dv |
= Y − | 1 |
| dp |
, |
| dt | dx |
dy | dz |
ρ | dy |
(10)
| dw |
+ u | dw |
+ v | dw |
+ w | dw |
= Z − | 1 |
| dp |
. |
| dt | dx |
dy | dz |
ρ | dz |
(11)
23. As a rule these equations are established immediately
by determining the component acceleration of the fluid particle
which is passing through (x, y, z) at the instant t of time considered,
and saying that the reversed acceleration or kinetic
reaction, combined with the impressed force per unit of mass
and pressure-gradient, will according to d’Alembert’s principle
form a system in equilibrium.
To determine the component acceleration of a particle, suppose F
to denote any function of x, y, z, t, and investigate the time rate of F
for a moving particle; denoting the change by DF/dt,
| DF |
= lt· | F(x + uδt, y + vδt, z + wδt, t + δt) − F(x, y, z, t) |
| dt | δt |
| = | dF |
+ u | dF |
+ v | dF |
+ w | dF |
; |
| dt | dx |
dy | dz |
(1)
and D/dt is called particle differentiation, because it follows the rate
of change of a particle as it leaves the point x, y, z; but
dF/dt, dF/dx, dF/dy, dF/dz
(2)
represent the rate of change of F at the time t, at the point, x, y, z,
fixed in space.
121
The components of acceleration of a particle of fluid are consequently
| Du |
= | du |
+ u | du |
+ v | du |
+ w | du |
, |
| dt | dt |
dx | dy |
dz |
(3)
| Dv |
= | dv |
+ u | dv |
+ v | dv |
+ w | dv |
, |
| dt | dt |
dx | dy |
dz |
(4)
| Dw |
= | dw |
+ u | dw |
+ v | dw |
+ w | dw |
, |
| dt | dt |
dx | dy |
dz |
(5)
leading to the equations of motion above.
If F (x, y, z, t) = 0 represents the equation of a surface containing
always the same particles of fluid,
| DF |
= 0, or | dF |
+ u | dF |
+ v | dF |
+ w | dF |
= 0, |
| dt | dt |
dx | dy |
dz |
(6)
which is called the differential equation of the bounding surface.
A bounding surface is such that there is no flow of fluid across it,
as expressed by equation (6). The surface always contains the same
fluid inside it, and condition (6) is satisfied over the complete surface,
as well as any part of it.
But turbulence in the motion will vitiate the principle that a
bounding surface will always consist of the same fluid particles,
as we see on the surface of turbulent water.
24. To integrate the equations of motion, suppose the impressed
force is due to a potential V, such that the force in any direction is the
rate of diminution of V, or its downward gradient; and then
X = −dV/dx, Y = −dV/dy, Z = −dV/dz;
(1)
and putting
| dw |
− | dv |
= 2ξ, | du |
− | dw |
= 2η, | dv |
− | du |
= 2ζ, |
| dy | dz |
dz | dx |
dx | dy |
(2)
| dξ |
+ | dη |
+ | dζ |
= 0, |
| dx | dy |
dz |
(3)
the equations of motion may be written
| du |
− 2vζ + 2wη + | dH |
= 0, |
| dt | dx |
(4)
| dv |
− 2wξ + 2uζ + | dH |
= 0, |
| dt | dy |
(5)
| dw |
− 2uη + 2wξ + | dH |
= 0, |
| dt | dz |
(6)
where
H = ∫ dp/ρ + V + ½q2,
(7)
q2 = u2 + v2 + w2,
(8)
and the three terms in H may be called the pressure head, potential
head, and head of velocity, when the gravitation unit is employed
and ½q2 is replaced by ½q2/g.
Eliminating H between (5) and (6)
| Dξ |
− ξ | du |
− η | dw |
− ζ | dv |
+ ξ ( | du |
+ | dv |
+ | dw |
) = 0, |
| dt | dx |
dx | dx |
dx | dy |
dz |
(9)
and combining this with the equation of continuity
| 1 |
| Dρ |
+ | du |
+ | dv |
+ | dw |
= 0, |
| ρ | dt |
dx | dy |
dz |
(10)
we have
| D |
( | ξ |
) − | ξ |
| du |
− | η |
| dv |
− | ζ |
| dw |
= 0, |
| dt | ρ |
ρ | dx |
ρ | dx |
ρ | dx |
(11)
with two similar equations.
Putting
ω2 = ξ2 + η2 + ζ2,
(12)
a vortex line is defined to be such that the tangent is in the direction
of ω, the resultant of ξ, η, ζ, called the components of molecular
rotation. A small sphere of the fluid, if frozen suddenly, would
retain this angular velocity.
If ω vanishes throughout the fluid at any instant, equation (11)
shows that it will always be zero, and the fluid motion is then called
irrotational; and a function φ exists, called the velocity function,
such that
u dx + v dy + w dz = −dφ,
(13)
and then the velocity in any direction is the space-decrease or
downward gradient of φ.
25. But in the most general case it is possible to have three
functions φ, ψ, m of x, y, z, such that
u dx + v dy + w dz = −dφ − m dψ,
(1)
as A. Clebsch has shown, from purely analytical considerations
(Crelle, lvi.); and then
| ξ = ½ | d(ψ, m) |
, η = ½ | d(ψ, m) |
, ζ = ½ | d(ψ, m) |
, |
| d(y, z) | d(z, x) |
d(x, y) |
(2)
and
| ξ | dψ |
+ η | dψ |
+ ζ | dψ |
= 0, ξ | dm |
+ η | dm |
+ ζ | dm |
= 0, |
| dx | dy |
dz | dx |
dy | dz |
(3)
so that, at any instant, the surfaces over which ψ and m are constant
intersect in the vortex lines.
Putting
(4)
the equations of motion (4), (5), (6) § 24 can be written
| dK |
− 2uζ + 2wη − | d(ψ,m) |
= 0, ..., ...; |
| dx | d(x,t) |
(5)
and therefore
| ξ | dK |
+ η | dK |
+ ζ | dK |
= 0. |
| dx | dy |
dz |
(6)
Equation (5) becomes, by a rearrangement,
| dK |
− | dψ |
( | dm |
+ u | dm |
+ v | dm |
+ w | dm |
) |
| dx | dx |
dt | dx |
dy | dz |
| + | dm |
( | dψ |
+ u | dψ |
+ v | dψ |
+ w | dψ |
) = 0, ..., ..., |
| dx | dt |
dx | dy |
dz |
(7)
| dK |
− | dψ |
| Dm |
+ | dm |
| Dψ |
= 0, ..., ..., |
| dx | dx |
dt | dx |
dt |
(8)
and as we prove subsequently (§ 37) that the vortex lines are composed
of the same fluid particles throughout the motion, the surface m and
ψ satisfies the condition of (6) § 23; so that K is uniform throughout
the fluid at any instant, and changes with the time only, and so
may be replaced by F(t).
26. When the motion is steady, that is, when the velocity at any
point of space does not change with the time,
| dK |
− 2vζ + 2wη = 0, ..., ... |
| dx |
(1)
| ξ | dK |
+ η | dK |
+ ζ | dK |
= 0, u | dK |
+ v | dK |
+ w | dK |
= 0, |
| dx | dy |
dz | dx |
dy | dz |
(2)
and
K = ∫ dp/ρ + V + ½q2 = H
(3)
is constant along a vortex line, and a stream line, the path of a fluid
particle, so that the fluid is traversed by a series of H surfaces, each
covered by a network of stream lines and vortex lines; and if the
motion is irrotational H is a constant throughout the fluid.
Taking the axis of x for an instant in the normal through a point
on the surface H = constant, this makes u = 0, ξ = 0; and in steady
motion the equations reduce to
dH/dν = 2vζ − 2wη = 2qω sin θ,
(4)
where θ is the angle between the stream line and vortex line; and
this holds for their projection on any plane to which dν is drawn
perpendicular.
In plane motion (4) reduces to
| dH |
= 2qζ = q ( | dQ |
+ | q |
), |
| dν | dv |
r |
(5)
if r denotes the radius of curvature of the stream line, so that
| 1 |
| dp |
+ | dV |
= | dH |
− | d ½q2 |
= | q2 |
, |
| ρ | dν |
dν | dν |
dν | r |
(6)
the normal acceleration.
The osculating plane of a stream line in steady motion contains
the resultant acceleration, the direction ratios of which are
| u | du |
+ v | du |
+ w | du |
= | d ½q2 |
− 2vζ + 2wη = | d ½q2 |
− | dH |
, ..., |
| dx | dy |
dz | dx |
dx | dx |
(7)
and when q is stationary, the acceleration is normal to the surface H
= constant, and the stream line is a geodesic.
Calling the sum of the pressure and potential head the statical
head, surfaces of constant statical and dynamical head intersect
in lines on H, and the three surfaces touch where the velocity is
stationary.
Equation (3) is called Bernoulli’s equation, and may be interpreted
as the balance-sheet of the energy which enters and leaves a given
tube of flow.
If homogeneous liquid is drawn off from a vessel so large that the
motion at the free surface at a distance may be neglected, then
Bernoulli’s equation may be written
H = p/ρ + z + q2/2g = P/ρ + h,
(8)
where P denotes the atmospheric pressure and h the height of the
free surface, a fundamental equation in hydraulics; a return has
been made here to the gravitation unit of hydrostatics, and Oz is
taken vertically upward.
In particular, for a jet issuing into the atmosphere, where p = P,
q2/2g = h − z,
(9)
or the velocity of the jet is due to the head k − z of the still free
surface above the orifice; this is Torricelli’s theorem (1643), the
foundation of the science of hydrodynamics.
27. Uniplanar Motion.—In the uniplanar motion of a homogeneous
liquid the equation of continuity reduces to
(1)
so that we can put
u = −dψ/dy, v = dψ/dx,
(2)
122
where ψ is a function of x, y, called the stream- or current-function;
interpreted physically, ψ − ψ0, the difference of the value of ψ at a
fixed point A and a variable point P is the flow, in ft.3/second, across
any curved line AP from A to P, this being the same for all lines in
accordance with the continuity.
Thus if dψ is the increase of ψ due to a displacement from P to P′,
and k is the component of velocity normal to PP′, the flow across
PP′ is dψ = k·PP′; and taking PP′ parallel to Ox, dψ = v dx; and
similarly dψ= −u dy with PP′ parallel to Oy; and generally dψ/ds
is the velocity across ds, in a direction turned through a right angle
forward, against the clock.
In the equations of uniplanar motion
| 2ζ = | dv |
− | du |
= | d2ψ |
+ | d2ψ |
= −∇2ψ, suppose, |
| dx | dy |
dx2 | dy2 |
(3)
so that in steady motion
| dH |
+ ∇2ψ | dψ |
= 0, | dH |
+ ∇2ψ | dψ |
= 0, | dH |
+ ∇2ψ = 0, |
| dx | dx |
dy | dy |
dψ |
(4)
and ∇2ψ must be a function of ψ.
If the motion ia irrotational,
| u = − | dφ |
= − | dψ |
, v = − | dφ |
= | dψ |
, |
| dx | dy |
dy | dx |
(5)
so that ψ and φ are conjugate functions of x and y,
φ + ψi = ƒ(x + yi), ∇2ψ = 0, ∇2φ = 0;
(6)
or putting
φ + ψi = w, x + yi = z, w = ƒ(z).
The curves φ = constant and ψ = constant form an orthogonal
system; and the interchange of φ and ψ will give a new state of
uniplanar motion, in which the velocity at every point is turned
through a right angle without alteration of magnitude.
For instance, in a uniplanar flow, radially inward towards O, the
flow across any circle of radius r being the same and denoted by
2πm, the velocity must be m/r, and
φ = m log r, ψ = mθ, φ + ψi =
m log reiθ, w = m log z.
(7)
Interchanging these values
ψ = m log r, φ = mθ, ψ + φi = m log reiθ
(8)
gives a state of vortex motion, circulating round Oz, called a straight
or columnar vortex.
A single vortex will remain at rest, and cause a velocity at any point
inversely as the distance from the axis and perpendicular to its direction;
analogous to the magnetic field of a straight electric current.
If other vortices are present, any one may be supposed to move
with the velocity due to the others, the resultant stream-function
being
ψ = Σm log r = log Πrm;
(9)
the path of a vortex is obtained by equating the value of ψ at the
vortex to a constant, omitting the rm of the vortex itself.
When the liquid is bounded by a cylindrical surface, the motion
of a vortex inside may be determined as due to a series of vortex-images,
so arranged as to make the flow zero across the boundary.
For a plane boundary the image is the optical reflection of the
vortex. For example, a pair of equal opposite vortices, moving on
a line parallel to a plane boundary, will have a corresponding pair
of images, forming a rectangle of vortices, and the path of a vortex
will be the Cotes’ spiral
r sin 2θ = 2a, or x−2 + y−2 = a−2;
(10)
this is therefore the path of a single vortex in a right-angled corner;
and generally, if the angle of the corner is π/n, the path is the Cotes’
spiral
r sin nθ = na.
(11)
A single vortex in a circular cylinder of radius a at a distance c
from the centre will move with the velocity due to an equal opposite
image at a distance a2/c, and so describe a circle with velocity
mc/(a2 − c2) in the periodic time 2π (a2 − c2)/m.
(12)
Conjugate functions can be employed also for the motion of liquid
in a thin sheet between two concentric spherical surfaces; the components
of velocity along the meridian and parallel in colatitude θ
and longitude λ can be written
| dφ |
= | 1 |
| dψ |
, | 1 |
| dψ |
= − | dψ |
, |
| dθ | sin θ |
dλ | sin θ |
dλ | dθ |
(13)
and then
φ + ψi = F (tan ½θ·eλi).
(14)
28. Uniplanar Motion of a Liquid due to the Passage of a Cylinder
through it.—A stream-function ψ must be determined to satisfy the
conditions
∇2ψ = 0, throughout the liquid;
(1)
ψ = constant, over any fixed boundary;
(2)
dψ/ds = normal velocity reversed over a solid boundary,
(3)
so that, if the solid is moving with velocity U in the direction Ox,
dψ/ds = −U dy/ds, or ψ + Uy = constant over the moving cylinder;
and ψ + Uy = ψ′ is the stream function of the relative motion of the
liquid past the cylinder, and similarly ψ − Vx for the component
velocity V along Oy; and generally
ψ′ = ψ + Uy − Vx
(4)
is the relative stream-function, constant over a solid boundary
moving with components U and V of velocity.
If the liquid is stirred up by the rotation R of a cylindrical body,
dψ/ds = normal velocity reversed
(5)
ψ + ½R (x2 + y2) = ψ′,
(6)
a constant over the boundary; and ψ′ is the current-function of
the relative motion past the cylinder, but now
V2ψ′ + 2R = 0,
(7)
throughout the liquid.
Inside an equilateral triangle, for instance, of height h,
ψ′ = −2Rαβγ/h,
(8)
where α, β, γ are the perpendiculars on the sides of the triangle.
In the general case ψ′ = ψ + Uy − Vx + ½R (x2 + y2) is the relative
stream function for velocity components, U, V, R.
29. Example 1.—Liquid motion past a circular cylinder.
Consider the motion given by
ω = U (z + a2/z),
(1)
so that
| ψ = U ( r + | a2 |
) cos θ = U ( 1 + | a2 |
) x, |
| r | r2 |
(2)
| φ = U ( r + | a2 |
) sin θ = U ( 1 + | a2 |
) y. |
| r | r2 |
(2)
Then ψ = 0 over the cylinder r = a, which may be considered a fixed
post; and a stream line past it along which ψ = Uc, a constant, is
the curve
| ( r − | a2 |
) sin θ = c, (x2 + y2) (y − c) − a2y = 0 |
| r |
(3)
a cubic curve (C3).
Over a concentric cylinder, external or internal, of radius r = b,
| ψ′ = ψ + U1y = [ U ( 1 − | a2 |
) + U1] y, |
| b2 |
(4)
and ψ′ is zero if
U1/U = (a2 − b2)/b2;
(5)
so that the cylinder may swim for an instant in the liquid without
distortion, with this velocity U1, and ω in (1) will give the liquid
motion in the interspace between the fixed cylinder r = a and the
concentric cylinder r = b, moving with velocity U1.
When b = 0, U1 = ∞; and when b = ∞, U1 = −U, so that at
infinity the liquid is streaming in the direction xO with velocity U.
If the liquid is reduced to rest at infinity by the superposition of
an opposite stream given by ω = −Uz, we are left with
ω = Ua2/z,
(6)
φ = U (a2/r) cos θ = Ua2x/(x2 + y2),
(7)
ψ = −U (a2/r) sin θ = −Ua2y/(x2 + y2),
(8)
giving the motion due to the passage of the Cylinder r = a with
velocity U through the origin O in the direction Ox.
If the direction of motion makes an angle θ′ with Ox,
| tan θ′ = | dφ |
/ | dφ |
= | 2xy |
= tan 2θ, θ = ½θ′, |
| dy | dx |
x2 − y2 |
(9)
and the velocity is Ua2/r2.
Along the path of a particle, defined by the C3 of (3),
| sin2 ½θ′ = | y2 |
= | y (y − c) |
, |
| x2 + y2 | a2 |
(10)
| ½ sin θ′ | dθ′ |
= | 2y − c |
| dy |
, |
| ds | a2 |
ds |
(11)
on the radius of curvature is ¼a2/(y − ½c), which shows that the curve
is an Elastica or Lintearia. (J. C. Maxwell, Collected Works, ii. 208.)
If φ1 denotes the velocity function of the liquid filling the cylinder
r = b, and moving bodily with it with velocity U1,
φ1 = −U1x,
(12)
and over the separating surface r = b
| φ |
= − | U |
( 1 + | a2 |
) = | a2 + b2 |
, |
| φ1 | U1 |
b2 | a2 − b2 |
(13)
and this, by § 36, is also the ratio of the kinetic energy in the annular
interspace between the two cylinders to the kinetic energy of the
liquid moving bodily inside r = b.
Consequently the inertia to overcome in moving the cylinder
r = b, solid or liquid, is its own inertia, increased by the inertia of
liquid (a2 + b2)/(a2 ~ b2) times the volume of the cylinder r = b;
this total inertia is called the effective inertia of the cylinder r = b,
at the instant the two cylinders are concentric.
123
With liquid of density ρ, this gives rise to a kinetic reaction to
acceleration dU/dt, given by
| πρb2 | a2 + b2 |
| dU |
= | a2 + b2 |
M′ | dU |
, |
| a2 − b2 | dt |
a2 − b2 | dt |
(14)
if M′ denotes the mass of liquid displaced by unit length of the
cylinder r = b. In particular, when a = ∞, the extra inertia is M′.
When the cylinder r = a is moved with velocity U and r = b with
velocity U1 along Ox,
| φ = U | a2 |
( | b2 |
+ r ) cos θ − U1 | b2 |
( r + | a2 |
) cos θ, |
| b2 − a2 | r |
b2 − a2 | r |
(15)
| ψ = −U | a2 |
( | b2 |
− r ) sin θ − U1 | b2 |
( r − | a2 |
) sin θ, |
| b2 − a2 | r |
b2 − a2 | r |
(16)
and similarly, with velocity components V and V1 along Oy
| φ = V | a2 |
( | b2 |
+ r ) cos θ − V1 | b2 |
( r + | a2 |
) cos θ, |
| b2 − a2 | r |
b2 − a2 | r |
(17)
| ψ = V | a2 |
( | b2 |
− r ) sin θ + V1 | b2 |
( r − | a2 |
) sin θ, |
| b2 − a2 | r |
b2 − a2 | r |
(18)
and then for the resultant motion
| w = (U2 + V2) | a2 |
| z |
+ | a2b2 |
| U + Vi |
| b2 − a2 | U + Vi |
b2 − a2 | z |
| −(U12 + V12) | b2 |
| z |
− | a2b2 |
| U1 + V1i |
. |
| b2 − a2 | U1 + V1i |
b2 − a2 | z |
(19)
The resultant impulse of the liquid on the cylinder is given by the
component, over r = a (§ 36),
| X = ∫ ρφ cos θ·a dθ = πρa2 ( U | b2 + a2 |
− U1 | 2b2 |
); |
| b2 − a2 | b2 − a2 |
(20)
and over r = b
| X1 = ∫ ρφ cos θ·b dθ = πρb2 ( U | 2a2 |
− U1 | b2 + a2 |
), |
| b2 − a2 | b2 − a2 |
(21)
and the difference X − X1 is the component momentum of the liquid
in the interspace; with similar expressions for Y and Y1.
Then, if the outside cylinder is free to move
| X1 = 0, | V1 |
= | 2a2 |
, X = πρa2U | b2 − a2 |
. |
| U | b2 + a2 |
b2 + a2 |
(22)
But if the outside cylinder is moved with velocity U1, and the
inside cylinder is solid or filled with liquid of density σ,
| X = −πρa2U, | U1 |
= | 2ρb2 |
, |
| U | ρ (b2 + a2) + σ (b2 − a2) |
| U − U1 |
= | (ρ − σ) (b2 − a2) |
, |
| U1 | ρ (b2 + a2) + σ (b2 − a2) |
(23)
and the inside cylinder starts forward or backward with respect to
the outside cylinder, according as ρ > or < σ.
30. The expression for ω in (1) § 29 may be increased by the
addition of the term
im log z = −mθ + im log r,
(1)
representing vortex motion circulating round the annulus of
liquid.
Considered by itself, with the cylinders held fixed, the vortex
sets up a circumferential velocity m/r on a radius r, so that the
angular momentum of a circular filament of annular cross section dA
is ρm dA, and of the whole vortex is ρmπ (b2 − a2).
Any circular filament can be started from rest by the application
of a circumferential impulse πρm dr at each end of a diameter; so
that a mechanism attached to the cylinders, which can set up a
uniform distributed impulse πρm across the two parts of a diameter
in the liquid, will generate the vortex motion, and react on the
cylinder with an impulse couple −ρmπa2 and ρmπb2, having resultant
ρmπ (b2 − a2), and this couple is infinite when b = ∞, as the
angular momentum of the vortex is infinite. Round the cylinder
r = a held fixed in the U current the liquid streams past with velocity
q′ = 2U sin θ + m/a;
(2)
and the loss of head due to this increase of velocity from U to q′ is
| q′2 − U2 |
= | (2U sin θ + m/a)2 − U2 |
, |
| 2g | 2g |
(3)
so that cavitation will take place, unless the head at a great distance
exceeds this loss.
The resultant hydrostatic thrust across any diametral plane
of the cylinder will be modified, but the only term in the loss
of head which exerts a resultant thrust on the whole cylinder is
2mU sin θ/ga, and its thrust is 2πρmU absolute units in the direction
Cy, to be counteracted by a support at the centre C; the liquid is
streaming past r = a with velocity U reversed, and the cylinder is
surrounded by a vortex. Similarly, the streaming velocity V
reversed will give rise to a thrust 2πρmV in the direction xC.
Now if the cylinder is released, and the components U and V are
reversed so as to become the velocity of the cylinder with respect
to space filled with liquid, and at rest at infinity, the cylinder will
experience components of force per unit length
(i.) − 2πρmV, 2πρmU, due to the vortex motion;
(ii.) − πρa2 dU/dt, − πρa2 dV/dt, due to the kinetic reaction of the liquid;
(iii.) 0, −π(σ − ρ) a2g, due to gravity,
taking Oy vertically upward, and denoting the density of the cylinder
by σ; so that the equations of motion are
| πρa2 | dU |
= − πρa2 | dU |
− 2πρmV, |
| dt | dt |
(4)
| πρa2 | dV |
= − πρa2 | dV |
+ 2πρmV − π (σ − ρ) a2g, |
| dt | dt |
(5)
or, putting m = a2ω, so that the vortex velocity is due to an angular
velocity ω at a radius a,
(σ + ρ) dU/dt + 2ρωV = 0,
(6)
(σ + ρ) dV/dt − 2ρωU + (σ-ρ) g = 0.
(7)
Thus with g = 0, the cylinder will describe a circle with angular
velocity 2ρω/(σ + ρ), so that the radius is (σ + ρ) v/2ρω, if the velocity
is v. With σ = 0, the angular velocity of the cylinder is 2ω; in this
way the velocity may be calculated of the propagation of ripples
and waves on the surface of a vertical whirlpool in a sink.
Restoring σ will make the path of the cylinder a trochoid; and
so the swerve can be explained of the ball in tennis, cricket, baseball,
or golf.
Another explanation may be given of the sidelong force, arising
from the velocity of liquid past a cylinder, which is encircled by a
vortex. Taking two planes x = ± b, and considering the increase of
momentum in the liquid between them, due to the entry and exit
of liquid momentum, the increase across dy in the direction Oy,
due to elements at P and P′ at opposite ends of the diameter PP′, is
ρ dy (U − Ua2r−2 cos 2θ + mr−1 sin θ) (Ua2r−2 sin 2θ + mr−1 cos θ)
+ ρ dy ( −U + Ua2r−2 cos 2θ + mr−1 sin θ) (Ua2r−2 sin 2θ − mr−1 cos θ)
= 2ρdymUr−1 (cos θ − a2r−2 cos 3θ),
|
(8)
and with y = b tan θ, r = b sec θ, this is
2ρmU dθ (1 − a2b−2 cos 3θ cos θ),
(9)
and integrating between the limits θ = ±½π, the resultant, as before,
is 2πρmU.
31. Example 2.—Confocal Elliptic Cylinders.—Employ the elliptic
coordinates η, ξ, and ζ = η + ξi, such that
z = c ch ζ, x = c ch η cos ξ, y = c sh η sin ζ;
(1)
then the curves for which η and ξ are constant are confocal ellipses
and hyperbolas, and
| J = | d(x, y) |
= c2 (ch2 η − cos2 ξ) |
| d(η, ξ) |
= (1/2)c2 (ch 2η − cos 2ξ) = r1r2 = OD2,
(2)
if OD is the semi-diameter conjugate to OP, and r1, r2 the focal
distances,
r1, r2 = c (ch η ± cos ξ);
(3)
r2 = x2 + y2 = c2 (ch2 η − sin2 ξ)
= ½c2 (ch 2η + cos 2ξ).
(4)
Consider the streaming motion given by
w = m ch (ζ − γ), γ = α + βi,
(5)
φ = m ch (η − α) cos (ξ − β), ψ = m sh (η − α) sin (ξ − β).
(6)
Then ψ = 0 over the ellipse η = α, and the hyperbola ξ = β, so that
these may be taken as fixed boundaries; and ψ is a constant on a C4.
Over any ellipse η, moving with components U and V of velocity,
ψ′ = ψ + Uy − Vx = [ m sh (η − α) cos β + Uc sh η ] sin ξ
- [ m sh (η − α) sin β + Vc ch η ] cos ξ;
(7)
so that ψ′ = 0, if
| U = − | m |
| sh (η − α) |
cos β, V = − | m |
| sh (η − α) |
sin β, |
| c | sh η |
c | ch η |
(8)
having a resultant in the direction PO, where P is the intersection of
an ellipse η with the hyperbola β; and with this velocity the ellipse
η can be swimming in the liquid, without distortion for an instant.
At infinity
| U = − | m |
e−a cos β = − | m |
cos β, |
| c | a − b |
| V = − | m |
e−a sin β = − | m |
sin β, |
| c | a − b |
(9)
a and b denoting the semi-axes of the ellipse α; so that the liquid is
streaming at infinity with velocity Q = m/(a + b) in the direction of
the asymptote of the hyperbola β.
An ellipse interior to η = α will move in a direction opposite to
the exterior current; and when η = 0, U = ∞, but V = (m/c) sh α sin β.
Negative values of η must be interpreted by a streaming motion
on a parallel plane at a level slightly different, as on a double Riemann
sheet, the stream passing from one sheet to the other across a cut
SS′ joining the foci S, S′. A diagram has been drawn by Col. R. L.
Hippisley.
124
The components of the liquid velocity q, in the direction of the
normal of the ellipse η and hyperbola ξ, are
−mJ−1 sh (η − α) cos (ξ − β), mJ−1 ch (η − α) sin (ξ − β).
(10)
The velocity q is zero in a corner where the hyperbola β cuts the
ellipse α; and round the ellipse α the velocity q reaches a maximum
when the tangent has turned through a right angle, and then
| q = Qea | √(ch 2α − cos 2β) |
; |
| sh 2α |
(11)
and the condition can be inferred when cavitation begins.
With β = 0, the stream is parallel to x0, and
φ = m ch (η − α) cos ξ
= −Uc ch (η − α) sh η cos ξ/sh (η − α)
(12)
over the cylinder η, and as in (12) § 29,
φ1 = −Ux = −Uc ch η cos ξ,
(13)
for liquid filling the cylinder; and
(14)
over the surface of η; so that parallel to Ox, the effective inertia
of the cylinder η, displacing M′ liquid, is increased by M′th η/th(η- α),
reducing when α = ∞ to M′ th η = M′ (b/a).
Similarly, parallel to Oy, the increase of effective inertia is
M′/th η th (η − α), reducing to M′/th η = M′ (a/b), when α = ∞, and
the liquid extends to infinity.
32. Next consider the motion given by
φ = m ch 2 (η − α) sin 2ξ, ψ = −m sh 2 (η − α) cos 2ξ;
(1)
in which ψ = 0 over the ellipse α, and
ψ′ = ψ + ½R (x2 + y2)
= [ −m sh 2 (η − α) + ¼Rc2 ] cos 2ξ + ¼Rc2 ch 2η,
(2)
which is constant over the ellipse η if
¼ Rc2 = m sh 2 (η − α);
(3)
so that this ellipse can be rotating with this angular velocity R for
an instant without distortion, the ellipse α being fixed.
For the liquid filling the interior of a rotating elliptic cylinder of
cross section
x2/a2 + y2/b2 = 1,
(4)
ψ1′ = m1 (x2/a2 + y2/b2)
(5)
with
∇2ψ1′ = −2R = −2m1 (1/a2 + 1/b2),
ψ1 = m1 (x2/a2 + y2/b2) − ½R (x2 + y2)
= −½R (x2 − y2) (a2 − b2) / (a2 + b2),
(6)
φ1 = Rxy (a2 − b2) / (a2 + b2),
w1 = φ1 + ψ1i = −½iR (x + yi)2 (a2 − b2) / (a2 + b2).
The velocity of a liquid particle is thus (a2 − b2)/(a2 + b2) of what
it would be if the liquid was frozen and rotating bodily with
the ellipse; and so the effective angular inertia of the liquid is
(a2 − b2)2/(a2 + b2)2 of the solid; and the effective radius of gyration,
solid and liquid, is given by
k2 = ¼(a2 + b2), and ¼(a2 − b2)2 / (a2 + b2).
(7)
For the liquid in the interspace between α and η,
| φ |
= | m ch 2 (η − α) sin 2ξ |
| φ1 | ¼ Rc2 sh 2η sin 2ξ (a2 − b2) / (a2 + b2) |
= 1/th 2 (η − α) th 2η;
(8)
and the effective k2 of the liquid is reduced to
¼ c2/th 2 (η − α) sh 2η,
(9)
which becomes ¼ c2/sh 2η = 1⁄8 (a2 − b2)/ab, when α = ∞, and the liquid
surrounds the ellipse η to infinity.
An angular velocity R, which gives components −Ry, Rx of
velocity to a body, can be resolved into two shearing velocities, −R
parallel to Ox, and R parallel to Oy; and then ψ is resolved into
ψ1 + ψ2, such that ψ1 + ½Rx2 and ψ2 + ½Ry2 is constant over the
boundary.
Inside a cylinder
φ1 + ψ1i = −½ iR (x + yi)2 a2 / (a2 + b2),
(10)
φ2 + ψ2i = ½ iR (x + yi)2 b2 / (a2 + b2),
(11)
and for the interspace, the ellipse α being fixed, and α1 revolving
with angular velocity R
φ1 + ψ1i = −1⁄8 iRc2 sh 2 (η − α + ξi) (ch 2α + 1) / sh 2 (α1 − α),
(12)
φ2 + ψ2i = 1⁄8 iRc2 sh 2 (η − α + ξi) (ch 2α − 1) / sh 2 (α1 − α),
(13)
satisfying the condition that ψ1 and ψ2 are zero over η = α, and over
η = α1
ψ1 + ½ Rx2 = 1⁄8 Rc2 (ch 2α1 + 1),
(14)
ψ2 + ½ Ry2 = 1⁄8 Rc2 (ch 2α1 − 1),
(15)
constant values.
In a similar way the more general state of motion may be analysed,
given by
w = m ch 2 (ζ − γ), γ = α + βi,
(16)
as giving a homogeneous strain velocity to the confocal system;
to which may be added a circulation, represented by an additional
term mζ in w.
Similarly, with
x + yi = c√[ sin (ξ + ηi) ]
(17)
the function
ψ = Qc sh ½ (η − α) sin ½ (ξ − β)
(18)
will give motion streaming past the fixed cylinder η = α, and dividing
along ξ = β; and then
x2 − y2 = c2 sin ξ ch η, 2xy = c2 cos ξ sh η.
(19)
In particular, with sh α = 1, the cross-section of η = α is
x4 + 6x2y2 + y4 = 2c4, or x4 + y4 = c4
(20)
when the axes are turned through 45°.
33. Example 3.—Analysing in this way the rotation of a rectangle
filled with liquid into the two components of shear, the stream
function ψ1 is to be made to satisfy the conditions
(i.) ∇2ψ1 = 0,
(ii.) ψ1 + ½Rx2 = ½Ra2, or ψ1 = 0 when x = ±a,
(iii.) ψ1 + ½Rx2 = ½Ra2, ψ1 = ½R (a2 − x2), when y = ± b.
|
Expanded in a Fourier series,
| a2 − x2 = | 32 |
a2 Σ | cos (2n + 1) ½ πx/a |
, |
| π3 | (2n + 1)3 |
(1)
so that
| ψ1 = R | 16 |
a2 Σ | cos (2n + 1) ½πx/a · ch (2n + 1) ½πy/a) |
, |
| π3 | (2n + 1)3 · ch (2n + 1) ½πb/a |
| w1 = φ1 + ψ1i = iR | 16 |
a2 Σ | cos (2n + 1) ½πz/a |
, |
| π3 | (2n + 1)3 ch (2n + 1) ½πb/a |
(2)
an elliptic-function Fourier series; with a similar expression for ψ2
with x and y, a and b interchanged; and thence ψ = ψ1 + ψ2.
Example 4.—Parabolic cylinder, axial advance, and liquid streaming
past.
The polar equation of the cross-section being
r1/2 cos ½θ = a1/2, or r + x = 2a,
(3)
the conditions are satisfied by
ψ′ = Ur sin θ − 2Ua1/2r1/2 sin ½θ = 2Ur1/2 sin ½θ (r1/2 cos ½θ − a1/2),
(4)
ψ = 2Ua1/2r1/2 sin ½θ = −U √ [ 2a (r − x) ],
(5)
w = −2Ua1/2z1/2,
(6)
and the resistance of the liquid is 2πρaV2/2g.
A relative stream line, along which ψ′ = Uc, is the quartic curve
| y − c = √ [ 2a (r − x) ], x = | (4a2y2 − (y − c)4 |
, r = | 4a2y2 + (y − c)4 |
, |
| 4a (y − c)2 | 4a (y − c)2 |
(7)
and in the absolute space curve given by ψ,
| dy |
= − | (y − c)2 |
, x = | 2ac |
− 2a log (y − c). |
| dx | 2ay |
y − c |
(8)
34. Motion symmetrical about an Axis.—When the motion of a
liquid is the same for any plane passing through Ox, and lies in the
plane, a function ψ can be found analogous to that employed in
plane motion, such that the flux across the surface generated by the
revolution of any curve AP from A to P is the same, and represented
by 2π (ψ − ψ0); and, as before, if dψ is the increase in ψ due to a
displacement of P to P′, then k the component of velocity normal
to the surface swept out by PP′ is such that 2πdψ = 2πyk·PP′; and
taking PP′ parallel to Oy and Ox,
u = −dψ/ydy, v = dψ/ydx,
(1)
and ψ is called after the inventor, “Stokes’s stream or current
function,” as it is constant along a stream line (Trans. Camb. Phil.
Soc., 1842; “Stokes’s Current Function,” R. A. Sampson, Phil.
Trans., 1892); and dψ/yds is the component velocity across ds in a
direction turned through a right angle forward.
In this symmetrical motion
| ξ = 0, η = 0, 2ζ = | d |
( | 1 |
| dψ |
) + | d |
( | 1 |
| dψ |
) |
| dx | y |
dx | dy |
y | dy |
| = | 1 |
( | d2ψ |
+ | d2ψ |
− | 1 |
| dψ |
) = − | 1 |
∇2ψ, |
| y | dx2 |
dy2 | y |
dy | y |
(2)
suppose; and in steady motion,
| dH |
+ | 1 |
| dψ |
∇2ψ = 0, | dH |
+ | 1 |
| dψ |
∇2ψ = 0, |
| dx | y2 |
dx | dy |
y2 | dy |
(3)
so that
2ζ/y = −y−2∇2ψ = dH/dψ
(4)
is a function of ψ, say ƒ′(ψ), and constant along a stream line;
dH/dv = 2qζ, H − ƒ(ψ) = constant,
(5)
throughout the liquid.
When the motion is irrotational,
| ζ = 0, u = − | dφ |
= − | 1 |
| dψ |
, v = − | dφ |
= | 1 |
| dψ |
, |
| dx | y |
dy | dy |
y | dx |
(6)
| ∇2ψ = 0, or | d2ψ |
+ | d2ψ |
− | 1 |
| dψ |
= 0. |
| dx2 | dy2 |
y | dy |
(7)
125
Changing to polar coordinates, x = r cos θ, y = r sin θ, the equation
(2) becomes, with cos θ = μ,
| r2 | d2ψ |
+ (1 − μ2) | d2ψ |
= 2 ζr3 sin θ, |
| dr2 | dμ |
(8)
of which a solution, when ζ = 0, is
| ψ = ( Arn+1 + | B |
) (1 − μ2) | dPn |
= ( Arn − 1 + | B |
) y2 | dPn |
, |
| rn | dμ |
rn+2 | dμ |
(9)
φ = { (n + 1) Arn − nBr−n−1 } Pn,
(10)
where Pn denotes the zonal harmonic of the nth order; also, in the
exceptional case of
ψ = A0 cos θ, φ = A0/r;
ψ = B0r, φ = −B0 log tan ½θ
= −½B0 sh−1 x/y.
|
(11)
Thus cos θ is the Stokes’ function of a point source at O, and
PA − PB of a line source AB.
The stream function ψ of the liquid motion set up by the passage
of a solid of revolution, moving with axial velocity U, is such that
| 1 |
| dψ |
= −U | dy |
, ψ + ½Uy2 = constant, |
| y | ds |
ds |
(12)
over the surface of the solid; and ψ must be replaced by ψ′ = ψ + ½Uy2
in the general equations of steady motion above to obtain the steady
relative motion of the liquid past the solid.
For instance, with n = 1 in equation (9), the relative stream
function is obtained for a sphere of radius a, by making it
ψ′ = ψ + ½Uy2 = ½U (r2 − a3/r) sin2 θ, ψ = −½Ua3 sin2 θ/r;
(13)
and then
φ′ = Ux (1 + ½a3/r2), φ = ½Ua3 cos θ/r2,
(14)
| − | dφ |
= U | a3 |
cos θ, − | dφ |
= ½U | a3 |
sin θ, |
| dr | r3 |
r dθ | r3 |
(15)
so that, if the direction of motion makes an angle ψ with Ox,
tan (ψ − θ) = ½ tan θ, tan ψ = 3 tan θ/(2 − tan2 θ),
(16)
Along the path of a liquid particle ψ′ is constant, and putting it
equal to ½Uc2,
(r2 − a3/r) sin2 θ = c2, sin2 θ = c2r / (r3 − a3),
(17)
the polar equation; or
y2 = c2r3 / (r3 − a3), r3 = a3y2 / (y2 − c2),
(18)
a curve of the 10th degree (C10).
In the absolute path in space
cos ψ = (2 − 3 sin2 θ) / √ (4 − sin2 θ), and sin3 θ = (y3 − c2y) / a3,
(19)
which leads to no simple relation.
The velocity past the surface of the sphere is
| 1 |
| dψ′ |
= ½U ( 2r + | a3 |
) | sin2 θ |
= 3⁄2 U sin θ, when r = a; |
| r sin θ | dr |
r2 | r sin θ |
(20)
so that the loss of head is
(9⁄4 sin2 θ − 1) U2/2g, having a maximum 5⁄4 U2/2g,
(21)
which must be less than the head at infinite distance to avoid
cavitation at the surface of the sphere.
With n = 2, a state of motion is given by
ψ = −½ Uy2a4 μ/r4, ψ′ = ½ Uy2 (1 − a4 μ/r4),
(22)
φ′ = Ux + φ, φ = −1⁄3 U (a4 / r3) P2, P2 = 3⁄2 μ2 − ½,
(23)
representing a stream past the surface r4 = a4μ.
35. A circular vortex, such as a smoke ring, will set up motion
symmetrical about an axis, and provide an illustration; a half
vortex ring can be generated in water by drawing a semicircular
blade a short distance forward, the tip of a spoon for instance.
The vortex advances with a certain velocity; and if an equal
circular vortex is generated coaxially with the first, the mutual
influence can be observed. The first vortex dilates and moves
slower, while the second contracts and shoots through the first;
after which the motion is reversed periodically, as if in a game of
leap-frog. Projected perpendicularly against a plane boundary,
the motion is determined by an equal opposite vortex ring, the
optical image; the vortex ring spreads out and moves more
slowly as it approaches the wall; at the same time the molecular
rotation, inversely as the cross-section of the vortex, is seen to
increase. The analytical treatment of such vortex rings is the
same as for the electro-magnetic effect of a current circulating
in each ring.
36. Irrotational Motion in General.—Liquid originally at rest in
a singly-connected space cannot be set in motion by a field of force
due to a single-valued potential function; any motion set up in
the liquid must be due to a movement of the boundary, and the
motion will be irrotational; for any small spherical element of the
liquid may be considered a smooth solid sphere for a moment, and
the normal pressure of the surrounding liquid cannot impart to it
any rotation.
The kinetic energy of the liquid inside a surface S due to the
velocity function φ is given by
| T = ½ρ ∫ ∫ ∫ [ ( | dφ |
) | 2 |
+ ( | dφ |
) | 2 |
+ ( | dφ |
) | 2 |
] dx dy dz, |
| dx | |
dy | |
dz | |
(1)
by Green’s transformation, dν denoting an elementary step along
the normal to the exterior of the surface; so that dφ/dν = 0 over
the surface makes T = 0, and then
| ( | dφ |
) | 2 |
+ ( | dφ |
) | 2 |
+ ( | dφ |
) | 2 |
= 0, | dφ |
= 0, | dφ |
= 0, | dφ |
= 0. |
| dx | |
dy | |
dz | |
dx | dy |
dz |
(2)
If the actual motion at any instant is supposed to be generated
instantaneously from rest by the application of pressure impulse
over the surface, or suddenly reduced to rest again, then, since no
natural forces can act impulsively throughout the liquid, the pressure
impulse ῶ satisfies the equations
| 1 |
| dῶ |
= −u, | 1 |
| dῶ |
= −v, | 1 |
| dῶ |
= ῶ, |
| ρ | dx |
ρ | dy |
ρ | dz |
(3)
ῶ = ρφ + a constant,
(4)
and the constant may be ignored; and Green’s transformation of
the energy T amounts to the theorem that the work done by an
impulse is the product of the impulse and average velocity, or half
the velocity from rest.
In a multiply connected space, like a ring, with a multiply valued
velocity function φ, the liquid can circulate in the circuits independently
of any motion of the surface; thus, for example,
φ = mθ = m tan−1 y/x
(5)
will give motion to the liquid, circulating in any ring-shaped figure
of revolution round Oz.
To find the kinetic energy of such motion in a multiply connected
space, the channels must be supposed barred, and the space made
acyclic by a membrane, moving with the velocity of the liquid;
and then if k denotes the cyclic constant of φ in any circuit, or the
value by which φ has increased in completing the circuit, the values
of φ on the two sides of the membrane are taken as differing by k,
so that the integral over the membrane
| ∫ ∫ φ | dφ |
dS = k ∫ ∫ | dφ |
dS, |
| dν | dν |
(6)
and this term is to be added to the terms in (1) to obtain the additional
part in the kinetic energy; the continuity shows that the
integral is independent of the shape of the barrier membrane, and
its position. Thus, in (5), the cyclic constant k = 2πm.
In plane motion the kinetic energy per unit length parallel to Oz
| T = ½ρ ∫ ∫ [ ( | dφ |
) | 2 |
+ ( | dφ |
) | 2 |
] dx dy = ½ρ ∫ ∫ [ ( | dψ |
) | 2 |
+ ( | dψ |
) | 2 |
] dx dy |
| dx | |
dy | |
dx | |
dy | |
| = ½ρ ∫ φ | dφ |
ds = ½ρ ∫ ψ | dψ |
ds. |
| dν | dν |
(7)
For example, in the equilateral triangle of (8) § 28, referred to coordinate
axes made by the base and height,
ψ′ = −2Rαβγ/h = −½ Ry [ (h − y)2 − 3x2 ] /h
(8)
ψ = ψ′ − ½R [ ( 1⁄3 h − y)2 + x2 ]
= −½R [ ½h3 + 1⁄3 h2y + h) (x2 − y2) − 3x2y + y3 ] /h
|
(9)
and over the base y = 0,
dx/dν = −dx/dy = + ½R ( 1⁄3 h2 − 3x2) / h, ψ = −½R ( 1⁄9 h2 + x2).
(10)
Integrating over the base, to obtain one-third of the kinetic
energy T,
| 1⁄3T = ½ρ ∫ | h / √3 |
¼R2 (3x4 − 1⁄27 h4) dx/h = ρR2 h4 / 135 √3 |
| −h / √3 |
(11)
so that the effective k2 of the liquid filling the triangle is given by
k2 = T / ½ρR2A = 2h2 / 45
= 2⁄5 (radius of the inscribed circle)2,
|
(12)
or two-fifths of the k2 for the solid triangle.
Again, since
dφ/dν = dψ/ds, dφ/ds = −dψ/dν,
(13)
T = ½ρ ∫ φ dψ = −½ρ ∫ ψ dφ.
(14)
With the Stokes’ function ψ for motion symmetrical about an
axis.
| T = ½ρ ∫ φ | dψ |
2πy ds = πρ ∫ φ dψ. |
| y ds |
(15)
37. Flow, Circulation, and Vortex Motion.—The line integral of
the tangential velocity along a curve from one point to another,
defined by
| ∫ ( u | dx |
+ v | dy |
+ w | dz |
) ds = ∫ (u dx + v dy + z dz), |
| ds | ds |
ds |
(1)
is called the “flux” along the curve from the first to the second
point; and if the curve closes in on itself the line integral round the
curve is called the “circulation” in the curve.
With a velocity function φ, the flow
−∫ dφ = φ1 − φ2,
(2)
126
so that the flow is independent of the curve for all curves mutually
reconcilable; and the circulation round a closed curve is zero, if
the curve can be reduced to a point without leaving a region for
which φ is single valued.
If through every point of a small closed curve the vortex lines are
drawn, a tube is obtained, and the fluid contained is called a vortex
filament.
By analogy with the spin of a rigid body, the component spin of
the fluid in any plane at a point is defined as the circulation round a
small area in the plane enclosing the point, divided by twice the
area. For in a rigid body, rotating about Oz with angular velocity ζ,
the circulation round a curve in the plane xy is
| ∫ ζ ( x | dy |
− y | dx |
) ds = ζ times twice the area. |
| ds | ds |
(3)
In a fluid, the circulation round an elementary area dxdy is
equal to
| u dx + ( v + | dv |
dx ) dy − ( u + | du |
dy ) dx − vdy = ( | dv |
− | du |
) dx dy, |
| dx | dy |
dx | dy |
(4)
so that the component spin is
(5)
in the previous notation of § 24; so also for the other two components
ξ and η.
Since the circulation round any triangular area of given aspect
is the sum of the circulation round the projections of the area on
the coordinate planes, the composition of the components of spin,
ξ, η, ζ, is according to the vector law. Hence in any infinitesimal
part of the fluid the circulation is zero round every small plane
curve passing through the vortex line; and consequently the circulation
round any curve drawn on the surface of a vortex filament
is zero.
If at any two points of a vortex line the cross-section ABC,
A′B′C′ is drawn of the vortex filament, joined by the vortex line
AA′, then, since the flow in AA′ is taken in opposite directions in
the complete circuit ABC AA′B′C′ A′A, the resultant flow in AA′
cancels, and the circulation in ABC, A′B′C′ is the same; this is
expressed by saying that at all points of a vortex filament ωα is
constant where α is the cross-section of the filament and ω the
resultant spin (W. K. Clifford, Kinematic, book iii.).
So far these theorems on vortex motion are kinematical; but
introducing the equations of motion of § 22,
| Du |
+ | dQ |
= 0, | Dv |
+ | dQ |
= 0, | Dw |
+ | dQ |
= 0, |
| dt | dx |
dt | dy |
dt | dz |
(6)
Q = ∫ dp/ρ + V,
(7)
and taking dx, dy, dz in the direction of u, v, w, and
dx : dy : dz = u : v : w,
| D |
( u dx + v dy + w dz ) = | Du |
dx + u | D dx |
+ ... = −dQ + ½ dq2, |
| dt | dt |
dt |
(8)
and integrating round a closed curve
| D |
∫ (u dx + v dy + w dz) = 0, |
| dt |
(9)
and the circulation in any circuit composed of the same fluid particles
is constant; and if the motion is differential irrotational and due
to a velocity function, the circulation is zero round all reconcilable
paths. Interpreted dynamically the normal pressure of the surrounding
fluid on a tube cannot create any circulation in the tube.
The circulation being always zero round a small plane curve
passing through the axis of spin in vortical motion, it follows conversely
that a vortex filament is composed always of the same fluid
particles; and since the circulation round a cross-section of a
vortex filament is constant, not changing with the time, it follows
from the previous kinematical theorem that αω is constant for all
time, and the same for every cross-section of the vortex filament.
A vortex filament must close on itself, or end on a bounding
surface, as seen when the tip of a spoon is drawn through the surface
of water.
Denoting the cross-section α of a filament by dS and its mass by
dm, the quantity ωdS/dm is called the vorticity; this is the same at
all points of a filament, and it does not change during the motion;
and the vorticity is given by ω cosεdS/dm, if dS is the oblique
section of which the normal makes an angle ε with the filament,
while the aggregate vorticity of a mass M inside a surface S is
M−1 ∫ ω cos ε dS.
Employing the equation of continuity when the liquid is homogeneous,
| 2 ( | dζ |
− | dη |
) = ∇2u, ... , ∇2 = − | d2 |
− | d2 |
− | d2 |
, |
| dy | dz |
dx2 | dy2 |
dz2 |
(10)
which is expressed by
∇2 (u, v, w) = 2 curl (ξ, η, ζ), (ξ, η, ζ) = ½ curl (u, v, w).
(11)
38. Moving Axes in Hydrodynamics.—In many problems, such as
the motion of a solid in liquid, it is convenient to take coordinate
axes fixed to the solid and moving with it as the movable trihedron
frame of reference. The components of velocity of the moving
origin are denoted by U, V, W, and the components of angular
velocity of the frame of reference by P, Q, R; and then if u, v, w
denote the components of fluid velocity in space, and u′, v′, w′ the
components relative to the axes at a point (x, y, z) fixed to the
frame of reference, we have
u = U + u′ − yR + zQ,
v = V + v′- zP + xR,
w = W + w′ − xQ + yP.
|
(1)
Now if k denotes the component of absolute velocity in a direction
fixed in space whose direction cosines are l, m, n,
k = lu + mv + nw;
(2)
and in the infinitesimal element of time dt, the coordinates of the
fluid particle at (x, y, z) will have changed by (u′, v′, w′)dt; so that
| Dk |
= | dl |
u + | dm |
v + | dn |
w |
| dt | dt |
dt | dt |
| + l ( | du |
+ u′ | du |
+ v′ | du |
+ w′ | du |
) |
| dt | dx |
dy | dz |
| + m ( | dv |
+ u′ | dv |
+ v′ | dv |
+ w′ | dv |
) |
| dt | dx |
dy | dz |
| + n ( | dw |
+ u′ | dw |
+ v′ | dw |
+ w′ | dw |
). |
| dt | dx |
dy | dz |
(3)
But as l, m, n are the direction cosines of a line fixed in space,
| dl |
= mR − nQ, | dm |
= nP − lR, | dn |
= lQ − mP; |
| dt | dt |
dt |
(4)
so that
| Dk |
= l ( | du |
− vR + wQ + u′ | du |
+ v′ | du |
+ w′ | du |
) + m (...) + n (...) |
| dt | dt |
dx | dy |
dz |
| = l ( X − | 1 |
| dp |
) + m ( Y − | 1 |
| dp |
) + n ( Z − | 1 |
| dp |
), |
| p | dx |
p | dy |
p | dz |
(5)
for all values of l, m, n, leading to the equations of motion with
moving axes.
When the motion is such that
| u = − | dφ |
− m | dψ |
, v = − | dφ |
− m | dψ |
, w = − | dφ |
− m | dψ |
, |
| dx | dx |
dy | dy |
dz | dz |
(6)
as in § 25 (1), a first integral of the equations in (5) may be written
| ∫ | dp |
+ V + ½q2 − | dφ |
− m | dψ |
+ (u − u′) ( | dφ |
+ m | dψ |
) |
| ρ | dt |
dt | dx |
dx |
| + (v − v′) ( | dφ |
+ m | dψ |
) + (w − w′) ( | dφ |
+ m | dψ |
) = F(t), |
| dy | dy |
dz | dz |
(7)
in which
| dφ |
− (u − u′) | dφ |
− (v − v′) | dφ |
− (w − w′) | dφ |
| dt | dx |
dy | dz |
| = | dφ |
− (U − yR + zQ) | dφ |
− (V − zP + xR) | dφ |
− (W − xQ + yP) | dφ |
| dt | dx |
dy | dz |
(8)
is the time-rate of change of φ at a point fixed in space, which is
left behind with velocity components u − u′, v − v′, w − w′.
In the case of a steady motion of homogeneous liquid symmetrical
about Ox, where O is advancing with velocity U, the equation (5)
of § 34
p/ρ + V + ½q′2 − ƒ (ψ′) = constant
(9)
becomes transformed into
| p |
+ V + ½q2 − | U |
| dψ |
+ ½U2 − ƒ (ψ + ½Uy2) = constant, |
| ρ | y |
dy |
(10)
ψ′ = ψ + ¼U y2,
(11)
subject to the condition, from (4) § 34,
y−2 ∇2ψ′ = −ƒ′(ψ′), y−2 ∇2ψ = −ƒ′ (ψ + ½Uy2).
(12)
Thus, for example, with
ψ′ = ¾U y2 (r2a−2 − 1), r2 = x2 + y2,
(13)
for the space inside the sphere r = a, compared with the value of
ψ′ in § 34 (13) for the space outside, there is no discontinuity of the
velocity in crossing the surface.
Inside the sphere
| 2ζ = | d |
( | 1 |
| dψ′ |
) + | d |
( | 1 |
| dψ′ |
) = | 15 |
U | y |
, |
| dx | y |
dx | dy |
y | dy |
2 | a2 |
(14)
so that § 34 (4) is satisfied, with
| ƒ′ (ψ′) = | 15 |
Ua−2, ƒ (ψ′) = | 15 |
Uψ′ a−2; |
| 2 | 2 |
(15)
and (10) reduces to
| p |
+ V − | 9 |
U { ( | x2 |
− 1 ) | 2 |
− ( | y2 |
− ½ ) | 2 |
} = constant; |
| ρ | 8 |
a2 | |
a2 | |
(16)
this gives the state of motion in M. J. M. Hill’s spherical vortex,
advancing through the surrounding liquid with uniform velocity.
39. As an application of moving axes, consider the motion of
liquid filling the ellipsoidal case
| x2 |
+ | y2 |
+ | z2 |
= 1; |
| a2 | b2 |
c2 |
(1)
and first suppose the liquid to be frozen, and the ellipsoid to be
127
rotating about the centre with components of angular velocity ξ,
η, ζ; then
u = − yζ + zη, v = − zξ + xζ, w = − xη + yξ.
(2)
Now suppose the liquid to be melted, and additional components of
angular velocity Ω1, Ω2, Ω3 communicated to the ellipsoidal case;
the additional velocity communicated to the liquid will be due to
a velocity-function
| φ = − Ω1 | b2 − c2 |
yz − Ω2 | c2 − a2 |
zx − Ω3 | a2 − b2 |
xy, |
| b2 + c2 | c2 + a2 |
a2 + b2 |
(3)
as may be verified by considering one term at a time.
If u′, v′, w′ denote the components of the velocity of the liquid
relative to the axes,
| u′ = u + yR − zQ = | 2a2 |
Ω3y − | 2a2 |
Ω2z, |
| a2 + b2 | c2 + a2 |
(4)
| v′ = v + zP − xR = | 2b2 |
Ω1z − | 2b2 |
Ω3x, |
| b2 + c2 | a2 + b2 |
(5)
| w′ = w + xQ − yP = | 2c2 |
Ω2x − | 2c2 |
Ω1y, |
| c2 + a2 | b2 + c2 |
(6)
P = Ω1 + ξ, Q = Ω2 + η, R = Ω3 + ζ.
(7)
Thus
| u′ | x |
+ v′ | y |
+ w′ | z |
= 0, |
| a2 | b2 |
c2 |
(8)
so that a liquid particle remains always on a similar ellipsoid.
The hydrodynamical equations with moving axes, taking into
account the mutual gravitation of the liquid, become
| 1 |
| dp |
+ 4πρAx + | du |
− vR + wQ + u′ | du |
+ v′ | du |
+ w′ | du |
= 0, ... , ... , |
| ρ | dx |
dt | dx |
dy | dz |
(9)
where
| A, B, C = ∫∞0 | abcdλ |
| (a2 + λ, b2 + λ, c2 + λ) P |
P2 = 4 (a2 + λ) (b2 + λ) (c2 + λ).
(10)
With the values above of u, v, w, u′, v′, w′, the equations become
of the form
| 1 |
| dp |
+ 4πρ Ax + αx + hy + gz = 0, |
| ρ | dx |
(11)
| 1 |
| dp |
+ 4πρBy + hx + βy + fz = 0, |
| ρ | dy |
(12)
| 1 |
| dp |
+ 4πρCz + gx + fy + γz = 0, |
| ρ | dz |
(13)
and integrating
pρ−1 + 2πρ (Ax2 + By2 + Cz2)
+ ½ (αx2 + βy2 + γz2 + 2fyz + 2gzx + 2hxy) = const.,
(14)
so that the surfaces of equal pressure are similar quadric surfaces,
which, symmetry and dynamical considerations show, must be
coaxial surfaces; and f, g, h vanish, as follows also by algebraical
reduction; and
| α = | 4c2(c2 − a2) |
Ω22 − ( | c2 − a2 |
Ω2 − η ) | 2 |
| (c2 + a2)2 | c2 + a2 |
|
| − | 4b2(a2 − b2) |
Ω32 − ( | a2 − b2 |
Ω3 − ζ ) | 2 |
, |
| (a2 + b2)2 | a2 + b2 |
|
(15)
with similar equations for β and γ.
If we can make
(4πρA + α) x2 = (4πρB + β) b2 = (4πρC + γ) c2,
(16)
the surfaces of equal pressure are similar to the external case, which
can then be removed without affecting the motion, provided α, β, γ
remain constant.
This is so when the axis of revolution is a principal axis, say Oz;
when
Ω1 = 0, Ω2 = 0, ξ = 0, η = 0.
(17)
If Ω3 = 0 or θ3 = ζ in addition, we obtain the solution of Jacobi’s
ellipsoid of liquid of three unequal axes, rotating bodily about the
least axis; and putting a = b, Maclaurin’s solution is obtained of
the rotating spheroid.
In the general motion again of the liquid filling a case, when a = b,
Ω3 may be replaced by zero, and the equations, hydrodynamical
and dynamical, reduce to
| dξ |
= − | 2c2 |
Ω2 ζ, | dη |
= | 2a2 |
Ω1 ζ, | dζ |
= | 2c2 |
(Ω2 ξ − Ω2 η) |
| dt | a2 + c2 |
dt | a2 + c2 |
dt | a2 + c2 |
(18)
| dΩ1 |
= Ω2 ζ + | a2 + c2 |
ηζ, | dΩ2 |
= −Ω1 ζ − | a2 + c2 |
ξζ; |
| dt | a2 − c2 |
dt | a2 − c2 |
(19)
of which three integrals are
(20)
| Ω12 + Ω22 = M + | (a2 + c2)2 |
ζ2, |
| 2c2 (a2 − c2) |
(21)
| Ω1 ξ + Ω2 ηN = + | a2 + c2 |
ζ2; |
| 4c2 |
(22)
and then
| ( | dζ |
) | 2 |
= | 4c4 |
(Ω2ξ − Ω12η)2 |
| dt | |
(a2 + c2) |
| = | 4c4 |
[ (ξ2 + η2) (Ω12 + Ω22) − (Ω1ξ + Ω2η)2 ] |
| (a2 + c2)2 |
| = | 4c4 |
[ LM − N2 + { | (a2 + c2)2 |
− M | a2 |
− N | a2 + c2 |
} ζ2 |
| (a2 + c2)2 | 2c2 (a2 + c2) |
c2 | 2c2 |
| − | (a2 + c2) (9a2 − c2) |
ζ4 ] = Z, |
| 16c4 (a2 − c2) |
(23)
where Z is a quadratic in ζ2, so that ζ is an elliptic function of t,
except when c = a, or 3a.
Put Ω1 = Ω cos φ, Ω2 = −Ω sin φ,
| Ω2 | dφ |
= | dΩ1 |
Ω2 − Ω1 | dΩ2 |
= Ω2ζ − | (a2 + c2) |
(Ω1ξ + Ω2η) ζ, |
| dt | dt |
dt | (a2 − c2) |
(24)
| dφ |
= ζ − | (a2 + c2) |
· |
|
, |
| dt | (a2 − c2) |
| M + | (a2 + c2)2 |
ζ2 |
| 2c2 (a2 − c2) | |
(25)
| φ = ∫ | ζ dζ |
− | a2 + c2 |
∫ | |
· | ζ dζ |
, |
| √Z | a2 − c2 |
| M + | (a2 + c2)2 |
ζ2 |
| 2c2 (a2 − c2) | | √Z |
(26)
which, as Z is a quadratic function of ζ2, are non-elliptic integrals;
so also for ψ, where ξ = ω cos ψ, η = −ω sin ψ.
In a state of steady motion
(27)
φ = ψ = nt, suppose,
(28)
Ω1ξ + Ω2η = Ωω,
(29)
| dφ |
= ζ − | a2 + c2 |
| ω |
ζ, |
| dt | a2 − c2 |
Ω |
(30)
| dψ |
= − | 2a2 |
| Ω |
ζ, |
| dt | a2 + c2 |
ω |
(31)
| 1 − | a2 + c2 |
| ω |
= − | 2a2 |
| Ω |
, |
| a2 − c2 | Ω |
a2 + c2 | ω |
(32)
| ( | ω |
− ½ | a2 + c2 |
) | 2 |
= | (a2 − c2) (9a2 − c2) |
, |
| Ω | a2 − c2 |
| 4 (a2 + c2) |
(33)
and a state of steady motion is impossible when 3a > c > a.
An experiment was devised by Lord Kelvin for demonstrating
this, in which the difference of steadiness was shown of a copper
shell filled with liquid and spun gyroscopically, according as the
shell was slightly oblate or prolate. According to the theory
above the stability is regained when the length is more than three
diameters, so that a modern projectile with a cavity more than
three diameters long should fly steadily when filled with water;
while the old-fashioned type, not so elongated, would be highly
unsteady; and for the same reason the gas bags of a dirigible
balloon should be over rather than under three diameters long.
40. A Liquid Jet.—By the use of the complex variable and its
conjugate functions, an attempt can be made to give a mathematical
interpretation of problems such as the efflux of water in a
jet or of smoke from a chimney, the discharge through a weir, the
flow of water through the piers of a bridge, or past the side of a
ship, the wind blowing on a sail or aeroplane, or against a wall,
or impinging jets of gas or water; cases where a surface of
discontinuity is observable, more or less distinct, which separates
the running stream from the dead water or air.
Uniplanar motion alone is so far amenable to analysis; the
velocity function φ and stream function ψ are given as conjugate
functions of the coordinates x, y by
w = ƒ(z) where z = x + yi, w = φ + ψi,
(1)
and then
| dw |
= | dφ |
+ i | dψ |
= −u + vi; |
| dz | dx |
dx |
(2)
so that, with u = q cos θ, v = q sin θ, the function
| ζ = −Q | dz |
= | Q |
= | Q |
(u + vi) = | Q |
(cos θ + i sin θ), |
| dw | (u − vi) |
q2 | q |
(3)
gives ζ as a vector representing the reciprocal of the velocity q in
direction and magnitude, in terms of some standard velocity Q.
To determine the motion of a jet which issues from a vessel with
plane walls, the vector ζ must be Constructed so as to have a constant
128
direction θ along a plane boundary, and to give a constant skin
velocity over the surface of a jet, where the pressure is constant.
It is convenient to introduce the function
Ω = log ζ = log (Q/q) + θi
(4)
 |
| Fig. 4. |
so that the polygon representing Ω conformally has a boundary
given by straight lines parallel to the coordinate axes; and then to
determine Ω and w as functions of a variable u (not to be confused
with the velocity component of q),
such that in the conformal representation
the boundary of the Ω
and w polygon is made to coincide
with the real axis of u.
It will be sufficient to give a
few illustrations.
Consider the motion where the
liquid is coming from an infinite
distance between two parallel
walls at a distance xx′ (fig. 4), and
issues in a jet between two edges A and A′; the wall xA being bent
at a corner B, with the external angle β = ½π/n.
The theory of conformal representation shows that the motion is
given by
| ζ = [ | √ (b − a′·u − a) + √(b − a·u − a′) |
] | 1/n |
, u = ae−πw/m; |
| √ (a − a′·u − b) | |
(5)
where u = a, a′ at the edge A, A′; u = b at a corner B; u = 0 across
xx′ where φ = ∞; and u = ∞, φ = ∞ across the end JJ′ of the jet,
bounded by the curved lines APJ, A′P′J′, over which the skin
velocity is Q. The stream lines xBAJ, xA′J′ are given by ψ = 0, m;
so that if c denotes the ultimate breadth JJ′ of the jet, where the
velocity may be supposed uniform and equal to the skin velocity Q,
m = Qc, c = m/Q.
If there are more B corners than one, either on xA or x′A′, the
expression for ζ is the product of corresponding factors, such as in (5).
Restricting the attention to a single corner B,
| ζn = ( | Q |
) | n |
(cos nθ + i sin nθ) = | √ (b − a′·u − a) + √ (b − a·u − a′) |
, |
| q | |
√ (a − a′·u − b) |
(6)
| ch nω = ch log ( | Q |
) | n |
cos nθ + i sh log ( | Q |
) | n |
sin nθ |
| q | |
q | |
| = ½(ζn + ζ−n) = √ | b − a′ |
√ | u − a |
, |
| a − a′ | u − b |
(7)
| sh nΩ = sh log ( | Q |
) cos nθ + i ch log ( | Q |
) | n |
sin nθ |
| q | q |
|
| = ½(ζn + ζ−n) = √ | b − a |
√ | u − a′ |
, |
| a − a′ | u − b |
(8)
∞ > a > b > 0 > a′ > −∞
(9)
and then
| dΩ |
= − | 1 |
| √ (b − a′·b − a′) |
, | dw |
= − | m |
, |
| du | 2n |
(u − b) √ (a − a·u − a′) | du |
πu |
(10)
the formulas by which the conformal representation is obtained.
For the Ω polygon has a right angle at u = a, a′, and a zero angle at
u = b, where θ changes from 0 to ½π/n and Ω increases by ½iπ/n; so
that
| dΩ |
= | A |
, where A = | √ (b − a·b − a′) |
. |
| du | (u − b) √ (u − a·u − a′) |
2n |
(11)
And the w polygon has a zero angle at u = 0, ∞, where ψ changes
from 0 to m and back again, so that w changes by im, and
| dw |
= | B |
, where B = − | m |
. |
| du | u |
π |
(12)
Along the stream line xBAPJ,
ψ = 0, u = ae−πφ/m;
(13)
and over the jet surface JPA, where the skin velocity is Q,
| dφ |
= −q = −Q, u = aeπsQ/m = aeπs/c, |
| ds |
(14)
denoting the arc AP by s, starting at u = a;
| ch nΩ = cos nθ = √ | b − a′ |
√ | u − a |
, |
| a − a′ | u − b |
(15)
| sh nΩ = i sin nθ = i √ | a − b |
√ | u − a′ |
, |
| a − a′ | u − b |
(16)
∞ > u = aeπs/c > a,
(17)
and this gives the intrinsic equation of the jet, and then the radius
of curvature
| ρ = − | ds |
= | 1 |
| dφ |
= | i |
| dw |
= | i |
| dw |
/ | dΩ |
| dθ | Q |
dθ | Q |
dΩ | Q |
du | du |
| = | c |
· | u − b |
| √ (u − a·u − a′) |
, |
| π | u |
√ (a − b·b − a′) |
(18)
not requiring the integration of (11) and (12)
If θ = α across the end JJ′ of the jet, where u = ∞, q = Q,
| ch nΩ = cos nα = √ | b − a′ |
, sh nΩ = i sin nα= i √ | a − b |
, |
| a − a′ | a − a′ |
(19)
Then
| cos 2nα − cos 2nθ = 2 | a − b·b − a′ |
= ½sin2 2nα | a − a′ |
| a − a′·u − b | u − b |
| sin 2nθ = 2 | √ (a − b.b − a′) √ (u − a·u − b′) |
| a − a′·u − b |
(20)
| = sin 2nα | √ (a − a·b − a′) |
; |
| u − b |
| 2n |
| c |
( 1 + | b |
) | √ (a − b·b − a′) |
| φ | ρ |
u − b | √ (u − a·u − a′) |
(21)
| = | a − a′ + (a + a′) cos 2nα − [ a + a′ + (a − a′) cos 2nα ] cos 2nθ |
× | cos 2nα − cos 2nθ |
. |
| (a − a′) sin2 2nα | sin 2nθ |
Along the wall AB, cos nθ = 0, sin nθ = 1,
a > u > b,
(22)
| ch nΩ = i sh log ( | Q |
) | n |
= i √ | b − a′ |
√ | a − u |
, |
| q | |
a − a′ | u − b |
(23)
| sh nΩ = i ch log ( | Q |
) | n |
= i √ | a − b |
√ | u − a′ |
, |
| q | |
a − a′ | u − b |
(24)
| ds |
= | ds |
| dφ |
= | m |
= | c |
| Q |
| du | dφ |
dt | πqu |
π | qu |
(25)
| π | AB |
= ∫ab | Q |
| du |
∫ [ | √ (a − b) √ (u − a′) + √ (b − a′) √ (a − u) |
] | 1/n |
| du |
. |
| c | q |
u | √ (a − a′) √ (u − b′) |
| u |
(26)
Along the wall Bx, cos nθ = 1, sin nθ = 0,
b > u > 0
(27)
| ch nΩ = ch log ( | Q |
) | n |
= √ | b − a′ |
√ | a − u |
, |
| q | |
a − a′ | b − u |
(28)
| sh nΩ = sh log ( | Q |
) | n |
= √ | a − b |
√ | u − a′ |
. |
| q | |
a − a′ | b − u |
(29)
At x where φ = ∞, u = 0, and q = q0,
| ( | Q |
) | n |
= √ | b − a′ |
√ | a |
+ √ | a − b |
√ | −a′ |
. |
| q0 | |
a − a′ | b |
a − a′ | q |
(30)
In crossing to the line of flow x′A′P′J′, ψ changes from 0 to m, so
that with q = Q across JJ′, while across xx′ the velocity is q0, so that
m = q0·xx′ = Q·JJ′
(31)
| JJ′ |
= | q0 |
[ √ | b − a′ |
√ | a |
− √ | a − b |
√ | −a′ |
] | 1/n |
, |
| xx′ | Q |
a − a′ | b |
a − a′ | b |
|
(32)
giving the contraction of the jet compared with the initial breadth
of the stream.
Along the line of flow x′A′P′J′, ψ = m, u = a′e−πφ/m, and from x′ to
A′, cos nθ = 1, sin nθ = 0,
| ch nΩ = ch log ( | Q |
) | n |
= √ | b − a′ |
√ | a − u |
, |
| q | |
a − a′ | b − u |
(33)
| sh nΩ = sh log ( | Q |
) | n |
= √ | a − b |
√ | u − a′ |
. |
| q | |
a − a′ | b − u |
(34)
0 > u > a′.
(35)
Along the jet surface A′J′, q = Q,
| ch nΩ = cos nθ = √ | b − a′ |
√ | a − u |
, |
| a − a′ | b − u |
(36)
| sh nΩ = i sin nθ = i √ | a − b |
√ | u − a′ |
. |
| a − a′ | b − u |
(37)
a′ > u = a′eπ/sc > −∞,
(38)
giving the intrinsic equation.
41. The first problem of this kind, worked out by H. v. Helmholtz,
of the efflux of a jet between two edges A and A1 in an infinite
wall, is obtained by the symmetrical duplication of the above, with
n = 1, b = 0, a′ = −∞, as in fig. 5,
| ch Ω = √ | u − a |
, sh Ω = √ | − a |
; |
| u | u |
(1)
and along the jet APJ, ∞ > u = aeπs/c > a,
| sh Ω = i sin θ − i √ | a |
= ie−1/2 πs/c, |
| u |
(2)
| PM = ∫∞s sinθ ds = ∫ e−½πs/c ds = | c |
e−1/2 πs/c = | c |
sin θ, |
| ½π | ½π |
(3)
129
so that PT = c/½π, and the curve AP is the tractrix; and the coefficient
of contraction, or
| breadth of the jet |
= | π |
. |
| breadth of the orifice | π + 2 |
(4)
A change of Ω and θ into nΩ and nθ will give the solution for
two walls converging symmetrically to the orifice AA1 at an angle π/n.
With n = ½, the reentrant walls are given of Borda’s mouthpiece,
and the coefficient of contraction becomes ½. Generally, by making
a′ = −∞, the line x′A′ may be taken as a straight stream line of
infinite length, forming an axis of symmetry; and then by duplication
the result can be obtained,
with assigned n, a,
and b, of the efflux from
a symmetrical converging
mouthpiece, or of the flow of water through the arches of a bridge,
with wedge-shaped piers to divide the stream.
 |
 |
| Fig. 5. |
Fig. 6. |
42. Other arrangements of the constants n, a, b, a′ will give the
results of special problems considered by J. M. Michell, Phil.
Trans. 1890.
Thus with a′ = 0, a stream is split symmetrically by a wedge of
angle π/n as in Bobyleff’s problem; and, by making a = ∞, the
wedge extends to infinity; then
| ch nΩ = √ | b |
, sh nΩ = √ | n |
. |
| b − u | b − u |
(1)
Over the jet surface ψ = m, q = Q,
u = − eπφ/m = − beπ2/c,
| ch Ω = cos nθ = √ | 1 |
, sh Ω = i sin nθ = i √ | eπ2/c |
, |
| eπ2/c + 1 | eπ2/c + 1 |
(2)
| e½π2/c = tan nθ, | ½π |
| ds |
= | 2n |
. |
| c | dθ |
sin 2nθ |
(3)
For a jet impinging normally on an infinite plane, as in fig. 6, n = 1,
e½π2/c = tan θ, ch (½πs/c) sin 2θ = 1,
(4)
sh ½πx/c = cot θ, sh ½πy/c = tan θ,
sh ½πx/c sh ½πy/c = 1, e½π(x + y)/c = e1/2 πx/c + e1/2 πy/c + 1.
(5)
With n = ½, the jet is reversed in direction, and the profile is the
catenary of equal strength.
In Bobyleff’s problem of the wedge of finite breadth,
| ch nΩ = √ | b |
√ | u − a |
, sh nΩ = √ | b − a |
√ | u |
, |
| a | u − b |
a | u − b |
(6)
| cos nα = √ | b |
, sin nα = √ | a − b |
, |
| a | a |
(7)
and along the free surface APJ, q = Q, ψ = 0, u = e−πφ/m = aeπs/c,
| cos nθ = cos nα √ | eπ2/c − 1 |
, |
| eπ2/c − cos2 nα |
| eπ2/c = | cos2 nα sin2 nθ |
, |
| sin2 nθ − sin2 nα |
(8)
the intrinsic equation, the other free surface A′P′J′ being given by
| eπ2/c = | cos2 nα sin2 nθ |
, |
| sin2 nα − sin2 nθ |
(9)
Putting n = 1 gives the case of a stream of finite breadth disturbed
by a transverse plane, a particular case of Fig. 7.
When a = b, α = 0, and the stream is very broad compared with
the wedge or lamina; so, putting w = w′(a − b)/a in the penultimate
case, and
u = ae−w ≈ a − (a − b)w′,
(10)
| ch nΩ = √ | w′ + 1 |
, sh nΩ = √ | 1 |
, |
| w′ | √ w′ |
(11)
in which we may write
w′ = φ + ψi.
(12)
Along the stream line xABPJ, ψ = 0; and along the jet surface
APJ, −1 > φ > −∞; and putting φ = −πs/c − 1, the intrinsic
equation is
πs/c = cot2 nθ,
(13)
which for n = 1 is the evolute of a catenary.
 |
| Fig. 7. |
43. When the barrier AA′ is held oblique to the current, the
stream line xB is curved to the branch point B on AA′ (fig. 7), and
so must be excluded from the
boundary of u; the conformal representation
is made now with
| dΩ |
= − | √ (b − a·b − a′) |
|
| du | (u − b) √ (u − a·u − a′) |
(1)
| dw |
= − | m |
| 1 |
− | m′ |
| 1 |
, |
| du | π |
u − j | π |
u − j |
| = − | m + m′ |
· | u − b |
, |
| π | u − j·u − j′ |
(2)
taking u = ∞ at the source where
φ = ∞, u = b at the branch point B, u = j, j′ at the end of the two
diverging streams where φ = −∞; while ψ = 0 along the stream
line which divides at B and passes through A, A′; and ψ = m, −m′
along the outside boundaries, so that m/Q, m′/Q is the final breadth
of the jets, and (m + m′)/Q is the initial breadth, c1 of the impinging
stream. Then
| ch ½Ω = √ | b − a′ |
√ | u − b |
, sh ½Ω = √ | b − a |
√ | u − a′ |
, |
| a − a′ | u − b |
a − a′ | u − b |
(3)
| ch Ω = | 2b − a − a′ |
− | N |
, |
| a − a′ | u − b |
| sh Ω = √ N | √ (2·a − u·u − a′) |
, |
| u − b |
| N = 2 | a − b·b − a′ |
. |
| a − a′ |
(4)
Along a jet surface, q = Q, and
chΩ = cos θ = cos α − ½sin2 α(a − a′) / (u − b),
(5)
if θ = α at the source x of the jet xB, where u = ∞; and supposing
θ = β, β′ at the end of the streams where u = j, j′,
| u − b |
= | ½sin2 α |
, | u − j |
½sin2 α | cosθ − cosβ |
, |
| a − a′ | cos α − cos θ |
a − a′ | (cos α − cos β) (cos α − cos θ) |
| u − j′ |
= ½sin2 α | cos θ − cos β′ |
; |
| a − a′ | (cosα − cos β′) (cos α − cosθ) |
(6)
and ψ being constant along a stream line
| dφ |
= | dw |
, Q | ds |
= | dφ |
= | dw |
| du |
, |
| du | du |
dθ | dθ |
du | dθ |
| πQ |
| ds |
= | π |
| ds |
= | (cos α − cos β) (cos α − cos β′) sin θ |
, |
| m + m′ | dθ |
c | dθ |
(cos α − cos θ) (cos θ − cos β) (cos θ − cos α′) |
| = | sin θ |
+ | cos α − cos β′ |
· | sin θ |
| cos α − cos θ | cos β − cos β′ |
cos θ − cos β |
| cos α − cos β |
· | sin θ |
, |
| cos β − cos β′ | cos θ − cos β′ |
(7)
giving the intrinsic, equation of the surface of a jet, with proper
attention to the sign.
From A to B, a > u > b, θ = 0,
| ch Ω = ch log | Q |
= cos α − ½ sin2 α | a − a′ |
| q | a − b |
| sh Ω = sh log | Q |
= | √ (a − u·u − a′) |
sinα |
| q | u − b |
| Q |
= | (u − b) cos α − ½ (a − a′) sin2 α + √ (a − u·u − a′) sin α |
| q | u − b |
(8)
| Q | ds |
= Q | ds |
| dφ |
= − | Q |
| dw |
| du | dφ |
du | q |
du |
| = | m + m′ |
· | (u − b) cos α − ½ (a − a′) sin2 α + √ (a − u·u − a′) sin α |
| π | j − u·u − j′ |
| π | AB |
= ∫ab | (2b − a − a′) (u − b) − 2(a − b) (b − a′) + 2√ (a − b·b − a′·a − u·u − a′) |
du, |
| c | a − a′·j − u·u − j′ |
(10)
with a similar expression for BA′.
The motion of a jet impinging on an infinite barrier is obtained
by putting j = a, j′ = a′; duplicated on the other side of the barrier,
the motion reversed will represent the direct collision of two jets of
unequal breadth and equal velocity. When the barrier is small
compared with the jet, α = β = β′, and G. Kirchhoff’s solution is
obtained of a barrier placed obliquely in an infinite stream.
Two corners B1 and B2 in the wall xA, with a′ = −∞, and n = 1,
will give the solution, by duplication, of a jet issuing by a reentrant
mouthpiece placed symmetrically in the end wall of the channel;
or else of the channel blocked partially by a diaphragm across the
middle, with edges turned back symmetrically, problems discussed
by J. H. Michell, A. E. H. Love and M. Réthy.
130
When the polygon is closed by the walls joining, instead of reaching
back to infinity at xx′, the liquid motion must be due to a
source, and this modification has been worked out by B. Hopkinson
in the Proc. Lond. Math. Soc., 1898.
Michell has discussed also the hollow vortex stationary inside a
polygon (Phil. Trans., 1890); the solution is given by
ch nΩ = sn w, sh nΩ = i cn w
(11)
so that, round the boundary of the polygon, ψ = K′, sin nθ = 0;
and on the surface of the vortex ψ = 0, q = Q, and
cos nθ = sn φ, nθ = ½π − am s/c,
(12)
the intrinsic equation of the curve.
This is a closed Sumner line for n = 1, when the boundary consists
of two parallel walls; and n = ½ gives an Elastica.
44. The Motion of a Solid through a Liquid.—An important
problem in the motion of a liquid is the determination of the state
of velocity set up by the passage of a solid through it; and thence
of the pressure and reaction of the liquid on the surface of the solid,
by which its motion is influenced when it is free.
Beginning with a single body in liquid extending to infinity, and
denoting by U, V, W, P, Q, R the components of linear and angular
velocity with respect to axes fixed in the body, the velocity function
takes the form
φ = Uφ1 + Vφ2 + Wφ3 + Pχ1 + Qχ2 + Rχ3,
(1)
where the φ’s and χ’s are functions of x, y, z, depending on the
shape of the body; interpreted dynamically, C − ρφ represents the
impulsive pressure required to stop the motion, or C + ρφ to start it
again from rest.
The terms of φ may be determined one at a time, and this problem
is purely kinematical; thus to determine φ1, the component U alone
is taken to exist, and then l, m, n, denoting the direction cosines of
the normal of the surface drawn into the exterior liquid, the function
φ1 must be determined to satisfy the conditions
(i.) ∇2φ1 = 0. throughout the liquid;
(ii.) dφ1/dυ = −l, the gradient of φ down the normal at the surface
of the moving solid;
(iii.) dφ1/dυ = 0, over a fixed boundary, or at infinity;
similarly for φ2 and φ3.
To determine χ1 the angular velocity P alone is introduced, and
the conditions to be satisfied are
(i.) ∇2χ1 = 0, throughout the liquid;
(ii.) dχ1/dυ = mz − ny, at the surface of the moving body, but zero over
a fixed surface, and at infinity; the same for χ2 and χ3.
For a cavity filled with liquid in the interior of the body, since the
liquid inside moves bodily for a motion of translation only,
φ1 = −x, φ2 = −y, φ3 = −z;
(2)
but a rotation will stir up the liquid in the cavity, so that the χ’s
depend on the shape of the surface.
The ellipsoid was the shape first worked out, by George Green, in
his Research on the Vibration of a Pendulum in a Fluid Medium (1833);
the extension to any other surface will form an important step in
this subject.
A system of confocal ellipsoids is taken
| x2 |
+ | y2 |
+ | z2 |
= 1 |
| a2 + λ | b2 + λ |
c2 + λ |
(3)
and a velocity function of the form
φ = xψ,
(4)
where ψ is a function of λ only, so that ψ is constant over an ellipsoid;
and we seek to determine the motion set up, and the form of ψ
which will satisfy the equation of continuity.
Over the ellipsoid, p denoting the length of the perpendicular from
the centre on a tangent plane,
| l = | px |
, m = | py |
, n = | pz |
| a2 + λ | b2 + λ |
c2 + λ |
(5)
| 1 = | p2x2 |
+ | p2y2 |
+ | p2z2 |
, |
| (a2 + λ)2 | (b2 + λ)2 |
(c2 + λ)2 |
p2 = (a2 + λ) l2 + (b2 + λ) m2 + (c2 + λ) n2,
= a2l2 + b2m2 + c2n2 + λ,
|
(7)
(8)
Thence
| dφ |
= | dx |
ψ + x | dψ |
| ds | ds |
ds |
| = | dx |
ψ + 2 (a2 + λ) | dψ |
l | dp |
, |
| ds | dλ |
ds |
(9)
so that the velocity of the liquid may be resolved into a component
-ψ parallel to Ox, and −2(a2 + λ)l dψ/dλ along the normal of the
ellipsoid; and the liquid flows over an ellipsoid along a line of slope
with respect to Ox, treated as the vertical.
Along the normal itself
| dφ |
{ ψ + 2(a2 + λ) | dψ |
} l, |
| ds | dλ |
(10)
so that over the surface of an ellipsoid where λ and ψ are constant,
the normal velocity is the same as that of the ellipsoid itself, moving
as a solid with velocity parallel to Ox
| U = −ψ − 2 (a2 + λ) | dψ |
, |
| dλ |
(11)
and so the boundary condition is satisfied; moreover, any ellipsoidal
surface λ may be supposed moving as if rigid with the velocity in
(11), without disturbing the liquid motion for the moment.
The continuity is secured if the liquid between two ellipsoids λ
and λ1, moving with the velocity U and U1 of equation (11), is
squeezed out or sucked in across the plane x = 0 at a rate equal to the
integral flow of the velocity ψ across the annular area α1 − α of the
two ellipsoids made by x = 0; or if
| αU − α1U1 = ∫λ1λ ψ | dα |
dλ, |
| dλ |
(12)
α = π√ (b2 + λ.c2 + λ).
(13)
Expressed as a differential relation, with the value of U from (11),
| d |
[ αψ + 2 (a2 + λ) α | dψ |
] − ψ | dα |
= 0, |
| dλ | dλ |
dλ |
(14)
| 3α | dψ |
+ 2 (a2 + λ) | d |
( α | dψ |
) = 0, |
| dλ | dλ |
dλ |
(15)
and integrating
| (a2 + λ)3/2 α | dψ |
= a constant, |
| dλ |
(16)
so that we may put
(17)
P2 = 4 (a2 + λ) (b2 + λ) (c2 + λ),
(18)
where M denotes a constant; so that ψ is an elliptic integral of the
second kind.
The quiescent ellipsoidal surface, over which the motion is entirely
tangential, is the one for which
| 2 (a2 + λ) | dψ |
+ ψ = 0, |
| dλ |
(19)
and this is the infinite boundary ellipsoid if we make the upper limit
λ1 = ∞.
The velocity of the ellipsoid defined by λ = 0 is then
| = | M |
− ∫∞0 | M dλ |
| abc | (a2 + λ)P |
(20)
with the notation
| A or Aλ = ∫∞λ | abc dλ |
| (a2 + λ) P |
(21)
so that in (4)
| φ = | M |
xA = | UxA |
, φ1 = | xAλ |
, |
| abc | 1 − A0 |
1 − A0 |
(22)
in (1) for an ellipsoid.
The impulse required to set up the motion in liquid of density ρ is
the resultant of an impulsive pressure ρφ over the surface S of the
ellipsoid, and is therefore
∫ ∫ ρφl dS = ρψ0 ∫ ∫ xl dS
= ρψ0 (volume of the ellipsoid) = ψ0W′,
(23)
where W′ denotes the weight of liquid displaced.
Denoting the effective inertia of the liquid parallel to Ox by αW′.
the momentum
αW′U = ψ0W′
(24)
(25)
in this way the air drag was calculated by Green for an ellipsoidal
pendulum.
Similarly, the inertia parallel to Oy and Oz is
| βW′ = | B0 |
W′, γW′ = | C0 |
W′, |
| 1 − B0 | 1 − C0 |
(26)
| Bλ, Cλ = ∫∞λ | abc dλ |
; |
| (b2 + λ, c2 + λ) P |
(27)
and
A + B + C = abc / ½P, A0 + B0 + C0 = 1.
(28)
For a sphere
a = b = c, A0 = B0 = C0 = 1⁄3, α = β = γ = ½,
(29)
131
so that the effective inertia of a sphere is increased by half the weight
of liquid displaced; and in frictionless air or liquid the sphere, of
weight W, will describe a parabola with vertical acceleration
(30)
Thus a spherical air bubble, in which W/W′ is insensible, will begin
to rise in water with acceleration 2g.
45. When the liquid is bounded externally by the fixed ellipsoid
λ = λ1, a slight extension will give the velocity function φ of the
liquid in the interspace as the ellipsoid λ = 0 is passing with velocity
U through the confocal position; φ must now take the form x(ψ + N),
and will satisfy the conditions in the shape
| φ = Ux | A + B1 + C1 |
= Ux |
| abc |
+ ∫λ1λ | abcdλ |
| a1b1c1 | (a2 + λ) P |
|
, |
| B0 + C0 − B1 − C1 |
| 1 − | abc |
− ∫λ10 | abcdλ |
| a1b1c1 | (a2 + λ) P |
|
(1)
and any confocal ellipsoid defined by λ, internal or external to
λ = λ1, may be supposed to swim with the liquid for an instant,
without distortion or rotation, with velocity along Ox
| U | Bλ + Cλ − B1 − C1 |
. |
| B0 + C0 − B1 − C1 |
Since − Ux is the velocity function for the liquid W′ filling the
ellipsoid λ = 0, and moving bodily with it, the effective inertia of the
liquid in the interspace is
| A0 + B1 + C1 |
W′. |
| B0 + C0 − B1 − C1 |
(2)
If the ellipsoid is of revolution, with b = c,
| φ = ½Ux | A + 2B1 |
, |
| B0 − B1 |
(3)
and the Stokes’ current function ψ can be written down
| ψ = − ½ Uy2 | B − B1 |
; |
| B0 − B1 |
(4)
reducing, when the liquid extends to infinity and B1 = 0, to
| φ = ½ Ux | A |
, ψ = − ½ Uy2 | B |
; |
| B0 | B0 |
(5)
so that in the relative motion past the body, as when fixed in the
current U parallel to xO,
| φ′ = ½Ux ( 1 + | A |
), ψ′ = ½Uy2 ( 1 − | B |
). |
| B0 | B0 |
(6)
Changing the origin from the centre to the focus of a prolate
spheroid, then putting b2 = pa, λ = λ′a, and proceeding to the limit
where a = ∞, we find for a paraboloid of revolution
| B = ½ | p |
, | B |
= | p |
, |
| p + λ′ | B0 |
p + λ′ |
(7)
(8)
with λ′ = 0 over the surface of the paraboloid; and then
ψ′ = ½ U [ y2 − p √ (x2 + y2) + px ];
(9)
ψ = −½ Up [ √ (x2 + y2) − x ];
(10)
φ = −½ Up log [ √ (x2 + y2) + x ].
(11)
The relative path of a liquid particle is along a stream line
ψ′ = ½ Uc2, a constant,
(12)
| x = | p2y2 − (y2 − c2)2 |
, √ (x2 + y2) = | p2y2 − (y2 − c2)2 |
| 2p (y2 − c2) | 2p (y2 − c2) |
(13)
a C4; while the absolute path of a particle in space will be given by
| dy |
= − | r − x |
= | y2 − c2 |
, |
| dx | y |
2py |
(14)
y2 − c2 = a2 e−x/p.
(15)
46. Between two concentric spheres, with
a2 + λ = r2, a2 + λ1 = a12,
(1)
A = B = C = a3 / 3r3,
| φ = ½ Ux | a3/r3 + 2 a3/a13 |
, ψ = ½ Uy2 | a3/r3 − a3/a13 |
; |
| 1 − a4/a12 | 1 − a3/a13 |
(2)
and the effective inertia of the liquid in the interspace is
| A0 + 2A1 |
W′ = ½ | a13 + 2a3 |
W′. |
| 2A0 − 2A1 | a13 − a3 |
(3)
When the spheres are not concentric, an expression for the effective
inertia can be found by the method of images (W. M. Hicks, Phil.
Trans., 1880).
The image of a source of strength μ at S outside a sphere of
radius a is a source of strength μa/ƒ at H, where OS = ƒ, OH = a2/ƒ,
and a line sink reaching from the image H to the centre O of
line strength −μ/a; this combination will be found to produce no
flow across the surface of the sphere.
Taking Ox along OS, the Stokes’ function at P for the source S
is μ cos PSx, and of the source H and line sink OH is μ(a/ƒ) cos PHx
and −(μ/a)(PO − PH); so that
| ψ = μ ( cos PSx + | a |
cos PHx − | PO − PH |
), |
| ƒ | a |
(4)
and ψ = −μ, a constant, over the surface of the sphere, so that there
is no flow across.
When the source S is inside the sphere and H outside, the line
sink must extend from H to infinity in the image system; to realize
physically the condition of zero flow across the sphere, an equal
sink must be introduced at some other internal point S′.
When S and S′ lie on the same radius, taken along Ox, the Stokes’
function can be written down; and when S and S′ coalesce a doublet
is produced, with a doublet image at H.
For a doublet at S, of moment m, the Stokes’ function is
| m | d |
cos PSx = −m | y2 |
; |
| dƒ | PS3 |
(5)
and for its image at H the Stokes’ function is
| m | d |
cos PHx = −m | a3 |
| y2 |
; |
| dƒ | ƒ3 |
PH3 |
(6)
so that for the combination
| ψ = my2 ( | a3 |
| 1 |
− | 1 |
) = m | y2 |
( | a3 |
− | ƒ3 |
), |
| ƒ3 | PH3 |
PS3 | ƒ3 |
PH3 | PS3 |
(7)
and this vanishes over the surface of the sphere.
There is ao Stokes’ function when the axis of the doublet at S
does not pass through O; the image system will consist of an
inclined doublet at H, making an equal angle with OS as the doublet
S, and of a parallel negative line doublet, extending from H to O,
of moment varying as the distance from O.
A distribution of sources and doublets over a moving surface
will enable an expression to be obtained for the velocity function
of a body moving in the presence of a fixed sphere, or inside it.
The method of electrical images will enable the stream function ψ′
to be inferred from a distribution of doublets, finite in number
when the surface is composed of two spheres intersecting at an
angle π/m, where m is an integer (R. A. Herman, Quart. Jour. of
Math. xxii.).
Thus for m = 2, the spheres are orthogonal, and it can be verified
that
| ψ′ = ½ Uy2 ( 1 − | a13 |
− | a23 |
+ | a3 |
), |
| r13 | r23 |
r3 |
(8)
where a1, a2, a = a1a2/√ (a12 + a22) is the radius of the spheres and
their circle of intersection, and r1, r2, r the distances of a point
from their centres.
The corresponding expression for two orthogonal cylinders will be
| ψ′ = Uy ( 1 − | a12 |
− | a22 |
+ | a2 |
). |
| r12 | r22 |
r2 |
(8)
With a2 = ∞, these reduce to
| ψ′ = ½Uy2 ( 1 − | a5 |
) | x |
, or Uy ( 1 − | a4 |
) | x |
, |
| r5 | a |
r4 | a |
(10)
for a sphere or cylinder, and a diametral plane.
Two equal spheres, intersecting at 120°, will require
| ψ′ = ½Uy2 [ | x |
− | a3 |
+ | a4 (a − 2x) |
+ | a3 |
− | a4 (a + 2x) |
], |
| a | 2r13 |
2r15 | 2r23 |
2r25 |
(11)
with a similar expression for cylinders; so that the plane x = 0
may be introduced as a boundary, cutting the surface at 60°. The
motion of these cylinders across the line of centres is the equivalent
of a line doublet along each axis.
47. The extension of Green’s solution to a rotation of the ellipsoid
was made by A. Clebsch, by taking a velocity function
φ = xyχ
(1)
for a rotation R about Oz; and a similar procedure shows that an
ellipsoidal surface λ may be in rotation about Oz without disturbing
the motion if
| R = − | [ 1/ (a2 + λ) + 1/ (b2 + λ) ] χ + 2 dx/dλ |
, |
| 1 / (b2 + λ) − 1 / (a2 + λ) |
(2)
and that the continuity of the liquid is secured if
| (a2 + λ)3/2 (b2 + λ)3/2 (c2 + λ) ½ | dχ |
= constant, |
| dλ |
(3)
| χ = ∫∞λ | N dλ |
= | N |
· | Bλ − Aλ |
; |
| (a2 + λ) (b2 + λ) P | abc |
a2 − b2 |
(4)
and at the surface λ = 0,
| R = − | [ (1/a2 + 1/b2) · N/abc · (B0 − A0)/(a2 − b2) ] − N/abc · 1/a2b2 |
, |
| 1/b2 − 1/a2 |
(5)
| N |
= R | 1/b2 − 1/a2 |
, |
| abc | 1/a2b2 − [ (1/a2 + 1/b2) · (B0 − A0) / (a2 − b2) ] |
(6)
| = R | (a2 − b2)2 / (a2 + b2) |
|
| (a2 − b2) / (a2 + b2) − (B0 − A0) |
132
The velocity function of the liquid inside the ellipsoid λ = 0 due
to the same angular velocity will be
φ1 = Rxy (a2 − b2) / (a2 + b2),
(7)
and on the surface outside
| φ0 = xyχ0 = xy | N |
| B0 − A0 |
, |
| abc | a2 − b2 |
(8)
so that the ratio of the exterior and interior value of φ at the surface
is
| φ0 |
= | B0 − A0 |
, |
| φ1 | (a2 − b2) / (a2 + b2) − (B0 − A0) |
(9)
and this is the ratio of the effective angular inertia of the liquid,
outside and inside the ellipsoid λ = 0.
The extension to the case where the liquid is bounded externally
by a fixed ellipsoid λ = λ1 is made in a similar manner, by putting
φ = xy (χ + M),
(10)
and the ratio of the effective angular inertia in (9) is changed to
| (B0 − A0) − (B1 − A1) + | a12 − b12 |
| abc |
|
| a12 + b12 | a1b1c1 | |
. |
| a2 − b2 |
− | a12 − b12 |
| abc |
− (B0 − A0) + (B1 − A1) |
| a2 + b2 | a12 + b12 |
a1b1c1 | |
(11)
Make c = ∞ for confocal elliptic cylinders; and then
| Aλ = ∫∞λ | ab |
= | ab |
( 1 − √ | b2 + λ |
), |
| (a2 + λ) √ (4a2 + λb2 + λ) | a2 − b2 |
a2 + λ |
(12)
| Bλ = | ab |
( √ | a2 + λ |
− 1 ), Cλ = 0; |
| a2 − b2 | b2 + λ |
and then as above in § 31, with
a = c ch α, b = c sh α, a1 = √ (a2 + λ) = c ch α1, b1 = c sh α1
(13)
the ratio in (11) agrees with § 31 (6).
As before in § 31, the rotation may be resolved into a shear-pair,
in planes perpendicular to Ox and Oy.
A torsion of the ellipsoidal surface will give rise to a velocity
function of the form φ = xyzΩ, where Ω can be expressed by the
elliptic integrals Aλ, Bλ, Cλ, in a similar manner, since
Ω = L ∫∞λ dλ / P3.
48. The determination of the φ’s and χ’s is a kinematical
problem, solved as yet only for a few cases, such as those discussed
above.
But supposing them determined for the motion of a body through
a liquid, the kinetic energy T of the system, liquid and body, is
expressible as a quadratic function of the components U, V, W, P,
Q, R. The partial differential coefficient of T with respect to a
component of velocity, linear or angular, will be the component of
momentum, linear or angular, which corresponds.
Conversely, if the kinetic energy T is expressed as a quadratic
function of x1, x2, x3, y1, y2, y3, the components of momentum, the
partial differential coefficient with respect to a momentum component
will give the component of velocity to correspond.
These theorems, which hold for the motion of a single rigid body,
are true generally for a flexible system, such as considered here for a
liquid, with one or more rigid bodies swimming in it; and they express
the statement that the work done by an impulse is the product
of the impulse and the arithmetic mean of the initial and final
velocity; so that the kinetic energy is the work done by the impulse
in starting the motion from rest.
Thus if T is expressed as a quadratic function of U, V, W, P, Q, R,
the components of momentum corresponding are
| x1 = | dT |
, x2 = | dT |
, x3 = | dT |
, |
| dU | dV |
dW |
(1)
| y1 = | dT |
, y2 = | dT |
, y3 = | dT |
; |
| dP | dQ |
dR |
but when it is expressed as a quadratic function of x1, x2, x3, y1,
y2, y3,
| U = | dT |
, V = | dT |
, W = | dT |
, |
| dx1 | dx2 |
dx3 |
(2)
| P = | dT |
, Q = | dT |
, R = | dT |
. |
| dy1 | dy2 |
dy3 |
The second system of expression was chosen by Clebsch and
adopted by Halphen in his Fonctions elliptiques; and thence the
dynamical equations follow
| X = | dx1 |
− x2 | dT |
+ x3 | dT |
, Y = ..., Z = ..., |
| dt | dy3 |
dy2 |
(3)
| L = | dy1 |
− y2 | dT |
+ y3 | dT |
− x2 | dT |
+ x3 | dT |
, M = ..., N = ..., |
| dt | dy3 |
dy2 | dx3 |
dx2 |
(4)
where X, Y, Z, L, M, N denote components of external applied force
on the body.
These equations are proved by taking a line fixed in space, whose
direction cosines are l, m, n, then
| dl |
= mR − nQ, | dm |
= nP − lR, | dn |
= lQ − mP. |
| dt | dt |
dt |
(5)
If P denotes the resultant linear impulse or momentum in this
direction
P = lx1 + mx2 + nx3,
(6)
| dP |
= | dl |
x1 + | dm |
x2 + | dn |
x3 |
| dt | dt |
dt | dt |
| + l | dx1 |
+ m | dx2 |
+ n | dx3 |
, |
| dt | dt |
dt |
| = l ( | dx1 |
− x2R + x3Q ) |
| dt |
| + m ( | dx2 |
− x3P + x1R ) |
| dt |
| + n ( | dx3 |
− x1Q + x2P ) |
| dt |
= lX + mY + nZ,
(7)
for all values of l, m, n.
Next, taking a fixed origin Ω and axes parallel to Ox, Oy, Oz
through O, and denoting by x, y, z the coordinates of O, and by G
the component angular momentum about Ω in the direction (l, m, n)
G = l (y1 − x2z + x3y)
+ m (y2 − x3x + x1z)
+ n (y3 − x1y + x2x).
|
(8)
Differentiating with respect to t, and afterwards moving the fixed
origin up to the moving origin O, so that
| x = y = z = 0, but | dx |
= U, | dy |
= V, | dz |
= W, |
| dt | dt |
dt |
| dG |
= l ( | dy1 |
− y2R + y3Q − x2W + x3V ) |
| dt | dt |
| + m ( | dy2 |
− y3P + y1R − x3U + x1W ) |
| dt |
| + n ( | dy3 |
− y1Q + y2P − x1V + x2U ) |
| dt |
= lL + mM + nN,
(9)
for all values of l, m, n.
When no external force acts, the case which we shall consider, there
are three integrals of the equations of motion
(i.) T = constant,
(ii.) x12 + x22+ x32 = F2, a constant,
(iii.) x1y1 + x2y2 + x3y3 = n = GF, a constant;
and the dynamical equations in (3) express the fact that x1, x2, x3
are the components of a constant vector having a fixed direction;
while (4) shows that the vector resultant of y1, y2, y3 moves as if
subject to a couple of components
x2W − x3V, x3U − x1W, x1V − x2U,
(10)
and the resultant couple is therefore perpendicular to F, the resultant
of x1, x2, x3, so that the component along OF is constant, as
expressed by (iii).
If a fourth integral is obtainable, the solution is reducible to a
quadrature, but this is not possible except in a limited series of cases,
investigated by H. Weber, F. Kötter, R. Liouville, Caspary,
Jukovsky, Liapounoff, Kolosoff and others, chiefly Russian mathematicians;
and the general solution requires the double-theta
hyperelliptic function.
49. In the motion which can be solved by the elliptic function, the
most general expression of the kinetic energy was shown by A.
Clebsch to take the form
T = ½p (x12 + x22) + ½p′x32
+ q (x1y1 + x2y2) + q′x3y3
+ ½r (y12 + y22) + ½r′y32
|
(1)
so that a fourth integral is given by
dy3 / dt = 0, y3 = constant;
(2)
| dx3 |
= x1 (qx2 + ry2) − x2 (qx1 + ry1) = r (x1y2 − x2y1), |
| dt |
(3)
| 1 |
( | dx3 |
) | 2 |
= (x12 + x22) (y12 + y22) − (x1y1 + x2y2)2 |
| r2 | dt |
|
= (x12 + x22) (y12 + y22) − (FG − x3y3)2
= (x12 + x22) (y12 + y22 + y32 − G2) − (Gx3 − Fy3)2,
|
(4)
in which
x12 + x22 = F2 − x32, x1y1 + x2y2 = FG − x3y3,
(5)
r (y12 + y22) = 2T − p(x12 + x22) − p′x32
− 2q (x1y1 + x2y2) − 2q′x3y3 − r′y32
= (p − p′) x32 + 2 (q − q′) x3y3 + m1,
|
(6)
m1 − 2T − pF2 − 2qFG − r1y32
(7)
so that
(8)
where X3 is a quartic function of x3, and thus t is given by an elliptic
133
integral of the first kind; and by inversion x3 is in elliptic function
of the time t. Now
(x1 − x2i) (y1 + y2i) = x1y1 + x2y2 + i (x1y2 − x2y1)
= FG − xy3y3 + i √ X3,
(9)
| y1 + y2i |
= | FG − x3y3 + i √ X3 |
, |
| x1 + x2i | x12 + x22 |
(10)
| d |
(x1 + x2i) = −i [ (q′ − q) x3 + r′y3 ] + irx3 (y1 + y2i), |
| dt |
(11)
| d |
log (x1 + x2i) = −(q′ − q) x3 − r′y3 + rx3 | FG − x3y3 + i √ X3 |
, |
| dti | F2 − x32 |
(12)
| d |
log √ | x1 + x2i |
= −(q′ − q) x3 − (r′ − r) y3 − Fr | Fy3 − Gx3 |
, |
| dti | x1 − x2i |
F2 − x32 |
(13)
requiring the elliptic integral of the third kind; thence the expression
of x1 + x2i and y1 + y2i.
Introducing Euler’s angles θ, φ, ψ,
x1 = F sin θ sin φ, x2 = F sin θ cos φ,
x1 + x2i = iF sin θε−ψi, x3 = F cos θ;
|
(14)
| sin θ | dψ |
= P sin φ + Q cos φ, |
| dt |
(15)
| F sin2 θ | dψ |
= | dT |
x1 + | dT |
x2 |
| dt | dy1 |
dy2 |
= (qx1 + ry1) x1 + (qx2 + ry2) x2
= q (x12 + x22) + r (x1y1 + x2y2)
= gF2 sin2 θ + r (FG − x3y3),
|
(16)
| ψ − qFt = ∫ | FG − x3y3 |
| Fr dx3 |
, |
| F2 − x32 | √ X3 |
(17)
elliptic integrals of the third kind.
Employing G. Kirchhoff’s expressions for X, Y, Z, the coordinates
of the centre of the body,
FX = y1 cos xY + y2 cos yY + y3 cos zY,
(18)
FY = −y1 cos xX + y2 cos yX + y3 cos zX,
(19)
G = y1 cos xZ + y2 cos yZ + y3 cos zZ,
(20)
F2(X2 + Y2) = y12 + y22 + y32 − G2,
(21)
| F(X + Yi) = | Fy3 − Gx3 + i √ X3 |
εψi. |
| √ (F2 − x32) |
(22)
Suppose x3 − F is a repeated factor of X3, then y3 = G, and
| X3 = (x3 − F)2 [ | p′ − p |
(x3 + F)2 + 2 | q′ − q |
G (x3 + F) − G2 ], |
| r | r |
(23)
and putting x3 − F = y,
| ( | dy |
) | 2 |
= r2y2 [ 4 | p′ − p |
F2 + 4 | q′ − q |
FG − G2 + 2 ( 2 | p′ − p |
F + | q′ − q |
G ) y + | p′ − p |
y2 ], |
| dt | |
r | r |
r | r |
r |
(24)
so that the stability of this axial movement is secured if
| A = 4 | p′ − p |
F2 + 4 | q′ − q |
FG − G2 |
| r | r |
(25)
is negative, and then the axis makes r√(-A)/π nutations per second.
Otherwise, if A is positive
| rt = ∫ | dy |
| y √ (A + 2By + Cy2) |
| = | 1 |
| sh−1 |
| √ A √ (A + 2By + Cy2) |
= | 1 |
| ch−1 |
| A + By |
, |
| √ A | ch−1 |
y√ (B2 ~ AC) | √A |
sh−1 | y √ (B2 ~ AC) |
(26)
and the axis falls away ultimately from its original direction.
A number of cases are worked out in the American Journal of
Mathematics (1907), in which the motion is made algebraical by the
use of the pseudo-elliptic integral. To give a simple instance,
changing to the stereographic projection by putting tan ½θ = x,
(Nx eψi)3/2 = (x + 1) √ X1 + i (x − 1) √ X2,
(27)
| X1 |
= ± ax4 + 2ax3 ± 3 (a + b) x2 + 2bx ± b, |
| X2 |
(28)
N3 = −8 (a + b),
(29)
will give a possible state of motion of the axis of the body; and the
motion of the centre may then be inferred from (22).
50. The theory preceding is of practical application in the
investigation of the stability of the axial motion of a submarine
boat, of the elongated gas bag of an airship, or of a spinning rifled
projectile. In the steady motion under no force of such a body in
a medium, the centre of gravity describes a helix, while the axis
describes a cone round the direction of motion of the centre of
gravity, and the couple causing precession is due to the displacement
of the medium.
In the absence of a medium the inertia of the body to translation
is the same in all directions, and is measured by the
weight W, and under no force the C.G. proceeds in a straight
line, and the axis of rotation through the C.G. preserves its
original direction, if a principal axis of the body; otherwise
the axis describes a cone, right circular if the body has uniaxial
symmetry, and a Poinsot cone in the general case.
But the presence of the medium makes the effective inertia
depend on the direction of motion with respect to the external
shape of the body, and on W′ the weight of fluid medium displaced.
Consider, for example, a submarine boat under water; the inertia
is different for axial and broadside motion, and may be represented
by
c1 = W + W′α, c2 = W + W′β,
(1)
where α, β are numerical factors depending on the external shape;
and if the C.G. is moving with velocity V at an angle φ with the axis,
so that the axial and broadside component of velocity is u = V cos φ,
v = V sin φ, the total momentum F of the medium, represented by
the vector OF at an angle θ with the axis, will have components,
expressed in sec. ℔,
| F cos θ = c1 | u |
= (W + W′α) | V |
cos φ, F sin θ = c2 | v |
= (W + W′β) | V |
. |
| g | g |
g | g |
(2)
Suppose the body is kept from turning as it advances; after t
seconds the C.G. will have moved from O to O′, where OO′ = Vt;
and at O′ the momentum is the same in magnitude as before, but
its vector is displaced from OF to O′F′.
For the body alone the resultant of the components of momentum
| W | V |
cos φ and W | V |
sin φ is W | V |
sec. ℔, |
| g | g |
g |
(3)
acting along OO′, and so is unaltered.
But the change of the resultant momentum F of the medium as
well as of the body from the vector OF to O′F′ requires an impulse
couple, tending to increase the angle FOO′, of magnitude, in sec.
foot-pounds
F·OO′·sin FOO′ = FVt sin (θ − φ),
(4)
equivalent to an incessant couple
N = FV sin (θ − φ)
= (F sin θ cos φ − F cos θ sin φ) V
= (c2 − c1) (V2 / g) sin φ cos φ
= W′ (β − α) uv / g.
|
(5)
This N is the couple in foot-pounds changing the momentum of the
medium, the momentum of the body alone remaining the same; the
medium reacts on the body with the same couple N in the opposite
direction, tending when c2 − c1 is positive to set the body broadside
to the advance.
An oblate flattened body, like a disk or plate, has c2 − c1 negative,
so that the medium steers the body axially; this may be verified by a
plate dropped in water, and a leaf or disk or rocket-stick or piece of
paper falling in air. A card will show the influence of the couple N if
projected with a spin in its plane, when it will be found to change its
aspect in the air.
An elongated body like a ship has c2 − c1 positive, and the couple N
tends to disturb the axial movement and makes it unstable, so that
a steamer requires to be steered by constant attention at the helm.
Consider a submarine boat or airship moving freely with the
direction of the resultant momentum horizontal, and the axis at a
slight inclination θ. With no reserve of buoyancy W = W′, and the
couple N, tending to increase θ, has the effect of diminishing the
metacentric height by h ft. vertical, where
| Wh tan θ = N = (c2 − c1) | c1 |
| u2 |
tan θ, |
| c2 | g |
(6)
| h = | c2 − c1 |
| c1 |
| u2 |
= (β − α) | 1 + α |
| u2 |
. |
| W | c2 |
g | 1 + β |
g |
(7)
51. An elongated shot is made to preserve its axial flight
through the air by giving it the spin sufficient for stability,
without which it would turn broadside to its advance; a top in
the same way is made to stand upright on the point in the
position of equilibrium, unstable statically but dynamically
stable if the spin is sufficient; and the investigation proceeds in
the same way for the two problems (see Gyroscope).
The effective angular inertia of the body in the medium is now
required; denote it by C1 about the axis of the figure, and by C2 about
a diameter of the mean section. A rotation about the axis of a
figure of revolution does not set the medium in motion, so that C1 is
the moment of inertia of the body about the axis, denoted by Wk12.
But if Wk22 is the moment of inertia of the body about a mean
diameter, and ω the angular velocity about it generated by an impulse
couple M, and M′ is the couple required to set the surrounding medium
in motion, supposed of effective radius of gyration k′,
Wk22ω = M − M′, W′k′2ω = M′,
(1)
(Wk22 + W′k′2) ω = M,
(2)
C2 = Wk22 + W′k′2 = (W + W′ε) k22,
(3)
in which we have put k′2 = εk2, where ε is a numerical factor depending
on the shape.
134
If the shot is spinning about its axis with angular velocity p, and
is preceding steadily at a rate μ about a line parallel to the resultant
momentum F at an angle θ, the velocity of the vector of angular
momentum, as in the case of a top, is
C1pμ sinθ − C2μ2 sin θ cos θ;
(4)
and equating this to the impressed couple (multiplied by g), that is, to
| gN = (c1 − c2) | c1 |
u2 tan θ, |
| c2 |
(5)
and dividing out sin θ, which equated to zero would imply perfect
centring, we obtain
| C2μ2 cos θ − C1pμ + (c2 − c1) | c1 |
u2 sec θ = 0. |
| c2 |
(6)
The least admissible value of p is that which makes the roots equal
of this quadratic in μ, and then
(7)
the roots would be imaginary for a value of p smaller than given by
| C12p2 − 4 (c2 − c1) | c1 |
C2u2 = 0, |
| c2 |
(8)
| p2 |
= 4 (c2 − c1) | c1 |
| C2 |
. |
| u2 | c2 |
C12 |
(9)
Table of Rifling for Stability of an Elongated Projectile, x Calibres long, giving δ the Angle of
Rifling, and n the Pitch of Rifling in Calibres.
| | Cast-iron Common Shell
ƒ = 2⁄3, S.G. 7.2. |
Palliser Shell
ƒ = ½, S.G. 8. |
Solid Steel Bullet
ƒ = 0, S.G. 8. |
Solid Lead Bullet
ƒ = 0, S.G. 10.9. |
| x | β − α | δ | n | δ | n | δ | n | δ | n |
| 1.0 | 0.0000 | 0° 0′ | Infinity | 0° 0′ | Infinity | 0° 0′ | Infinity | 0° 0′ | Infinity |
| 2.0 | 0.4942 | 2 49 | 63.87 | 2 32 | 71.08 | 2 29 | 72.21 | 2 08 | 84.29 |
| 2.5 | 0.6056 | 3 46 | 47.91 | 3 23 | 53.32 | 3 19 | 54.17 | 2 51 | 63.24 |
| 3.0 | 0.6819 | 4 41 | 38.45 | 4 13 | 42.79 | 4 09 | 43.47 | 3 38 | 50.74 |
| 3.5 | 0.7370 | 5 35 | 32.13 | 5 02 | 35.75 | 4 58 | 36.33 | 4 15 | 42.40 |
| 4.0 | 0.7782 | 6 30 | 27.60 | 5 51 | 30.72 | 5 45 | 31.21 | 4 56 | 36.43 |
| 4.5 | 0.8100 | 7 24 | 24.20 | 6 40 | 26.93 | 6 32 | 27.36 | 5 37 | 31.94 |
| 5.0 | 0.8351 | 8 16 | 21.56 | 7 28 | 23.98 | 7 21 | 24.36 | 6 18 | 28.44 |
| 6.0 | 0.8721 | 10 05 | 17.67 | 9 04 | 19.67 | 8 56 | 19.98 | 7 40 | 23.33 |
| 10.0 | 0.9395 | 16 57 | 10.31 | 15 19 | 11.47 | 15 05 | 11.65 | 13 00 | 13.60 |
| Infinity | 1.0000 | 90 00 | 0.00 | 90 00 | 0.00 | 90 00 | 0.00 | 90 00 | 0.00 |
If the shot is moving as if fired from a gun of calibre d inches, in
which the rifling makes one turn in a pitch of n calibres or nd inches,
so that the angle δ of the rifling is given by
tan δ = πd / nd = ½ dp / u,
(10)
which is the ratio of the linear velocity of rotation ½dp to u, the
velocity of advance,
| tan2 δ = | π2 |
= | d2p2 |
= (c2 − c1) | c1 |
| C2d2 |
| n2 | 4u2 |
c2 | C12 |
| = | W′ |
(β − α) | |
· |
| ( 1 + | W′ |
ε ) ( | k1 |
) | 2 |
| W | d |
| |
. |
| W |
|
|
(11)
For a shot in air the ratio W′/W is so small that the square may
be neglected, and formula (11) can be replaced for practical purpose
in artillery by
| tan2 δ = | π2 |
= | W′ |
(β − α) ( | k2 |
) | 2 |
/ ( | k1 |
) | 4 |
, |
| n2 | W |
d | |
d | |
(12)
if then we can calculate β, α, or β − α for the external shape of the
shot, this equation will give the value of δ and n required for stability
of flight in the air.
The ellipsoid is the only shape for which α and β have so far been
determined analytically, as shown already in § 44, so we must restrict
our calculation to an egg-shaped bullet, bounded by a prolate
ellipsoid of revolution, in which, with b = c,
| A0 = ∫∞0 | ab2 dλ |
= ∫∞0 | ab2 dλ |
, |
| (a2 + λ) √ [ 4 (a2 + λ) (b2 + λ)2 ] | 2 (a2 + λ)3/2 (b2 + λ) |
(13)
A0 + 2B0 = 1,
(14)
| a = | A0 |
, β = | B0 |
= | 1 − A0 |
= | 1 |
. |
| 1 − A0 | 1 − B0 |
1 + A0 | 1 + 2α |
(15)
The length of the shot being denoted by l and the calibre by d, and
the length in calibres by x
l / d = 2a / 2b = x,
(16)
| A0 = | x |
ch−1x − | 1 |
, |
| (x2− 1)3/2 | x2 − 1 |
(17)
| 2B0 = | − x |
ch−1x + | x2 |
, |
| (x2 − 1)3/2 | x2 + 1 |
(18)
| x2A0 + 2B0 = | x sh−1 √ (x2 − 1) |
= | x |
log [ x + √ (x2 − 1) ]. |
| √ (x2 − 1) | √ (x2 − 1) |
(19)
If σ denotes the density of the metal, and if the shell has a cavity
homothetic with the external ellipsoidal shape, a fraction f of the
linear scale; then the volume of a round shot being 1⁄6 π d3, and
1⁄6 π d3 x of a shot x calibres long
W = 1⁄6 πd3 x (i − ƒ3) σ,
(20)
| Wk12 = 1⁄6 πd3 x | d2 |
(1 − ƒ5) σ, |
| 10 |
(21)
| Wk22 = 1⁄6 πd3 x | l2 + d2 |
(1 − ƒ5) σ. |
| 20 |
(22)
If ρ denotes the density of the air or medium
W′ = 1⁄6 πd3 xρ,
(23)
(24)
| k12 |
= | 1 |
| 1 − ƒ5 |
, | k22 |
= | x2 + 1 |
, |
| d2 | 10 |
1 − ƒ3 | k12 |
2 |
(25)
| tan2 δ = | ρ |
(β − α) | x2 + 1 |
, |
| σ | 1⁄5 (1 − ƒ5) |
(26)
in which σ/ρ may be replaced by 800 times the S.G. of the metal,
taking water as 800 times denser than air on the average, in
round numbers, and formula (10) may be written n tan δ = π, or
nδ = 180, when δ is a small angle, and given in degrees.
From this formula (26) the table following has been calculated
by A. G. Hadcock, and the results are in agreement with practical
experience.
52. In the steady motion the centre of the shot describes a helix,
with axial velocity
| u cos θ = v sin θ = ( l + | c1 |
tan2 θ ) u cos θ ≈ u sec θ, |
| c2 |
(1)
and transverse velocity
| u sin θ − v cos θ = ( l − | c1 |
) u sin θ ≈ (β − α) u sin θ; |
| c2 |
(2)
and the time of completing a turn of the spiral is 2π/μ.
When μ has the critical value in (7),
| 2π |
= | 4π |
| C2 |
cos θ = | 2π |
(x2 + 1) cos θ, |
| μ | p |
C1 | p |
(3)
which makes the circumference of the cylinder on which the helix
is wrapped
| 2π |
(u sin θ − v cos θ = | 2πu |
(β − α) (x2 + 1) sin2 θ cos θ |
| μ | p |
= nd (β − α) (x2 + 1) sin θ cos θ,
(4)
and the length of one turn of the helix
| 2π |
(u cos θ + v sin θ) = nd (x2 + 1); |
| μ |
(5)
thus for x = 3, the length is 10 times the pitch of the rifling.
53. The Motion of a Perforated Solid in Liquid.—In the preceding
investigation, the liquid stops dead when the body is brought to rest;
and when the body is in motion the surrounding liquid moves in a
uniform manner with respect to axes fixed in the body, and the
force experienced by the body from the pressure of the liquid on its
surface is the opposite of that required to change the motion of the
liquid; this has been expressed by the dynamical equations given
above. But if the body is perforated, the liquid can circulate through
a hole, in reentrant stream lines linked with the body, even while
the body is at rest; and no reaction from the surface can influence
this circulation, which may be supposed started in the ideal manner
described in § 29, by the application of impulsive pressure across an
ideal membrane closing the hole, by means of ideal mechanism
connected with the body. The body is held fixed, and the reaction
of the mechanism and the resultant of the impulsive pressure on the
surface are a measure of the impulse, linear ξ, η, ζ, and angular
λ, μ, ν, required to start the circulation.
135
This impulse will remain of constant magnitude, and fixed
relatively to the body, which thus experiences an additional reaction
from the circulation which is the opposite of the force required to
change the position in space of the circulation impulse; and these
extra forces must be taken into account in the dynamical equations.
An article may be consulted in the Phil. Mag., April 1893, by
G. H. Bryan, in which the analytical equations of motion are
deduced of a perforated solid in liquid, from considerations purely
hydrodynamical.
The effect of an external circulation of vortex motion on the
motion of a cylinder has been investigated in § 29; a similar procedure
will show the influence of circulation through a hole in a solid,
taking as the simplest illustration a ring-shaped figure, with uniplanar
motion, and denoting by ξ the resultant axial linear
momentum of the circulation.
As the ring is moved from O to O′ in time t, with velocity Q, and
angular velocity R, the components of liquid momentum change
from
αM′U + ξ and βM′V along Ox and Oy
to
αM′U′+ ξ and βM′V′ along O′x′ and O′y′,
(1)
the axis of the ring changing from Ox to O′x′; and
U = Q cos θ, V = Q sin θ,
U′ = Q cos (θ − Rt), V′ = Q sin (θ − Rt),
|
(2)
so that the increase of the components of momentum, X1, Y1, and N1,
linear and angular, are
X1 = (αM′U′ + ξ) cos Rt − αM′U − ξ − βM′V′ sin Rt
=(α − β)M′Q sin (θ − Rt) sin Rt − ξ ver Rt
|
(3)
Y1 = (αM′U′ + ξ) sin Rt + βM′V′ cos Rt − βM′V
= (α − β) M′Q cos (θ − Rt) sin Rt + ξ sin RT,
|
(4)
N1 = [ −(αM′U′ + ξ) sin (θ − Rt) + βM′V′ cos (θ − Rt) ] OO′
= [ −(α − β) M′Q cos (θ − Rt) sin (θ − Rt) − ξ sin (θ − Rt) ] Qt.
|
(5)
The components of force, X, Y, and N, acting on the liquid at O,
and reacting on the body, are then
X = lt. X1/t = (α − β) M′QR sin θ = (α − β) M′VR,
(6)
Y = lt. Y1/t = (α − β) M′QR cos θ + ξR = (α − β) M′UR + ξR,
(7)
Z = lt. Z1/t = −(α − β) M′Q2 sin θ cos θ − ξQ sin θ
= [ −(α − β) M′U + ξ ] V.
(8)
Now suppose the cylinder is free; the additional forces acting on
the body are the components of kinetic reaction of the liquid
| −αM′ ( | dU |
− VR ), −βM′ ( | dV |
+ UR ), εC′ | dR |
, |
| dt | dt |
dt |
(9)
so that its equations of motion are
| M ( | dU |
− VR ) = −αM′ ( | dU |
− VR ) − (α − β) M′VR, |
| dt | dt |
(10)
| M ( | dV |
+ UR ) = −βM′ ( | dV |
+ UR ) − (α − β) M′UR − ξR, |
| dt | dt |
(11)
| C | dR |
= −εC′ | dR |
+ (α − β) M′UV + ξV; |
| dt | dt |
(12)
and putting as before
M + αM′ = c1, M + βM′ = c2, C + εC′ = C3,
(13)
(14)
| c2 | dV |
+ (c1U + ξ) R = 0, |
| dt |
(15)
| c3 | dR |
− (c1U + ξ − c2U) V = 0; |
| dt |
(16)
showing the modification of the equations of plane motion, due to
the component ξ of the circulation.
The integral of (14) and (15) may be written
c1U + ξ = F cos θ, c2V = − F sin θ,
(17)
| dx |
= U cos θ − V sin θ = | F cos2 θ |
+ | F sin2 θ |
− | ξ |
cos θ, |
| dt | c1 |
c2 | c1 |
(18)
| dμ |
= U sin θ + V cos θ = ( | F |
− | F |
) sin θ cos θ − | ξ |
sin θ, |
| dt | c1 |
c2 | c1 |
(19)
| C3 | d2θ |
= ( | F2 |
− | F2 |
) sin θ cos θ − | Fξ |
sin θ = F | dμ |
, |
| dt2 | c1 |
c2 | c1 |
dt |
(20)
| C3 | dθ |
= Fy = √ [ − | F2 cos2 θ |
− | F2 sin2 θ |
+ 2 | Fξ |
cos θ + H ]; |
| dt | c1 |
c2 | c1 |
(21)
so that cos θ and y is an elliptic function of the time.
When ξ is absent, dx/dt is always positive, and the centre of the
body cannot describe loops; but with ξ, the influence may be great
enough to make dx/dt change sign, and so loops occur, as shown in
A. B. Basset’s Hydrodynamics, i. 192, resembling the trochoidal
curves, which can be looped, investigated in § 29 for the motion of
a cylinder under gravity, when surrounded by a vortex.
The branch of hydrodynamics which discusses wave motion in a
liquid or gas is given now in the articles Sound and Wave; while
the influence of viscosity is considered under Hydraulics.
References.—For the history and references to the original
memoirs see Report to the British Association, by G. G. Stokes (1846),
and W. M. Hicks (1882). See also the Fortschritte der Mathematik,
and A. E. H. Love, “Hydrodynamik” in the Encyklöpadie der
mathematischen Wissenschaften (1901).
(A. G. G.)
HYDROMEDUSAE, a group of marine animals, recognized
as belonging to the Hydrozoa (q.v.) by the following characters.
(1) The polyp (hydropolyp) is of simple structure, typically much
longer than broad, without ectodermal oesophagus or mesenteries,
such as are seen in the anthopolyp (see article Anthozoa); the
mouth is usually raised above the peristome on a short conical
elevation or hypostome; the ectoderm is without cilia.
(2) With very few exceptions, the polyp is not the only type of
individual that occurs, but alternates in the life-cycle of a given
species, with a distinct type, the medusa (q.v.), while in other
cases the polyp-stage may be absent altogether, so that only
medusa-individuals occur in the life-cycle.
The Hydromedusae represent, therefore, a sub-class of the
Hydrozoa. The only other sub-class is the Scyphomedusae
(q.v.). The Hydromedusae contrast with the Scyphomedusae
in the following points. (1) The polyp, when present, is without
the strongly developed longitudinal retractor muscles, forming
ridges (taeniolae) projecting into the digestive cavity, seen in the
scyphistoma or scyphopolyp. (2) The medusa, when present,
has a velum and is hence said to be craspedote; the nervous
system forms two continuous rings running above and below
the velum; the margin of the umbrella is not lobed (except
in Narcomedusae) but entire; there are characteristic differences
in the sense-organs (see below, and Scyphomedusae); and
gastral filaments (phacellae), subgenital pits, &c., are absent.
(3) The gonads, whether formed in the polyp or the medusa,
are developed in the ectoderm.
The Hydromedusae form a widespread, dominant and highly
differentiated group of animals, typically marine, and found in
all seas and in all zones of marine life. Fresh-water forms,
however, are also known, very few as regards species or genera,
but often extremely abundant as individuals. In the British
fresh-water fauna only two genera, Hydra and Cordylophora, are
found; in America occurs an additional genus, Microhydra.
The paucity of fresh-water forms contrasts sharply, with the great
abundance of marine genera common in all seas and on every
shore. The species of Hydra, however, are extremely common
and familiar inhabitants of ponds and ditches.
In fresh-water Hydromedusae the life-cycle is usually secondarily
simplified, but in marine forms the life-cycle may be
extremely complicated, and a given species often passes in the
course of its history through widely different forms adapted to
different habitats and modes of life. Apart from larval or
embryonic forms there are found typically two types of person,
as already stated, the polyp and the medusa, each of which may
vary independently of the other, since their environment and
life-conditions are usually quite different. Hence both polyp
and medusa present characters for classification, and a given
species, genus or other taxonomic category may be defined
by polyp-characters or medusa-characters or by both combined.
If our knowledge of the life-histories of these organisms were
perfect, their polymorphism would present no difficulties to
classification; but unfortunately this is far from being the case.
In the majority of cases we do not know the polyp corresponding
to a given medusa, or the medusa that arises from a given polyp.1
Even when a medusa is seen to be budded, from a polyp under
observation in an aquarium, the difficulty is not always solved,
since the freshly-liberated, immature medusa may differ greatly
from the full-grown, sexually-mature medusa after several
months of life on the high seas (see figs. 11, B, C, and 59, a, b, c).
To establish the exact relationship it is necessary not only to
breed but to rear the medusa, which cannot always be done in
136
confinement. The alternative is to fish all stages of the medusa
in its growth in the open sea, a slow and laborious method in
which the chance of error is very great, unless the series of stages
is very complete.
At present, therefore, classifications of the Hydromedusae
have a more or less tentative character, and are liable to revision
with increased knowledge of the life-histories of these organisms.
Many groups bear at present two names, the one representing
the group as defined by polyp-characters, the other as defined
by medusa-characters. It is not even possible in all cases to be
certain that the polyp-group corresponds exactly to the medusa-group,
especially in minor systematic categories, such as families.
The following is the main outline of the classification that is
Adopted in the present article. Groups founded on polyp-characters
are printed in ordinary type, those founded on medusa-characters
in italics. For definitions of the groups see below.
Sub-class Hydromedusae (Hydrozoa Craspedota).
Order I. Eleutheroblastea.
” II. Hydroidea (Leptolinae).
Sub-order 1. Gymnoblastea (Anthomedusae).
” 2. Calyptoblastea (Leptomedusae).
Order III. Hydrocorallinae.
” IV. Graptolitoidea.
” V. Trachylinae.
Sub-order 1. Trachomedusae.
” 2. Narcomedusae.
Order VI. Siphonophora.
Sub-order 1. Chondrophorida.
” 2. Calycophorida.
” 3. Physophorida.
” 4. Cystophorida.
|
Organization and Morphology of the Hydromedusae.
 |
| Fig. 1.—Diagram of a typical
Hydropolyp. |
|
a, Hydranth;
b, Hydrocaulus;
c, Hydrorhiza;
t, Tentacle;
ps, Perisarc, forming in the
region of the hydranth
a cup or hydrotheca(h, t),—which,
however, is only
found in polyps of the
order Calyptoblastea. |
As already stated, there occur in the Hydromedusae two
distinct types of person, the polyp and the medusa; and either
of them is capable of non-sexual reproduction by budding, a
process which may lead to the
formation of colonies, composed
of more or fewer individuals combined
and connected together.
The morphology of the group
thus falls naturally into four
sections—(1) the hydropolyp, (2)
the polyp-colony, (3) the hydromedusa,
(4) the medusa-colonies.
Since, however, medusa-colonies
occur only in one group, the Siphonophora,
and divergent views
are held with regard to the
morphological interpretation of
the members of a siphonophore,
only the first three of the above
subdivisions of hydromedusa
morphology will be dealt with
here in a general way, and the
morphology of the Siphonophora
will be considered under the heading
of the group itself.
1. The Hydropolyp (fig. 1)—The
general characters of this organism
are described above and in the
articles Hydrozoa and Polyp. It
is rarely free, but usually fixed and
incapable of locomotion. The foot
by which it is attached often sends
out root-like processes—the hydrorhiza
(c). The column (b) is generally long, slender and stalk-like
(hydrocaulus). Just below the crown of tentacles, however,
the body widens out to form a “head,” termed, the hydranth (a),
containing a stomach-like dilatation of the digestive cavity. On the
upper face of the hydranth the crown of tentacles (t) surrounds the
peristome, from which rises the conical hypostome, bearing the
mouth at its extremity. The general ectoderm covering the surface
of the body has entirely lost the cilia present in the earlier larval
stages (planula), and may be naked, or clothed in a cuticle or exoskeleton,
the perisarc (ps), which in its simplest condition is a
chitinous membrane secreted by the ectoderm. The perisarc when
present invests the hydrorhiza and hydrocaulus; it may stop short
below the hydranth, or it may extend farther. In general there are
two types of exoskeleton, characteristic of the two principal divisions
of the Hydroidea. In the Gymnoblastea the perisarc either stops
below the hydranth, or, if continued on to it, forms a closely-fitting
investment extending as a thin cuticle as far as the bases of the
tentacles (e.g. Bimeria, see G. J. Allman [1],2 pl. xii. figs, 1 and 3).
In the Calyptoblastea the perisarc is always continued above the
hydrocaulus, and forms a cup, the hydrangium or hydrotheca (h, t),
standing off from the body, into which the hydranth can be retracted
for shelter and protection.
 |
| From Allman’s Gymnoblastic Hydroids, by permission of the Council of the Ray
Society. |
| Fig. 2.—Stauridium productum, portion of the colony magnified;
p, polyp; rh, hydrorhiza. |
 |
| Fig. 3.—Diagram of
Corymorpha. A, A hydriform
person giving rise
to medusiform persons
by budding from the
margin of the disk; B,
free swimming medusa
(Steenstrupia of Forbes)
detached from the same,
with manubrial genitalia,
(Anthomedusae) and only
one tentacle. (After Allman). |
The architecture of the hydropolyp, simple though it be, furnishes a
long series of variations affecting each part of the body. The greatest
variation, however, is seen in the tentacles. As regards number, we
find in the aberrant forms Protohydra and Microhydra tentacles
entirely absent. In the curious hydroid Monobrachium a single
tentacle is present, and the same is the
case in Clathrozoon; in Amphibrachium
and in Lar (fig. 11, A) the polyp bears
two tentacles only. The reduction of
the tentacles in all these forms may be
correlated with their mode of life, and
especially with living in a constant
current of water, which brings food-particles
always from one direction and
renders a complete whorl or circle of
tentacles unnecessary. Thus Microhydra
lives amongst Bryozoa, and appears to
utilize the currents produced by these
animals. Protohydra occurs in oyster-banks
and Monobrachium also grows on
the shells of bivalves, and both these
hydroids probably fish in the currents
produced by the lamellibranchs. Amphibrachium
grows in the tissues of a
sponge, Euplectella, and protrudes its
hydranth into the canal-system of the
sponge; and Lar grows on the tubes of
the worm Sabella. With the exception
of these forms, reduced for the most part
in correlation with a semi-parasitic mode
of life, the tentacles are usually numerous.
It is rare to find in the polyp a regular,
symmetrical disposition of the tentacles
as in the medusa. The primitive number
of four in a whorl is seen, however, in
Stauridium (fig. 2) and Cladonema
(Allman [1], pl. xvii.), and in Clavatella
each whorl consists regularly of eight
(Allman, loc. cit. pl. xviii.). As a rule,
however, the number in a whorl is
irregular. The tentacles may form a
single whorl, or more than one; thus
in Corymorpha (fig. 3) and Tubularia
(fig. 4) there are two circlets; in Stauridium
(fig. 2) several; in Coryne and Cordylophora the tentacles are
scattered irregularly over the elongated hydranth.
 |
| Fig. 4.—Diagram of Tubularia
indivisa. A single hydriform person
a bearing a stalk carrying numerous
degenerate medusiform persons or
sporosacs b. (After Allman.) |
As regards form, the tentacles show a number of types, of which
the most important are (1) filiform, i.e. cylindrical or tapering from
137
base to extremity, as in Clava (fig. 5); (2) capitate, i.e. knobbed
at the extremity, as in Coryne (see Allman, loc. cit. pl. iv.); (3)
branched, a rare form in the polyp, but seen in Cladocoryne (see
Allman, loc. cit. p. 380, fig. 82). Sometimes more than one type of
form is found in the same
polyp; in Pennaria and
Stauridium (fig. 2) the upper
whorls are capitate, the lower
filiform. Finally, as regards
structure, the tentacles may
retain their primitive hollow
nature, or become solid by
obliteration of the axial
cavity.
The hypostome of the
hydropolyp may be small, or,
on the other hand, as in
Eudendrium (Allman, loc. cit.
pls. xiii., xiv.), large and
trumpet-shaped. In the
curious polyp Myriothela the
body of the polyp is differentiated
into nutritive and
reproductive portions.
Histology.—The ectoderm
of the hydropolyp is chiefly
sensory, contractile and protective
in function. It may
also be glandular in places. It consists of two regions, an external
epithelial layer and a more internal sub-epithelial layer.
The epithelial layer consists of (1) so-called “indifferent” cells
secreting the perisarc or cuticle and modified to form glandular cells
in places; for example, the adhesive cells in the foot. (2) Sensory
cells, which may be fairly numerous in places, especially on the
tentacles, but which occur always scattered and isolated, never
aggregated to form sense-organs as in the medusa. (3) Contractile
or myo-epithelial cells, with the cell prolonged at the base into a
contractile muscle-fibre (fig. 6, B). In the hydropolyp the ectodermal
muscle-fibres are always directed longitudinally. Belonging primarily
to the epithelial layer, the muscular cells may become secondarily
sub-epithelial.
 |
| From Allman’s Gymnoblastic Hydroids, by permission of the Council of the Ray
Society. |
| Fig. 5.—Colonies of Clava. A, Clava squamata, magnified. B,
C. multicornis, natural size; p, polyp; gon, gonophores; rh,
hydrorhiza. |
The sub-epithelial layer consists primarily of the so-called interstitial
cells, lodged between the narrowed basal portions of the
epithelial cells. From them are developed two distinct types of
histological elements; the genital cells and the cnidoblasts or mother-cells
of the nematocysts. The sub-epithelial layer thus primarily
constituted may be recruited by immigration from without of other
elements, more especially by nervous (ganglion) cells and muscle-cells
derived from the epithelial layer. In its fullest development,
therefore, the sub-epithelial layer consists of four classes of
cell-elements.
 |
| Fig. 6 A.—Portion of the body-wall of Hydra, showing ectoderm
cells above, separated by “structureless lamella” from three
flagellate endoderm cells below. The latter are vacuolated, and
contain each a nucleus and several dark granules. In the middle
ectoderm cell are seen a nucleus and three nematocysts, with
trigger hairs projecting beyond the cuticle. A large nematocyst,
with everted thread, is seen in the right-hand ectodermal cell.
(After F. E. Schulze.) |
The genital cells are simple wandering cells (archaeocytes), at first
minute and without any specially distinctive features, until they
begin to develop into germ-cells. According to Wulfert [60] the
primitive germ-cells of Gonothyraea can be distinguished soon after
the fixation of the planula, appearing amongst the interstitial cells
of the ectoderm. The germ-cells are capable of extensive migrations,
not only in the body of the same polyp, but also from parent to bud
through many non-sexual generations of polyps in a colony (A.
Weismann [58]).
 |
| Fig. 6 B.—Epidermo-muscular
cells of Hydra. m, muscular-fibre
processes. (After Kleinenberg,
from Gegenbaur.) |
 |
| Fig. 7.—Diagrams to show the structure
of Nematocysts and their mode of
working. (After Iwanzov.) |
a, Undischarged nematocyst.
b, Commencing discharge.
c, Discharge complete.
cn, Cnidocil.
N, Nucleus of cnidoblast.
o.c, Outer capsule.
x, Plug closing the opening of the outer capsule.
i.c., Inner capsule, continuous with the
wall of the filament, f.
b, Barbs. |
The cnidoblasts are the mother-cells of the nematocysts, each
cell producing one nematocyst in its interior. The complete nematocyst
(fig. 7) is a spherical or oval capsule containing a hollow thread,
usually barbed, coiled in its interior. The capsule has a double wall,
an outer one (o.c.), tough and rigid
in nature, and an inner one (i.c.)
of more flexible consistence. The
outer wall of the capsule is incomplete
at one pole, leaving an
aperture through which the thread
is discharged. The inner membrane
is continuous with the wall
of the hollow thread at a spot immediately
below the aperture in the
outer wall, so that the thread itself
(f) is simply a hollow prolongation
of the wall of the inner capsule inverted and pushed into its cavity.
The entire nematocyst is enclosed in the cnidoblast which formed
it. When the nematocyst is completely developed, the cnidoblast
passes outwards so as to occupy a superficial position in the ectoderm,
and a delicate protoplasmic process of sensory nature, termed the
cnidocil (cn) projects from the cnidoblast like a fine hair or cilium.
Many points in the development and mechanism of the nematocyst
are disputed, but it is tolerably certain (1) that the cnidocil is of
sensory nature, and that stimulation, by contact with prey or in other
ways, causes a reflex discharge of the nematocyst; (2) that the discharge
is an explosive change whereby the in-turned thread is
suddenly everted and turned inside out, being thus shot through the
opening in the outer wall of the capsule, and forced violently into
the tissues of the prey, or, it may be, of an enemy; (3) that the thread
inflicts not merely a mechanical wound, but instils an irritant poison,
numbing and paralysing in its action. The points most in dispute
are, first, how the explosive discharge is brought about, whether
by pressure exerted external to the capsule (i.e. by contraction of
the cnidoblast) or by internal pressure. N. Iwanzov [27] has brought
forward strong grounds for the latter view, pointing out that the
cnidoblast has no contractile mechanism and that measurements
show discharged capsules to be on the average slightly larger than
undischarged ones. He believes that the capsule contains a substance
which swells very rapidly when brought into contact with
water, and that in the undischarged condition the capsule has its
opening closed by a plug of protoplasm (x, fig. 7) which prevents
138
access of water to the contents; when the cnidocil is stimulated it
sets in action a mechanism or perhaps a series of chemical changes
by which the plug is dissolved or removed; as a result water penetrates
into the capsule and causes its contents to swell, with the
result that the thread is
everted violently. A
second point of dispute
concerns the spot at which
the poison is lodged.
Iwanzov believes it to be
contained within the
thread itself before discharge,
and to be introduced
into the tissues of
the prey by the eversion
of the thread. A third
point of dispute is whether
the nematocysts are
formed in situ, or whether
the cnidoblasts migrate
with them to the region
where they are most
needed; the fact that in
Hydra, for example, there
are no interstitial cells in
the tentacles, where nematocysts
are very abundant,
is certainly in favour of
the view that the cnidoblasts
migrate on to the
tentacles from the body,
and that like the genital
cells the cnidoblasts are
wandering cells.
The muscular tissue
consists primarily of processes
from the bases of
the epithelial cells, processes
which are contractile
in nature and may be
distinctly striated. A
further stage in evolution
is that the muscle-cells
lose their connexion with
the epithelium and come
to lie entirely beneath it,
forming a sub-epithelial
contractile layer, developed
chiefly in the tentacles
of the polyp. The
evolution of the ganglion-cells,
is probably similar;
an epithelial cell develops
processes of nervous nature
from the base, which come
into connexion with the
bases of the sensory cells, with the muscular cells, and with the
similar processes of other nerve-cells; next the nerve-cell loses
its connexion with the outer epithelium and becomes a sub-epithelial
ganglion-cell which is closely connected with the muscular layer,
conveying stimuli from the sensory cells to the contractile elements.
The ganglion-cells of Hydromedusae are generally very small.
In the polyp the nervous tissue
is always in the form of a
scattered plexus, never concentrated
to form a definite
nervous system as in the medusa.
 |
| From Gegenbaur’s Elements of Comparative
Anatomy. |
| Fig. 8.—Vacuolated Endoderm
Cells of cartilaginous
consistence from the axis of the
tentacle of a Medusa (Cunina). |
The endoderm of the polyp is
typically a flagellated epithelium
of large cells (fig. 6), from the bases
of which arise contractile muscular
processes lying in the plane of
the transverse section of the body.
In different parts of the coelenteron
the endoderm may be of
three principal types—(1)
digestive endoderm, the primitive
type, with cells of large
size and considerably vacuolated, found in the hydranth; some
of these cells may become special glandular cells, without
flagella or contractile processes; (2) circulatory endoderm, without
vacuoles and without basal contractile processes, found in the hydrorhiza
and hydrocaulus; (3) supporting endoderm (fig. 8), seen in solid
tentacles as a row of cubical vacuolated cells, occupying the axis
of the tentacle, greatly resembling notochordal tissue, particularly
that of Amphioxus at a certain stage of development; as a fourth
variety of endodermal cells excretory cells should perhaps be reckoned,
as seen in the pores in the foot of Hydra and elsewhere (cf. C. Chun,
Hydrozoa [1], pp. 314, 315).
The mesogloea in the hydropolyp is a thin elastic layer, in which
may be lodged the muscular fibres and ganglion cells mentioned above,
but which never contains any connective tissue or skeletogenous
cells or any other kind of special mesogloeal corpuscles.
 |
| From Allman’s Gymnoblastic Hydroids, by permission of
the Council of the Ray Society. |
| Fig. 9.—Colony of Hydractinia echinata, growing
on the Shell of a Whelk. Natural size. |
 |
| From Allman’s Gymnoblastic Hydroids,
by permission of the Council of the Ray
Society. |
| Fig. 10.—Polyps from a Colony
of Hydractinia, magnified. dz,
dactylozoid; gz, gastrozoid: b,
blastostyle; gon, gonophores;
rh, hydrorhiza. |
2. The Polyp-colony.—All known hydropolyps possess the power
of reproduction by budding, and the buds produced may become
either polyps or
medusae. The
buds may all become
detached
after a time and
give rise to
separate and independent
individuals,
as in the
common Hydra,
in which only
polyp-individuals
are produced and
sexual elements
are developed
upon the polyps
themselves; or,
on the other
hand, the polyp-individuals produced by budding may remain
permanently in connexion with the parent polyp, in which case
sexual elements are never developed on polyp-individuals but
only on medusa-individuals, and a true colony is formed. Thus
the typical hydroid colony starts from a “founder” polyp, which
in the vast majority of cases is fixed, but which may be floating, as in
Nemopsis, Pelagohydra, &c. The founder-polyp usually produces by
budding polyp-individuals, and these in their turn produce other
buds. The polyps are all non-sexual individuals whose function
is purely nutritive. After a time the polyps, or certain of them,
produce by budding medusa-individuals, which sooner or later
develop sexual elements; in some cases, however, the founder-polyp
remains solitary, that is
to say, does not produce polyp-buds,
but only medusa-buds,
from the first (Corymorpha, fig. 3,
Myriothela, &c.). In primitive
forms the medusa-individuals
are set free before reaching
sexual maturity and do not contribute
anything to the colony.
In other cases, however, the
medusa-individuals become
sexually mature while still attached
to the parent polyp, and
are then not set free at all, but
become appanages of the hydroid
colony and undergo degenerative
changes leading to reduction and
even to complete obliteration of
their original medusan structure.
In this way the hydroid colony
becomes composed of two portions
of different function, the
nutritive “trophosome,” composed
of non-sexual polyps, and
the reproductive “gonosome,”
composed of sexual medusa-individuals,
which never exercise
a nutritive function while attached
to the colony. As a
general rule polyp-buds are produced
from the hydrorhiza and
hydrocaulus, while medusa-buds
are formed on the hydranth. In
some cases, however, medusa-buds
are formed on the hydrorhiza,
as in Hydrocorallines.
In such a colony of connected
individuals, the exact limits of
the separate “persons” are not
always clearly marked out.
Hence it is necessary to distinguish
between, first, the “zooids,”
indicated in the case of the polyps
by the hydranths, each with
mouth and tentacles; and,
secondly, the “coenosarc,” or
common flesh, which cannot
be assigned more to one individual than another, but consists
of a more or less complicated network of tubes, corresponding to the
hydrocaulus and hydrorhiza of the primitive independent polyp-individual.
The coenosarc constitutes a system by which the
digestive cavity of any one polyp is put into communication with
that of any other individual either of the trophosome or gonosome.
In this manner the food absorbed by one individual contributes
to the welfare of the whole colony, and the coenosarc has the
139
function of circulating and distributing nutriment through the
colony.
The hydroid colony shows many variations in form and architecture
which depend simply upon differences in the methods in which
polyps are budded.
 |
| After Hincks, Forbes, and Browne. A and B modified
from Hincks; C modified from Forbes’s Brit. Naked-eyed
Medusae. |
| Fig. 11.—Lar sabellarum and two stages
of its Medusa, Willia stellata. A, colony of
Lar; B and C, young and adult medusae. |
 |
| Fig. 12.—Colony of Bougainvillea
fruticosa, natural size, attached to the
underside of a piece of floating timber.
(After Allman.) |
In the first place,
buds may be produced
only from the hydrorhiza,
which grows out
and branches to form
a basal stolon, typically
net-like, spreading over
the substratum to
which the founder-polyp
attached itself.
From the stolon the
daughter-polyps grow
up vertically. The result
is a spreading or
creeping colony, with
the coenosarc in the
form of a root-like
horizontal network (fig.
5, B; 11, A). Such a
colony may undergo
two principal modifications.
The meshes of
the basal network may
become very small or
virtually obliterated, so
that the coenosarc becomes
a crust of tubes
tending to fuse together,
and covered over by
a common perisarc.
Encrusting colonies of
this kind are seen in
Clava squamata (fig.
5, A) and Hydractinia
(figs. 9, 10), the latter
having the perisarc
calcified. A further
very important modification
is seen when the
tubes of the basal
perisarc do not remain
spread out in one plane,
but grow in all planes
forming a felt-work;
the result is a massive
colony, such as is seen in the so-called Hydrocorallines (fig. 60),
where the interspaces between the coenosarcal tubes are filled up
with calcareous matter, or coenosteum, replacing the chitinous
perisarc. The result is a stony, solid mass, which contributes to
the building up of coral reefs. In massive colonies of this kind no
sharp distinction can be drawn between hydrorhiza and hydrocaulus
in the coenosarc; it
is practically all hydrorhiza.
Massive colonies may assume
various forms and are often
branching or tree-like. A further
peculiarity of this type of
colony is that the entire coenosarcal
complex is covered externally
by a common layer
of ectoderm; it is not clear
how this covering layer is
developed.
In the second place, the
buds may be produced from
the hydrocaulus, growing out
laterally from it; the result
is an arborescent, tree-like
colony (figs. 12, 13). Budding
from the hydrocaulus may be
combined with budding from
the hydrorhiza, so that numerous
branching colonies arise
from a common basal stolon.
In the formation of arborescent
colonies, two sharply
distinct types of budding are
found, which are best described
in botanical terminology
as the monopodial or
racemose, and the sympodial
or cymose types respectively; each is characteristic of one of the
two sub-orders of the Hydroidea, the Gymnoblastea and Calyptoblastea.
In the monopodial method (figs. 12, 14) the founder-polyp is,
theoretically, of unlimited growth in a vertical direction, and as it
grows up it throws out buds right and left alternately, so that the
first bud produced by it is the lowest down, the second bud is above
the first, the third above this again, and so on. Each bud produced
by the founder proceeds to grow and to bud in the same way as the
founder did, producing a side branch of the main stem. Hence, in a
colony of gymnoblastic hydroids, the oldest polyp of each system,
that is to say, of the main stem or of a branch, is the topmost polyp;
the youngest polyp of the system is the one nearest to the topmost
polyp; and the axis of the system is a true axis.
 |
| Fig. 13.—Portion of colony of Bougainvillea fruticosa
(Anthomedusae-Gymnoblastea) more magnified. (From Lubbock, after
Allman.) |
 |
| Fig. 14.—Diagrams of the monopodial method of budding, shown
in five stages (1-5). F, the founder-polyp; 1, 2, 3, 4, the succession
of polyps budded from the founder-polyp; a′, b′, c′, the succession
of polyps budded from 1; a2, b2, polyps budded from 2; a3, polyp
budded from 3. |
 |
| Fig. 15.—Diagram of sympodial budding,
biserial type, shown in five stages (1-5). F,
founder-polyp; 1, 2, 3, 4, 5, 6, succession of
polyps budded from the founder; a, b, c,
second series of polyps budded from the founder;
a3, b3, series budded from 3. |
 |
| Fig. 16.—Diagram of sympodial
budding, uniserial type, shown
in four stages (1-4). F, founder-polyp;
1, 2, 3, succession of polyps
budded from the founder. |
 |
| Fig. 17.—Diagram of sympodial budding,
simple unbranched Plumularia-type. F,
founder; 1-8, main axis formed by biserial
budding from founder; a-e, pinnule formed
by uniserial budding from founder; a¹-d¹,
branch formed by similar budding from 1;
a2-d2 from 2, and so forth. |
In the sympodial method of budding, on the other hand, the
founder-polyp is of limited growth, and forms a bud from its side,
which is also of limited growth, and forms a bud in its turn, and so on
(figs. 15, 16). Hence, in a colony of calyptoblastic hydroids, the
oldest polyp of a system is the lowest; the youngest polyp is the topmost
140
one; and the axis of the system is a false axis composed of
portions of each of the consecutive polyps. In this method of budding
there are two
types. In one, the
biserial type (fig.
15), the polyps produce
buds right
and left alternately,
so that the
hydranths are
arranged in a zigzag
fashion, forming
a “scorpioid
cyme,” as in Obelia
and Sertularia. In
the other, the uniserial
type (fig. 16),
the buds are
formed always on
the same side,
forming a “helicoid
cyme,” as in
Hydrallmania,
according to H.
Driesch, in which,
however, the
primitively uniserial
arrangement
becomes masked later by secondary torsions of the hydranths.
In a colony formed by sympodial budding, a polyp always produces
first a bud, which contributes to the system to which it belongs, i.e.
continues the stem or branch of which its parent forms a part. The
polyp may then form a second
bud, which becomes the starting
point of a new system, the
beginning, that is, of a new
branch; and even a third bud,
starting yet another system,
may be produced from the same
polyp. Hence the colonies of
Calyptoblastea may be complexly
branched, and the budding
may be biserial throughout,
uniserial throughout, or
partly one, partly the other.
Thus in Plumularidae (figs. 17,
18) there is formed a main stem
by biserial budding; each polyp
on the main stem forms a
second bud, which usually
forms a side branch or pinnule
by uniserial budding. In this
way are formed the familiar feathery colonies of Plumularia, in
which the pinnules are all in one plane, while in the allied Antennularia
the pinnules are arranged in whorls round the main biserial
stem. The pinnules never branch again, since in the uniserial mode
of budding a polyp
never forms a second
polyp-bud. On the
other hand, a polyp
on the main stem may
form a second bud
which, instead of forming
a pinnule by uniserial
budding, produces
by biserial budding
a branch, from
which pinnules arise as
from the main stem
(fig. 18—3, 6). Or a
polyp on the main
stem, after having
budded a second time
to form a pinnule,
may give rise to a
third bud, which
starts a new biserial
system, from which
uniserial pinnules arise
as from the main stem—type
of Aglaophenia
(fig. 19). The laws of
budding in hydroids
have been worked out
in an interesting
manner by H. Driesch [13], to whose memoirs the reader must be
referred for further details.
Individualization of Polyp-Colonies.—As in other cases where
animal colonies are formed by organic union of separate individuals,
there is ever a tendency for the polyp-colony as a whole to act as a
single individual, and for the members to become subordinated to
the needs of the colony and to undergo specialization for particular
functions, with the result that they simulate organs and their individuality
becomes masked to a greater or less degree. Perhaps the
earliest of such specializations is connected with the reproductive
function. Whereas primitively any polyp in a colony may produce
medusa-buds, in many hydroid colonies medusae are budded only by
certain polyps termed blastostyles (fig. 10, b). At first not differing
in any way from other
polyps (fig. 5), the blastostyles
gradually lose their
nutritive function and the
organs connected with it;
the mouth and tentacles
disappear, and the blastostyle
obtains the nutriment
necessary for its activity by
way of the coenosarc. In
the Calyptoblastea, where
the polyps are protected
by special capsules of the
perisarc, the gonothecae enclosing
the blastostyles
differ from the hydrothecae
protecting the hydranths
(fig. 54).
 |
 |
| Fig. 18.—Diagram showing method
of branching in the Plumularia-type;
compare with fig. 17. Polyps 3 and 6,
instead of producing uniserial pinnules,
have produced biserial branches (31, 32,
33, 34; 61-63), which give off uniserial
branches in their turn. |
Fig. 19.—Diagram showing method of branching
in the Aglaophenia-type. Polyp 7 has produced
as its first bud, 8; as its second bud, a7,
which starts a uniserial pinnule; and as a third
bud I7, which starts a biserial branch (II7-VI7)
that repeats the structure of the main stem and
gives off pinnules. The main stem is indicated
by-·-·-·, the new stem by ······. |
In other colonies the two
functions of the nutritive
polyp, namely, capture and
digestion of food, may be
shared between different
polyps (fig. 10). One class
of polyps, the dactylozoids
(dz), lose their mouth and
stomach, and become elongated
and tentacle-like,
showing great activity of
movement. Another class,
the gastrozoids (gz), have the tentacles reduced or absent, but have
the mouth and stomach enlarged. The dactylozoids capture food,
and pass it on to the gastrozoids, which swallow and digest it.
Besides the three types of individual above mentioned, there are
other appendages of hydroid colonies, of which the individuality is
doubtful. Such are the “guard-polyps” (machopolyps) of Plumularidae,
which are often regarded as individuals of the nature of dactylozoids,
but from a study of the mode of budding in this hydroid
family Driesch concluded that the guard-polyps were not true
polyp-individuals, although each is enclosed in a small protecting
cup of the perisarc, known as a nematophore. Again, the spines
arising from the
basal crust of
Podocoryne have
been interpreted
by some authors
as reduced polyps.
3. The Medusa.—In
the Hydromedusae
the
medusa-individual
occurs, as already
stated, in one of
two conditions,
either as an independent
organism
leading a true life
in the open seas,
or as a subordinate
individuality in
the hydroid
colony, from which
it is never set free;
it then becomes a
mere reproductive
appendage or gonophore,
losing successively
its organs
of sense, locomotion
and nutrition,
until its
medusoid nature
and organization
become scarcely
recognizable.
Hence it is convenient to consider the morphology of the medusa
from these two aspects.
(a) The Medusa as an Independent Organism.—The general
structure and characteristics of the medusa are described elsewhere
(see articles Hydrozoa and Medusa), and it is only necessary here to
deal with the peculiarities of the Hydromedusa.
 |
 |
| From Allman’s Gymnoblastic Hydroids, by permission of
the Council of the Ray Society. |
From Allman’s Gymnoblastic Hydroids, by permission of
the Council of the Ray Society. |
| Fig. 20.—Cladonema radiatum, the medusa
walking on the basal branches of its tentacles
(t), which are turned up over the body. |
Fig. 21.—Clavatella prolifera, ambulatory
medusa. t, tentacles; oc, ocelli. |
As regards habit of life the vast majority of Hydromedusae are
141
pelagic organisms, floating on the surface of the open sea, propelling
themselves feebly by the pumping movements of the umbrella
produced by contraction of the sub-umbral musculature, and
capturing their prey with their tentacles. The genera Cladonema
(fig. 20) and Clavatella
(fig. 21), however, are
ambulatory,
creeping forms, living
in rock-pools and
walking, as it were,
on the tips of the
proximal branches of
each of the tentacles,
while the remaining
branches serve for
capture of food.
Cladonema still has
the typical medusan
structure, and is able
to swim about, but in
Clavatella the umbrella
is so much reduced,
that swimming
is no longer possible.
The remarkable
medusa Mnestra
parasites is ecto-parasitic
throughout life
on the pelagic mollusc
Phyllirrhoe, attached
to it by the sub-umbral
surface, and
its tentacles have
become rudimentary
or absent. It is interesting
to note that Mnestra has been shown by J. W. Fewkes
[15] and R. T. Günther [19] to belong to the same family (Cladonemidae)
as Cladonema and Clavatella, and it is reasonable to suppose
that the non-parasitic ancestor of Mnestra was, like the other two
genera, an ambulatory
medusa which
acquired louse-like
habits. In some
species of the genus
Cunina (Narcomedusae)
the youngest
individuals (actinulae)
are parasitic on
other medusae (see
below), but in later
life the parasitic
habit is abandoned.
No other instances
are known of sessile
habit in Hydromedusae.
 |
| After E. T. Browne, from Proc.
Zool. Soc. of London. |
| Fig. 22.—Corymorpha
nutans, adult female
Medusa. Magnified 10
diameters. |
The external form of the Hydromedusae varies from that of a deep
bell or thimble, characteristic of the Anthomedusae, to the shallow
saucer-like form characteristic of the Leptomedusae. It is usual for
the umbrella to have an even, circular, uninterrupted margin; but
in the order Narcomedusae secondary
down-growths between the tentacles
produce a lobed, indented margin to
the umbrella. The marginal tentacles
are rarely absent in non-parasitic forms,
and are typically four in number, corresponding
to the four perradii marked
by the radial canals. Interradial tentacles
may be also developed, so that
the total number present may be increased
to eight or to an indefinitely
large number. In Willia, Geryonia, &c.,
however, the tentacles and radial
canals are on the plan of six instead of
four (figs. 11 and 26). On the other
hand, in some cases the tentacles are
less in number than the perradii; in
Corymorpha (figs. 3 and 22) there is but
a single tentacle, while two are found
in Amphinema and Gemmaria (Anthomedusae),
and in Solmundella
bitentaculata (fig. 67) and Aeginopsis
hensenii (fig. 23) (Narcomedusae). The
tentacles also vary considerably in
other ways than in number: first, in
form, being usually simple, with a basal bulb, but in Cladonemidae
they are branched, often in complicated fashion; secondly,
in grouping, being usually given off singly, and at regular intervals
from the margin of the umbrella, but in Margelidae and in some
Trachomedusae they are given off in tufts or bunches (fig. 24);
thirdly, in position and origin, being usually implanted on the
extreme edge of the umbrella, but in Narcomedusae they become
secondarily shifted and are given off high up on the ex-umbrella
(figs. 23 and 25); and, fourthly, in structure, being hollow or solid,
as in the polyp. In some medusae, for instance, the remarkable
deep-sea family Pectyllidae, the tentacles may bear suckers, by which
the animal may attach itself temporarily. It should be mentioned
finally that the tentacles are very contractile
and extensible, and may therefore present
themselves, in one and the same individual, as
long, drawn-out threads, or in the form of short
corkscrew-like ringlets; they may stream
downwards from the sub-umbrella, or be held
out horizontally, or be directed upwards over
the ex-umbrella (fig. 23). Each species of
medusa usually has a characteristic method of carrying its
tentacles.
 |
 |
| After O. Maas, Die
craspedoten Medusen der
Plankton Expedition, by
permission of Lipsius and
Tischer. |
After O. Maas, Craspedoten Medusen der Siboga-Expedition,
by permission of E. S. Brill & Co. |
| Fig. 23.—Aeginopsis
hensenii,
slightly magnified,
showing the manner
in which the tentacles
are carried in
life. |
Fig. 24.—Rathkea octonemalis. |
 |
| After O. Maas, Medusae, in Prince of
Monaco’s series. |
| Fig. 25.—Aeginura grimaldii. |
The sub-umbrella invariably shows a velum as an inwardly
projecting ridge or rim at its margin, within the circle of tentacles;
hence the medusae of this sub-class are termed craspedote. The
manubrium is absent altogether in the fresh-water medusa Limnocnida,
in which the diameter of the mouth exceeds half that of the
umbrella; on the other hand, the manubrium may attain a great
length, owing to the centre of the sub-umbrella with the stomach
being drawn into it, as it were, to form a long proboscis, as in Geryonia.
The mouth may be a simple, circular pore at the extremity of the
manubrium, or by folding of the edges it may become square or shaped
like a Maltese cross, with four corners and four lips. The corners of
the mouth may then be drawn
out into lobes or lappets, which
may have a branched or
fringed outline (fig. 27), and
in Margelidae the subdivisions
of the fringe simulate tentacles
(fig. 24).
The internal anatomy of the
Hydromedusae shows numerous
variations. The stomach
may be altogether lodged in
the manubrium, from which
the radial canals then take
origin directly as in Geryonia
(Trachomedusae); it may be
with or without gastric
pouches. The radial canals
may be simple or branched,
primarily four, rarely six in
number. The ring-canal is
drawn out in Narcomedusae
into festoons corresponding
with the lobes of the margin,
and may be obliterated altogether (Solmaris). In this order the radial
canals are represented only by wide gastric pouches, and in the family
Solmaridae are suppressed altogether, so that the tentacles and the
festoons of the ring-canal arise directly from the stomach. In
Geryonia, centripetal canals, ending blindly, arise from the ring-canal
and run in a radial direction towards the centre of the umbrella
(fig. 26).
Histology of the Hydromedusa.—The histology described above
for the polyp may be taken as the primitive type, from which that
142
of the medusa differs only in greater elaboration and differentiation
of the cell-elements, which are also more concentrated to form
distinct tissues.
 |
| Fig. 26.—Carmarina (Geryonia) hastata, one of the Trachomedusae.
(After Haeckel.) |
|
a, Nerve ring.
a′, Radial nerve.
b, Tentaculocyst.
c, Circular canal.
e, Radiating canal.
g″. Ovary.
h, Peronia or cartilaginous process ascending from the
cartilaginous margin of the disk centripetally in the
outer surface of the jelly-like disk; six of these are
perradial, six interradial, corresponding to the twelve
solid larval tentacles, resembling those of Cunina. |
k, Dilatation (stomach) of the manubrium.
l, Jelly of the disk.
p, Manubrium.
t, Tentacle (hollow and tertiary, i.e. preceded by six perradial
and six interradial solid larval tentacles).
u, Cartilaginous margin of the disk covered by thread-cells.
v. Velum. |
 |
| After O. Maas in Results of
the “Albatross” Expedition,
Museum of Comparative
Zoology, Cambridge, Mass.,
U.S.A. |
| Fig. 27.—Stomotoca
divisa, one of the Tiaridae
(Anthomedusae). |
The ectoderm furnishes the general epithelial covering of the body,
and the muscular tissue, nervous system and sense-organs. The
external epithelium is flat on the ex-umbral surface, more columnar
on the sub-umbral surface, where it forms the muscular tissue of the
sub-umbrella and the velum. The nematocysts of the ectoderm
may be grouped to form batteries on the tentacles, umbrellar margin
and oral lappets. In places the nematocysts may be crowded so
thickly as to form a tough, supporting, “chondral” tissue, resembling
cartilage, chiefly developed at the margin of the umbrella and forming
streaks or bars supporting the tentacles
(“Tentakelspangen,” peronia) or the tentaculocysts
(“Gehörspangen,” otoporpae).
The muscular tissue of the Hydromedusae
is entirely ectodermal. The
muscle-fibres arise as processes from the
bases of the epithelial cells; such cells
may individually become sub-epithelial
in position, as in the polyp; or, in places
where muscular tissue is greatly developed,
as in the velum or sub-umbrella,
the entire muscular epithelium may be
thrown into folds in order to increase its
surface, so that a deeper sub-epithelial
muscular layer becomes separated completely
from a more superficial body-epithelium.
In its arrangement the muscular tissue
forms two systems: the one composed
of striated fibres arranged circularly, that
is to say, concentrically round the central
axis of the umbrella; the other of non-striated
fibres running longitudinally,
that is to say, in a radial direction from,
or (in the manubrium) parallel to, the same ideal axis. The
circular system is developed continuously over the entire sub-umbral
surface, and the velum represents a special local development
of this system, at a region where it is able to act at the greatest
mechanical advantage in producing the contractions of the umbrella
by which the animal progresses. The longitudinal system is discontinuous,
and is subdivided into proximal, medial and distal
portions. The proximal portion forms the retractor muscles of the
manubrium, or proboscis, well developed, for example, in Geryonia.
The medial portion forms radiating tracts of fibres, the so-called
“bell-muscles” running underneath, and parallel to, the radial
canals; when greatly developed, as in Tiaridae, they form ridges,
so-called mesenteries, projecting into the sub-umbral cavity.
The distal portions form the muscles of the tentacles. In contrast
with the polyp, the longitudinal muscle-system is entirely
ectodermal, there being no endodermal muscles in craspedote
medusae.
 |
 |
| Fig. 28.—Muscular Cells of Medusae
(Lizzia). The uppermost is a purely muscular
cell from the sub-umbrella; the two lower are
epidermo-muscular cells from the base of a
tentacle; the upstanding nucleated portion
forms part of the epidermal mosaic on the
free surface of the body. (After Hertwig.) |
After O. Maas, Craspedoten Medusen der Siboga
Expedition, by permission of E. S. Brill & Co. |
| Fig. 29.—Tiaropsis rosea (Ag. and Mayer)
showing the eight adradial Statocysts, each
close to an Ocellus. Cf. fig. 30. |
The nervous system of the medusa consists of sub-epithelial
ganglion-cells, which form, in the first place, a diffuse plexus of nervous
tissue, as in the
polyp, but developed
chiefly on the sub-umbral
surface; and
which are concentrated,
in the second
place, to form a
definite central nervous
system, never
found in the polyp.
In Hydromedusae
the central nervous
system forms two
concentric nerve-rings
at the margin
of the umbrella, near
the base of the velum.
One, the “upper”
or ex-umbral nerve-ring,
is derived from
the ectoderm on the ex-umbral side of the velum; it is the larger
of the two rings, containing more numerous but smaller ganglion-cells,
and innervates the tentacles. The other, the “lower” or sub-umbral
nerve-ring, is derived from the ectoderm on the sub-umbral
side of the velum; it contains fewer but larger ganglion-cells and
innervates the muscles of the velum (see diagram in article Medusae).
The two nerve-rings are connected by fibres passing from one to the
other.
The sensory cells are slender epithelial cells, often with a cilium
or stiff protoplasmic process, and should perhaps be regarded as the
only ectoderm-cells which retain the primitive ciliation of the larval
ectoderm, otherwise lost in all Hydrozoa. The sense-cells form,
in the first place, a diffuse system of scattered sensory cells, as in the
polyp, developed chiefly on the manubrium, the tentacles and the
margin of the umbrella, where they form a sensory ciliated epithelium
covering the nerve-centres; in the second place, the sense-cells are
concentrated to form
definite sense-organs,
situated always at
the margin of the
umbrella, hence often
termed “marginal
bodies.” The possession
of definite sense-organs
at once distinguishes
the medusa
from the polyp, in
which they are never
found.
The sense-organs of
medusae are of two
kinds—first, organs
sensitive to light,
usually termed ocelli
(fig. 29); secondly,
organs commonly
termed otocysts, on
account of their resemblance
to the auditory
vesicles of higher
animals, but serving
for the sense of
balance and orientation,
and therefore
given the special name
of statocysts (fig. 30). The sense-organs may be tentaculocysts, i.e.
modifications of a tentacle, as in Trachylinae, or developed from the
margin of the umbrella, in no connexion with a tentacle (or, if so
connected, not producing any modification in the tentacle), as in
Leptolinae. In Hydromedusae the sense-organs are always exposed
at the umbrellar margin (hence Gymnophthalmata), while in Scyphomedusae
they are covered over by flaps of the umbrellar margin
(hence Steganophthalmata).
 |
 |
| Modified after Linko, Traveaux Soc. Imp. Nat., St.
Petersbourg, xxix. |
Modified after O. and R, Hertwig, Nervensystem
und Sinnesorgane der Medusen, by
permission of F. C. W. Vogel. |
| Fig. 30.—Section of a Statocyst and
Ocellus of Tiaropsis diademata; cf. fig. 29. |
Fig. 31.—Section of a Statocyst of
Mitrocoma annae. |
ex, Ex-umbral ectoderm.
sub, Sub-umbral ectoderm.
c.c, Circular canal.
v, Velum.
st.e, Cavity of statocyst.
con, Concrement-cell with otolith. |
sub, Sub-umbral ectoderm.
c.c, Circular canal.
v, Velum.
st.c, Cavity of statocyst.
con, Concrement-cell with otolith. |
The statocysts present in general the structure of either a knob
or a closed vesicle, composed of (1) indifferent supporting epithelium:
(2) sensory, so-called auditory epithelium of slender cells, each
143
bearing at its free upper end a stiff bristle and running out at its base
into a nerve-fibre; (3) concrement-cells, which produce intercellular
concretions, so-called otoliths.
By means of
vibrations or shocks
transmitted through the
water, or by displacements
in the balance or
position of the animal,
the otoliths are caused
to impinge against the
bristles of the sensory
cells, now on one side,
now on the other, causing
shocks or stimuli which
are transmitted by the
basal nerve-fibre to the
central nervous system.
Two stages in the development
of the otocyst
can be recognized, the
first that of an open pit
on a freely-projecting
knob, in which the otoliths
are exposed, the
second that of a closed
vesicle, in which the otoliths
are covered over.
Further, two distinct
types of otocyst can be
recognized in the Hydromedusae:
that of the Leptolinae, in which the entire organ is
ectodermal, concrement-cells and all, and the organ is not a tentaculocyst;
and that of the Trachylinae, in which the organ is a
tentaculocyst, and the concrement-cells
are endodermal,
derived from the endoderm
of the modified tentacle, while
the rest of the organ is ectodermal.
 |
 |
| Modified after O. and R, Hertwig, Nervensystem
und Sinnesorgane der Medusen, by
permission of F. C. W. Vogel. |
Modified after O. and R, Hertwig,
Nervensystem und Sinnesorgane der
Medusen, by permission of F. C. W.
Vogel. |
| Fig. 32.—Section of a Statocyst
of Phialidium. |
Fig. 33.—Optical Section of
a Statocyst of Octorchis. |
ex, Ex-umbral ectoderm.
sub, Sub-umbral ectoderm.
v, Velum.
st.c, Cavity of statocyst.
con, Concrement-cell with otolith. |
con, Concrement-cell with otolith.
st.c, Cavity of statocyst. |
In the Leptolinae the otocysts
are seen in their first
stage in Mitrocoma annae
(fig. 31) and Tiaropsis (figs. 29,
30) as an open pit at the base
of the velum, on its sub-umbral
side. The pit has its
opening turned towards the
sub-umbral cavity, while its
base or fundus forms a bulge,
more or less pronounced, on
the ex-umbral side of the
velum. At the fundus are
placed the concrement-cells
with their conspicuous otoliths
(con) and the inconspicuous
auditory cells, which are
connected with. the sub-umbral
nerve-ring. From
the open condition arises
the closed condition very
simply by closing up of the
aperture of the pit. We then find the typical otocyst of the
Leptomedusae, a vesicle bulging on the ex-umbral side of the velum
(figs. 32, 33). The otocysts are placed on the outer wall of the
vesicle (the fundus of the original pit) or on its sides; their arrangement
and number vary greatly and furnish useful characters for
distinguishing genera. The sense-cells are innervated, as before,
from the sub-umbral nerve-ring. The inner wall of the vesicle
(region of closure) is frequently thickened to form a so-called “sense-cushion,”
apparently a ganglionic offshoot from the sub-umbral
nerve-ring. In many
Leptomedusae the otocysts
are very small, inconspicuous
and embedded
completely in the
tissues; hence they may
be easily overlooked in
badly-preserved material,
and perhaps are present
in many cases where they
have been said to have
been wanting.
 |
 |
| After O. and R, Hertwig, Nervensystem und Sinnesorgane
der Medusen, by permission of F. C. W.
Vogel. |
After O. and R, Hertwig, Nervensystem und Sinnesorgane
der Medusen, by permission of F. C. W.
Vogel. |
| Fig. 34.—Tentaculocyst (statorhabd)
of Cunina solmaris. n.c, Nerve-cushion;
end, endodermal concrement-cells; con,
otolith. |
Fig. 35.—Tentaculocyst of Cunina lativentris. |
| |
ect, Ectoderm.
n.c, Nerve-cushion.
end, Endodermal concrement-cells.
con, Otolith. |
In the Trachylinae the
simplest condition of the
otocyst is a freely projecting
club, a so-called
statorhabd (figs. 34, 35),
representing a tentacle
greatly reduced in size,
covered with sensory
ectodermal epithelium
(ect.), and containing an
endodermal core (end.),
which is at first continuous
with the endoderm
of the ring-canal, but
later becomes separated
from it. In the endoderm
large concretions are formed (con.). Other sensory cells with long
cilia cover a sort of cushion (n.c.) at the base of the club; the club
may be long and the
cushion small, or the
cushion large and the
club small. The whole
structure is innervated,
like the tentacles, from
the ex-umbral nerve-ring.
An advance towards the
second stage is seen in
such a form as Rhopalonema
(fig. 36), where the
ectoderm of the cushion
rises up in a double fold
to enclose the club in a
protective covering forming
a cup or vesicle, at
first open distally; finally
the opening closes and
the closed vesicle may
sink inwards and be
found far removed from
the surface, as in Geryonia
(fig. 37).
 |
 |
| Fig. 36.—Simple tentaculocyst of Rhopalonema
velatum. The process carrying the otolith
or concretion hk, formed by endoderm cells, is
enclosed by an upgrowth forming the “vesicle,”
which is not yet quite closed in at the top.
(After Hertwig.) |
After O. and R, Hertwig, Nervensystem und Sinnesorgane
der Medusen, by permission of F. C. W. Vogel. |
| Fig. 37.—Section of statocyst of Geryonia
(Carmarina hastata). |
| |
st.c, Statocyst containing the minute tentaculocyst.
nr1, Ex-umbral nerve-ring.
nr2, Sub-umbral nerve-ring.
ex, Ex-umbral ectoderm.
sub, Sub-umbral ectoderm.
c.c, Circular canal.
v, Velum. |
The ocelli are seen in
their simplest form as a
pigmented patch of ectoderm,
which consists of
two kinds of cells—(1)
pigment-cells, which are
ordinary indifferent cells
of the epithelium containing pigment-granules, and (2) visual cells,
slender sensory epithelial cells of the usual type, which may develop
visual cones or
rods at their free
extremity. The
ocelli occur
usually either on
the inner or outer
sides of the tentacles;
if on the
inner side, the
tentacle is turned
upwards and
carried over the
ex-umbrella, so
as to expose the
ocellus to the
light; if the
ocellus be on the
outer side of a
tentacle, two
nerves run round
the base of the
tentacle to it. In
other cases ocelli may occur between tentacles, as in Tiaropsis (fig. 29).
The simple form of ocellus described in the foregoing paragraph
may become folded into a pit or cup, the interior of which becomes
filled with a clear gelatinous secretion forming a sort of vitreous
144
body. The distal portion of the vitreous body may project from the
cavity of the cup, forming a non-cellular lens as in Lizzia (fig. 28).
Beyond this simple condition the visual organs of the Hydromedusae
do not advance, and are far from reaching the wonderful development
of the eyes of Scyphomedusae (Charybdaea).
Besides the ordinary type of ocellus just described, there is found
in one genus (Tiaropsis) a type of ocellus in which the visual elements
are inverted, and
have their cones
turned away from
the light, as in the
human retina (fig.
30). In this case
the pigment-cells
are endodermal,
forming a cup of
pigment in which
the visual cones
are embedded. A
similar ocellus is
formed in Aurelia
among the Scyphomedusae
(q.v.).
Other sense
organs of Hydromedusae
are the
so-called sense-clubs
or cordyli
found in a few
Leptomedusae,
especially in those
genera in which
otocysts are inconspicuous
or absent
(fig. 39). Each
cordylus is a tentacle-like
structure with an endodermal axis containing an
axial cavity which may be continuous with the ring-canal, or may
be partially occluded. Externally the cordylus is covered, by very
flattened ectoderm, and bears no otoliths or sense-cells, but the base
of the club rests upon the ex-umbral nerve-ring. Brooks regards these
organs as sensory, serving for the sense of balance, and representing
a primitive stage of the tentaculocysts of Trachylinae; Linko, on
the other hand, finding no nerve-elements connected with them,
regards them as digestive (?) in function.
The sense-organs of the two fresh-water medusae Limnocodium
and Limnocnida are peculiar and of rather doubtful nature (see E. T.
Browne [10]).
 |
| Fig. 38.—Ocellus of
Lizzia koellikeri. oc,
Pigmented ectodermal
cells; l, lens. (After
Hertwig.) |
The endoderm of the medusa shows the same general types of
structure as in the polyp, described above. We can distinguish (1)
digestive endoderm, in the stomach, often
with special glandular elements; (2) circulatory
endoderm, in the radial and ring-canals;
(3) supporting endoderm in the axes
of the tentacles and in the endoderm-lamella;
the latter is primitively a double
layer of cells, produced by concrescence
of the ex-umbral and sub-umbral layers of
the coelenteron, but it is usually found as a
single layer of flattened cells (fig. 40); in
Geryonia, however, it remains double, and
the centripetal canals arise by parting of
the two layers; (4) excretory endoderm,
lining pores at the margin of the umbrella,
occurring in certain Leptomedusae as so-called
“marginal tubercles,” opening, on
the one hand, into the ring-canal and, on
the other hand, to the exterior by “marginal
funnels,” which debouch into the sub-umbral
cavity above the velum. As has been described
above, the endoderm may also contribute
to the sense-organs, but such
contributions are always of an accessory
nature, for instance, concrement-cells in
the otocysts, pigment in the ocelli, and
never of sensory nature, sense-cells being
in all cases ectodermal.
The reproductive cells may be regarded as belonging primarily
to neither ectoderm nor endoderm, though lodged in the ectoderm
in all Hydromedusae. As described for the polyp, they are wandering
cells capable of extensive migrations before reaching the particular
spot at which they ripen. In the Hydromedusae they usually, if
not invariably, ripen in the ectoderm, but in the neighbourhood of the
main sources of nutriment, that is to say, not far from the stomach.
Hence the gonads are found on the manubrium in Anthomedusae
generally; on the base of the manubrium, or under the gastral
pouches, or in both these situations (Octorchidae), or under the radial
canals, in Trachomedusae; under the gastral pouches or radial
canals, in Narcomedusae. When ripe, the germ-cells are dehisced
directly to the exterior.
 |
 |
| After W. K. Brooks, Journal of Morphology, x.,
by permission of Ginn & Co. |
Fig. 40.—Portions of Sections through
the Disk of Medusae—the upper one of
Lizzia, the lower of Aurelia. (After
Hertwig.) |
| Fig. 39.—Section of a Cordylus of
Laodice. |
c.c, Circular canal.
v, Velum.
t, Tentacle.
c, Cordylus, composed of flattened
ectoderm ec covering a large-celled
endodermal axis en. |
el, Endoderm lamella.
m, Muscular processes of the ectoderm-cells in cross section.
d, Ectoderm.
en, Endoderm lining the enteric cavity.
e, Wandering endoderm cells of the gelatinous substance. |
Hydromedusae are of separate sexes, the only known exception
being Amphogona apsteini, one of the Trachomedusae (Browne [9]).
Moreover, all the medusae budded from a given hydroid colony are
either male or female, so that even the non-sexual polyp must be
considered to have a latent sex. (In Hydra, on the other hand, the
individual is usually hermaphrodite.) The medusa always reproduces
itself sexually, and in some cases non-sexually also. The non-sexual
reproduction takes the
form of fission, budding
or sporogony, the details
of which are described
below. Buds may be produced
from the manubrium,
radial canals,
ring-canal, or tentacle-bases,
or from an aboral
stolon (Narcomedusae).
In all cases only medusa-buds
are produced, never
polyp-buds.
The mesogloea of the
medusa is largely developed
and of great
thickness in the umbrella.
The sub-epithelial tissues,
i.e. the nervous and muscular
cells, are lodged
in the mesogloea, but in
Hydromedusae it never
contains tissue-cells or
mesogloeal corpuscles.
(b) The Medusae as a
Subordinate Individuality.—It
has been shown
above that polyps are
budded only from polyps
and that the medusae
may be budded either
from polyps or from
medusae. In any case the
daughter-individuals produced from the buds may be imagined as
remaining attached to the parent and forming a colony of individuals
in organic connexion with one another, and thus three possible cases
arise. The first case gives a colony entirely composed of polyps, as
in many Hydroidea. The second case gives a colony partly composed
of polyp-individuals, partly of medusa-individuals, a possibility also
realized in many colonies of Hydroidea. The third case gives a colony
entirely composed of medusa-individuals, a possibility perhaps
realized in the Siphonophora, which will be discussed in dealing with
this group.
The first step towards the formation of a mixed hydroid colony is
undoubtedly a hastening of the sexual maturity of the medusa-individual.
Normally the medusae are liberated in quite an immature
state; they swim
away, feed, grow and
become adult mature
individuals. From the
bionomical point of
view, the medusa is to
be considered as a
means of spreading the
species, supplementing
the deficiencies of the
sessile polyp. It may
be, however, that increased
reproductiveness
becomes of greater
importance to the
species than wide diffusion;
such a condition
will be brought about if
the medusae mature
quickly and are either
set free in a mature
condition or remain in
the shelter of the polyp-colony,
protected from
risks of a free life in the
open sea. In this way
the medusa sinks from
an independent personality
to an organ of the polyp-colony, becoming a so-called
medusoid gonophore, or bearer of the reproductive organs, and losing
gradually all organs necessary for an independent existence, namely
those of sense, locomotion and nutrition.
In some cases both free medusae and gonophores may be produced
from the same hydroid colony. This is the case in Syncoryne mirabilis
(Allman [1], p. 278) and in Campanularia volubilis; in the latter,
free medusae are produced in summer, gonophores in winter
(Duplessis [14]). Again in Pennaria, the male medusae are set free
145
in a state of maturity, and have ocelli; the female medusae remain
attached and have no sense organs.
 |
| Modified from Weismann, Entstehung der Sexualzellen bei den Hydromedusen. |
| Fig. 41.—Diagrams of the Structure of the Gonophores of
various Hydromedusae, based on the figures of G. J. Allman and
A. Weismann. |
A, “Meconidium” of Gonothyraea.
B, Type of Tubularia.
C, Type of Garveia, &c.
D, Type of Plumularia, Agalma, &c.
E, Type of Coryne, Forskalia, &c.
F, G, H, Sporosacs.
F, With simple spadix.
G, With spadix prolonged (Eudendrium).
H, With spadix branched (Cordylophora). |
s.c, Sub-umbral cavity.
t, Tentacles.
c.c, Circular canal,
g, Gonads.
sp, Spadix.
e.l, Endoderm-lamella.
ex, Ex-umbral ectoderm.
ect, Ectotheca. |
 |
| After Allman, Gymnoblastic Hydroids, by permission of the
Council of the Ray Society. |
| Fig. 42.—Gonophores of Dicoryne conferta. |
A, A male gonophore still enclosed in its ectotheca.
B and C, Two views of a female gonophore after liberation.
t, Tentacles.
ov, Ova, two carried on each female gonophore.
sp, Testis. |
The gonophores of different hydroids differ greatly in structure
from one another, and form a series showing degeneration of the
medusa-individual, which is gradually stripped, as it were, of its
characteristic features of medusan organization and finally reduced to
the simplest structure. A very early stage in the degeneration is well
exemplified by the so-called “meconidium” of Gonothyraea (fig.
41, A). Here the medusoid, attached by the centre of its ex-umbral
surface, has lost its velum and sub-umbral muscles, its sense organs
and mouth, though still retaining rudimentary tentacles. The
gonads (g) are produced on the manubrium, which has a hollow
endodermal axis, termed the spadix (sp.), in open communication
with the coenosarc of the polyp-colony and serving for the nutrition
of the generative cells. A very similar condition is seen in Tubularia
(fig. 41, B), where, however, the tentacles have quite disappeared,
and the circular rim formed by the margin of the umbrella has nearly
closed over the manubrium leaving only a small aperture through
which the embryos emerge. The next step is illustrated by the
female gonophores of Cladocoryne, where the radial and ring-canals
have become obliterated by coalescence of their walls, so that the
entire endoderm of the umbrella is in the condition of the endoderm-lamella.
Next the opening of the umbrella closes up completely
and disappears, so that the sub-umbral cavity forms a closed space
surrounding the manubrium, on which the gonads are developed;
such a condition is seen in the male gonophore of Cladocoryne and in
Garveia (fig. 41, C), where, however, there is a further complication in
the form of an adventitious envelope or ectotheca (ect.) split off from
the gonophore as a protective covering, and not present in Cladocoryne.
The sub-umbral cavity (s.c.) functions as a brood-space
for the developing embryos, which are set free by rupture of the wall.
It is evident that the outer envelope of the gonophore represents the
ex-umbral ectoderm (ex.), and that the inner ectoderm lining the
cavity represents the sub-umbral ectoderm of the free medusa.
The next step is the gradual obliteration of the sub-umbral cavity
(s.c.) by disappearance of which the sub-umbral ectoderm comes into
contact with the ectoderm of the manubrium. Such a type is found
in Plumularia and also in Agalma (fig. 41, D); centrally is seen the
spadix (sp.), bearing the generative cells (g), and external to these (1)
a layer of ectoderm representing the epithelium of the manubrium;
(2) the layer of sub-umbral ectoderm; (3) the endoderm-lamella
(e.l.); (4) the ex-umbral ectoderm (ex.); and (5) there may or may
not be present also an ectotheca. Thus the gonads are covered over
by at least four layers of epithelium, and since these are unnecessary,
presenting merely obstacles to the dehiscence of the gonads, they
gradually undergo reduction. The sub-umbral ectoderm and that
covering the manubrium undergo concrescence to form a single layer
(fig. 41, E), which finally disappears altogether, and the endoderm-lamella
disappears. The gonophore is now reduced to its simplest
condition, known as the sporosac (fig. 41, F, G, H), and consists of the
spadix bearing the gonads covered by a single layer of ectoderm (ex.),
with or without the addition of an ectotheca. It cannot be too
strongly emphasized, however, that the sporosac should not be compared
simply with the manubrium of the medusa, as is sometimes
done. The endodermal spadix (sp.) of the sporosac represents the
endoderm of the manubrium; the ectodermal lining of the sporosac
(ex.) represents the ex-umbral ectoderm of the medusa; and the
intervening layers,
together with the
sub-umbral cavity,
have disappeared.
The spadix, as the
organ of nutrition
for the gonads,
may be developed
in various ways,
being simple (fig.
41, F) or branched
(fig. 41, H); in
Eudendrium (fig.
41, G) it curls
round the single
large ovum.
The hydroid
Dicoryne is remarkable
for the
possession of gonophores,
which are
ciliate and become
detached and
swim away by
means of their
cilia. Each such
sporosac has two
long tentacle-like
processes thickly
ciliated.
It has been
maintained that
the gonads of
Hydra represent
sporosacs or gonophores
greatly reduced,
with the
last traces of
medusoid structure
completely
obliterated. There
is, however, no
evidence whatever
for this, the gonads
of Hydra being
purely ectodermal
structures, while
all medusoid gonophores
have an endodermal portion. Hydra is, moreover, bisexual,
in contrast with what is known of hydroid colonies.
In some Leptomedusae the gonads are formed on the radial
canals and form protruding masses resembling sporosacs superficially,
but not in structure. Allman, however, regarded this type
of gonad as equivalent to a sporosac, and considered the medusa
bearing them as a non-sexual organism, a “blastocheme” as he
termed it, producing by budding medusoid gonophores. As medusae
are known to bud medusae from the radial canals there is nothing
impossible in Allman’s theory, but it cannot be said to have received
satisfactory proof.
Reproduction and Ontogeny of the Hydromedusae.
Nearly every possible method of reproduction occurs amongst
the Hydromedusae. In classifying methods of generation it is
usual to make use of the sexual or non-sexual nature of the
reproduction as a primary difference, but a more scientific
classification is afforded by the distinction between tissue-cells
146
(histocytes) and germinal cells, actual or potential (archaeocytes),
amongst the constituent cells of the animal body. In
this way we may distinguish, first, vegetative reproduction, the
result of discontinuous growth of the tissues and cell-layers
of the body as a whole, leading to (1) fission, (2) autotomy, or
(3) vegetative budding; secondly, germinal reproduction, the
result of the reproductive activity of the archaeocytes or germinal
tissue. In germinal reproduction the proliferating cells may be
undifferentiated, so-called primitive germ-cells, or they may be
differentiated as sexual cells, male or female, i.e. spermatozoa
and ova. If the germ-cells are undifferentiated, the offspring
may arise from many cells or from a single cell; the first type
is (4) germinal budding, the second is (5) sporogony. If the germ-cells
are differentiated, the offspring arises by syngamy or sexual
union of the ordinary type between an ovum and spermatozoon,
so-called fertilization, of the ovum, or by parthenogenesis, i.e.
development of an ovum without fertilization. The only one of
these possible modes of reproduction not known to occur in
Hydromedusae is parthenogenesis.
(1) True fission or longitudinal division of an individual into
two equal and similar daughter-individuals is not common but
occurs in Gastroblasta, where it has been described in detail by
Arnold Lang [30].
(2) Autotomy, sometimes termed transverse fission, is the name
given to a process of unequal fission in which a portion of the
body separates off with subsequent regeneration. In Tubularia
by a process of decapitation the hydranths may separate off
and give rise to a separate individual, while the remainder of
the body grows a new hydranth. Similarly in Schizocladium
portions of the hydrocaulus are cut off to form so-called “spores,”
which grow into new
individuals (see
Allman [1]).
 |
 |
| Much modified from C. Chun, “Coelenterata,” in
Bronn’s Tierreich. |
Fig. 44.—Diagrams of Medusa budding with
the formation of an entocodon. The endoderm
is shaded, the ectoderm left clear. |
| Fig. 43.—Direct Budding of Cunina. |
A, B, C, E, F, In vertical section.
D, Sketch of external view.
st, Stomach.
m, Manubrium.
t. Tentacle.
s.o, Sense organ.
v, Velum.
s.c, Sub-umbral cavity.
n.s, Nervous system. |
A, B, C, D, F, Successive stages in vertical section.
E, Transverse section of a stage similar to D.
Gc, Entocodon.
s.c, Cavity of entocodon, forming the future sub-umbral cavity.
st, Stomach.
r.c, Radial canal.
c.c, Circular canal.
e.l, Endoderm lamella.
m, Manubrium.
v, Velum.
t, Tentacle. |
(3) Vegetative budding
is almost universal
in the Hydromedusae.
By budding
is understood the
formation of a new individual
from a fresh
growth of undifferentiated
material. It
is convenient to distinguish
buds that
give rise to polyps
from those that form
medusae.
(a) The Polyp.—The
buds that form polyps
are very simple in
mode of formation.
Four stages may be
distinguished; the first
is a simple outgrowth
of both layers, ectoderm
and endoderm,
containing a prolongation
of the coelenteric
cavity; in the second
stage the tentacles
grow out as secondary
diverticula from the
side of the first outgrowth;
in the third
stage the mouth is
formed as a perforation
of the two layers;
and, lastly, if the bud
is to be separated, it
becomes nipped off
from the parent polyp and begins a free existence.
(b) The Medusae.—Two types of budding must be distinguished—the
direct, so-called, palingenetic type, and the indirect, so-called
coenogenetic type.
The direct type of budding is rare, but is seen in Cunina and
Millepora. In Cunina there arises, first, a simple outgrowth of both
layers, as in a polyp-bud (fig. 43, A); in this the mouth is formed
distally as a perforation (B); next the sides of the tube so formed
bulge out laterally near the attachment to form the umbrella, while
the distal undilated portion of the tube represents the manubrium
(C); the umbrella
now grows out
into a number of
lobes or lappets,
and the tentacles
and tentaculocysts
grow out, the
former in a notch
between two
lappets, the latter
on the apex of each
lappet (D, E);
finally, the velum
arises as a growth
of the ectoderm
alone, the whole
bud shapes itself,
so to speak, and
the little medusa is
separated off by
rupture of the thin
stalk connecting it
with the parent (F).
The direct method
of medusa-budding
only differs from
the polyp-bud by
its greater complexity
of parts and
organs.
The indirect
mode of budding
(figs. 44, 45) is the
commonest method
by which medusa-buds
are formed.
It is marked by the
formation in the
bud of a characteristic
structure
termed the entocodon
(Knospenkern,
Glockenkern).
 |
| Fig. 45.—Modifications of the method of
budding shown in fig. 44, with solid Entocodon
(Gc.) and formation of an ectotheca (ect.). |
The first stage is
a simple hollow
outgrowth of both
body-layers (fig. 44,
A); at the tip of
this is formed a
thickening of the
ectoderm, arising
primitively as a
hollow ingrowth
(fig. 44, B), but
more usually as a
solid mass of ectoderm-cells
(fig. 45,
A). The ectodermal
ingrowth is the
entocodon (Gc.); it
bulges into, and
pushes down, the
endoderm at the
apex of the bud,
and if solid it soon
acquires a cavity (fig. 44, C, s.c.). The cavity of the entocodon
increases continually in size, while the endoderm pushes up at the
sides of it to form a cup with hollow walls, enclosing but not quite
surrounding the
entocodon, which
remains in contact
at its outer side
with the ectoderm
covering the bud
(fig. 44, D, v). The
next changes that
take place are
chiefly in the endoderm-cup
(fig. 44,
D, E); the cavity
between the two
walls of the cup
becomes reduced
by concrescence to
form the radial
canals (r.c.), ring-canal (c.c.), and endoderm-lamella (e.l., fig. 44, E),
and at the same time the base of the cup is thrust upwards to form
the manubrium (m), converting the cavity of the entocodon into a
147
space which is crescentic or horse-shoe-like in section. Next tentacles
(t, fig. 44, F) grow out from the ring-canal, and the double
plate of ectoderm on the distal side of the entocodon becomes
perforated, leaving a circular rim composed of two layers of ectoderm,
the velum (v) of the medusa. Finally, a mouth is formed by breaking
through at the apex of the manubrium, and the now fully-formed
medusa becomes
separated by rupture
of the stalk
of the bud and
swims away.
 |
| Fig. 46.—Diagrams to show the significance
of the Entocodon in Medusa-buds. (Modified
from a diagram given by A. Weismann.) |
I, Ideally primitive method of budding, in
which the mouth is formed first (Ia),
next the tentacles (Ib), and lastly the
umbrella.
II, Method. of Cunina; (a) the mouth arises,
next the umbrella (b), and lastly the tentacles
(c).
III, Hypothetical transition from II to the indirect
method with an entocodon; the
formation of the manubrium is retarded,
that of the umbrella hastened (IIIa, b).
IV, a, b, c, budding with an entocodon (cf.
fig. 44).
V, Budding with a solid entocodon (cf. fig. 45). |
If the bud, however,
is destined to
give rise not to a
free medusa, but
to a gonophore,
the development
is similar but becomes
arrested at
various points, according
to the
degree to which
the gonophore is
degenerate. The
entocodon is
usually formed,
proving the medusoid
nature of the
bud, but in sporosacs
the entocodon
may be rudimentary
or absent
altogether. The
process of budding
as above described
may be varied or
complicated in
various ways;
thus a secondary,
amnion-like, ectodermal
covering
or ectotheca (fig.
45, C, ect.) may be
formed over all, as
in Garveia, &c.;
or the entocodon
may remain solid
and without cavity
until after the
formation of the
manubrium, or
may never acquire
a cavity at all, as
described above
for the gonophores.
Phylogenetic Significance
of the
Entocodon.—It is
seen from the
foregoing account
of medusa-budding
that the entocodon
is a very
important constituent
of the bud,
furnishing some of
the most essential
portions of the
medusa; its cavity
becomes the sub-umbral
cavity,
and its lining furnishes
the ectodermal
epithelium
of the manubrium
and of the sub-umbral cavity as far as the edge of the velum.
Hence the entocodon represents a precocious formation of the
sub-umbral surface, equivalent to the peristome of the polyp,
differentiated in the bud prior to other portions of the organism
which must be regarded as antecedent to it in phylogeny.
If the three principal organ-systems of the medusa, namely mouth,
tentacles and umbrella, be considered in the light of phylogeny,
it is evident that the manubrium bearing the mouth must be the
oldest, as representing a common property of all the Coelentera,
even of the gastrula embryo of all Enterozoa. Next in order come
the tentacles, common to all Cnidaria. The special property of the
medusa is the umbrella, distinguishing the medusa at once from
other morphological types among the Coelentera. If, therefore, the
formation of these three systems of organs took place according to
a strictly phylogenetic sequence, we should expect them to appear
in the order set forth above (fig. 46, Ia, b, c). The nearest approach
to the phylogenetic sequence is seen in the budding of Cunina, where
the manubrium and mouth appear first, but the umbrella is formed
before the tentacles (fig. 46, IIa, b, c). In the indirect or coenogenetic
method of budding, the first two members of the sequence
exhibited by Cunina change places, and the umbrella is formed first,
the manubrium next, and then the tentacles; the actual mouth-perforation
being delayed to the very last (fig. 46, IVa, b, c). Hence
the budding of medusae exemplifies very clearly a common phenomenon
in development, a phylogenetic series of events completely
dislocated in the ontogenetic time-sequence.
The entocodon is to be regarded, therefore, not as primarily an
ingrowth of ectoderm, but rather as an upgrowth of both body-layers,
in the form of a circular rim (IVa), representing the umbrellar
margin; it is comparable to the bulging that forms the umbrella in
the direct method of budding, but takes place before a manubrium
is formed, and is greatly reduced in size, so as to become a little pit.
By a simple modification, the open pit becomes a solid ectodermal
ingrowth, just as in Teleostean fishes the hollow medullary tube, or
the auditory pit of other vertebrate embryos, is formed at first as a
solid cord of cells, which acquires a cavity secondarily. Moreover,
the entocodon, however developed, gives rise at first to a closed
cavity, representing a closing over of the umbrella, temporary in
the bud destined to be a free medusa, but usually permanent in the
sessile gonophore. As has been shown above, the closing up of the
sub-umbral cavity is one of the earliest degenerative changes in the
evolution of the gonophore, and we may regard it as the umbrellar
fold taking on a protective function, either temporarily for the bud
or permanently for the gonophore.
To sum up, the entocodon is a precocious formation of the umbrella,
closing over to protect the organs in the umbrellar cavity. The
possession of an entocodon proves the medusa-nature of the bud,
and can only be explained on the theory that gonophores are degenerate
medusae, and is inexplicable on the opposed view that
medusae are derived from gonophores secondarily set free. In the
sporosac, however, the medusa-individual has become so degenerate
that even the documentary proof, so to speak, of its medusoid
nature may have been destroyed, and only circumstantial evidence
of its nature can be produced.
4. Germinal Budding.—This method of budding is commonly
described as budding from a single body-layer, instead of from
both layers. The layer that produces the bud is invariably the
ectoderm, i.e. the layer in which, in Hydromedusae, the generative
cells are lodged; and in some cases the buds are produced in the
exact spot in which later the gonads appear. From these facts,
and from those of the sporogony, to be described below, we may
regard budding to this type as taking place from the germinal
epithelium rather than from ordinary ectoderm.
(a) The Polyp.—Budding from the ectoderm alone has been
described by A. Lang [29] in Hydra and other polyps. The tissues
of the bud become differentiated into ectoderm and endoderm, and
the endoderm of the bud becomes secondarily continuous with that
of the parent, but no part of the parental endoderm contributes
to the building up of the daughter-polyp. Lang regarded this
method of budding as universal in polyps, a notion disproved by
O. Seeliger [52] who went to the opposite extreme and regarded the
type of budding described by Lang as non-existent. In view,
however, both of the statements and figures of Lang and of the facts
to be described presently for medusae (Margellium), it is at least
theoretically possible that both germinal and vegetative budding may
occur in polyps as well as in medusae.
(b) The Medusa.—The clearest instance of germinal budding is
furnished by Margellium (Rathkea) octopunctatum, one of the
Margelidae. The budding of this medusa has been worked out in
detail by Chun (Hydrozoa, [1]), to whom the reader must be referred
for the interesting laws of budding regulating the sequence and
order of formation of the buds.
The buds of Margellium are produced on the manubrium in each of
the four interradii, and they arise from the ectoderm, that is to say,
the germinal epithelium, which later gives rise to the gonads. The
buds do not appear simultaneously but successively on each of the
four sides of the manubrium, thus:  and secondary buds
may be produced on the medusa-buds before the latter are set free
as medusae. Each bud arises as a thickening of the epithelium, which
first forms two or three layers (fig. 47, A), and becomes separated into
a superficial layer, future ectoderm, surrounding a central mass, future
endoderm (fig. 47, B). The ectodermal epithelium on the distal side
of the bud becomes thickened, grows inwards, and forms a typical
entocodon (fig. 37, D, E, F). The remaining development of the bud
is just as described above for the indirect method of medusa-budding
(fig. 47, G, H). When the bud is nearly complete, the body-wall of
the parent immediately below it becomes perforated, placing the
coelenteric cavity of the parent in secondary communication with
that of the bud (H), doubtless for the better nutrition of the latter.
and secondary buds
may be produced on the medusa-buds before the latter are set free
as medusae. Each bud arises as a thickening of the epithelium, which
first forms two or three layers (fig. 47, A), and becomes separated into
a superficial layer, future ectoderm, surrounding a central mass, future
endoderm (fig. 47, B). The ectodermal epithelium on the distal side
of the bud becomes thickened, grows inwards, and forms a typical
entocodon (fig. 37, D, E, F). The remaining development of the bud
is just as described above for the indirect method of medusa-budding
(fig. 47, G, H). When the bud is nearly complete, the body-wall of
the parent immediately below it becomes perforated, placing the
coelenteric cavity of the parent in secondary communication with
that of the bud (H), doubtless for the better nutrition of the latter.
148
Especially noteworthy in the germinal budding of Margellium
is the formation of the entocodon, as in the vegetative budding of
the indirect type.
5. Sporogony.—This method of reproduction has been described
by E. Metchnikoff in Cunina and allied genera. In individuals
either of the male or female sex, germ-cells which are quite undifferentiated
and neutral in character, become amoeboid, and
wander into the endoderm. They divide each into two sister-cells,
one of which—the spore—becomes enveloped by the other.
The spore-cell multiplies by division, while the enveloping cell
is nutrient and protective. The spore cell gives rise to a
“spore-larva,”
which is set free in the coelenteron and grows into a
medusa. Whether sporogony occurs also in the polyp or not
remains to be proved.
6. Sexual Reproduction and Embryology.—The ovum of Hydromedusae
is usually one of a large number of oögonia, and grows
at the expense of its sister-cells. No regular follicle is formed,
but the oöcyte absorbs nutriment from the remaining oögonia.
In Hydra the oöcyte is a large amoeboid cell, which sends out
pseudopodia amongst the oögonia and absorbs nutriment from
them. When the oöcyte is full grown, the residual oögonia
die off and disintegrate.
 |
| Fig. 47.—Budding from the Ectoderm (germinal epithelium) in
Margellium. (After C. Chun.) |
A, The epithelium becomes two-layered.
B, The lower layer forms a solid mass of cells, which (C)
becomes a vesicle, the future endoderm, containing the
coelenteric cavity (coel), while the outer layer
furnishes the future ectoderm.
D, E, F, a thickening of the ectoderm on the distal side of
the bud forms an entocodon (Gc). |
G,H, Formation of the medusae.
s.c, Sub-umbral cavity.
r.c, Radial canal.
st, Stomach, which in H acquires a secondary communication
with the digestive cavity of the mother.
cc, Circular canal.
v, Velum.
t, Tentacle. |
The spermatogenesis and maturation and fertilization of the
germ-cells present nothing out of the common and need not be
described here. These processes have been studied in detail
by A. Brauer [2] for Hydra.
The general course of the development is described in the article
Hydrozoa. We may distinguish the following series of stages:
(1) ovum; (2) cleavage, leading to formation of a blastula; (3)
formation of an inner mass or parenchyma, the future endoderm,
by immigration or delamination, leading to the so-called parenchymula-stage;
(4) formation of an archenteric cavity, the future
coelenteron, by a splitting of the internal parenchyma, and of a
blastopore, the future mouth, by perforation at one pole, leading to
the gastrula-stage; (5) the outgrowth of tentacles round the mouth
(blastopore), leading to the actinula-stage; and (6) the actinula
becomes the polyp or medusa in the manner described elsewhere
(see articles Hydrozoa, Polyp and Medusa). This is the full, ideal
development, which is always contracted or shortened to a greater or
less extent. If the embryo is set free as a free-swimming, so-called
planula-larva, in the blastula, parenchymula, or gastrula stage, then
a free actinula stage is not found; if, on the other hand, a free
actinula occurs, then there is no free planula stage.
The cleavage of the ovum follows two types, both seen in Tubularia
(Brauer [3]). In the first, a cleavage follows each nuclear division;
in the second, the nuclei multiply by division a number of times,
and then the ovum divides into as many blastomeres as there are
nuclei present. The result of cleavage in all cases is a typical
blastula, which when set free becomes oval and develops a flagellum
to each cell, but when not set free, it remains spherical in form and
has no flagella.
The germ-layer formation is always by immigration or delamination,
never by invagination. When the blastula is oval and free-swimming
the inner mass is formed by unipolar immigration from
the hinder pole. When the blastula is spherical and not set free, the
germ-layer formation is always multipolar, either by immigration
or by delamination, i.e. by tangential division of the cells of the
blastoderm, as in Geryonia, or by a mixture of immigration and
delamination, as in Hydra, Tubularia, &c. The blastopore is formed
as a secondary perforation at one spot, in free-swimming forms
at the hinder pole. Formation of archenteron and blastopore may,
however, be deferred till a later stage (actinula or after).
The actinula stage is usually suppressed or not set free, but it is
seen in Tubularia (fig. 48), where it is ambulatory, in Gonionemus
(Trachomedusae), and in Cunina (Narcomedusae),
where it is parasitic.
 |
| Modified from a plate by L.
Agassiz, Contributions to Nat.
Hist. U.S., iv. |
| Fig. 48.—Free Actinula
of Tubularia. |
In Leptolinae the embryonic development
culminates in a polyp, which is
usually formed by fixation of a planula
(parenchymula), rarely by fixation of an
actinula. The planula may fix itself (1)
by one end, and then becomes the hydrocaulus
and hydranth, while the hydrorhiza
grows out from the base; or (2)
partly by one side and then gives rise to
the hydrorhiza as well as to the other
parts of the polyp; or (3) entirely by its
side, and then forms a recumbent hydrorhiza
from which a polyp appears to be
budded as an upgrowth.
In Trachylinae the development produces always a medusa, and
there is no polyp-stage. The medusa arises direct from the actinula-stage
and there is no entocodon formed, as in the budding described
above.
Life-cycles of the Hydromedusae.—The life-cycle of the Leptolinae
consists of an alternation of generations in which non-sexual individuals,
polyps, produce by budding sexual individuals, medusae,
which give rise by the sexual process to the non-sexual polyps again,
so completing the cycle. Hence the alternation is of the type termed
metagenesis. The Leptolinae are chiefly forms belonging to the inshore
fauna. The Trachylinae, on the other hand, are above all
oceanic forms, and have no polyp-stage, and hence there is typically
no alternation in their life-cycle. It is commonly assumed that the
Trachylinae are forms which have lost the alternation of generations
possessed by them ancestrally, through secondary simplification of
the life-cycle. Hence the Trachylinae are termed “hypogenetic”
medusae to contrast them with the metagenetic Leptolinae. The
whole question has, however, been argued at length by W. K. Brooks
[4], who adduces strong evidence for a contrary view, that is to say,
for regarding the direct type of development seen in Trachylinae as
more primitive, and the metagenesis seen in Leptolinae as a secondary
complication introduced into the life-cycle by the acquisition of
larval budding. The polyp is regarded, on this view, as a form
phylogenetically older than the medusa, in short, as nothing more
than a sessile actinula. In Trachylinae the polyp-stage is passed
over, and is represented only by the actinula as a transitory embryonic
stage. In Leptolinae the actinula becomes the sessile polyp
which has acquired the power of budding and producing individuals
either of its own or of a higher rank; it represents a persistent larval
stage and remains in a sexually immature condition as a neutral
individual, sex being an attribute only of the final stage in the development,
namely the medusa. The polyp of the Leptolinae has
reached the limit of its individual development and is incapable of
becoming itself a medusa, but only produces medusa-buds; hence a
true alternation of generations is produced. In Trachylinae also the
beginnings of a similar metagenesis can be found. Thus in Cunina
octonaria, the ovum develops into an actinula which buds daughter-actinulae;
all of them, both parent and offspring, develop into
medusae, so that there is no alternation of generations, but only
larval multiplication. In Cunina parasitica, however, the ovum
develops into an actinula, which buds actinulae as before, but only
the daughter-actinulae develop into medusae, while the original,
parent-actinula dies off; here, therefore, larval budding has led to a
true alternation of generations. In Gonionemus the actinula becomes
fixed and polyp-like, and reproduces by budding, so that here also an
alternation of generations may occur. In the Leptolinae we must
first substitute polyp for actinula, and then a condition is found which
can be compared to the case of Cunina parasitica or Gonionemus, if
we suppose that neither the parent-actinula (i.e. founder-polyp) nor
its offspring by budding (polyps of the colony) have the power of
becoming medusae, but only of producing medusae by budding.
For further arguments and illustrations the reader must be referred
to Brooks’s most interesting memoir. The whole theory is one most
149
intimately connected with the question of the relation between polyp
and medusa, to be discussed presently. It will be seen elsewhere,
however, that whatever view may be held as to the origin of metagenesis
in Hydromedusae, in the case of Scyphomedusae (q.v.) no
other view is possible than that the alternation of generations is the
direct result of larval proliferation.
To complete our survey of life-cycles in the Hydromedusae it is
necessary to add a few words about the position of Hydra and its
allies. If we accept the view that Hydra is a true sexual polyp, and
that its gonads are not gonophores (i.e. medusa-buds) in the extreme
of degeneration, then it follows from Brooks’s theory that Hydra
must be descended from an archaic form in which the medusan type
of organization had not yet been evolved. Hydra must, in short, be
a living representative of the ancestor of which the actinula-stage is
a transient reminiscence in the development of higher forms. It
may be pointed out in this connexion that the fixation of Hydra is
only temporary, and that the animal is able at all times to detach
itself, to move to a new situation, and to fix itself again. There is no
difficulty whatever in regarding Hydra as bearing the same relation
to the actinula-stage of other Hydromedusae that a Rotifer bears to
a trochophore-larva or a fish to a tadpole.
The Relation of Polyp and Medusa.—Many views have been put
forward as to the morphological relationship between the two
types of person in the Hydromedusae. For the most part,
polyp and medusa have been regarded as modifications of a
common type, a view supported by the existence, among Scyphomedusae
(q.v.), of sessile polyp-like medusae (Lucernaria, &c.).
R. Leuckart in 1848 compared medusae in general terms to
flattened polyps. G. J. Allman [1] put forward a more detailed
view, which was as follows. In some polyps the tentacles are
webbed at the base, and it was supposed that a medusa was a
polyp of this kind set free, the umbrella being a greatly developed
web or membrane extending between the tentacles. A very
different theory was enunciated by E. Metchnikoff. In some
hydroids the founder-polyp, developed from a planula after fixation,
throws out numerous outgrowths from the base to form the
hydrorhiza; these outgrowths may be radially arranged so as to
form by contact or coalescence a flat plate. Mechnikov considered
the plate thus formed at the base of the polyp as equivalent
to the umbrella, and the body of the polyp as equivalent to the
manubrium, of the medusa; on this view the marginal tentacles
almost invariably present in medusae are new formations, and
the tentacles of the polyp are represented in the medusa by the
oral arms which may occur round the mouth, and which sometimes,
e.g. in Margelidae, have the appearance and structure of
tentacles. Apart from the weighty arguments which the development
furnishes against the theories of Allman and Mechnikov,
it may be pointed out that neither hypothesis gives a satisfactory
explanation of a structure universally present in medusae of
whatever class, namely the endoderm-lamella, discovered by
the brothers O. and R. Hertwig. It would be necessary to regard
this structure as a secondary extension of the endoderm in the
tentacle-web, on Allman’s theory, or between the outgrowths
of the hydrorhiza, on Mechnikov’s hypothesis. The development,
on the contrary, shows unequivocally that the endoderm-lamella
arises as a local coalescence of the endodermal linings of a
primitively extensive gastral space.
The question is one intimately connected with the view taken
as to the nature and individuality of polyp, medusa and gonophore
respectively. On this point the following theories have
been put forward.
1. The theory that the medusa is simply an organ, which has
become detached and has acquired a certain degree of independence,
like the well-known instance of the hectocotyle of the cuttle-fish.
On this view, put forward by E. van Beneden and T. H. Huxley, the
sporosac is the starting-point of an evolution leading up through the
various types of gonophores to the free medusa as the culminating
point of a phyletic series. The evidence against this view may be
classed under two heads: first, comparative evidence; hydroids
very different in their structural characters and widely separate in
the systematic classification of these organisms may produce medusae
very similar, at least so far as the essential features of medusan
organization are concerned; on the other hydroids closely allied,
perhaps almost indistinguishable, may produce gonophores in the one
case, medusae in the other; for example, Hydractinia (gonophores)
and Podocoryne (medusae), Tubularia (gonophores) and Ectopleura
(medusae), Coryne (gonophores) and Syncoryne (medusae), and so on.
If it is assumed that all these genera bore gonophores ancestrally,
then medusa of similar type must have been evolved quite independently
in a great number of cases. Secondly, there is the evidence
from the development, namely, the presence of the entocodon in the
medusa-bud, a structure which, as explained above, can only be
accounted for satisfactorily by derivation from a medusan type of
organization. Hence it may be concluded that the gonophores are
degenerate medusae, and not that the medusae are highly elaborated
gonophores, as the organ-theory requires.
2. The theory that the medusa is an independent individual, fully
equivalent to the polyp in this respect, is now universally accepted
as being supported by all the facts of comparative morphology and
development. The question still remains open, however, which of
the two types of person may be regarded as the most primitive, the
most ancient in the race-history of the Hydromedusae. F. M.
Balfour put forward the view that the polyp was the more primitive
type, and that the medusa is a special modification of the polyp for
reproductive purposes, the result of division of labour in a polyp-colony,
whereby special reproductive persons become detached and
acquire organs of locomotion for spreading the species. W. K.
Brooks, on the other hand, as stated above, regards the medusa as
the older type and looks upon both polyp and medusa, in the Hydromedusae,
as derived from a free-swimming or floating actinula, the
polyp being thus merely a fixed nutritive stage, possessing secondarily
acquired powers of multiplication by budding.
The Hertwigs when they discovered the endoderm-lamella showed
on morphological grounds that polyp and medusa are independent
types, each produced by modification in different directions of a
more primitive type represented in development by the actinula-stage.
If a polyp, such as Hydra, be regarded simply as a sessile
actinula, we must certainly consider the polyp to be the older type,
and it may be pointed out that in the Anthozoa only polyp-individuals
occur. This must not be taken to mean, however, that the
medusa is derived from a sessile polyp; it must be regarded as a
direct modification of the more ancient free actinula form, without
primitively any intervening polyp-stage, such as has been introduced
secondarily into the development of the Leptolinae and represents a
revival, so to speak, of an ancestral form or larval stage, which has
taken on a special role in the economy of the species.
Systematic Review of the Hydromedusae
Order I. Eleutheroblastea.—Simple polyps which become
sexually mature and which also reproduce non-sexually, but
without any medusoid stage in the life-cycle.
The sub-order includes the family Hydridae, containing the
common fresh-water polyps of the genus Hydra. Certain other
forms of doubtful affinities have also been referred provisionally
to this section.
Hydra.—This genus comprises fresh-water polyps of simple structure.
The body bears tentacles, but shows no division into hydrorhiza,
hydrocaulus or hydranth; it is temporarily fixed and has no perisarc.
The polyp is usually hermaphrodite, developing both ovaries and
testes in the same individual. There is no free-swimming planula
larva, but the stage corresponding to it is passed over in an enveloping
cyst, which is secreted round the embryo by its own ectodermal
layer, shortly after the germ-layer formation is complete, i.e. in the
parenchymula-stage. The envelope is double, consisting of an external
chitinous stratified shell, and an internal thin elastic membrane.
Protected by the double envelope, the embryo is set free as a so-called
“egg,” and in Europe it passes the winter in this condition. In the
spring the embryo bursts its shell and is set free as a minute actinula
which becomes a Hydra.
Many species are known, of which three are common in European
waters. It has been shown by C. F. Jickeli (28) that the species are
distinguishable by the characters of their nematocysts. They also
show characteristic differences in the egg (Brauer [2]). In Hydra
viridis the polyp is of a green colour and produces a spherical egg
with a smooth shell which is dropped into the mud. H. grisea is
greyish in tint and produces a spherical egg with a spiky shell,
which also is dropped into the mud. H. fusca (= H. vulgaris) is brown
in colour, and produces a bun-shaped egg, spiky on the convex
surface, and attached to a water-weed or some object by its flattened
side. Brauer found a fourth species, similar in appearance to H.
fusca, but differing from the three other species in being of separate
sexes, and in producing a spherical egg with a knobby shell, which is
attached like that of H. fusca.
The fact already noted that the species of Hydra can be distinguished
by the characters of their nematocysts is a point of great
interest. In each species, two or three kinds of nematocysts occur,
some large, some small, and for specific identification the nematocysts
must be studied collectively in each species. It is very remarkable
that this method of characterizing and diagnozing species
has never been extended to the marine hydroids. It is quite possible
that the characters of the nematocysts might afford data as useful
to the systematist in this group as do the spicules of sponges, for
instance. It would be particularly interesting to ascertain how the
nematocysts of a polyp are related to those possessed by the medusa
budded from it, and it is possible that in this manner obscure questions
of relationship might be cleared up.
150
 |
| Fig. 49.—Diagram showing possible
modifications of persons of a gymnoblastic
Hydromedusa. (After Allman.) |
a, Hydrocaulus (stem).
b, Hydrorhiza (root).
c, Enteric cavity.
d, Endoderm.
e, Ectoderm.
f, Perisarc, (horny case).
g, Hydranth (hydriform person) expanded.
g′, Hydranth (hydriform person) contracted.
h, Hypostome, bearing mouth at its extremity.
k, Sporosac springing from the hydrocaulus.
k′, Sporosac springing from m, a modified hydriform person (blastostyle): the
genitalia are seen surrounding the spadix or manubrium.
l, Medusiform person or medusa.
m, Blastostyle. |
Protohydra is a marine genus characterized by the absence of
tentacles, by a great similarity to Hydra in histological structure, and
by reproduction by transverse fission. It was found originally in an
oyster-farm at Ostend. The sexual reproduction is unknown. For
further information see C. Chun (Hydrozoa [1]. Pl. I.).
Polypodium hydriforme Ussow is a fresh-water form parasitic on
the eggs of the sterlet. A “stolon” of unknown origin produces
thirty-two buds, which become as many Polypodia; each has
twenty-four tentacles and divides by fission repeated twice into four
individuals, each with six tentacles. The daughter-individuals grow,
form the full number
of twenty-four tentacles
and divide again. The
polyps are free and walk
on their tentacles. See
Ussow [54].
Tetraplatia volitans
Viguier is a remarkable
floating marine form.
See C. Viguier [56] and
Delage and Hérouard
(Hydrozoa [2]).
Haleremita Schaudinn.
See F. Schaudinn
[50] and Delage and
Hérouard (Hydrozoa
[2]).
In all the above-mentioned
genera, with
the exception of Hydra,
the life-cycle is so imperfectly
known that
their true position cannot
be determined in
the present state of
our knowledge. They
may prove eventually
to belong to other
orders. Hence only the
genus Hydra can be
considered as truly representing
the order
Eleutheroblastea. The
phylogenetic position
of this genus has been
discussed above.
Order II. Hydroidea
seu Leptolinae.—Hydromedusae
with alternation
of generations
(metagenesis) in which
a non-sexual polyp-generation
(trophosome)
produces by
budding a sexual
medusa-generation
(gonosome). The
polyp may be solitary,
but more usually produces
polyps by
budding and forms
a polyp-colony. The polyp usually has the body distinctly
divisible into hydranth, hydrocaulus and hydrorhiza, and is
usually clothed in a perisarc. The medusae may be set free or
may remain attached to the polyp-colony and degenerate into
a gonophore. When fully developed the medusa is characterized
by the sense organs being composed entirely of ectoderm,
developed independently of the tentacles, and innervated from
the sub-umbral nerve-ring.
The two kinds of persons present in the typical Hydroidea make
the classification of the group extremely difficult, for reasons explained
above. Hence the systematic arrangement that follows
must be considered purely provisional. A natural classification
of the Hydroidea has yet to be put forward. Many genera and
families are separated by purely artificial characters, mere shelf-and-bottle
groupings devised, for the convenience of the museum
curator and the collector. Thus many subdivisions are diagnosed by
setting free medusae in one case, or producing gonophores in another,
although it is very obvious, as pointed out above, that a genus producing
medusae may be far more closely allied to one producing
gonophores than to another producing medusae, or vice versa, and
that in some cases the production of medusae or gonophores varies
with the season or the sex. Moreover, P. Hallez [22] has recently
shown that hydroids hitherto regarded as distinct species are only
forms of the same species grown under different conditions.
Sub-Order 1. Hydroidea Gymnoblastea (Anthomedusae).—Trophosome without hydrothecae or gonothecae, with monopodial
type of budding. Gonosome with free medusae or
gonophores; medusae usually with ocelli, never with otocysts.
The gymnoblastic polyp usually has a distinct perisarc investing
the hydrorhiza and the hydrocaulus, sometimes also the hydranth
as far as the bases of the tentacles (Bimeria); but in such cases
the perisarc forms a closely-fitting investment or cuticule on
the hydranth, never a hydrotheca standing off from it, as in the
next sub-order. The polyps may be solitary, or form colonies,
which may be of the spreading or encrusting type, or arborescent,
and then always of monopodial growth and budding. In some
cases, any polyp of the colony may bud medusae; in other
cases, only certain polyps, the blastostyles, have this power.
When blastostyles are present, however, they are never enclosed
in special gonothecae as in the next sub-order. In this sub-order
the characters of the hydranth are very variable, probably owing
to the fact that it is exposed and not protected by a hydrotheca,
as in Calyptoblastea.
 |
 |
| Fig. 50.—Sarsia
(Dipurena) gemnifera.
b, The long manubrium,
bearing medusiform
buds; a, mouth. |
Fig. 51.—Sarsia prolifera.
Ocelli are seen at the base of the
tentacles, and also (as an exception)
groups of medusiform
buds. |
Speaking generally, three principal types of hydranth can be
distinguished, each with subordinate varieties of form.
1. Club-shaped hydranths with numerous tentacles, generally
scattered irregularly, sometimes with a spiral arrangement, or in
whorls (“verticillate”).
(a) Tentacles filiform; type of Clava (fig. 5), Cordylophora, &c.
(b) Tentacles capitate, simple; type of Coryne and Syncoryne;
Myriothela is an aberrant form with some of the tentacles
modified as “claspers” to hold the ova.
(c) Tentacles capitate, branched, wholly or in part; type of
Cladocoryne.
(d) Tentacles filiform or capitate, tending to be arranged in
definite whorls; type of Stauridium (fig. 2), Cladonema
and Pennaria.
2. Hydranth more shortened, daisy-like in form, with two whorls
of tentacles, oral and aboral.
(a) Tentacles filiform, simple, radially arranged or scattered
irregularly; type of Tubularia (fig. 4), Corymorpha (fig. 3),
Nemopsis, Pelagohydra, &c.
(b) Tentacles with a bilateral arrangement, branched tentacles
in addition to simple filiform ones; type of Branchiocerianthus.
3. Hydranth with a single circlet of tentacles.
(a) With filiform tentacles; the commonest type, seen in
Bougainvillea (fig. 13), Eudendrium, &c.
(b) With capitate tentacles; type of Clavatella.
4. Hydranth with tentacles reduced below four; type of Lar
(fig. 11), Monobrachium, &c.
151
The Anthomedusa in form is generally deep, bell-shaped.
The sense organs are typically ocelli, never otocysts. The gonads
are borne on the manubrium, either forming a continuous ring
(Codonid type), or four masses or pairs of masses (Oceanid type).
The tentacles may be scattered singly round the margin of the
umbrella (“monerenematous”) or arranged in tufts (“lophonematous”);
in form they may be simple or branched (Cladonemid
type); in structure they may be hollow (“coelomerinthous”);
or solid (“pycnomerinthous”). When sessile gonophores are
produced, they may show all stages of degeneration.
Classification.—Until quite recently the hydroids (Gymnoblastea)
and the medusae (Anthomedusae) have been classified separately,
since the connexion between them was insufficiently known. Delage
and Hérouard (Hydrozoa [2]) were the first to make an heroic
attempt to unite the two classifications into one, to which Hickson
(Hydrozoa [4]) has made some additions and slight modifications.
The classification given here is for the most part that of Delage and
Hérouard. It is certain, however, that no such classification can be
considered final at present, but must undergo continual revision in
the future. With this reservation we may recognize fifteen well-characterized
families and others of more doubtful nature. Certain
discrepancies must also be noted.
1. Margelidae (= medusa-family Margelidae + hydroid families
Bougainvillidae, Dicorynidae, Bimeridae and Eudendridae). Trophosome
arborescent, with hydranths of Bougainvillea-type; gonosome
free medusae or gonophores, the medusae with solid tentacles in
tufts (lophonematous). Common genera are the hydroid Bougainvillea
(figs. 12, 13), and the medusae Hippocrene (budded from
Bougainvillea), Margelis, Rathkea (fig. 24), and Margellium. Other
hydroids are Garveia, Bimeria, Eudendrium and Heterocordyle, with
gonophores, and Dicoryne with peculiar sporosacs.
 |
| After Haeckel, System der Medusen, by permission of Gustav
Fischer. |
| Fig. 52.—Tiara pileata, L. Agassiz. |
2. Podocorynidae (= medusa-families Thamnostomidae and Cytaeidae
+ hydroid families Podocorynidae and Hydractiniidae). Trophosome
encrusting with hydranths of Bougainvillea-type, polyps differentiated
into blastostyles, gastrozoids and dactylozoids; gonosome free
medusae or gonophores. The typical genus is the well-known
hydroid Podocoryne,
budding
the medusa known
as Dysmorphosa;
Thamnostylus,
Cytaeis, &c., are
other medusae
with unknown
hydroids. Hydractinia
(figs. 9, 10)
is a familiar
hydroid genus,
bearing gonophores.
3. Cladonemidae.—Trophosome,
polyps with two
whorls of tentacles,
the lower
filiform, the upper
capitate; gonosome,
free medusae,
with tentacles
solid and
branched. The
type-genus Cladonema
(fig. 20) is a
common British
form.
4. Clavatellidae.—Trophosome,
polyps with a
single whorl of
capitate tentacles;
gonosome, free
medusae, with tentacles
branched,
solid. Clavatella
(fig. 21), with a
peculiar ambulatory
medusa is a
British form.
5. Pennariidae.—Trophosome,
polyps with an
upper circlet of numerous capitate tentacles, and a lower circlet of filiform
tentacles. Pennaria, with a free medusa known as Globiceps, is a
common Mediterranean form. Stauridium (fig. 2) is a British hydroid.
6. Tubulariidae.—Trophosome, polyps with two whorls of tentacles,
both filiform. Tubularia (fig. 4), a well-known British hydroid,
bears gonophores.
7. Corymorphidae (including the medusa-family Hybocodonidae).—Trophosome
solitary polyps, with two whorls of tentacles; gonosome,
free medusae or gonophores. Corymorpha (fig. 3), a well-known
British genus, sets free a medusa known as Steenstrupia (fig.
22). Here belong the deep-sea genera Monocaulus and Branchiocerianthus,
including the largest
hydroid polyps known, both
genera producing sessile gonophores.
 |
| After Haeckel, System der Medusen, by
permission of Gustav Fischer. |
| Fig. 53.—Pteronema darwinii.
The apex of the stomach is prolonged
into a brood pouch containing
embryos. |
8. Dendroclavidae.—Trophosome,
polyp with filiform tentacles
in three or four whorls. Dendroclava,
a hydroid, produces the
medusa known as Turritopsis.
9. Clavidae (including the
medusa-family Tiaridae (figs. 27
and 51). Trophosome, polyps
with scattered filiform tentacles;
gonosome, medusae or gonophores,
the medusae with hollow
tentacles. Clava (fig. 5), a
common British hydroid, produces
gonophores; so also does
Cordylophora, a form inhabiting
fresh or brackish water. Turris
produces free medusae. Amphinema
is a medusan genus of unknown
hydroid.
10. Bythotiaridae.—Trophosome
unknown; gonosome, free
medusae, with deep, bell-shaped
umbrella, with interradial gonads
on the base of the stomach, with
branched radial canals, and correspondingly
numerous hollow tentacles. Bythotiara, Sibogita.
11. Corynidae (= hydroid families
Corynidae, Syncorynidae and
Cladocorynidae + medusan family
Sarsiidae).—Trophosome polyps
with capitate tentacles, simple or
branched, scattered or verticillate;
gonosome, free medusae or gonophores.
Coryne, a common British
hydroid, produces gonophores;
Syncoryne, indistinguishable from
it, produces medusae known as Sarsia (fig. 51). Cladocoryne is
another hydroid genus; Codonium and Dipurena (fig. 50) are medusan
genera.
12. Myriothelidae.—The genus Myriothela is a solitary polyp with
scattered capitate tentacles, producing sporosacs.
13. Hydrolaridae.—Trophosome (only known in one genus),
polyps with two tentacles forming a creeping colony; gonosome,
free medusae with four, six or more radial canals, giving off one or
more lateral branches which run to the margin of the umbrella, with
the stomach produced into four, six or more lobes, upon which the
gonads are developed; the mouth with four lips or with a folded
margin; the tentacles simple, arranged evenly round the margin of
the umbrella. The remarkable hydroid Lar (fig. 11) grows upon the
tubes of the worm Sabella and produces a medusa known as Willia.
Another medusan genus is Proboscidactyla.
14. Monobrachiidae.—The genus Monobrachium is a colony-forming
hydroid which grows upon the shells of bivalve molluscs,
each polyp having but a single tentacle. It buds medusae, which,
however, are as yet only known in an immature condition (C.
Mereschkowsky [41]).
15. Ceratellidae.—Trophosome polyps forming branching colonies
of which the stem and main branches are thick and composed of a
network of anastomosing coenosarcal tubes covered by a common
ectoderm and supported by a thick chitinous perisarc; hydranths
similar to those of Coryne; gonosome, sessile gonophores. Ceratella,
an exotic genus from the coast of East Africa, New South Wales and
Japan. The genera Dehitella Gray and Dendrocoryne Inaba should
perhaps be referred to this family; the last-named is regarded by
S. Goto [16] as the type of a distinct family, Dendrocorynidae.
Doubtful families, or forms difficult to classify, are: Pteronemidae,
Medusae of Cladonemid type, with hydroids for the most part unknown.
The British genus Gemmaria, however, is budded from a
hydroid referable to the family Corynidae. Pteronema (fig. 53).
Nemopsidae, for the floating polyp Nemopsis, very similar to
Tubularia in character; the medusa, on the other hand, is very
similar to Hippocrene (Margelidae). See C. Chun (Hydrozoa [1]).
Pelagohydridae, for the floating polyp Pelagohydra, Dendy, from
New Zealand. The animal is a solitary polyp bearing a great number
of medusa-buds. The body, representing the hydranth of an
ordinary hydroid, has the aboral portion modified into a float, from
which hangs down a proboscis bearing the mouth. The float is
covered with long tentacles and bears the medusa-buds. The
proboscis bears at its extremity a circlet of smaller oral tentacles.
Thus the affinities of the hydranth are clearly, as Dendy points out,
152
with a form such as Corymorpha, which also is not fixed but only
rooted in the mud. The medusae, on the other hand, have the
tentacles in four tufts of (in the buds) five each, and thus resemble
the medusae of the
family Margelidae.
See A. Dendy [12].
 |
| Fig. 54.—Diagram showing possible modifications
of the persons of a Calyptoblastic
Hydromedusa. Letters a to h same as in
fig. 49. i, The horny cup or hydrotheca of
the hydriform persons; l, medusiform person
springing from m, a modified, hydriform
person (blastostyle); n, the horny case or
gonangium enclosing the blastostyle and
its buds. This and the hydrotheca i give
origin to the name Calyptoblastea. (After
Allman.) |
Perigonimus.—This
common British hydroid
belongs by its
characters to the
family Bougainvillidae;
it produces,
however, a medusa
of the genus Tiara (fig.
52), referable to the
family Clavidae; a
fact sufficient to indicate
the tentative
character of even the
most modern classifications
of this order.
Sub-order II.
Hydroidea Calyptoblastea
(Leptomedusae).—Trophosome
with polyps
always differentiated
into nutritive and
reproductive individuals
(blastostyles)
enclosed in hydrothecae
and gonothecae
respectively;
with sympodial type
of budding. Gonosome
with free medusae
or gonophores;
the medusae typically
with otocysts,
sometimes with cordyli
or ocelli (figs.
54, 55).
 |
| Fig. 55.—View of the Oral Surface of
one of the Leptomedusae (Irene pellucida,
Haeckel), to show the numerous
tentacles and the otocysts. |
ge, Genital glands.
M, Manubrium.
ot, Otocysts.
rc, The four radiating canals.
Ve, The velum. |
The calyptoblastic
polyp of the nutritive
type is very uniform in character, its tendency to variation
being limited, as it were, by the enclosing hydrotheca. The
hydranth almost always has a single circlet of tentacles, like
the Bougainvillea-type, in the preceding sub-order; an exception
is the curious genus Clathrozoon, in which the hydranth has
a single tentacle. The
characteristic hydrotheca
is formed by the bud at
an early stage (fig. 56);
when complete it is an
open cup, in which the
hydranth develops and
can be protruded from the
opening for the capture
of food, or is withdrawn
into it for protection.
Solitary polyps are unknown
in this sub-order;
the colony may be creeping
or arborescent in form;
if the latter, the budding
of the polyps, as already
stated, is of the sympodial
type, and either
biserial, forming stems
capable of further branching,
or uniserial, forming
pinnules not capable of further branching. In the biserial type
the polyps on the two sides of the stem have primitively an
alternating, zigzag arrangement; but, by a process of differential
growth, quickened in the 1st, 3rd, 5th, &c., members of the
stem, and retarded in the 2nd, 4th, 6th, &c., members, the polyps
may assume secondarily positions opposite to one another on
the two sides of the stem. Other variations in the mode of
growth or budding bring about further differences in the building
up of the colony, which are not in all cases properly understood
and cannot be described in detail here. The stem may contain
a single coenosarcal tube (“monosiphonic”) or several united
in a common perisarc (“polysiphonic”). An important variation
is seen, in the form of the hydrotheca itself, which may come
off from the main stem by a stalk, as in Obelia, or may be
sessile, without a stalk, as in Sertularia.
 |
| After Allman, Gymnoblastic Hydroids, by permission of
the council of the Ray Society. |
| Fig. 56.—Diagrams to show the mode of
formation of the Hydrotheca and Gonotheca
in Calyptoblastic Hydroids. A-D are stages
common to both; from D arises the hydrotheca
(E) or the gonotheca (F); th, theca;
st, stomach; t, tentacles; m, mouth; mb,
medusa-buds. |
In many Calyptoblastea there occur also reduced defensive
polyps or dactylozoids, which in this sub-order have received
the special name of sarcostyles. Such are the “snake-like zoids”
of Ophiodes and other genera, and as such are generally interpreted
the “machopolyps”
of the
Plumularidea.
These organs are
supported by cuplike
structures of the
perisarc, termed
nematophores, regarded
as modified
hydrothecae supporting
the specialized
polyp-individuals.
They are
specially characteristic
of the family
Plumularidae.
The medusa-buds,
as already stated,
are always produced
from blastostyles,
reduced non-nutritive
polyps without
mouth or tentacles.
An apparent, but
not real, exception
is Halecium halecinum,
in which the
blastostyle is produced
from the side
of a nutritive polyp,
and both are enclosed
in a common
theca without a
partition between
them (Allman [1]
p. 50, fig. 24). The
gonotheca is formed in its early stage in the same way as the
hydrotheca, but the remains of the hydranth persists as an
operculum closing the capsule, to be withdrawn when the
medusae or genital products are set free (fig. 56).
The blastostyles, gonophores and gonothecae furnish a series of variations
which can best be considered as so many stages of evolution.
Stage 1, seen in Obelia. Numerous medusae are budded successively
within the gonotheca and set free; they swim off and mature in the
open sea (Allman [1], p. 48, figs. 18, 19).
Stage 2, seen in Gonothyraea. Medusae, so-called “meconidia,”
are budded but not liberated; each in turn, when it reaches sexual
maturity, is protruded from the gonotheca by elongation of the
stalk, and sets free the embryos, after which it withers and is replaced
by another (Allman [1], p. 57, fig. 28).
Stage 3, seen in Sertularia.—The gonophores are reduced in varying
degree, it may be to sporosacs; they are budded successively from
the blastostyle, and each in turn, when ripe, protrudes the spadix
through the gonotheca (fig. 57, A, B). The spadix forms a gelatinous
cyst, the so-called acrocyst (ac), external to the gonotheca (gth),
enclosing and protecting the embryos. Then the spadix withers,
leaving the embryos in the acrocyst, which may be further protected
by a so-called marsupium, a structure formed by tentacle-like
processes growing out from the blastostyle to enclose the acrocyst,
each such process being covered by perisarc like a glove-finger
secreted by it (fig. 57, C). (Allman [1], pp. 50, 51, figs. 21-24;
Weismann [58], p. 170, pl. ix., figs. 7, 8.)
153
Stage 4, seen in Plumularidae.—The generative elements are
produced in structures termed corbulae, formed by reduction
and modification of branches of the colony. Each corbula
contains a central row of blastostyles enclosed and protected
by lateral rows of branches representing stunted buds (Allman [1],
p. 66, fig. 30).
 |
| After Allman, Gymnoblastic Hydroids, by permission of the
council of the Ray Society. |
| Fig. 57.—Diagrams to show the mode of
formation of an Acrocyst and a Marsupium.
In A two medusa-buds are seen within the gonotheca
(gth), the upper more advanced than the
lower one. In B the spadix of the upper bud has
protruded itself through the top of the gonotheca
and the acrocyst (ac) is secreted round it.
In C the marsupium (m) is formed as finger-like
process from the summit of the blastostyle, enclosing
the acrocyst; b, medusa-buds on the
blastostyle. |
The Leptomedusa in form is generally shallow, more or less
saucer-like, with velum less developed than in Anthomedusae
(fig. 55). The characteristic sense-organs are ectodermal otocysts,
absent, however, in some genera, in which case cordyli
may replace them. When otocysts are present, they are at least
eight in number, situated adradially, but are often very numerous.
The cordyli are scattered on the ring-canal. Ocelli, if present,
are borne on the tentacle-bulbs. The tentacles are usually
hollow, rarely solid (Obelia). In number they are rarely less than
four, but in Dissonema there are only two. Primitively there
are four perradial tentacles, to which may be added four interradial,
or they may become very numerous and are then scattered
evenly round the margin, never arranged in tufts or clusters.
In addition to
tentacles, there
may be marginal
cirri (Laodice)
with a solid
endodermal axis,
spirally coiled,
very contractile,
and bearing a
terminal battery
of nematocysts.
The gonads are developed
typically
beneath the radial
canals or below
the stomach or
its pouches, often
stretching as long
bands on to the
base of the manubrium.
In Octorchidae
(fig. 58)
each such band
is interrupted,
forming one mass
at the base of the
manubrium and
another below the
radial canal in
each radius, in all
eight separate gonad-masses, as the name implies. In some
Leptomedusae excretory “marginal tubercles” are developed
on the ring-canal.
Classification.—As in the Gymnoblastea, the difficulty of uniting
the hydroid and medusan systems into one scheme of classification
is very great in the present state of our knowledge. In a great many
Leptomedusae the hydroid stage is as yet unknown, and it is by no
means certain even that they possess one. It is quite possible that
some of these medusae will be found to be truly hypogenetic, that is
to say, with a life-cycle secondarily simplified by suppression of
metagenesis. At present, ten recent and one extinct family of
Calyptoblastea (Leptomedusae) may be recognized provisionally:
1. Eucopidae (figs. 55, 59).—Trophosome with stalked hydrothecae;
gonosome, free medusae with otocysts and four, rarely six
or eight, unbranched radial canals. Two of the commonest British
hydroids belong to this family, Obelia and Clytia. Obelia forms
numerous polyserial stems of the characteristic zigzag pattern growing
up from a creeping basal stolon, and buds the medusa of the same
name. In Clytia the polyps arise singly from the stolon, and the
medusa is known as Phialidium (fig. 59).
2. Aequoridae.—Trophosome only known in one genus (Polycanna),
and similar to the preceding; gonosome, free medusae with
otocysts and with at least eight radial canals, often a hundred or
more, simple or branched. Aequorea is a common medusa.
3. Thaumantidae.—Trophosome only known in one genus (Thaumantias),
similar to that of the Eucopidae; gonosome, free medusae
with otocysts inconspicuous or absent, with usually four, sometimes
eight, rarely more than eight, radial canals, simple and unbranched,
along which the gonads are developed, with numerous tentacles
bearing ocelli and with marginal sense-clubs. Laodice and Thaumantias
are representative genera.
4. Berenicidae.—Trophosome unknown; gonosome, free medusae,
with four or six radial canals, bearing the gonads, with numerous
tentacles, between which occur sense-clubs, without otocysts.
Berenice, Staurodiscus, &c.
 |
| After Haeckel, System der Medusen, by permission of Gustav Fischer. |
| Fig. 58.—Octorchandra canariensis, from life. |
5. Polyorchidae.—Trophosome unknown; gonosome, free medusae
of deep form, with radial canals branched in a feathery manner, and
bearing gonads on the main canal, but not on the branches, with
numerous hollow tentacles bearing ocelli, and without otocysts.
Polyorchis, Spirocodon.
6. Campanularidae.--Trophosome as in Eucopidae; gonosome,
sessile gonophores. Many common or well-known genera belong
here, such as Halecium, Campanularia, Gonothyraea, &c.
7. Lafoëidae.—Trophosome as in the preceding; gonosome, free
medusae or gonophores, the medusae with large open otocysts.
The hydroid genus Lafoëa is remarkable for producing gonothecae on
the hydrorhiza, each containing a blastostyle which bears a single
gonophore; this portion of the colony was formerly regarded as an
independent parasitic hydroid, and was named Coppinia. Medusan
genera are Mitrocoma, Halopsis, Tiaropsis (fig. 29, &c.).
(So far as the characters of the trophosome are concerned, the
seven preceding families are scarcely distinguishable, and they form
a section apart, contrasting sharply with the families next to be
mentioned, in none of which are free medusae liberated from the
colony, so that only the characters of the trophosome need be considered.)
 |
| After E. T. Browne, Proc. Zool. Soc. of London, 1896. |
| Fig. 59.—Three stages in the development of Phialidium temporarium.
a, The youngest stage, is magnified about 22 diam.; b,
older, is magnified about 8 diam.; c, the adult medusa, is magnified. |
8. Sertularidae.—Hydrothecae sessile, biserial, alternating or
opposite on the stem. Sertularia and Sertularella are two very
common genera of this family.
9. Plumularidae.—Hydrothecae sessile, biserial on the main stem,
uniserial on the lateral branches or pinnules, which give the colony
its characteristic feathery form; with nematophores. A very
abundant and prolific family; well-known British genera are
Plumularia, Antennularia and Aglaophenia.
10. Hydroceratinidae.—This family contains the single Australian
species Clathrozoon wilsoni Spencer, in which a massive hydrorhiza
154
bears sessile hydrothecae, containing hydranths each with a single
tentacle, and numerous nematophores. See W. B. Spencer [53].
11. Dendrograptidae, containing fossil (Silurian) genera, such as
Dendrograptus and Thamnograptus, of doubtful affinities.
 |
| Fig. 60.—Portion of the
calcareous corallum of Millepora
nodosa, showing the
cyclical arrangement of the
pores occupied by the “persons”
or hydranths. About
twice the natural size. (From
Moseley.) |
Order III. Hydrocorallinae.—Metagenetic colony-forming
Hydromedusae, in which the polyp-colony forms a massive,
calcareous corallum into which the polyps can be retracted;
polyp-individuals always of two kinds, gastrozoids and dactylozoids;
gonosome either free medusae or sessile gonophores.
The trophosome consists of a mass
of coenosarcal tubes anastomosing
in all planes. The interspaces
between the tubes are filled up
by a solid mass of lime, consisting
chiefly of calcium carbonate,
which replaces the chitinous perisarc
of ordinary hydroids and forms
a stony corallum or coenosteum
(fig. 60). The surface of the
coenosteum is covered by a layer
of common ectoderm, containing
large nematocysts, and is perforated
by pores of two kinds,
gastropores and dactylopores,
giving exit to gastrozoids and
dactylozoids respectively, which
are lodged in vertical pore-canals
of wider calibre than the coenosarcal
canals of the general network.
The coenosteum increases
in size by new growth at the surface; and in the deeper,
older portions of massive forms the tissues die off after a certain
time, only the superficial region retaining its vitality down to a
certain depth. The living tissues at the surface are cut off
from the underlying dead portions by horizontal partitions
termed tabulae, which are formed successively as the coenosteum
increases in age and size. If the coenosteum of Millepora be
broken across, each pore-canal (perhaps better termed a polyp-canal)
is seen to be interrupted by a series of transverse
partitions, representing successive periods of growth with
separation from the underlying dead portions.
 |
| Fig. 61.—Enlarged view of the surface of a living Millepora,
showing five dactylozooids surrounding a central gastrozooid. (From
Moseley.) |
 |
| Fig. 62.—Diagrams illustrating the successive
stages in the development of the
cyclosystems of the Stylasteridae. (After
Moseley.) |
1, Sporadopora dichotoma.
2, 3, Allopora nobilis.
4, Allopora profunda.
5, Allopora miniacea.
6, Astylus subviridis.
7, Distichopora coccinea.
s, Style.
dp, Dactylopore.
gp, Gastropore.
b, In fig. 6, inner horseshoe-shaped mouth of gastropore. |
Besides the wider vertical pore-canals and the narrower,
irregular coenosarcal canals, the coenosteum may contain, in its
superficial portion, chambers or ampullae, in which the reproductive
zoids (medusae or gonophores) are budded from the
coenosarc.
The gastropores and dactylopores are arranged in various
ways at the surface, a common pattern being the formation of a
cyclosystem (fig. 60), in which a central gastrozoid is surrounded
by a ring of dactylozoids (fig. 61). In such a system the dactylopores
may be confluent with the gastropore, so that the entire
cyclosystem presents itself as a single aperture subdivided by
radiating partitions,
thus having a superficial
resemblance to
a madreporarian
coral with its radiating
septa (figs. 62
and 63).
The gastrozoids
usually bear short
capitate tentacles,
four, six or twelve
in number; but in
Astylus (fig. 63) they
have no tentacles.
The dactylozoids
have no mouth; in
Milleporidae they
have short capitate
tentacles, but lack
tentacles in Stylasteridae.
The gonosome consists
of free medusae
in Milleporidae,
which are budded
from the apex of a
dactylozoid in Millepora
murrayi, but in
other species from
the coenosarcal
canals. The medusae
are produced by direct budding, without an entocodon in the
bud. They are liberated in a mature condition, and probably
live but a short time, merely sufficient to spread the species.
The manubrium bearing the gonads is
mouthless, and the umbrella is without
tentacles, sense-organs, velum or radial
canals. In the Stylasteridae sessile gonophores
are formed, always by budding
from the coenosarc. In Distichopora the
gonophores have radial canals, but in
other genera they are sporosacs with no
trace of medusoid structure.
 |
| Fig. 63.—Portion of
the corallum of Astylus
subviridis (one of the
Stylasteridae), showing
cyclosystems placed at
intervals on the
branches, each with a
central gastropore and
zone of slit-like dactylopores.
(After
Moseley.) |
Classification.—Two families are known:—
1. Milleporidae.—Coenosteum massive,
irregular in form; pores scattered irregularly
or in cyclosystems, without styles, with
transverse tabulae; free medusae. A single
genus, Millepora (figs. 60, 61).
2. Stylasteridae.—Coenosteum arborescent,
sometimes fanlike, with pores only
on one face, or on the lateral margins of the
branches; gastropores with tabulae only in
two genera, but with (except in Astylus) a
style, i.e. a conical, thorn-like projection
from the base of the pore, sometimes found
also in dactylopores; sessile gonophores.
Sporadopora has the pores scattered irregularly.
Distichopora has the pores arranged
in rows. Stylaster has cyclosystems. In
Allopora the cyclostems resemble the calyces
of Anthozoan corals. In Cryptohelia the
cyclosystem is covered by a cap or operculum.
In Astylus (fig. 63) styles are
absent.
Affinities of the Hydrocorallinae.—There
can be no doubt that the forms comprised
in this order bear a close relationship to the
Hydroidea, especially the sub-order Gymnoblastea,
with which they should perhaps be
classed in a natural classification. A hydrocoralline
may be regarded as a form of
hydroid colony in which the coenosarc
forms a felt-work ramifying in all planes, and in which the
chitinous perisarc is replaced by a massive calcareous skeleton. So
far as the trophosome is concerned, the step from an encrusting
155
hydroid such as Hydractinia to the hydrocoralline Millepora is not
great.
Hickson considers that the families Milleporidae and Stylasteridae
should stand quite apart from one another and should not be united
in one order. The nearest approach to the Stylasteridae is perhaps
to be found in Ceratella, with its arborescent trophosome formed of
anastomosing coenosarcal tubes supported by a thick perisarc and
covered by a common ectoderm. Ceratella stands in much the same
relation to the Stylasteridae that Hydractinia does to the Milleporidae,
in both cases the chitinous perisarc being replaced by the
solid coenosteum to which the hydrocorallines owe the second half
of their name.
Order IV. Graptolitoidea (Rhabdophora, Allman).—This
order has been constituted for a peculiar group of palaeozoic
fossils, which have been interpreted as the remains of the skeletons
of Hydrozoa of an extinct type.
A typical graptolite consists of an axis bearing a series of
tooth-like projections, like a saw. Each such projection is regarded
as representing a cup or hydrotheca, similar to those borne
by a calyptoblastic hydroid, such as Sertularia. The supposed
hydrothecae may be present on one side of the axis only (monoprionid)
or on both sides (diprionid); the first case may be
conjectured to be the result of uniserial (helicoid) budding, the
second to be produced by biserial (scorpioid) budding. In one
division (Retiolitidae) the axis is reticulate. In addition to the
stems bearing cups, there are found vesicles associated with
them, which have been interpreted as gonothecae or as floats,
that is to say, air-bladders, acting as hydrostatic organs for a
floating polyp-colony.
Since no graptolites are known living, or, indeed, since palaeozoic
times, the interpretation of their structure and affinities
must of necessity be extremely conjectural, and it is by no means
certain that they are Hydrozoa at all. It can only be said that
their organization, so far as the state of their preservation
permits it to be ascertained, offers closer analogies with the
Hydrozoa, especially the Calyptoblastea, than with any other
existing group of the animal kingdom.
See the treatise of Delage and Hérouard (Hydrozoa, [4]), and the
article Graptolites.
Order V. Trachylinea.—Hydromedusae without alternation
of generations, i.e. without a hydroid phase; the medusa
develops directly from the actinula larva, which may, however,
multiply by budding. Medusae with sense-organs represented
by otocysts derived from modified tentacles (tentaculocysts),
containing otoliths of endodermal origin, and innervated from
the ex-umbral nerve-ring.
This order, containing the typical oceanic medusae, is divided
into two sub-orders.
Sub-order 1. Trachomedusae.—Tentacles given off from
the margin of the umbrella, which is entire, i.e. not lobed or
indented; tentaculocysts usually enclosed in vesicles; gonads
on the radial canals. The medusae of this order are characterized
by the tough, rigid consistence of the umbrella, due partly to
the dense nature of the mesogloea, partly to the presence of a
marginal rim of chondral tissue, consisting of thickened ectoderm
containing great numbers of nematocysts, and forming, as it
were, a cushion-tyre supporting the edge of the umbrella. Prolongations
from the rim of chondral tissue may form clasps
or peronia supporting the tentacles. The tentacles are primarily
four in number, perradial, alternating with four interradial
tentaculocysts, but both tentacles and sense-organs may be
multiplied and the primary perradii may be six instead of four
(fig. 26). The tentacles are always solid, containing an axis
of endoderm-cells resembling notochordal tissue or plant-parenchyma,
and are but moderately flexible. The sense-organs
are tentaculocysts which are usually enclosed in vesicles and
may be sunk far below the surface. The gonads are on the
radial canals or on the stomach (Ptychogastridae), and each
gonad may be divided into two by a longitudinal sub-umbral
muscle-tract. The radial canals are four, six, eight or more,
and in some genera blindly-ending centripetal canals are present
(fig. 26). The stomach may be drawn out into the manubrium,
forming a proboscis (“Magenstiel”) of considerable length.
The development of the Trachomedusae, so far as it is known,
shows an actinula-stage which is either free (larval) or passed
over in the egg (foetal) as in Geryonia; in no case does there
appear to be a free planula-stage. The actinula, when free,
may multiply by larval budding, but in all cases both the original
actinula and all its descendants become converted into medusae,
so that there is no alternation
of generations.
In Gonionemus the actinula
becomes attached
and polyp-like and reproduces
by budding.
 |
| After Haeckel, System der Medusen, by permission
of Gustav Fischer. |
| Fig. 64. Olindias mülleri. |
The Trachomedusae are
divided into the following
families:
1. Petasidae (Petachnidae).—Four
radial canals,
four gonads; stomach not
prolonged into the manubrium,
which is relatively
short; tentaculocysts free.
Petasus and other genera
make up this family,
founded by Haeckel, but
no other naturalist has
ever seen them, and it is
probable that they are
simply immature forms of
other genera.
2. Olindiadae, with four
radial canals and four
gonads; manubrium
short; ring-canals giving
off blind centripetal
canals; tentaculocysts
enclosed. Olindias mülleri
(fig. 64) is a common
Mediterranean species.
Other genera are Aglauropsis,
Gossea and Gonionemus;
the last named
bears adhesive suckers on
the tentacles. Some doubt
attaches to the position
of this family. It has
been asserted that the
tentaculocysts are entirely
ectodermal and that either
the family should be
placed amongst the Leptomedusae,
or should form,
together with certain Leptomedusae, an entirely distinct order.
In Gonionemus, however, the concrement-cells are endodermal.
3. Trachynemidae.—Eight radial canals, eight gonads, stomach
not prolonged into manubrium; tentaculocysts
enclosed. Rhopalonema, Trachynema,
&c.
 |
| After E. T. Browne, Proc. Zool.
Soc. of London. |
| Fig. 65.—Aglantha rosea (Forbes), a British medusa. |
4. Ptychogastridae (Pectyllidae).—As
in the preceding, but with suckers on
the tentacles. Ptychogastria Allman
(= Pectyllis), a deep-sea form.
5. Aglauridae.—Eight radial canals,
two, four or eight gonads; tentacles
numerous; tentaculocysts free; stomach
prolonged into manubrium. Aglaura,
Aglantha (fig. 65), &c., with eight gonads;
Stauraglaura with four; Persa with two.
Amphogona, hermaphrodite, with male
and female gonads on alternating radial
canals.
6. Geryonidae.—Four or six radial
canals; gonads band-like; stomach
prolonged into a manubrium of great
length; tentaculocysts enclosed. Liriope,
&c., with four radial canals; Geryonia,
Carmarina (fig. 26), &c., with six.
7. Halicreidae.—Eight very broad
radial canals; ex-umbrella often provided
with lateral outgrowths; tentacles
differing in size, but in a single row.
Halicreas.
Sub-order 2. Narcomedusae.—Margin of the umbrella-lobed,
tentacles arising from the ex-umbrella at some distance
from the margin; tentaculocysts exposed, not enclosed in
vesicles; gonads on the sub-umbral floor of the stomach or of
the gastric pouches.
156
 |
| Fig. 66.—Cunina rhododactyla, one
of the Narcomedusae. (After Haeckel.) |
c, Circular canal.
h, “Otoporpae” or centripetal process of the marginal cartilaginous ring connected with tentaculocyst.
k, Stomach.
l, Jelly of the disk.
r, Radiating canal (pouch of stomach).
tt, Tentacles.
tw, Tentacle root. |
The Narcomedusae exhibit peculiarities of form and structure
which distinguish them at once from all other Hydromedusae.
The umbrella is shallow and has the margin supported by a
rim of thickened ectoderm, as in the Trachomedusae, but not
so strongly developed. The tentacles are not inserted on the
margin of the umbrella, but arise high up on the ex-umbral
surface, and the umbrella is prolonged into lobes corresponding
to the interspaces between the tentacles. The condition of
things can be imagined by supposing that in a medusa primitively
of normal build, with tentacles at the margin, the umbrella
has grown down past the insertion of the tentacles. As a result
of this extension of the umbrellar margin, all structures belonging
to this region, namely, the ring-canal, the nerve-rings, and the
rim of thickened ectoderm,
do not run an even course,
but are thrown into festoons,
caught up under
the insertion of each tentacle
in such a way that
the ring-canal and its accompaniments
form in each
notch of the umbrellar
margin an inverted V, the
apex of which corresponds
to the insertion of the
tentacle; in some cases
the limbs of the V may run
for some distance parallel
to one another, and may
be fused into one, giving a
figure better compared to
an inverted Y. Thus the
ectodermal rim runs
round the edge of each
lobe of the umbrella and then passes upwards towards
the base of the tentacle from the re-entering angle between
two adjacent lobes, to form with its fellow of the next
lobe a tentacle-clasp or peronium, i.e. a streak of thickened
ectoderm supporting the tentacle. Similarly the ring-canal
runs round the edge of the lobe as the so-called festoon-canal,
and then runs upwards under the peronium to the base of the
tentacle as one of a pair of peronial canals, the limbs of the V-like
figure already mentioned. The nerve-rings have a similar
course. The tentaculocysts are implanted round the margins
of the lobes of the umbrella and may be supported by prolongations
of the ectodermal rim termed otoporpae (Gehörspangen).
The radial canals are represented by wide gastric pouches, and
may be absent, so that the tentacles arise directly from the
stomach (Solmaridae). The tentacles are always solid, as in
Trachomedusae.
The development of the Narcomedusae is in the main similar
to that of the Trachomedusae, but shows some remarkable
features. In Aeginopsis a planula is formed by multipolar
immigration. The two ends of the planula become greatly
lengthened and give rise to the two primary tentacles of the
actinula, of which the mouth arises from one side of the planula.
Hence the principal axis of the future medusa corresponds,
not to the longitudinal axis of the planula, but to a transverse
axis. This is in some degree parallel to the cases described
above, in which a planula gives rise to the hydrorhiza, and buds
a polyp laterally.
In Cunina and allied genera the actinula, formed in the manner
described, has a hypostome of great length, quite disproportionate
to the size of the body, and is further endowed with the power
of producing buds from a stolon arising from the aboral side of
the body. In these species the actinula is parasitic upon another
medusa; for instance, Cunoctantha octonaria upon Turritopsis,
C. proboscidea upon Liriope or Geryonia. The parasite effects
a lodgment in the host either by invading it as a free-swimming
planula, or, apparently, in other cases, as a spore-embryo which is
captured and swallowed as food by the host. The parasitic actinula
is found attached to the proboscis of the medusa; it thrusts its
greatly elongated hypostome into the mouth of the medusa
and nourishes itself upon the food in the digestive cavity of
its host. At the same time it produces buds from an aboral
stolon. The buds become medusae by the direct method of
budding described above. In some cases the buds do not become
detached at once, but the stolon continues to grow and to produce
more buds, forming a “bud-spike” (Knospenähre), which
consists of the axial stolon bearing medusa-buds in all stages
of development. In such cases the original parent-actinula
does not itself become a medusa, but remains arrested in development
and ultimately dies off, so that a true alternation of generations
is brought about. It is in these parasitic forms that we
meet with the method of reproduction by sporogony described
above.
In other Narcomedusae, e.g. Cunoctantha fowleri Browne,
buds are formed from the sub-umbrella on the under side of the
stomach pouches, where later the gonads are developed.
Classification.—Three families of Narcomedusae are recognized
(see O. Maas [40]):
 |
| After O. Maas, Craspedoten Medusen der
Siboga Expedition, by permission of E. S.
Brill & Co. |
| Fig. 67.—Solmundella bitentaculata
(Quoy and Gaimard). |
1. Cunanthidae.—With broad gastric pouches which are simple,
i.e. undivided, and “pernemal,” i.e. correspond in position with the
tentacles. Cunina (fig. 66)
with more than eight tentacles;
Cunoctantha with eight
tentacles, four perradial, four
interradial.
2. Aeginidae.—Radii a multiple
of four, with radial gastric
pouches bifurcated or subdivided;
the tentacles are
implanted in the notch between
the two subdivisions of each
(primary) gastric pouch, hence
the (secondary) gastric pouches
appear to be “internemal”
in position, i.e. to alternate in
position with the tentacles.
Aegina, with four tentacles and
eight pouches; Aeginura (fig.
25), with eight tentacles and
sixteen pouches; Solmundella
(fig. 67), with two tentacles and
eight pouches; Aeginopsis
(fig. 23), with two or four
tentacles and sixteen pouches.
3. Solmaridae.—No gastric
pouches; the numerous tentacles
arise direct from the
stomach, into which also the
peronial canals open, so that
the ring-canal is cut up into separate festoons. Solmaris, Pegantha,
Polyxenia, &c. To this family should be referred, probably, the genus
Hydroctena, described by C. Dawydov [11a] and regarded by him
as intermediate between Hydromedusae and Ctenophora. See
O. Maas [35].
Appendix to the Trachylinae.
Of doubtful position, but commonly referred to the Trachylinae,
are the two genera of fresh-water medusae, Limnocodium and
Limnocnida.
Limnocodium sowerbyi was first discovered in the Victoria regia
tank in the Botanic Gardens, Regent’s Park, London. Since then
it has been discovered in other botanic gardens in various parts of
Europe, its two most recent appearances being at Lyons (1901) and
Munich (1905), occurring always in tanks in which the Victoria regia
is cultivated, a fact which indicates that tropical South America is
its original habitat. In the same tanks a small hydroid, very similar
to Microhydra, has been found, which bears medusa-buds and is
probably the stock from which the medusa is budded. It is a remarkable
fact that all specimens of Limnocodium hitherto seen have
been males; it may be inferred from this either that only one polyp-stock
has been introduced into Europe, from which all the medusae
seen hitherto have been budded, or perhaps that the female medusa
is a sessile gonophore, as in Pennaria. The male gonads are carried on
the radial canals.
Limnocnida tanganyicae was discovered first in Lake Tanganyika,
but has since been discovered also in Lake Victoria and in the
river Niger. It differs from Limnocodium in having practically no
manubrium but a wide mouth two-thirds the diameter of the umbrella
across. It buds medusae from the margin of the mouth in May and
June, and in August and September the gonads are formed in the
place where the buds arose. The hydroid phase, if any, is not
known.
Both these medusae have sense-organs of a peculiar type, which
are said to contain an endodermal axis like the sense-organs of
Trachylinae, but the fact has recently been called in question for
157
Limnocodium by S. Goto, who considers the genus to be allied to
Olindias. Allman, on the other hand, referred Limnocodium to the
Leptomedusae.
In this connexion must be mentioned, finally, the medusae budded
from the fresh-water polyp Microhydra. The polyp-stages of Limnocodium
and Microhydra are extremely similar in character. In both
cases the hydranth is extremely reduced and has no tentacles, and
the polyp forms a colony by budding from the base. In Limnocodium
the body secretes a gelatinous mucus to which adhere
particles of mud, &c., forming a protective covering. In Microhydra
no such protecting case is formed. In view of the great resemblance
between Microhydra and the polyp of Limnocodium, it might be
expected that the medusae to which they give origin would also be
similar. As yet, however, the medusa of Microhydra has only been
seen in an immature condition, but it shows some well-marked
differences from Limnocodium, especially in the structure of the
tentacles, which furnish useful characters for distinguishing species
amongst medusae. The possession of a polyp-stage by Limnocodium
and Microhydra furnishes an argument against placing them in the
Trachylinae. Their sense-organs require renewed investigations.
(Browne [10] and [10a].)
Order VI. Siphonophora.—Pelagic floating Hydrozoa with
great differentiation of parts, each performing a special function;
generally regarded as colonies showing differentiation of individuals
in correspondence with a physiological division of
labour.
 |
| Fig. 68.—Diagram showing possible
modifications of medusiform
and hydriform persons of a colony
of Siphonophora. The thick black
line represents endoderm, the thinner
line ectoderm. (After Allman.) |
n, Pneumatocyst.
k, Nectocalyces (swimming bells).
l, Hydrophyllium (covering-piece).
i, Generative medusiform person.
g, Palpon with attached palpacle, h.
e, Siphon with branched grappling tentacle, f.
m, Stem. |
A typical Siphonophore is a stock or cormus consisting of a
number of appendages placed in organic connexion with one
another by means of a coenosarc. The coenosarc does not
differ in structure from that already described in colonial
Hydrozoa. It consists of a hollow tube, or tubes, of which the
wall is made up of the two body-layers, ectoderm and endoderm,
and the cavity is a continuation
of the digestive cavities
of the nutritive and other
appendages, i.e. of the coelenteron.
The coenosarc may
consist of a single elongated
tube or stolon, forming
the stem or axis of the
cormus on which, usually,
the appendages are arranged
in groups termed cormidia;
or it may take the form of a
compact mass of ramifying,
anastomosing tubes, in which
case the cormus as a whole
has a compact form and cormidia
are not distinguishable.
In the Disconectae the
coenosarc forms a spongy
mass, the “centradenia,”
which is partly hepatic in
function, forming the so-called
liver, and partly excretory.
The appendages show
various types of form and
structure corresponding to
different functions. The cormus
is always differentiated
into two parts; an upper
portion termed the nectosome,
in which the appendages are
locomotor or hydrostatic in
function, that is to say, serve
for swimming or floating;
and a lower portion termed
the siphosome, bearing appendages
which are nutritive,
reproductive or simply protective in function.
Divergent views have been held by different authors both as
regards the nature of the cormus as a whole, and as regards
the homologies of the different types of appendages borne
by it.
The general theories of Siphonophoran morphology are discussed
below, but in enumerating the various types of appendages it is
convenient to discuss their morphological interpretation at the same
time.
 |
| After A. Agassiz, from Lankester’s Treatise on
Zoology. |
| Fig. 69.—Porpita, seen from above,
showing the pneumatophore and expanded
palpons. |
In the nectosome one or more of the following types of appendage
occur:—
1. Swimming-bells, termed nectocalyces or nectophores (fig. 68, k),
absent in Chondrophorida and Cystophorida; they are contractile and
resemble, both in appearance, structure and function, the umbrella
of a medusa, with radial canals, ring-canal and velum; but they
are without manubrium,
tentacles or sense-organs,
and are always bilaterally
symmetrical, a peculiarity
of form related with the
fact that they are attached
on one side to the stem.
A given cormus may bear
one or several nectocalyces,
and by their contractions
they propel the
colony slowly along, like
so many medusae harnessed
together. In cases
where the cormus has no
pneumatophore the topmost
swimming bell may
contain an oil-reservoir or
oleocyst.
2. The pneumatophore
or air-bladder (fig. 68, n),
for passive locomotion,
forming a float which
keeps the cormus at or
near the surface of the
water. The pneumatophore
arises from the ectoderm as a pit or invagination, part of
which forms a gas-secreting gland, while the rest gives rise to an
air-sack lined by a chitinous cuticle. The orifice of invagination
forms a pore which may be closed up or may form a protruding
duct or funnel. As in the analogous swim-bladder of fishes, the
gas in the pneumatophore can be secreted or absorbed, whereby
the specific gravity of the body can be diminished or increased, so
as to cause it to float nearer the surface or at a deeper level.
Never more than one pneumatophore is found in a cormus, and
when present it is always situated at the highest point above the
swimming bells, if these are present also. In Velella the pneumatophore
becomes of complex structure and sends air-tubes, lined by a
chitin and resembling tracheae, down into the compact coenosarc,
thus evidently serving a respiratory as well as a hydrostatic
function.
Divergent views have been held as to the morphological
significance of the pneumatophore. E. Haeckel regarded the
whole structure as a glandular ectodermal pit formed on the ex-umbral
surface of a medusa-person. C. Chun and, more recently, R.
Woltereck [59], on the other hand, have shown that the ectodermal
pit which gives rise to the pneumatophore represents an entocodon.
Hence the cavity of the air-sack is equivalent to a sub-umbral
cavity in which no manubrium is formed, and the pore or orifice of
invagination would represent the margin of the umbrella. In the
wall of the sack is a double layer of endoderm, the space between
which is a continuation of the coelenteron. By coalescence of the
endoderm-layers, the coelenteron may be reduced to vessels, usually
eight in number, opening into a ring-sinus surrounding the pore.
Thus the disposition of the endoderm-cavities is roughly comparable
to the gastrovascular system of a medusa.
The difference between the theories of Haeckel and Chun is connected
with a further divergence in the interpretation of the stem or
axis of the cormus. Haeckel regards it as the equivalent of the
manubrium, and as it is implanted on the blind end of the pneumatophore,
such a view leads necessarily to the air-sack and gland being a
development on the ex-umbral surface of the medusa-person. Chun
and Woltereck, on the other hand, regard the stem as a stolo prolifer
arising from the aboral pole, that is to say, from the ex-umbrella,
similar to that which grows out from the ex-umbral surface of the
embryo of the Narcomedusae and produces buds, a view which is
certainly supported by the embryological evidence to be adduced
shortly.
In the siphosome the following types of appendages occur:—
1. Siphons or nutritive appendages, from which the order takes its
name; never absent and usually present in great numbers (fig. 68, e).
Each is a tube dilated at or towards the base and containing a mouth
at its extremity, leading into a stomach placed in the dilatation
already mentioned. The siphons have been compared to the manubrium
of a medusa-individual, or to polyps, and hence are sometimes
termed gastrozoids.
2. Palpons (fig. 68, g), present in some genera, especially in
Physonectae; similar to the siphons but without a mouth, and purely
tactile in function, hence sometimes termed dactylozoids. If a
distal pore or aperture is present, it is excretory in function; such
varieties have been termed “cystons” by Haeckel.
158
3. Tentacles (“Fangfäden”), always present, and implanted one
at the base of each siphon (fig. 68, f). The tentacles of siphonophores
may reach a great length and have a complex structure. They may
bear accessory filaments or tentilla (f′), covered thickly with batteries
of nematocysts, to which these organisms owe their great powers of
offence and defence.
4. Palpacles (“Tastfäden”), occurring together with palpons, one
implanted at the base of each palpon (fig. 68, h). Each palpacle is
a tactile filament, very extensile, without accessory filaments or
nematocysts.
5. Bracts (“hydrophyllia”), occur in Calycophorida and some
Physophorida as scale-like appendages protecting other parts (fig.
68, l). The mesogloea is greatly developed in them and they are
often of very tough consistency. By Haeckel they
are considered homologous with the umbrella of a
medusa.
 |
| From G. H. Fowler, after A. Agassiz, Lankester’s Treatise on Zoology. |
| Fig. 70.—Diagram of the structure of Velella, showing the central and
peripheral thirds of a half-section of the colony, the middle third being
omitted. The ectoderm is indicated by close hatching, the endoderm by
light hatching, the mesogloea by thick black lines, the horny skeleton of
the pneumatophore and sail by dotting. |
BL, Blastostyle.
C, Centradenia.
D, Palpon.
EC, Edge of colony prolonged beyond the pneumatophore.
G, Cavity of the large central siphon. |
M, Medusoid gonophores.
PN, Primary central chamber, and
PN′, concentric chamber of the pneumatophore, showing
an opening to the exterior and a “trachea.”
S, Sail. |
6. Gonostyles, appendages which produce by budding
medusae or gonophores, like the blastostyles of a hydroid
colony. In their most primitive form they are seen in
Velella as “gonosiphons,” which possess mouths like
the ordinary sterile siphons and bud free medusae. In
other forms they have no mouths. They may be
branched, so-called “gonodendra,” and amongst them
may occur special forms of palpons, “gonopalpons.”
The gonostyles have been compared to the blastostyles
of a hydroid colony, or to the manubrium of a
medusa which produces free or sessile medusa-buds.
7. Gonophores, produced either on the gonostyles
already mentioned or budded, as in hydrocorallines,
from the coenosarc, i.e. the stem (fig. 68, i.). They
show every transition between free medusae and
sporosacs, as already described, for hydroid colonies.
Thus in Velella free medusae are produced,
which have been described as an independent
genus of medusae, Chrysomitra.
In other types the medusae may be set
free in a mature condition as the so-called “genital swimming
bells,” comparable to the Globiceps of Pennaria. The most usual
condition, however, is that in which sessile medusoid gonophores or
sporosacs are produced.
 |
| From G. H. Fowler, after G.
Cuvier, Lankester’s Treatise on
Zoology. |
| Fig. 71.—Upper surface
of Velella, showing
pneumatophore and sail. |
The various types of appendages described in the foregoing may
be arranged in groups termed cormidia. In forms with a compact
coenosarc such as Velella, Physalia, &c., the separate cormidia cannot
be sharply distinguished, and such a condition is described technically
as one with “scattered” cormidia. In forms in which, on the
other hand, the coenosarc forms an elongated, tubular axis or stem,
the appendages are arranged as regularly recurrent cormidia along it,
and the cormidia are then said to be “ordinate.” In such cases the
oldest cormidia, that is to say, those furthest from the nectosome,
may become detached (like the segments
or proglottides of a tape-worm) and
swim off, each such detached cormidium
then becoming a small free cormus
which, in many cases, has been given an
independent generic name. A cormidium
may contain a single nutritive siphon
(“monogastric”) or several siphons
(“polygastric”):
The following are some of the forms
of cormidia that occur:—
1. The eudoxome (Calycophorida), consisting
of a bract, siphon, tentacle and
gonophore; when free it is known as
Eudoxia.
2. The ersaeome (Calycophorida), made up of the same appendages
as the preceding type but with the addition of a nectocalyx; when
free termed Ersaea.
3. The rhodalome of some Rhodalidae, consisting of siphon, tentacle
and one or more gonophores.
4. The athorome of Physophora, &c., consisting of siphon, tentacle,
one or more palpons with palpacles, and one or more gonophores.
5. The crystallome of Anthemodes, &c., similar to the athorome but
with the addition of a
group of bracts.
 |
| Fig. 72.—A, Diphyes campanulata;
B, a group of appendages (cormidium) of
the same Diphyes. (After C. Gegenbaur.) |
a, Axis of the colony.
m, Nectocalyx.
c, Sub-umbral cavity of nectocalyx.
v, Radial canals of nectocalyx.
o, Orifice of nectocalyx.
t, Bract.
n, Siphon.
g, Gonophore.
i, Tentacle. |
Embryology of the
Siphonophora.—The fertilized
ovum gives rise
to a parenchymula, with
solid endoderm, which is
set free as a free-swimming
planula larva, in
the manner already described
(see Hydrozoa).
The planula has its two
extremities dissimilar
(Bipolaria-larva). The
subsequent development
is slightly different according
as the future
cormus is headed by a
pneumatophore (Physophorida,
Cystophorida)
or by a nectocalyx (Calycophorida).
(i.) Physophorida,
for example
Halistemma (C.
Chun, Hydrozoa
[1]). The planula
becomes elongated
and broader
towards one pole,
at which a pit or
invagination of the
ectoderm arises.
Next the pit closes
up to form a
vesicle with a pore,
and so gives rise
to the pneumatophore.
From the
broader portion of
the planula an
outgrowth arises
which becomes the
first tentacle of
the cormus. The
endoderm of the
planula now acquires
a cavity,
and at the
narrower pole a
mouth is formed,
giving rise to the
primary siphon.
Thus from the
original planula three appendages are, as it were, budded off, while
the planula itself mostly gives rise to coenosarc, just as in some
hydroids the planula is converted chiefly into hydrorhiza.
(ii.) Calycophorida, for example, Muggiaea. The planula develops,
on the whole, in a similar manner, but the ectodermal invagination
arises, not at the pole of the planula, but on the side of its
broader portion, and gives rise, not to a pneumatophore, but to a
nectocalyx, the primary swimming bell or protocodon (“Fallschirm”)
which is later thrown off and replaced by secondary swimming bells,
metacodons, budded from the coenosarc.
159
From a comparison of the two embryological types there can be no
doubt on two points; first, that the pneumatophore and the protocodon
are strictly homologous, and, therefore if the nectocalyx is
comparable to the umbrella of a medusa, as seems obvious, the
pneumatophore must be so too; secondly, that the coenosarcal axis
arises from the ex-umbrella of the medusa and cannot be compared
to a manubrium, but is strictly comparable to the “bud-spike” of a
Narcomedusan.
Theories of Siphonophore Morphology.—The many theories that
have been put forward as to the interpretation of the cormus
and the various parts are set forth and discussed in the
treatise of Y. Delage and E. Hérouard (Hydrozoa [4]) and more
recently by R. Woltereck [59], and only a brief analysis can be
given here.
 |
| After C. Gegenbaur. |
| Fig. 73.—Physophora hydrostatica. |
a′, Pneumatocyst.
t, Palpons.
a, Axis of the colony.
m, Nectocalyx.
o, Orifice of nectocalyx.
n, Siphon.
g, Gonophore.
i, Tentacle. |
In the first place the cormus has been regarded as a single individual
and its appendages as organs. This is the so-called “polyorgan”
theory, especially connected
with the name of Huxley;
but it must be borne in mind that
Huxley regarded all the forms
produced, in any animal, between
one egg-generation and the next,
as constituting in the lump one
single individual. Huxley, therefore,
considered a hydroid colony,
for example, as a single individual,
and each separate polyp or medusa
budded from it as having the
value of an organ and not of an
individual. Hence Huxley’s view
is not so different from those held
by other authors as it seems to
be at first sight.
In more recent years Woltereck
[59] has supported Huxley’s view
of individuality, at the same time
drawing a fine distinction between
“individual” and “person.” The
individual is the product of sexual
reproduction; a person is an individual
of lower rank, which may
be produced asexually. A Siphonophore
is regarded as a single
individual composed of numerous
zoids, budded from the primary
zoid (siphon) produced from the
planula. Any given zoid is a
person-zoid if equivalent to the
primary zoid, an organ-zoid if
equivalent only to a part of it.
Woltereck considers the siphonophores
most nearly allied to the
Narcomedusae, producing like
the buds from an aboral stolon,
the first bud being represented
by the pneumatophore or protocodon,
in different cases.
Contrasting, in the second place,
with the polyorgan theory are the
various “polyperson” theories
which interpret the Siphonophore
cormus as a colony composed of
more or fewer individuals in organic
union with one another. On
this interpretation there is still
room for considerable divergence
of opinion as regards detail. To
begin with, it is not necessary on
the polyperson theory to regard
each appendage as a distinct individual;
it is still possible to
compare appendages with parts
of an individual which have become separated from one another
by a process of “dislocation of organs.” Thus a bract may be
regarded, with Haeckel, as a modified umbrella of a medusa,
a siphon as its manubrium, and a tentacle as representing a
medusan tentacle shifted in attachment from the margin to the
sub-umbrella; or a siphon may be compared with a polyp, of which
the single tentacle has become shifted so as to be attached to the
coenosarc and so on. Some authors prefer, on the other hand, to
regard every appendage as a separate individual, or at least as a
portion of an individual, of which other portions have been lost or
obliterated.
A further divergence of opinion arises from differences in the
interpretation of the persons composing the colony. It is possible to
regard the cormus (1) as a colony of medusa-persons, (2) as a colony
of polyp-persons, (3) as composed partly of one, partly of the other.
It is sufficient here to mention briefly the views put forward on this
point by C. Chun and R. Haeckel.
Chun (Hydrozoa [1]) maintains the older views of Leuckart and
Claus, according to which the cormus is to be compared to a floating
hydroid colony. It may be regarded as derived from floating polyps
similar to Nemopsis or Pelagohydra, which by budding produce a
colony of polyps and also form medusa-buds. The polyp-individuals
form the nutritive siphosome or trophosome. The medusa-buds
are either fertile or sterile. If fertile they become free medusae
or sessile gonophores. If sterile they remain attached and locomotor
in function, forming the nectosome, the pneumatophore
and swimming-bells.
Haeckel, on the other hand, is in accordance with Balfour in
regarding a Siphonophore as a medusome, that is to say, as a colony
composed of medusoid persons or organs entirely. Haeckel considers
that the Siphonophores have two distinct ancestral lines of
evolution:
1. In the Disconanthae, i.e. in such forms as Velella, Porpita, &c.,
the ancestor was an eight-rayed medusa (Disconula) which acquired a
pneumatophore as an ectodermal pit on the ex-umbrella, and in
which the organs (manubrium, tentacles, &c.) became secondarily
multiplied, just as they do in Gastroblasta as the result of incomplete
fission. The nearest living allies of the ancestral Disconula are to
be sought in the Pectyllidae.
 |
| After Haeckel, from Lankester’s Treatise on Zoology. |
| Fig. 74.—Stephalia corona, a young colony. |
p, Pneumatophore .
n, Nectocalyx.
l, Aurophore. |
lo, Orifice of the aurophore.
s, Siphon.
t, Tentacle. |
2. In the Siphonanthae, i.e. in all other Siphonophores, the ancestral
form was a Siphonula, a bilaterally symmetrical Anthomedusa
with a single long tentacle (cf. Corymorpha), which became displaced
from the margin to the sub-umbrella. The Siphonula produced
buds on the manubrium, as many Anthomedusae are known
to do, and these by reduction or dislocation of parts gave rise to
the various appendages of the colony. Thus the umbrella of the
Siphonula became the protocodon, and its manubrium, the axis or
stolon, which, by a process of dislocation of organs, escaped, as it
were, from the sub-umbrella through a cleft and became secondarily
attached to the ex-umbrella. It must be pointed out that, however
probable Haeckel’s theory may be in other respects, there is not the
slightest evidence for any such cleft in the umbrella having been
present at any time, and that the embryological evidence, as already
pointed out, is all against any homology between the stem and a
manubrium, since the primary siphon does not become the stem,
which arises from the ex-umbral side of the protocodon and is
strictly comparable to a stolon.
Classification.—The Siphonophora may be divided, following
Delage and Hérouard, into four sub-orders:
I. Chondrophorida (Disconectae Haeckel, Tracheophysae
Chun). With an apical chambered pneumatophore, from which
tracheal tubes may take origin (fig. 70); no nectocalyces or
bracts; appendages all on the lower side of the pneumatophore
arising from a compact coenosarc, and consisting of a central
160
principal siphon, surrounded by gonosiphons, and these again
by tentacles.
Three families: (1) Discalidae, for Discalia and allied genera, deep-sea
forms not well known; (2) Porpitidae for the familiar genus
Porpita (fig. 69) and its allies; and (3) Velellidae, represented by the
well-known genus Velella (figs. 70, 71), common in the Mediterranean
and other seas.
II. Calycophorida (Calyconectae, Haeckel). Without pneumatophore,
with one, two, rarely more nectocalyces.
Three families: (1) Monophyidae, with a single nectocalyx;
examples Muggiaea, sometimes found in British seas, Sphaeronectes,
&c.; (2) Diphyidae, with two nectocalyces; examples Diphyes (fig.
72), Praya, Abyla, &c.; and (3) Polyphyidae, with numerous nectocalyces;
example Hippopodius, Stephanophyes and other genera.
 |
| From G. H. Fowler, modified after G. Cuvier and E. Haeckel, Lankester’s Treatise
on Zoology. |
| Fig. 75.—A. Physalia, general view, diagrammatic; B, cormidium
of Physalia; D, palpon; T, palpacle; G, siphon; GP,
gonopalpon; M ♂, male gonophore; M ♀, female gonophore, ultimately
set free. |
III. Physophorida (Physonectae + Auronectae, Haeckel).
With an apical pneumatophore, not divided into chambers,
followed by a series of nectocalyces or bracts.
A great number of families and genera are referred to this group,
amongst which may be mentioned specially—(1) Agalmidae, containing
the genera Stephanomia, Agalma, Anthemodes, Halistemma,
&c.; (2) Apolemidae, with the genus Apolemia and its allies;
(3) Forskaliidae, with Forskalia and allied forms; (4) Physophoridae,
for Physophora (fig. 73) and other genera, (5) Anthophysidae, for
Anthophysa, Athorybia, &c.; and lastly the two families (6) Rhodalidae
and (7) Stephalidae (fig. 74), constituting the group Auronectae
of Haeckel. The Auronectae are peculiar deep-sea forms, little known
except from Haeckel’s descriptions, in which the large pneumatophore
has a peculiar duct, termed the aurophore, placed on its lower
side in the midst of a circle of swimming-bells.
IV. Cystophorida (Cystonectae, Haeckel). With a very large
pneumatophore not divided into chambers, but without nectocalyces
or bracts. Two sections can be distinguished, the
Rhizophysina, with long tubular coenosarc-bearing ordinate
cormidia, and Physalina, with compact coenosarc-bearing
scattered cormidia.
A type of the Rhizophysina is the genus Rhizophysa. The
Physalina comprise the families Physalidae and Epibulidae, of
which the types are Physalia (figs. 74, 75) and Epibulia, respectively.
Physalia, known commonly as the Portuguese man-of-war, is remarkable
for its great size, its brilliant colours, and its terrible stinging
powers.
Bibliography.—In addition to the works cited below, see the
general works cited in the article Hydrozoa, in some of which very
full bibliographies will be found.
1. G. J. Allman, “A Monograph of the Gymnoblastic or Tubularian
Hydroids,” Ray Society (1871-1872); 2. A. Brauer, “Über die
Entwickelung von Hydra,” Zeitschr. f. wiss. Zool. lii. (1891), pp. 169-216,
pls. ix.-xii.; 3. “Über die Entstehung der Geschlechtsprodukte
und die Entwickelung von Tubularia mesembryanthemum Allm.,”
t.c. pp. 551-579, pls. xxxiii.-xxxv.; 4. W. K. Brooks, “The Life-History
of the Hydromedusae: a discussion of the Origin of the
Medusae, and of the significance of Metagenesis,” Mem. Boston Soc.
Nat. Hist. iii. (1886), pp. 259-430, pis. xxxvii.-xliv.; 5. “The
Sensory Clubs of Cordyli of Laodice,” Journ. Morphology, x. (1895),
pp. 287-304, pl. xvii.; 6. E. T. Browne, “On British Hydroids and
Medusae,” Proc. Zool. Soc. (1896), pp. 459-500, pls. xvi., xvii., (1897),
pp. 816-835, pls. xlviii. xlix. 12 text-figs.; 7. “Biscayan Medusae,”
Trans. Linn. Soc. x. (1906), pp. 163-187, pl. xiii.; 8. “Medusae” in
Herdman, Rep. Pearl Oyster Fisheries, Gulf of Manaar, iv. (1905),
pp. 131-166, 4 pls.; 9. “Hydromedusae with a Revision of the
Williadae and Petasidae,” Fauna and Geogr. Maldive and Laccadive
Archipelagos, ii. (1904), pp. 722-749, pls. liv.-lvii.; 10. “On
the Freshwater Medusa liberated by Microhydra ryderi, Potts,
and a Comparison with Limnocodium,” Quart. Journ. Micr. Sci. I
(1906), pp. 635, 645, pl. xxxvii.; 10a. “On the Freshwater Medusa
Limnocnida tanganicae” Budgett Memorial Volume (Cambridge,
1908, pp. 471-482, pl. xxviii.; 11. C. Claus, “Über die Struktur der
Muskelzellen und über den Körperbau von Mnestra parasites
Krohn,” Verhandl. zool. bot. Ges. Wien, xxv. (1876), pp. 9-12, pl. i.;
11a. C. Dawydov, “Hydroctena salenskii,” Mém. Acad. Imp. St.
Pétersbourg (viii.) xiv. No. 9 (1903), 17 pp., 1 pl.; 12. A. Dendy,
“On a Free-swimming Hydroid, Pelagohydra mirabilis,” n. gen. et
sp., Quart. Journ. Micr. Sci. xlvi. (1903), pp. 1-24, pls. i. ii.; 13. H.
Driesch, “Tektonische Studien an Hydroidpolypen,” (1) Jen.
Zeitschr., xxiv. (1890), pp. 189-226, 12 figs.; (2) t.c. pp. 657-688,
6 figs.; (3) ibid. xxv. (1891), pp. 467-479, 3 figs.; 14. G. Duplessis,
“On Campanularia volubilis,” Soc. Vaud. Bull. 13 (Lausanne, 1874-1875);
15. J. W. Fewkes, “On Mnestra,” Amer. Natural., xviii.
(1884), pp. 197-198, 3 figs.; 16. S. Goto, “Dendrocoryne Inaba,
Vertreterin einer neuen Familie der Hydromedusen,” Annot. Zool.
Tokyo, i. (1897), pp. 93-104, pl. vi., figs. 106-113; 17. “The Craspe
dote Medusa Olindias and some of its Natural Allies,” Mark Anniversary
Volume (New York, 1903), pp. 1-22, 3 pls.; 18. H. Grenacher,
“Über die Nesselkapseln von Hydra,” Zool. Anz. xviii. (1895),
pp. 310-321, 7 figs.; 19. R. T. Günther, “On the Structure and
Affinities of Mnestra parasites Krohn; with a revision of the Classification
of the Cladonemidae,” Mitt. Stat. Neapel, xvi. (1903), pp.
35-62, pls. ii. iii.; 20. E. Haeckel, “Das System der Medusen,”
Denkschr. med.-nat.-wiss. Ges. (Jena, 1879-1881); 21. “Deep Sea
Medusae,” in Reports of the Challenger Expedition, Zool. iv. pt. 2
(London, 1882); 22. P. Hallez, “Bougainvillia fruticosa Allm. est
le faciès d’eau agitée du Bougainvillia ramosa Van Ben.” C.-R. Acad.
Sci. Paris, cxl. (1905), pp. 457-459; 23. O. & R. Hertwig, Der
Organismus der Medusen (Jena, 1878), 70 pp., 3 pls.; 24. Das
Nervensystem und die Sinnesorgane der Medusen (Leipzig, 1878), 186
pp., 10 pls.; 25. S. J. Hickson, “The Medusae of Millepora,” Proc.
Roy. Soc. lxvi. (1899), pp. 6-10, 10 figs.; 26. T. Hincks, A History of
British Hydroid Zoophytes (2 vols., London, 1868); 27. N. Iwanzov,
“Über den Bau, die Wirkungsweise und die Entwickelung der
Nesselkapseln von Coelenteraten,” Bull. Soc. Imp. Natural, Moscou
(1896), pp. 323-355, 4 pls.; 28. C. F. Jickeli, “Der Bau der Hydroidpolypen,”
(1) Morph. Jahrbuch, viii. (1883), pp. 373-416, pls. xvi.-xviii.;
(2) t.c., pp. 580-680, pls. xxv.-xxviii.; 29. Albert Lang,
“Über die Knospung bei Hydra und einigen Hydropolypen,”
Zeitschr. f. wiss. Zool. liv. (1892), pp. 365-384, pl. xvii.; 30. Arnold
Lang, “Gastroblasta Raffaelei. Eine durch eine Art unvollständiger
Theilung entstehende Medusen-Kolonie,” Jena Zeitschr.
xix. (1886), pp. 735-762, pls. xx., xxi.; 31. A. Linko, “Observations
sur les méduses de la mer Blanche,” Trav. Soc. Imp. Nat. St Pétersbourg,
xxix. (1899); 32. “Über den Bau der Augen bei den Hydromedusen,”
Zapiski Imp. Akad. Nauk (Mém. Acad. Imp. Sci.) St
Pétersbourg (8) x. 3 (1900), 23 pp., 2 pls.; 33. O. Maas, “Die craspedoten
Medusen,” in Ergebn. Plankton Expedition, ii. (Kiel and Leipzig,
1893), 107 pp., 8 pls., 3 figs.; 34. “Die Medusen,” Mem. Mus.
Comp. Zool. Harvard, xxiii. (1897), i.; 35. “On Hydroctena,” Zool.
Centralbl. xi. (1904), pp. 240-243; 36. “Revision des méduses
appartenant aux familles des Cunanthidae et des Aeginidae, et
groupement nouveau des genres,” Bull. Mus. Monaco, v. (1904),
8 pp.; 37. “Revision der Cannotiden Haeckels,” SB. K. Bayer.
Akad. xxxiv. (1904), pp. 421-445; 38. “Meduses,” Result. Camp.
161
Sci. Monaco, xxviii. (1904), 71 pp., 6 pls.; 39. “Die craspedoten
Medusen der Siboga-Expedition,” Uitkomst. Siboga-Exped. x. (1905),
84 pp., 14 pls.; 40. “Die arktischen Medusen (ausschliesslich der
Polypomedusen),” Fauna arctica, iv. (1906), pp. 479-526; 41. C.
Mereschkowsky, “On a new Genus of Hydroids (Monobrachium)
from the White Sea, with a short description of other new Hydroids,”
Ann. Mag. Nat. Hist. (4) xx. (1877), pp. 220-229, pls. v. vi.; 42.
E. Metchinkoft, “Studien über die Entwickelung der Medusen und
Siphonophoren,” Zeitschr. f. wiss. Zool. xxiv. (1874), pp. 15-83, pls.
i.-xii.; 43. “Vergleichend-embryologische Studien” (Geryoniden,
Cunina), ibid. xxxvi. (1882), pp. 433-458, pl. xxviii.; 44. Embryologische
Studien an Medusen (Vienna, 1886), 150 pp., 12 pls., 10 figs.;
45. “Medusologische Mittheilungen,” Arb. zool. Inst. Wien, vi.
(1886), pp. 237-266, pls. xxii. xxiii.; 46. L. Murbach, “Beiträge zur
Kenntnis der Anatomie und Entwickelung der Nesselorgane der
Hydroiden,” Arch. f. Naturgesch. lx. i. (1894), pp. 217-254, pl. xii.;
47. “Preliminary Note on the Life-History of Gonionemus,” Journ.
Morph. xi. (1895), pp. 493-496; 48. L. Murbach and C. Shearer,
“On Medusae from the Coast of British Columbia and Alaska,”
Proc. Zool. Soc. (1903), ii. pp. 164-191, pls. xvii.-xxii.; 49. H. F.
Perkins, “The Development of Gonionema murbachii,” Proc. Acad.
Nat. Sci. Philadelphia (1902), pp. 750-790, pls. xxxi-xxxiv.; 50.
F. Schaudinn, “Über Haleremita cumulans, n. g. n. sp., einen
marinen Hydroidpolypen,” SB. Ges. natforsch. Freunde Berlin (1894),
pp. 226-234, 8 figs.; 51. F. E. Schulze, “On the Structure and
Arrangement of the Soft Parts in Euplectella aspergillum” (Amphibrachium),
Tr. R. Soc. Edinburgh, xxix. (1880), pp. 661-673, pl.
xvii.; 52. O. Seeliger, “Über das Verhalten der Keimblätter bei
der Knospung der Cölenteraten,” Zeitschr. f. wiss. Zool. lviii. (1894),
pp. 152-188, pls. vii.-ix.; 53. W. B. Spencer, “A new Family of
Hydroidea (Clathrozoon), together with a description of the Structure
of a new Species of Plumularia,” Trans. Roy. Soc. Victoria (1890),
pp. 121-140, 7 pls.; 54. M. Ussow, “A new Form of Fresh-water
Coelenterate” (Polypodium), Ann. Mag. Nat. Hist. (5) xviii. (1886),
pp. 110-124, pl. iv.; 55. E. Vanhöffen, “Versuch einer natürlichen
Gruppierung der Anthomedusen,” Zool. Anzeiger, xiv. (1891), pp.
439-446; 56. C. Viguier, “Études sur les animaux inférieurs de la
baie d’Alger” (Tetraplatia), Arch. Zool. Exp. Gen. viii. (1890), pp.
101-142, pls. vii.-ix.; 57. J. Wagner, “Recherches sur l’organisation
de Monobrachium parasiticum Méréjk,” Arch. biol. x. (1890),
pp. 273-309, pls. viii. ix.; 58. A. Weismann, Die Entstehung der
Sexualzellen bei den Hydromedusen (Jena, 1883); 59. R. Woltereck,
“Beiträge zur Ontogenie und Ableitung des Siphonophorenstocks,”
Zeitschr. f. wiss. Zool. lxxxii. (1905), pp. 611-637, 21 text-figs.;
60. J. Wulfert, “Die Embryonalentwickelung von Gonothyraea
loveni Allm.,” Zeitschr. f. wiss. Zool. lxxi. (1902), pp. 296-326, pls.
xvi.-xviii.
(E. A. M.)
1 In some cases hydroids have been reared in aquaria from ova
of medusae, but these hydroids have not yet been found in the sea
(Browne [10 a]).
2 The numbers in square brackets [] refer to the bibliography at
the end of this article; but when the number is preceded by the
word Hydrozoa, it refers to the bibliography at the end of the article
Hydrozoa.
HYDROMETER (Gr. ὕδωρ, water, and μέτρον, a measure), an
instrument for determining the density of bodies, generally of
fluids, but in some cases of solids. When a body floats in a
fluid under the action of gravity, the weight of the body is equal
to that of the fluid which it displaces (see Hydromechanics). It
is upon this principle that the hydrometer is constructed, and it
obviously admits of two modes of application in the case of fluids:
either we may compare the weights of floating bodies which are
capable of displacing the same volume of different fluids, or we
may compare the volumes of the different fluids which are displaced
by the same weight. In the latter case, the densities of
the fluids will be inversely proportional to the volumes thus
displaced.
The hydrometer is said by Synesius Cyreneus in his fifth letter
to have been invented by Hypatia at Alexandria,1 but appears
to have been neglected until it was reinvented by Robert Boyle,
whose “New Essay Instrument,” as described in the Phil. Trans.
for June 1675, differs in no essential particular from Nicholson’s
hydrometer. This instrument was devised for the purpose of
detecting counterfeit coin, especially guineas and half-guineas.
In the first section of the paper (Phil. Trans. No. 115, p. 329) the
author refers to a glass instrument exhibited by himself many
years before, and “consisting of a bubble furnished with a long
and slender stem, which was to be put into several liquors, to
compare and estimate their specific gravities.” This seems to
be the first reference to the hydrometer in modern times.
In fig. 1 C represents the instrument used for guineas, the
circular plates A representing plates of lead, which are used as
ballast when lighter coins than guineas are examined. B
represents “a small glass instrument for estimating the specific
gravities of liquors,” an account of which was promised by Boyle
in the following number of the Phil. Trans., but did not appear.
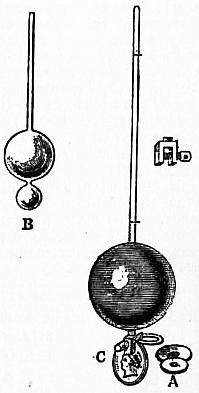 |
| Fig. 1.—Boyle’s New
Essay Instrument. |
The instrument represented at B (fig. 1), which is copied from
Robert Boyle’s sketch in the Phil. Trans. for 1675, is generally
known as the common hydrometer.
It is usually made of glass, the lower
bulb being loaded with mercury or
small shot which serves as ballast,
causing the instrument to float with
the stem vertical. The quantity of
mercury or shot inserted depends upon
the density of the liquids for which
the hydrometer is to be employed, it
being essential that the whole of the
bulb should be immersed in the heaviest
liquid for which the instrument is used,
while the length and diameter of the
stem must be such that the hydrometer
will float in the lightest liquid
for which it is required. The stem is
usually divided into a number of equal
parts, the divisions of the scale being
varied in different instruments, according
to the purposes for which they are
employed.
Let V denote the volume of the instrument
immersed (i.e. of liquid displaced)
when the surface of the liquid in which the hydrometer
floats coincides with the lowest division of the scale, A the
area of the transverse section of the stem, l the length of a scale
division, n the number of divisions on the stem, and W the weight
of the instrument. Suppose the successive divisions of the scale to
be numbered 0, 1, 2 ... n starting with the lowest, and let w0,
W1, w2 ... wn be the weights of unit volume of the liquids in which
the hydrometer sinks to the divisions 0, 1, 2 ... n respectively.
Then, by the principle of Archimedes,
W = Vw0; or w0 = W / V. Also
W = (V + lA) w1; or w1 = W/(V + lA),
wp2 = W / (V + plA), and
wn= W / (V + nlA),
|
or the densities of the several liquids vary inversely as the respective
volumes of the instrument immersed in them; and, since the
divisions of the scale correspond to equal increments of volume
immersed, it follows that the densities of the several liquids in
which the instrument sinks to the successive divisions form a
harmonic series.
If V = NlA then N expresses the ratio of the volume of the instrument
up to the zero of the scale to that of one of the scale-divisions.
If we suppose the lower part of the instrument replaced by a uniform
bar of the same sectional area as the stem and of volume V, the
indications of the instrument will be in no respect altered, and the
bottom of the bar will be at a distance of N scale-divisions below
the zero of the scale.
In this case we have wp = W/(N + p)lA; or the density of the
liquid varies inversely as N + p, that is, as the whole number of
scale-divisions between the bottom of the tube and the plane of
flotation.
If we wish the successive divisions of the scale to correspond to
equal increments in the density of the corresponding liquids, then
the volumes of the instrument, measured up to the successive
divisions of the scale, must form a series in harmonical progression,
the lengths of the divisions increasing as we go up the stem.
The greatest density of the liquid for which the instrument described
above can be employed is W/V, while the least density is
W/(V + nlA), or W/(V + v), where v represents the volume of the stem
between the extreme divisions of the scale. Now, by increasing v,
leaving W and V unchanged, we may increase the range of the instrument
indefinitely. But it is clear that if we increase A, the sectional
area of the stem, we shall diminish l, the length of a scale-division
corresponding to a given variation of density, and thereby proportionately
diminish the sensibility of the instrument, while
diminishing the section A will increase l and proportionately increase
the sensibility, but will diminish the range over which the instrument
can be employed, unless we increase the length of the stem in
the inverse ratio of the sectional area. Hence, to obtain great
sensibility along with a considerable range, we require very long
slender stems, and to these two objections apply in addition to the
question of portability; for, in the first place, an instrument with
a very long stem requires a very deep vessel of liquid for its complete
immersion, and, in the second place, when most of the stem is above
162
the plane of flotation, the stability of the instrument when floating
will be diminished or destroyed. The various devices which have
been adopted to overcome this difficulty will be described in the
account given of the several hydrometers which have been hitherto
generally employed.
The plan commonly adopted to obviate the necessity of inconveniently
long stems is to construct a number of hydrometers as
nearly alike as may be, but to load them differently, so that the scale-divisions
at the bottom of the stem of one hydrometer just overlap
those at the top of the stem of the preceding. By this means a set
of six hydrometers, each having a stem rather more than 5 in. long,
will be equivalent to a single hydrometer with a stem of 30 in.
But, instead of employing a number of instruments differing only in
the weights with which they are loaded, we may employ the same
instrument, and alter its weight either by adding mercury or shot to
the interior (if it can be opened) or by attaching weights to the exterior.
These two operations are not quite equivalent, since a weight
added to the interior does not affect the volume of liquid displaced
when the instrument is immersed up to a given division of the scale,
while the addition of weights to the exterior increases the displacement.
This difficulty may be met, as in Keene’s hydrometer, by
having all the weights of precisely the same volume but of different
masses, and never using the instrument except with one of these
weights attached.
 |
| Fig. 2.—Clarke’s
Hydrometer. |
The first hydrometer intended for the determination of the
densities of liquids, and furnished with a set of weights to be
attached when necessary, was that constructed
by Mr Clarke (instrument-maker)
and described by J. T. Desaguliers in the
Philosophical Transactions for March and
April 1730, No. 413, p. 278. The following
is Desaguliers’s account of the instrument
(fig. 2):—
“After having made several fruitless trials
with ivory, because it imbibes spirituous liquors,
and thereby alters its gravity, he (Mr Clarke)
at last made a copper hydrometer, represented
in fig. 2, having a brass wire of about 1 in. thick
going through, and soldered into the copper
ball Bb. The upper part of this wire is filed flat
on one side, for the stem of the hydrometer,
with a mark at m, to which it sinks exactly in
proof spirits. There are two other marks, A and
B, at top and bottom of the stem, to show
whether the liquor be 1⁄10th above proof (as when
it sinks to A), or 1⁄10th under proof (as when it
emerges to B), when a brass weight such as C
has been screwed on to the bottom at c. There
are a great many such weights, of different sizes, and marked to be
screwed on instead of C, for liquors that differ more than 1⁄10th from
proof, so as to serve for the specific gravities in all such proportions
as relate to the mixture of spirituous liquors, in all the variety
made use of in trade. There are also other balls for showing the
specific gravities quite to common water, which make the instrument
perfect in its kind.”
Clarke’s hydrometer, as afterwards constructed for the purposes
of the excise, was provided with thirty-two weights to adapt it to
spirits of different specific gravities, and eleven smaller weights,
or “weather weights” as they were called, which were attached
to the instrument in order to correct for variations of temperature.
The weights were adjusted for successive intervals of 5° F., but
for degrees intermediate between these no additional correction
was applied. The correction for temperature thus afforded was
not sufficiently accurate for excise purposes, and William Speer
in his essay on the hydrometer (Tilloch’s Phil. Mag., 1802, vol.
xiv.) mentions cases in which this imperfect compensation led
to the extra duty payable upon spirits which were more than 10%
over proof being demanded on spirits which were purposely
diluted to below 10% over proof in order to avoid the charge.
Clarke’s hydrometer, however, remained the standard instrument
for excise purposes from 1787 until it was displaced by that of
Sikes.
Desaguliers himself constructed a hydrometer of the ordinary
type for comparing the specific gravities of different kinds of
water (Desaguliers’s Experimental Philosophy, ii. 234). In
order to give great sensibility to the instrument, the large glass
ball was made nearly 3 in. in diameter, while the stem consisted of
a wire 10 in. in length and only 1⁄40in. in diameter. The instrument
weighed 4000 grains, and the addition of a grain caused it to
sink through an inch. By altering the quantity of shot in the
small balls the instrument could be adapted for liquids other than
water.
To an instrument constructed for the same purpose, but on a
still larger scale than that of Desaguliers, A. Deparcieux added
a small dish on the top of the stem for the reception of the
weights necessary to sink the instrument to a convenient depth.
The effect of weights placed in such a dish or pan is of course
the same as if they were placed within the bulb of the instrument,
since they do not alter the volume of that part which is immersed.
 |
| Fig. 3.—Nicholson’s
Hydrometer. |
The first important improvement in the hydrometer after
its reinvention by Boyle was introduced by G. D. Fahrenheit,
who adopted the second mode of construction above referred to,
arranging his instrument so as always to
displace the same volume of liquid, its
weight being varied accordingly. Instead of
a scale, only a single mark is placed upon the
stem, which is very slender, and bears at the
top a small scale pan into which weights are
placed until the instrument sinks to the mark
upon its stem. The volume of the displaced
liquid being then always the same, its density
will be proportional to the whole weight
supported, that is, to the weight of the
instrument together with the weights required
to be placed in the scale pan.
Nicholson’s hydrometer (fig. 3) combines the
characteristics of Fahrenheit’s hydrometer and of Boyle’s essay
instrument.2 The following is the description given of it by
W. Nicholson in the Manchester Memoirs, ii. 374:—
“AA represents a small scale. It may be taken off at D. Diameter
1½ in., weight 44 grains.
“B a stem of hardened steel wire. Diameter 1⁄100 in.
“E a hollow copper globe. Diameter 28⁄10 in. Weight with stem
369 grains.
“FF a stirrup of wire screwed to the globe at C.
“G a small scale, serving likewise as a counterpoise. Diameter
1½ in. Weight with stirrup 1634 grains.
“The other dimensions may be had from the drawing, which is
one-sixth of the linear magnitude of the instrument itself.
“In the construction it is assumed that the upper scale shall
constantly carry 1000 grains when the lower scale is empty, and the
instrument sunk in distilled water at the temperature of 60° Fahr.
to the middle of the wire or stem. The length of the stem is arbitrary,
as is likewise the distance of the lower scale from the surface of the
globe. But, the length of the stem being settled, the lower scale may
be made lighter, and, consequently, the globe less, the greater its
distance is taken from the surface of the globe; and the contrary.”
In comparing the densities of different liquids, it is clear that
this instrument is precisely equivalent to that of Fahrenheit,
and must be employed in the same manner, weights being placed
in the top scale only until the hydrometer sinks to the mark on the
wire, when the specific gravity of the liquid will be proportional
to the weight of the instrument together with the weights in the
scale.
In the subsequent portion of the paper above referred to,
Nicholson explains how the instrument may be employed as a
thermometer, since, fluids generally expanding more than the
solids of which the instrument is constructed, the instrument
will sink as the temperature rises.
To determine the density of solids heavier than water with this
instrument, let the solid be placed in the upper scale pan, and let
the weight now required to cause the instrument to sink in distilled
water at standard temperature to the mark B be denoted by w,
while W denotes the weight required when the solid is not present.
Then W − w is the weight of the solid. Now let the solid be placed
in the lower pan, care being taken that no bubbles of air remain
attached to it, and let w1 be the weight now required in the scale pan.
This weight will exceed w in consequence of the water displaced by
the solid, and the weight of the water thus displaced will be W1 − w,
which is therefore the weight of a volume of water equal to that of
the solid. Hence, since the weight of the solid itself is W − w, its
density must be (W − w)/(w1 − w).
The above example illustrates how Nicholson’s or Fahrenheit’s
hydrometer may be employed as a weighing machine for small
weights.
In all hydrometers in which a part only of the instrument
163
is immersed, there is a liability to error in consequence of the
surface tension, or capillary action, as it is frequently called, along
the line of contact of the instrument and the surface of the liquid
(see Capillary Action). This error diminishes as the diameter
of the stem is reduced, but is sensible in the case of the thinnest
stem which can be employed, and is the chief source of error in
the employment of Nicholson’s hydrometer, which otherwise
would be an instrument of extreme delicacy and precision.
The following is Nicholson’s statement on this point:—
“One of the greatest difficulties which attends hydrostatical
experiments arises from the attraction or repulsion that obtains at
the surface of the water. After trying many experiments to obviate
the irregularities arising from this cause, I find reason to prefer the
simple one of carefully wiping the whole instrument, and especially
the stem, with a clean cloth. The weights in the dish must not be
esteemed accurate while there is either a cumulus or a cavity in the
water round the stem.”
It is possible by applying a little oil to the upper part of the
bulb of a common or of a Sikes’s hydrometer, and carefully
placing it in pure water, to cause it to float with the upper part
of the bulb and the whole of the stem
emerging as indicated in fig. 4, when it
ought properly to sink almost to the top
of the stem, the surface tension of the
water around the circumference of the
circle of contact, AA′, providing the
additional support required.
 |
| Fig. 4. |
The universal hydrometer of G. Atkins,
described in the Phil. Mag. for 1808,
xxxi. 254, is merely Nicholson’s hydrometer
with the screw at C projecting
through the collar into which it is screwed,
and terminating in a sharp point above the
cup G. To this point soft bodies lighter
than water (which would float if placed in
the cup) could be attached, and thus completely
immersed. Atkins’s instrument was
constructed so as to weigh 700 grains, and
when immersed to the mark on the stem
in distilled water at 60° F. it carried 300
grains in the upper dish. The hydrometer
therefore displaced 1000 grains of distilled
water at 60° F. and hence the specific gravity
of any other liquid was at once indicated
by adding 700 to the number of grains in the
pan required to make the instrument sink to
the mark on the stem. The small divisions on the scale corresponded
to differences of 1⁄10th of a grain in the weight of the instrument.
The “Gravimeter,” constructed by Citizen Guyton and described
in Nicholson’s Journal, 4to, i. 110, differs from Nicholson’s instrument
in being constructed of glass, and having a cylindrical bulb
about 21 centimetres in length and 22 millimetres in diameter.
Its weight is so adjusted that an additional weight of 5 grammes
must be placed in the upper pan to cause the instrument to sink
to the mark on the stem in distilled water at the standard temperature.
The instrument is provided with an additional piece, or “plongeur,”
the weight of which exceeds 5 grammes by the weight of water which
it displaces; that is to say, it is so constructed as to weigh 5 grammes
in water, and consists of a glass envelope filled with mercury. It is
clear that the effect of this “plongeur,” when placed in the lower
pan, is exactly the same as that of the 5 gramme weight in the upper
pan. Without the extra 5 grammes the instrument weighs about 20
grammes, and therefore floats in a liquid of specific gravity .8.
Thus deprived of its additional weight it may be used for spirits.
To use the instrument for liquids of much greater density than
water additional weights must be placed in the upper pan, and the
“plongeur” is then placed in the lower pan for the purpose of giving
to the instrument the requisite stability.
Charles’s balance areometer is similar to Nicholson’s hydrometer,
except that the lower basin admits of inversion, thus enabling the
instrument to be employed for solids lighter than water, the inverted
basin serving the same purpose as the pointed screw in
Atkins’s modification of the instrument.
Adie’s sliding hydrometer is of the ordinary form, but can be
adjusted for liquids of widely differing specific gravities by drawing
out a sliding tube, thus changing the volume of the hydrometer
while its weight remains constant.
The hydrometer of A. Baumé, which has been extensively used in
France, consists of a common hydrometer graduated in the following
manner. Certain fixed points were first determined upon the stem
of the instrument. The first of these was found by immersing the
hydrometer in pure water, and marking the stem at the level of
the surface. This formed the zero of the scale. Fifteen standard
solutions of pure common salt in water were then prepared, containing
respectively 1, 2, 3, ... 15% (by weight) of dry salt. The
hydrometer was plunged in these solutions in order, and the stem
having been marked at the several surfaces, the degrees so obtained
were numbered 1, 2, 3, ... 15. These degrees were, when necessary,
repeated along the stem by the employment of a pair of compasses
till 80 degrees were marked off. The instrument thus adapted to
the determination of densities exceeding that of water was called the
hydrometer for salts.
The hydrometer intended for densities less than that of water,
or the hydrometer for spirits, is constructed on a similar principle.
The instrument is so arranged that it floats in pure water with
most of the stem above the surface. A solution containing 10%
of pure salt is used to indicate the zero of the scale, and the point at
which the instrument floats when immersed in distilled water at
10° R. (54½° F.) is numbered 10. Equal divisions are then marked
off upwards along the stem as far as the 50th degree.
The densities corresponding to the several degrees of Baumé’s
hydrometer are given by Nicholson (Journal of Philosophy, i. 89) as
follows:—
Baumé’s Hydrometer for Spirits. Temperature 10° R.
| Degrees. | Density. | Degrees. | Density. | Degrees. | Density. |
| 10 | 1.000 | 21 | .922 | 31 | .861 |
| 11 | .990 | 22 | .915 | 32 | .856 |
| 12 | .985 | 23 | .909 | 33 | .852 |
| 13 | .977 | 24 | .903 | 34 | .847 |
| 14 | .970 | 25 | .897 | 35 | .842 |
| 15 | .963 | 26 | .892 | 36 | .837 |
| 16 | .955 | 27 | .886 | 37 | .832 |
| 17 | .949 | 28 | .880 | 38 | .827 |
| 18 | .943 | 29 | .874 | 39 | .822 |
| 19 | .935 | 30 | .867 | 40 | .817 |
| 20 | .928 | | | | |
Baume’s Hydrometer for Salts.
| Degrees. | Density. | Degrees. | Density. | Degrees. | Density. |
| 0 | 1.000 | 27 | 1.230 | 51 | 1.547 |
| 3 | 1.020 | 30 | 1.261 | 54 | 1.594 |
| 6 | 1.040 | 33 | 1.295 | 57 | 1.659 |
| 9 | 1.064 | 36 | 1.333 | 60 | 1.717 |
| 12 | 1.089 | 39 | 1.373 | 63 | 1.779 |
| 15 | 1.114 | 42 | 1.414 | 66 | 1.848 |
| 18 | 1.140 | 45 | 1.455 | 69 | 1.920 |
| 21 | 1.170 | 48 | 1.500 | 72 | 2.000 |
| 24 | 1.200 | | | | |
 |
| Fig. 5.—Jones’s
Hydrometer. |
Carrier’s hydrometer was very similar to that of Baumé, Cartier
having been employed by the latter to construct his instruments for
the French revenue. The point at which the instrument floated in
distilled water was marked 10° by Cartier, and 30°
on Carrier’s scale corresponded to 32° on Baumé’s.
Perhaps the main object for which hydrometers
have been constructed is the determination of the
value of spirituous liquors, chiefly for revenue
purposes. To this end an immense variety of
hydrometers have been devised, differing mainly
in the character of their scales.
In Speer’s hydrometer the stem has the form
of an octagonal prism, and upon each of the eight
faces a scale is engraved, indicating the percentage
strength of the spirit corresponding to the several
divisions of the scale, the eight scales being
adapted respectively to the temperature 35°, 40°,
45°, 50°, 55°, 60°, 65° and 70° F. Four small pins,
which can be inserted into the counterpoise of the
instrument, serve to adapt the instrument to the
temperatures intermediate between those for which
the scales are constructed. William Speer was
supervisor and chief assayer of spirits in the port
of Dublin. For a more complete account of this
instrument see Tilloch’s Phil. Mag., xiv. 151.
 |
| Fig. 6. |
The hydrometer constructed by Jones, of Holborn,
consists of a spheroidal bulb with a rectangular
stem (fig. 5). Between the bulb and
counterpoise is placed a thermometer, which
serves to indicate the temperature of the liquid,
and the instrument is provided with three weights
which can be attached to the top of the stem. On
the four sides of the stem AD are engraved four
scales corresponding respectively to the unloaded
instrument, and to the instrument loaded with the
respective weights. The instrument when unloaded
serves for the range from 74 to 47 over proof; when loaded with the
first weight it indicates from 46 to 13 over proof, with the second
weight from 13 over proof to 29 under proof, and with the third
164
from 29 under proof to pure water, the graduation corresponding to
which is marked W at the bottom of the fourth scale. One side of the
stem AD is shown in fig. 5, the other three in fig. 6. The thermometer
is also provided with four scales corresponding to the scales
above mentioned. Each scale has its zero in the middle corresponding
to 60° F. If the mercury in the thermometer
stand above this zero the spirit must
be reckoned weaker than the hydrometer indicates
by the number on the thermometer
scale level with the top of the mercury, while
if the thermometer indicate a temperature
lower than the zero of the scale (60° F.) the
spirit must be reckoned stronger by the scale
reading. At the side of each of the four
scales on the stem of the hydrometer is engraved
a set of small numbers indicating the
contraction in volume which would be experienced
if the requisite amount of water (or
spirit) were added to bring the sample tested
to the proof strength.
The hydrometer constructed by Dicas of
Liverpool is provided with a sliding scale which
can be adjusted for different temperatures, and
which also indicates the contraction in volume
incident on bringing the spirit to proof strength. It is provided
with thirty-six different weights which, with the ten divisions on the
stem, form a scale from 0 to 370. The employment of so many
weights renders the instrument ill-adapted for practical work where
speed is an object.
 |
| Fig. 7.—Atkins’s
Hydrometer. |
This instrument was adopted by the United States in 1790, but
was subsequently discarded by the Internal Revenue Service for
another type. In this latter form the observations have to be made
at the standard temperature of 60° F., at which the graduation 100
corresponds to proof spirit and 200 to absolute alcohol. The need
of adjustable weights is avoided by employing a set of five instruments,
graduated respectively 0°-100°, 80°-120°, 100°-140°, 130°-170°,
160°-200°. The reading gives the volume of
proof spirit equivalent to the volume of liquor;
thus the readings 80° and 120° mean that 100
volumes of the test liquors contain the same
amount of absolute alcohol as 80 and 120
volumes of proof spirit respectively. Proof
spirit is defined in the United States as a
mixture of alcohol and water which contains
equal volumes of alcohol and water at 60° F.,
the alcohol having a specific gravity of 0.7939
at 60° as compared with water at its maximum
density. The specific gravity of proof spirit is
0.93353 at 60°; and 100 volumes of the
mixture is made from 50 volumes of absolute
alcohol and 53.71 volumes of water.
Quin’s universal hydrometer is described in
the Transactions of the Society of Arts, viii.
98. It is provided with a sliding rule to adapt
it to different temperatures, and has four scales,
one of which is graduated for spirits and the
other three serve to show the strengths of
worts. The peculiarity of the instrument consists
in the pyramidal form given to the stem,
which renders the scale-divisions more nearly
equal in length than they would be on a prismatic
stem.
Atkins’s hydrometer, as originally constructed,
is described in Nicholson’s Journal, 8vo, ii.
276. It is made of brass, and is provided
with a spheroidal bulb the axis of which is
2 in. in length, the conjugate diameter being 1½
in. The whole length of the instrument is
8 in., the stem square of about 1⁄8-in. side, and the
weight about 400 grains. It is provided with
four weights, marked 1, 2, 3, 4, and weighing
respectively 20, 40, 61 and 84 grains, which can
be attached to the shank of the instrument at
C (fig. 7) and retained there by the fixed weight
B. The scale engraved upon one face of the
stem contains fifty-five divisions, the top and
bottom being marked 0 or zero and the alternate
intermediate divisions (of which there are
twenty-six) being marked with the letters of the alphabet in order.
The four weights are so adjusted that, if the instrument floats with
the stem emerging as far as the lower division 0 with one of the
weights attached, then replacing the weight by the next heavier
causes the instrument to sink through the whole length of the scale
to the upper division 0, and the first weight produces the same effect
when applied to the naked instrument. The stem is thus virtually
extended to five times its length, and the number of divisions increased
practically to 272. When no weight is attached the instrument
indicates densities from .806 to .843; with No. 1 it registers
from .843 to .880, with No. 2 from .880 to .918, with No. 3 from .918
to .958, and with No. 4 from .958 to 1.000, the temperature being
55° F. It will thus be seen that the whole length of the stem corresponds
to a difference of density of about .04, and one division to
about .00074, indicating a difference of little more than 1⁄3% in the
strength of any sample of spirits.
The instrument is provided with a sliding rule, with scales corresponding
to the several weights, which indicate the specific gravity
corresponding to the several divisions of the hydrometer scale compared
with water at 55° F. The slider upon the rule serves to adjust
the scale for different temperatures, and then indicates the strength
of the spirit in percentages over or under proof. The slider is also
provided with scales, marked respectively Dicas and Clarke, which
serve to show the readings which would have been obtained had the
instruments of those makers been employed. The line on the scale
marked “concentration” indicates the diminution in volume
consequent upon reducing the sample to proof strength (if it is over
proof, O.P.) or upon reducing proof spirit to the strength of the
sample (if it is under proof, U.P.). By applying the several weights
in succession in addition to No. 4 the instrument can be employed for
liquids heavier than water; and graduations on the other three sides
of the stem, together with an additional slide rule, adapt the instrument
for the determination of the strength of worts.
Atkins subsequently modified the instrument (Nicholson’s Journal,
8vo, iii. 50) by constructing the different weights of different
shapes, viz. circular, square, triangular and pentagonal, instead
of numbering them 1, 2, 3 and 4 respectively, a figure of the
weight being stamped on the sliding rule opposite to every letter in
the series to which it belongs, thus diminishing the probability of
mistakes. He also replaced the letters on the stem by the corresponding
specific gravities referred to water as unity. Further
information concerning these instruments and the state of hydrometry
in 1803 will be found in Atkins’s pamphlet On the Relation
between the Specific Gravities and the Strength of Spirituous Liquors
(1803); or Phil. Mag. xvi. 26-33, 205-212, 305-312; xvii. 204-210
and 329-341.
In Gay-Lussac’s alcoholometer the scale is divided into 100 parts
corresponding to the presence of 1, 2, ... % by volume of alcohol at
15° C., the highest division of the scale corresponding to the purest
alcohol he could obtain (density .7947) and the lowest division
corresponding to pure water. A table provides the necessary
corrections for other temperatures.
Tralles’s hydrometer differs from Gay-Lussac’s only in being
graduated at 4° C. instead of 15° C., and taking alcohol of density
.7939 at 15.5° C. for pure alcohol instead of .7947 as taken by Gay-Lussac
(Keene’s Handbook of Hydrometry).
In Beck’s hydrometer the zero of the scale corresponds to density
1.000 and the division 30 to density .850, and equal divisions on
the scale are continued as far as is required in both directions.
 |
| Fig. 8.—Sike’s
Hydrometer. |
In the centesimal hydrometer of Francœur the volume of the
stem between successive divisions of the scale is always 1⁄100th of the
whole volume immersed when the instrument floats
in water at 4° C. In order to graduate the stem
the instrument is first weighed, then immersed in
distilled water at 4° C., and the line of flotation
marked zero. The first degree is then found by
placing on the top of the stem a weight equal to
1⁄100th of the weight of the instrument, which increases
the volume immersed by 1⁄100th of the original
volume. The addition to the top of the stem of
successive weights, each 1⁄100th of the weight of the
instrument itself, serves to determine the successive
degrees. The length of 100 divisions of the
scale, or the length of the uniform stem the volume
of which would be equal to that of the hydrometer
up to the zero graduation, Francœur called the
“modulus” of the hydrometer. He constructed
his instruments of glass, using different instruments
for different portions of the scale (Francœur, Traité
d’aréométrie, Paris, 1842).
Dr Boriés of Montpellier constructed a hydrometer
which was based upon the results of his
experiments on mixtures of alcohol and water.
The interval between the points corresponding to
pure alcohol and to pure water Boriés divided
into 100 equal parts, though the stem was prolonged
so as to contain only 10 of these divisions,
the other 90 being provided for by the addition of 9
weights to the bottom of the instrument as in Clarke’s hydrometer.
The instrument which has now been exclusively used for revenue
purposes for nearly a century is that associated with the name of
Bartholomew Sikes, who was correspondent to the Board of Excise
from 1774 to 1783, and for some time collector of excise for Hertfordshire.
Sikes’s hydrometer, on account of its similarity to that of Boriés,
appears to have been borrowed from that instrument. It is made
of gilded brass or silver, and consists of a spherical ball A (fig. 8),
1.5 in. in diameter, below which is a weight B connected with the
ball by a short conical stem C. The stem D is rectangular in section
and about 3½ in. in length. This is divided into ten equal parts, each
of which is subdivided into five. As in Boriés’s instrument, a series
of 9 weights, each of the form shown at E, serves to extend the scale
165
to 100 principal divisions. In the centre of each weight is a hole
capable of admitting the lowest and thickest end of the conical stem
C, and a slot is cut into it just wide enough to allow the upper part
of the cone to pass. Each weight can thus be dropped on to the
lower stem so as to rest on the counterpoise B. The weights are
marked 10, 20, ... 90; and in using the instrument that weight
must be selected which will allow it to float in the liquid with a
portion only of the stem submerged. Then the reading of the scale
at the line of flotation, added to the number on the weight, gives the
reading required. A small supernumerary weight F is added, which
can be placed upon the top of the stem. F is so adjusted that when
the 60 weight is placed on the lower stem the instrument sinks to
the same point in distilled water when F is attached as in proof
spirit when F is removed. The best instruments are now constructed
for revenue purposes of silver, heavily gilded, because it was found
that saccharic acid contained in some spirits attacked brass behind
the gilding.
The following table gives the specific gravities corresponding to the
principal graduations on Sikes’s hydrometer at 60° F. and 62° F.,
together with the corresponding strengths of spirits. The latter are
based upon the tables of Charles Gilpin, clerk to the Royal Society,
for which the reader is referred to the Phil. Trans. for 1794. Gilpin’s
work is a model for its accuracy and thoroughness of detail, and his
results have scarcely been improved upon by more recent workers.
The merit of Sikes’s system lies not so much in the hydrometer as in
the complete system of tables by which the readings of the instrument
are at once converted into percentage of proof-spirit.
Table showing the Densities corresponding to the Indications of
Sike’s Hydrometer.
Sike’s
Indications. | 60° F. | 62° F. |
| Density. | Proof
Spirit
per
cent. | Density. | Proof
Spirit
per
cent. |
| 0 | .815297 | 167.0 | .815400 | 166.5 |
| 1 | .816956 | 166.1 | .817059 | 165.6 |
| 2 | .818621 | 165.3 | .818725 | 164.8 |
| 3 | .820294 | 164.5 | .820397 | 163.9 |
| 4 | .821973 | 163.6 | .822077 | 163.1 |
| 5 | .823659 | 162.7 | .823763 | 162.3 |
| 6 | .825352 | 161.8 | .825457 | 161.4 |
| 7 | .827052 | 160.9 | .827157 | 160.5 |
| 8 | .828759 | 160.0 | .828864 | 159.6 |
| 9 | .830473 | 159.1 | .830578 | 158.7 |
| 10 | .832195 | 158.2 | .832300 | 157.8 |
| 11 | .833888 | 157.3 | .833993 | 156.8 |
| 12 | .835587 | 156.4 | .835692 | 155.9 |
| 13 | .837294 | 155.5 | .837400 | 155.0 |
| 14 | .839008 | 154.6 | .839114 | 154.0 |
| 15 | .840729 | 153.7 | .840835 | 153.1 |
| 16 | .842458 | 152.7 | .842564 | 152.1 |
| 17 | .844193 | 151.7 | .844299 | 151.1 |
| 18 | .845936 | 150.7 | .846042 | 150.1 |
| 19 | .847685 | 149.7 | .847792 | 149.1 |
| 20 | .849442 | 148.7 | .849549 | 148.1 |
| 20B | .849393 | 148.7 | .849500 | 148.1 |
| 21 | .851122 | 147.6 | .851229 | 147.1 |
| 22 | .852857 | 146.6 | .852964 | 146.1 |
| 23 | .854599 | 145.6 | .854707 | 145.1 |
| 24 | .856348 | 144.6 | .856456 | 144.0 |
| 25 | .858105 | 143.5 | .858213 | 142.9 |
| 26 | .859869 | 142.4 | .859978 | 141.8 |
| 27 | .861640 | 141.3 | .861749 | 140.8 |
| 28 | .863419 | 140.2 | .863528 | 139.7 |
| 29 | .865204 | 139.1 | .865313 | 138.5 |
| 30 | .866998 | 138.0 | .867107 | 137.4 |
| 30B | .866991 | 138.0 | .867100 | 137.4 |
| 31 | .868755 | 136.9 | .868865 | 136.2 |
| 32 | .870526 | 135.7 | .870636 | 135.1 |
| 33 | .872305 | 134.5 | .872415 | 133.9 |
| 34 | .874090 | 133.4 | .874200 | 132.8 |
| 35 | .875883 | 132.2 | .873994 | 131.6 |
| 36 | .877684 | 131.0 | .877995 | 130.4 |
| 37 | .879492 | 129.8 | .879603 | 129.1 |
| 38 | .881307 | 128.5 | .881419 | 127.9 |
| 39 | .883129 | 127.3 | .883241 | 126.7 |
| 40 | .884960 | 126.0 | .885072 | 125.4 |
| 40B | .884888 | 126.0 | .885000 | 125.4 |
| 41 | .886689 | 124.8 | .886801 | 124.2 |
| 42 | .888497 | 123.5 | .888609 | 122.9 |
| 43 | .890312 | 122.2 | .890425 | 121.6 |
| 44 | .892135 | 120.9 | .892248 | 120.3 |
| 45 | .893965 | 119.6 | .894078 | 119.0 |
| 46 | .895803 | 118.3 | .895916 | 117.6 |
| 47 | .897647 | 116.9 | .897761 | 116.3 |
| 48 | .899509 | 115.6 | .899614 | 114.9 |
| 49 | .901360 | 114.2 | .901417 | 113.5 |
| 50 | .903229 | 112.8 | .903343 | 112.1 |
| 50B | .903186 | 112.8 | .903300 | 112.1 |
| 51 | .905024 | 111.4 | .905138 | 110.7 |
| 52 | .906869 | 110.0 | .906983 | 109.3 |
| 53 | .908722 | 108.6 | .908837 | 107.9 |
| 54 | .910582 | 107.1 | .910697 | 106.5 |
| 55 | .912450 | 105.6 | .912565 | 105.0 |
| 56 | .914326 | 104.2 | .914441 | 103.5 |
| 57 | .916209 | 102.7 | .916323 | 102.0 |
| 58 | .918100 | 101.3 | .918216 | 100.5 |
| 59 | .919999 | 99.7 | .820115 | 98.9 |
| 60 | .921906 | 98.1 | .922022 | 97.4 |
| 60B | .921884 | 98.1 | .922000 | 97.4 |
| 61 | .923760 | 96.6 | .923877 | 95.9 |
| 62 | .925643 | 95.0 | .925760 | 94.2 |
| 63 | .927534 | 93.3 | .927652 | 92.6 |
| 64 | .929433 | 91.7 | .929550 | 90.9 |
| 65 | .931339 | 90.0 | .931457 | 89.2 |
| 66 | .933254 | 88.3 | .933372 | 87.5 |
| 67 | .935176 | 86.5 | .935294 | 85.8 |
| 68 | .937107 | 84.7 | .937225 | 84.0 |
| 69 | .939045 | 82.9 | .939163 | 82.2 |
| 70 | .940991 | 81.1 | .941110 | 80.3 |
| 70B | .940981 | 81.1 | .941100 | 80.3 |
| 71 | .942897 | 79.2 | .943016 | 78.4 |
| 72 | .944819 | 77.3 | .944938 | 76.5 |
| 73 | .946749 | 75.3 | .946869 | 74.5 |
| 74 | .948687 | 73.3 | .948807 | 72.5 |
| 75 | .950634 | 71.2 | .950753 | 70.4 |
| 76 | .952588 | 69.0 | .952708 | 68.2 |
| 77 | .954550 | 66.8 | .954670 | 66.0 |
| 78 | .956520 | 64.4 | .956641 | 63.5 |
| 79 | .958498 | 61.9 | .958619 | 61.1 |
| 80 | .960485 | 59.4 | .960606 | 58.5 |
| 80B | .960479 | 59.4 | .960600 | 58.5 |
| 81 | .962433 | 56.7 | .962555 | 55.8 |
| 82 | .964395 | 53.9 | .964517 | 53.0 |
| 83 | .966366 | 50.9 | .966488 | 50.0 |
| 84 | .968344 | 47.8 | .968466 | 47.0 |
| 85 | .970331 | 44.5 | .970453 | 43.8 |
| 86 | .972325 | 41.0 | .972448 | 40.4 |
| 87 | .974328 | 37.5 | .974451 | 36.9 |
| 88 | .976340 | 34.0 | .976463 | 33.5 |
| 89 | .978359 | 30.6 | .978482 | 30.1 |
| 90 | .980386 | 27.2 | .980510 | 26.7 |
| 90B | .980376 | 27.2 | .980500 | 26.7 |
| 91 | .982371 | 23.9 | .982496 | 23.6 |
| 92 | .984374 | 20.8 | .984498 | 20.5 |
| 93 | .986385 | 17.7 | .986510 | 17.4 |
| 94 | .988404 | 14.8 | .988529 | 14.5 |
| 95 | .990431 | 12.0 | .990557 | 11.7 |
| 96 | .992468 | 9.3 | .992593 | 9.0 |
| 97 | .994512 | 6.7 | .994637 | 6.5 |
| 98 | .996565 | 4.1 | .996691 | 4.0 |
| 99 | .998626 | 1.8 | .998752 | 1.6 |
| 100 | 1.000696 | 0.0 | 1.000822 | 0.0 |
In the above table for Sikes’s hydrometer two densities are given
corresponding to each of the degrees 20, 30, 40, 50, 60, 70, 80 and 90,
indicating that the successive weights belonging to the particular
instrument for which the table has been calculated do not quite
agree. The discrepancy, however, does not produce any sensible
error in the strength of the corresponding spirit.
A table which indicates the weight per gallon of spirituous liquors
for every degree of Sikes’s hydrometer is printed in 23 and 24 Vict. c.
114, schedule B. This table differs slightly from that given above,
which has been abridged from the table given in Keene’s Handbook
of Hydrometry, apparently on account of the equal divisions on
Sikes’s scale having been taken as corresponding to equal increments
of density.
Sikes’s hydrometer was established for the purpose of collecting
the revenue of the United Kingdom by Act of Parliament, 56 Geo.
III. c. 140, by which it was enacted that “all spirits shall be deemed
and taken to be of the degree of strength which the said hydrometers
called Sikes’s hydrometers shall, upon trial by any officer or officers
of the customs or excise, denote such spirits to be.” This act came
into force on January 5, 1817, and was to have remained in force until
August 1, 1818, but was repealed by 58 Geo. III. c. 28, which established
Sikes’s hydrometer on a permanent footing. By 3 and 4 Will. IV.
c. 52, § 123, it was further enacted that the same instruments and
methods should be employed in determining the duty upon imported
spirits as should in virtue of any Act of Parliament be employed
in the determination of the duty upon spirits distilled at
home. It is the practice of the officers of the inland revenue to adjust
Sikes’s hydrometer at 62° F., that being the temperature at which the
imperial gallon is defined as containing 10 ℔ avoirdupois of distilled
water. The specific gravity of any sample of spirits thus determined,
when multiplied by ten, gives the weight in pounds per imperial
gallon, and the weight of any bulk of spirits divided by this number
gives its volume at once in imperial gallons.
Mr (afterwards Colonel) J. B. Keene, of the Hydrometer Office,
London, has constructed an instrument after the model of Sikes’s,
but provided with twelve weights of different masses but equal
volumes, and the instrument is never used without having one of
these attached. When loaded with either of the lightest two weights
the instrument is specifically lighter than Sikes’s hydrometer when
unloaded, and it may thus be used for specific gravities as low as
that of absolute alcohol. The volume of each weight being the same,
the whole volume immersed is always the same when it floats at the
same mark whatever weight may be attached.
Besides the above, many hydrometers have been employed for
special purposes. Twaddell’s hydrometer is adapted for densities
greater than that of water. The scale is so arranged that the reading
multiplied by 5 and added to 1000 gives the specific gravity with
reference to water as 1000. To avoid an inconveniently long stem,
different instruments are employed for different parts of the scale
as mentioned above.
The lactometer constructed by Dicas of Liverpool is adapted for
the determination of the quality of milk. It resembles Sikes’s
hydrometer in other respects, but is provided with eight weights.
It is also provided with a thermometer and slide rule, to reduce the
readings to the standard temperature of 55° F. Any determination
of density can be taken only as affording prima facie evidence of the
quality of milk, as the removal of cream and the addition of water are
operations which tend to compensate each other in their influence on
the density of the liquid, so that the lactometer cannot be regarded
as a reliable instrument.
The marine hydrometers, as supplied by the British government
to the royal navy and the merchant marine, are glass instruments
with slender stems, and generally serve to indicate specific gravities
from 1.000 to 1.040. Before being issued they are compared
with a standard instrument, and their errors determined. They
are employed for taking observations of the density of sea-water.
The salinometer is a hydrometer originally intended to indicate
the strength of the brine in marine boilers in which sea-water is
employed. Saunders’s salinometer consists of a hydrometer which
floats in a chamber through which the water from the boiler is
allowed to flow in a gentle stream, at a temperature of 200° F.
The peculiarity of the instrument consists in the stream of water,
as it enters the hydrometer chamber, being made to impinge against
a disk of metal, by which it is broken into drops, thus liberating the
steam, which would otherwise disturb the instrument.
The use of Sikes’s hydrometer necessitates the employment of a
considerable quantity of spirit. For the testing of spirits in bulk no
more convenient instrument has been devised, but where very small
quantities are available more suitable laboratory methods must be
adopted.
In England, the Finance Act 1907 (7 Ed. VII. c. 13), section 4,
provides as follows: (1) The Commissioners of Customs and the
Commissioners of Inland Revenue may jointly make regulations
authorizing the use of any means described in the regulations for
ascertaining for any purpose the strength or weight of spirits. (2)
Where under any enactment Sykes’s (sic) Hydrometer is directed to
be used or may be used for the purpose of ascertaining the strength
or weight of spirits, any means so authorized by regulations may be
used instead of Sykes’s Hydrometer and references to Sykes’s Hydrometer
in any enactment shall be construed accordingly. (3) Any
regulations made under this section shall be published in the London,
Edinburgh and Dublin Gazette, and shall take effect from the date of
publication, or such later date as may be mentioned in the regulations
for the purpose. (4) The expression “spirits” in this section has the
same meaning as in the Spirits Act 1880.
(W. G.)
1 In Nicholson’s Journal, iii. 89, Citizen Eusebe Salverte
calls attention to the poem “De Ponderibus et Mensuris” generally
ascribed to Rhemnius Fannius Palaemon, and consequently 300 years
older than Hypatia, in which the hydrometer is described and
attributed to Archimedes.
2 Nicholson’s Journal, vol. i. p. 111, footnote.
HYDROPATHY, the name given, from the Greek, to the
“water-cure,” or the treatment of disease by water, used
outwardly and inwardly. Like many descriptive names, the
word “hydropathy” is defective and even misleading, the active
agents in the treatment being heat and cold, of which water
166
is little more than the vehicle, and not the only one. Thermotherapeutics
(or thermotherapy) is a term less open to objection.
Hydropathy, as a formal system, dates from about 1829,
when Vincenz Priessnitz (1801-1851), a farmer of Gräfenberg
in Silesia, Austria, began his public career in the paternal
homestead, extended so as to accommodate the increasing
numbers attracted by the fame of his cures. Two English
works, however, on the medical uses of water had been translated
into German in the century preceding the rise of the movement
under Priessnitz. One of these was by Sir John Floyer (1649-1734),
a physician of Lichfield, who, struck by the remedial use
of certain springs by the neighbouring peasantry, investigated
the history of cold bathing, and published in 1702 his Ψυχρολουσία,
or the History of Cold Bathing, both Ancient and Modern.”
The book ran through six editions within a few years, and the
translation was largely drawn upon by Dr J. S. Hahn of Silesia,
in a work published in 1738, On the Healing Virtues of Cold
Water, Inwardly and Outwardly applied, as proved by Experience.
The other work was that of Dr James Currie (1756-1805) of
Liverpool, entitled Medical Reports on the Effects of Water, Cold
and Warm, as a remedy in Fevers and other Diseases, published
in 1797, and soon after translated into German by Michaelis
(1801) and Hegewisch (1807). It was highly popular, and first
placed the subject on a scientific basis. Hahn’s writings had
meanwhile created much enthusiasm among his countrymen,
societies having been everywhere formed to promote the medicinal
and dietetic use of water; and in 1804 Professor Örtel of Ansbach
republished them and quickened the popular movement by
unqualified commendation of water drinking as a remedy for all
diseases. In him the rising Priessnitz found a zealous advocate,
and doubtless an instructor also.
At Gräfenberg, to which the fame of Priessnitz drew people of
every rank and many countries, medical men were conspicuous
by their numbers, some being attracted by curiosity, others by
the desire of knowledge, but the majority by the hope of cure
for ailments which had as yet proved incurable. Many records
of experiences at Gräfenberg were published, all more or less
favourable to the claims of Priessnitz, and some enthusiastic
in their estimate of his genius and penetration; Captain Claridge
introduced hydropathy into England in 1840, his writings and
lectures, and later those of Sir W. Erasmus Wilson (1809-1884),
James Manby Gully (1808-1883) and Edward Johnson, making
numerous converts, and filling the establishments opened soon
after at Malvern and elsewhere. In Germany, France and
America hydropathic establishments multiplied with great
rapidity. Antagonism ran high between the old practice and
the new. Unsparing condemnation was heaped by each on the
other; and a legal prosecution, leading to a royal commission
of inquiry, served but to make Priessnitz and his system stand
higher in public estimation.
Increasing popularity diminished before long that timidity
which had in great measure prevented trial of the new method
from being made on the weaker and more serious class of cases,
and had caused hydropathists to occupy themselves mainly with
a sturdy order of chronic invalids well able to bear a rigorous
regimen and the severities of unrestricted crisis. The need of a
radical adaptation to the former class was first adequately
recognized by John Smedley, a manufacturer of Derbyshire,
who, impressed in his own person with the severities as well as
the benefits of “the cold water cure,” practised among his workpeople
a milder form of hydropathy, and began about 1852 a
new era in its history, founding at Matlock a counterpart of the
establishment at Gräfenberg.
Ernst Brand (1826-1897) of Berlin, Räljen and Theodor von
Jürgensen of Kiel, and Karl Liebermeister (1833-1901) of
Basel, between 1860 and 1870, employed the cooling bath in
abdominal typhus with striking results, and led to its introduction
to England by Dr Wilson Fox. In the Franco-German
war the cooling bath was largely employed, in conjunction
frequently with quinine; and it now holds a recognized position
in the treatment of hyperpyrexia. The wet sheet pack has
become part of medical practice; the Turkish bath, introduced
by David Urquhart (1805-1877) into England on his return from
the East, and ardently adopted by Dr Richard Barter (1802-1870)
of Cork, has become a public institution, and, with the
“morning tub” and the general practice of water drinking, is
the most noteworthy of the many contributions by hydropathy to
public health (see Baths, ad fin.).
The appliances and arrangements by means of which heat and
cold are brought to bear on the economy are—(a) Packings, hot
and cold, general and local, sweating and cooling; (b) hot air and
steam baths; (c) general baths, of hot water and cold; (d) sitz,
spinal, head and foot baths; (e) bandages (or compresses), wet and
dry; also (f) fomentations and poultices, hot and cold, sinapisms,
stupes, rubbings and water potations, hot and cold.
(a) Packings.—The full pack consists of a wet sheet enveloping
the body, with a number of dry blankets packed tightly over it, including
a macintosh covering or not. In an hour or less these are
removed and a general bath administered. The pack is a derivative,
sedative, sudorific and stimulator of cutaneous excretion. There
are numerous modifications of it, notably the cooling pack, where
the wrappings are loose and scanty, permitting evaporation, and
the application of indefinite duration, the sheet being rewetted as it
dries; this is of great value in protracted febrile conditions. There
are also local packs, to trunk, limbs or head separately, which are
derivative, soothing or stimulating, according to circumstance and
detail.
(b) Hot air baths, the chief of which is the Turkish (properly,
the Roman) bath, consisting of two or more chambers ranging in
temperature from 120° to 212° or higher, but mainly used at 150° for
curative purposes. Exposure is from twenty minutes up to two hours
according to the effect sought, and is followed by a general bath, and
occasionally by soaping and shampooing. It is stimulating, derivative,
depurative, sudorific and alterative, powerfully promoting tissue
change by increase of the natural waste and repair. It determines
the blood to the surface, reducing internal congestions, is a potent
diaphoretic, and, through the extremes of heat and cold, is an effective
nervous and vascular stimulant and tonic. Morbid growths and
secretions, as also the uraemic, gouty and rheumatic diathesis, are
beneficially influenced by it. The full pack and Turkish bath have
between them usurped the place and bettered the function of the
once familiar hot bath. The Russian or steam bath and the lamp
bath are primitive and inferior varieties of the modern Turkish
bath, the atmosphere of which cannot be too dry and pure.
(c) General baths comprise the rain (or needle), spray (or rose),
shower, shallow, plunge, douche, wave and common morning
sponge baths, with the dripping sheet, and hot and cold spongings,
and are combinations, as a rule, of hot and cold water. They
are stimulating, tonic, derivative and detergent.
(d) Local baths comprise the sitz (or sitting), douche (or spouting),
spinal, foot and head baths, of hot or cold water, singly or in combination,
successive or alternate. The sitz, head and foot baths are
used “flowing” on occasion. The application of cold by “Leiter’s
tubes” is effective for reducing inflammation (e.g. in meningitis
and in sunstroke); in these a network of metal or indiarubber
tubing is fitted to the part affected, and cold water kept continuously
flowing through them. Rapid alternations of hot and cold
water have a powerful effect in vascular stasis and lethargy of the
nervous system and absorbents, yielding valuable results in local
congestions and chronic inflammations.
(e) Bandages (or compresses) are of two kinds,—cooling, of wet
material left exposed for evaporation, used in local inflammations
and fevers; and heating, of the same, covered with waterproof
material, used in congestion, external or internal, for short or long
periods. Poultices, warm, of bread, linseed, bran, &c., changed but
twice in twenty-four hours, are identical in action with the heating
bandage, and superior only in the greater warmth and consequent
vital activity their closer application to the skin ensures.
(f) Fomentations and poultices, hot or cold, sinapisms, stupes,
rubefacients, irritants, frictions, kneadings, calisthenics, gymnastics,
electricity, &c., are adjuncts largely employed.
Bibliography.—Among the numerous earlier works on hydropathy,
the following are worth mention: Balbirnie, Water Cure in
Consumption (1847), Hydropathic Aphorisms (1856) and A Plea for
the Turkish Bath (1862); Beni-Barde, Traité d’hydrothérapie (1874);
Claridge, Cold Water Cure, or Hydropathy (1841), Facts and Evidence
in Support of Hydropathy (1843) and Cold Water, Tepid Water and
Friction Cure (1849); Dunlop, Philosophy of the Bath (1873); Floyer,
Psychrolousia, or the History of Cold-Bathing, &c. (1702); J. S. Hahn
(Schweidnitz), Observations on the Healing Virtues of Cold Water
(1738); Hunter, Hydropathy for Home Use (1879); E. W. Lane,
Hydropathy, or the Natural System of Medical Treatment (1857);
R. J. Lane, Life at the Water Cure (1851); Shew, Hydropathic Family
Physician (1857); Smedley, Practical Hydropathy (1879); Smethurst,
Hydrotherapia, or the Water Cure (1843); Wainwright, Inquiry into
the Nature and Use of Baths (1737); Weiss, Handbook of Hydropathy
(1844); Wilson Principles and Practice of the Cold Water
Cure (1854) and The Water Cure (1859). A useful recent work
dealing comprehensively with the subject is Richard Metcalfe’s
Rise and Progress of Hydropathy (1906).
167
HYDROPHOBIA (Gr. ὕδωρ, water, and ϕόβος, fear; so called
from the symptom of dread of water), or Rabies (Lat. for “madness”),
an acute disease, occurring chiefly in certain of the lower
animals, particularly the canine species, and liable to be communicated
by them to other animals and to man.
In Dogs, &c.—The occurrence of rabies in the fox, wolf, hyaena,
jackal, raccoon, badger and skunk has been asserted; but there
is every probability that it is originally a disease of the dog.
It is communicated by inoculation to nearly all, if not all, warm-blooded
creatures. The transmission from one animal to another
only certainly takes place through inoculation with viruliferous
matters. The malady is generally characterized at a certain
stage by an irrepressible desire in the animal to act offensively
with its natural weapons—dogs and other carnivora attacking
with their teeth, herbivora with their hoofs or horns, and birds
with their beaks, when excited ever so slightly. In the absence
of excitement the malady may run its course without any fit of
fury or madness.
Symptoms.—The disease has been divided into three stages or
periods, and has also been described as appearing in at least two
forms, according to the peculiarities of the symptoms. But, as a
rule, one period of the disease does not pass suddenly into another,
the transition being almost imperceptible; and the forms do not
differ essentially from each other, but appear merely to constitute
varieties of the same disease, due to the natural disposition of the
animal, or other modifying circumstances. These forms have been
designated true or furious rabies (Fr. rage vrai; Ger. rasende Wuth)
and dumb rabies (Fr. rage mue; Ger. stille Wuth).
The malady does not commence with fury and madness, but in a
strange and anomalous change in the habits of the dog: it becomes
dull, gloomy, and taciturn, and seeks to isolate itself in out-of-the-way
places, retiring beneath chairs and to odd corners. But in its retirement
it cannot rest: it is uneasy and fidgety, and no sooner has
it lain down than suddenly it jumps up in an agitated manner,
walks backwards and forwards several times, again lies down and
assumes a sleeping attitude, but has only maintained it for a few
minutes when it is once more moving about. Again it retires to its
corner, to the farthest recess it can find, and huddles itself up into
a heap, with its head concealed beneath its chest and fore-paws.
This state of continual agitation and inquietude is in striking contrast
with its ordinary habits, and should therefore receive attention.
Not unfrequently there are a few moments when the creature appears
more lively than usual, and displays an extraordinary amount of
affection. Sometimes there is a disposition to gather up straw,
thread, bits of wood, &c., which are industriously carried away; a
tendency to lick anything cold, as iron, stones, &c., is also observed
in many instances; and there is also a desire evinced to lick other
animals. Sexual excitement is also frequently an early symptom.
At this period no disposition to bite is observed; the animal is docile
with its master and obeys his voice, though not so readily as before,
nor with the same pleased countenance. There is something strange
in the expression of its face, and the voice of its owner is scarcely able
to make it change from a sudden gloominess to its usual animated
aspect. These symptoms gradually become more marked; the
restlessness and agitation increase. If on straw the dog scatters and
pulls it about with its paws, and if in a room it scratches and tumbles
the cushions or rugs on which it usually lies. It is incessantly on
the move, rambling about, scratching the ground, sniffing in corners
and at the doors, as if on the scent or seeking for something. It
indulges in strange movements, as if affected by some mental influences
or a prey to hallucinations. When not excited by any
external influence it will remain for a brief period perfectly still and
attentive, as if watching something, or following the movements of
some creature on the wall; then it will suddenly dart forward and
snap at the vacant air, as if pursuing an annoying object, or endeavouring
to seize a fly. At another time it throws itself, yelling
and furious, against the wall, as if it heard threatening voices on the
other side, or was bent on attacking an enemy. Nevertheless, the
animal is still docile and submissive, for its master’s voice will bring
it out of its frenzy. But the saliva is already virulent, and the excessive
affection which it evinces at intervals, by licking the hands or
face of those it loves, renders the danger very great should there
be a wound or abrasion. Until a late period in the disease the
master’s voice has a powerful influence over the animal. When
it has escaped from all control and wanders erratically abroad,
ferocious and restless, and haunted by horrid phantoms, the familiar
voice yet exerts its influence, and it is rare indeed that it attacks
its master.
There is no dread of water in the rabid dog; the animal is generally
thirsty, and if water be offered will lap it with avidity, and swallow
it at the commencement of the disease. And when, at a later period,
the constriction about the throat—symptomatic of the disease—renders
swallowing difficult, the dog will none the less endeavour to
drink, and the lappings are as frequent and prolonged when deglutition
becomes impossible. So little dread has the rabid dog of water
that it will ford streams and swim rivers; and when in the ferocious
stage it will even do this in order to attack other creatures on the
opposite side.
At the commencement of the disease the dog does not usually
refuse to eat, and some animals are voracious to an unusual degree.
But in a short time it becomes fastidious, only eating what it usually
has a special predilection for. Soon, however, this gives place to a
most characteristic symptom—either the taste becomes extremely
depraved or the dog has a fatal and imperious desire to bite and
ingest everything. The litter of its kennel, wool from cushions,
carpets, stockings, slippers, wood, grass, earth, stones, glass, horse-dung,
even its own faeces and urine, or whatever else may come in
its way, are devoured. On examination of the body of a dog which
has died of rabies it is so common to find in the stomach a quantity
of dissimilar and strange matters on which the teeth have been
exercised that, if there was nothing known of the animal’s history,
there would be strong evidence of its having been affected with the
disease. When a dog, then, is observed to gnaw and eat suchlike
matters, though it exhibits no tendency to bite, it should be suspected.
The mad dog does not usually foam at the mouth to any great
extent at first. The mucus of the mouth is not much increased in
quantity, but it soon becomes thicker, viscid, and glutinous, and
adheres to the angles of the mouth, fauces and teeth. It is at this
period that the thirst is most ardent, and the dog sometimes furiously
attempts to detach the saliva with its paws; and if after a while
it loses its balance in these attempts and tumbles over, there can no
longer be any doubt as to the nature of the malady. There is another
symptom connected with the mouth in that form of the disease
named “dumb madness” which has frequently proved deceptive.
The lower jaw drops in consequence of paralysis of its muscles, and
the mouth remains open. The interior is dry from the air passing
continually over it, and assumes a deep red tint, somewhat masked
by patches of dust or earth, which more especially adhere to the upper
surface of the tongue and to the lips. The strange alteration produced
in the dog’s physiognomy by its constantly open mouth and the dark
colour of the interior is rendered still more characteristic by the dull,
sad, or dead expression of the animal’s eyes. In this condition the
creature is not very dangerous, because generally it could not bite if
it tried—indeed there does not appear to be much desire to bite in
dumb madness; but the saliva is none the less virulent, and accidental
inoculations with it, through imprudent handling, will prove
as fatal as in the furious form. The mouth should not be
touched,—numerous deaths having occurred through people thinking the
dog had some foreign substance lodged in its throat, and thrusting
their fingers down to remove it. The sensation of tightness which
seems to exist at the throat causes the dog to act as if a bone were
fixed between its teeth or towards the back of its mouth, and to
employ its fore-paws as if to dislodge it. This is a very deceptive
symptom, and may prove equally dangerous if caution be not observed.
Vomiting of blood or a chocolate-coloured fluid is witnessed
in some cases, and has been supposed to be due to the foreign substances
in the stomach, which abrade the lining membrane; this,
however, is not correct, as it has been observed in man.
The voice of the rabid dog is very peculiar, and so characteristic
that to those acquainted with it nothing more is needed to prove
the presence of the disease. Those who have heard it once or twice
never forget its signification. Owing to the alterations taking place
in the larynx the voice becomes hoarse, cracked and stridulous, like
that of a child affected with croup—the “voix du coq,” as the French
have it. A preliminary bark is made in a somewhat elevated tone
and with open mouth; this is immediately succeeded by five, six
or eight decreasing howls, emitted when the animal is sitting or
standing, and always with the nose elevated, which seem to come
from the depths of the throat, the jaws not coming together and
closing the mouth during such emission, as in the healthy bark.
This alteration in the voice is frequently the first observable indication
of the malady, and should at once attract attention. In dumb
madness the voice is frequently lost from the very commencement—hence
the designation.
The sensibility of the mad dog appears to be considerably
diminished, and the animal appears to have lost the faculty of expressing
the sensations it experiences: it is mute under the infliction
of pain, though there can be no doubt that it still has peripheral
sensation to some extent. Burning, beating and wounding produce
much less effect than in health, and the animal will even mutilate
itself with its teeth. Suspicion, therefore, should always strongly
attach to a dog which does not manifest a certain susceptibility to
painful impressions and receives punishment without any cry or
complaint. There is also reason for apprehension when a dog
bites itself persistently in any part of its body. A rabid dog is usually
stirred to fury at the sight of one of its own species; this test has
been resorted to by Henrie Marie Bouley (1814-1885) to dissipate
doubts as to the existence of the disease when the diagnosis is otherwise
uncertain. As soon as the suspected animal, if it is really rabid,
finds itself in the presence of another of its species it at once assumes
the aggressive, and, if allowed, will bite furiously. All rabid animals
indeed become excited, exasperated, and furious at the sight of a dog,
and attack it with their natural weapons, even the timid sheep
when rabid butts furiously at the enemy before which in health it
would have fled in terror. This inversion of sentiment is sometimes
168
valuable in diagnosing the malady; it is so common that it may be
said to be present in every case of rabies. When, therefore, a dog,
contrary to its habits and natural inclination, becomes suddenly
aggressive to other dogs, it is time to take precautions.
In the large majority of instances the dog is inoffensive in the
early period of the disease to those to whom it is familiar. It then
flies from its home and either dies, is killed as “mad,” or returns in
a miserable plight, and in an advanced stage of the malady, when
the desire to bite is irresistible. It is in the early stage that sequestration
and suppressive measures are most valuable. The dogs which
propagate the disease are usually those that have escaped from
their owners. After two or three days, frequently in about twelve
hours, more serious and alarming symptoms appear, ferocious
instincts are developed, and the desire to do injury is irrepressible.
The animal has an indefinable expression of sombre melancholy
and cruelty. The eyes have their pupils dilated, and emit flashes
of light when they are not dull and heavy; they always appear so
fierce as to produce terror in the beholder; they are red, and their
sensibility to light is increased; and wrinkles, which sometimes
appear on the forehead, add to the repulsive aspect of the animal.
If caged it flies at the spectator, emitting its characteristic howl or
bark, and seizing the iron bars with its teeth, and if a stick be thrust
before it this is grasped and gnawed. This fury is soon succeeded by
lassitude, when the animal remains insensible to every excitement.
Then all at once it rouses up again, and another paroxysm of fury
commences. The first paroxysm is usually the most intense, and the
fits vary in duration from some hours to a day, and even longer;
they are ordinarily briefer in trained and pet dogs than in those which
are less domesticated, but in all the remission is so complete after the
first paroxysm that the animals appear to be almost well, if not in
perfect health. During the paroxysms respiration is hurried and
laboured, but tranquil during the remissions. There is an increase of
temperature, and the pulse is quick and hard. When the animal is
kept in a dark place and not excited, the fits of fury are not observed.
Sometimes it is agitated and restless in the manner already described.
It never becomes really furious or aggressive unless excited by external
objects—the most potent of these, as has been said, being another
dog, which, however, if it be admitted to its cage, it may not at
once attack. The attacked animal rarely retaliates, but usually
responds to the bites by acute yells, which contrast strangely with
the silent anger of the aggressor, and tries to hide its head with
its paws or beneath the straw. These repeated paroxysms hurry
the course of the disease. The secretion and flowing of a large
quantity of saliva from the mouth are usually only witnessed in
cases in which swallowing has become impossible, the mouth being
generally dry. At times the tongue, nose and whole head appear
swollen. Other dogs frequently shun one which is rabid, as if aware
of their danger.
The rabid dog, if lodged in a room or kept in a house, is continually
endeavouring to escape; and when it makes its escape it goes freely
forward, as if impelled by some irresistible force. It travels considerable
distances in a short time, perhaps attacking every living
creature it meets—preferring dogs, however, to other animals, and
these to mankind; cats, sheep, cattle and horses are particularly
liable to be injured. It attacks in silence, and never utters a snarl
or a cry of anger; should it chance to be hurt in return it emits
no cry or howl of pain. The degree of ferocity appears to be related
to natural disposition and training. Some dogs, for instance, will
only snap or give a slight bite in passing, while others will bite
furiously, tearing the objects presented to them, or which they
meet in their way, and sometimes with such violence as to injure
their mouth and break their teeth, or even their jaws. If chained,
they will in some cases gnaw the chain until their teeth are worn
away and the bones laid bare. The rabid dog does not continue
its progress very long. Exhausted by fatigue and the paroxysms
of madness excited in it by the objects it meets, as well as by hunger,
thirst, and also, no doubt, by the malady, its limbs soon become
feeble; the rate of travelling is lessened and the walk is unsteady,
while its drooping tall, head inclined towards the ground, open
mouth, and protruded tongue (of a leaden colour or covered with
dust) give the distressed creature a very striking and characteristic
physiognomy. In this condition, however, it is much less to be
dreaded than in its early fits of fury, since it is no longer capable
or desirous of altering its course or going out of its way to attack
an animal or a man not immediately in the path. It is very probable
that its fast-failing vision, deadened scent, and generally diminished
perception prevent its being so readily impressed or excited by
surrounding objects as it previously was. To each paroxysm,
which is always of short duration, there succeeds a degree of exhaustion
as great as the fits have been violent and oft repeated.
This compels the animal to stop; then it shelters itself in obscure
places—frequently in ditches by the roadside—and lies there in a
somnolescent state for perhaps hours. There is great danger, nevertheless,
in disturbing the dog at this period; for when roused from
its torpor it has sometimes sufficient strength to inflict a bite.
This period, which may be termed the second stage, is as variable
in its duration as the first, but it rarely exceeds three or four days.
The above-described phenomena gradually merge into those of the
third or last period, when symptoms of paralysis appear, which are
speedily followed by death. During the remission in the paroxysms
these paralytic symptoms are more particularly manifested in the
hind limbs, which appear as if unable to support the animal’s weight,
and cause it to stagger about; or the lower jaw becomes more or
less drooping, leaving the parched mouth partially open. Emaciation
rapidly sets in, and the paroxysms diminish in intensity, while the
remissions become less marked. The physiognomy assumes a still
more sinister and repulsive aspect; the hair is dull and erect; the
flanks are retracted; the eyes lose their lustre and are buried in
the orbits, the pupil being dilated, and the cornea dull and semi-opaque;
very often, even at an early period, the eyes squint, and
this adds still more to the terrifying appearance of the poor dog.
The voice, if at all heard, is husky, the breathing laborious, and the
pulse hurried and irregular. Gradually the paralysis increases, and
the posterior extremities are dragged as if the animal’s back were
broken, until at length it becomes general; it is then the prelude
to death. Or the dog remains lying in a state of stupor, and can
only raise itself with difficulty on the fore-limbs when greatly excited.
In this condition it may yet endeavour to bite at objects within its
reach. At times convulsions of a tetanic character appear in certain
muscles; at other times these are general. A comatose condition
ensues, and the rabid dog, if permitted to die naturally, perishes,
in the great majority of cases, from paralysis and asphyxia.
In dumb madness there is paralysis of the lower jaw, which imparts
a curious and very characteristic physiognomy to the dog;
the voice is also lost, and the animal can neither eat nor drink.
In this condition the creature remains with its jaw pendent and
the mouth consequently wide open, showing the flaccid or swollen
tongue covered with brownish matter, and a stringy gelatinous-looking
saliva lying between it and the lower lip and coating the
fauces, which sometimes appear to be inflamed. Though the
animal is unable to swallow fluids, the desire to drink is nevertheless
intense; for the creature will thrust its face into the vessel of
water in futile attempts to obtain relief, even until the approach
of death. Water may be poured down its throat without inducing
a paroxysm. The general physiognomy and demeanour of the poor
creature inspire the beholder with pity rather than fear. The
symptoms due to cerebral excitement are less marked than in the
furious form of the disease; the agitation is not so considerable,
and the restlessness, tendency to run away, and desire to bite are
nearly absent; generally the animal is quite passive. Not unfrequently
one or both eyes squint, and it is only when very much
excited that the dog may contrive to close its mouth. Sometimes
there is swelling about the pharynx and the neck; when the tongue
shares in this complication it hangs out of the mouth. In certain
cases there is a catarrhal condition of the membrane lining the
nasal cavities, larynx, and bronchi; sometimes the animal testifies
to the existence of abdominal pain, and the faeces are then soft or
fluid. The other symptoms—such as the rapid exhaustion and
emaciation, paralysis of the posterior limbs towards the termination
of the disease, as well as the rapidity with which it runs its course—are
the same as in the furious form.
The simultaneous occurrence of furious and dumb madness has
frequently been observed in packs of fox-hounds. Dumb madness
differs, then, from the furious type in the paralysis of the lower
jaw, which hinders the dog from biting, save in very exceptional
circumstances; the ferocious instincts are also in abeyance; and
there is no tendency to aggression. It has been calculated that
from 15 to 20% of rabid dogs have this particular form of the
disease. Puppies and young dogs chiefly have furious rabies.
These are the symptoms of rabies in the dog; but it is not likely,
nor is it necessary, that they will all be present in every case. In
other species the symptoms differ more or less from those manifested
by the dog, but they are generally marked by a change in
the manner and habits of the creatures affected, with strong indications
of nervous disturbance, in the majority of species amounting
to ferociousness and a desire to injure, timid creatures becoming
bold and aggressive.
In Human Beings.—The disease of hydrophobia has been
known from early times, and is alluded to in the works of Aristotle,
Xenophon, Plutarch, Virgil, Horace, Ovid and many others, as
well as in those of the early writers on medicine. Celsus gives
detailed instructions respecting the treatment of men who have
been bitten by rabid dogs, and dwells on the dangers attending
such wounds. After recommending suction of the bitten part
by means of a dry cupping glass, and thereafter the application
of the actual cautery or of strong caustics, and the employment
of baths and various internal remedies, he says: “Idque cum
ita per triduum factum est, tutus esse homo a periculo videtur.
Solet autem ex eo vulnere, ubi parum occursum est, aquae
timor nasci, ὑδροφοβίαν Graeci appellant. Miserrimum genus
morbi; in quo simul aeger et siti et aquae metu cruciatur;
quo oppressis in angusto spes est.” Subsequently Galen described
minutely the phenomena of hydrophobia, and recommended
the excision of the wounded part as a protection against
169
the disease. Throughout many succeeding centuries little or
nothing was added to the facts which the early physicians had
made known upon the subject. The malady was regarded with
universal horror and dread, and the unfortunate sufferers were
generally abandoned by all around them and left to their terrible
fate. In later times the investigations of Boerhaave, Gerard
van Swieten (1700-1772), John Hunter, François Magendie
(1783-1855), Gilbert Breschet (1784-1845), Virchow, Albert
Reder, as also of William Youatt (1776-1847), George Fleming,
Meynell, Karl Hertwig (1798-1881), and others, have furnished
important information; but all these were put into the
shade by the researches of Pasteur.
The disease is communicated by the secretions of the mouth
of the affected animal entering a wound or abrasion of the human
skin or mucous membrane. In the great majority of cases
(90%) this is due to the bite of a rabid dog, but bites of rabid
cats, wolves, foxes, jackals, &c. are occasionally the means of
conveying the disease. Numerous popular fallacies still prevail
on the subject of hydrophobia. Thus it is supposed that the bite
of an angry dog may produce the disease, and all the more if the
animal should subsequently develop symptoms of rabies. The
ground for this erroneous notion is the fact, which is unquestionable,
that animals in whom rabies is in the stage of incubation,
during which there are few if any symptoms, may by their bites
convey the disease, though fortunately during this early stage
they are little disposed to bite. The bite of a non-rabid animal,
however enraged, cannot give rise to hydrophobia.
The period of incubation of the disease, or that time which
elapses between the introduction of the virus and the development
of the symptoms, appears to vary in a remarkable degree,
being in some cases as short as a fortnight, and in others as long
as several months or even years. On an average it seems to be
from about six weeks to three months, but it mainly depends
on the part bitten; bites on the head are the most dangerous.
The incubation period is also said to be shorter in children.
The rare instances of the appearance of hydrophobia many years
after the introduction of the poison are always more or less open
to question as to subsequent inoculation.
When the disease is about to declare itself it not unfrequently
happens that the wound, which had quickly and entirely healed
after the bite, begins to exhibit evidence of irritation or inflammatory
action, or at least to be the seat of morbid sensations
such as numbness, tingling or itching. The symptoms characterizing
the premonitory stage are great mental depression and
disquietude, together with restlessness and a kind of indefinite
fear. There is an unusual tendency to talk, and the articulation
is abrupt and rapid. Although in some instances the patients
will not acknowledge that they have been previously bitten,
and deny it with great obstinacy, yet generally they are well
aware of the nature of their malady, and speak despairingly of
its consequences. There is in this early stage a certain amount
of constitutional disturbance showing itself by feverishness, loss
of appetite, sleeplessness, headache, great nervous excitability,
respiration of a peculiar sighing or sobbing character, and even
occasionally a noticeable aversion to liquids. These symptoms—constituting
what is termed the melancholic stage—continue in
general for one or two days, when they are succeeded by the
stage of excitement in which all the characteristic phenomena
of the malady are fully developed. Sometimes the disease first
shows itself in this stage, without antecedent symptoms.
The agitation of the sufferer now becomes greatly increased,
and the countenance exhibits anxiety and terror. There is
noticed a marked embarrassment of the breathing, but the most
striking and terrible features of this stage are the effects produced
by attempts to swallow fluids. The patient suffers from
thirst and desires eagerly to drink, but on making the effort is
seized with a most violent suffocative paroxysm produced by
spasm of the muscles of swallowing and breathing, which continues
for several seconds, and is succeeded by a feeling of
intense alarm and distress. With great caution and determination
the attempt is renewed, but only to be followed with a
repetition of the seizure, until the unhappy sufferer ceases from
sheer dread to try to quench the thirst which torments him.
Indeed the very thought of doing so suffices to bring on a choking
paroxysm, as does also the sound of the running of water. The
patient is extremely sensitive to any kind of external impression;
a bright light, a loud noise, a breath of cool air, contact with
any one, are all apt to bring on one of these seizures. But
besides these suffocative attacks there also occur general convulsions
affecting the whole muscular system of the body, and
occasionally a condition of tetanic spasm. These various
paroxysms increase in frequency and severity with the advance
of the disease, but alternate with intervals of comparative
quiet, in which, however, there is intense anxiety and more or
less constant difficulty of breathing, accompanied with a peculiar
sonorous expiration, which has suggested the notion that the
patient barks like a dog. In many instances there is great
mental disturbance, with fits of maniacal excitement, in which
he strikes at every one about him, and accuses them of being
the cause of his sufferings—these attacks being succeeded by
calm intervals in which he expresses great regret for his violent
behaviour. During all this stage of the disease the patient is
tormented with a viscid secretion accumulating in his mouth,
which from dread of swallowing he is constantly spitting about
him. There may also be noticed snapping movements of the
jaws as if he were attempting to bite, but these are in reality
a manifestation of the spasmodic action which affects the
muscles generally. There is no great amount of fever, but there
is constipation, diminished flow of urine, and often sexual
excitement.
After two or three days of suffering of the most terrible
description the patient succumbs, death taking place either in a
paroxysm of choking, or on the other hand in a tranquil manner
from exhaustion, all the symptoms having abated, and the
power of swallowing returned before the end. The duration of
the disease from the first declaration of the symptoms is generally
from three to five days.
Apart from the inoculation method (see below), the treatment
of most avail is that which is directed towards preventing the
absorption of the poison into the system. This may be accomplished
by excision of the part involved in the bite of the rabid
animal, or, where this from its locality is impracticable, in the
application to the wound of some chemical agent which will
destroy the activity of the virus, such as potassa fusa, lunar
caustic (nitrate of silver), or the actual cautery in the form of a
red-hot wire. The part should be thoroughly acted on by these
agents, no matter what amount of temporary suffering this may
occasion. Such applications should be resorted to immediately
after the bite has been inflicted, or as soon thereafter as possible.
Further, even though many hours or days should elapse, these
local remedies should still be applied; for if, as appears probable,
some at least of the virus remains for long at the injured part,
the removal or effectual destruction of this may prevent the dread
consequences of its absorption. Every effort should be made to
tranquillize and reassure the patient.
Two special points of interest have arisen in recent years in
connexion with this disease. One is the Pasteur treatment by
inoculation with rabic virus (see also Parasitic Diseases), and
the other was the attempt of the government to exterminate
rabies in the British Isles by muzzling dogs.
The Pasteur treatment was first applied to human beings in
1885 after prolonged investigation and experimental trial on
animals. It is based on the fact that a virus, capable
of giving rabies by inoculation, can be extracted
Pasteur treatment.
from the tissues of a rabid animal and then intensified
or attenuated at pleasure. It appears that the strength
of the rabic virus, as determined by inoculation, is constant in
the same species of animal, but is modified by passing through
another species. For instance, the natural virus of dogs is always
of the same strength, but when inoculated into monkeys it becomes
weakened, and the process of attenuation can be carried on by
passing the virus through a succession of monkeys, until it
loses the power of causing death. If this weakened virus is
then passed back through guinea-pigs, dogs or rabbits, it regains
170
its former strength. Again, if it be passed through a succession
of dogs it becomes intensified up to a maximum of strength
which is called the virus fixe. Pasteur further discovered that
the strength can be modified by temperature and by keeping
the dried tissues of a rabid animal containing the virus. Thus,
if the spinal cord of a rabid dog be preserved in a dry state, the
virus loses strength day by day. The system of treatment
consists in making an emulsion of the cord and graduating the
strength of the dose by using a succession of cords, which have
been kept for a progressively diminishing length of time. Those
which have been kept for fourteen days are used as a starting-point,
yielding virus of a minimum strength. They are followed
by preparations of diminishing age and increasing strength,
day by day, up to the maximum, which is three days old. These
are successively injected into the circulatory system. The
principle is the artificial acquisition by the patient of resistance
to the rabic virus, which is presumed to be already in the system
but has not yet become active, by accustoming him gradually
to its toxic effect, beginning with a weak form and progressively
increasing the dose. It is not exactly treatment of the disease,
because it is useless or nearly so when the disease has commenced,
nor is it exactly preventive, for the patient has already been
bitten. It must be regarded as a kind of anticipatory cure.
The cords are cut into sections and preserved dry in sterilized
flasks plugged with cotton-wool. Another method of preparing
the inoculatory virus, which has been devised by Guido Tizzoni
and Eugenio Centanni, consists in subjecting the virus fixe to
peptic digestion by diluted gastric juice for varying periods of
time.
The first patient was treated by Pasteur’s system in July
1885. He was successively inoculated with emulsions made from
cords that had been kept fourteen and ten days, then eleven
and eight days, then eight, seven, six days, and so on. Two
forms of treatment are now used—(1) the “simple,” in which
the course from weak to strong virus is extended over nine days;
(2) the “intensive,” in which the maximum is reached in seven
days. The latter is used in cases of very bad bites and those of
some standing, in which it is desirable to lose no time. Two
days are compressed into one at the commencement by making
injections morning and evening instead of once a day, so that the
fifth-day cord is reached in four days instead of six, as in the
“simple” treatment. When the maximum—the third-day
cord—is reached the injections are continued with fifth-, fourth-,
and third-day cords. The whole course is fifteen days in the
simple treatment and twenty-one in the intensive. The doses
injected range from 1 to 3 cubic centimetres. Injections are
made alternately into the right and left flanks. The following
table shows the number treated from 1886 to 1905, with the
mortality.
| Year. | Patients
Treated. | Deaths. | Mortality
per cent. |
| 1886 | 2671 | 25 | .94 |
| 1887 | 1770 | 14 | .79 |
| 1888 | 1622 | 9 | .55 |
| 1889 | 1830 | 7 | .38 |
| 1890 | 1540 | 5 | .32 |
| 1891 | 1559 | 4 | .25 |
| 1892 | 1790 | 4 | .22 |
| 1893 | 1648 | 6 | .36 |
| 1894 | 1387 | 7 | .50 |
| 1895 | 1520 | 5 | .33 |
| 1896 | 1308 | 4 | .30 |
| 1897 | 1521 | 6 | .39 |
| 1898 | 1465 | 3 | .20 |
| 1899 | 1614 | 4 | .25 |
| 1900 | 1419 | 10 | .70 |
| 1901 | 1318 | 5 | .37 |
| 1902 | 1105 | 2 | .18 |
| 1903 | 630 | 4 | .65 |
| 1904 | 757 | 5 | .66 |
| 1905 | 727 | 4 | .54 |
These figures do not include cases which develop hydrophobia
during treatment or within fifteen days after treatment is completed,
for it is held that persons who die within that period
have their nervous centres invaded by virus before the cure has
time to act. The true mortality should therefore be considerably
higher. For instance, in 1898 three deaths came within this
category, which just doubles the mortality; and in 1899 the
additional deaths were six, bringing the mortality up to two-and-a-half
times that indicated in the table. When, however, the
additional deaths are included the results remain sufficiently
striking, if two assumptions are granted—(1) that all the persons
treated have been bitten by rabid animals; (2) that a large
proportion of persons so bitten usually have hydrophobia.
Unfortunately, both these assumptions lack proof, and therefore
the evidence of the efficacy of the treatment cannot be said to
satisfy a strictly scientific standard. With regard to the first point,
the patients are divided into three categories—(1) those bitten by
an animal the rabidity of which is proved by the development
of rabies in other animals bitten by it or inoculated from its
spinal cord; (2) those bitten by an animal pronounced rabid
on a veterinary examination; (3) those bitten by an animal
suspected of being rabid. The number of patients in each category
in 1898 was (1) 141, (2) 855, (3) 469; and in 1899 it was (1) 152,
(2) 1099, (3) 363. As might be expected, the vast majority came
under the second and third heads, in which the evidence of rabidity
is doubtful or altogether lacking. With regard to the second
point, the proportion of persons bitten by rabid animals who
ordinarily develop hydrophobia has only been “estimated”
from very inadequate data. Otto Bollinger from a series of
collected statistics states that before the introduction of the
Pasteur treatment, of patients bitten by dogs undoubtedly rabid
47% died, the rate being 33% in those whose wounds had been
cauterized and 83% when there had been no local treatment.
If the number of rabid dogs be compared with the deaths from
hydrophobia in any year or series of years, it can hardly be very
high. For instance, in 1895, 668 dogs, besides other animals,
were killed and certified to be rabid in England, and the deaths
from hydrophobia were twenty. Of course this proves nothing,
as the number of persons bitten is not known, but the difference
between the amount of rabies and of hydrophobia is suggestively
great in view of the marked propensity of rabid dogs to bite,
nor is it accounted for by the fact that some of the persons bitten
were treated at the Institut Pasteur. A comparison of the annual
mortality from hydrophobia in France before and after the introduction
of the treatment would afford decisive evidence as to
its efficacy; but unfortunately no such comparison can be made
for lack of vital statistics in that country. The experience of
the Paris hospitals, however, points to a decided diminution of
mortality. On the whole it must be said, in the absence of further
data, that the Pasteur treatment certainly diminishes the danger
of hydrophobia from the bites of rabid animals.
More recently treatment with an anti-rabic serum has been
suggested (see Parasitic Diseases). Victor Babes and Lepp
and later Guido Tizzoni and Eugenio Centanni have worked out
a method of serum treatment curative and protective. In this
method not the rabic poison itself, as in the Pasteur treatment,
but the protective substance formed is injected into the tissues.
The serum of a vaccinated animal is capable of neutralizing the
power of the virus of rabies not only when mixed with the virus
before injection but even when injected simultaneously or within
twenty-four hours after the introduction of the virus. These
authors showed that the serum of a rabbit protects a rabbit
better than does the serum of a dog, and vice versa. At the end
of twenty days’ injections they found they could obtain such a
large quantity of anti-rabic substance in the serum of an animal,
that even 1 part of serum to 25,000 of the body weight would
protect an animal. This process differs from that of Pasteur
in so far as that in place of promoting the formation of the
antidote within the body of the patient, by a process of vaccination
with progressively stronger and stronger virus, this part of
the process is carried on in an animal, Babes using the dog and
Centanni the sheep, the blood serum of which is injected. This
method of vaccination is useful as a protective to those in charge
of kennels.
171
The attempt to stamp out rabies in Great Britain was an
experiment undertaken by the government in the public interest.
The principal means adopted were the muzzling of
dogs in infected areas, and prolonged quarantine for
Muzzling order in England.
imported animals. The efficacy of dog-muzzling
in checking the spread of rabies and diminishing its
prevalence has been repeatedly proved in various countries.
Liable as other animals may be to the disease, in England at
least the dog is pre-eminently the vehicle of contagion and the
great source of danger to human beings. There is a difference
of opinion on the way in which muzzling acts, though there can
be none as to the effect it produces in reducing rabies. Probably
it acts rather by securing the destruction of ownerless and stray—which
generally includes rabid—dogs than by preventing biting;
for though it may prevent snapping, even the wire-cage muzzle
does not prevent furious dogs from biting, and it is healthy, not
rabid, dogs that wear the muzzle. It has therefore been suggested
that a collar would have the same effect, if all collarless dogs
were seized; but the evidence goes to show that it has not,
perhaps because rabid dogs are more likely to stray from home
with their collars, which are constantly worn, than with muzzles
which are not, and so escape seizure. Moreover, it is much easier
for the police to see whether a dog is wearing a muzzle or not
than it is to make sure about the collar. However this may be,
the muzzle has proved more efficacious, but it was not applied
systematically in England until a late date. Sometimes the
regulations were in the hands of the government, and sometimes
they were left to local authorities; in either case they were
allowed to lapse as soon as rabies had died down. In April
1897 the Board of Agriculture entered on a systematic attempt
to exterminate rabies by the means indicated. The plan was to
enforce muzzling over large areas in which the disease existed,
and to maintain it for six months after the occurrence of the
last case. In spite of much opposition and criticism, this was
resolutely carried out under Mr Walter Long, the responsible
minister, and met with great success. By the spring of 1899—that
is, in two years—the disease had disappeared in Great
Britain, except for one area in Wales; and, with this exception,
muzzling was everywhere relaxed in October 1899. It was taken
off in Wales also in the following May, no case having occurred
since November 1899. Rabies was then pronounced extinct.
During the summer of 1900, however, it reappeared in Wales, and
several counties were again placed under the order. The year
1901 was the third in succession in which no death from hydrophobia
was registered in the United Kingdom. In the ten years
preceding 1899, 104 deaths were registered, the death-rate
reaching 30 in 1889 and averaging 29 annually. In 1902 two
deaths from hydrophobia were registered. From that date to
June 1909 (the latest available for the purpose of this article)
no death from hydrophobia was notified in the United Kingdom.
See Annales de l’Institut Pasteur, from 1886; Journal of the
Board of Agriculture, 1899; Makins, “Hydrophobia,” in Treves’s
System of Surgery; Woodhead, “Rabies,” in Allbutt’s System of
Medicine.
HYDROSPHERE (Gr. ὕδωρ, water, and σφαῖρα, sphere), in
physical geography, a name given to the whole mass of the water
of the oceans, which fills the depressions in the earth’s crust,
and covers nearly three-quarters of its surface. The name is
used in distinction from the atmosphere, the earth’s envelope
of air, the lithosphere (Gr. λίθος, rock) or solid crust of the earth,
and the centrosphere or interior mass within the crust. To
these “spheres” some writers add, by figurative usage, the
terms “biosphere,” or life-sphere, to cover all living things,
both animals and plants, and “psychosphere,” or mind-sphere,
covering all the products of human intelligence.
HYDROSTATICS (Gr. ὕδωρ, water, and the root στα-, to cause
to stand), the branch of hydromechanics which discusses the
equilibrium of fluids (see Hydromechanics).
HYDROXYLAMINE, NH2OH, or hydroxy-ammonia, a compound
prepared in 1865 by W. C. Lossen by the reduction of
ethyl nitrate with tin and hydrochloric acid. In 1870 E. Ludwig
and T. H. Hein (Chem. Centralblatt, 1870, 1, p. 340) obtained it
by passing nitric oxide through a series of bottles containing tin
and hydrochloric acid, to which a small quantity of platinum
tetrachloride has been added; the acid liquid is poured off
when the operation is completed, and sulphuretted hydrogen is
passed in; the tin sulphide is filtered off and the filtrate evaporated.
The residue is extracted by absolute alcohol, which dissolves
the hydroxylamine hydrochloride and a little ammonium
chloride; this last substance is removed as ammonium platino-chloride,
and the residual hydroxylamine hydrochloride is
recrystallized. E. Divers obtains it by mixing cold saturated
solutions containing one molecular proportion of sodium nitrate,
and two molecular proportions of acid sodium sulphite, and
then adding a saturated solution of potassium chloride to the
mixture. After standing for twenty-four hours, hydroxylamine
potassium disulphonate crystallizes out. This is boiled for some
hours with water and the solution cooled, when potassium
sulphate separates first, and then hydroxylamine sulphate.
E. Tafel (Zeit. anorg. Chem., 1902, 31, p. 289) patented an electrolytic
process, wherein 50% sulphuric acid is treated in a divided
cell provided with a cathode of amalgamated lead, 50% nitric
acid being gradually run into the cathode compartment. Pure
anhydrous hydroxylamine has been obtained by C. A. Lobry de
Bruyn from the hydrochloride, by dissolving it in absolute
methyl alcohol and then adding sodium methylate. The precipitated
sodium chloride is filtered, and the solution of hydroxylamine
distilled in order to remove methyl alcohol, and finally
fractionated under reduced pressure. The free base is a colourless,
odourless, crystalline solid, melting at about 30° C., and boiling
at 58° C. (under a pressure of 22 mm.). It deliquesces and
oxidizes on exposure, inflames in dry chlorine and is reduced to
ammonia by zinc dust. Its aqueous solution is strongly alkaline,
and with acids it forms well-defined stable salts. E. Ebler and
E. Schott (J. pr. Chem., 1908, 78, p. 289) regard it as acting with
the formula NH2·OH towards bases, and as NH3:O towards acids,
the salts in the latter case being of the oxonium type. It is a
strong reducing agent, giving a precipitate of cuprous oxide
from alkaline copper solutions at ordinary temperature, converting
mercuric chloride to mercurous chloride, and precipitating
metallic silver from solutions of silver salts. With
aldehydes and ketones it forms oximes (q.v.). W. R. Dunstan
(Jour. Chem. Soc., 1899, 75, p. 792) found that the addition of
methyl iodide to a methyl alcohol solution of hydroxylamine
resulted in the formation of trimethyloxamine, N(CH3)3O.
Many substituted hydroxylamines are known, substitution taking
place either in the α or β position  . β-phenylhydroxyl-amine,
C6H5NH·OH·, is obtained in the reduction of nitrobenzene
in neutral solution (e.g. by the action of the aluminium-mercury
couple and water), but better, according to C. Goldschmidt (Ber.,
1896, 29, p. 2307) by dissolving nitrobenzene in ten times its weight
of ether containing a few cubic centimetres of water, and heating
with excess of zinc dust and anhydrous calcium chloride for three
hours on a water bath. It also appears as an intermediate product
in the electrolytic reduction of nitrobenzene in sulphuric acid
solution. By gentle oxidation it yields nitrosobenzene. Derivatives
of the type R2N·OH result in the action of the Grignard reagent on
amyl nitrite. Dihydroxy-ammonia or nitroxyl, NH(OH)2, a very
unstable and highly reactive substance, has been especially studied
by A. Angeli (see A. W. Stewart, Recent Advances in Physical and
Inorganic Chemistry, 1909).
. β-phenylhydroxyl-amine,
C6H5NH·OH·, is obtained in the reduction of nitrobenzene
in neutral solution (e.g. by the action of the aluminium-mercury
couple and water), but better, according to C. Goldschmidt (Ber.,
1896, 29, p. 2307) by dissolving nitrobenzene in ten times its weight
of ether containing a few cubic centimetres of water, and heating
with excess of zinc dust and anhydrous calcium chloride for three
hours on a water bath. It also appears as an intermediate product
in the electrolytic reduction of nitrobenzene in sulphuric acid
solution. By gentle oxidation it yields nitrosobenzene. Derivatives
of the type R2N·OH result in the action of the Grignard reagent on
amyl nitrite. Dihydroxy-ammonia or nitroxyl, NH(OH)2, a very
unstable and highly reactive substance, has been especially studied
by A. Angeli (see A. W. Stewart, Recent Advances in Physical and
Inorganic Chemistry, 1909).
HYDROZOA, one of the most widely spread and prolific
groups of aquatic animals. They are for the most part marine
in habitat, but a familiar fresh-water form is the common Hydra
of ponds and ditches, which gives origin to the name of the class.
The Hydrozoa comprise the hydroids, so abundant on all shores,
most of which resemble vegetable organisms to the unassisted
eye; the hydrocorallines, which, as their name implies, have a
massive stony skeleton and resemble corals; the jelly-fishes so
called; and the Siphonophora, of which the species best known
by repute is the so-called “Portuguese man-of-war” (Physalia),
dreaded by sailors on account of its terrible stinging powers.
In external form and appearance the Hydrozoa exhibit such
striking differences that there would seem at first sight to be
little in common between the more divergent members of the
group. Nevertheless there is no other class in the animal kingdom
with better marked characteristics, or with more uniform
172
morphological peculiarities underlying the utmost diversity of
superficial characters.
All Hydrozoa, in the first place, exhibit the three structural
features distinctive of the Coelentera (q.v.). (1) The body is built
up of two layers only, an external protective and sensory layer,
the ectoderm, and an internal digestive layer, the endoderm.
(2) The body contains but a single internal cavity, the coelenteron
or gastrovascular space, which may be greatly ramified, but is not
shut off into cavities distinct from the central digestive space.
(3) The generative cells are produced in either the ectoderm or
endoderm, and not in a third layer arising in the embryo, distinct
from the two primary layers; in other words, there is no mesoderm
or coelom.
To these three characters the Hydrozoa add a fourth which
is distinctive of the subdivision of the Coelenterata termed the
Cnidaria; that is to say, they always possess peculiar stinging
organs known as nettle-cells, or nematocysts (Cnidae), each
produced in a cell forming an integral part of the animal’s
tissues. The Hydrozoa are thus shown to belong to the group
of Coelenterata Cnidaria, and it remains to consider more fully
their distinctive features, and in particular those which mark
them off from the other main division of the Cnidaria, the
Anthozoa (q.v.), comprising the corals and sea-anemones.
The great diversity, to which reference has already been made,
in the form and structure of the Hydrozoa is due to two principal
causes. In the first place, we find in this group two distinct
types of person or individual, the polyp and the medusa (qq.v.),
each capable of a wide range of variations; and when both
polyp and medusa occur in the life-cycle of the same species,
as is frequently the case, the result is an alternation of generations
of a type peculiarly characteristic of the class. In the
second place, the power of non-sexual reproduction by budding
is practically of universal occurrence among the Hydrozoa, and
by the buds failing to separate from the parent stock, colonies are
produced, more or less complicated in structure and often of
great size. We find that polyps may either bud other polyps or
may produce medusae, and that medusae may bud medusae,
though never, apparently, polyps. Hence we have a primary
subdivision of the colonies of Hydrozoa into those produced by
budding of polyps and those produced by budding of medusae.
The former may contain polyp-persons and medusa-persons,
either one kind alone or both kinds combined; the latter will
contain only medusa-persons variously modified.
The morphology of the Hydrozoa reduces itself, therefore,
to a consideration of the morphology of the polyp, of the medusa
and of the colony. Putting aside the last-named, for a detailed
account of which see Hydromedusae, we can best deal with the
peculiarities of the polyp and medusa from a developmental
point of view.
In the development of the Hydrozoa, and indeed of the Cnidaria
generally, the egg usually gives rise to an oval larva which swims
about by means of a coating of cilia on the surface of the body.
This very characteristic larva is termed a planula, but though very
uniform externally, the planulae of different species, or of the same
species at different periods, do not always represent the same stage
of embryonic development internally. On examining more minutely
the course of the development, it is found that the ovum goes
through the usual process of cleavage, always total and regular in
this group, and so gives rise to a hollow sphere or ovoid with the
wall composed of a single layer of cells, and containing a spacious
cavity, the blastocoele or segmentation-cavity. This is the blastula
stage occurring universally in all Metazoa, probably representing
an ancestral Protozoan colony in phylogeny. Next the blastula
gives rise to an internal mass of cells (fig. 1, hy) which come from the
wall either by immigration (fig. 1, A) or by splitting off (delamination).
The formation of an inner cell-mass converts the single-layered
blastula (monoblastula) into a double-layered embryo
(diblastula) which may be termed a parenchymula, since at first
the inner cell-mass forms an irregular parenchyma which may
entirely fill up and obliterate the segmentation cavity (fig. 1, B).
At a later stage, however, the cells of the inner mass arrange themselves
in a definite layer surrounding an internal cavity (fig. 1, C, al),
which soon acquires an opening to the exterior at one pole, and so
forms the characteristic embryonic stage of all Enterozoa known as
the gastrula (fig. 2). In this stage the body is composed of two
layers, ectoderm (d) externally, and endoderm (c) internally, surrounding
a central cavity, the archenteron (b), which communicates
with the exterior by a pore (a), the blastopore.
 |
| From Balfour, after Kowalewsky. |
| Fig. 1.—Formation of the Diblastula of Eucope (one of the
Calyptoblastic Hydromedusae) by immigration. A, B, C, three successive
stages. ep, Ectoderm; hy, endoderm; al, enteric cavity. |
 |
| From Gegenbaur’s Elements
of Comparative Anatomy. |
| Fig. 2.—Diagram of a Diblastula. |
a, Blastopore.
b, Archenteric cavity.
c, Endoderm.
d, Ectoderm. |
Thus a planula larva may be a blastula, or but slightly advanced
beyond this stage, or it may be (and most usually is) a parenchymula;
or in some cases (Scyphomedusae) it may be a gastrula. It should
be added that the process of development, the gastrulation as it is
termed, may be shortened by the immigration of cells taking place
at one pole only, and in a connected layer with orderly arrangement,
so that the gastrula stage is reached at once from the blastula without
any intervening parenchymula stage. This is a process of gastrulation
by invagination which is found in all animals above the Coelenterata,
but which is very rare in the Cnidaria, and is known only in
the Scyphomedusae amongst the Hydrozoa.
After the gastrula stage, which is found as a developmental stage
in all Enterozoa, the embryo of the Hydrozoa proceeds to develop
characters which are peculiar to the Coelenterata
only. Round the blastopore hollow
outgrowths, variable in number, arise by the
evagination of the entire body-wall, both
ectoderm and endoderm. Each outgrowth contains
a prolongation of the archenteric cavity
(compare figs. 2 and 3, A). In this way is
formed a ring of tentacles, the most characteristic
organs of the Cnidaria. They surround
a region which is termed the peristome, and
which contains in the centre the blastopore,
which becomes the adult mouth. The archenteron
becomes the gastrovascular system
or coelenteron. Between the ectoderm and
endoderm a gelatinous supporting layer,
termed the mesogloea, makes its appearance.
The gastrula has now become an actinula,
which may be termed the distinctive larva of
the Cnidaria, and doubtless represents in a
transitory manner the common ancestor of
the group. In no case known, however, does
the actinula become the adult, sexually mature
individual, but always undergoes further
modifications, whereby it develops into either a polyp or a medusa.
To become a polyp, the actinula (fig. 3, A) becomes attached to
some firm object by the pole farthest from the mouth, and its growth
preponderates in the direction of the principal axis, that is to say, the
axis passing through the mouth (fig. 3, a-b). As a result the body
becomes columnar in form (fig. 3, B), and without further change
passes into the characteristic polyp-form (see Polyp).
 |
| Fig. 3.—Diagram showing the change of the Actinula (A) into a
Polyp (B); a-b, principal (vertical) axis; c-d, horizontal axis. The
endoderm is shaded, the ectoderm is left clear. |
 |
| Fig. 4.—Diagram showing the change of the Actinula into a
Medusa. A, Vertical section of the actinula; a-b and c-d as in fig. 3, B,
transitional stage, showing preponderating growth in the horizontal
plane. C, C′, D, D′, two types of medusa organization; C and D are
composite sections, showing a radius (R) on one side, an interradius
(IR) on the other; C’ and D’ are plans; the mouth and manubrium
are indicated at the centre, leading into the gastral cavity subdivided
by the four areas of concrescence in each interradius (IR). t,
tentacle; g.p, gastric pouch; r.c, radial canal not present in C
and C′; c.c, circular or ring-canal; e.l, endoderm-lamella formed
by concrescence. For a more detailed diagram of medusa-structure
see article Medusa. |
It is convenient to distinguish two types of polyp by the names
hydro polyp and anthopolyp, characteristic of the Hydrozoa and
173
Anthozoa respectively. In the hydropolyp the body is typically
elongated, the height of the column being far greater than the
diameter. The peristome is relatively small and the mouth is generally
raised on a projecting spout or hypostome. The ectoderm loses entirely
the ciliation which it had in the planula and actinula stages and commonly
secretes on its external surface a protective or supporting investment,
the perisarc. Contrasting with this, the anthopolyp is
generally of squat form, the diameter often exceeding the height;
the peristome is wide, a hypostome is lacking, and the ectoderm,
or so much of it as is exposed, i.e. not covered by secretion of skeletal
or other investment, retains its ciliation throughout life. The
internal structural differences are even more characteristic. In the
hydropolyp the blastopore of the embryo forms the adult mouth
situated at the extremity of the hypostome, and the ectoderm and
endoderm meet at this point. In the anthopolyp the blastopore is
carried inwards by an in-pushing of the body-wall of the region of
the peristome, so that the adult mouth is an opening leading into a
short ectodermal oesophagus or stomodaeum, at the bottom of
which is the blastopore. Further, in the hydropolyp the digestive
cavity either remains simple and undivided and circular in transverse
section, or may show ridges projecting internally, which in this case
are formed of endoderm alone, without any participation of the
mesogloea. In the anthopolyp, on the other hand, the digestive
cavity is always subdivided by so-called mesenteries, in-growths
of the endoderm containing vertical lamellae of mesogloea (see
Anthozoa). In short, the hydropolyp is characterized by a more
simple type of organization than the anthopolyp, and is in most
respects less modified from the actinula type of structure.
Returning now to the actinula, this form may, as already stated,
develop into a medusa, a type of individual found only in the
Hydrozoa, as here understood. To become a medusa, the actinula
grows scarcely at all in the direction of the principal axis, but greatly
along a plane at right angles to it. Thus the body becomes umbrella-shaped,
the concave side representing the peristome, and the convex
side the column, of the polyp. Hence the tentacles are found at the
edge of the umbrella, and the hypostome forms usually a projecting
tube, with the mouth at the extremity, forming the manubrium or
handle of the umbrella. The medusa has a pronounced radial symmetry,
and the positions of the primary tentacles, usually four in
number, mark out the so-called radii, alternating with which are
four interradii. The ectoderm retains its ciliation only in the
sensory organs. The mesogloea becomes enormously increased in
quantity (hence the popular name “jelly-fish”), and in correlation
with this the endoderm-layer lining the coelenteron becomes pressed
together in the interradial areas and undergoes concrescence,
forming a more or less complicated gastrovascular system (see
Medusa). It is sufficient to state here that the medusa is usually a
free-swimming animal, floating mouth downwards on the open seas,
but in some cases it may be attached by its aboral pole, like a polyp,
to some firm basis, either temporarily or permanently.
Thus the development of the two types of individual seen in the
Hydrozoa may be summarized as follows:—

This development, though probably representing the primitive
sequence of events, is never actually found in its full extent, but is
always abbreviated by omission or elimination of one or more of
the stages. We have already seen that the parenchymula stage is
passed over when the gastrulation is of the invaginate type. On the
other hand, the parenchymula may develop directly into the actinula
or even into the polyp, with suppression of the intervening steps.
Great apparent differences may also be brought about by variations
in the period at which the embryo is set free as a larva, and since two
free-swimming stages, planula and actinula, are unnecessary, one or
other of them is always suppressed. A good example of this is seen
in two common genera of British hydroids, Cordylophora and Tabularia.
In Cordylophora the embryo is set free at the parenchymula
stage as a planula which fixes itself and develops into a polyp, both
gastrula and actinula stages being suppressed. In Tubularia, on the
other hand, the parenchymula develops into an actinula within the
maternal tissues, and is then set free, creeps about for a time, and
after fixing itself, changes into a polyp; hence in this case the
planula-stage, as a free larva, is entirely suppressed.
The Hydrozoa may be defined, therefore, as Cnidaria in which
two types of individual, the polyp and the medusa, may be present,
each type developed along divergent lines from the primitive actinula
form. The polyp (hydropolyp) is of simple structure and never has
an ectodernal oesophagus or mesenteries.1 The general ectoderm
loses its cilia, which persist only in the sensory cells, and it frequently
secretes external protective or supporting structures. An internal
mesogloeal skeleton is not found.
The class is divisible into two main divisions or sub-classes, Hydromedusae
and Scyphomedusae, of which definitions and detailed
systematic accounts will be found under these headings.
General Works on Hydrozoa.—C. Chun, “Coelenterata
(Hohlthiere),” Bronn’s Klassen und Ordnungen des Thier-Reichs
ii. 2 (1889 et seq.); Y. Delage, and E. Hérouard, Traité de zoologie
concrète, ii. part 2, Les Coelentérés (1901); G. H. Fowler, “The
Hydromedusae and Scyphomedusae” in E. R. Lankester’s Treatise
on Zoology, ii. chapters iv. and v. (1900); S. J. Hickson, “Coelenterata
and Ctenophora,” Cambridge Natural History, i. chapters
x.-xv. (1906).
(E. A. M.)
HYENA, a name applicable to all the representatives of the
mammalian family Hyaenidae, a group of Carnivora (q.v.) allied
to the civets. From all other large Carnivora except the African
hunting-dog, hyenas are distinguished by having only four toes
on each foot, and are further characterized by the length of the
fore-legs as compared with the hind pair, the non-retractile claws,
and the enormous strength of the jaws and teeth, which enables
them to break the hardest bones and to retain what they have
seized with unrelaxing grip.
174
 |
| Fig. 1.—The Striped Hyena (Hyaena striata). |
 |
| Fig. 2.—The Spotted Hyena (Hyaena crocuta). |
The striped hyena (Hyaena striata) is the most widely distributed
species, being found throughout India, Persia, Asia
Minor, and North and East Africa, the East African form
constituting a distinct race, H. striata schillingsi; while there
are also several distinct Asiatic races. The species resembles
a wolf in size, and is greyish-brown In colour, marked with
indistinct longitudinal stripes of a darker hue, while the legs are
transversely striped. The hairs on the body are long, especially
on the ridge of the neck and back, where they form a distinct
mane, which is continued along the tail. Nocturnal in habits,
it prefers by day the gloom of caves and ruins, or of the burrows
which it occasionally forms, and issues forth at sunset, when it
commences its unearthly howling. When the animal is excited,
the howl changes into what has been compared to demoniac
laughter, whence the name of “laughing-hyena.” These
creatures feed chiefly on carrion, and thus perform useful service
by devouring remains which might otherwise pollute the air.
Even human dead are not safe from their attacks, their powerful
claws enabling them to gain access to newly interred bodies in
cemeteries. Occasionally (writes Dr W. T. Blanford) sheep or
goats, and more often dogs, are carried off, and the latter, at all
events, are often taken alive to the animal’s den. This species
appears to be solitary in habits, and it is rare to meet with more
than two together. The cowardice of this hyena is proverbial;
despite its powerful teeth, it rarely attempts to defend itself.
A very different animal is the spotted hyena, Hyaena (Crocuta)
crocuta, which has the sectorial teeth of a more cat-like type,
and is marked by dark-brown spots on a yellowish ground, while
the mane is much less distinct. At the Cape it was formerly
common, and occasionally committed great havoc among the
cattle, while it did not hesitate to enter the Kaffir dwellings at
night and carry off children sleeping by their mothers. By
persistent trapping and shooting, its numbers have now been
considerably reduced, with the result, however, of making it
exceedingly wary, so that it is not readily caught in any trap
with which it has had an opportunity of becoming acquainted.
Its range extends from Abyssinia to the Cape. The Abyssinian
form has been regarded as a distinct species, under the name
of H. liontiewi, but this, like various more southern forms, is
but regarded as a local race. The brown hyena (H. brunnea)
is South African, ranging to Angola on the west and Kilimanjaro
on the east. In size it resembles the striped hyena, but differs
in appearance, owing to the fringe of long hair covering the neck
and fore part of the back. The general hue is ashy-brown, with
the hair lighter on the neck (forming a collar), chest and belly;
while the legs are banded with dark brown. This species is not
often seen, as it remains concealed during the day. Those
frequenting the coast feed on dead fish, crabs and an occasional
stranded whale, though they are also a danger to the sheep and
cattle kraal. Strand-wolf is the local name at the Cape.
Although hyenas are now confined to the warmer regions of the
Old World, fossil remains show that they had a more northerly
range during Tertiary times; the European cave-hyena being a
form of the spotted species, known as H. crocuta spelaea. Fossil
hyenas occur in the Lower Pliocene of Greece, China, India,
&c.; while remains indistinguishable from those of the striped
species have been found in the Upper Pliocene of England and
Italy.
HYÈRES, a town in the department of the Var in S.E. France,
11 m. by rail E. of Toulon. In 1906 the population of the commune
was 17,790, of the town 10,464; the population of the former
was more than doubled in the last decade of the 19th century.
Hyères is celebrated (as is also its fashionable suburb, Costebelle,
nearer the seashore) as a winter health resort. The town proper
is situated about 2½ m. from the seashore, and on the south-western
slope of a steep hill (669 ft., belonging to the Maurettes
chain, 961 ft.), which is one of the westernmost spurs of the
thickly wooded Montagnes des Maures. It is sheltered from the
north-east and east winds, but is exposed to the cold north-west
wind or mistral. Towards the south and south-east a fertile
plain, once famous for its orange groves, but now mainly covered
by vineyards and farms, stretches to the sea, while to the south-west,
across a narrow valley, rises a cluster of low hills, on which is
the suburb of Costebelle. The older portion of the town is still
surrounded, on the north and east, by its ancient, though
dilapidated medieval walls, and is a labyrinth of steep and dirty
streets. The more modern quarter which has grown up at the
southern foot of the hill has handsome broad boulevards and
villas, many of them with beautiful gardens, filled with semi-tropical
plants. Among the objects of interest in the old town
are: the house (Rue Rabaton, 7) where J. B. Massillon (1663-1742),
the famous pulpit orator, was born; the parish church
of St Louis, built originally in the 13th century by the Cordelier
or Franciscan friars, but completely restored in the earlier part
of the 19th century; and the site of the old château, on the
summit of the hill, now occupied by a villa. The plain between
the new town and the sea is occupied by large nurseries, an
excellent jardin d’acclimatation, and many market gardens, which
supply Paris and London with early fruits and vegetables,
especially artichokes, as well as with roses in winter. There are
extensive salt beds (salines) both on the peninsula of Giens, S.
of the town, and also E. of the town. To the east of the Giens
peninsula is the fine natural harbour of Hyères, as well as three
thinly populated islands (the Stoechades of the ancients),
Porquerolles, Port Cros and Le Levant, which are grouped
together under the common name of Îles d’Hyères.
The town of Hyères seems to have been founded in the 10th
century, as a place of defence against pirates, and takes its name
from the aires (hierbo in the Provençal dialect), or threshing-floors
for corn, which then occupied its site. It passed from the
possession of the viscounts of Marseilles to Charles of Anjou,
count of Provence, and brother of St Louis (the latter landed
here in 1254, on his return from Egypt). The château was
175
dismantled by Henri IV., but thanks to its walls, the town resisted
in 1707 an attack made by the duke of Savoy.
See Ch. Lenthéric, La Provence Maritime ancienne et moderne
(chap. 5) (Paris, 1880).
(W. A. B. C.)
HYGIEIA, in Greek mythology, the goddess of health. It
seems probable that she was originally an abstraction, subsequently
personified, rather than an independent divinity of very
ancient date. The question of the original home of her worship
has been much discussed. The oldest traces of it, so far as is
known at present, are to be found at Titane in the territory of
Sicyon, where she was worshipped together with Asclepius, to
whom she appears completely assimilated, not an independent
personality. Her cult was not introduced at Epidaurus till a
late date, and therefore, when in 420 B.C. the worship of Asclepius
was introduced at Athens coupled with that of Hygieia, it is not
to be inferred that she accompanied him from Epidaurus, or
that she is a Peloponnesian importation at all. It is most
probable that she was invented at the time of the introduction
of Asclepius, after the sufferings caused by the plague had
directed special attention to sanitary matters. The already
existing worship of Athena Hygieia had nothing to do with
Hygieia the goddess of health, but merely denoted the recognition
of the power of healing as one of the attributes of Athena, which
gradually became crystallized into a concrete personality.
At first no special relationship existed between Asclepius and
Hygieia, but gradually she came to be regarded as his daughter,
the place of his wife being already secured by Epione. Later
Orphic hymns, however, and Herodas iv. 1-9, make her the wife
of Asclepius. The cult of Hygieia then spread concurrently with
that of Asclepius, and was introduced at Rome from Epidaurus
in 293, by which time she may have been admitted (which was not
the case before) into the Epidaurian family of the god. Her
proper name as a Romanized Greek importation was Valetudo,
but she was gradually identified with Salus, an older genuine
Italian divinity, to whom a temple had already been erected in
302. While in classical times Asclepius and Hygieia are simply
the god and goddess of health, in the declining years of paganism
they are protecting divinities generally, who preserve mankind
not only from sickness but from all dangers on land and sea.
In works of art Hygieia is represented, together with Asclepius,
as a maiden of benevolent appearance, wearing the chiton and
giving food or drink to a serpent out of a dish.
See the article by H. Lechat in Daremberg and Saglio’s Dictionnaire
des antiquités, with full references to authorities; and E.
Thrämer in Roscher’s Lexikon der Mythologie, with a special section
on the modern theories of Hygieia.
HYGIENE (Fr. hygiène, from Gr. ὑγιαίνειν, to be healthy),
the science of preserving health, its practical aim being to render
“growth more perfect, decay less rapid, life more vigorous,
death more remote.” The subject is thus a very wide one,
embracing all the agencies which affect the physical and mental
well-being of man, and it requires acquaintance with such
diverse sciences as physics, chemistry, geology, engineering,
architecture, meteorology, epidemiology, bacteriology and
statistics. On the personal or individual side it involves consideration
of the character and quality of food and of water
and other beverages; of clothing; of work, exercise and sleep;
of personal cleanliness, of special habits, such as the use of
tobacco, narcotics, &c.; and of control of sexual and other
passions. In its more general and public aspects it must take
cognizance of meteorological conditions, roughly included under
the term climate; of the site or soil on which dwellings are
placed; of the character, materials and arrangement of dwellings,
whether regarded individually or in relation to other houses
among which they stand; of their heating and ventilation; of
the removal of excreta and other effete matters; of medical
knowledge relating to the incidence and prevention of disease;
and of the disposal of the dead.
These topics will be found treated in such articles as Dietetics,
Food, Food-Preservation, Adulteration, Water, Heating,
Ventilation, Sewerage, Bacteriology, Housing, Cremation,
&c. For legal enactments which concern the sanitary well-being
of the community, see Public Health.
HYGINUS, eighth pope. It was during his pontificate (c.
137-140) that the gnostic heresies began to manifest themselves
at Rome.
HYGINUS (surnamed Gromaticus, from gruma, a surveyor’s
measuring-rod), Latin writer on land-surveying, flourished in
the reign of Trajan (A.D. 98-117). Fragments of a work on
legal boundaries attributed to him will be found in C. F. Lachmann,
Gromatici Veteres, i. (1848).
A treatise on Castrametation (De Munitionibus Castrorum), also
attributed to him, is probably of later date, about the 3rd century
A.D. (ed. W. Gemoll, 1879; A. von Domaszewski, 1887).
HYGINUS, GAIUS JULIUS, Latin author, a native of Spain
(or Alexandria), was a pupil of the famous Cornelius Alexander
Polyhistor and a freedman of Augustus, by whom he was made
superintendent of the Palatine library (Suetonius, De Grammaticis,
20). He is said to have fallen into great poverty in his
old age, and to have been supported by the historian Clodius
Licinus. He was a voluminous author, and his works included
topographical and biographical treatises, commentaries on Helvius
Cinna and the poems of Virgil, and disquisitions on agriculture
and bee-keeping. All these are lost.
Under the name of Hyginus two school treatises on mythology are
extant: (1) Fabularum Liber, some 300 mythological legends and
celestial genealogies, valuable for the use made by the author of
the works of Greek tragedians now lost; (2) De Astronomia, usually
called Poetica Astronomica, containing an elementary treatise on
astronomy and the myths connected with the stars, chiefly based on
the Καταστερισμοί of Eratosthenes. Both are abridgments and both
are by the same hand; but the style and Latinity and the elementary
mistakes (especially in the rendering of the Greek originals) are held
to prove that they cannot have been the work of so distinguished
a scholar as C. Julius Hyginus. It is suggested that these treatises
are an abridgment (made in the latter half of the 2nd century) of
the Genealogiae of Hyginus by an unknown grammarian, who added
a complete treatise on mythology.
Editions.—Fabulae, by M. Schmidt (1872); De Astronomia, by
B. Bunte (1875); see also Bunte, De C. Julii Hygini, Augusti Liberti,
Vita et Scriptis (1846).
HYGROMETER (Gr. ὁγρός, moist, μέτρον, a measure), an
instrument for measuring the absolute or relative amount of
moisture in the atmosphere; an instrument which only
qualitatively determines changes in the humidity is termed a
“hygroscope.” The earlier instruments generally depended for
their action on the contraction or extension of substances when
exposed to varying degrees of moisture; catgut, hair, twisted
cords and wooden laths, all of which contract with an increase in
the humidity and vice versa, being the most favoured materials.
The familiar “weather house” exemplifies this property. This
toy consists of a house provided with two doors, through which
either a man or woman appears according as the weather is
about to be wet or fine. This action is effected by fixing a catgut
thread to the base on which the figures are mounted, in such
a manner that contraction of the thread rotates the figures so
that the man appears and extension so that the woman appears.
Many of the early forms are described in C. Hutton, Math. and
Phil. Dictionary (1815). The modern instruments, which utilize
other principles, are described in Meteorology: II. Methods and
Apparatus.
HYKSOS, or “Shepherd Kings,” the name of the earliest
invaders of Egypt of whom we have definite evidence in tradition.
Josephus (c. Apion. i. 14), who identifies the Hyksos with the
Israelites, preserves a passage from the second book of Manetho
giving an account of them. (It may be that Josephus had it, not
direct from Manetho’s writings, but through the garbled version
of some Alexandrine compiler.) In outline it is as follows. In
the days of a king of Egypt named Timaeus the land was suddenly
invaded from the east by men of ignoble race, who conquered
it without a struggle, destroyed cities and temples, and slew or
enslaved the inhabitants. At length they elected a king named
Salatis, who, residing at Memphis, made all Egypt tributary,
and established garrisons in different parts, especially eastwards,
fearing the Assyrians. He built also a great fortress at Avaris,
in the Sethroite nome, east of the Bubastite branch of the Nile.
Salatis was followed in succession by Beon, Apachnas, Apophis,
Jannas and Asses. These six kings reigned 198 years and 10
months, and all aimed at extirpating the Egyptians. Their
whole race was named Hyksos, i.e. “shepherd kings,” and
176
some say they were Arabs (another explanation found by
Josephus is “captive shepherds”). When they and their
successors had held Egypt for 511 years, the kings of the Thebais
and other parts of Egypt rebelled, and a long and mighty war
began. Misphragmuthosis worsted the “Shepherds” and
shut them up in Avaris; and his son Thutmosis, failing to
capture the stronghold, allowed them to depart; whereupon
they went forth, 240,000 in number, established themselves
in Judea and built Jerusalem.
In Manetho’s list of kings, the six above named (with many
variations in detail) form the XVth dynasty, and are called
“six foreign Phoenician kings.” The XVIth dynasty is of
thirty-two “Hellenic (sic?) shepherd kings,” the seventeenth
is of “shepherds and Theban kings” (reigning simultaneously).
The lists vary greatly in different versions, but the above seems
the most reasonable selection of readings to be made. For
“Hellenic” see below. The supposed connexion with the
Israelites has made the problem of the Hyksos attractive, but
light is coming upon it very slowly. In 1847 E. de Rougé
proved from a fragment of a story in the papyri of the British
Museum, that Apopi was one of the latest of the Hyksos kings,
corresponding to Aphobis; he was king of the “pest” and
suppressed the worship of the Egyptian gods, and endeavoured
to make the Egyptians worship his god Setekh or Seti; at
the same time an Egyptian named Seqenenrē reigned in Thebes,
more or less subject to Aphobis. The city of Hawari (Avaris)
was also mentioned in the fragment.
In 1850 a record of the capture of this city from the Hyksos
by Ahmosi, the founder of the eighteenth dynasty, was discovered
by the same scholar. A large class of monuments was afterwards
attributed to the Hyksos, probably in error. Some statues
and sphinxes, found in 1861 by Mariette at Tanis (in the north-east
of the Delta), which had been usurped by later kings, had
peculiar “un-Egyptian” features. One of these bore the name
of Apopi engraved lightly on the shoulder; this was evidently
a usurper’s mark, but from the whole circumstances it was
concluded that these, and others of the same type of features
found elsewhere, must have belonged to the Hyksos. This
view held the field until 1893, when Golénischeff produced an
inferior example bearing its original name, which showed that
in this case it represented Amenemhe III. In consequence
it is now generally believed that they all belong to the twelfth
dynasty. Meanwhile a headless statue of a king named Khyan,
found at Bubastis, was attributed on various grounds to the
Hyksos, the soundest arguments being his foreign name and
the boastful un-Egyptian epithet “beloved of his ka,” where
“beloved of Ptah” or some other god was to be expected.
His name was immediately afterwards recognized on a lion
found as far away from Egypt as Bagdad. Flinders Petrie then
pointed out a group of kings named on scarabs of peculiar type,
which, including Khyan, he attributed to the period between
the Old Kingdom and the New, while others were in favour of
assigning them all to the Hyksos, whose appellation seemed
to be recognizable in the title Hek-khos, “ruler of the barbarians,”
borne by Khyan. The extraordinary importance of Khyan was
further shown by the discovery of his name on a jar-lid at Cnossus
in Crete. Semitic features were pointed out in the supposed
Hyksos names, and Petrie was convinced of their date by his
excavations of 1905-1906 in the eastern Delta. Avaris is generally
assigned to the region towards Pelusium on the strength of its
being located in the Sethroite nome by Josephus, but Petrie
thinks it was at Tell el-Yahudiyeh (Yehudia), where Hyksos
scarabs are common. From the remains of fortifications there
he argues that the Hyksos were uncivilized desert people,
skilled in the use of the bow, and must thus have destroyed
by their archery the Egyptian armies trained to fight hand-to-hand;
further, that their hordes were centered in Syria, but were
driven thence by a superior force in the East to take refuge
in the islands and became a sea-power—whence the strange
description “Hellenic” in Manetho, which most editors have
corrected to ἀλλοί, “others.” Besides the statue of Khyan,
blocks of granite with the name of Apopi have been found in
Upper Egypt at Gebelen and in Lower Egypt at Bubastis. The
celebrated Rhind mathematical papyrus was copied in the
reign of an Apopi from an original of the time of Amenemhe III.
Large numbers of Hyksos scarabs are found in Upper and
Lower Egypt, and they are not unknown in Palestine. Khyan’s
monuments, inconspicuous as they are, actually extend over
a wider area—from Bagdad to Cnossus—than those of any other
Egyptian king.
It is certain that this mysterious people were Asiatic, for
they are called so by the Egyptians. Though Seth was an
Egyptian god, as god of the Hyksos he represents some Asiatic
deity. The possibility of a connexion between the Hyksos
and the Israelites is still admitted in some quarters. Hatred
of these impious foreigners, of which there is some trace in
more than one text, aroused amongst the Egyptians (as nothing
ever did before or since) that martial spirit which carried the
armies of Tethmosis to the Euphrates.
Besides the histories of Egypt, see J. H. Breasted, Ancient
Records of Egypt; Historical Documents ii. 4, 125; G. Maspero,
Contes populaires, 3me éd. p. 236; W. M. F. Petrie, Hyksos
and Israelite Cities, p. 67; Golénischeff in Recueil de travaux, xv.
p. 131.
(F. Ll. G.)
HYLAS, In Greek legend, son of Theiodamas, king of the
Dryopians in Thessaly, the favourite of Heracles and his companion
on the Argonautic expedition. Having gone ashore at
Kios in Mysia to fetch water, he was carried off by the nymphs
of the spring in which he dipped his pitcher. Heracles sought
him in vain, and the answer of Hylas to his thrice-repeated cry
was lost in the depths of the water. Ever afterwards, in memory
of the threat of Heracles to ravage the land if Hylas were not
found, the inhabitants of Kios every year on a stated day roamed
the mountains, shouting aloud for Hylas (Apollonius Rhodius
i. 1207; Theocritus xiii.; Strabo xii. 564; Propertius i. 20;
Virgil, Ecl. vi. 43). But, although the legend is first told in
Alexandrian times, the “cry of Hylas” occurs long before as
the “Mysian cry” in Aeschylus (Persae, 1054), and in Aristophanes
(Plutus, 1127) “to cry Hylas” is used proverbially of
seeking something in vain. Hylas, like Adonis and Hyacinthus,
represents the fresh vegetation of spring, or the water of a fountain,
which dries up under the heat of summer. It is suggested
that Hylas was a harvest deity and that the ceremony gone
through by the Kians was a harvest festival, at which the figure
of a boy was thrown into the water, signifying the dying vegetation-spirit
of the year.
See G. Türk in Breslauer Philologische Abhandlungen, vii. (1895);
W. Mannhardt, Mythologische Forschungen (1884).
HYLOZOISM (Gr. ὕλη, matter, ζωή, life), in philosophy, a
term applied to any system which explains all life, whether
physical or mental, as ultimately derived from matter (“cosmic
matter,” Weldstoff). Such a view of existence has been common
throughout the history of thought, and especially among physical
scientists. Thus the Ionian school of philosophy, which began
with Thales, sought for the beginning of all things in various
material substances, water, air, fire (see Ionian School). These
substances were regarded as being in some sense alive, and
taking some active part in the development of being. This
primitive hylozoism reappeared in modified forms in medieval
and Renaissance thought, and in modern times the doctrine of
materialistic monism is its representative. Between modern
materialism and hylozoism proper there is, however, the distinction
that the ancients, however vaguely, conceived the
elemental matter as being in some sense animate if not actually
conscious and conative.
HYMEN, or Hymenaeus, originally the name of the song sung
at marriages among the Greeks. As usual the name gradually
produced the idea of an actual person whose adventures gave
rise to the custom of this song. He occurs often in association
with Linus and Ialemus, who represent similar personifications,
and is generally called a son of Apollo and a Muse. As the son
of Dionysus and Aphrodite, he was regarded as a god of fruitfulness.
In Attic legend he was a beautiful youth who, being in
love with a girl, followed her in a procession to Eleusis disguised
as a woman, and saved the whole band from pirates. As reward
177
he obtained the girl in marriage, and his happy married life
caused him ever afterwards to be invoked in marriage songs
(Servius on Virgil, Aen. i. 651). According to another story,
he was a youth who was killed by the fall of his house on his
wedding day; hence he was invoked, to propitiate him and avert
a similar fate from others (Servius, loc. cit.). He is represented
in works of art as an effeminate-looking, winged youth, carrying
a bridal torch and wearing a nuptial veil. The marriage song
was sung, with musical accompaniment, during the procession
of the bride from her parents’ house to that of the bridegroom,
Hymenaeus being invoked at the end of each portion.
See R. Schmidt, De Hymenaeo el Talasio (1886), and J. A. Hild in
Daremberg and Saglis’s Dictionnaire des antiquités.
HYMENOPTERA (Gr. ὑμήν, a membrane, and πτερόν, a wing),
a term used in zoological classification for one of the most important
orders of the class Hexapoda (q.v.). The order was founded
by Linnaeus (Systema Naturae, 1735), and is still recognized by
all naturalists in the sense proposed by him, to include
the saw-flies, gall-flies, ichneumon-flies and their allies, ants,
wasps and bees. The relationship of the Hymenoptera to
other orders of insects is discussed in the article Hexapoda,
but it may be mentioned
here that in
structure the highest
members of the order
are remarkably specialized,
and that in the
perfection of their instincts
they stand at
the head of all insects
and indeed of all invertebrate
animals. About
30,000 species of Hymenoptera
are now known.
 |
| After C. L. Marlatt, Bur. Ent. Bull. 3, N.S., U.S. Dept. Agric. |
| Fig. 1.—A, Front of head of Saw-fly (Pachynematus); a,
labrum; b, clypeus; c, vertex; d, d, antennal cavities. C and
D, Mandibles. E, First maxilla; a, cardo; b, stipes; c, galea;
d, lacinia; e, palp. B, Second maxillae (Labium); a, mentum;
b, ligula (between the two galeae); c, c, palps. Magnified. |
 |
 |
| |
After C. Janet, Mem.
Soc. Zool. France (1898). |
| Fig. 2.—Jaws of
Hive-bee (Apis
mellifica). Magnified
about 6½ times.
a, mandible; b, c,
palp and lacinia
of first maxilla;
d, e, g, h, mentum,
palp, fused laciniae
(ligula or “tongue”)
and galea of 2nd
maxillae. |
Fig. 3.—Median
section through mid-body
of female Red
Ant (Myrmica rubra).
H, Head; 1, 2, 3,
the thoracic segments;
i., ii., the
first and second abdominal
segments;
i., being the propodeum. |
Characters.—In all
Hymenoptera the mandibles
(fig. 1, C, D) are
well developed, being
adapted, as in the more
lowly winged insects, such
as the Orthoptera, for
biting. The more generalized
Hymenoptera have
the second maxillae but
slightly modified, their
inner lobes being fused to
form a ligula (fig. 1, B, b).
In the higher families this
structure becomes elongated (fig. 2, g) so as to form an elaborate
sucking-organ or “tongue.” These insects are able, therefore, to
bite as well as to suck, whereas most insects which have acquired
the power of suction have lost that of biting. Both fore- and hind-wings
are usually present, both pairs being membranous, the hind-wings
small and not folded when at rest, each provided along the
costa with a row of curved hooks which catch on to a fold along the
dorsum of the adjacent fore-wing during flight. A large number of
Hymenoptera are, however, entirely wingless—at least as regards one
sex or form of the species. One of the most remarkable features is
the close union of the foremost abdominal segment (fig. 3, i.) with
the metathorax, of which it often seems to form a part, the apparent
first abdominal segment being, in such case, really the second (fig.
3, ii.). The true first segment, which undergoes a more or less complete
fusion with the thorax is known as the “median segment”
or propodeum. In female Hymenoptera the typical insectan
ovipositor with its three pairs of processes is well developed, and in
the higher families this organ becomes functional as a sting (fig. 5),—used
for offence and defence. As regards their life history, all
Hymenoptera undergo a “complete” metamorphosis. The larva
is soft-skinned (eruciform), being either a caterpillar (fig. 6, b) or a legless
grub (fig. 7, a), and the pupa is free (fig. 7, c), i.e. with the appendages
not fixed to the body, as is the case in the pupa of most moths.
 |
| Fig. 4.—Fore-Wings of Hymenoptera. |
1. Tenthredinidae (Hylotoma)—
1, marginal; 2, appendicular;
3, 4, 5, 6, radial or submarginal;
7, 8, 9, median or
discoidal; 10, sub-costal;
11, 12, cubital or branchial;
and 13, anal or lanceolate
cellules; a, b, c, submarginal
nervures; d, basal nervures;
e, f, recurrent nervures; st,
stigma; co, costa. |
2. Cynipidae (Cynips).
3. Chalcididae (Perilampus).
4. Proctotrypidae (Codrus).
5. Mymaridae (Mymar).
6. Braconidae (Bracon).
7. Ichneumonidae (Trogus).
8. Chrysididae (Cleptes).
9. Formicidae (Formica).
10. Vespidae (Vespa).
11. Apidae (Apathus). |
Structure.—The head of a hymenopterous insect bears three simple
eyes (ocelli) on the front and vertex in addition to the large compound
eyes. The feelers are generally simple in type, rarely showing serrations
or prominent appendages; but one or two basal segments
are frequently differentiated to form an elongate “scape,” the
remaining segments—carried at an elbowed angle to the scape—making
up the “flagellum”; the segments of the flagellum often
bear complex sensory organs. The general characters of the jaws
have been mentioned above, and in detail there is great variation
in these organs among the different families. The sucking tongue
of the Hymenoptera has often been compared with the hypopharynx
of other insects. According to D. Sharp, however, the hypopharynx
is present in all Hymenoptera as a distinct structure at the base of
the “tongue,” which must be regarded as representing the fused
laciniae of the second maxillae. In the thorax the pronotum and
prosternum are closely associated with the mesothorax, but the pleura
of the prothorax are usually shifted far forwards, so that the fore-legs
are inserted just behind the head. A pair of small plates—the tegulae—are
very generally present at the bases of the fore-wings. The
union of the first abdominal segment with the metathorax has been
178
already mentioned. The second (so-called “first”) abdominal
segment is often very constricted, forming the “waist” so characteristic
of wasps and ants for example. The constriction of this segment
and its very perfect articulation with the propodeum give great
mobility to the abdomen, so that the ovipositor or sting can be used
with the greatest possible accuracy and effect.
Mention has already been made of the series of curved hooks along
the costa of the hind-wing; by means of this arrangement the two
wings of a side are firmly joined together during flight, which thus
becomes particularly accurate. The wings in the Hymenoptera show
a marked reduction in the number of nervures as compared with more
primitive insects. The main median nervure, and usually also
the sub-costal become united with the radial, while the branches of
radial, median and cubital nervures pursuing a transverse or recurrent
course across the wing, divide its area into a number of
areolets or “cells,” that are of importance in classification. Among
many of the smaller Hymenoptera we find that the wings are almost
destitute of nervures. In the hind-wings—on account of their reduced
size—the nervures are even more reduced than in the fore-wings.
The legs of Hymenoptera are of the typical insectan form, and
the foot is usually composed of five segments. In many families
the trochanter appears to be represented by two small segments,
there being thus an extra joint in the leg. It is almost certain that
the distal of these two segments really belongs to the thigh, but the
ordinary nomenclature will be used in the present article, as this
character is of great importance in discriminating families, and
the two segments in question are referred to the trochanter by most
systematic writers.
 |
| After C. Janet, Aiguillon de la Myrmica rubra (Paris, 1898). |
| Fig. 5.—Ovipositor or Sting of Red Ant (Myrmica rubra) Queen.
Magnified. The right sheath C (outer process of the ninth abdominal
segment—9) is shown in connexion with the guide B formed by the
inner processes of the 9th segment. The stylet A (process of the
8th abdominal segment—8) is turned over to show its groove a,
which works along the tongue or rail b. |
The typical insectan ovipositor, so well developed among the
Hymenoptera, consists of three pairs of processes (gonapophyses)
two of which belong to the ninth abdominal segment and one to
the eighth. The latter are the cutting or piercing stylets (fig. 5, A)
of the ovipositor, while the two outer processes of the ninth segment
are modified into sheaths or feelers (fig. 5, C) and the two inner
processes form a guide (fig. 5, B) on which the stylets work, tongues
or rails on the “guide” fitting accurately into longitudinal grooves
on the stylet. In the different families of the Hymenoptera, there
are various modifications of the ovipositor, in accord with the
habits of the insects and the purposes to which the organ is put.
The sting of wasps, ants and bees is a modified ovipositor and is
used for egg-laying by the fertile females, as well as for defence.
Most male Hymenoptera have processes which form claspers or
genital armature. These processes are not altogether homologous
with those of the ovipositor, being formed by inner and outer lobes
of a pair of structures on the ninth abdominal segment.
Many points of interest are to be noted in the internal structure
of the Hymenoptera. The gullet leads into a moderate-sized crop,
and several pairs of salivary glands open into the mouth. The crop
is followed by a proventriculus which, in the higher Hymenoptera,
forms the so-called “honey stomach,” by the contraction of whose
wails the solid and liquid food can be separated, passed on into the
digestive stomach, or held in the crop ready for regurgitation into
the mouth. Behind the digestive stomach are situated, as usual,
intestine and rectum, and the number of kidney (Malpighian) tubes
varies from only six to over a hundred, being usually great.
In the female, each ovary consists of a large number of ovarian
tubes, in which swollen chambers containing the egg-cells alternate
with smaller chambers enclosing nutrient material. In connexion
with the ovipositor are two poison-glands, one acid and the other
alkaline in its secretion. The acid gland consists of one, two or
more tubes, with a cellular coat of several layers, opening into a
reservoir whence the duct leads to the exterior. The alkaline gland
is an irregular tube with a single cellular layer, its duct opening
alongside that of the acid reservoir. These glands are most strongly
developed when the ovipositor is modified into a sting.
Development.—Parthenogenesis is of normal occurrence in the
life-cycle of many Hymenoptera. There are species of gall-fly in
which males are unknown, the unfertilized eggs always developing
into females. On the other hand, in certain saw-flies and among
the higher families, the unfertilized eggs, capable of development,
usually give rise to male insects (see Bee). The larvae of most saw-flies
feeding on the leaves of plants are caterpillars (fig. 6, b) with
numerous abdominal pro-legs, but in most families of Hymenoptera
the egg is laid in such a situation that an abundant food-supply is
assured without exertion on the part of the larva, which is consequently
a legless grub, usually white in colour, and with soft flexible
cuticle (fig. 7, a). The organs and instincts for egg-laying and food-providing
are perhaps the most remarkable features in the economy
of the Hymenoptera. Gall-fly grubs are provided with vegetable
food through the eggs being laid by the mother insect within plant
tissues. The ichneumon pierces the body of a caterpillar and lays
her eggs where the grubs will find abundant animal food. A digging-wasp
hunts for insect prey and buries it with the egg, while a true
wasp feeds her brood with captured insects, as a bird her fledglings.
Bees store honey and pollen to serve as food for their young. Thus
we find throughout the order a degree of care for offspring unreached
by other insects, and this family-life has, in the best known
of the Hymenoptera—ants, wasps and bees—developed into an
elaborate social organization.
Social Life.—The development of a true insect society among
the Hymenoptera is dependent on a differentiation among
the females between individuals with well-developed ovaries
(“queens”) whose special function is reproduction; and individuals
with reduced or aborted ovaries (“workers”) whose
duty is to build the nest, to gather food and to tend and feed
the larvae. Among the wasps the workers may only differ from
the queens in size, and individuals intermediate between the
two forms of female may be met with. Further, the queen wasp,
and also the queen humble-bee, commences unaided the work of
building and founding a new nest, being afterwards helped by
her daughters (the workers) when these have been developed.
In the hive-bee and among ants, on the other hand, there are
constant structural distinctions between queen and worker, and
the function of the queen bee in a hive is confined to egg-laying,
the labour of the community being entirely done by the workers.
Many ants possess several different forms of worker, adapted for
special duties. Details of this fascinating subject are given in the
special articles Ant, Bee and Wasp (q.v.).
Habits and Distribution.—Reference has been already made to
the various methods of feeding practised by Hymenoptera in
the larval stage, and the care taken of or for the young throughout
the order leads in many cases to the gathering of such food
by the mother or nurse. Thus, wasps catch flies; worker ants
make raids and carry off weak insects of many kinds; bees
gather nectar from flowers and transform it into honey within
their stomachs—largely for the sake of feeding the larvae in
the nest. The feeding habits of the adult may agree with that
of the larva, or differ, as in the ease of wasps which feed their
grubs on flies, but eat principally vegetable food themselves.
The nest-building habit is similarly variable. Digging wasps
make simple holes in the ground; many burrowing bees form
branching tunnels; other bees excavate timber or make their
brood-chambers in hollow plant-stems; wasps work up with
their saliva vegetable fibres bitten off tree-bark to make paper;
social bees produce from glands in their own bodies the wax
whence their nest-chambers are built. The inquiline habit
(“cuckoo-parasitism”), when one species makes use of the labour
of another by invading the nest and laying her eggs there, is of
frequent occurrence among Hymenoptera; and in some cases the
larva of the intruder is not content with taking the store of food
provided, but attacks and devours the larva of the host.
Most Hymenoptera are of moderate or small size, the giants
of the order—certain saw-flies and tropical digging-wasps—never
reach the bulk attained by the largest beetles, while the
wing-spread is narrow compared with that of many dragon-flies
and moths. On the other hand, there are thousands of
very small species, and the tiny “fairy-flies” (Mymaridae),
whose larvae live as parasites in the eggs of various insects, are
179
excessively minute for creatures of such complex organization.
Hymenoptera are probably less widely distributed than Aptera,
Coleoptera or Diptera, but they are to be found in all except the
most inhospitable regions of the globe. The order is, with few
exceptions, terrestrial or aerial in habit. Comparatively only a
few species are, for part of their lives, denizens of fresh water;
these, as larvae, are parasitic on the eggs or larvae of other
aquatic insects, the little hymenopteron, Polynema natans,
one of the “fairy-flies”—swims through the water by strokes
of her delicate wings in search of a dragon-fly’s egg in which to
lay her own egg, while the rare Agriotypus dives after the case
of a caddis-worm. It is of interest that the waters have been
invaded by the parasitic group of the Hymenoptera, since in
number of species this is by far the largest of the order. No
group of terrestrial insects escapes their attacks—even larvae
boring in wood are detected by ichneumon flies with excessively
long ovipositors. Not a few cases are known in which a parasitic
larva is itself pierced by the ovipositor of a “hyperparasite,”
and even the offspring of the latter may itself fall a victim to the
attack of a “tertiary parasite.”
Fossil History.—Very little is known of the history of the Hymenoptera
previous to the Tertiary epoch, early in which, as we know
from the evidence of many Oligocene and Miocene fossils, all the
more important families had been differentiated. Fragments of
wings from the Lias and Oolitic beds have been referred to ants and
bees, but the true nature of these remains is doubtful.
Classification.—Linnaeus divided the Hymenoptera into two
sections—the Terebrantia, whose females possess a cutting or
piercing ovipositor, and the Aculeata, in which the female organ
is modified into a sting. This nomenclature was adopted by
P. A. Latreille and has been in general use until the present day.
A closely similar division of the order results from T. Hartig’s
character drawn from the trochanter—whether of two segments
or undivided—the groups being termed respectively Ditrocha
and Monotrocha. But the most natural division is obtained by
the separation of the saw-flies as a primitive sub-order, characterized
by the imperfect union of the first abdominal segment
with the thorax, and by the broad base of the abdomen, so that
there is no median constriction or “waist,” and by the presence
of thoracic legs—usually also of abdominal pro-legs—in the larva.
All the other families of Hymenoptera, including the gall-flies,
ichneumons and aculeates, have the first abdominal segment
closely united with the thorax, the second abdominal segment
constricted so as to form a narrow stalk or “waist,” and legless
larvae without a hinder outlet to the food-canal. These two sub-orders
are usually known as the Sessiliventra and Petioliventra
respectively, but the names Symphyta and Apocrita proposed in
1867 by C. Gerstaecker have priority, and should not be replaced.
Symphyta.
This sub-order, characterized by the “sessile,” broad-based
abdomen, whose first segment is imperfectly united with the thorax,
and by the usually caterpillar-like larvae with legs, includes the
various groups of saw-flies. Three leading families may be
mentioned. The Cephidae, or stem saw-flies, have an elongate
pronotum, a compressed abdomen, and a single spine on the shin
of the fore-leg. The soft, white larvae have the thoracic legs very
small and feed in the stems of various plants. Cephus pygmaeus is
a well-known enemy of corn crops. The Siricidae (“wood-wasps”)
are large elongate insects also with one spine on each fore-shin, but
with the pronotum closely joined to the mesothorax. The ovipositor
is long and prominent, enabling the female insect to lay her eggs in
the wood of trees, where the white larvae, whose legs are excessively
short, tunnel and feed. These insects are adorned with bands of
black and yellow, or with bright metallic colours, and on account
of their large size and formidable ovipositors they often cause
needless alarm to persons unfamiliar with their habits. The
Tenthredinidae, or true saw-flies, are distinguished by two spines on
each fore-shin, while the larvae are usually caterpillars, with three
pairs of thoracic legs, and from six to eight pairs of abdominal pro-legs
the latter not possessing the hooks found on the pro-legs of
lepidopterous caterpillars. Most saw-fly larvae devour leaves, and
the beautifully serrate processes of the ovipositor are well adapted
for egg-laying in plant tissues. Some saw-fly larvae are protected
by a slimy secretion (fig. 6, c) and a few live concealed in galls.
In the form of the feelers, the wing-neuration and minor structural
details there is much diversity among the saw-flies. They have
been usually regarded as a single family, but W. H. Ashmead has
lately differentiated eleven families of them.
Apocrita.
This sub-order includes the vast majority of the Hymenoptera,
characterized by the narrowly constricted waist in the adult and by
the legless condition of the larva. The trochanter is simple in some
genera and divided in others. With regard to the minor divisions
of this group, great difference of opinion has prevailed among
students. In his recent classification Ashmead (1901) recognizes
seventy-nine families arranged under eight “super-families.” The
number of species included in this division is enormous, and the
multiplication of families is, to some extent, a natural result of
increasingly close study. But the distinctions between many of
these rest on comparatively slight characters, and it is likely that
the future discovery of new genera may abolish many among such
distinctions as may now be drawn. It seems advisable, therefore,
in the present article to retain the wider conception of the family
that has hitherto contented most writers on the Hymenoptera.
Ashmead’s “super-families” have, however, been adopted as—founded
on definite structural characters—they probably indicate
relationship more nearly than the older divisions founded mostly
on habit. The Cynipoidea include the gall-flies and their parasitic
relations. In the Chalcidoidea, Ichneumonoidea and Proctotrypoidea
will be found nearly all the “parasitic Hymenoptera” of
older classifications. The Formicoidea are the ants. The group
of Fossores, or “digging-wasps,” is divided by Ashmead, one section
forming the Sphecoidea, while the other, together with the Chrysidae
and the true wasps, make up the Vespoidea. The Apoidea consists
of the bees only.
 |
| After Marlatt, Ent. Circ. 26, U.S. Dept. Agric. |
| Fig. 6.—a, Pear Saw-fly (Eriocampoides limacina); b, larva without,
and c, with its slimy protective coat; e, cocoon; f, larva
before pupation; g, pupa, magnified; d, leaves with larvae. |
 |
| After Howard, Ent. Tech. Bull. 5 U.S. Dept. Agric. |
| Fig. 7.—Chalcid (Dibrachys boucheanus), a hyper-parasite. |
a, Larva.
d, Its head more highly magnified.
b, Female fly. |
c, Pupa of male.
e, Feeler. |
Cynipoidea.—In this division the ovipositor issues from the ventral
surface of the abdomen; the pronotum reaches back to the tegulae;
the trochanter has two segments; the fore-wing (fig. 4, 2) has no
stigma, but one or two areolets. The feelers with twelve to fifteen
segments are thread-like and straight. All the insects included in
this group are small and form two families—the Cynipidae and the
Figitidae. They are the “gall-flies,” many of the species laying
eggs in various plant-tissues where the presence of the larva causes
the formation of a pathological growth or gall, always of a definite
form and characteristic of the species; the “oak-apple” and the
180
bedeguar of the rose are familiar examples. Other flies of this
group have the inquiline habit, laying their eggs in the galls of
other species, while others again pierce the cuticle of maggots or
aphids, in whose bodies their larvae live as parasites.
Chalcidoidea.—This division resembles the Cynipoidea in the
position of the ovipositor, and in the two segmented trochanters.
The fore-wing also has no stigma, and the whole wing is almost
destitute of nervures and areolets, while the pronotum does not
reach back to the tegulae, and the feelers are elbowed (fig. 7). The
vast majority of this group, including nearly 5000 known species,
are usually reckoned as a single family, the Chalcididae, comprising
small insects, often of bright metallic colours, whose larvae are
parasitic in insects of various orders. The “fig-insects,” whose
presence in ripening figs is believed essential to the proper development
of the fruit, belong to Blastophaga and other genera of this
family. They are remarkable in having wingless males and winged
females. The “polyembryonic” development of an Encyrtus, as
studied by P. Marchal, is highly remarkable. The female lays her
egg in the egg of a small ermine moth (Hyponomeuta) and the egg
gives rise not to a single embryo but to a hundred, which develop
as the host-caterpillar develops, being found at a later stage within
the latter enveloped in a flexible tube.
The Mymaridae or “fairy-flies” are distinguished from the
Chalcididae by their narrow fringed wings (figs. 4, 5) and by the
situation of the ovipositor just in front of the tip of the abdomen.
They are among the most minute of all insects and their larvae are
probably all parasitic in insects’ eggs.
 |
| After Riley and Howard, Insect Life, vol. i. |
| Fig. 8.—Ichneumon Fly (Rhyssa per-suasoria)
ovipositing. |
Ichneumonoidea.—The ten thousand known species included in
this group agree with the Cynipoidea and Chalcidoidea in the
position of the ovipositor and in the jointed trochanters, but are
distinguished by the fore-wing possessing a distinct stigma and
usually a typical series of nervures and areolets (figs. 4, 8). Many of
the species are of fair size. They lay their eggs (fig. 8) in the bodies
of insects and their larvae belonging to various orders. A few
small families such as the Evaniidae and the Stephanidae are included
here, but the vast majority of the group fall into two large
families, the Ichneumonidae
and the Braconidae,
the former distinguished
by the presence of two
median (or discoidal) cells
in the fore-wing (figs. 4, 7),
while the latter has only
one (figs. 4, 6). Not a few
of these insects, however,
are entirely wingless. On
account of their work in
destroying plant-eating
insects, the ichneumon-flies
are of great economic
importance.
Proctotrypoidea.—This
group may be distinguished
from the preceding
by the position
of the ovipositor at the extreme apex of the abdomen, and
from the groups that follow (with very few exceptions) by
the jointed trochanters of the legs. The pronotum reaches
back to the tegulae. The Pelecinidae—included here by Ashmead—are
large insects with remarkably elongate abdomens
and undivided trochanters. All the other members of the group
may be regarded as forming a single family—the Proctotrypidae,
including an immense number of small parasitic Hymenoptera, not
a few of which are wingless. Of special interest are the transformations
of Platygaster, belonging to this family, discovered by M.
Ganin, and familiarized to English readers through the writings of
Sir J. Lubbock (Lord Avebury). The first larva is broad in front
and tapers behind to a “tail” provided with two divergent processes,
so that it resembles a small crustacean. It lives in the grub
of a gall-midge and it ultimately becomes changed into the usual
white and fleshy hymenopterous larva. The four succeeding
sections, in which the ovipositor is modified into a sting (always
exserted from the tip of the abdomen) and the trochanters are with
few exceptions simple, form the Aculeata of Linnaeus.
Formicoidea.—The ants which form this group are readily distinguished
by the differentiation of the females into winged “queens”
and wingless “workers.” The pronotum extends back to the wing-bases,
and the “waist” is greatly constricted and marked by one or
two “nodes.” The differentiation of the females leads to a complex
social life, the nesting habits of ants and the various industries that
they pursue being of surpassing interest (see Ant).
Vespoidea.—This section includes a number of families characterized
by the backward extension of the prothorax to the tegulae
and distinguished from the ants by the absence of “nodes” at the
base of the abdomen. The true wasps have the fore-wings folded
lengthwise when at rest and the fore-legs of normal build—not
specialized for digging. The Vespidae or social wasps have “queens”
and “workers” like the ants, but both these forms of female are
winged; the claws on their fret are simple. In the Eumenidae or
solitary wasps the female sex is undifferentiated, and the foot claws
are toothed. (For the habits of these insects see Wasp.) The
Chrysididae or ruby wasps are small insects with a very hard cuticle
exhibiting brilliant metallic colours—blue, green and crimson.
Only three or four abdominal segments are visible, the hinder segments
being slender and retracted to form a telescope-like tube in
which the ovipositor lies. When the ovipositor is brought into
use this tube is thrust out. The eggs are laid in the nests of various
bees and wasps, the chrysid larva living as a “cuckoo” parasite.
The Trigonalidae, a small family whose larvae are parasitic in
wasps’ nests, also probably belong here.
The other families of the Vespoidea belong to the series of “Fossores”
or digging-wasps. In two of the families—the Mutillidae
and Thynnidae—the females are wingless and the larvae live as
parasites in the larvae of other insects; the female Mutilla enters
bumble-bees’ nests and lays her eggs in the bee-grubs. In the other
families both sexes are winged, and the instinct and industry of the
females are among the most wonderful in the Hymenoptera. They
make burrows wherein they place insects or spiders which they have
caught and stung, laying their eggs beside the victim so that the
young larvae find themselves in presence of an abundant and
appropriate food-supply. Valuable observations on the habits
of these insects are due to J. H. Fabre and G. W. and E. Peckham.
The prey is sometimes stung in the neighbourhood of the nerve
ganglia, so that it is paralysed but not killed, the grub of the fossorial
wasp devouring its victim alive; but this instinct varies in perfection,
and in many cases the larva flourishes equally whether its prey be
killed or not. The females have a wonderful power of finding their
burrows on returning from their hunting expeditions. Among the
Vespoid families of fossorial wasps, the Pompilidae are the most
important. They are recognizable by their slender and elongate
hind-legs; many of them provision their burrows with spiders.
The Sapygidae are parasitic on bees, while the Scoliidae are large,
robust and hairy insects, many of which prey upon the grubs of
chafers.
Sphecoidea.—In this division are included the rest of the “digging-wasps,”
distinguished from the Vespoidea by the short pronotum
not reaching backward to the tegulae. They have usually been
reckoned as forming a single, very large family—the Sphegidae—but
ten or twelve subdivisions of the group are regarded as distinct
families by Ashmead and others. Great diversity is shown in the
details of structure, habits and nature of the prey. Species of
Sphex, studied by Fabre, provisioned their brood-chambers with
crickets. Pelopoeus hunts spiders, while Ammophila catches caterpillars
for the benefit of her young. Fabre states that the last-named
insect uses a stone for the temporary closing of her burrow,
and the Peckhams have seen a female Ammophila take a stone
between her mandibles and use it as a hammer for pounding down
the earth over her finished nest. The habits of Bembex are of especial
interest. The female, instead of provisioning her burrow with a
supply of food that will suffice the larva for its whole life, brings
fresh flies with which she regularly feeds her young. In this instinct
we have a correspondence with the habits of social wasps and bees.
Yet it may be thought that the usual instinct of the “digging-wasps”
to capture and store up food in an underground burrow for
the benefit of offspring which they will never see is even more surprising.
The habit of some genera is to catch the prey before making
their tunnel, but more frequently the insect digs her nest, and then
hunts for prey to put into it.
Apoidea.—The bees which make up this group agree with the
Sphecoidea in the short pronotum, but may be distinguished from
all other Hymenoptera by the widened first tarsal segment and the
plumose hairs on head and body. They are usually regarded as
forming a single family—the Apidae—but there is very great
diversity in structural details, and Ashmead divides them into
fourteen families. The “tongue,” for example, is short and obtuse
or emarginate in Colletes and Prosopis, while in all other bees it is
pointed at the tip. But in Andrena and its allies it is comparatively
short, while in the higher genera, such as Apis and Bombus, it is
elongate and flexible, forming a most elaborate and perfect organ for
taking liquid food. Bees feed on honey and pollen. Most of the
genera are “solitary” in habit, the female sex being undifferentiated;
but among the humble-bees and hive-bees we find, as in
social wasps and ants, the occurrence of workers, and the consequent
elaboration of a wonderful insect-society. (See Bee.)
Bibliography.—The literature of several special families of the
Hymenoptera will be found under the articles Ant, Bee, Ichneumon-Fly,
Wasp, &c., referred to above. Among earlier students on
structure may be mentioned P. A. Latreille, Familles naturelles du
règne animal (Paris, 1825), who recognized the nature of the
“median segment.” C. Gerstaecker (Arch. f. Naturg. xx., 1867)
and F. Brauer (Sitzb. K. Akad. Wiss. Wien. lxxxv., 1883) should
also be consulted on this subject. For internal anatomy, specially
the digestive organs, see L. Dufour, Mém. savants étrangers, vii.
(1841), and Ann. Sci. Nat. Zool. (4), i. 1854. For nervous system H.
Viallanes, Ann. Sci. Nat. Zool. (7), ii. iv. 1886-1887, and F. C.
Kenyon, Journ. Comp. Neurol. vi., 1896. For poison and other
glands, see L. Bordas, Ann. Sci. Nat. Zool. (7) xix., 1895. For the
sting and ovipositor H. Dewitz, Zeits. wiss. Zool. xxv., 1874,
xxviii., 1877, and F. Zander, ib. lxvi., 1899. For male genital
armature S. A. Peytoureau, Morphologie de l’armure génitale des
181
insectes (Bordeaux, 1895), and E. Zander, Zeits. wiss. Zool. lxvii.,
1900. The systematic student of Hymenoptera is greatly helped
by C. G. de Dalla Torre’s Catalogus Hymenopterorum (10 vols.,
Leipzig, 1893-1902). For general classifications see F. W. Konow,
Entom. Nachtr. (1897), and W. H. Ashmead, Proc. U.S. Nat. Mus.
xxiii., 1901; the latter paper deals also especially with the Ichneumonoidea
of the globe. For habits and life histories of Hymenoptera
see J. Lubbock (Lord Avebury), Ants, Bees and Wasps (9th ed.,
London, 1889); C. Janet, Études sur les fourmis, les guêpes et les
abeilles (Paris, &c., 1893 and onwards); and G. W. and E. G.
Peckham, Instincts and Habits of Solitary Wasps (Madison, Wis.
U.S.A., 1898). Monographs of most of the families of British
Hymenoptera have now been published. For saw-flies and gall-flies,
see P. Cameron’s British Phytophagous Hymenoptera (4 vols.,
London, Roy. Soc., 1882-1893). For Ichneumonoidea, C. Morley’s
Ichneumons of Great Britain (Plymouth, 1903, &c.), and T. A.
Marshall’s “British Braconidae,” Trans. Entom. Soc., 1885-1899.
The smaller parasitic Hymenoptera have been neglected in this
country since A. H. Haliday’s classical papers Entom. Mag. i.-v.,
(1833-1838) but Ashmead’s “North American Proctotrypidae” (Bull.
U.S. Nat. Mus. xlv., 1893) is valuable for the European student.
For the Fossores, wasps, ants and bees see E. Saunders, Hymenoptera
Aculeata of the British Islands (London, 1896). Exhaustive references
to general systematic works will be found in de Dalla Torre’s
Catalogue mentioned above. Of special value to English students are
C. T. Bingham’s Fauna of British India, “Hymenoptera” (London,
1897 and onwards), and P. Cameron’s volumes on Hymenoptera in
the Biologia Centrali-Americana. F. Smith’s Catalogues of Hymenoptera
in the British Museum (London, 1853-1859) are well
worthy of study.
(G. H. C.)
HYMETTUS (Ital. Monte Matto, hence the modern name
Trello Vouni), a mountain in Attica, bounding the Athenian
plain on the S.E. Height, 3370 ft. It was famous in ancient
times for its bees, which gathered honey of peculiar flavour
from its aromatic herbs; their fame still persists. The spring
mentioned by Ovid (Ars Amat. iii. 687) is probably to be recognized
near the monastery of Syriani or Kaesariani on the
western slope. This may be identical with that known as Κύλλον Πήρα, said to be a remedy for barrenness in women. The marble
of Hymettus, which often has a bluish tinge, was used extensively
for building in ancient Athens, and also, in early times, for
sculpture; but the white marble of Pentelicus was preferred
for both purposes.
See E. Dodwell, Classical and Topographical Tour (1819), i. 483.
HYMNS.—1. Classical Hymnody.—The word “hymn”
(ὕμνος) was employed by the ancient Greeks1 to signify a song
or poem composed in honour of gods, heroes or famous men,
or to be recited on some joyful, mournful or solemn occasion.
Polymnia was the name of their lyric muse. Homer makes
Alcinous entertain Odysseus with a “hymn” of the minstrel
Demodocus, on the capture of Troy by the wooden horse. The
Works and Days of Hesiod begins with an invocation to the Muses
to address hymns to Zeus, and in his Theogonia he speaks of
them as singing or inspiring “hymns” to all the divinities, and
of the bard as “their servant, hymning the glories of men of
old, and of the gods of Olympus.” Pindar calls by this name odes,
like his own, in praise of conquerors at the public games of Greece.
The Athenian dramatists (Euripides most frequently) use the
word and its cognate verbs in a similar manner; they also
describe by them metrical oracles and apophthegms, martial,
festal and hymeneal songs, dirges and lamentations or incantations
of woe.
Hellenic hymns, according to this conception of them, have
come down to us, some from a very early and others from a late
period of Greek classical literature. Those which passed by the
name of Homer2 were already old in the time of Thucydides.
They are mythological poems (several of them long), in hexameter
verse—some very interesting. That to Apollo contains
a traditionary history of the origin and progress of the Delphic
worship; those on Hermes and on Dionysus are marked by
much liveliness and poetical fancy. Hymns of a like general
character, but of less interest (though these also embody some
fine poetical traditions of the Greek mythology, such as the story
of Teiresias, and that of the wanderings of Leto), were written
in the 3rd century before Christ, by Callimachus of Cyrene.
Cleanthes, the successor of Zeno, composed (also in hexameters)
an “excellent and devout hymn” (as it is justly called by
Cudworth, in his Intellectual System) to Zeus, which is preserved
in the Eclogae of Stobaeus, and from which Aratus borrowed
the words, “For we are also His offspring,” quoted by St Paul
at Athens. The so-called Orphic hymns, in hexameter verse,
styled τελεταί, or hymns of initiation into the “mysteries”
of the Hellenic religion, are productions of the Alexandrian school,—as
to which learned men are not agreed whether they are
earlier or later than the Christian era.
The Romans did not adopt the word “hymn”; nor have we
many Latin poems of the classical age to which it can properly
be applied. There are, however, a few—such as the simple
and graceful “Dianae sumus in fide” (“Dian’s votaries are we”)
of Catullus, and “Dianam tenerae dicite virgines” (“Sing to
Dian, gentle maidens”) of Horace—which approach much more
nearly than anything Hellenic to the form and character of
modern hymnody.
2. Hebrew Hymnody.—For the origin and idea of Christian
hymnody we must look, not to Gentile, but to Hebrew sources.
St Augustine’s definition of a hymn, generally accepted by
Christian antiquity, may be summed up in the words, “praise
to God with song” (“cum cantico”); Bede understood the
“canticum” as properly requiring metre; though he thought
that what in its original language was a true hymn might retain
that character in an unmetrical translation. Modern use has
enlarged the definition; Roman Catholic writers extend it to
the praises of saints; and the word now comprehends rhythmical
prose as well as verse, and prayer and spiritual meditation as
well as praise.
The modern distinction between psalms and hymns is arbitrary
(see Psalms). The former word was used by the LXX. as a
generic designation, probably because it implied an accompaniment
by the psaltery (said by Eusebius to have been of very
ancient use in the East) or other instruments. The cognate
verb “psallere” has been constantly applied to hymns, both in
the Eastern and in the Western Church; and the same compositions
which they described generically as “psalms” were
also called by the LXX. “odes” (i.e. songs) and “hymns.”
The latter word occurs, e.g. in Ps. lxxii. 20 (“the hymns of
David the son of Jesse”), in Ps. lxv. 1, and also in the Greek
titles of the 6th, 54th, 55th, 67th and 76th (this numbering of
the psalms being that of the English version, not of the LXX.).
The 44th chapter of Ecclesiasticus, “Let us now praise famous
men,” &c., is entitled in the Greek πατέρων ὕμνος, “The Fathers’
Hymn.” Bede speaks of the whole book of Psalms as called
“liber hymnorum,” by the universal consent of Hebrews,
Greeks and Latins.
In the New Testament we find our Lord and His apostles
singing a hymn (ὑμνήσαντες ἐξῆλθον), after the institution of
the Lord’s Supper; St Paul and Silas doing the same (ὕμνουν τὸν θεόν) in their prison at Philippi; St James recommending
psalm-singing (ψαλλέτω), and St Paul “psalms and hymns
and spiritual songs” (ψαλμοῖς καὶ ὕμνοις καὶ ῲδαῖς πνευματικαῖς)
St Paul also, in the 14th chapter of the first epistle to the Corinthians,
speaks of singing (ψαλῶ) and of every man’s psalm
(ἕκαστος ὑμῶν ψαλμὸν ἕχει). In a context which plainly has reference
to the assemblies of the Corinthian Christians for common
worship. All the words thus used were applied by the LXX.
to the Davidical psalms; it is therefore possible that these only
may be intended, in the different places to which we have
referred. But there are in St Paul’s epistles several passages
(Eph. v. 14; 1 Tim. iii. 16; 1 Tim. vi. 15, 16; 2 Tim. ii. 11, 12)
which have so much of the form and character of later Oriental
hymnody as to have been supposed by Michaelis and others to
be extracts from original hymns of the Apostolic age. Two of
them are apparently introduced as quotations, though not
found elsewhere in the Scriptures. A third has not only rhythm,
but rhyme. The thanksgiving prayer of the assembled disciples,
recorded in Acts iv., is both in substance and in manner poetical;
182
and in the canticles, “Magnificat,” “Benedictus,” &c., which
manifestly followed the form and style of Hebrew poetry, hymns
or songs, proper for liturgical use, have always been recognized
by the church.
3. Eastern Church Hymnody.—The hymn of our Lord, the
precepts of the apostles, the angelic song at the nativity, and
“Benedicite omnia opera” are referred to in a curious metrical
prologue to the hymnary of the Mozarabic Breviary as precedents
for the practice of the Western Church. In this respect,
however, the Western Church followed the Eastern, in which
hymnody prevailed from the earliest times.
Philo describes the Theraputae (q.v.) of the neighbourhood of
Alexandria as composers of original hymns, which (as well as
old) were sung at their great religious festivals—the
people listening in silence till they came to the closing
Therapeutae.
strains, or refrains, at the end of a hymn or stanza (the
“acroteleutia” and “ephymnia”), in which all, women as well
as men, heartily joined. These songs, he says, were in various
metres (for which he uses a number of technical terms); some
were choral, some not; and they were divided into variously
constructed strophes or stanzas. Eusebius, who thought that
the Theraputae were communities of Christians, says that the
Christian practice of his own day was in exact accordance
with this description.
The practice, not only of singing hymns, but of singing them
antiphonally, appears, from the well-known letter of Pliny to
Trajan, to have been established in the Bithynian
churches at the beginning of the 2nd century. They
Antiphonal singing.
were accustomed “stato die ante lucem convenire,
carmenque Christo, quasi Deo, dicere secum invicem.”
This agrees well, in point of time, with the tradition recorded
by the historian Socrates, that Ignatius (who suffered martyrdom
about A.D. 107) was led by a vision or dream of angels
singing hymns in that manner to the Holy Trinity to introduce
antiphonal singing into the church of Antioch, from which it
quickly spread to other churches. There seems to be an allusion
to choral singing in the epistle of Ignatius himself to the Romans,
where he exhorts them, “χορὸς γελῳδίαν” (“having formed themselves
into a choir”), to “sing praise to the Father in Christ
Jesus.” A statement of Theodoret has sometimes been supposed
to refer the origin of antiphonal singing to a much later date;
but this seems to relate only to the singing of Old Testament
Psalms (τὴν Δαυιδικὴν μελῳδίαν), the alternate chanting of
which, by a choir divided into two parts, was (according to that
statement) first introduced into the church of Antioch by two
monks famous in the history of their time, Flavianus and Diodorus,
under the emperor Constantius II.
Other evidence of the use of hymns in the 2nd century is
contained in a fragment of Caius, preserved by Eusebius, which
refers to “all the psalms and odes written by faithful
brethren from the beginning,” as “hymning Christ, the
2nd century.
Word of God, as God.” Tertullian also, in his description
of the “Agapae,” or love-feasts, of his day, says that, after
washing hands and bringing in lights, each man was invited to
come forward and sing to God’s praise something either taken
from the Scriptures or of his own composition (“ut quisque de
Sacris Scripturis vel proprio ingenio potest”). George Bull,
bishop of St David’s, believed one of those primitive compositions
to be the hymn appended by Clement of Alexandria to his
Paedagogus; and Archbishop Ussher considered the ancient
morning and evening hymns, of which the use was enjoined by
the Apostolical Constitutions, and which are also mentioned in
the “Tract on Virginity” printed with the works of St Athanasius,
and in St Basil’s treatise upon the Holy Spirit, to belong
to the same family. Clement’s hymn, in a short anapaestic
metre, beginning στόμιον πώλων ἀδαῶν (or, according to some
editions, βασιλεῦ ἁγίων, λόγε πανδαμάτωρ—translated by the
Rev. A. Chatfield, “O Thou, the King of Saints, all-conquering
Word”), is rapid, spirited and well-adapted for singing. The
Greek “Morning Hymn” (which, as divided into verses by
Archbishop Ussher in his treatise De Symbolis, has a majestic
rhythm, resembling a choric or dithyrambic strophe) is the
original form of “Gloria in Excelsis,” still said or sung, with
some variations, in all branches of the church which have not
relinquished the use of liturgies. The Latin form of this hymn
(of which that in the English communion office is an exact
translation) is said, by Bede and other ancient writers, to have
been brought into use at Rome by Pope Telesphorus, as early as
the time of the emperor Hadrian. A third, the Vesper or “Lamp-lighting”
hymn (“φῶς ἱλαρὸν ἁγίας δόξης”—translated by
Canon Bright “Light of Gladness, Beam Divine”), holds its
3rd century.
place to this day in the services of the Greek rite.
In the 3rd century Origen seems to have had in his
mind the words of some other hymns or hymn of like
character, when he says (in his treatise Against Celsus): “We
glorify in hymns God and His only begotten Son; as do also the
Sun, the Moon, the Stars and all the host of heaven. All these,
in one Divine chorus, with the just among men, glorify in hymns
God who is over all, and His only begotten Son.” So highly
were these compositions esteemed in the Syrian churches that
the council which deposed Paul of Samosata from the see of
Antioch in the time of Aurelian justified that act, in its synodical
letter to the bishops of Rome and Alexandria, on this ground
(among others) that he had prohibited the use of hymns of that
kind, by uninspired writers, addressed to Christ.
After the conversion of Constantine, the progress of hymnody
became closely connected with church controversies. There
had been in Edessa, at the end of the 2nd or early in the 3rd
century, a Gnostic writer of conspicuous ability, named Bardesanes,
who was succeeded, as the head of his sect or school, by
his son Harmonius. Both father and son wrote hymns, and set
them to agreeable melodies, which acquired, and in the 4th
century still retained, much local popularity. Ephraem Syrus,
the first voluminous hymn-writer whose works remain to us,
thinking that the same melodies might be made useful to the
faith, if adapted to more orthodox words, composed to them a
large number of hymns in the Syriac language, principally in
tetrasyllabic, pentasyllable and heptasyllabic metres, divided
into strophes of from 4 to 12, 16 and even 20 lines each. When
a strophe contained five lines, the fifth was generally an
“ephymnium,” detached in sense, and consisting of a prayer,
invocation, doxology or the like, to be sung antiphonally, either
in full chorus or by a separate part of the choir. The Syriac
Chrestomathy of August Hahn (Leipzig, 1825), and the third
volume of H. A. Daniel’s Thesaurus Hymnologicus (Leipzig,
1841-1856), contain specimens of these hymns. Some of them
have been translated into (unmetrical) English by the Rev.
Henry Burgess (Select Metrical Hymns of Ephrem Syrus, &c.,
1853). A considerable number of those so translated are on
subjects connected with death, resurrection, judgment, &c.,
and display not only Christian faith and hope, but much simplicity
and tenderness of natural feeling. Theodoret speaks
of the spiritual songs of Ephraem as very sweet and profitable,
and as adding much, in his (Theodoret’s) time, to the brightness
of the commemorations of martyrs in the Syrian Church.
The Greek hymnody contemporary with Ephraem followed,
with some licence, classical models. One of its favourite metres
was the Anacreontic; but it also made use of the short
anapaestic, Ionic, iambic and other lyrical measures, as well as
the hexameter and pentameter. Its principal authors were
Methodius, bishop of Olympus, who died about A.D. 311, Synesius,
who became bishop of Ptolemais in Cyrenaica in 410, and
Gregory Nazianzen, for a short time (380-381) patriarch of
Constantinople. The merits of these writers have been perhaps
too much depreciated by the admirers of the later Greek
“Melodists.” They have found an able English translator in
the Rev. Allen Chatfield (Songs and Hymns of Earliest Greek
Christian Poets, London, 1876). Among the most striking of
their works are μνώεο Χριστέ (“Lord Jesus, think of me”), by
Synesius; σὲ τὸν ἄφθιτον μονάρχην (“O Thou, the One Supreme”)
and τί σοι θέλεις γενέσθαι (“O soul of mine, repining”), by Gregory;
also ἄνωθεν παρθένοι (“The Bridegroom cometh”), by Methodius.
There continued to be Greek metrical hymn-writers, in a similar
style, till a much later date. Sophronius, patriarch of Jerusalem
183
in the 7th century, wrote seven Anacreontic hymns; and St
John Damascene, one of the most copious of the second school
of “Melodists,” was also the author of some long compositions
in trimeter iambics.
An important development of hymnody at Constantinople
arose out of the Arian controversy. Early in the 4th century
Athanasius had rebuked, not only the doctrine of Arius,
but the light character of certain hymns by which he
Period of Arian controversy.
endeavoured to make that doctrine popular. When,
towards the close of that century (398), St John
Chrysostom was raised to the metropolitan see, the Arians,
who were still numerous at Constantinople, had no places of
worship within the walls; but they were in the habit of coming
into the city at sunset on Saturdays, Sundays and the greater
festivals, and congregating in the porticoes and other places of
public resort, where they sung, all night through, antiphonal
songs, with “acroteleutia” (closing strains, or refrains), expressive
of Arian doctrine, often accompanied by taunts and
insults to the orthodox. Chrysostom was apprehensive that this
music might draw some of the simpler church people to the Arian
side; he therefore organized, in opposition to it, under the
patronage and at the cost of Eudoxia, the empress of Arcadius
(then his friend), a system of nightly processional hymn-singing,
with silver crosses, wax-lights and other circumstances of
ceremonial pomp. Riots followed, with bloodshed on both sides,
and with some personal injury to the empress’s chief eunuch,
who seems to have officiated as conductor or director of the
church musicians. This led to the suppression, by an imperial
edict, of all public Arian singing; while in the church the
practice of nocturnal hymn-singing on certain solemn occasions,
thus first introduced, remained an established institution.
It is not improbable that some rudiments of the peculiar
system of hymnody which now prevails throughout the Greek
communion, and whose affinities are rather to the
Hebrew and Syriac than to the classical forms, may
Greek system of hymnody.
have existed in the church of Constantinople, even
at that time. Anatolius, patriarch of Constantinople
in the middle of the 5th century, was the precursor of that
system; but the reputation of being its proper founder belongs
to Romanos, of whom little more is known than that he wrote
hymns still extant, and lived towards the end of that century.
The importance of that system in the services of the Greek
church may be understood from the fact that Dr J. M. Neale
computed four-fifths of the whole space (about 5000 pages)
contained in the different service-books of that church to be
occupied by hymnody, all in a language or dialect which has
ceased to be anywhere spoken.
The system has a peculiar technical terminology, in which the
words “troparion,” “ode,” “canon” and “hirmus” (εἶρμος) chiefly
require explanation.
The troparion is the unit of the system, being a strophe or stanza,
seen, when analysed, to be divisible into verses or clauses, with
regulated caesuras, but printed in the books as a single prose sentence,
without marking any divisions. The following (turned into English,
from a “canon” by John Mauropus) may be taken as an example:
“The never-sleeping Guardian, | the patron of my soul, | the guide
of my life, | allotted me by God, | I hymn thee, Divine Angel | of
Almighty God.” Dr Neale and most other writers regard all these
“troparia” as rhythmical or modulated prose. Cardinal J. B.
Pitra, on the other hand, who in 1867 and 1876 published two
learned works on this subject, maintains that they are really metrical,
and governed by definite rules of prosody, of which he lays down
sixteen. According to him, each “troparion” contains from three
to thirty-three verses; each verse varies from two to thirteen
syllables, often in a continuous series, uniform, alternate or reciprocal,
the metre being always syllabic, and depending, not on the
quantity of vowels or the position of consonants, but on an harmonic
series of accents.
In various parts of the services solitary troparia are sung, under
various names, “contacion,” “oecos,” “cathisma,” &c., which mark
distinctions either in their character or in their use.
An ode is a song or hymn compounded of several similar “troparia,”—usually
three, four or five. To these is always prefixed a typical
or standard “troparion,” called the hirmus, by which the syllabic
measure, the periodic series of accents, and in fact the whole structure
and rhythm of the stanzas which follow it are regulated. Each
succeeding “troparion” in the same “ode” contains the same
number of verses, and of syllables in each verse, and similar accents
on the same or equivalent syllables. The “hirmus” may either
form the first stanza of the “ode” itself, or (as is more frequently
the case) may be taken from some other piece; and, when so taken,
it is often indicated by initial words only, without being printed at
length. It is generally printed within commas, after the proper
rubric of the “ode.” A hymn in irregular “stichera” or stanzas,
without a “hirmus,” is called “idiomelon.” A system of three or
four odes is “triodion” or “tetraodion.”
A canon is a system of eight (theoretically nine) connected odes,
the second being always suppressed. Various pauses, relieved by
the interposition of other short chants or readings, occur during
the singing of a whole “canon.” The final “troparion” in each
ode of the series is not unfrequently detached in sense (like the
“ephymnia” of Ephraem Syrus), particularly when it is in the (very
common) form of a “theotokion,” or ascription of praise to the
mother of our Lord, and when it is a recurring refrain or burden.
There were two principal periods of Greek hymnography
constructed on these principles—the first that of Romanos and
his followers, extending over the 6th and 7th centuries, the
second that of the schools which arose during the Iconoclastic
controversy in the 8th century, and which continued for some
centuries afterwards, until the art itself died out.
The works of the writers of the former period were collected
in Tropologia, or church hymn-books, which were held in high
esteem till the 10th century, when they ceased to be
regarded as church-books, and so fell into neglect.
School of Romanos.
They are now preserved only in a very small number
of manuscripts. From three of these, belonging to public
libraries at Moscow, Turin and Rome, Cardinal Pitra has printed,
in his Analecta, a number of interesting examples, the existence
of which appears to have been unknown to Dr Neale, and which,
in the cardinal’s estimation, are in many respects superior to
the “canons,” &c., of the modern Greek service-books, from
which all Neale’s translations (except some from Anatolius)
are taken. Cardinal Pitra’s selections include twenty-nine works
by Romanos, and some by Sergius, and nine other known, as
well as some unknown, authors. He describes them as having
generally a more dramatic character than the “melodies”
of the later period, and a much more animated style; and he
supposes that they may have been originally sung with dramatic
accompaniments, by way of substitution for the theatrical
performances of Pagan times. As an instance of their peculiar
character, he mentions a Christmas or Epiphany hymn by
Romanos, in twenty-five long strophes, in which there is, first,
an account of the Nativity and its accompanying wonders, and
then a dialogue between the wise men, the Virgin mother and
Joseph. The magi arrive, are admitted, describe the moral
and religious condition of Persia and the East, and the cause
and adventures of their journey, and then offer their gifts. The
Virgin intercedes for them with her Son, instructs them in some
parts of Jewish history, and ends with a prayer for the salvation
of the world.
The controversies and persecutions of the 8th and succeeding
centuries turned the thoughts of the “melodists” of the great
monasteries of the Studium at Constantinople and
St Saba in Palestine and their followers, and those of
Melodists.
the adherents of the Greek rite in Sicily and South Italy
(who suffered much from the Saracens and the Normans), into
a less picturesque but more strictly theological course; and the
influence of those controversies, in which the final success of the
cause of “Icons” was largely due to the hymns, as well as to
the courage and sufferings, of these confessors, was probably the
cause of their supplanting, as they did, the works of the older
school. Cardinal Pitra gives them the praise of having discovered
a graver and more solemn style of chant, and of having done
much to fix the dogmatic theology of their church upon its
present lines of near approach to the Roman.
Among the “melodists” of this latter Greek school there
were many saints of the Greek church, several patriarchs
and two emperors—Leo the Philosopher, and Constantine
Porphyrogenitus, his son. Their greatest poets were Theodore
and Joseph of the Studium, and Cosmas and John (called
Damascene) of St Saba. Neale translated into English verse
several selected portions, or centoes, from the works of these
and others, together with four selections from earlier works by
184
Anatolius. Some of his translations—particularly “The day is
past and over,” from Anatolius, and “Christian, dost thou see
them,” from Andrew of Crete—have been adopted into hymn-books
used in many English churches; and the hymn “Art thou
weary,” which is rather founded upon than translated from
one by Stephen the Sabaite, has obtained still more general
popularity.
4. Western Church Hymnody.—It was not till the 4th century
that Greek hymnody was imitated in the West, where its introduction
was due to two great lights of the Latin Church—St
Hilary of Poitiers and St Ambrose of Milan.
Hilary was banished from his see of Poitiers in 356, and was
absent from it for about four years, which he spent in Asia
Minor, taking part during that time in one of the councils of
the Eastern Church. He thus had full opportunity of becoming
acquainted with the Greek church music of that day; and he
wrote (as St Jerome, who was thirty years old when Hilary died,
and who was well acquainted with his acts and writings, and spent
some time in or near his diocese, informs us) a “book of hymns,”
to one of which Jerome particularly refers, in the preface to the
second book of his own commentary on the epistle to the
Galatians. Isidore, archbishop of Seville, who presided over
the fourth council of Toledo, in his book on the offices of
the church, speaks of Hilary as the first Latin hymn-writer;
that council itself, in its 13th canon, and the prologue
to the Mozarabic hymnary (which is little more than a
versification of the canon), associate his name, in this respect,
with that of Ambrose. A tradition, ancient and widely
spread, ascribed to him the authorship of the remarkable
“Hymnum dicat turba fratrum, hymnum cantus personet”
(“Band of brethren, raise the hymn, let your song the
hymn resound”), which is a succinct narrative, in hymnal
form, of the whole gospel history; and is perhaps the earliest
example of a strictly didactic hymn. Both Bede and Hincmar
much admired this composition, though the former does not
mention, in connexion with it, the name of Hilary. The private
use of hymns of such a character by Christians in the West may
probably have preceded their ecclesiastical use; for Jerome
says that in his day those who went into the fields might hear
“the ploughman at his hallelujahs, the mower at his hymns,
and the vine-dresser singing David’s psalms.” Besides this,
seven shorter metrical hymns attributed to Hilary are still extant.
Of the part taken by Ambrose, not long after Hilary’s death,
in bringing the use of hymns into the church of Milan, we have
a contemporary account from his convert, St Augustine.
Justina, mother of the emperor Valentinian, favoured
Ambrose.
the Arians, and desired to remove Ambrose from his see. The
“devout people,” of whom Augustine’s mother, Monica, was one,
combined to protect him, and kept guard in the church. “Then,”
says Augustine, “it was first appointed that, after the manner
of the Eastern churches, hymns and psalms should be sung,
lest the people should grow weary and faint through sorrow;
which custom has ever since been retained, and has been followed
by almost all congregations in other parts of the world.” He
describes himself as moved to tears by the sweetness of these
“hymns and canticles”:—“The voices flowed into my ears;
the truth distilled into my heart; I overflowed with devout
affections, and was happy.” To this time, according to an
uncertain but not improbable tradition which ascribed the
composition of the “Te Deum” to Ambrose, and connected
it with the conversion of Augustine, is to be referred the commencement
of the use in the church of that sublime unmetrical
hymn.
It is not, however, to be assumed that the hymnody thus
introduced by Ambrose was from the first used according to the
precise order and method of the later Western ritual. To bring
it into (substantially) that order and method appears to have been
the work of St Benedict. Walafrid Strabo, the earliest ecclesiastical
writer on this subject (who lived at the beginning of the
9th century), says that Benedict, on the constitution of the
religious order known by his name (about 530), appointed
the Ambrosian hymns to be regularly sung in his offices for the
canonical hours. Hence probably originated the practice of
the Italian churches, and of others which followed their example,
to sing certain hymns (Ambrosian, or by the early successors of
the Ambrosian school) daily throughout the week, at “Vespers,”
“Lauds” and “Nocturns,” and on some days at “Compline”
also—varying them with the different ecclesiastical seasons
and festivals, commemorations of saints and martyrs and other
special offices. Different dioceses and religious houses had their
own peculiarities of ritual, including such hymns as were approved
by their several bishops or ecclesiastical superiors, varying in
detail, but all following the same general method. The national
rituals, which were first reduced into a form substantially like
that which has since prevailed, were probably those of Lombardy
and of Spain, now known as the “Ambrosian” and the
“Mozarabic.” The age and origin of the Spanish ritual are
uncertain, but it is mentioned in the 7th century by Isidore,
bishop of Seville. It contained a copious hymnary, the original
form of which may be regarded as canonically approved by the
fourth council of Toledo (633). By the 13th canon of that council,
an opinion (which even then found advocates) against the use in
churches of any hymns not taken from the Scriptures—apparently
the same opinion which had been held by Paul of Samosata—was
censured; and it was ordered that such hymns should be
used in the Spanish as well as in the Gallican churches, the penalty
of excommunication being denounced against all who might
presume to reject them.
The hymns of which the use was thus established and
authorized were those which entered into the daily and other
offices of the church, afterwards collected in the “Breviaries”;
in which the hymns “proper” for “the week,” and for “the
season,” continued for many centuries, with very few exceptions,
to be derived from the earliest epoch of Latin Church poetry—reckoning
that epoch as extending from Hilary and Ambrose
to the end of the pontificate of Gregory the Great. The
“Ambrosian” music, to which those hymns were generally
sung down to the time of Gregory, was more popular and congregational
than the “Gregorian,” which then came into use,
and afterwards prevailed. In the service of the mass it was
not the general practice, before the invention of sequences in
the 9th century, to sing any hymns, except some from the
Scriptures esteemed canonical, such as the “Song of the Three
Children” (“Benedicite omnia opera”). But to this rule
there were, according to Walafrid Strabo, some occasional
exceptions; particularly in the case of Paulinus, patriarch
of Aquileia under Charlemagne, himself a hymn-writer, who
frequently used hymns, composed by himself or others, in the
eucharistic office, especially in private masses.
Some of the hymns called “Ambrosian” (nearly 100 in
number) are beyond all question by Ambrose himself, and the
rest probably belong to his time or to the following century.
Four, those beginning “Aeterne rerum conditor” (“Dread
Framer of the earth and sky”), “Deus Creator omnium”
(“Maker of all things, glorious God”), “Veni Redemptor
Gentium” (“Redeemer of the nations, come”) and “Jam
surgit hora tertia” (“Christ at this hour was crucified”), are
quoted as works of Ambrose by Augustine. These, and others
by the hand of the same master, have the qualities most valuable
in hymns intended for congregational use. They are short
and complete in themselves; easy, and at the same time elevated
in their expression and rhythm; terse and masculine in thought
and language; and (though sometimes criticized as deficient
in theological precision) simple, pure and not technical in their
rendering of the great facts and doctrines of Christianity, which
they present in an objective and not a subjective manner. They
have exercised a powerful influence, direct or indirect, upon
many of the best works of the same kind in all succeeding
generations. With the Ambrosian hymns are properly classed
those of Hilary, and the contemporary works of Pope Damasus I.
(who wrote two hymns in commemoration of saints), and of
Prudentius, from whose Cathemerina (“Daily Devotions”)
and Peristephana (“Crown-songs for Martyrs”), all poems of
considerable, some of great length—about twenty-eight hymns,
185
found in various Breviaries, were derived. Prudentius was a
layman, a native of Saragossa, and it was in the Spanish ritual
that his hymns were most largely used. In the Mozarabic
Breviary almost the whole of one of his finest poems (from which
most churches took one part only, beginning “Corde natus
ex parentis”) was appointed to be sung between Easter and
Ascension-Day, being divided into eight or nine hymns; and
on some of the commemorations of Spanish saints long poems
from his Peristephana were recited or sung at large. He is
entitled to a high rank among Christian poets, many of the hymns
taken from his works being full of fervour and sweetness, and
by no means deficient in dignity or strength.
These writers were followed in the 5th and early in the 6th
century by the priest Sedulius, whose reputation perhaps
exceeded his merit; Elpis, a noble Roman lady
(considered, by an erroneous tradition, to have been
5th and 6th centuries.
the wife of the philosophic statesman Boetius);
Pope Gelasius I.; and Ennodius, bishop of Pavia.
Sedulius and Elpis wrote very little from which hymns could be
extracted; but the small number taken from their compositions
obtained wide popularity, and have since held their ground.
Gelasius was of no great account as a hymn-writer; and the
works of Ennodius appear to have been known only in Italy
and Spain. The latter part of the 6th century produced Pope
Gregory the Great and Venantius Fortunatus, an Italian poet,
the friend of Gregory, and the favourite of Radegunda, queen of
the Franks, who died (609) bishop of Poitiers. Eleven hymns
of Gregory, and twelve or thirteen (mostly taken from longer
poems) by Fortunatus, came into general use in the Italian,
Gallican and British churches. Those of Gregory are in a style
hardly distinguishable from the Ambrosian; those of Fortunatus
are graceful, and sometimes vigorous. He does not, however,
deserve the praise given to him by Dr Neale, of having struck
out a new path in Latin hymnody. On the contrary, he may
more justly be described as a disciple of the school of Prudentius,
and as having affected the classical style, at least as much as
any of his predecessors.
The poets of this primitive epoch, which closed with the 6th
century, wrote in the old classical metres, and made use of a considerable
variety of them—anapaestic, anacreontic, hendecasyllabic,
asclepiad, hexameters and pentameters and others. Gregory and
some of the Ambrosian authors occasionally wrote in sapphics;
but the most frequent measure was the iambic dimeter, and, next
to that, the trochaic. The full alcaic stanza does not appear to
have been used for church purposes before the 16th century, though
some of its elements were. In the greater number of these works,
a general intention to conform to the rules of Roman prosody is
manifest; but even those writers (like Prudentius) in whom that
conformity was most decided allowed themselves much liberty of
deviation from it. Other works, including some of the very earliest,
and some of conspicuous merit, were of the kind described by Bede
as not metrical but “rhythmical”—i.e. (as he explains the term
“rhythm”), “modulated to the ear in imitation of different metres.”
It would be more correct to call them metrical—(e.g. still trochaic
or iambic, &c., but, according to new laws of syllabic quantity, depending
entirely on accent, and not on the power of vowels or the
position of consonants)—laws by which the future prosody of all
modern European nations was to be governed. There are also, in
the hymns of the primitive period (even in those of Ambrose),
anticipations—irregular indeed and inconstant, but certainly not
accidental—of another great innovation, destined to receive important
developments, that of assonance or rhyme, in the final
letters or syllables of verses. Archbishop Trench, in the introduction
to his Sacred Latin Poetry, has traced the whole course of the
transition from the ancient to the modern forms of versification,
ascribing it to natural and necessary causes, which made such
changes needful for the due development of the new forms of spiritual
and intellectual life, consequent upon the conversion of the Latin-speaking
nations to Christianity.
From the 6th century downwards we see this transformation
making continual progress, each nation of Western Christendom
adding, from time to time, to the earlier hymns in its
service-books others of more recent and frequently
6th century downwards.
of local origin. For these additions, the commemorations
of saints, &c., as to which the devotion of one
place often differed from that of another, offered especial opportunities.
This process, while it promoted the development
of a medieval as distinct from the primitive style, led also to much
deterioration in the quality of hymns, of which, perhaps, some of
the strongest examples may be found in a volume published in
1865 by the Irish Archaeological Society from a manuscript in the
library of Trinity College, Dublin. It contains a number of
hymns by Irish saints of the 6th, 7th and 8th centuries—in
several instances fully rhymed, and in one mixing Erse and Latin
barbarously together, as was not uncommon, at a much later date,
in semi-vernacular hymns of other countries. The Mozarabic
Breviary, and the collection of hymns used in the Anglo-Saxon
churches, published in 1851 by the Surtees Society (chiefly from
a Benedictine MS. In the college library of Durham, supplemented
by other MSS. in the British Museum), supply many further illustrations
of the same decline of taste:—such Sapphics, e.g., as
the “Festum insigne prodiit coruscum” of Isidore, and the
“O veneranda Trinitas laudanda” of the Anglo-Saxon books.
The early medieval period, however, from the time of Gregory
the Great to that of Hildebrand, was far from deficient in the production
of good hymns, wherever learning flourished. Bede
in England, and Paul “the Deacon”—the author of a fairly
classical sapphic ode on St John the Baptist—in Italy, were
successful followers of the Ambrosian and Gregorian styles.
Eleven metrical hymns are attributed to Bede by Cassander;
and there are also in one of Bede’s works (Collectanea et flores)
two rhythmical hymns of considerable length on the Day of
Judgment, with the refrains “In tremendo die” and “Attende
homo,” both irregularly rhymed, and, in parts, not unworthy
of comparison with the “Dies Irae.” Paulinus, patriarch of
Aquileia, contemporary with Paul, wrote rhythmical trimeter
iambics in a manner peculiar to himself. Theodulph, bishop of
Orleans (793-835), author of the famous processional hymn for
Palm Sunday in hexameters and pentameters, “Gloria, laus, et
honor tibi sit, Rex Christe Redemptor” (“Glory and honour and
laud be to Thee, King Christ the Redeemer”), and Hrabanus
Maurus, archbishop of Mainz, the pupil of Alcuin, and the most
learned theologian of his day, enriched the church with some
excellent works. Among the anonymous hymns of the same
period there are three of great beauty, of which the influence may
be traced in most, if not all, of the “New Jerusalem” hymns of
later generations, including those of Germany and Great Britain:—“Urbs
beata Hierusalem” (“Blessed city, heavenly Salem”);
“Alleluia piis edite laudibus” (“Alleluias sound ye in strains
of holy praise”—called, from its burden, “Alleluia perenne”);
and “Alleluia dulce carmen” (“Alleluia, song of sweetness”),
which, being found in Anglo-Saxon hymnaries certainly older
than the Conquest, cannot be of the late date assigned to it, in
his Mediaeval Hymns and Sequences, by Neale. These were
followed by the “Chorus novae Hierusalem” (“Ye Choirs of
New Jerusalem”) of Fulbert, bishop of Chartres. This group of
hymns is remarkable for an attractive union of melody, imagination,
poetical colouring and faith. It represents, perhaps, the
best and highest type of the middle school, between the severe
Ambrosian simplicity and the florid luxuriance of later times.
Another celebrated hymn, which belongs to the first medieval
period, is the “Veni Creator Spiritus” (“Come, Holy Ghost,
our souls inspire”). The earliest recorded occasion of
its use is that of a translation (898) of the relics of St
Veni Creator.
Marcellus, mentioned in the Annals of the Benedictine
order. It has since been constantly sung throughout Western
Christendom (as versions of it still are in the Church of England),
as part of the appointed offices for the coronation of kings, the
consecration and ordination of bishops and priests, the assembling
of synods and other great ecclesiastical solemnities. It has been
attributed—probably in consequence of certain corruptions in
the text of Ekkehard’s Life of Notker (a work of the 13th century)—to
Charlemagne. Ekkehard wrote in the Benedictine monastery
Notker.
of St Gall, to which Notker belonged, with full access
to its records; and an ignorant interpolator, regardless
of chronology, added, at some later date, the word “Great” to
the name of “the emperor Charles,” wherever it was mentioned
in that work. The biographer relates that Notker—a man of a
gentle, contemplative nature, observant of all around him, and
accustomed to find spiritual and poetical suggestions in common
186
sights and sounds—was moved by the sound of a mill-wheel to
compose his “sequence” on the Holy Spirit, “Sancti Spiritus
adsit nobis gratia” (“Present with us ever be the Holy Spirit’s
grace”); and that, when finished, he sent it as a present to
“the emperor Charles,” who in return sent him back, “by the
same messenger,” the hymn “Veni Creator,” which (says Ekkehard)
the same “Spirit had inspired him to write” (“Sibi idem
Spiritus inspiraverat”). If this story is to be credited—and,
from its circumstantial and almost dramatic character, it has an
air of truth—the author of “Veni Creator” was not Charlemagne,
but his grandson the emperor Charles the Bald. Notker himself
long survived that emperor, and died in 912.
The invention of “sequences” by Notker may be regarded
as the beginning of the later medieval epoch of Latin hymnody.
In the eucharistic service, in which (as has been stated)
hymns were not generally used, it had been the practice,
Sequences.
except at certain seasons, to sing “laud,” or “Alleluia,”
between the epistle and the gospel, and to fill up what would
otherwise have been a long pause, by extending the cadence
upon the two final vowels of the “Alleluia” into a protracted
strain of music. It occurred to Notker that, while preserving
the spirit of that part of the service, the monotony of the interval
might be relieved by introducing at that point a chant of praise
specially composed for the purpose. With that view he produced
the peculiar species of rhythmical composition which obtained
the name of “sequentia” (probably from following after the
close of the “Alleluia”), and also that of “prosa,” because its
structure was originally irregular and unmetrical, resembling in
this respect the Greek “troparia,” and the “Te Deum,” “Benedicite”
and canticles. That it was in some measure suggested
by the forms of the later Greek hymnody seems probable, both
from the intercourse (at that time frequent) between the Eastern
and Western churches, and from the application by Ekkehard,
in his biography and elsewhere (e.g. in Lyndwood’s Provinciale),
of some technical terms, borrowed from the Greek terminology,
to works of Notker and his school and to books containing them.
Dr Neale, in a learned dissertation prefixed to his collection of
sequences from medieval Missals, and enlarged in a Latin letter to
H. A. Daniel (printed in the fifth volume of Daniel’s Thesaurus
hymnologicus), investigated the laws of caesura and modulation which
are discoverable in these works. Those first brought into use were
sent by their author to Pope Nicholas I., who authorized their use,
and that of others composed after the same model by other brethren
of St Gall, in all churches of the West.
Although the sequences of Notker and his school, which then
rapidly passed into most German, French and British Missals,
were not metrical, the art of “assonance” was much practised in
them. Many of those in the Sarum and French Missals have every
verse, and even every clause or division of a verse, ending with the
same vowel “a”—perhaps with some reference to the terminal
letter of “Alleluia.” Artifices such as these naturally led the way
to the adaptation of the same kind of composition to regular metre
and fully developed rhyme. Neale’s full and large collection, and
the second volume of Daniel’s Thesaurus, contain numerous examples,
both of the “proses,” properly so called, of the Notkerian type, and
of those of the later school, which (from the religious house to
which its chief writer belonged) has been called “Victorine.” Most
Missals appear to have contained some of both kinds. In the
majority of those from which Neale’s specimens are taken, the
metrical kind largely prevailed; but in some (e.g. those of Sarum
and Liége) the greater number were Notkerian.
Of the sequence on the Holy Ghost, sent by Notker (according
to Ekkehard) to Charles the Bald, Neale says that it “was in
use all over Europe, even in those countries, like Italy and Spain,
which usually rejected sequences”; and that, “in the Missal
of Palencia, the priest was ordered to hold a white dove in his
hands, while intoning the first syllables, and then to let it go.”
Another of the most remarkable of Notker’s sequences, beginning
“Media in vita” (“In the midst of life we are in death”), is
said to have been suggested to him while observing some workmen
engaged in the construction of a bridge over a torrent near his
monastery. Catherine Winkworth (Christian Singers of Germany,
1869) states that this was long used as a battle-song, until the
custom was forbidden, on account of its being supposed to
exercise a magical influence. A translation of it (“Mitten
wir im Leben sind”) is one of Luther’s funeral hymns; and
all but the opening sentence of that part of the burial service
of the Church of England which is directed to be “said or sung”
at the grave, “while the corpse is made ready to be laid into
the earth,” is taken from it.
The “Golden Sequence,” “Veni, sancte Spiritus” (“Holy
Spirit, Lord of Light”), is an early example of the transition
of sequences from a simply rhythmical to a metrical form. Archbishop
Trench, who esteemed it “the loveliest of all the hymns
in the whole circle of Latin sacred poetry,” inclined to give
credit to a tradition which ascribes its authorship to Robert II.,
king of France, son of Hugh Capet. Others have assigned to
it a later date—some attributing it to Pope Innocent III.,
and some to Stephen Langton, archbishop of Canterbury. Many
translations, in German, English and other languages, attest
its merit. Berengarius of Tours, St Bernard of Clairvaux
and Abelard, in the 11th century and early in the 12th, followed
in the same track; and the art of the Victorine school was
carried to its greatest perfection by Adam of St Victor (who
died between 1173 and 1194)—“the most fertile, and” (in the
concurrent judgment of Archbishop Trench and Neale) “the
greatest of the Latin hymnographers of the Middle Ages.”
The archbishop’s selection contains many excellent specimens
of his works.
But the two most widely celebrated of all this class of
compositions—works which have exercised the talents of the
greatest musical composers, and of innumerable
translators in almost all languages—are the “Dies
Dies Irae.
Stabat Mater.
Aquinas.
Irae” (“That day of wrath, that dreadful day”), by Thomas
of Celano, the companion and biographer of St Francis of Assisi,
and the “Stabat Mater dolorosa” (“By the cross
sad vigil keeping”) of Jacopone, or Jacobus de
Benedictis, a Franciscan humorist and reformer,
who was persecuted by Pope Boniface VIII. for his satires on
the prelacy of the time, and died in 1306. Besides these, the 13th
century produced the famous sequence “Lauda Sion salvatorem”
(“Sion, lift thy voice and sing”), and the four other well-known
sacramental hymns of St Thomas Aquinas, viz. “Pange lingua
gloriosi corporis mysterium” (“Sing, my tongue,
the Saviour’s glory”), “Verbum supernum prodiens”
(“The Word, descending from above”—not to be confounded
with the Ambrosian hymn from which it borrowed the first
line), “Sacris solemniis juncta sint gaudia” (“Let us with
hearts renewed our grateful homage pay”), and “Adoro Te
devote, latens Deitas” (“O Godhead hid, devoutly I adore
Thee”)—a group of remarkable compositions, written by him
for the then new festival of Corpus Christi, of which he induced
Pope Urban IV. (1261-1265) to decree the observance. In
these (of which all but “Adoro Te devote” passed rapidly into
breviaries and missals) the doctrine of transubstantiation is
set forth with a wonderful degree of scholastic precision; and
they exercised, probably, a not unimportant influence upon the
general reception of that dogma. They are undoubtedly works
of genius, powerful in thought, feeling and expression.
These and other medieval hymn-writers of the 12th and 13th
centuries may be described, generally, as poet-schoolmen.
Their tone is contemplative, didactic, theological;
they are especially fertile and ingenious in the field
Medieval hymns.
of mystical interpretation. Two great monasteries
in the East had, in the 8th and 9th centuries, been the principal
centres of Greek hymnology; and, in the West, three monasteries—St
Gall, near Constance (which was long the especial seat of
German religious literature), Cluny in Burgundy and St Victor,
near Paris—obtained a similar distinction. St Gall produced,
besides Notker, several distinguished sequence writers, probably
his pupils—Hartmann, Hermann and Gottschalk—to the last
of whom Neale ascribes the “Alleluiatic Sequence” (“Cantemus
cuncti melodum nunc Alleluia”), well known in England through
his translation, “The strain upraise of joy and praise.” The
chief poets of Cluny were two of its abbots, Odo and Peter the
Venerable (1122-1156), and one of Peter’s monks, Bernard
of Morlaix, who wrote the remarkable poem on “Contempt
of the World” in about 3000 long rolling “leonine-dactylic”
verses, from parts of which Neale’s popular hymns, “Jerusalem
187
the golden,” &c., are taken. The abbey of St Victor, besides
Adam and his follower Pistor, was destined afterwards to produce
the most popular church poet of the 17th century.
There were other distinguished Latin hymn-writers of the
later medieval period besides those already mentioned. The
name of St Bernard of Clairvaux cannot be passed
over with the mere mention of the fact that he was the
Bernard of Clairvaux.
author of some metrical sequences. He was, in truth,
the father, in Latin hymnody, of that warm and
passionate form of devotion which some may consider to apply
too freely to Divine Objects the language of human affection,
but which has, nevertheless, been popular with many devout
persons, in Protestant as well as Roman Catholic churches.
F. von Spee, “Angelus Silesius,” Madame Guyon, Bishop Ken,
Count Zinzendorf and Frederick William Faber may be regarded
as disciples in this school. Many hymns, in various languages,
have been founded upon St Bernard’s “Jesu dulcis memoria”
(“Jesu, the very thought of Thee”), “Jesu dulcedo cordium”
(“Jesu, Thou joy of loving hearts”) and “Jesu Rex admirabilis”
(“O Jesu, King most wonderful”)—three portions of one
poem, nearly 200 lines long. Pietro Damiani, the friend of
Pope Gregory VII, Marbode, bishop of Rennes, in the 11th,
Hildebert, archbishop of Tours, in the 12th, and St Bonaventura
in the 13th centuries, are other eminent men who added poetical
fame as hymnographers to high public distinction.
Before the time of the Reformation, the multiplication of
sequences (often as unedifying in matter as unpoetical in style)
had done much to degrade the common conception of hymnody.
In some parts of France, Portugal, Sardinia and Bohemia,
their use in the vernacular language had been allowed. In
Germany also there were vernacular sequences as early as the
12th century, specimens of which may be seen in the third
chapter of C. Winkworth’s Christian Singers of Germany.
Scoffing parodies upon sequences are said to have been among
the means used in Scotland to discredit the old church services.
After the 15th century they were discouraged at Rome. They
retained for a time some of their old popularity among German
Protestants, and were only gradually relinquished in France.
A new “prose,” in honour of St Maxentia, is among the compositions
of Jean Baptiste Santeul; and Dr Daniel’s second volume
closes with one written in 1855 upon the dogma of the Immaculate
Conception.
The taste of the Renaissance was offended by all deviations from
classical prosody and Latinity. Pope Leo X. directed the whole
body of the hymns in use at Rome to be reformed; and
the Hymni novi ecclesiastici juxta veram metri et Latinitatis
normam,
Roman revision of hymns.
prepared by Zacharie Ferreri (1479-1530), a
Benedictine of Monte Cassino, afterwards a Carthusian
and bishop of Guardia, to whom Leo had committed that task,
appeared at Rome in 1525, with the sanction of a later pope, Clement
VII. The next step was to revise the whole Roman Breviary.
That undertaking, after passing through several stages under
different popes (particularly Pius V. and Clement VIII.), was at last
brought to a conclusion by Urban VIII., in 1631. From this revised
Breviary a large number of medieval hymns, both of the earlier
and the later periods, were excluded; and in their places many new
hymns, including some by Pope Urban himself, and some by Cardinal
Bellarmine and another cardinal (Silvius Antonianus) were introduced.
The hymns of the primitive epoch, from Hilary to Gregory
the Great, for the most part retained their places (especially in the
offices for every day of the week); and there remained altogether
from seventy to eighty of earlier date than the 11th century.
Those, however, which were so retained were freely altered, and by
no means generally improved. The revisers appointed by Pope
Urban (three learned Jesuits—Strada, Gallucci and Petrucci)
professed to have made “as few changes as possible” in the works
of Ambrose, Gregory, Prudentius, Sedulius, Fortunatus and other
“poets of great name.” But some changes, even in those works,
were made with considerable boldness; and the pope, in the “constitution”
by which his new book was promulgated, boasted that,
“with the exception of a very small number (’perpaucis’), which
were either prose or merely rhythmical, all the hymns had been made
conformable to the laws of prosody and Latinity, those which could
not be corrected by any milder method being entirely rewritten.”
The latter fate befel, among others, the beautiful “Urbs beata
Hierusalem,” which now assumed the form (to many, perhaps,
better known), of “Caelestis urbs Jerusalem.” Of the “very few”
which were spared, the chief were “Ave maris stella” (“Gentle star
of ocean”), “Dies Irae,” “Stabat Mater dolorosa,” the hymns of
Thomas Aquinas, two of St Bernard and one Ambrosian hymn,
“Jesu nostra Redemptio” (“O Jesu, our Redemption”), which
approaches nearer than others to the tone of St Bernard. A then
recent hymn of St Francis Xavier, with scarcely enough merit of
any kind to atone for its neglect of prosody, “O Deus, ego amo Te”
(“O God, I love Thee, not because”), was at the same time introduced
without change. This hymnary of Pope Urban VIII. is now
in general use throughout the Roman Communion.
The Parisian hymnary underwent three revisions—the first in
1527, when a new “Psaltery with hymns” was issued. In this
such changes only were made as the revisers thought
justifiable upon the principle of correcting supposed
Parisian revisions.
corruptions of the original text. Of these, the transposition,
“Urbs Jerusalem beata,” instead of “Urbs beata Hierusalem,”
may be taken as a typical example. The next revision was in 1670-1680,
under Cardinal Péréfixe, preceptor of Louis XIV., and Francis
Harlay, successively archbishops of Paris, who employed for this
purpose Claude Santeul, of the monastery of St Magloire, and,
through him, obtained the assistance of other French scholars, including
his more celebrated brother, Jean Baptiste Santeul, of the
abbey of St Victor—better known as “Santolius Victorinus.”
The third and final revision was completed in 1735, under the
primacy of Cardinal Archbishop de Vintimille, who engaged for it
the services of Charles Coffin, then rector of the university of Paris.
Many old hymns were omitted in Archbishop Harlay’s Breviary, and
a large number of new compositions, by the Santeuls and others, was
introduced. It still, however, retained in their old places (without
further changes than had been made in 1527) about seventy of
earlier date than the 11th century—including thirty-one Ambrosian,
one by Hilary, eight by Prudentius, seven by Fortunatus, three by
Paul the Deacon, two each by Sedulius, Elpis, Gregory and Hrabanus
Maurus, “Veni Creator” and “Urbs Jerusalem beata.” Most of
these disappeared in 1735, although Cardinal Vintimille, in his
preface, professed to have still admitted the old hymns, except when
the new were better—(“veteribus hymnis locus datus est, nisi
quibus, ob sententiarum vim, elegantiam verborum, et teneriores
pietatis sensus, recentiores anteponi satius visum est”). The number
of the new was, at the same time, very largely increased. Only
twenty-one more ancient than the 16th century remained, of which
those belonging to the primitive epoch were but eight, viz. four
Ambrosian, two by Fortunatus and one each by Prudentius and
Gregory. The number of Jean Baptiste Santeul’s hymns rose to
eighty-nine; those by Coffin—including some old hymns, e.g.
“Jam lucis orto sidere” (“Once more the sun is beaming bright”),
which he substantially re-wrote—were eighty-three; those of other
modern French writers, ninety-seven. Whatever opinion may be
entertained of the principles on which these Roman and Parisian
revisions proceeded, it would be unjust to deny very high praise as
hymn-writers to several of their poets, especially to Coffin and Jean
Baptiste Santeul. The noble hymn by Coffin, beginning—
| “O luce qui mortalibus | “O Thou who in the light dost dwell, |
| Lates inaccessa, Deus, | To mortals unapproachable, |
| Praesente quo sancti tremunt | Where angels veil them from Thy rays, |
| Nubuntque vultus angeli,” | And tremble as they gaze,” |
and several others of his works, breathe the true Ambrosian spirit;
and though Santeul (generally esteemed the better poet of the two)
delighted in alcaics, and did not greatly affect the primitive manner,
there can be no question as to the excellence of such hymns as his
“Fumant Sabaeis templa vaporibus” (“Sweet incense breathes
around”), “Stupete gentes, fit Deus hostia” (“Tremble, ye Gentile
lands”), “Hymnis dum resonat curia caelitum” (“Ye in the house
of heavenly morn”), and “Templi sacratas pande, Sion, fores”
(“O Sion, open wide thy gates”). It is a striking testimony to the
merits of those writers that such accomplished translators as the
Rev. Isaac Williams and the Rev. John Chandler appear (from the
title-page of the latter, and the prefaces of both) to have supposed
their hymns to be “ancient” and “primitive.” Among the other
authors associated with them, perhaps the first place is due to the
Abbé Besnault, of Sens, who contributed to the book of 1735 the
“Urbs beata vera pacis Visio Jerusalem,” in the opinion of Neale
“much superior” to the “Caelestis urbs Jerusalem” of the Roman
Breviary. This stood side by side with the “Urbs Jerusalem beata”
of 1527 (in the office for the dedication of churches) till 1822, when the
older form was at last finally excluded by Archbishop de Quelen.
The Parisian Breviary of 1735 remained in use till the national
French service-books were superseded (as they have lately been,
generally, if not universally) by the Roman. Almost all French
dioceses followed, not indeed the Breviary, but the example, of
Paris; and before the end of the 18th century the ancient Latin
hymnody was all but banished from France.
In some parts of Germany, after the Reformation, Latin hymns
continued to be used even by Protestants. This was the case at
Halberstadt until quite a recent date. In England, a few are
still occasionally used in the older universities and colleges.
Modern Latin hymns.
Some, also, have been composed in both countries since
the Reformation. The “Carmina lyrica” of Johann
Jakob Balde, a native of Alsace, and a Jesuit priest in Bavaria, have
received high commendation from very eminent German critics,
particularly Herder and Augustus Schlegel. Some of the Latin
hymns of William Alard (1572-1645), a Protestant refugee from
188
Belgium, and pastor in Holstein, have been thought worthy of a place
in Archbishop Trench’s selection. Two by W. Petersen (printed
at the end of Haberkorn’s supplement to Jacobi’s Psalmodia Germanica)
are good in different ways—one, “Jesu dulcis amor meus”
(“Jesus, Thee my soul doth love”), being a gentle melody of spiritual
devotion, and the other, entitled Spes Sionis, violently controversial
against Rome. An English hymn of the 17th century, in the
Ambrosian style, “Te Deum Patrem colimus” (“Almighty Father,
just and good”), is sung on every May-Day morning by the choristers
of Magdalen College, Oxford, from the top of the tower of their chapel;
and another in the style of the Renaissance, of about the same date,
“Te de profundis, summe Rex” (“Thee from the depths, Almighty
King”), long formed part of a grace formerly sung by the scholars of
Winchester College.
5. German Hymnody.—Luther was a proficient in and a lover
of music. He desired (as he says in the preface to his hymn-book
of 1545) that this “beautiful ornament” might “in
a right manner serve the great Creator and His Christian
Luther.
people.” The persecuted Bohemian or Hussite Church, then
settled on the borders of Moravia under the name of “United
Brethren,” had sent to him, on a mission in 1522, Michael Weiss,
who not long afterwards published a number of German translations
from old Bohemian hymns (known as those of the
“Bohemian Brethren”), with some of his own. These Luther
highly approved and recommended. He himself, in 1522,
published a small volume of eight hymns, which was enlarged
to 63 in 1527, and to 125 in 1545. He had formed what he called
a “house choir” of musical friends, to select such old and
popular tunes (whether secular or ecclesiastical) as might be
found suitable, and to compose new melodies, for church use.
His fellow labourers in this field (besides Weiss) were Justus
Jonas, his own especial colleague; Paul Eber, the disciple and
friend of Melanchthon; John Walther, choirmaster successively
to several German princes, and professor of arts, &c., at Wittenberg;
Nicholas Decius, who from a monk became a Protestant
teacher in Brunswick, and translated the “Gloria in Excelsis,”
&c.; and Paul Speratus, chaplain to Duke Albert of Prussia
in 1525. Some of their works are still popular in Germany.
Weiss’s “Funeral Hymn,” “Nun lasst uns den Leib begraben”
(“Now lay we calmly in the grave”); Eber’s “Herr Jesu
Christ, wahr Mensch und Gott” (“Lord Jesus Christ, true Man
and God”), and “Wenn wir in höchsten Nöthen sein” (“When
in the hour of utmost need”); Walther’s “New Heavens and
new Earth” (“Now fain my joyous heart would sing”);
Decius’s “To God on high be thanks and praise”; and Speratus’s
“Salvation now has come for all,” are among those which
at the time produced the greatest effect, and are still best
remembered.
Luther’s own hymns, thirty-seven in number (of which about
twelve are translations or adaptations from Latin originals),
are for the principal Christian seasons; on the sacraments,
the church, grace, death, &c.; and paraphrases of seven psalms,
of a passage in Isaiah, and of the Lord’s Prayer, Ten Commandments,
Creed, Litany and “Te Deum.” There is also a very
touching and stirring song on the martyrdom of two youths
by fire at Brussels, in 1523-1524. Homely and sometimes
rugged in form, and for the most part objective in tone, they are
full of fire, manly simplicity and strong faith. Three rise above
the rest. One for Christmas, “Vom Himmel hoch da komm
ich her” (“From Heaven above to earth I come”), has a
reverent tenderness, the influence of which may be traced in
many later productions on the same subject. That on salvation
through Christ, of a didactic character, “Nun freuet euch,
lieben Christen g’mein” (“Dear Christian people, now rejoice”),
is said to have made many conversions, and to have been once
taken up by a large congregation to silence a Roman Catholic
preacher in the cathedral of Frankfort. Pre-eminent above all
is the celebrated paraphrase of the 46th Psalm: “Ein’ feste
Burg ist unser Gott” (“A sure stronghold our God is He”)—“the
production” (as Ranke says) “of the moment in which
Luther, engaged in a conflict with a world of foes, sought strength
in the consciousness that he was defending a divine cause which
could never perish.” Carlyle compares it to “a sound of Alpine
avalanches, or the first murmur of earthquakes.” Heine called
it “the Marseillaise of the Reformation.”
Luther spent several years in teaching his people at Wittenberg
to sing these hymns, which soon spread over Germany. Without
adopting the hyperbolical saying of Coleridge, that “Luther
did as much for the Reformation by his hymns as by his translation
of the Bible,” it may truly be affirmed, that, among the
secondary means by which the success of the Reformation was
promoted, none was more powerful. They were sung everywhere—in
the streets and fields as well as the churches, in the
workshop and the palace, “by children in the cottage and by
martyrs on the scaffold.” It was by them that a congregational
character was given to the new Protestant worship. This success
they owed partly to their metrical structure, which, though
sometimes complex, was recommended to the people by its
ease and variety; and partly to the tunes and melodies (many of
them already well known and popular) to which they were set.
They were used as direct instruments of teaching, and were
therefore, in a large measure, didactic and theological; and it
may be partly owing to this cause that German hymnody came
to deviate, so soon and so generally as it did, from the simple
idea expressed in the ancient Augustinian definition, and to
comprehend large classes of compositions which, in most other
countries, would be thought hardly suitable for church use.
The principal hymn-writers of the Lutheran school, in the
latter part of the 16th century, were Nikolaus Selnecker, Herman
and Hans Sachs, the shoemaker of Nuremberg, also
known in other branches of literature. All these
Followers of Luther
wrote some good hymns. They were succeeded by
men of another sort, to whom F. A. Cunz gives the
name of “master-singers,” as having raised both the poetical
and the musical standard of German hymnody:—Bartholomäus
Ringwaldt, Ludwig Helmbold, Johannes Pappus, Martin Schalling,
Rutilius and Sigismund Weingartner. The principal topics
of their hymns (as if with some foretaste of the calamities
which were soon to follow) were the vanity of earthly things,
resignation to the Divine will, and preparation for death
and judgment. The well-known English hymn, “Great God,
what do I see and hear,” is founded upon one by Ringwaldt.
Of a quite different character were two of great beauty and
universal popularity, composed by Philip Nicolai, a Westphalian
pastor, during a pestilence in 1597, and published by him,
with fine chorales, two years afterwards. One of these (the
“Sleepers wake! a voice is calling,” of Mendelssohn’s oratorio,
St Paul) belongs to the family of Advent or New Jerusalem
hymns. The other, a “Song of the believing soul concerning the
Heavenly Bridegroom” (“Wie schön leucht’t uns der Morgenstern”—“O
morning Star, how fair and bright”), became the
favourite marriage hymn of Germany.
The hymns produced during the Thirty Years’ War are characteristic
of that unhappy time, which (as Miss Winkworth says)
“caused religious men to look away from this world,”
and made their songs more and more expressive of
Period of Thirty Years’ War.
personal feelings. In point of refinement and graces
of style, the hymn-writers of this period excelled
their predecessors. Their taste was chiefly formed by the influence
of Martin Opitz, the founder of what has been called
the “first Silesian school” of German poetry, who died comparatively
young in 1639, and who, though not of any great
original genius, exercised much power as a critic. Some of the
best of these works were by men who wrote little. In the famous
battle-song of Gustavus Adolphus, published (1631) after the
victory of Breitenfeld, for the use of his army, “Verzage nicht
du Häuflein klein” (“Fear not, O little flock, the foe”), we have
almost certainly a composition of the hero-king himself, the
versification corrected by his chaplain Jakob Fabricius (1593-1654)
and the music composed by Michael Altenburg, whose
name has been given to the hymn. This, with Luther’s paraphrase
of the 67th Psalm, was sung by Gustavus and his soldiers
before the battle of Lützen in 1632. Two very fine hymns,
one of prayer for deliverance and peace, the other of trust in
God under calamities, were written about the same time by
Matthäus Löwenstern, a saddler’s son, poet, musician and
statesman, who was ennobled after the peace by the emperor
189
Ferdinand III. Martin Rinckhart, in 1636, wrote the “Chorus
of God’s faithful children” (“Nun danket alle Gott”—“Now
thank we all our God”), introduced by Mendelssohn in his
“Lobgesang,” which has been called the “Te Deum” of Germany,
being usually sung on occasions of public thanksgiving. Weissel,
in 1635, composed a beautiful Advent hymn (“Lift up your heads,
ye mighty gates”), and J. M. Meyfart, professor of theology at
Erfurt, in 1642, a fine adaptation of the ancient “Urbs beata
Hierusalem.” The hymn of trust in Providence by George
Neumark, librarian to that duke of Weimar (“Wer nur den
lieben Gott lässt walten”—“Leave God to order all thy ways”),
is scarcely, if at all, inferior to that of Paul Gerhardt on the same
theme. Paul Flemming, a great traveller and lover of nature,
who died in 1639, also wrote excellent compositions, coloured
by the same tone of feeling; and some, of great merit, were
composed, soon after the close of the war, by Louisa Henrietta,
electress of Brandenburg, granddaughter of the famous admiral
Coligny, and mother of the first king of Prussia. With these
may be classed (though of later date) a few striking hymns of
faith and prayer under mental anxiety, by Anton Ulrich, duke
of Brunswick.
The most copious, and in their day most esteemed, hymn-writers
of the first half of the 17th century, were Johann Heermann
and Johann Rist. Heermann, a pastor in Silesia,
the theatre (in a peculiar degree) of war and persecution,
Rist.
experienced in his own person a very large share of the
miseries of the time, and several times narrowly escaped a
violent death. His Devoti musica cordis, published in 1630,
reflects the feelings natural under such circumstances. With a
correct style and good versification, his tone is subjective, and
the burden of his hymns is not praise, but prayer. Among his
works (which enter largely into most German hymn-books),
two of the best are the “Song of Tears” and the “Song of
Comfort,” translated by Miss Winkworth in her Christian
Singers of Germany. Rist published about 600 hymns, “pressed
out of him,” as he said, “by the cross.” He was a pastor, and
son of a pastor, in Holstein, and lived after the peace to enjoy
many years of prosperity, being appointed poet-laureate to the
emperor and finally ennobled. The bulk of his hymns, like those
of other copious writers, are of inferior quality; but some,
particularly those for Advent, Epiphany, Easter Eve and on
Angels, are very good. They are more objective than those of
Heermann, and written, upon the whole, in a more manly spirit.
Dach.
Next to Heermann and Rist in fertility of production,
and above them in poetical genius, was Simon Dach,
professor of poetry at Königsberg, who died in 1659. Miss
Winkworth ranks him high among German poets, “for the
sweetness of form and depth of tender contemplative emotion
to be found in his verses.”
The fame of all these writers was eclipsed in the latter part of
the same century by three of the greatest hymnographers whom
Germany has produced—Paul Gerhardt (1604-1676),
Johann Franck (1618-1677) and Johann Scheffler
Gerhardt.
(1624-1677), the founder of the “second Silesian school,” who
assumed the name of “Angelus Silesius.” Gerhardt is by universal
consent the prince of Lutheran poets. His compositions,
which may be compared, in many respects, to those of the
Christian Year, are lyric poems, of considerable length, rather
than hymns, though many hymns have been taken from them.
They are, with few exceptions, subjective, and speak the language
of individual experience. They occupy a middle ground between
the masculine simplicity of the old Lutheran style and the highly
wrought religious emotion of the later pietists, towards whom
they on the whole incline. Being nearly all excellent, it is not
easy to distinguish among the 123 those which are entitled
to the highest praise. Two, which were written one during the
war and the other after the conclusion of peace, “Zeuch ein zu
deinen Thoren” (“Come to Thy temple here on earth”), and
“Gottlob, nun ist erschollen” (“Thank God, it hath resounded”),
are historically interesting. Of the rest, one is well
known and highly appreciated in English through Wesley’s
translation, “Commit thou all thy ways”; and the evening
and spring-tide hymns (“Now all the woods are sleeping” and
“Go forth, my heart, and seek delight”) show an exquisite
feeling for nature; while nothing can be more tender and
pathetic than “Du bist zwar mein und bleibest mein” (“Thou’rt
Franck.
mine, yes, still thou art mine own”), on the death of
his son. Franck, who was burgomaster of Guben in
Lusatia, has been considered by some second only to Gerhardt.
If so, it is with a great distance between them. His approach to
the later pietists is closer than that of Gerhardt. His hymns
were published, under the title of Geistliche und weltliche Gedichte,
in 1674, some of them being founded on Ambrosian and other
Latin originals. Miss Winkworth gives them the praise of a
condensed and polished style and fervid and impassioned thought.
It was after his conversion to Roman Catholicism that
Scheffler.
Scheffler adopted the name of “Angelus Silesius,”
and published in 1657 his hymns, under a fantastic title, and with
a still more fantastic preface. Their keynote is divine love;
they are enthusiastic, intense, exuberant in their sweetness,
like those of St Bernard among medieval poets. An adaptation
of one of them, by Wesley, “Thee will I love, my Strength, my
Tower,” is familiar to English readers. Those for the first
Sunday after Epiphany, for Sexagesima Sunday and for Trinity
Sunday, in Lyra Germanica, are good examples of his excellences,
with few of his defects. His hymns are generally so free from
the expression, or even the indirect suggestion, of Roman
Catholic doctrine, that it has been supposed they were written
before his conversion, though published afterwards. The evangelical
churches of Germany found no difficulty in admitting
them to that prominent place in their services which they have
ever since retained.
Towards the end of the 17th century, a new religious school
arose, to which the name of “Pietists” was given, and of which
Philipp Jakob Spener was esteemed the founder.
He and his pupils and successors, August Hermann
Pietists.
Francke and Anastasius Freylinghausen, all wrote hymns.
Spener’s hymns are not remarkable, and Francke’s are not
numerous. Freylinghausen was their chief singer; his rhythm
is lively, his music florid; but, though his book attained extraordinary
popularity, he was surpassed in solid merit by other
less fertile writers of the same school. The “Auf hinauf zu
deiner Freude” (“Up, yes, upward to thy gladness”) of Schade
may recall to an English reader a hymn by Seagrave, and more
than one by Lyte; the “Malabarian hymn” (as it was called by
Jacobi) of Johann Schütz, “All glory to the Sovereign Good,”
has been popular in England as well as Germany; and one of
the most exquisite strains of pious resignation ever written is
“Whate’er my God ordains is right,” by Samuel Rodigast.
Joachim Neander, a schoolmaster at Düsseldorf, and a friend
of Spener and Schütz (who died before the full development of
the “Pietistic” school), was the first man of eminence
in the “Reformed” or Calvinistic Church who imitated
Neander.
Lutheran hymnody. This he did, while suffering persecution
from the elders of his own church for some other religious
practices, which he had also learnt from Spener’s example. As
a poet, he is sometimes deficient in art; but there is feeling,
warmth and sweetness in many of his “Bundeslieder” or
“Songs of the Covenant,” and they obtained general favour,
both in the Reformed and in Lutheran congregations. The
Summer Hymn (“O Thou true God alone”) and that on the
glory of God in creation (“Lo, heaven and earth and sea and air”)
are instances of his best style.
With the “Pietists” may be classed Benjamin Schmolke and
Dessler, representatives of the “Orthodox” division of Spener’s
school; Philipp Friedrich Hiller, their leading poet in
South Germany; Gottfried Arnold and Gerhard
Schmolke.
Tersteegen, who were practically independent of ecclesiastical
organization, though connected, one with the “Orthodox”
and the other with the “Reformed” churches; and Nikolaus
Ludwig, Graf von Zinzendorf. Schmolke, a pastor in Silesia,
called the Silesian Rist (1672-1737), was perhaps the most
voluminous of all German hymn-writers. He wrote 1188
religious poems and hymns, a large proportion of which do not
190
rise above mediocrity. His style, if less refined, is also less
subjective and more simple than that of most of his contemporaries.
Among his best and most attractive works, which
indeed, it would be difficult to praise too highly, are the
“Hosianna David’s Sohn,” for Palm Sunday—much resembling
a shorter hymn by Jeremy Taylor; and the Ascension, Whitsuntide
and Sabbath hymns—“Heavenward doth our journey
tend,” “Come deck our feast to-day,” and “Light of light,
Dessler.
Hiller.
enlighten me.” Dessler was a greater poet than
Schmolke. Few hymns, of the subjective kind, are
better than his “I will not let Thee go, Thou Help in time of
need,” “O Friend of souls, how well is me,” and “Now, the
pearly gates unfold.” Hiller (1699-1769), was a pastor
in Württemberg who, falling into ill-health during the
latter part of his ministry, published a Geistliche Liederhöstlein in a
didactic vein, with more taste than power, but (as Miss Winkworth
says) in a tone of “deep, thoughtful, practical piety.” They
were so well adapted to the wants of his people that to this day
Hiller’s Casket is prized, next to their Bibles, by the peasantry of
Württemberg; and the numerous emigrants from that part of
Germany to America and other foreign countries generally
Arnold.
take it with them wherever they go. Arnold, a
professor at Giessen, and afterwards a pastor in
Brandenburg, was a man of strong will, uncompromising
character and austere views of life, intolerant and controversial
towards those whose doctrine or practice he disapproved, and
more indifferent to separatism and sectarianism than the
“orthodox” generally thought right. His hymns, like those
of Augustus M. Toplady, whom in these respects he resembled,
unite with considerable strength more gentleness and breadth
of sympathy than might be expected from a man of such a
Tersteegen.
character. Tersteegen (1697-1769), who never formally
separated himself from the “Reformed” communion,
in which he was brought up, but whose sympathies
were with the Moravians and with Zinzendorf, was, of all the more
copious German hymn-writers after Luther, perhaps the most
remarkable man. Pietist, mystic and missionary, he was also a
great religious poet. His 111 hymns were published In 1731, in
a volume called Geistlicher Blumengärtlein inniger Seelen.
They are intensely individual, meditative and subjective.
Wesley’s adaptations of two—“Lo! God is here; let us adore,”
and “Thou hidden Love of God, whose source”—are well known.
Among those translated by Miss Winkworth, “O God, O Spirit,
Light of all that live,” and “Come, brethren, let us go,” are
specimens which exhibit favourably his manner and power.
Miss Cox speaks of him as “a gentle heaven-inspired soul,
whose hymns are the reflection of a heavenly, happy life, his mind
being full of a child-like simplicity”; and his own poem on
the child-character, which Miss Winkworth has appropriately
connected with Innocents’ day (“Dear Soul, couldst thou
become a child”)—one of his best compositions, exquisitely
conceived and expressed—shows that this was in truth the
ideal which he sought to realize. The hymns of Zinzendorf
Zinzendorf.
are often disfigured by excess in the application of the
language and imagery of human affections to divine
objects; and this blemish is also found in many
later Moravian hymns. But one hymn, at least, of Zinzendorf
may be mentioned with unqualified praise, as uniting the merits
of force, simplicity and brevity—“Jesu, geh voran” (“Jesus,
lead the way”), which is taught to most children of religious
parents in Germany. Wesley’s “Jesus, Thy blood and righteousness”
is a translation from Zinzendorf.
The transition from Tersteegen and Zinzendorf to Gellert
and Klopstock marks strongly the reaction against Pietism
which took place towards the middle of the 18th
century. The Geistlichen Oden und Lieder of Christian
Gellert.
F. Gellert were published in 1757, and are said to have been
received with an enthusiasm almost like that which “greeted
Luther’s hymns on their first appearance.” It is a proof of the
moderation both of the author and of his times that they were
largely used, not only by Protestant congregations, but in
those German Roman Catholic churches in which vernacular
services had been established through the influence of the
emperor Joseph II. They became the model which was followed
by most succeeding hymn-writers, and exceeded all others
in popularity till the close of the century, when a new wave of
thought was generated by the movement which produced the
French Revolution. Since that time they have been, perhaps,
too much depreciated. They are, indeed, cold and didactic, as
compared with Scheffler or Tersteegen; but there is nevertheless
in them a spirit of genuine practical piety; and, if not marked
by genius, they are pure in taste, and often terse, vigorous and
graceful.
Klopstock, the author of the Messiah, cannot be considered
great as a hymn-writer, though his “Sabbath Hymn” (of
Klopstock.
which there is a version in Hymns from the Land
of Luther) is simple and good. Generally his hymns
(ten of which are translated in Sheppard’s Foreign Sacred
Lyre) are artificial and much too elaborate.
Of the “romantic” school, which came in with the French
Revolution, the two leading writers are Friedrich Leopold von
Hardenberg, called “Novalis,” and Friedrich de la Motte
Fouqué, the celebrated author of Undine and Sintram—both
romance-writers, as well as poets. The genius of Novalis was
early lost to the world; he died in 1801, not thirty years old.
Some of his hymns are very beautiful; but even in such works
as “Though all to Thee were faithless,” and “If only He is
mine,” there is a feeling of insulation and of despondency as to
good in the actual world, which was perhaps inseparable from his
Fouqué.
ecclesiastical idealism. Fouqué survived till 1843.
In his hymns there is the same deep flow of feeling,
richness of imagery and charm of expression which distinguishes
his prose works. The two missionary hymns—“Thou, solemn
Ocean, rollest to the strand,” and “In our sails all soft and
sweetly”—and the exquisite composition which finds its motive
in the gospel narrative of blind Bartimeus, “Was du vor tausend
Jahren” (finely translated both by Miss Winkworth and by Miss
Cox), are among the best examples.
The later German hymn-writers of the 19th century belong,
generally, to the revived “Pietistic” school. Some of the best,
Johann Baptist von Albertini, Friedrich Adolf
Krummacher, and especially Karl Johann Philipp Spitta
Spitta.
(1801-1859) have produced works not unworthy of the fame of
their nation. Mr Massie, the able translator of Spitta’s Psalter
und Harfe (Leipzig, 1833), speaks of it as having “obtained for
him in Germany a popularity only second to that of Paul Gerhardt.”
In Spitta’s poems (for such they generally are, rather
than hymns) the subjective and meditative tone is tempered,
not ungracefully, with a didactic element; and they are not
disfigured by exaggerated sentiment, or by a too florid and
rhetorical style.
6. British Hymnody.—After the Reformation, the development
of hymnody was retarded, in both parts of Great Britain,
by the example and influence of Geneva. Archbishop Cranmer
appears at one time to have been disposed to follow Luther’s
course, and to present to the people, in an English dress, some at
least of the hymns of the ancient church. In a letter to King
Henry VIII. (October 7, 1544), among some new “processions”
which he had himself translated, into English, he mentions the
Easter hymn, “Salve, festa dies, toto memorabilis aevo”
(“Hail, glad day, to be joyfully kept through all generations”),
of Fortunatus. In the “Primer” of 1535 (by Marshall) and the
one of 1539 (by Bishop Hilsey of Rochester, published by order
of the vicar-general Cromwell) there had been several rude
English hymns, none of them taken from ancient sources. King
Henry’s “Primer” of 1545 (commanded by his injunction of the
6th of May 1545 to be used throughout his dominions) was formed
on the model of the daily offices of the Breviary; and it contains
English metrical translations from some of the best-known
Ambrosian and other early hymns. But in the succeeding reign
different views prevailed. A new direction had been given to the
taste of the “Reformed” congregations in France and Switzerland
by the French metrical translation of the Old Testament Psalms,
which appeared about 1540. This was the joint work of Clement
191
Marot, valet or groom of the chamber to Francis I., and Theodore
Beza, then a mere youth, fresh from his studies at Orleans.
Marot’s psalms were dedicated to the French king and the
ladies of France, and, being set to popular airs, became fashionable.
They were sung by Francis himself, the queen,
the princesses and the courtiers, upon all sorts of secular
Marot’s Psalms.
occasions, and also, more seriously and religiously, by
the citizens and the common people. They were soon perceived
to be a power on the side of the Reformation. Calvin, who
had settled at Geneva in the year of Marot’s return to Paris,
was then organizing his ecclesiastical system. He rejected the
hymnody of the breviaries and missals, and fell back upon the
idea, anciently held by Paul of Samosata, and condemned by the
fourth council of Toledo, that whatever was sung in churches
ought to be taken out of the Scriptures. Marot’s Psalter, appearing
thus opportunely, was introduced into his new system of
worship, and appended to his catechism. On the other hand,
it was interdicted by the Roman Catholic priesthood. Thus it
became a badge to the one party of the “reformed” profession,
and to the other of heresy.
The example thus set produced in England the translation
commonly known as the “Old Version” of the Psalms. It was
begun by Thomas Sternhold, whose position in the
household of Henry VIII., and afterwards of Edward
Sternhold and Hopkins.
VI., was similar to that of Marot with Francis I., and
whose services to the former of those kings were rewarded
by a substantial legacy under his will. Sternhold published
versions of nineteen Psalms, with a dedication to King
Edward, and died soon afterwards. A second edition appeared
in 1551, with eighteen more Psalms added, of Sternhold’s translating,
and seven others by John Hopkins, a Suffolk clergyman.
The work was continued during Queen Mary’s reign by British
refugees at Geneva, the chief of whom were William Whittingham,
afterwards dean of Durham, who succeeded John Knox as
minister of the English congregation there, and William Kethe
or Keith, said by Strype to have been a Scotsman. They
published at Geneva in 1556 a service-book, containing fifty-one
English metrical psalms, which number was increased, in later
editions, to eighty-seven. On the accession of Queen Elizabeth,
this Genevan Psalmody was at once brought into use in England—first
(according to a letter of Bishop Jewell to Peter Martyr,
dated 5th March 1560) in one London church, from which it
quickly spread to others both in London and in other cities.
Jewell describes the effect produced by large congregations, of
as many as 6000 persons, young and old, women and children,
singing it after the sermons at St Paul’s Cross—adding, “Id
sacrificos et diabolum aegre habet; vident enim sacras conciones
hoc pacto profundius descendere in hominum animos.” The
first edition of the completed “Old Version” (containing forty
Psalms by Sternhold, sixty-seven by Hopkins, fifteen by Whittingham,
six by Kethe and the rest by Thomas Norton the
dramatist, Robert Wisdom, John Marckant and Thomas Churchyard)
appeared in 1562.
In the meantime, the Books of Common Prayer, of 1549, 1552
and 1559, had been successively established as law by the acts of
uniformity of Edward VI. and Queen Elizabeth. In these no
provision was made for the use of any metrical psalm or hymn on
any occasion whatever, except at the consecration of bishops and
the ordination of priests, in which offices (first added in 1552) an
English version of “Veni Creator” (the longer of the two now in use)
was appointed to be “said or sung.” The canticles, “Te Deum,”
“Benedicite,” the Nicene and Athanasian Creeds, the “Gloria in
Excelsis,” and some other parts of the communion and other special
offices were also directed to be “said or sung”; and, by general
rubrics, the chanting of the whole service was allowed.
The silence, however, of the rubrics in these books as to any other
singing was not meant to exclude the use of psalms not expressly
appointed, when they could be used without interfering with the
prescribed order of any service. It was expressly provided by
King Edward’s first act of uniformity (by later acts made applicable
to the later books) that it should be lawful “for all men, as well in
churches, chapels, oratories or other places, to use openly any
psalms or prayers taken out of the Bible, at any due time, not letting
or omitting thereby the service, or any part thereof, mentioned in
the book.” And Queen Elizabeth, by one of the injunctions issued
in the first year of her reign, declared her desire that the provision
made, “in divers collegiate and also some parish churches, for
singing in the church, so as to promote the laudable service of music,”
should continue. After allowing the use of “a modest and distinct
song in all parts of the common prayers of the church, so that the
same may be as plainly understanded as if it were read without
singing,” the injunction proceeded thus—“And yet, nevertheless,
for the comforting of such that delight in music, it may be permitted
that in the beginning or in the end of the Common Prayer, either at
morning or evening, there may be sung an hymn, or such like song
to the praise of Almighty God, in the best sort of melody and music
that may be conveniently devised, having respect that the sentence”
(i.e. sense) “of hymn may be understanded and perceived.”
The “Old Version,” when published (by John Daye, for the
Stationers’ Company, “cum gratia et privilegio Regiae Majestatis”),
bore upon the face of it that it was “newly set forth, and allowed
to be sung of the people in churches, before and after morning and
evening prayer, as also before and after the sermon.” The question
of its authority has been at different times much debated, chiefly by
Peter Heylyn and Thomas Warton on one side (both of whom disliked
and disparaged it), and by William Beveridge, bishop of St Asaph,
and the Rev. H. J. Todd on the other. Heylyn says, it was “permitted
rather than allowed,” which seems to be a distinction without
much difference. “Allowance,” which is all that the book claimed
for itself, is authorization by way of permission, not of commandment.
Its publication in that form could hardly have been licensed,
nor could it have passed into use as it did without question, throughout
the churches of England, unless it had been “allowed” by some
authority then esteemed to be sufficient. Whether that authority
was royal or ecclesiastical does not appear, nor (considering the
proviso in King Edward’s act of uniformity, and Queen Elizabeth’s
injunctions) is it very important. No inference can justly be drawn
from the inability of inquirers, in Heylyn’s time or since, to discover
any public record bearing upon this subject, many public documents
of that period having been lost.
In this book, as published in 1562, and for many years afterwards,
there were (besides the versified Psalms) eleven metrical
versions of the “Te Deum,” canticles, Lord’s Prayer (the best
of which is that of the “Benedicite”); and also “Da pacem,
Domine,” a hymn suitable to the times, rendered into English
from Luther; two original hymns of praise, to be sung before
morning and evening prayer; two penitential hymns (one of
them the “humble lamentation of a sinner”); and a hymn
of faith, beginning, “Lord, in Thee is all my trust.” In these
respects, and also in the tunes which accompanied the words
(stated by Dr Charles Burney, in his History of Music, to be
German, and not French), there was a departure from the
Genevan platform. Some of these hymns, and some of the psalms
also (e.g. those by Robert Wisdom, being alternative versions),
were omitted at a later period; and many alterations and
supposed amendments were from time to time made by unknown
hands in the psalms which remained, so that the text, as
now printed, is in many places different from that of 1562.
In Scotland, the General Assembly of the kirk caused to be
printed at Edinburgh in 1564, and enjoined the use of, a book
entitled
Scotch Psalms.
The Form of Prayers and Ministry of the
Sacraments used in the English Church at Geneva,
approved and received by the Church of Scotland;
whereto, besides that was in the former books, are also added sundry
other prayers, with the whole Psalms of David in English metre.
This contained, from the “Old Version,” translations of forty
Psalms by Sternhold, fifteen by Whittingham, twenty-six by
Kethe and thirty-five by Hopkins. Of the remainder two were
by John Pulleyn (one of the Genevan refugees, who became
archdeacon of Colchester); six by Robert Pont, Knox’s son-in-law,
who was a minister of the kirk, and also a lord of session;
and fourteen signed with the initials I. C., supposed to be John
Craig; one was anonymous, eight were attributed to N., two to
M. and one to T. N. respectively.
So matters continued in both churches until the Civil War.
During the interval, King James I. conceived the project of
himself making a new version of the Psalms, and appears to have
translated thirty-one of them—the correction of which, together
with the translation of the rest, he entrusted to Sir William
Alexander, afterwards earl of Stirling. Sir William having
completed his task, King Charles I. had it examined and approved
by several archbishops and bishops of England, Scotland and
Ireland, and caused it to be printed in 1631 at the Oxford University
Press, as the work of King James; and, by an order
192
under the royal sign manual, recommended its use in all churches
of his dominions. In 1634 he enjoined the Privy Council of
Scotland not to suffer any other psalms, “of any edition whatever,”
to be printed in or imported into that kingdom. In 1636
it was republished, and was attached to the famous Scottish
service-book, with which the troubles began in 1637. It need
hardly be added that the king did not succeed in bringing this
Psalter into use in either kingdom.
When the Long Parliament undertook, in 1642, the task of
altering the liturgy, its attention was at the same time directed
to psalmody. It had to judge between two rival translations
of the Psalms—one by Francis Rouse, a member of the House
of Commons, afterwards one of Cromwell’s councillors and
finally provost of Eton; the other by William Barton, a clergyman
of Leicester. The House of Lords favoured Barton, the
House of Commons Rouse, who had made much use of the labours
of Sir William Alexander. Both versions were printed by order
of parliament, and were referred for consideration to the Westminster
Assembly. They decided in favour of Rouse. His
version, as finally amended, was published in 1646, under an
order of the House of Commons dated 14th November 1645.
In the following year it was recommended by the parliament
to the General Assembly at Edinburgh, who appointed a committee,
with large powers, to prepare a revised Psalter, recommending
to their consideration not only Rouse’s book but that
of 1564, and two other versions (by Zachary Boyd and Sir
William Mure of Rowallan), then lately executed in Scotland.
The result of the labours of this committee was the “Paraphrase”
of the Psalms, which, in 1649-1650, by the concurrent authority
of the General Assembly and the committee of estates, was
ordered to be exclusively used throughout the church of Scotland.
Some use was made in the preparation of this book of the versions
to which the attention of the revisers had been directed, and
also of Barton’s; but its basis was that of Rouse. It was
received in Scotland with great favour, which it has ever since
retained; and it is fairly entitled to the praise of striking a
tolerable medium between the rude homeliness of the “Old,”
and the artificial modernism of the “New” English versions—perhaps
as great a success as was possible for such an undertaking.
Sir Walter Scott is said to have dissuaded any attempt to alter
it, and to have pronounced it, “with all its acknowledged
occasional harshness, so beautiful, that any alterations must
eventually prove only so many blemishes.” No further step
towards any authorized hymnody was taken by the kirk of
Scotland till the following century.
In England, two changes bearing on church hymnody were
made upon the revision of the prayer-book after the Restoration,
in 1661-1662. One was the addition, in the offices for consecrating
bishops and ordaining priests, of the shorter version
of “Veni Creator” (“Come, Holy Ghost, our souls inspire”),
as an alternative form. The other, and more important, was
the insertion of the rubric after the third collect, at morning
and evening prayer: “In quires and places where they sing,
here followeth the anthem.” By this rubric synodical and
parliamentary authority was given for the interruption, at that
point, of the prescribed order of the service by singing an anthem,
the choice of which was left to the discretion of the minister.
Those actually used, under this authority, were for some time
only unmetrical passages of scripture, set to music by Blow,
Purcell and other composers, of the same kind with the
anthems still generally sung in cathedral and collegiate
churches. But the word “anthem” had no technical signification
which could be an obstacle to the use under this rubric of
metrical hymns.
The “New Version” of the Psalms, by Dr Nicholas Brady and
the poet-laureate Nahum Tate (both Irishmen), appeared in 1696,
under the sanction of an order in council of William
III., “allowing and permitting” its use “in all such
Tate and Brady.
churches, chapels and congregations as should think fit
to receive it.” Dr Compton, bishop of London, recommended it
to his diocese. No hymns were then appended to it; but the
authors added a “supplement” in 1703, which received an
exactly similar sanction from an order in council of Queen
Anne. In that supplement there were several new versions
of the canticles, and of the “Veni Creator”; a variation of the
old “humble lamentation of a sinner”; six hymns for Christmas,
Easter and Holy Communion (all versions or paraphrases of
scripture), which are still usually printed at the end of the
prayer-books containing the new version; and a hymn “on
the divine use of music”—all accompanied by tunes. The
authors also reprinted, with very good taste, the excellent
version of the “Benedicite” which appeared in the book of
1562. Of the hymns in this “supplement,” one (“While
shepherds watched their flocks by night”) greatly exceeded
the rest in merit. It has been ascribed to Tate, but it has a
character of simplicity unlike the rest of his works.
The relative merits of the “Old” and “New” versions
have been very variously estimated. Competent judges have
given the old the praise, which certainly cannot be
accorded to the new, of fidelity to the Hebrew. In
Old and new versions compared.
both, it must be admitted, that those parts which
have poetical merit are few and far between; but
a reverent taste is likely to be more offended by the frequent
sacrifice, in the new, of depth of tone and accuracy of sense
to a fluent commonplace correctness of versification and
diction, than by any excessive homeliness in the old. In both,
however, some psalms, or portions of psalms, are well
enough rendered to entitle them to a permanent place in
the hymn-books—especially the 8th, and parts of the 18th
Psalm, by Sternhold; the 57th, 84th and 100th, by Hopkins;
the 23rd, 34th and 36th, and part of the 148th, by Tate and
Brady.
The judgment which a fastidious critic might be disposed
to pass upon both these books may perhaps be considerably
mitigated by comparing them with the works of other
labourers in the same field, of whom Holland, in his interesting
volumes entitled Psalmists of Great Britain, enumerates above
150. Some of them have been real poets—the celebrated earl
of Surrey, Sir Philip Sidney and his sister the countess of
Pembroke, George Sandys, George Wither, John Milton and
John Keble. In their versions, as might be expected, there
are occasional gleams of power and beauty, exceeding anything
to be found in Sternhold and Hopkins, or Tate and Brady;
but even in the best these are rare, and chiefly occur where the
strict idea of translation has been most widely departed from.
In all of them, as a rule, the life and spirit, which in prose versions
of the psalms are so wonderfully preserved, have disappeared.
The conclusion practically suggested by so many failures is
that the difficulties of metrical translation, always great,
are in this case insuperable; and that, while the psalms like
other parts of scripture are abundantly suggestive of motive
and material for hymnographers, it is by assimilation and
adaptation, and not by any attempt to transform their exact
sense into modern poetry, that they may be best used for this
purpose.
The order in council of 1703 is the latest act of any public authority
by which an express sanction has been given to the use of psalms
or hymns in the Church of England. At the end, indeed, of many
Prayer-books, till about the middle of the 19th century, there were
commonly found, besides some of the hymns sanctioned by that
order in council, or of those contained in the book of 1562, a sacramental
and a Christmas hymn by Doddridge; a Christmas hymn
(varied by Martin Madan) from Charles Wesley; an Easter hymn
of the 18th century, beginning “Jesus Christ has risen to-day”;
and abridgments Bishop Ken’s Morning and Evening Hymns.
These additions first began to be made in or about 1791, in London
editions of the Prayer-book and Psalter, at the mere will and
pleasure (so far as appears) of the printers. They had no sort of
authority.
In the state of authority, opinion and practice disclosed by
the preceding narrative may be found the true explanation of
the fact that, in the country of Chaucer, Spenser,
Shakespeare and Milton, and notwithstanding the
English congregational hymnody.
example of Germany, no native congregational
hymnody worthy of the name arose till after the commencement
of the 18th century. Yet there was no want of
193
appreciation of the power and value of congregational church
music. Milton could write, before 1645:—
“There let the pealing organ blow
To the full-voiced quire below
In service high, and anthems clear,
As may with sweetness through mine ear
Dissolve me into ecstasies,
And bring all Heaven before mine eyes.”
|
Thomas Mace, in his Music’s Monument (1676), thus described
the effect of psalm-singing before sermons by the congregation
in York Minster on Sundays, during the siege of 1644: “When
that vast concording unity of the whole congregational chorus
came thundering in, even so as it made the very ground shake
under us, oh, the unutterable ravishing soul’s delight! in the
which I was so transported and wrapt up in high contemplations
that there was no room left in my whole man, body, soul and
spirit, for anything below divine and heavenly raptures; nor
could there possibly be anything to which that very singing
might be truly compared, except the right apprehension or
conceiving of that glorious and miraculous quire, recorded in
the scriptures at the dedication of the temple.” Nor was there
any want of men well qualified, and by the turn of their minds
predisposed, to shine in this branch of literature. Some (like
Sandys, Boyd and Barton) devoted themselves altogether to
paraphrases of other scriptures as well as the psalms. Others
(like George Herbert, and Francis and John Quarles) moralized,
meditated, soliloquized and allegorized in verse. Without
reckoning these, there were a few, even before the Restoration,
who came very near to the ideal of hymnody.
First in time is the Scottish poet John Wedderburn, who
translated several of Luther’s hymns, and in his Compendious
Book of Godly and Spiritual Songs added others of his
own (or his brothers’) composition. Some of these
Wedderburn.
poems, published before 1560, are of uncommon
excellence, uniting ease and melody of rhythm, and structural
skill, with grace of expression, and simplicity, warmth and reality
of religious feeling. Those entitled “Give me thy heart,”
“Go, heart,” and “Leave me not,” which will be found in a
collection of 1860 called Sacred Songs of Scotland, require little,
beyond the change of some archaisms of language, to adapt them
for church or domestic use at the present day.
Next come the two hymns of “The new Jerusalem,” by an
English Roman Catholic priest signing himself F. B. P. (supposed
to be “Francis Baker, Presbyter”), and by another
Scottish poet, David Dickson, of which the history
Dickson.
is given by Dr Bonar in his edition of Dickson’s work. This
(Dickson’s), which begins “O mother dear, Jerusalem,” and
has long been popular in Scotland, is a variation and amplification
by the addition of a large number of new stanzas of the English
original, beginning “Jerusalem, my happy home,” written in
Queen Elizabeth’s time, and printed (as appears by a copy in
the British Museum) about 1616, when Dickson was still young.
Both have an easy natural flow, and a simple happy rendering of
the beautiful scriptural imagery upon the subject, with a spirit
of primitive devotion uncorrupted by medieval peculiarities.
The English hymn of which some stanzas are now often sung
in churches is the true parent of the several shorter forms,—all
of more than common merit,—which, in modern hymn-books,
begin with the same first line, but afterwards deviate from
the original. Kindred to these is the very fine and faithful
translation, by Dickson’s contemporary Drummond of Hawthornden
of the ancient “Urbs beata Hierusalem” (“Jerusalem,
that place divine”). Other ancient hymns (two of Thomas
Aquinas, and the “Dies Irae”) were also well translated, in
1646, by Richard Crashaw, after he had become a Roman
Catholic and had been deprived by the parliament of his fellowship
at Cambridge.
Conspicuous among the sacred poets of the first two Stuart
reigns in England was George Wither. His Hymnes and Songs
of the Church appeared in 1622-1623, under a patent
of King James I., by which they were declared “worthy
Wither.
and profitable to be inserted, in convenient manner and due
place, into every English Psalm-book to metre.” His Hallelujah
(in which some of the former Hymnes and Songs were repeated)
followed in 1641. Some of the Hymnes and Songs were set to
music by Orlando Gibbons, and those in both books were written
to be sung, though there is no evidence that the author contemplated
the use of any of them in churches. They included
hymns for every day in the week (founded, as those contributed
nearly a century afterwards by Charles Coffin to the Parisian
Breviary also were, upon the successive works of the days of
creation); hymns for all the church seasons and festivals, including
saints’ days; hymns for various public occasions; and hymns
of prayer, meditation and instruction, for all sorts and conditions
of men, under a great variety of circumstances—being at once
a “Christian Year” and a manual of practical piety. Many
of them rise to a very high point of excellence,—particularly
the “general invitation to praise God” (“Come, O come, in
pious lays”), with which Hallelujah opens; the thanksgivings
for peace and for victory, the Coronation Hymn, a Christmas,
an Epiphany, and an Easter Hymn, and one for St Bartholomew’s
day (Hymns 1, 74, 75, and 84 in part i., and 26, 29, 36 and 54
in part ii. of Hallelujah).
John Cosin, afterwards bishop of Durham, published in 1627
a volume of “Private Devotions,” for the canonical hours and
Cosin.
other occasions. In this there are seven or eight
hymns of considerable merit,—among them a very good
version of the Ambrosian “Jam lucis orto sidere,” and the
shorter version of the “Veni Creator,” which was introduced
after the Restoration into the consecration and ordination
services of the Church of England.
The hymns of Milton (on the Nativity, Passion, Circumcision
Milton.
and “at a Solemn Music”), written about 1629, in
his early manhood, were probably not intended for
singing; but they are odes full of characteristic beauty and
power.
During the Commonwealth, in 1654, Jeremy Taylor published
at the end of his Golden Grove, twenty-one hymns, described
by himself as “celebrating the mysteries and chief
Jeremy Taylor.
festivals of the year, according to the manner of the
ancient church, fitted to the fancy and devotion of
the younger and pious persons, apt for memory, and to be joined,
to their other prayers.” Of these, his accomplished editor,
Bishop Heber, justly says:—
“They are in themselves, and on their own account, very interesting
compositions. Their metre, indeed, which is that species of
spurious Pindaric which was fashionable with his contemporaries,
is an obstacle, and must always have been one, to their introduction
into public or private psalmody; and the mixture of that alloy of
conceits and quibbles which was an equally frequent and still greater
defilement of some of the finest poetry of the 17th century will
materially diminish their effect as devotional or descriptive odes.
Yet, with all these faults, they are powerful, affecting, and often
harmonious; there are many passages of which Cowley need not
have been ashamed, and some which remind us, not disadvantageously,
of the corresponding productions of Milton.”
He mentions particularly the advent hymn (“Lord, come
away”), part of the hymn “On heaven,” and (as “more regular
in metre, and in words more applicable to public devotion”)
the “Prayer for Charity” (“Full of mercy, full of love”).
The epoch of the Restoration produced in 1664 Samuel
Crossman’s Young Man’s Calling, with a few “Divine Meditations”
in verse attached to it; in 1668 John Austin’s
Restoration period.
Devotions in the ancient way of offices, with psalms,
hymns and prayers for every day in the week and every
holyday in the year; and in 1681 Richard Baxter’s
Poetical Fragments. In these books there are altogether seven
or eight hymns, the whole or parts of which are extremely good:
Crossman’s “New Jerusalem” (“Sweet place, sweet place
alone”), one of the best of that class, and “My life’s a shade,
my days”; Austin’s “Hark, my soul, how everything,” “Fain
would my thoughts fly up to Thee,” “Lord, now the time
returns,” “Wake all my hopes, lift up your eyes”; and Baxter’s
“My whole, though broken heart, O Lord,” and “Ye holy
angels bright.” Austin’s Offices (he was a Roman Catholic)
seem to have attracted much attention. Theophilus Dorrington,
in 1686, published variations of them under the title of Reformed
194
Devotions; George Hickes, the non-juror, wrote one of his
numerous recommendatory prefaces to S. Hopton’s edition;
and the Wesleys, in their earliest hymn-book, adopted hymns
from them, with little alteration. These writers were followed
by John Mason in 1683, and Thomas Shepherd in 1692,—the
former, a country clergyman, much esteemed by Baxter and other
Nonconformists; the latter himself a Nonconformist, who
finally emigrated to America. Between these two men there was
a close alliance, Shepherd’s Penitential Cries being published
as an addition to the Spiritual Songs of Mason. Their hymns
came into early use in several Nonconformist congregations;
but, with the exception of one by Mason (“There is a stream
which issues forth”), they are not suitable for public singing.
In those of Mason there is often a very fine vein of poetry;
and later authors have, by extracts or centoes from different
parts of his works (where they were not disfigured by his general
quaintness), constructed several hymns of more than average
excellence.
Three other eminent names of the 17th century remain to be
mentioned, John Dryden, Bishop Ken and Bishop Simon
Patrick; with which may be associated that of Addison, though
he wrote in the 18th century.
Dryden’s translation of “Veni Creator” a cold and laboured
performance, is to be met with in many hymn-books. Abridgments
of Ken’s morning and evening hymns are in all.
These, with the midnight hymn, which is not inferior
to them, first appeared In 1697, appended to the third
Dryden, Ken.
edition of the author’s Manual of Prayers for Winchester Scholars.
Between these and a large number of other hymns (on the
attributes of God, and for the festivals of the church) published
by Bishop Ken after 1703 the contrast is remarkable. The
universal acceptance of the morning and evening hymns is due
to their transparent simplicity, warm but not overstrained
devotion, and extremely popular style. Those afterwards
published have no such qualities. They are mystical, florid, stiff,
Patrick
Addison.
didactic and seldom poetical, and deserve the neglect
into which they have fallen. Bishop Patrick’s hymns
were chiefly translations from the Latin, most of them from
Prudentius. The best is a version of “Alleluia dulce carmen.”
Of the five attributed to Addison, not more than three
are adapted to public singing; one (“The spacious
firmament on high”) is a very perfect and finished composition,
taking rank among the best hymns in the English language.3
From the preface to Simon Browne’s hymns, published in
1720, we learn that down to the time of Dr Watts the only
hymns known to be “in common use, either in private families
or in Christian assemblies,” were those of Barton, Mason and
Shepherd, together with “an attempt to turn some of George
Herbert’s poems into common metre,” and a few sacramental
hymns by authors now forgotten, named Joseph Boyse (1660-1728)
and Joseph Stennett. Of the 1410 authors of original
British hymns enumerated in Daniel Sedgwick’s catalogue,
published in 1863, 1213 are of later date than 1707; and, if any
correct enumeration could be made of the total number of hymns
of all kinds published in Great Britain before and after that date,
the proportion subsequent to 1707 would be very much larger.
The English Independents, as represented by Dr Isaac Watts,
have a just claim to be considered the real founders of modern
English hymnody. Watts was the first to understand the nature
of the want, and, by the publication of his Hymns in 1707-1709,
and Psalms (not translations, but hymns founded on psalms)
in 1709, he led the way in providing for it. His immediate
followers were Simon Browne and Philip Doddridge. Later in
the 18th century, Joseph Hart, Thomas Gibbons, Miss Anne
Steele, Samuel Medley, Samuel Stennett, John Ryland, Benjamin
Beddome and Joseph Swain succeeded to them.
Among these writers, most of whom produced some hymns of
merit, and several are extremely voluminous, Isaac Watts and
Philip Doddridge are pre-eminent. It has been the
fashion with some to disparage Watts, as if he had
Watts.
never risen above the level of his Hymns for Little Children. No
doubt his taste is often faulty, and his style very unequal, but,
looking to the good, and disregarding the large quantity of inferior
matter, it is probable that more hymns which approach to a very
high standard of excellence, and are at the same time suitable
for congregational use, may be found in his works than in those
of any other English writer. Such are “When I survey the
wondrous cross,” “Jesus shall reign where’er the sun” (and also
another adaptation of the same 72nd Psalm), “Before Jehovah’s
awful throne” (first line of which, however, is not his, but
Wesley’s), “Joy to the world, the Lord is come,” “My soul,
repeat His praise,” “Why do we mourn departing friends,”
“There is a land of pure delight,” “Our God, our help in ages
past,” “Up to the hills I lift mine eyes,” and many more. It
is true that in some of these cases dross is found in the original
poems mixed with gold; but the process of separation, by selection
without change, is not difficult. As long as pure nervous
English, unaffected fervour, strong simplicity and liquid yet
manly sweetness are admitted to be characteristics of a good
hymn, works such as these must command admiration.
Doddridge is, generally, much more laboured and artificial;
but his place also as a hymn-writer ought to be determined, not
by his failures, but by his successes, of which the
number is not inconsiderable. In his better works
Doddridge.
he is distinguished by a graceful and pointed, sometimes even
a noble style. His “Hark, the glad sound, the Saviour comes”
(which is, indeed, his masterpiece), is as sweet, vigorous and
perfect a composition as can anywhere be found. Two other
hymns, “How gentle God’s commands,” and that which, in
a form slightly varied, became the “O God of Bethel, by whose
hand,” of the Scottish “Paraphrases,” well represent his softer
manner.
Of the other followers in the school of Watts, Miss Anne Steele
(1717-1778) is the most popular and perhaps the best. Her
hymn beginning “Far from these narrow scenes of night”
deserves high praise, even by the side of other good performances
on the same subject.
The influence of Watts was felt in Scotland, and among the
first whom it reached there was Ralph Erskine. This seems
to have been after the publication of Erskine’s Gospel Sonnets,
which appeared in 1732, five years before he joined his brother
Ebenezer in the Secession Church. The Gospel Sonnets became,
as some have said, a “people’s classic”; but there is in them
very little which belongs to the category of hymnody. More
than nineteen-twentieths of this very curious book are occupied
with what are, in fact, theological treatises and catechisms,
mystical meditations on Christ as a bridegroom or husband,
and spiritual enigmas, paradoxes, and antithetical conceits,
versified, it is true, but of a quality of which such lines as—
“Faith’s certain by fiducial arts,
Sense by its evidential facts,”
|
may be taken as a sample. The grains of poetry scattered
through this large mass of Calvinistic divinity are very few;
yet in one short passage of seven stanzas (“O send me down a
draught of love”), the fire burns with a brightness so remarkable
as to justify a strong feeling of regret that the gift which this
writer evidently had in him was not more often cultivated.
Another passage, not so well sustained, but of considerable
195
beauty (part of the last piece under the title “The believer’s
soliloquy”), became afterwards, in the hands of John Berridge,
the foundation of a very striking hymn (“O happy saints, who
walk in light”).
After his secession, Ralph Erskine published two paraphrases
of the “Song of Solomon,” and a number of other “Scripture
songs,” paraphrased, in like manner, from the Old and New
Testaments. In these the influence of Watts became very
apparent, not only by a change in the writer’s general style, but
by the direct appropriation of no small quantity of matter from
Dr Watts’s hymns, with variations which were not always
improvements. His paraphrases of I Cor. i. 24; Gal. vi. 14; Heb.
vi. 17-19; Rev. v. 11, 12, vii. 10-17, and xii. 7-12 are little else
than Watts transformed. One of these (Rev. vii. 10-17) is
interesting as a variation and improvement, intermediate
between the original and the form which it ultimately assumed
as the 66th “Paraphrase” of the Church of Scotland, of Watts’s
“What happy men or angels these,” and “These glorious
minds, how bright they shine.” No one can compare it with
its ultimate product, “How bright these glorious spirits shine,”
without perceiving that William Cameron followed Erskine, and
only added finish and grace to his work,—both excelling Watts,
in this instance, in simplicity as well as in conciseness.
Of the contributions to the authorized “Paraphrases” (with
the settlement of which committees of the General Assembly of
the Church of Scotland were occupied from 1745, or
earlier, till 1781), the most noteworthy, besides the
Scottish paraphrases.
two already mentioned, were those of John Morrison
and those claimed for Michael Bruce. The obligations of
these “Paraphrases” to English hymnody, already traced in
some instances (to which may be added the adoption from
Addison of three out of the five “hymns” appended to them),
are perceptible in the vividness and force with which these
writers, while adhering with a severe simplicity to the sense of
the passages of Scripture which they undertook to render,
fulfilled the conception of a good original hymn. Morrison’s
“The race that long in darkness pined” and “Come, let us to
the Lord our God,” and Bruce’s “Where high the heavenly
temple stands” (if this was really his), are well entitled to that
praise. The advocates of Bruce in the controversy, not yet
closed, as to the poems said to have been entrusted by him to
John Logan, and published by Logan in his own name, also
claim for him the credit of having varied the paraphrase “Behold,
the mountain of the Lord,” from its original form, as printed
by the committee of the General Assembly in 1745, by some
excellent touches.
Attention must now be directed to the hymns produced
by the “Methodist” movement, which began about 1738,
and which afterwards became divided, between those
esteemed Arminian, under John Wesley, those who
Methodist hymns.
adhered to the Moravians, when the original alliance
between that body and the founders of Methodism was dissolved,
and the Calvinists, of whom Whitfield was the leader, and Selina,
countess of Huntingdon, the patroness. Each of these sections
had its own hymn-writers, some of whom did, and others did not,
secede from the Church of England. The Wesleyans had Charles
Wesley, Robert Seagrave and Thomas Olivers; the Moravians,
John Cennick, with whom, perhaps, may be classed John Byrom,
who imbibed the mystical ideas of some of the German schools;
the Calvinists, Augustus Montague Toplady, John Berridge,
William Williams, Martin Madan, Thomas Haweis, Rowland Hill,
John Newton and William Cowper.
Among all these writers, the palm undoubtedly belongs to
Charles Wesley. In the first volume of hymns published by the
two brothers are several good translations from the
German, believed to be by John Wesley, who, although
Charles Wesley.
he translated and adapted, is not supposed to have
written any original hymns; and the influence of German
hymnody, particularly of the works of Paul Gerhardt, Scheffler,
Tersteegen and Zinzendorf, may be traced in a large proportion of
Charles Wesley’s works. He is more subjective and meditative
than Watts and his school; there is a didactic turn, even in his
most objective pieces, as, for example, in his Christmas and
Easter hymns; most of his works are supplicatory, and his faults
are connected with the same habit of mind. He is apt to repeat
the same thoughts, and to lose force by redundancy—he runs
sometimes even to a tedious length; his hymns are not always
symmetrically constructed, or well balanced and finished off.
But he has great truth, depth and variety of feeling; his diction
is manly and always to the point; never florid, though sometimes
passionate and not free from exaggeration; often vivid and
picturesque. Of his spirited style there are few better examples
than “O for a thousand tongues to sing,” “Blow ye the trumpet,
blow,” “Rejoice, the Lord is King” and “Come, let us join our
friends above”; of his more tender vein, “Happy soul, thy days
are ended”; and of his fervid contemplative style (without
going beyond hymns fit for general use), “O Thou who earnest
from above,” “Forth in Thy name, O Lord, I go” and “Eternal
beam of light divine.” With those whose taste is for hymns in
which warm religious feelings are warmly and demonstratively expressed,
“Jesus, lover of my soul,” is as popular as any of these.
Of the other Wesleyan hymn-writers, Olivers, originally a
Olivers.
Welsh shoemaker and afterwards a preacher, is the most remarkable.
He is the author of only two works, both
odes, in a stately metre, and from their length unfit for
congregational singing, but one of them, “The God of Abraham
praise,” an ode of singular power and beauty.
The Moravian Methodists produced few hymns now available
for general use. The best are Cennick’s “Children of the heavenly
King” and Hammond’s “Awake and sing the song of
Moses and the Lamb,” the former of which (abridged),
Cennick, Hammond, Byrom.
and the latter as varied by Madan, are found in many
hymn-books, and are deservedly esteemed. John
Byrom, whose name we have thought it convenient to
connect with these, though he did not belong to the Moravian
community, was the author of a Christmas hymn (“Christians
awake, salute the happy morn”) which enjoys great popularity;
and also of a short subjective hymn, very fine both in feeling and
in expression, “My spirit longeth for Thee within my troubled
breast.”
The contributions of the Calvinistic Methodists to English
hymnody are of greater extent and value. Few writers of hymns
had higher gifts than Toplady, author of “Rock of
ages,” by some esteemed the finest in the English
Toplady.
language. He was a man of ardent temperament, enthusiastic
zeal, strong convictions and great energy of character. “He
had,” says one of his biographers, “the courage of a lion, but his
frame was brittle as glass.” Between him and John Wesley
there was a violent opposition of opinion, and much acrimonious
controversy; but the same fervour and zeal which made him
an intemperate theologian gave warmth, richness and spirituality
to his hymns. In some of them, particularly those which, like
“Deathless principle, arise,” are meditations after the German
manner, and not without direct obligation to German originals,
the setting is somewhat too artificial; but his art is never inconsistent
with a genuine flow of real feeling. Others (e.g.
“When languor and disease invade” and “Your harps, ye
trembling saints”) fail to sustain to the end the beauty with
which they began, and would have been better for abridgment.
But in all these, and in most of his other works, there is great
force and sweetness, both of thought and language, and an easy
and harmonious versification.
Berridge, William Williams (1717-1791) and Rowland Hill, all
men remarkable for eccentricity, activity and the devotion of
their lives to the special work of missionary preaching,
though not the authors of many good hymns, composed,
Berridge, Williams and R. Hill.
or adapted from earlier compositions, some of great
merit. One of Berridge, adapted from Erskine, has
been already mentioned; another, adapted from Watts, is
“Jesus, cast a look on me.” Williams, a Welshman, who wrote
“Guide me, O Thou great Jehovah,” was especially an apostle of
Calvinistic Methodism in his own country, and his hymns are
still much used in the principality. Rowland Hill wrote the
popular hymn beginning “Exalted high at God’s right hand.”
196
If, however, the number as well as the quality of good hymns
available for general use is to be regarded, the authors of the
Olney Hymns are entitled to be placed at the head of
all the writers of this Calvinistic school. The greater
Cowper and Newton.
number of the Olney Hymns are, no doubt, homely
and didactic; but to the best of them, and they are
no inconsiderable proportion, the tenderness of Cowper and the
manliness of John Newton (1725-1807) give the interest of
contrast, as well as that of sustained reality. If Newton carried
to some excess the sound principle laid down by him, that
“perspicuity, simplicity and ease should be chiefly attended to,
and the imagery and colouring of poetry, if admitted at all,
should be indulged very sparingly and with great judgment,”
if he is often dry and colloquial, he rises at other times into
“soul-animating strains,” such as “Glorious things of thee are
spoken, Zion, city of our God”; and sometimes (as in “Approach,
my soul, the mercy seat”) rivals Cowper himself in depth of
feeling. Cowper’s hymns in this book are, almost without
exception, worthy of his name. Among them are “Hark, my
soul, it is the Lord,” “There is a fountain filled with blood,”
“Far from the world, O Lord, I flee,” “God moves in a mysterious
way” and “Sometimes a light surprises.” Some,
perhaps, even of these, and others of equal excellence (such as
“O for a closer walk with God”), speak the language of a
special experience, which, in Cowper’s case, was only too real,
but which could not, without a degree of unreality not desirable
in exercises of public worship, be applied to themselves by all
ordinary Christians.
During the first quarter of the 19th century there were not
many indications of the tendency, which afterwards became
manifest, to enlarge the boundaries of British hymnody.
The Remains of Henry Kirke White, published by
19th-century hymns.
R. Grant.
Bowdler.
Southey in 1807, contained a series of hymns, some of
which are still in use; and a few of Bishop Heber’s hymns
and those of Sir Robert Grant, which, though offending rather
too much against John Newton’s canon, are well
known and popular, appeared between 1811 and 1816,
in the Christian Observer. In John Bowdler’s Remains, published
soon after his death in 1815, there are a few more of
the same, perhaps too scholarlike, character. But
the chief hymn-writers of that period were two clergymen of
the Established Church—one in Ireland, Thomas Kelly, and
the other in England, William Hurn—who both became Nonconformists,
and the Moravian poet, James Montgomery (1771-1854),
a native of Scotland.
Kelly was the son of an Irish judge, and in 1804 published
a small volume of ninety-six hymns, which grew in successive
editions till, in the last before his death in 1854, they
amounted to 765. There is, as might be expected,
Kelly.
in this great number a large preponderance of the didactic
and commonplace. But not a few very excellent hymns may
be gathered from them. Simple and natural, without the vivacity
and terseness of Watts or the severity of Newton, Kelly has
some points in common with both those writers, and he is less
subjective than most of the “Methodist” school. His hymns
beginning “Lo! He comes, let all adore Him,” and “Through
the day Thy love hath spared us,” have a rich, melodious movement;
and another, “We sing the praise of Him who died,”
is distinguished by a calm, subdued power, rising gradually from
a rather low to a very high key.
Hurn published in 1813 a volume of 370 hymns, which were
Hurn.
afterwards increased to 420. There is little in them which
deserves to be saved from oblivion; but one at least,
“There is a river deep and broad,” may bear comparison
with the best of those which have been produced upon
the same, and it is rather a favourite, theme.
The Psalms and Hymns of James Montgomery were published
in 1822 and 1825, though written earlier. More cultivated
Montgomery.
and artistic than Kelly, he is less simple and natural.
His “Hail to the Lord’s Anointed,” “Songs of praise
the angels sang” and “Mercy alone can meet my
case” are among his most successful efforts.
During this period, the collections of miscellaneous hymns
for congregational use, of which the example was set by the
Wesleys, Whitfield, Toplady and Lady Huntingdon,
had greatly multiplied; and with them the practice
Collections of hymns.
(for which, indeed, too many precedents existed in
the history of Latin and German hymnody) of every
collector altering the compositions of other men without scruple,
to suit his own doctrine or taste; with the effect, too generally,
of patching and disfiguring, spoiling and emasculating the
works so altered, substituting neutral tints for natural colouring,
and a dead for a living sense. In the Church of England the
use of these collections had become frequent in churches and
chapels, principally in cities and towns, where the sentiments
of the clergy approximated to those of the Nonconformists.
In rural parishes, when the clergy were not of the “Evangelical”
school, they were generally held in disfavour; for which, even
if doctrinal prepossessions had not entered into the question, the
great want of taste and judgment often manifested in their
compilation, and perhaps also the prevailing mediocrity of
the bulk of the original compositions from which most of them
were derived, would be enough to account. In addition to this,
the idea that no hymns ought to be used in any services of the
Church of England, except prose anthems after the third collect,
without express royal or ecclesiastical authority, continued
down to that time largely to prevail among high churchmen.
Two publications, which appeared almost simultaneously
in 1827—Bishop Heber’s Hymns, with a few added by Dean
Milman, and John Keble’s Christian Year (not a hymn-book,
Heber, Milman, Keble.
but one from which several admirable hymns
have been taken, and the well-spring of many streams
of thought and feeling by which good hymns have
since been produced)—introduced a new epoch, breaking down
the barrier as to hymnody which had till then existed between
the different theological schools of the Church of England.
Mant.
In this movement Richard Mant, bishop of Down,
was also one of the first to co-operate. It soon received
a great additional impulse from the increased attention which,
about the same time, began to be paid to ancient hymnody,
and from the publication in 1833 of Bunsen’s Gesangbuch.
Among its earliest fruits was the Lyra apostolica, containing
hymns, sonnets and other devotional poems, most of them
originally contributed by some of the leading authors of the
Tracts for the Times to the British Magazine; the finest
of which is the pathetic “Lead, kindly Light, amid th’ encircling
gloom,” by Cardinal Newman—well known, and universally
Newman.
admired. From that time hymns and hymn-writers
rapidly multiplied in the Church of England,
and in Scotland also. Nearly 600 authors whose publications
were later than 1827 are enumerated in Sedgwick’s catalogue of
1863, and about half a million hymns are now in existence.
Works, critical and historical, upon the subject of hymns, have
also multiplied; and collections for church use have become
innumerable—several of the various religious denominations,
and many of the leading ecclesiastical and religious societies,
having issued hymn-books of their own, in addition to those
compiled for particular dioceses, churches and chapels, and to
books (like Hymns Ancient and Modern, published 1861, supplemented
1889, revised edition, 1905) which have become
popular without any sanction from authority. To mention
all the authors of good hymns since the commencement of this
new epoch would be impossible; but probably no names could
be chosen more fairly representative of its characteristic merits,
and perhaps also of some of its defects, than those of Josiah
Conder and James Edmeston among English Nonconformists;
Henry Francis Lyte and Charlotte Elliott among evangelicals in
the Church of England; John Mason Neale and Christopher
Wordsworth, bishop of Lincoln, among English churchmen
of the higher school; Arthur Penrhyn Stanley, Edward H.
Plumptre, Frances Ridley Havergal; and in Scotland, Dr
Horatius Bonar, Dr Norman Macleod and Dr George Matheson.
American hymn-writers belong to the same schools, and have
been affected by the same influences. Some of them have
197
enjoyed a just reputation on both sides of the Atlantic. Among
those best known are John Greenleaf Whittier, Bishop Doane,
Dr W. A. Muhlenberg and Thomas Hastings; and it is difficult
to praise too highly such works as the Christmas hymn, “It came
upon the midnight clear,” by Edmund H. Sears; the Ascension
hymn, “Thou, who didst stoop below,” by Mrs S. E. Miles;
two by Dr Ray Palmer, “My faith looks up to Thee, Thou
Lamb of Calvary,” and “Jesus, Thou joy of loving hearts,”
the latter of which is the best among several good English
versions of “Jesu, dulcedo, cordium”; and “Lord of all being,
throned afar,” by Oliver Wendell Holmes.
The more modern “Moody and Sankey” hymns (see Moody,
D. L.) popularized a new Evangelical type, and the Salvation
Army has carried this still farther.
7. Conclusion.—The object aimed at in this article has been
to trace the general history of the principal schools of ancient
and modern hymnody, and especially the history of its use in
the Christian church. For this purpose it has not been thought
necessary to give any account of the hymns of Racine, Madame
Guyon and others, who can hardly be classed with any school,
nor of the works of Caesar Malan of Geneva (1787-1864) and
other quite modern hymn-writers of the Reformed churches in
Switzerland and France.
On a general view of the whole subject, hymnody is seen to
have been a not inconsiderable factor in religious worship.
It has been sometimes employed to disseminate and popularize
particular views, but its spirit and influence has been, on the whole,
catholic. It has embodied the faith, trust and hope, and no
small part of the inward experience, of generation after generation
of men, in many different countries and climates, of many
different nations, and in many varieties of circumstances and
condition. Coloured, indeed, by these differences, and also
by the various modes in which the same truths have been
apprehended by different minds and sometimes reflecting
partial and imperfect conceptions of them, and errors with which
they have been associated in particular churches, times and
places, its testimony is, nevertheless, generally the same. It
has upon it a stamp of genuineness which cannot be mistaken.
It bears witness to the force of a central attraction more powerful
than all causes of difference, which binds together times
ancient and modern, nations of various race and language,
churchmen and nonconformists, churches reformed and unreformed;
to a true fundamental unity among good Christians;
and to a substantial identity in their moral and spiritual
experience.
(S.)
The regular practice of hymnody in English musical history
dates from the beginning of the 16th century. Luther’s verses
were adapted sometimes to ancient church melodies, sometimes to
tunes of secular songs, and sometimes had music composed for them
by himself and others. Many rhyming Latin hymns are of earlier
date whose tunes are identified with them, some of which tunes,
with the subject of their Latin text, are among the Reformer’s
appropriations; but it was he who put the words of praise and
prayer into the popular mouth, associated with rhythmical music
which aided to imprint the words upon the memory and to enforce
their enunciation. In conjunction with his friend Johann Walther,
Luther issued a collection of poems for choral singing in 1524, which
was followed by many others in North Germany. The English
versions of the Psalms by Sternhold and Hopkins and their predecessors,
and the French version by Clement Marot and Theodore
Beza, were written with the same purpose of fitting sacred minstrelsy
to the voice of the multitude. Goudimel in 1566 and Claudin le
Jeune in 1607 printed harmonizations of tunes that had then become
standard for the Psalms, and in England several such publications
appeared, culminating in Thomas Ravenscroft’s famous collection,
The Whole Book of Psalms (1621); in all of these the arrangements
of the tunes were by various masters. The English practice of
hymn-singing was much strengthened on the return of the exiled
reformers from Frankfort and Geneva, when it became so general
that, according to Bishop Jewell, thousands of the populace who
assembled at Paul’s Cross to hear the preaching would join in the
singing of psalms before and after the sermon.
The placing of the choral song of the church within the lips of
the people had great religious and moral influence; it has had also
its great effect upon art, shown in the productions of the North
German musicians ever since the first days of the Reformation,
which abound in exercises of scholarship and imagination wrought
upon the tunes of established acceptance. Some of these are accompaniments
to the tunes with interludes between the several strains,
and some are compositions for the organ or for orchestral instruments
that consist of such elaboration of the themes as is displayed
in accompaniments to voices, but of far more complicated and extended
character. A special art-form that was developed to a very
high degree, but has passed into comparative disuse, was the
structure of all varieties of counterpoint extemporaneously upon
the known hymn-tunes (chorals), and several masters acquired
great fame by success in its practice, of whom J. A. Reinken (1623-1722),
Johann Pachelbel (1653-1706), Georg Boehm and the
great J. S. Bach are specially memorable. The hymnody of North
Germany has for artistic treatment a strong advantage which is
unpossessed by that of England, in that for the most part the same
verses are associated with the same tunes, so that, whenever the
text or the music is heard, either prompts recollection of the other,
whereas in England tunes were always and are now often composed
to metres and not to poems; any tune in a given metre is available
for every poem in the same, and hence there are various tunes to
one poem, and various poems to one tune.4 In England a tune
is named generally after some place—as “York,” “Windsor,”
“Dundee,”—or by some other unsignifying word; in North Germany
a tune is mostly named by the initial words of the verses to
which it is allied, and consequently, whenever it is heard, whether
with words or without, it necessarily suggests to the hearer the
whole subject of that hymn of which it is the musical moiety undivorceable
from the literary half. Manifold as they are, knowledge
of the choral tunes is included in the earliest schooling of every
Lutheran and every Calvinist in Germany, which thus enables all
to take part in performance of the tunes, and hence expressly the
definition of “choral.” Compositions grounded on the standard
tune are then not merely school exercises, but works of art which
link the sympathies of the writer and the listener, and aim at expressing
the feeling prompted by the hymn under treatment.
Bibliography: I. Ancient.—George Cassander, Hymni ecclesiastici
(Cologne, 1556); Georgius Fabricius, Poëtarum veterum
ecclesiasticorum (Frankfort, 1578); Cardinal J. M. Thomasius,
Hymnarium in Opera, ii. 351 seq. (Rome, 1747); A. J. Rambach,
Anthologie christlicher Gesänge (Altona, 1817); H. A. Daniel,
Thesaurus hymnologicus (Leipzig, 5 vols., 1841-1856); J. M.
Neale, Hymni ecclesiae et sequentiae (London, 1851-1852); and
Hymns of the Eastern Church (1863). The dissertation prefixed to the
second volume of the Acta sanctorum of the Bollandists; Cardinal J.
B. Pitra, Hymnographie de l’église grecque (1867), Analecta sacra
(1876); W. Christ and M. Paranikas, Anthologia Graeca carminum
Christianorum (Leipzig, 1871); F. A. March, Latin Hymns with English
Notes (New York, 1875); R. C. Trench, Sacred Latin Poetry (London,
4th ed., 1874); J. Pauly, Hymni breviarii Romani (Aix-la-Chapelle,
3 vols., 1868-1870); Pimont, Les Hymnes du bréviaire romain
(vols. 1-3, 1874-1884, unfinished); A. W. F. Fischer, Kirchenlieder-Lexicon
(Gotha, 1878-1879); J. Kayser, Beiträge zur Geschichte der
ältesten Kirchenhymnen (1881); M. Manitius, Geschichte der christlichen
lateinischen Poesie (Stuttgart, 1891); John Julian, Dictionary
of Hymnology (1892, new ed. 1907). For criticisms of metre, see
also Huemer, Untersuchungen über die ältesten christlichen Rhythmen
(1879); E. Bouvy, Poètes et mélodes (Nîmes, 1886); C. Krumbacher,
Geschichte der byzantinischen Literatur (Munich, 1897, p. 700 seq.);
J. M. Neale, Latin dissertation prefixed to Daniel’s Thesaurus, vol. 5;
and D. J. Donahoe, Early Christian Hymns (London, 1909).
II. Medieval.—Walafrid Strabo’s treatise, ch. 25, De hymnis, &c.;
Radulph of Tongres, De psaltario observando (14th century);
Clichtavaens, Elucidatorium ecclesiasticum (Paris, 1556); Faustinus
Arevalus, Hymnodia Hispanica (Rome, 1786); E. du Méril, Poésies
populaires latines antérieures au XIIIe siècle (Paris, 1843); J. Stevenson,
Latin Hymns of the Anglo-Saxon Church (Surtees Society, Durham,
1851); Norman, Hymnarium Sarisburiense (London, 1851); J. D.
Chambers, Psalter, &c., according to the Sarum use (1852); F. J.
Mone, Lateinische Hymnen des Mittelalters (Freiburg, 3 vols., 1853-1855);
Ph. Wackernagel, Das deutsche Kirchenlied von der ältesten
Zeit bis zum Anfang des 17. Jahrhunderts, vol. i. (Leipzig, 1864); E.
Dümmler, Poëtae latini aevi Carolini (1881-1890); the Hymnologische
Beiträge: Quellen und Forschungen zur Geschichte der lateinischen
Hymnendichtung, edited by C. Blume and G. M. Dreves (Leipzig,
1897); G. C. F. Mohnike, Hymnologische Forschungen; Klemming,
Hymni et sequentiae in regno Sueciae (Stockholm, 4 vols.,
1885-1887); Das katholische deutsche Kirchenlied (vol. i. by K.
Severin Meister, 1862, vol. ii. by W. Baumker, 1883); the “Hymnodia
Hiberica,” Spanische Hymnen des Mittelalters, vol. xvi.
(1894); the “Hymnodia Gotica,” Mozarabische Hymnen des
altspanischen Ritus, vol. xxvii. (1897); J. Dankó, Vetus hymnarium
ecclesiasticae Hungariae (Budapest, 1893); J. H. Bernard and R.
Atkinson, The Irish Liber Hymnorum (2 vols., London, 1898);
C. A. J. Chevalier, Poésie liturgique du moyen âge (Paris, 1893).
III. Modern.—J. C. Jacobi, Psalmodia Germanica (1722-1725
and 1732, with supplement added by J. Haberkorn, 1765); F. A.
Cunz, Geschichte des deutschen Kirchenliedes (Leipzig, 1855); Baron
von Bunsen, Versuch eines allgemeinen Gesang- und Gebetbuches
198
(1833) and Allgemeines evangelisches Gesang- und Gebetbuch (1846);
Catherine Winkworth, Christian Singers of Germany (1869) and
Lyra Germanica (1855); Catherine H. Dunn, Hymns from the
German (1857); Frances E. Cox, Sacred Hymns from the German
(London, 1841); Massie, Lyra domestica (1860); Appendix on
Scottish Psalmody in D. Laing’s edition of Baillie’s Letters and
Journals (1841-1842); J. and C. Wesley, Collection of Psalms and
Hymns (1741); Josiah Miller, Our Hymns, their Authors and Origin
(1866); John Gadsby, Memoirs of the Principal Hymn-writers
(3rd ed., 1861); L. C. Biggs, Annotations to Hymns Ancient and
Modern (1867); Daniel Sedgwick, Comprehensive Index of Names
of Original Authors of Hymns (2nd ed., 1863); R. E. Prothero, The
Psalms in Human Life (1907); C. J. Brandt and L. Helweg, Den
danske Psalmedigtning (Copenhagen, 1846-1847); J. N. Skaar,
Norsk Salmehistorie (Bergen, 1879-1880); H. Schück, Svensk
Literaturhistoria (Stockholm, 1890); Rudolf Wolkan, Geschichte der
deutschen Literatur in Böhmen, 246-256, and Das deutsche Kirchenlied
der böhm. Brüder (Prague, 1891); Zahn, Die geistlichen Lieder der
Brüder in Böhmen, Mähren u. Polen (Nuremberg, 1875); and J.
Müller, “Bohemian Brethren’s Hymnody,” in J. Julian’s Dictionary
of Hymnology.
For account of hymn-tunes, &c., see W. Cowan and James Love,
Music of the Church Hymnody and the Psalter in Metre (London,
1901); and Dickinson, Music in the History of the Western Church
(New York, 1902); S. Kümmerle, Encyklopädie der evangelischen
Kirchenmusik (4 vols., 1888-1895); Chr. Palmer, Evangelische
Hymnologie (Stuttgart, 1865); and P. Urto Kornmüller, Lexikon
der kirchlichen Tonkunst (1891).
1 The history of the “hymn” naturally begins with Greece, but
it may be found in some form much earlier; Assyria and Egypt
have left specimens, while India has the Vedic hymns, and Confucius
collected “praise songs” in China.
2 See Greek Literature.
3 The authorship of this and of one other, “When all thy mercies,
O my God,” has been made a subject of controversy,—being claimed
for Andrew Marvell (who died in 1678), in the preface to Captain E.
Thompson’s edition (1776) of Marvell’s Works. But this claim does
not appear to be substantiated. The editor did not give his readers
the means of judging as to the real age, character or value of a manuscript
to which he referred; he did not say that these portions of it
were in Marvell’s handwriting; he did not even himself include
them among Marvell’s poems, as published in the body of his edition;
and he advanced a like claim on like grounds to two other poems, in
very different styles, which had been published as their own by
Tickell and Mallet. It is certain that all the five hymns were first
made public in 1712, in papers contributed by Addison to the Spectator
(Nos. 441, 453, 465, 489, 513), in which they were introduced in a
way which might have been expected if they were by the hand
which wrote those papers, but which would have been improbable,
and unworthy of Addison, if they were unpublished works of a writer
of so much genius, and such note in his day, as Marvell. They are
all printed as Addison’s in Dr Johnson’s British Poets.
4 The old tune for the 100th Psalm and Croft’s tune for the 104th
are almost the only exceptions, unless “God save the King” may be
classed under “hymnody.” In Scotland also the tune for the 124th
Psalm is associated with its proper text.
HYPAETHROS (Gr. ὕπαιθρος, beneath the sky, in the open
air, ὑπό, beneath, and αἰθήρ, air), the Greek term quoted by
Vitruvius (iii. 2) for the opening in the middle of the roof of
decastyle temples, of which “there was no example in Rome,
but one in Athens in the temple of Jupiter Olympius, which is
octastyle.” But at the time he wrote (c. 25 B.C.) the cella of this
temple was unroofed, because the columns which had been provided
to carry, at all events, part of the ceiling and roof had been
taken away by Sulla in 80 B.C. The decastyle temple of Apollo
Didymaeus near Miletus was, according to Strabo (c. 50 B.C.),
unroofed, on account of the vastness of its cella, in which precious
groves of laurel bushes were planted. Apart from these two
examples, the references in various writers to an opening of
some kind in the roofs of temples dedicated to particular deities,
and the statement of Vitruvius, which was doubtless based on
the writings of Greek authors, that in decastyle or large temples
the centre was open to the sky and without a roof (medium autem
sub divo est sine tecto), render the existence of the hypaethros
probable in some cases; and therefore C. R. Cockerell’s discovery
in the temple at Aegina of two fragments of a coping-stone, in
which there were sinkings on one side to receive the tiles and
covering tiles, has been of great importance in the discussion
of this subject. In the conjectural restoration of the opaion
or opening in the roof shown in Cockerell’s drawing, it has been
made needlessly large, having an area of about one quarter of
the superficial area of the cella between the columns, and since
in the Pantheon at Rome the relative proportions of the central
opening in the dome and the area of the Rotunda are 1: 22,
and the light there is ample, in the clearer atmosphere of Greece
it might have been less. The larger the opening the more conspicuous
would be the notch in the roof which is so greatly objected
to; in this respect T. J. Hittorff would seem to be nearer the
truth when, in his conjectural restoration of Temple R. at Selinus,
he shows an opaion about half the relative size shown in Cockerell’s
of that at Aegina, the coping on the side elevation being much
less noticeable. The problem was apparently solved in another
way at Bassae, where, in the excavations of the temple of Apollo
by Cockerell and Baron Haller von Hallerstein, three marble
tiles were found with pierced openings in them about 18 in. by
10 in.; five of these pierced tiles on either side would have amply
lighted the interior of the cella, and the amount of rain passing
through (a serious element to be considered in a country where
torrential rains occasionally fall) would not be very great or
more than could be retained to dry up in the cella sunk pavement.
In favour of both these methods of lighting the interior of the
cella, the sarcophagus tomb at Cyrene, about 20 ft. long, carved
in imitation of a temple, has been adduced, because, on the top
of the roof and in its centre, there is a raised coping, and a similar
feature is found on a tomb found near Delos; an example from
Crete now in the British Museum shows a pierced tile on each
side of the roof, and a large number of pierced tiles have been
found in Pompeii, some of them surrounded with a rim identical
with that of the marble tiles at Bassae. On the other hand,
there are many authorities, among them Dr W. Dörpfeld, who
have adhered to their original opinion that it was only through
the open doorway that light was ever admitted into the cella,
and with the clear atmosphere of Greece and the reflections
from the marble pavement such lighting would be quite sufficient.
There remains still another source of light to be considered,
that passing through the Parian marble tiles of the roof; the
superior translucency of Parian to any other marble may have
suggested its employment for the roofs of temples, and if, in the
framed ceilings carried over the cella, openings were left, some
light from the Parian tile roof might have been obtained. It
is possibly to this that Plutarch refers when describing the ceiling
and roof of the temple of Demeter at Eleusis, where the columns
in the interior of the temple carried a ceiling, probably constructed
of timbers crossing one another at right angles, and one or more
of the spaces was left open, which Xenocles surmounted by a
roof formed of tiles.
James Fergusson put forward many years ago a conjectural
restoration in which he adopted a clerestory above the superimposed
columns inside the cella; in order to provide the light
for these windows he indicated two trenches in the roof, one on each
side, and pointed out that the great Hall of Columns at Karnak was
lighted in this way with clerestory windows; but in the first place
the light in the latter was obtained over the flat roofs covering lower
portions of the hall, and in the second place, as it rarely rains in
Thebes, there could be no difficulty about the drainage, while in
Greece, with the torrential rains and snow, these trenches would be
deluged with water, and with all the appliances of the present day
it would be impossible to keep these clerestory windows watertight.
There is, however, still another objection to Fergusson’s
theory; the water collecting in these trenches on the roof would
have to be discharged, for which Fergusson’s suggestions are quite
inadequate, and the gargoyles shown in the cella wall would make
the peristyle insupportable just at the time when it was required
for shelter. No drainage otherwise of any kind has ever been found
in any Greek temple, which is fatal to Fergusson’s view. Nor is it
in accordance with the definition “open to the sky.” English
cathedrals and churches are all lighted by clerestory windows, but
no one has described them as open to the sky, and although Vitruvius’s
statements are sometimes confusing, his description is far too
clear to leave any misunderstanding as to the lighting of temples
(where it was necessary on account of great length) through an
opening in the roof.
There is one other theory which has been put forward, but which
can only apply to non-peristylar temples,—that light and air was
admitted through the metopes, the apertures between the beams
crossing the cella,—and it has been assumed that because Orestes
was advised in one of the Greek plays to climb up and look through
the metopes of the temple, these were left open; but if Orestes could
look in, so could the birds, and the statue of the god would be
defiled. The metopes were probably filled in with shutters of
some kind which Orestes knew how to open.
(R. P. S.)
HYPALLAGE (Gr. ὑπαλλαγή, interchange or exchange), a
rhetorical figure, in which the proper relation between two words
according to the rules of syntax are inverted. The stock instance
is that in Virgil, Aen. iii. 61, where dare classibus austros, to
give winds to the fleet, is put for dare classes austris, to give the
fleet to the winds. The term is also loosely applied to figures
of speech properly known as “metonymy” and, generally, to
any striking turn of expression.
HYPATIA (Ὑπατία) (c. A.D. 370-415) mathematician and
philosopher, born in Alexandria, was the daughter of Theon,
also a mathematician and philosopher, author of scholia on
Euclid and a commentary on the Almagest, in which it is suggested
that he was assisted by Hypatia (on the 3rd book). After
lecturing in her native city, Hypatia ultimately became the
recognized head of the Neoplatonic school there (c. 400). Her
great eloquence and rare modesty and beauty, combined with
her remarkable intellectual gifts, attracted to her class-room a
large number of pupils. Among these was Synesius, afterwards
(c. 410) bishop of Ptolemaïs, several of whose letters to her,
full of chivalrous admiration and reverence, are still extant.
Suidas, misled by an incomplete excerpt in Photius from the life
of Isidorus (the Neoplatonist) by Damascius, states that Hypatia
199
was the wife of Isidorus; but this is chronologically impossible,
since Isidorus could not have been born before 434 (see Hoche in
Philologus). Shortly after the accession of Cyril to the patriarchate
of Alexandria in 412, owing to her intimacy with Orestes,
the pagan prefect of the city, Hypatia was barbarously murdered
by the Nitrian monks and the fanatical Christian mob (March
415). Socrates has related how she was torn from her chariot,
dragged to the Caesareum (then a Christian church), stripped
naked, done to death with oyster-shells (ὀστράκοις ἀνεῖλον
perhaps “cut her throat”) and finally burnt piecemeal. Most
prominent among the actual perpetrators of the crime was one
Peter, a reader; but there seems little reason to doubt Cyril’s
complicity (see Cyril of Alexandria).
Hypatia, according to Suidas, was the author of commentaries
on the Arithmetica of Diophantus of Alexandria, on the Conics
of Apollonius of Perga and on the astronomical canon (of
Ptolemy). These works are lost; but their titles, combined with
expressions in the letters of Synesius, who consulted her about
the construction of an astrolabe and a hydroscope, indicate that
she devoted herself specially to astronomy and mathematics.
Little is known of her philosophical opinions, but she appears
to have embraced the intellectual rather than the mystical side
of Neoplatonism, and to have been a follower of Plotinus rather
than of Porphyry and Iamblichus. Zeller, however, in his
Outlines of Greek Philosophy (1886, Eng. trans. p. 347), states
that “she appears to have taught the Neoplatonic doctrine in the
form in which Iamblichus had stated it.” A Latin letter to
Cyril on behalf of Nestorius, printed in the Collectio nova conciliorum,
i. (1623), by Stephanus Baluzius (Étienne Baluze, q.v.),
and sometimes attributed to her, is undoubtedly spurious. The
story of Hypatia appears in a considerably disguised yet still
recognizable form in the legend of St Catherine as recorded in
the Roman Breviary (November 25), and still more fully in the
Martyrologies (see A. B. Jameson, Sacred and Legendary Art (1867)
ii. 467.)
The chief source for the little we know about Hypatia is the account
given by Socrates (Hist. ecclesiastica, vii. 15). She is the subject of an
epigram by Palladas in the Greek Anthology (ix. 400). See Fabricius,
Bibliotheca Graeca (ed. Harles), ix. 187; John Toland, Tetradymus
(1720); R. Hoche in Philologus (1860), xv. 435; monographs by
Stephan Wolf (Czernowitz, 1879), H. Ligier (Dijon, 1880) and W. A.
Meyer (Heidelberg, 1885), who devotes attention to the relation of
Hypatia to the chief representatives of Neoplatonism; J. B. Bury,
Hist. of the Later Roman Empire (1889), i. 208,317; A. Güldenpenning,
Geschichte des oströmischen Reiches unter Arcadius und Theodosius II.
(Halle, 1885), p. 230; Wetzer and Welte, Kirchenlexikon, vi.
(1889), from a Catholic standpoint. The story of Hypatia also forms
the basis of the well-known historical romance by Charles Kingsley
(1853).
HYPERBATON (Gr. ὑπέρβατον, a stepping over), the name of a
figure of speech, consisting of a transposition of words from their
natural order, such as the placing of the object before instead of
after the verb. It is a common method of securing emphasis.
HYPERBOLA, a conic section, consisting of two open branches,
each extending to infinity. It may be defined in several ways.
The in solido definition as the section of a cone by a plane at a
less inclination to the axis than the generator brings out the
existence of the two infinite branches if we imagine the cone
to be double and to extend to infinity. The in plano definition,
i.e. as the conic having an eccentricity greater than unity, is a
convenient starting-point for the Euclidian investigation. In
projective geometry it may be defined as the conic which intersects
the line at infinity in two real points, or to which it is possible
to draw two real tangents from the centre. Analytically, it is
defined by an equation of the second degree, of which the highest
terms have real roots (see Conic Section).
While resembling the parabola in extending to infinity, the curve
has closest affinities to the ellipse. Thus it has a real centre, two
foci, two directrices and two vertices; the transverse axis, joining
the vertices, corresponds to the major axis of the ellipse, and the
line through the centre and perpendicular to this axis is called the
conjugate axis, and corresponds to the minor axis of the ellipse;
about these axes the curve is symmetrical. The curve does not
appear to intersect the conjugate axis, but the introduction of
imaginaries permits us to regard it as cutting this axis in two unreal
points. Calling the foci S, S′, the real vertices A, A′, the extremities
of the conjugate axis B, B’ and the centre C, the positions of B, B′
are given by AB = AB′ = CS. If a rectangle be constructed about
AA′ and BB′, the diagonals of this figure are the “asymptotes”
of the curve; they are the tangents from the centre, and hence
touch the curve at infinity. These two lines may be pictured in the
in solido definition as the section of a cone by a plane through its
vertex and parallel to the plane generating the hyperbola. If the
asymptotes be perpendicular, or, in other words, the principal axes
be equal, the curve is called the rectangular hyperbola. The hyperbola
which has for its transverse and conjugate axes the transverse
and conjugate axes of another hyperbola is said to be the conjugate
hyperbola.
Some properties of the curve will be briefly stated: If PN be the
ordinate of the point P on the curve, AA’ the vertices, X the meet of
the directrix and axis and C the centre, then PN2: AN·NA′: :
SX2: AX·A′X, i.e. PN2 is to AN·NA′ in a constant ratio. The circle
on AA’ as diameter is called the auxiliarly circle; obviously AN·NA’
equals the square of the tangent to this circle from N, and hence the
ratio of PN to the tangent to the auxiliarly circle from N equals the
ratio of the conjugate axis to the transverse. We may observe
that the asymptotes intersect this circle in the same points as the
directrices. An important property is: the difference of the focal
distances of any point on the curve equals the transverse axis.
The tangent at any point bisects the angle between the focal distances
of the point, and the normal is equally inclined to the focal
distances. Also the auxiliarly circle is the locus of the feet of the perpendiculars
from the foci on any tangent. Two tangents from any
point are equally inclined to the focal distance of the point. If the
tangent at P meet the conjugate axis in t, and the transverse in N,
then Ct. PN = BC2; similarly if g and G be the corresponding intersections
of the normal, PG : Pg : : BC2 : AC2. A diameter is a line
through the centre and terminated by the curve: it bisects all chords
parallel to the tangents at its extremities; the diameter parallel to
these chords is its conjugate diameter. Any diameter is a mean
proportional between the transverse axis and the focal chord parallel
to the diameter. Any line cuts off equal distances between the curve
and the asymptotes. If the tangent at P meets the asymptotes in
R, R′, then CR·CR′ = CS2. The geometry of the rectangular hyperbola
is simplified by the fact that its principal axes are equal.
Analytically the hyperbola is given by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
wherein ab > h2. Referred to the centre this becomes
Ax2 + 2Hxy + By2 + C = 0; and if the axes of coordinates be the
principal axes of the curve, the equation is further simplified to
Ax2 − By2 = C, or if the semi-transverse axis be a, and the semi-conjugate
b, x2/a2 − y2/b2 = 1. This is the most commonly used form.
In the rectangular hyperbola a = b; hence its equation is x2 − y2 = 0.
The equations to the asymptotes are x/a = ±y/b and x = ±y respectively.
Referred to the asymptotes as axes the general equation
becomes xy = k2; obviously the axes are oblique in the general
hyperbola and rectangular in the rectangular hyperbola. The values
of the constant k2 are ½(a2 + b2) and ½a2 respectively. (See
Geometry: Analytical; Projective.)
HYPERBOLE (from Gr. ὑπερβάλλειν, to throw beyond), a
figure of rhetoric whereby the speaker expresses more than
the truth, in order to produce a vivid impression; hence, an
exaggeration.
HYPERBOREANS (Ὑπερβόρεοι, Ὑπερβόρειοι), a mythical
people intimately connected with the worship of Apollo. Their
name does not occur in the Iliad or the Odyssey, but Herodotus
(iv. 32) states that they were mentioned in Hesiod and in the
Epigoni, an epic of the Theban cycle. According to Herodotus,
two maidens, Opis and Arge, and later two others, Hyperoche
and Laodice, escorted by five men, called by the Delians Perphereës,
were sent by the Hyperboreans with certain offerings
to Delos. Finding that their messengers did not return, the
Hyperboreans adopted the plan of wrapping the offerings in
wheat-straw and requested their neighbours to hand them on
to the next nation, and so on, till they finally reached Delos.
The theory of H. L. Ahrens, that Hyperboreans and Perphereës
are identical, is now widely accepted. In some of the dialects
of northern Greece (especially Macedonia and Delphi) φ had a
tendency to become β. The original form of Περφερέες was
ὑπερφερέται or ὑπέρφοροι (“those who carry over”), which
becoming ὑπέρβοροι gave rise to the popular derivation from
βορέας (“dwellers beyond the north wind”). The Hyperboreans
were thus the bearers of the sacrificial gifts to Apollo
over land and sea, irrespective of their home, the name being
given to Delphians, Thessalians, Athenians and Delians. It is
objected by O. Schröder that the form Περφερέες requires a passive
meaning, “those who are carried round the altar,” perhaps
dancers like the whirling dervishes; distinguishing them from
the Hyperboreans, he explains the latter as those who live “above
200
the mountains,” that is, in heaven. Under the influence of the
derivation from βορέας, the home of the Hyperboreans was
placed in a region beyond the north wind, a paradise like the
Elysian plains, inaccessible by land or sea, whither Apollo could
remove those mortals who had lived a life of piety. It was a
land of perpetual sunshine and great fertility; its inhabitants
were free from disease and war. The duration of their life was
1000 years, but if any desired to shorten it, he decked himself
with garlands and threw himself from a rock into the sea. The
close connexion of the Hyperboreans with the cult of Apollo
may be seen by comparing the Hyperborean myths, the characters
of which by their names mostly recall Apollo or Artemis (Agyieus,
Opis, Hecaergos, Loxo), with the ceremonial of the Apolline
worship. No meat was eaten at the Pyanepsia; the Hyperboreans
were vegetarians. At the festival of Apollo at Leucas
a victim flung himself from a rock into the sea, like the Hyperborean
who was tired of life. According to an Athenian decree
(380 B.C.) asses were sacrificed to Apollo at Delphi, and Pindar
(Pythia, x. 33) speaks of “hecatombs of asses” being offered to
him by the Hyperboreans. As the latter conveyed sacrificial
gifts to Delos hidden in wheat-straw, so at the Thargelia a sheaf
of corn was carried round in procession, concealing a symbol of
the god (for other resemblances see Crusius’s article). Although
the Hyperborean legends are mainly connected with Delphi and
Delos, traces of them are found in Argos (the stories of Heracles,
Perseus, Io), Attica, Macedonia, Thrace, Sicily and Italy (which
Niebuhr indeed considers their original home). In modern times
the name has been applied to a group of races, which includes the
Chukchis, Koryaks, Yukaghirs, Ainus, Gilyaks and Kamchadales,
inhabiting the arctic regions of Asia and America. But if
ever ethnically one, the Asiatic and American branches are now
as far apart from each other as they both are from the Mongolo-Tatar
stock.
See O. Crusius in Roscher’s Lexikon der Mythologie; O. Schröder
in Archiv für Religionswissenschaft (1904), viii. 69; W. Mannhardt,
Wald- und Feldkulte (1905); L. R. Farnell, Cults of the Greek
States (1907), iv. 100.
HYPEREIDES (c. 390-322 B.C.), one of the ten Attic orators,
was the son of Glaucippus, of the deme of Collytus. Having
studied under Isocrates, he began life as a writer of speeches
for the courts, and in 360 he prosecuted Autocles, a general
charged with treason in Thrace (frags. 55-65, Blass). At the
time of the so-called “Social War” (358-355) he accused
Aristophon, then one of the most influential men at Athens,
of malpractices (frags. 40-44, Blass), and impeached Philocrates
(343) for high treason. From the peace of 346 to 324 Hypereides
supported Demosthenes in the struggle against Macedon; but
in the affair of Harpalus he was one of the ten public prosecutors
of Demosthenes, and on the exile of his former leader he became
the head of the patriotic party (324). After the death of
Alexander, he was the chief promoter of the Lamian war against
Antipater and Craterus. After the decisive defeat at Crannon
(322), Hypereides and the other orators, whose surrender was
demanded by Antipater, were condemned to death by the
Athenian partisans of Macedonia. Hypereides fled to Aegina,
but Antipater’s emissaries dragged him from the temple of
Aeacus, where he had taken refuge, and put him to death;
according to others, he was taken before Antipater at Athens
or Cleonae. His body was afterwards removed to Athens for
burial.
Hypereides was an ardent pursuer of “the beautiful,” which
in his time generally meant pleasure and luxury. His temper
was easy-going and humorous; and hence, though in his development
of the periodic sentence he followed Isocrates, the essential
tendencies of his style are those of Lysias, whom he surpassed,
however, in the richness of his vocabulary and in the variety of
his powers. His diction was plain and forcible, though he
occasionally indulged in long compound words probably borrowed
from the Middle Comedy, with which, and with the everyday
life of his time, he was in full sympathy. His composition was
simple. He was specially distinguished for subtlety of expression,
grace and wit, as well as for tact in approaching his case and
handling his subject matter. Sir R. C. Jebb sums up the criticism
of pseudo-Longinus (De sublimitate, 34) in the phrase—“Hypereides
was the Sheridan of Athens.”
Seventy-seven speeches were attributed to Hypereides, of which
twenty-five were regarded as spurious even by ancient critics.
It is said that a MS. of most of the speeches was in existence in the
16th century in the library of Matthias Corvinus, king of Hungary,
at Ofen, but was destroyed at the capture of the city by the Turks
in 1526. Only a few fragments were known until comparatively
recent times. In 1847 large fragments of his speeches Against
Demosthenes (see above) and For Lycophron (incidentally interesting
as elucidating the order of marriage processions and other details
of Athenian life, and the Athenian government of Lemnos), and the
whole of the For Euxenippus (c. 330, a locus classicus on εἰσαγγελίαι or
state prosecutions), were found in a tomb at Thebes in Egypt, and
in 1856 a considerable portion of a λόγος παρανόμων, a Funeral Oration
over Leosthenes and his comrades who had fallen in the Lamian war,
the best extant specimen of epideictic oratory (see Babington,
Churchill). Towards the end of the century further discoveries
were made of the conclusion of the speech Against Philippides
(dealing with a γραφὴ παρανόμων, or indictment for the proposal of
an unconstitutional measure, arising out of the disputes of the
Macedonian and anti-Macedonian parties at Athens), and of the whole
of the Against Athenogenes (a perfumer accused of fraud in the sale
of his business). These have been edited by F. G. Kenyon (1893).
An important speech that is lost is the Deliacus (frags. 67-75, Blass)
on the presidency of the Delian temple claimed by both Athens and
Delos, which was adjudged by the Amphictyons to Athens.
On Hypereides generally see pseudo-Plutarch, Decem oratorum
vitae; F. Blass, Attische Beredsamkeit, iii.; R. C. Jebb, Attic
Orators, ii. 381. A full list of editions and articles is given in F.
Blass, Hyperidis orationes sex cum ceterarum fragmentis (1894,
Teubner series), to which may be added I. Bassi, Le Quattro Orazioni
di Iperide (introduction and notes, 1888), and J. E. Sandys in
Classical Review (January 1895) (a review of the editions of Kenyon
and Blass). For the discourse against Athenogenes see H. Weil,
Études sur l’antiquité grecque (1900).
HYPERION, in Greek mythology, one of the Titans, son of
Uranus and Gaea and father of Helios, the sun-god (Hesiod,
Theog. 134, 371; Apollodorus i. 1. 2). In the well-known
passage in Shakespeare (Hamlet, i. 2: “Hyperion to a satyr,”
where as in other poets the vowel -i- though really long, is
shortened for metrical reasons) Hyperion is used for Apollo as
expressive of the idea of beauty. The name is often used as
an epithet of Helios, who is himself sometimes called simply
Hyperion. It is explained as (1) he who moves above (ὑπερ-ιων),
but the quantity of the vowel is against this; (2) he who is
above (ὑπερι-ων). Others take it to be a patronymic in form,
like Κρονῖων, Μολῖων.
HYPERSTHENE, a rock-forming mineral belonging to the
group of orthorhombic pyroxenes. It differs from the other
members (enstatite [q.v.] and bronzite) of this group in containing
a considerable amount of iron replacing magnesium: the
chemical formula is (Mg, Fe)SiO3. Distinctly developed crystals
are rare, the mineral being usually found as foliated masses
embedded in those igneous rocks—norite, hypersthene-andesite,
&c.—of which it forms an essential constituent. The coarsely
grained labradorite-hypersthene-rock (norite) of the island of
St Paul off the coast of Labrador has furnished the most typical
material; and for this reason the mineral has been known as
“Labrador hornblende” or paulite. The colour is brownish-black,
and the pleochrism strong; the hardness is 6, and the
specific gravity 3.4-3.5. On certain surfaces it displays a brilliant
copper-red metallic sheen or schiller, which has the same origin
as the bronzy sheen of bronzite (q.v.), but is even more pronounced.
Like bronzite, it is sometimes cut and polished for ornamental
purposes.
(L. J. S.)
HYPERTROPHY (Gr. ὑπέρ, over, and τροφή, nourishment),
a term in medicine employed to designate an abnormal increase
in bulk of one or more of the organs or component tissues of the
body (see Pathology). In its strict sense this term can only
be applied where the increase affects the natural textures of a
part, and is not applicable where the enlargement is due to the
presence of some extraneous morbid formation. Hypertrophy
of a part may manifest itself either by simply an increase in
the size of its constituents, or by this combined with an increase
in their number (hyperplasia). In many instances both are
associated.
201
The conditions giving rise to hypertrophy are the reverse
of those described as producing Atrophy (q.v.). They are
concisely stated by Sir James Paget as being chiefly or only
three, namely: (1) the increased exercise of a part in its healthy
functions; (2) an increased accumulation in the blood of the
particular materials which a part appropriates to its nutrition
or in secretion; and (3) an increased afflux of healthy blood.
Illustrations are furnished of the first of these conditions by
the high development of muscular tissue under habitual active
exercise; of the second in the case of obesity, which is an hypertrophy
of the fatty tissues, the elements of which are furnished
by the blood; and of the third in the occasional overgrowth of
hair in the neighbourhood of parts which are the seat of inflammation.
Obviously therefore, in many instances, hypertrophy
cannot be regarded as a deviation from health, but rather on
the contrary as indicative of a high degree of nutrition and
physical power. Even in those cases where it is found associated
with disease, it is often produced as a salutary effort of nature
to compensate for obstructions or other difficulties which have
arisen in the system, and thus to ward off evil consequences.
No better example of this can be seen than in the case of certain
forms of heart disease, where from defect at some of the natural
orifices of that organ the onward flow of the blood is interfered
with, and would soon give rise to serious embarrassment to the
circulation, were it not that behind the seat of obstruction
the heart gradually becomes hypertrophied, and thus acquires
greater propelling power to overcome the resistance in front.
Again, it has been noticed, in the case of certain double organs
such as the kidneys, that when one has been destroyed by disease
the other has become hypertrophied to such a degree as enables
it to discharge the functions of both.
Hypertrophy may, however, in certain circumstances constitute
a disease, as in goitre and elephantiasis (q.v.), and also
in the case of certain tumours and growths (such as cutaneous
excrescences, fatty tumours, mucous polypi, &c.), which are
simply enlargements of normal textures. Hypertrophy does
not in all cases involve an increase in bulk; for, just as in
atrophy there may be no diminution in the size of the affected
organ, so in hypertrophy there may be no increase. This is
apt to be the case where certain only of the elements of an organ
undergo increase, while the others remain unaffected or are
actually atrophied by the pressure of the hypertrophied tissue,
as is seen in the disease known as cirrhosis of the liver.
A spurious hypertrophy is observed in the rare disease to which
G. B. Duchenne applied the name of pseudo-hypertrophic paralysis.
This ailment, which appears to be confined to children, consists
essentially of a progressive loss of power accompanied with a
remarkable enlargement of certain muscles or groups of muscles,
more rarely of the whole muscular system. This increase of
bulk is, however, not a true hypertrophy, but rather an excessive
development of connective tissue in the substance of the muscles,
the proper texture of which tends in consequence to undergo
atrophy or degeneration. The appearance presented by a child
suffering from this disease is striking. The attitude and gait
are remarkably altered, the child standing with shoulders thrown
back, small of the back deeply curved inwards, and legs wide
apart, while walking is accompanied with a peculiar swinging
or rocking movement. The calves of the legs, the buttocks,
the muscles of the back, and occasionally other muscles, are
seen to be unduly enlarged, and contrast strangely with the
general feebleness. The progress of the disease is marked by
increasing failure of locomotory power, and ultimately by complete
paralysis of the limbs. The malady is little amenable to
treatment, and, although often prolonged for years, generally
proves fatal before the period of maturity.
HYPNOTISM, a term now in general use as covering all that
pertains to the art of inducing the hypnotic state, or hypnosis,
and to the study of that state, its conditions, peculiarities and
effects. Hypnosis is a condition, allied to normal sleep (Gr.
ὕπνος), which can be induced in a large majority of normal
persons. Its most characteristic and constant symptom is
the increased suggestibility of the subject (see Suggestion).
Other symptoms are very varied and differ widely in different
subjects and in the same subject at different times. There can
be no doubt that the increased suggestibility and all the other
symptoms of hypnosis imply some abnormal condition of the
brain of a temporary and harmless nature. It would seem
that in all ages and in almost all countries individuals have
occasionally fallen into abnormal states of mind more or less
closely resembling the hypnotic state, and have thereby excited
the superstitious wonder of their fellows. In some cases the
state has been deliberately induced, in others it has appeared
spontaneously, generally under the influence of some emotional
excitement. The most familiar of these allied states is the
somnambulism or sleep-walking to which some persons seem to
be hereditarily disposed. Of a rather different type are the
states of ecstasy into which religious enthusiasts have occasionally
fallen and which were especially frequent among the peoples
of Europe during the middle ages. While in this condition
individuals have appeared to be insensitive to all impressions
made on their sense-organs, even to such as would excite acute
pain in normal persons, have been capable of maintaining rigid
postures for long periods of time, have experienced vivid
hallucinations, and have produced, through the power of the
imagination, extraordinary organic changes in the body, such
as the bloody stigmata on the hands and feet in several well-attested
instances. It has been proved in recent years that
effects of all these kinds may be produced by hypnotic suggestion.
Different again, but closely paralleled by some subjects in hypnosis,
is the state of latah into which a certain proportion of
persons of the Malay race are liable to fall. These persons, if
their attention is suddenly and forcibly drawn to any other
person, will begin to imitate his every action and attitude, and
may do so in spite of their best efforts to restrain their imitative
movements. Among the half-bred French-Canadians of the
forest regions of Canada occur individuals, known as “jumpers,”
who are liable to fall suddenly into a similar state of abject
imitativeness, and the same peculiar behaviour has been observed
among some of the remote tribes of Siberia.
The deliberate induction of states identical with, or closely
allied to, hypnosis is practised by many barbarous and savage
peoples, generally for ceremonial purposes. Thus, certain
dervishes of Algiers are said to induce in themselves, by the aid
of the sound of drums, monotonous songs and movements, a
state in which they are insensitive to pain, and a similar practice
of religious devotees is reported from Tibet. Perhaps the most
marvellous achievement among well-attested cases of this sort
is that of certain yogis of Hindustan; by long training and
practice they seem to acquire the power of arresting almost
completely all their vital functions. An intense effort of abstraction
from the impressions of the outer world, a prolonged fixation
of the eyes upon the nose or in some other strained position and
a power of greatly slowing the respiration, these seem to be
important features of their procedure for the attainment of their
abnormal states.
In spite of the wide distribution in time and space, and the
not very infrequent occurrence, of these instances of states
identical with or allied to hypnosis, some three centuries of
enthusiastic investigation and of bitter controversy were required
to establish the occurrence of the hypnotic state among the facts
accepted by the world of European science. Scientific interest
in them may be traced back at least as far as the end of the 16th
century. Paracelsus had founded the “sympathetic system”
of medicine, according to which the stars and other bodies,
especially magnets, influence men by means of a subtle emanation
or fluid that pervades all space. J. B. van Helmont, a distinguished
man of science of the latter part of the 16th century,
extended this doctrine by teaching that a similar magnetic fluid
radiates from men, and that it can be guided by their wills to
influence directly the minds and bodies of others. In the middle
of the 17th century there appeared in England several persons
who claimed to have the power of curing diseases by stroking
with the hand. Notable amongst these was Valentine Greatrakes,
of Affane, in the county of Waterford, Ireland, who was born in
202
February 1628, and who attracted great attention in England
by his supposed power of curing the king’s evil, or scrofula.
Many of the most distinguished scientific and theological men
of the day, such as Robert Boyle and R. Cudworth, witnessed
and attested the cures supposed to be effected by Greatrakes,
and thousands of sufferers crowded to him from all parts of
the kingdom. About the middle of the 18th century John Joseph
Gassner, a Roman Catholic priest in Swabia, took up the notion
that the majority of diseases arose from demoniacal possession,
and could only be cured by exorcism. His method was undoubtedly
similar to that afterwards followed by Mesmer and
others, and he had an extraordinary influence over the nervous
systems of his patients. Gassner, however, believed his power
to be altogether supernatural.
But it was not until the latter part of the 18th century that
the doctrine of a magnetic fluid excited great popular interest
and became the subject of fierce controversy in the scientific
world. F. A. Mesmer (q.v.), a physician of Vienna, was largely
instrumental in bringing the doctrine into prominence. He
developed it by postulating a specialized variety of magnetic
fluid which he called animal magnetism; and he claimed to be
able to cure many diseases by means of this animal magnetism,
teaching, also, that it may be imparted to and stored up in inert
objects, which are thereby rendered potent to cure disease.
It would seem that Mesmer himself was not acquainted with
the artificial somnambulism which for nearly a century was called
mesmeric or magnetic sleep, and which is now familiar as hypnosis
of a well-marked degree. It was observed and described about
the year 1780 by the marquis de Puységur, a disciple of Mesmer,
who showed that, while subjects were in this state, not only could
some of their diseases be cured, but also their movements could
be controlled by the “magnetizer,” and that they usually
remembered nothing of the events of the period of sleep when
restored to normal consciousness. These are three of the most
important features of hypnosis, and the modern study of hypnotism
may therefore be said to have been initiated at this date by
Puységur. For, though it is probable that this state had often
been induced by the earlier magnetists, they had not recognized
that the peculiar behaviour of their patients resulted from their
being plunged into this artificial sleep, but had attributed all
the symptoms they observed to the direct physical action of
external agents upon the patients.
The success of Mesmer and his disciples, especially great in
the fashionable world, led to the appointment in Paris of a
royal commission for the investigation of their claims. The
commission, which included men of great eminence, notably
A. L. Lavoisier and Benjamin Franklin, reported in the year
1784 that it could not accept the evidence for the existence of
the magnetic fluid; but it did not express an opinion as to the
reality of the cures said to be effected by its means, nor as to the
nature of the magnetic sleep. This report and the social upheavals
of the following years seem to have abolished the public
interest in “animal magnetism” for the space of one generation;
after which Alexandre Bertrand, a Parisian physician, revived
it by his acute investigations and interpretations of the phenomena.
Bertrand was the first to give an explanation of the facts
of the kind that is now generally accepted. He exhibited the
affinity of the “magnetic sleep” to ordinary somnambulism, and
he taught that the peculiar effects are to be regarded as due to the
suggestions of the operator working themselves out in the mind
and body of the “magnetized” subject, i.e. he regarded the
influence of the magnetizer as exerted in the first instance on
the mind of the subject and only indirectly through the mind
upon the body. Shortly after this revival of public interest,
namely in the year 1831, a committee of the Academy of Medicine
of Paris reported favourably upon “magnetism” as a therapeutic
agency, and before many years had elapsed it was
extensively practised by the physicians of all European countries,
with few exceptions, of which England was the most notable.
Most of the practitioners of this period adhered to the doctrine
of the magnetic fluid emanating from the operator to his patient,
and the acceptance of this doctrine was commonly combined
with belief in phrenology, astrology and the influence of metals
and magnets, externally applied, in curing disease and in producing
a variety of strange sensations and other affections of the
mind. These beliefs, claiming to rest upon carefully observed
facts, were given a new elaboration and a more imposing claim
to be scientifically established by the doctrine of odylic force
propounded by Baron Karl von Reichenbach. In this mass
of ill-based assertion and belief the valuable truths of “animal
magnetism” and the psychological explanations of them given
by Bertrand were swamped and well-nigh lost sight of. For it
was this seemingly inseparable association between the facts of
hypnotism and these bizarre practices and baseless beliefs that
blinded the larger and more sober part of the scientific world,
and led them persistently to assert that all this group of alleged
phenomena was a mass of quackery, fraud and superstition.
And the fact that magnetism was practised for pecuniary gain,
often in a shameless manner, by exponents who claimed to cure
by its means every conceivable ill, rendered this attitude on the
part of the medical profession inevitable and perhaps excusable,
though not justifiable. It was owing to this baleful association
that John Elliotson, one of the leading London physicians of that
time, who became an ardent advocate of “magnetism” and who
founded and edited the Zoist in the interests of the subject,
was driven out of the profession. This association may perhaps
be held, also, to excuse the hostile attitude of the medical
profession towards James Esdaile, a surgeon, who, practising
in a government hospital in Calcutta among the natives of India,
performed many major operations, such as the amputation of
limbs, painlessly and with the most excellent results by aid of
the “magnetic” sleep. For both Elliotson and Esdaile, though
honourable practitioners, accepted the doctrine of the “magnetic”
fluid and many of the erroneous beliefs that commonly were
bound up with it.
In 1841 James Braid, a surgeon of Manchester, rediscovered
independently Bertrand’s physiological and psychological explanations
of the facts, carried them further, and placed
“hypnotism,” as he named the study, on a sound basis. Braid
showed that subjects in “magnetic” sleep, far from being in a
profoundly insensitive condition, are often abnormally susceptible
to impressions on the senses, and showed that many of the
peculiarities of their behaviour were due to suggestions, made
verbally or otherwise, but unintentionally, by the operator or
by onlookers.
It seems, on looking back on the history of hypnotism, that at
this time it was in a fair way to secure general recognition as a
most interesting subject of psychological study and a valuable
addition to the resources of the physician. But it was destined
once more to be denied its rights by official science and to fall
back into disrepute. This was due to the coincidence about the
year 1848 of two events of some importance, namely—the discovery
of the anaesthetic properties of chloroform and the sudden
rise of modern spiritualism. The former afforded a very convenient
substitute for the most obvious practical application
of hypnotism, the production of anaesthesia during surgical
operations; the latter involved it once more in a mass of fraud
and superstition, and, for the popular mind, drove it back to the
region of the marvellous, the supernatural and the dangerous,
made it, in fact, once more a branch of the black art.
From this time onward there took place a gradual differentiation
of the “animal magnetism” of the 18th century into two
diverging branches, hypnotism and spiritualism, two branches
which, however, are not yet entirely separated and, perhaps,
never will be. At the same time the original system of “animal
magnetism” has lived on in an enfeebled condition and is now
very nearly, though not quite, extinct.
In the development of hypnotism since the time of Braid we
may distinguish three lines, the physiological, the psychological
and the pathological. The last may be dismissed in a few words.
Its principal representative was J. M. Charcot, who taught at
the Salpêtrière in Paris that hypnosis is essentially a symptom
of a morbid condition of hysteria or hystero-epilepsy. This
doctrine, which, owing to the great repute enjoyed by Charcot,
203
has done much to retard the application of hypnotism, is now
completely discredited. The workers of the physiological party
attached special importance to the fixation of the eyes, or to
other forms of long continued and monotonous, or violent, sensory
stimulation in the induction of hypnosis. They believed that by
acting on the senses in these ways they induced a peculiar condition
of the nervous system, which consisted in the temporary
abolition of the cerebral functions and the consequent reduction
of the subject to machine-like unconscious automatism. The
leading exponent of this view was R. Heidenhain, professor of
physiology at Breslau, whose experimental investigations played
a large part in convincing the scientific world of the genuineness
of the leading symptoms of hypnosis. The purely psychological
doctrine of hypnosis puts aside all physical and physiological influences
and effects as of but little or no importance, and seeks
a psychological explanation of the induction of hypnosis and of
all the phenomena. This dates from 1884, when H. Bernheim,
professor of medicine at Nancy, published his work De la Suggestion
(republished in 1887 with a second part on the therapeutics
of hypnotism). Bernheim was led to the study of hypnotism
by A. A. Liébeault, who for twenty years had used it very
largely and successfully in his general practice among the poor
of Nancy. Liébeault rediscovered independently, and Bernheim
made known to the world the truths, twice previously discovered
and twice lost sight of, that expectation is a most important
factor in the induction of hypnosis, that increased suggestibility
is its essential symptom, and that in general the operator works
upon his patient by mental influences. Although they went too far
in the direction of ignoring the peculiarity of the state of the brain
in hypnosis and the predisposing effect of monotonous sensory
stimulation, and in seeking to identify hypnosis with normal
sleep, the views of the Nancy investigators have prevailed, and
are now in the main generally accepted. Their methods of verbal
suggestion have been adopted by leading physicians in almost
all civilized countries and have been proved to be efficacious
in the relief of many disorders; and as a method of psychological
investigation hypnotism has proved, especially in the hands of
the late Ed. Gurney, of Dr Pierre Janet and of other investigators,
capable of throwing much light on the constitution of the mind,
has opened up a number of problems of the deepest interest,
and has done more than any other of the many branches of
modern psychology to show the limitations and comparative
barrenness of the old psychology that relied on introspection
alone and figured as a department of general philosophy. In
England, “always the last to enter into the general movement
of the European mind,” the prejudice, incredulity and ignorant
misrepresentation with which hypnotism has everywhere
been received have resisted its progress more stubbornly than
elsewhere; but even in England its reality and its value as a
therapeutic agent have at last been officially recognized. In
1892, just fifty years after Braid clearly demonstrated the facts
and published explanations of them almost identical with those
now accepted, a committee of the British Medical Association
reported favourably upon hypnotism after a searching investigation;
it is now regularly employed by a number of physicians of
high standing, and the formation in 1907 of “The Medical Society
for the Study of Suggestive Therapeutics” shows that the footing
it has gained is likely to be made good.
Induction of Hypnosis.—It has now been abundantly proved
that hypnosis can be induced in the great majority of normal
persons, provided that they willingly submit themselves to the
process. Several of the most experienced operators have succeeded
in hypnotizing more than 90% of the cases they have
attempted, and most of them are agreed that failure to induce
hypnosis in any case is due either to lack of skill and tact on
the part of the operator, or to some unfavourable mental condition
of the subject. It has often been said that some races or
peoples are by nature more readily hypnotizable than others;
of the French people especially this has been maintained. But
there is no sufficient ground for this statement. The differences
that undoubtedly obtain between populations of different
regions in respect to the ease or difficulty with which a large
proportion of all persons can be hypnotized are sufficiently
explained by the differences of the attitude of the public towards
hypnotism; in France, e.g., and especially in Nancy, hypnotism
has been made known to the public chiefly as a recognized
auxiliary to the better known methods of medical treatment,
whereas in England the medical profession has allowed the public
to make acquaintance with hypnotism through the medium of
disgusting stage-performances whose only object was to raise a
laugh, and has, with few exceptions, joined in the general chorus
of condemnation and mistrust. Hence in France patients
submit themselves with confidence and goodwill to hypnotic
treatment, whereas in England it is still necessary in most cases
to remove an ill-based prejudice before the treatment can be
undertaken with hope of success. For the confidence and goodwill
of the patient are almost essential to success, and even after
hypnosis has been induced on several occasions a patient may
be so influenced by injudicious friends that he cannot again
be hypnotized or, if hypnotized, is much less amenable to the
power of suggestion. Various methods of hypnotization are
current, but most practitioners combine the methods of Braid
and of Bernheim. After asking the patient to resign himself
passively into their hands, and after seating him in a comfortable
arm-chair, they direct him to fix his eyes upon some small
object held generally in such a position that some slight muscular
strain is involved in maintaining the fixation; they then suggest
to him verbally the idea or expectation of sleep and the sensations
that normally accompany the oncoming of sleep, the heaviness
of the eyes, the slackness of the limbs and so forth; and
when the eyes show signs of fatigue, they either close them
by gentle pressure or tell the subject to close them. Many also
pass their hands slowly and regularly over the face, with or
without contact. The old magnetizers attached great importance
to such “passes,” believing that by them the “magnetic fluid”
was imparted to the patient; but it seems clear that, in so far
as they contribute to induce hypnosis, it is in their character
merely of gentle, monotonous, sensory stimulations. A well-disposed
subject soon falls into a drowsy state and tends to pass
into natural sleep; but by speech, by passes, or by manipulating
his limbs the operator keeps in touch with him, keeps his waning
attention open to the impressions he himself makes. Most subjects
then find it difficult or impossible to open their eyes or to
make any other movement which is forbidden or said to be
impossible by the operator, although they may be fully conscious
of all that goes on about them and may have the conviction that
if they did but make an effort they could break the spell. This
is a light stage of hypnosis beyond which some subjects can
hardly be induced to pass and beyond which few pass at the first
attempt. But on successive occasions, or even on the first
occasion, a favourable subject passes into deeper stages of
hypnosis. Many attempts have been made to distinguish clearly
marked and constantly occurring stages. But it seems now clear
that the complex of symptoms displayed varies in all cases with
the idiosyncrasies of the subject and with the methods adopted
by the operator. In many subjects a waxy rigidity of the limbs
appears spontaneously or can be induced by suggestion; the
limbs then retain for long periods without fatigue any position
given them by the operator. The most susceptible subjects
pass into the stage known as artificial somnambulism. In this
condition they continue to respond to all suggestions made by
the operator, but seem as insensitive to all other impressions as a
person in profound sleep or in coma; and on awaking from this
condition they are usually oblivious of all that they have heard,
said or done during the somnambulistic period. When in this
last condition patients are usually more profoundly influenced by
suggestions, especially post-hypnotic suggestions, than when in
the lighter stages; but the lighter stages suffice for the production
of many therapeutic effects. When a patient is completely
hypnotized, his movements, his senses, his ideas and, to
some extent, even the organic processes over which he has no
voluntary control become more or less completely subject to
the suggestions of the operator; and usually he is responsive
to the operator alone (rapport) unless he is instructed by the
204
latter to respond also to the suggestions of other persons. If
left to himself the hypnotized subject will usually awake to his
normal state after a period which is longer in proportion to the
depth of hypnosis; and the deeper stages seem to pass over into
normal sleep. The subject can in almost every case be brought
quickly back to the normal state by the verbal command of the
operator.
The Principal Effects produced by Suggestion during Hypnosis.—The
subject may not only be rendered incapable of contracting
any of the muscles of the voluntary system, but may also be
made to use them with extraordinarily great or sustained force
(though by no means in all cases). He can with difficulty refrain
from performing any action commanded by the operator, and
usually carries out any simple command without hesitation.
Any one of the sense-organs, or any sensory region such as the
skin or deep tissues of one limb may be rendered anaesthetic by
verbal suggestion, aided perhaps by some gentle manipulation
of the part. On this fact depends the surgical application of
hypnotism. Sceptical observers are always inclined to doubt the
genuineness of the anaesthesia produced by a mere word of
command, but the number of surgical operations performed under
hypnotic anaesthesia suffices to put its reality beyond all question.
A convincing experiment may, however, be made on
almost any good subject. Anaesthesia of one eye may be
suggested and its reality tested in the following way. Anaesthesia
of the left eye may be suggested, and the subject be instructed to
fix his gaze on a distant point and to give some signal as soon
as he sees the operator’s finger in the peripheral field of
view. The operator then brings his finger slowly from behind
and to the right forwards towards the subject’s line of sight.
The subject signals as soon as it crosses the normal temporal
boundary of the field of view of the right eye. The operator then
brings his finger forward from a point behind and to the left of
the subject’s head. The subject allows it to cross the monocular
field of the left eye and signals only when the finger enters the
field of vision of the right eye across its nasal boundary. Since
few persons, other than physiologists or medical men, are aware
of the relations of the boundaries of the monocular and binocular
fields of vision, the success of this experiment affords proof that
the finger remains invisible to the subject during its passage
across the monocular field of the left eye. The abolition of pain,
especially of neuralgias, the pain of rheumatic and other inflammations,
which is one of the most valuable applications of
hypnotism, is an effect closely allied to the production of such
anaesthesia.
It has often been stated that in hypnosis the senses may be
rendered extraordinarily acute or hyperaesthetic, so that impressions
too faint to affect the senses of the normal person
may be perceived by the hypnotized subject; but in view of the
fact that most observers are ignorant of the normal limits of
sensitivity and discrimination, all such statements must be
received with caution, until we have more convincing evidence
than has yet been brought forward.
Positive and Negative Hallucinations are among the most
striking effects of hypnotic suggestion. A good subject may be
made to experience an hallucinatory perception of almost any
object, the more easily the less unusual and out of harmony
with the surroundings is the suggested object. He may, e.g.,
be given a blank card and asked if he thinks it a good photograph
of himself. He may then assent and describe the photograph in
some detail, and, what is more astonishing, he may pick out the
card as the one bearing the photograph, after it has been mixed
with other similar blank cards. This seems to be due to the part
played by points de repère, insignificant details of surface or
texture, which serve as an objective basis around which the
hallucinatory image is constructed by the pictorial imagination
of the subject. A negative hallucination may be induced by
telling the subject that a certain object or person is no longer
present, when he ignores in every way that object or person.
This is more puzzling than the positive hallucination and will be
referred to again in discussing the theory of hypnosis. Both
kinds of hallucination tend to be systematically and logically
developed; if, e.g., the subject is told that a certain person is no
longer visible, he may become insensitive to impressions made on
any sense by that person.
Delusions, or false beliefs as to their present situation or
past experiences may be induced in many subjects. On being
assured that he is some other person, or that he is in some
strange situation, the subject may accept the suggestion and
adapt his behaviour with great histrionic skill to the induced
delusion. It is probable that many, perhaps all, subjects are
vaguely aware, as we sometimes are in dreams, that the delusions
and hallucinations they experience are of an unreal nature.
In the lighter stages of hypnosis a subject usually remembers
the events of his waking life, but in the deeper stages he is apt,
while remembering the events of previous hypnotic periods, to be
incapable of recalling his normal life; but in this respect, as also
in respect to the extent to which on awaking he remembers the
events of the hypnotic period, the suggestions of the operator
usually play a determining part.
Among the organic changes that have been produced by
hypnotic suggestion are slowing or acceleration of the cardiac and
respiratory rhythms; rise and fall of body-temperature through
two or three degrees; local erythema and even inflammation
of the skin with vesication or exudation of small drops of blood;
evacuation of the bowel and vomiting; modifications of the
secretory activity of glands, especially of the sweat-glands.
Post-hypnotic Effects.—Most subjects in whom any appreciable
degree of hypnosis can be induced show some susceptibility to
post-hypnotic suggestion, i.e. they may continue to be influenced,
when restored to the fully waking state, by suggestions made
during hypnosis, more especially if the operator suggests that
this shall be the case; as a rule, the deeper the stage of hypnosis
reached, the more effective are post-hypnotic suggestions. The
therapeutic applications of hypnotism depend in the main upon
this post-hypnotic continuance of the working of suggestions.
If a subject is told that on awaking, or on a certain signal, or
after the lapse of a given interval of time from the moment of
awaking, he will perform a certain action, he usually feels some
inclination to carry out the suggestion at the appropriate moment.
If he remembers that the action has been suggested to him he
may refuse to perform it, and if it is one repugnant to his moral
nature, or merely one that would make him appear ridiculous,
he may persist in his refusal. But if the action is of a simple
and ordinary nature he will usually perform it, remarking that
he cannot be comfortable till it is done. If the subject was deeply
hypnotized and remembers nothing of the hypnotic period, he
will carry out the post-hypnotic suggestion in almost every case,
no matter how complicated or absurd it may be, so long as it is
not one from which his normal self would be extremely averse;
and he will respond appropriately to the suggested signals,
although he is not conscious of their having been named; he
will often perform the action in a very natural way, and will,
if questioned, give some more or less adequate reason for it.
Such actions, determined by post-hypnotic suggestions of which
no conscious memory remains, may be carried out even after the
lapse of many weeks or even months. Inhibitions of movement,
anaesthesia, positive and negative hallucinations, and delusions
may also be made to persist for brief periods after the termination
of hypnosis; and organic effects, such as the action of the
bowels, the oncoming of sleep and the cessation of pain, may be
determined by post-hypnotic suggestion. In short, it may be said
that in a good subject all the kinds of suggestion which will
take effect during hypnosis will also be effective if given as
post-hypnotic
suggestions.
Theory of the Hypnotic State.—Very many so called theories
of hypnosis have been propounded, but few of them demand
serious consideration. One author ascribes all the symptoms
to cerebral anaemia, another to cerebral congestion, a third to
temporary suppression of the functions of the cerebrum, a fourth
to abnormal cerebral excitability, a fifth to the independent
functioning of one hemisphere. Another seeks to explain all the
facts by saying that in hypnosis our normal consciousness disappears
and is replaced by a dream-consciousness; and yet
205
another by the assumption that every human organism comprises
two mental selves or personalities, a normal one and one
which only comes into activity during sleep and hypnosis.
Most of these “theories” would, even if true, carry us but a
little way towards a complete understanding of the facts. There
is, however, one theory or principle of explanation which is
now gradually taking shape under the hands of a number of the
more penetrating workers in this field, and which does seem to
render intelligible many of the principle facts. This is the
theory of mental dissociation.
It is clear that a theory of hypnosis must attempt to give
some account of the peculiar condition of the brain which is
undoubtedly present as an essential feature of the state. It is
therefore not enough to say with Bernheim that hypnosis is a
state of abnormally increased suggestibility produced by suggestion;
nor is it enough, though it is partially true, to say that it
is a state of mono-ideism or one of abnormally great concentration
of attention. Any theory must be stated in terms of
physiological psychology, it must take account of both the
psychical and the nervous peculiarities of the hypnotic state;
it must exhibit the physiological condition as in some degree
similar to that obtaining in normal sleep; but principally it
must account for that abnormally great receptivity for ideas,
and that abnormally intense and effective operation of ideas so
received, which constitute abnormally great suggestibility.
The theory of mental dissociation may be stated in purely
mental terms, or primarily in terms of nervous structure and
function, and the latter mode of statement is probably the
more profitable at the present time. The increased effectiveness
of ideas might be due to one of two conditions: (1) it might
be that certain tracts of the brain or the whole brain were in a
condition of abnormally great excitability; or (2) an idea
might operate more effectively in the mind and on the body,
not because it, or the underlying brain-process was more intense
than normally, but because it worked out its effects free from
the interference of contrary or irrelevant ideas that might
weaken its force. It is along this second line that the theory
of mental dissociation attempts to explain the increased suggestibility
of hypnosis. To understand the theory we must bear
in mind the nature of mental process in general and of its nervous
concomitants. Mental process consists in the interplay, not
merely of ideas, but rather of complex dispositions which are
the more or less enduring conditions of the rise of ideas to consciousness.
Each such disposition seems capable of remaining
inactive or quiescent for long periods, and of being excited in
various degrees, either by impressions made upon the sense-organs
or by the spread of excitement from other dispositions.
When its excitement rises above a certain pitch of intensity,
the corresponding idea rises to the focus of consciousness.
These dispositions are essential factors of all mental process,
the essential conditions of all mental retention. They may be
called simply mental dispositions, their nature being left undefined;
but for our present purpose it is advantageous to regard
them as neural dispositions, complex functional groups of nervous
elements or neurones. The neurones of each such group must
be conceived as being so intimately connected with one another
that the excitement of any part of the group at once spreads
through the whole group or disposition, so that it always functions
as a unit. The whole cerebrum must be conceived as consisting
of a great number of such dispositions, inextricably interwoven,
but interconnected in orderly fashion with very various degrees
of intimacy; groups of dispositions are very intimately connected
to form neural systems, so that the excitement of any one member
of such a system tends to spread in succession to all the other
members. On the other hand, it is a peculiarity of the reciprocal
relations of all such dispositions and systems that the excitement
of any one to such a degree that the corresponding idea rises
to consciousness prevents or inhibits the excitement of others,
i.e. all of them are in relations of reciprocal inhibition with
one another (see Muscle and Nerve). The excitement of dispositions
associated together to form a system tends towards
some end which, either immediately or remotely, is an action,
a bodily movement, in many cases a movement of the organs
of speech only. Now we know from many exact experiments
that the neural dispositions act and react upon one another to
some extent, even when they are excited only in so feeble a
degree that the corresponding ideas do not rise to consciousness.
In the normal state of the brain, then, when any idea is present
to consciousness, the corresponding neural disposition is in a
state of dominant excitement, but the intensity of that excitement
is moderated, depressed or partially inhibited by the
sub-excitement of many rival or competing dispositions of
other systems with which it is connected. Suppose now that
all the nervous connexions between the multitudinous dispositions
of the cerebrum are by some means rendered less
effective, that the association-paths are partially blocked or
functionally depressed; the result will be that, while the most
intimate connexions, those between dispositions of any one
system remain functional or permeable, the weaker less intimate
connexions, those between dispositions belonging to different
systems will be practically abolished for the time being; each
system of dispositions will then function more or less as an
isolated system, and its activity will no longer be subject to the
depressing or inhibiting influence of other systems; therefore
each system, on being excited in any way, will tend to its end
with more than normal force, being freed from all interferences;
that is to say, each idea or system of ideas will tend to work
itself out and to realize itself in action immediately, without
suffering the opposition of antagonistic ideas which, in the
normal state of the brain, might altogether prevent its realization
in action.
The theory of mental dissociation assumes that the abnormal
state of the brain that obtains during hypnosis is of this kind,
a temporary functional depression of all, or of many of the
associations or nervous links between the neural dispositions;
that is, it regards hypnosis as a state of relative dissociation.
The lighter the stage of hypnosis the slighter is the degree of
dissociation, the deeper the stage the more nearly complete
is the dissociation.
It is not essential that the theory should explain in what
change this stage of dissociation consists, but a view compatible
with all that we know of the functions of the central nervous
system may be suggested. The connexions between neural
dispositions involve synapses or cell-junctions, and these seem
to be the places of variable resistance which demarcate the dispositions
and systems; and there is good reason to think that
their resistances vary with the state of the neurones which they
connect, being lowered when these are excited and raised when
their excitement ebbs. Now, in the waking state, the varied
stimuli, which constantly rain upon all the sense-organs, maintain
the whole cerebrum in a state of sub-excitement, keep all the
cerebral neurones partially charged with free nervous energy.
When the subject lies down to sleep or submits himself to the
hypnotizer he arrests as far as possible the flow of his thoughts,
and the sensory stimuli are diminished in number and intensity.
Under these conditions the general cerebral activity tends to
subside, the free energy with which the cerebral neurones are
charged ebbs away, and the synaptic resistances rise proportionally;
then the effect of sensory impressions tends to be
confined to the lower nervous level, and the brain tends to
come to rest. If this takes place the condition of normal sleep
is realized. But in inducing hypnosis the operator, by means
of his words and manipulations, keeps one system of ideas
and the corresponding neural system in activity, namely, the
ideas connected with himself; thus he keeps open one channel
of entry to the brain and mind, and through this one open
channel he can introduce whatever ideas he pleases; and the
ideas so introduced then operate with abnormally great effect
because they work in a free field, unchecked by rival ideas and
tendencies.
This theory of relative dissociation has two great merits:
in the first place it goes far towards enabling us to understand
in some degree most of the phenomena of hypnosis; secondly,
we have good evidence that dissociation really occurs in deep
206
hypnosis and in some allied states. Any one may readily work
out for himself the application of the theory to the explanation
of the power of the operator’s suggestions to control movement,
to induce anaesthesia, hallucinations and delusions, and to
exert on the organic processes an influence greater than can
be exerted by mental processes in the normal state of the brain.
But the positive evidence of the occurrence of dissociation is
a matter of great psychological interest and its nature must
be briefly indicated. The phenomena of automatic speech
and writing afford the best evidence of cerebral dissociation.
Many persons can, while in an apparently normal or but very
slightly abnormal condition, produce automatic writing, i.e.
intelligibly written sentences, in some cases long connected
passages, of whose import they have no knowledge, their self-conscious
intelligence being continuously directed to some
other task. The carrying out of post-hypnotic suggestions
affords in many cases similar evidence. Thus a subject may be
told that after waking he will perform some action when a
given signal, such as a cough, is repeated for the fifth time.
In the post-hypnotic state he remains unaware of his instructions,
is not conscious of noting the signals, and yet carries out the
suggestion at the fifth signal, thereby proving that the signals
have been in some sense noted and counted. Many interesting
varieties of this experiment have been made, some of much
greater complexity; but all agreeing in indicating that the
suggested action is prepared for and determined by cerebral
processes that do not affect the consciousness of the subject,
but seem to occur as a system of processes detached from the
main stream of cerebral activity; that is to say, they imply
the operation of relatively dissociated neural systems.
Many authorities go further than this; they argue that,
since actions of the kind described are determined by processes
which involve operations, such as counting, that we are
accustomed to regard as distinctly mental in character and that
normally involve conscious activity, we must believe that in
these cases also consciousness or psychical activity is involved,
but that it remains as a separate system or stream of consciousness
concurrent with the normal or personal consciousness.
In recent years the study of various abnormal mental states,
especially the investigations by French physicians of severe forms
of hysteria, have brought to light many facts which seem to
justify this assumption of a secondary stream of consciousness,
a co- or sub-consciousness coexistent with the personal consciousness;
although, from the nature of the case, an absolute proof
of such co-consciousness can hardly be obtained. The co-consciousness
seems to vary in degree of complexity and coherence
from a mere succession of fragmentary sensations to an organized
stream of mental activity, which may rival in all respects the
primary consciousness; and in cases of the latter type it is usual
to speak of the presence of a secondary personality. The co-consciousness
seems in the simpler cases, e.g. in cases of hysterical
or hypnotic anaesthesia, to consist of elements split off from the
normal primary consciousness, which remains correspondingly
poorer; and the assumption is usually made that such a stream
of co-consciousness is the psychical correlate of groups and
systems of neurones dissociated from the main mass of cerebral
neurones. If, in spite of serious objections, we entertain this
conception, we find that it helps us to give some account of various
hypnotic phenomena that otherwise remain quite inexplicable;
some such conception seems to be required more particularly
by the facts of negative hallucination and the execution of
post-hypnotic suggestions involving such operations as counting
and exact discrimination without primary consciousness.
Supernormal Hypnotic Phenomena.—The facts hitherto considered,
strange and perplexing as many of them are, do not
seem to demand for their explanation any principles of action
fundamentally different from those operative in the normal
human mind. But much of the interest that has centred in
hypnotism in recent years has been due to the fact that some
of its manifestations seem to go beyond all such principles of
explanation, and to suggest the reality of modes of influence
and action that science has not hitherto recognized. Of these
by far the best attested are the post-hypnotic unconscious
reckoning of time and telepathy or “thought-transference”
(for the latter see Telepathy). The post-hypnotic reckoning
and noting of the lapse of time seems in some instances to have
been carried out, in the absence of all extraneous aids and with
complete unconsciousness on the part of the normal personality,
with such extreme precision that the achievement cannot be
accounted for by any intensification of any faculty that we at
present recognize or understand. Thus, Dr Milne Bramwell
has reported the case of a patient who, when commanded in
hypnosis to perform some simple action after the lapse of many
thousands of minutes, would carry out the suggestion punctually
to the minute, without any means of knowing the exact time
of day at which the suggestion was given or the time of day at
the moment its performance fell due; more recently a similar
case, even more striking in some respects, has been carefully
observed and described by Dr T. W. Mitchell. Other reported
phenomena, such as telaesthesia or clairvoyance, and telekinesia,
are hardly sufficiently well attested to demand serious consideration
in this place.
Medical Applications of Hypnotism.—The study and practice
of hypnotism is not yet, and probably never will be, regarded
as a normal part of the work of the general practitioner. Its
successful application demands so much time, tact, and special
experience, that it will probably remain, as it is now, and as it
is perhaps desirable that it should remain, a specialized branch
of medical practice. In England it is only in recent years that
it has been possible for a medical man to apply it in his practice
without incurring professional odium and some risk of loss of
reputation. That, in certain classes of cases, it may effect a cure
or bring relief when all other modes of treatment are of no avail
is now rapidly becoming recognized; but it is less generally
recognized that it may be used with great advantage as a supplement
to other modes of treatment in relieving symptoms that
are accentuated by nervous irritability or mental disturbance.
A third wide field of usefulness lies before it in the cure of undesirable
habits of many kinds. Under the first heading may
be put insomnia, neuralgia, neurasthenia, hysteria in almost all
its many forms; under the second, inflammations such as that of
chronic rheumatism, contractures and paralyses resulting from
gross lesion of the brain, epilepsy, dyspepsia, menstrual irregularities,
sea-sickness; under the third, inebriety, the morphia
and other drug habits, nail-biting, enuresis nocturna, masturbation,
constipation, facial and other twitchings. In pronounced
mental diseases hypnotism seems to be almost useless; for in
general terms it may be said that it can be applied most effectively
where the brain, the instrument through which it works, is sound
and vigorous. The widespread prejudice against the use of
hypnotism is no doubt largely due to the marvellous and (to
most minds) mysterious character of the effects producible by
its means; and this prejudice may be expected to diminish as
our insight into the mode of its operation deepens. The more
purely bodily results achieved by hypnotic suggestion become
in some degree intelligible if we regard it as a powerful means of
diverting nervous energy from one channel or organ to others,
so as to give physiological rest to an overworked organ or tissue,
or so as to lead to the atrophy of one nervous habit and the replacement
of it by a more desirable habit. And in the cure of
those disorders which involve a large mental element the essential
part played by it is to drive out some habitually recurrent idea
and to replace it by some idea, expectation or conviction of
healthy tendency.
It seems clear that the various systems of “mind-curing”
in the hands of persons lacking all medical training, which are
now so frequently the cause of distressing and needless disasters,
owe their rapid spread to the fact that the medical profession
has hitherto neglected to attach sufficient importance to the
mental factor in the causation and cure of disease; and it seems
clear, too, that a more general and more intelligent appreciation
of the possibilities of hypnotic treatment would constitute the
best means at the disposal of the profession for combating this
growing evil.
207
The Dangers of Hypnotism.—Much has been written on this
head of late years, and some of the enthusiastic advocates of
hypnotic treatment have done harm to their cause by ignoring
or denying in a too thoroughgoing manner the possibility of
undesirable results of the spread of the knowledge and practice
of hypnotism. Like all powerful agencies, chloroform or morphia,
dynamite or strong electric currents, hypnotic suggestion can
only be safely used by those who have special knowledge and
experience, and, like them, it is liable to abuse. There is little
doubt that, if a subject is repeatedly hypnotized and made to
entertain all kinds of absurd delusions and to carry out very
frequently post-hypnotic suggestions, he may be liable to some
ill-defined harm; also, that an unprincipled hypnotizer might
secure an undue influence over a naturally weak subject.
But there is no ground for the belief that hypnotic treatment,
applied with good intentions and reasonable care and judgment,
does or can produce deleterious effects, such as weakening of the
will or liability to fall spontaneously into hypnosis. All physicians
of large experience in hypnotic practice are in agreement in respect
to this point. But some difference of opinion exists as to the
possibility of deliberately inducing a subject to commit improper
or criminal actions during hypnosis or by post-hypnotic suggestion.
There is, however, no doubt that subjects retain even in
deep hypnosis a very considerable power of resistance to any
suggestion that is repugnant to their moral nature; and it has
been shown that, on some cases in which a subject in hypnosis
is made to perform some ostensibly criminal action, such as
firing an unloaded pistol at a bystander or putting poison into a
cup for him to drink, he is aware, however obscurely, of the unreal
nature of the situation. Nevertheless it must be admitted that
a person lacking in moral sentiments might be induced to commit
actions from which in the normal state he would abstain, if only
from fear of punishment; and it is probable that a skilful and
evil-intentioned operator could in some cases so deceive a well-disposed
subject as to lead him into wrong-doing. The proper
precaution against such dangers is legislative regulation of the
practice of hypnotism such as is already enforced in some
countries.
Bibliography.—The literature of hypnotism has increased in
volume at a rapid rate during recent years. Of recent writings the
following may be mentioned as among the most important:—Treatment
by Hypnotism and Suggestion by C. Lloyd Tuckey, M.D. (5th ed.,
London, 1907); Hypnotism, its History, Practice and Theory, by
J. Milne Bramwell, M.B. (2nd ed., London, 1906); Hypnotism, by
Albert Moll (5th ed., London, 1901). All these three books give good
general accounts of hypnotism, the first being the most strictly
medical, the last the most general in its treatment. See also Hypnotism:
or Suggestion in Psycho-Therapy, by August Forel (translated
from the 5th German ed. by G. H. W. Armit, London, 1906); a
number of papers by Ed. Gurney, and by Ed. Gurney and F. W. H.
Myers in Proc. of the Soc. for Psychical Research, especially “The
Stages of Hypnotism,” in vol. ii.; also some more recent papers in
the same journal by other hands; chapter on Hypnotism in Human
Personality and its Survival of bodily Death, by F. W. H. Myers
(London, 1903); The Psychology of Suggestion, by Boris Sidis, Ph.D.
(New York, 1898); “Zur Psychologie der Suggestion,” by Prof.
Th. Lipp, and other papers in the Zeitschrift für Hypnotismus. Of
special historical interest are the following:—Étude sur le zoomagnétisme,
par A. A. Liébeault (Paris, 1883); Hypnotisme, suggestion,
psycho-thérapie, par Prof. Bernheim (Paris, 1891); Braid on
Hypnotism (a new issue of James Braid’s Neurypnology), edited by
A. E. Waite (London, 1899); Traité du somnambulisme, by A.
Bertrand (Paris, 1826). A full bibliography is appended to Dr
Milne Bramwell’s Hypnotism.
(W. McD.)
HYPOCAUST (Gr. ὑπόκαυστον: ὑπό, beneath, and καυείν,
to burn), the term given to the chamber formed under the floors
of the Roman baths, through which the hot air from the furnace
passed, sometimes to a single flue, as in the case of the tepidarium,
but in the calidarium and sweating-room to a series of flues
placed side by side forming the lining of the walls. The floor
of the hot-air chamber consisted of tiles, 2 ft. square, laid on a
bed of concrete; on this a series of dwarf piers 2 ft. high were
built of 8-in. square tiles placed about 16 in. apart, which carried
the floor of the hall or room; this floor was formed of a bed of
concrete covered with layers of pounded bricks and marble
cement, on which the marble pavement in slabs or tesserae was
laid. In colder countries, as for instance in Germany and
England, the living rooms were all heated in a similar way, and
round Trèves (Trier) both systems have been found in two or
three Roman villas, with the one flue for the ordinary rooms and
several wall flues for the hot baths. In England these hypocausts
are found in every Roman settlement, and the chief
interest in these is centred in the magnificent mosaic pavements
with which the principal rooms were laid. Many of the pavements
found in London and elsewhere have been preserved in the
British or the Guildhall museums; and in some of the provincial
towns, such as Leicester and Lincoln, they remain in situ many
feet below the present level of the town.
HYPOCHONDRIASIS (synonyms—“the spleen,” “the
vapours”), a medical term (from τὸ ὑποχόνδριον, τὰ ὑποχόνδρια,
the soft part of the body immediately under the χόνδρος or cartilage
of the breast-bone) given by the ancients, and indeed by physicians
down to the time of William Cullen, to diseases or derangements
of one or more of the abdominal viscera. Cullen (Clinical
Lectures, 1777) classified it amongst nervous diseases, and Jean
Pierre Falret (1794-1870) more fully described it as a morbid
condition of the nervous system characterized by depression of
feeling and false beliefs as to an impaired state of the health.
The subjects of hypochondriasis are for the most part members
of families in which hereditary predisposition to degradation of
the nervous system is strong, or those who have suffered from
morbid influences affecting this system during the earlier years of
life. It may be dependent on depressing disease affecting the
general system, but under such circumstances it is generally
so complicated with the symptoms of hysteria as to render
differentiation difficult (see Hysteria). Hypochondriasis is
often handed down from one generation to another in its individual
form, but it is also not unfrequently to be met with in
an individual as the sole manifestation in him of a family tendency
to insanity. In its most common form it is manifested by simple
false belief as to the state of the health, the intellect being otherwise
unaffected. We may instance the “vapourish” woman or
the “splenetic” as terms society has applied to its milder
manifestations. Such persons are constantly asserting a weak
state of health although no palpable cause can be discovered.
In its more definite phases pain or uneasy sensations are referred
by the patient to some particular region, generally the abdomen,
the heart or the head. That these are subjective is apparent
from the fact that the general health is good: all the functions of
the various systems are duly performed; the patient eats and
sleeps well; and, when any circumstance temporarily overrides
the false belief, he is happy and comfortable. No appeal to the
reason is of any avail, and the hypochondriac idea so dominates
his existence as to render him unable to perform the ordinary
duties of life. In its most aggravated form hypochondriasis
amounts to actual insanity, delusions arising as to the existence
of living creatures in the intestines or brain, or to the effect
that the body is materially changed; e.g. into glass, wood, &c.
The symptoms of this condition may be remittent; they may
even disappear for years, and only return on the advent of some
exciting cause. Suicide is occasionally committed in order to
escape from the constant misery. Recovery can only be looked
for by placing the patient under such morally hygienic conditions
as may help to turn his mind to other matters. (See also
Neuropathology.)
HYPOCRISY, pretence, or false assumption of a high character,
especially in regard to religious belief or practice. The Greek
ὑπόκρισις, from which the word is derived through the Old
French, meant primarily the acting of a part on the stage, from
ὑποκρίνεσθαι, to give an answer, to speak dialogue, play a part
on the stage, hence to practice dissimulation.
HYPOSTASIS, in theology, a term frequently occurring in the
Trinitarian controversies of the 4th and 5th centuries. According
to Irenaeus (i. 5, 4) it was introduced into theology by Gnostic
writers, and in earliest ecclesiastical usage appears, as among
the Stoics, to have been synonymous with οὐσία. Thus Dionysius
of Rome (cf. Routh, Rel. Sacr. iii. 373) condemns the attempt
to sever the Godhead into three separate hypostases and three
deities, and the Nicene Creed in the anathemas speaks of
208
ὲξ ἑτέρας ὑποστάσεως ἢ οὐσίας. Alongside, however, of this persistent
interchange there was a desire to distinguish between the
terms, and to confine ὑπόστασις to the Divine persons. This
tendency arose in Alexandria, and its progress may be seen in
comparing the early and later writings of Athanasius. That
writer, in view of the Arian trouble, felt that it was better to
speak of οὐσία as “the common undifferentiated substance of
Deity,” and ὑπόστασις as “Deity existing in a personal mode,
the substance of Deity with certain special properties” (οὐσία μετά τινων ἰδιωμάτων). At the council of Alexandria in 362 the
phrase τρεῖς ὑποστάσεις was permitted, and the work of this
council was supplemented by Basil, Gregory of Nazianzus and
Gregory of Nyssa in the formula μία οὐσία, τρεῖς ὑποστάσεις or
μία οὐσία ἐν τρίσιν ὑποστάσεσιν.
The results arrived at by these Cappadocian fathers were stated
in a later age by John of Damascus (De orth. fid. iii. 6), quoted in
R. L. Ottley, The Doctrine of the Incarnation, ii. 257.
HYPOSTYLE, in architecture, the term applied to a hall,
the flat ceiling of which is supported by columns, as in the Hall
of Columns at Karnak. In this case the columns flanking the
central avenue are of greater height than those of the side aisles,
and this admits of openings in the wall above the smaller columns,
through which light is admitted over the aisle roof, through
clerestory windows.
HYPOSULPHITE OF SODA, the name originally given to
the substance known in chemistry as sodium thiosulphate,
Na2S2O3; the earlier name is still commonly used, especially by
photographers, who employ this chemical as a fixer. In systematic
chemistry, sodium hyposulphite is a salt of hyposulphurous
acid, to which Schutzenberger gave the formula H2SO2, but
which Bernthsen showed to be H2S2O4. (See Sulphur.)
HYPOTHEC (Lat. hypotheca, Gr. ὑποθήκη), in Roman law,
the most advanced form of the contract of pledge. A specific
thing may be given absolutely to a creditor on the understanding
that it is to be given back when the creditor’s debt is paid;
or the property in the thing may be assigned to the creditor
while the debtor is allowed to remain in possession, the creditor
as owner being able to take possession if his debt is not discharged.
Here we have the kind of security known as pledge
and mortgage respectively. In the hypotheca, the property
does not pass to the creditor, nor does he get possession, but he
acquires a preferential right to have his debt paid out of the
hypothecated property; that is, he can sell it and pay himself
out of the proceeds, or in default of a purchaser he can become
the owner himself. The name and the principle have passed
into the law of Scotland, which distinguishes between conventional
hypothecs, as bottomry and respondentia, and tacit hypothecs
established by law. Of the latter the most important is the
landlord’s hypothec for rent (corresponding to distress in the law
of England), which extends over the produce of the land and the
cattle and sheep fed on it, and over stock and horses used in
husbandry. The law of agricultural hypothec long caused much
discontent in Scotland; its operation was restricted by the
Hypothec Amendment (Scotland) Act 1867, and finally by the
Hypothec Abolition (Scotland) Act 1880 it was enacted that
the “landlord’s right of hypothec for the rent of land, including
the rent of any buildings thereon, exceeding two acres in extent,
let for agriculture or pasture, shall cease and determine.” By
the same act and by the Agricultural Holdings (Scotland) Act
1883 other rights and remedies for rent, where the right of
hypothec had ceased, were given to the landlord.
HYPOTHESIS (from Gr. ὑποτιθέναι, to put under; cf.
Lat. suppositio, from sub-ponere), in ordinary language, an
explanation, supposition or assumption, which is put forward
in the absence of ascertained facts or causes. Both in ordinary
life and in the acquisition of scientific knowledge hypothesis
is all-important. A detective’s work consists largely in forming
and testing hypothesis. If an astronomer is confronted by some
phenomenon which has no obvious explanation he may postulate
some set of conditions which from his general knowledge of the
subject would or might give rise to the phenomenon in question;
he then tests his hypothesis until he discovers whether it does
or does not conflict with the facts. An example of this process
is that of the discovery of the planet Neptune: certain perturbations
of the orbit of Uranus had been observed, and it was seen
that these could be explained on the hypothesis of the existence
of a then unknown planet, and this hypothesis was verified
by actual observation. The progress of inductive knowledge is
by the formation of successive hypotheses, and it frequently
happens that the demolition of one or even many hypotheses
is the direct road to a new and accurate hypothesis, i.e. to fresh
knowledge. A hypothesis may, therefore, turn out to be entirely
wrong, yet it may be of the greatest practical use.
The recognition of the importance of hypotheses has led to
various attempts at drawing up exact rules for their formation,
but logicians are generally agreed that only very elementary
principles can be laid down. Thus a hypothesis must contain
nothing which is at variance with known facts or principles:
it should not postulate conditions which cannot be verified
empirically. J. S. Mill (Logic III. xiv. 4) laid down the principle
that a hypothesis is not “genuinely scientific” if it is “destined
always to remain a hypothesis”: it must “be of such a nature
as to be either proved or disproved by comparison with observed
facts”: in the same spirit Bacon said that in searching for
causes in nature “Deum semper excipimus.” Mill’s principle,
though sound in the abstract, has, except in a few cases, little
practical value in determining the admissibility of hypotheses,
and in practice any rule which tends to discourage hypothesis
is in general undesirable. The most satisfactory check on
hypothesis is expert knowledge in the particular field of research
by which rigorous tests may be applied. This test is roughly
of two kinds, first by the ultimate principles or presuppositions
on which a particular branch of knowledge rests, and second
by the comparison of correlative facts. Useful light is shed on
this distinction by Lotze, who contrasts (Logic, § 273) postulates
(“absolutely necessary assumptions without which the content
of the observation with which we are dealing would contradict
the laws of our thought”) with hypotheses, which he defines
as conjectures, which seek “to fill up the postulate thus abstractly
stated by specifying the concrete causes, forces or processes,
out of which the given phenomenon really arose in this
particular case, while in other cases maybe the same postulate
is to be satisfied by utterly different though equivalent combinations
of forces or active elements.” Thus a hypothesis may be
ruled out by principles or postulates without any reference to
the concrete facts which belong to that division of the subject
to explain which the hypothesis is formulated. A true hypothesis,
therefore, seeks not merely to connect or colligate two separate
facts, but to do this in the light of and subject to certain fundamental
principles. Various attempts have been made to classify
hypotheses and to distinguish “hypothesis” from a “theory”
or a mere “conjecture”: none of these have any great practical
importance, the differences being only in degree, not in kind.
The adjective “hypothetical” is used, in the same sense,
both loosely in contradistinction to “real” or “actual,” and
technically in the phrases “hypothetical judgment” and
“hypothetical syllogism.” (See Logic and Syllogism.)
See Naville, La Logique de l’hypothèse (1880), and textbooks of
logic, e.g. those of Jevons, Bosanquet, Joseph; Liebmann, Der
Klimax d. Theorien.
HYPOTRACHELIUM (Gr. ὑποτραχήλιον, the lower part of
the neck, τράχηλος), in classical architecture, the space between
the annulet of the echinus and the upper bed of the shafts,
including, according to C. R. Cockerell, the three grooves or
sinkings found in some of the older examples, as in the temple
of Neptune at Paestum and the temple of Aphaea at Aegina;
there being only one groove in the Parthenon, the Theseum and
later examples. In the temple of Ceres and the so-called Basilica
at Paestum the hypotrachelium consists of a concave sinking
carved with vertical lines suggestive of leaves, the tops of which
project forward. A similar decoration is found in the capital
of the columns flanking the tomb of Agamemnon at Mycenae,
but here the hypotrachelium projects forward with a cavetto
moulding, and is carved with triple leaves like the buds of a
209
rose. In the Roman Doric Order the term was sometimes
applied to that which is generally known as the “necking,”
the space between the fillet and the annulet.
HYPSOMETER (Gr. ὕψος, height, μέτρον, a measure), an
instrument for measuring heights which employs the principles
that the boiling-point of a liquid is lowered by diminishing
the pressure, and that the barometric pressure varies with the
height of the point of observation. The instrument consists
of a cylindrical vessel in which the liquid, usually water, is boiled,
surmounted by a jacketed column, in the outer partitions of
which the vapour circulates, while in the central one a thermometer
is placed. To deduce the height of the station from
the observed boiling-point, it is necessary to know the relation
existing between the boiling-point and pressure, and also between
the pressure and height of the atmosphere.
HYRACOIDEA, a suborder of ungulate mammals represented
at the present day only by the Syrian hyrax (Procavia syriaca),
the “coney” of the Bible, and its numerous African relatives,
all of which may be included in the single genus Procavia (or
Hyrax), and consequently in the family Procaviidae. These
creatures have no proper English name, and are generally known
as hyraxes, from the scientific term (Hyrax) by which they were
for many years designated—a term which has unfortunately
had to give place to the earlier Procavia. In size these animals
may be compared roughly to rabbits and hares; and they have
rodent-like habits, hunching up their backs after the fashion of
some foreign members of the hare-family, more especially the
Liu-Kiu rabbit. In the matter of nomenclature these animals
have been singularly unfortunate. In the title “hyrax” they
have, for instance, usurped the Greek name for the shrew-mouse;
while in the Bible they have been given the old English name
for the rabbit. Perhaps rock-rabbit would be the best name.
At the Cape they are known to the Dutch as dass (badger),
which has been anglicized into “dassie.”
 |
| Fig. 1.—The Cape Hyrax (Procavia capensis). |
As regards the recent forms, the dentition in the fully adult animal
consists only of incisors and cheek-teeth, the formula being i. ½,
c. 0⁄0, p. 4⁄4 m. 3⁄3. There is, however, a minute upper canine developed
at first, which is early shed; and in extinct forms this tooth was
functional and molar-like. The upper incisors have persistent
pulps, and are curved longitudinally, forming a semicircle as in
rodents; they are, however, not flattened from before backwards
as in that order, but prismatic, with an antero-external, an antero-internal
and a posterior surface, the first two only being covered
with enamel; their tips are consequently not chisel-shaped, but
sharp-pointed. They are preceded by functional, rooted milk-teeth.
The lower incisors have long tapering roots, but not of persistent
growth; and are straight, directed somewhat forwards, with awl-shaped,
tri-lobed crowns. Behind the incisors is a considerable gap,
followed by the cheek-teeth, which are all contiguous, and formed
almost exactly on the pattern of some of the perissodactyle ungulates.
The milk-dentition includes three pairs of incisors and
one of canines in each jaw. The hyoid arch is unlike that of any
known mammal. The dorsal and lumbar vertebrae are very numerous,
28 to 30, of which 21 or 22 bear ribs. The tail is extremely
short. There are no clavicles. In the fore foot, the three middle
toes are subequally developed, the fifth is present, but smaller, and
the first is rudimentary, although, in one species at least, all its
normal bones are present. The terminal phalanges of the four
outer digits are small, somewhat conical and flattened in form.
The carpus has a distinct os centrale. There is a slight ridge on the
femur in the place of a third trochanter. The fibula is complete,
thickest at its upper end, where it generally unites with the tibia.
The articulation between the tibia and astragalus is more complex
than in other mammals, the end of the malleolus entering into it.
The hind-foot is very like that of a rhinoceros, having three well-developed
toes. There is no trace of a first toe, and the fifth meta-tarsal
is represented by a small nodule. The terminal phalange of
the inner (or second) digit is deeply cleft, and has a peculiar long
curved claw, the others having short broad nails. The stomach is
formed upon much the same principle as that of the horse or rhinoceros,
but is more elongated transversely and divided by a constriction
into two cavities—a large left cul de sac, lined by a very dense white
epithelium, and a right pyloric cavity, with a thick, soft, vascular
lining. The intestinal canal is long, and has, in addition to the
ordinary short, but capacious and sacculated caecum at the commencement
of the colon, lower down, a pair of large, conical, pointed
caeca. The liver is much subdivided, and there is no gall-bladder.
The brain resembles that of typical ungulates far more than that
of rodents. The testes are permanently abdominal. The ureters
open into the fundus of the bladder as in some Rodents. The
female has six teats, of which four are inguinal and two axillary,
and the placenta is zonary and deciduous. There is a gland on the
back.
 |
| Fig. 2.—Skull and Dentition of Tree-Hyrax (Procavia dorsalis). |
The more typical members of the genus are terrestrial in their
habits, and their cheek-teeth have nearly the same pattern as in
rhinoceroses; while the interval between the upper incisors is
less than the width of the teeth; and the lower incisors are only
slightly notched at the cutting edge. Vertebrae: C. 7, D. 22, L. 8,
S. 6, C. 6. Of this form the earliest known species, P. capensis, is
the type; but there are many other species, as P. syriaca, and P.
brucei from Syria and eastern Africa. They inhabit mountainous
and rocky regions, and live on the ground. In a second section the
molar teeth have the same pattern as in Palaeotherium (except that
the third lower molar has but two lobes); the interval between the
upper incisors exceeds the width of the teeth; and the lower incisors
have distinctly tri-lobed crowns. Vertebrae: C. 7, D. 21, L. 7, S. 5,
C. 10. The members of this section frequent the trunks and large
branches of trees, sleeping in holes. There are several species from
Western and South Africa, as P. arboreus and P. dorsalis. The
members of both groups appear to have a power like that possessed
by geckos of clinging to vertical surfaces of rocks and trees by the
soles of their feet.
Extinct Hyracoids.—For many years extinct representatives
of the Hyracoidea were unknown, partly owing to the fact that
certain fossils were not recognized as really belonging to that group.
The longest known of these was originally named Leptodon graecus,
but, on account of the preoccupation of the generic title, the designation
has been changed to Pliohyrax graecus. This animal, whose
remains occur in the Lower Pliocene of both Attica and Samos, was
about the size of a donkey, and possessed three pairs of upper incisor
teeth, of which the innermost were large and trihedral, recalling
those of the existing genus. On the other hand, the two outer
pairs of incisors were in contact with one another and with the
canines, so as to form on each side a series continuous with the
cheek-teeth.
The next representatives of the group occur in the Upper Eocene
beds of the Fayum district of Egypt, where the genera Saghatherium
and Megalohyrax occur. These are regarded as representing a
distinct family, the Saghatheriidae, characterized by the possession
of the full series of twenty-two teeth in the upper jaw, among
which the first pair of incisors was modified to form trihedral rootless
tusks, while the two remaining pairs were separated from one
another and from the teeth in front by gaps. The canine was like
a premolar, and in contact with the first tooth of that series; and
the cheek-teeth were short-crowned, with the premolar simpler than
the molars, and a third lobe to the last lower tooth of the latter
210
series. The members of this genus were small or medium-sized
ungulates with single-rooted incisors. On the other hand, the
representatives of the contemporary genus Megalohyrax were approximately
as large as Pliohyrax, and in some instances had double
roots to the second and third incisors.
It is now possible to define the suborder Hyracoidea as including
ungulates with a centrale in the carpus, plantigrade feet, in which
the first and fifth toes are reduced in greater or less degree, and
clavicles and a foramen in the lower end of the humerus are absent.
The femur has a small third trochanter, the radius and ulna and
tibia and fibula are respectively separate, at least in the young, and
the fibula articulates with the astragalus. The earlier forms had the
full series of 44 teeth, with the premolars simpler than the molars;
but in the later types the canines and some of the incisors disappear,
and at least the hinder premolars become molar-like. In all cases
the first upper incisors are large and rootless.
That the group originated in Africa there can be no reasonable
doubt; and it is remarkable that so early as the Upper Eocene the
types in existence differed comparatively little in structure from the
modern forms. In fact the hyraxes were then almost as distinct
from other mammals as they are at the present day.
See also C. W. Andrews, Descriptive Catalogue of the Tertiary
Vertebrata of the Fayum, British Museum (1906).
(R. L.*)
HYRCANIA. (1) An ancient district of Asia, south of the
Caspian Sea, and bounded on the E. by the river Oxus, called
Virkana, or “Wolf’s Land,” in Old Persian. It was a wide and
indefinite tract. Its chief city is called Tape by Strabo, Zadracarta
by Arrian (probably the modern Astarabad). The latter
is evidently the same as Carta, mentioned by Strabo as an
important city. Little is known of the history of the country.
Xenophon says it was subdued by the Assyrians; Curtius that
6000 Hyrcanians were in the army of Darius III. (2) Two
towns named Hyrcania are mentioned, one in Hyrcania, the
other in Lydia. The latter is said to have derived its name from a
colony of Hyrcanians, transported thither by the Persians.
HYRCANUS (Ὑρκανός), a Greek surname, of unknown origin,
borne by several Jews of the Maccabaean period.
John Hyrcanus I., high priest of the Jews from 135 to 105 B.C.,
was the youngest son of Simon Maccabaeus. In 137 B.C. he,
along with his brother Judas, commanded the force which
repelled the invasion of Judaea led by Cendebeus, the general
of Antiochus VII. Sidetes. On the assassination of his father
and two elder brothers by Ptolemy, governor of Jericho, his
brother-in-law, in February 135, he succeeded to the high priesthood
and the supreme authority in Judaea. While still engaged
in the struggle with Ptolemy, he was attacked by Antiochus
with a large army (134), and compelled to shut himself up in
Jerusalem; after a severe siege peace was at last secured only
on condition of a Jewish disarmament, and the payment of an
indemnity and an annual tribute, for which hostages were taken.
In 129 he accompanied Antiochus as a vassal prince on his ill-fated
Parthian expedition; returning, however, to Judaea
before winter, he escaped the final disaster. By the judicious
mission of an embassy to Rome he now obtained confirmation
of the alliance which his father had previously made with the
growing western power; at the same time he availed himself
of the weakened state of the Syrian monarchy under Demetrius
II. to overrun Samaria, and also to invade Idumaea, which he
completely subdued, compelling its inhabitants to receive
circumcision and accept the Jewish faith. After a long period
of rest he directed his arms against the town of Samaria, which,
in spite of the intervention of Antiochus, his sons Antigonus and
Aristobulus ultimately took, and by his orders razed to the ground
(c. 100 B.C.). He died in 105, and was succeeded by Aristobulus,
the eldest of his five sons. The external policy of Hyrcanus
was marked by considerable energy and tact, and, aided as it was
by favouring circumstances, was so successful as to leave the
Jewish nation in a position of independence and of influence such
as it had not known since the days of Solomon. During its
later years his reign was much disturbed, however, by the contentions
for ascendancy which arose between the Pharisees and
Sadducees, the two rival sects or parties which then for the first
time (under those names at least) came into prominence.
Josephus has related the curious circumstances under which he
ultimately transferred his personal support from the former to the
latter.
John Hyrcanus II., high priest from 78 to 40 B.C., was the
eldest son of Alexander Jannaeus by his wife Alexandra, and
was thus a grandson of the preceding. When his father died in
78, he was by his mother forthwith appointed high priest, and
on her death in 69 he claimed the succession to the supreme civil
authority also; but, after a brief and troubled reign of three
months, he was compelled to abdicate both kingly and priestly
dignities in favour of his more energetic and ambitious younger
brother Aristobulus II. In 63 it suited the policy of Pompey
that he should be restored to the high priesthood, with some
semblance of supreme command, but of much of this semblance
even he was soon again deprived by the arrangement of the
pro-consul Gabinius, according to which Palestine was in 57 B.C.
divided into five separate circles (σύνοδοι, συνέδρια). For services
rendered to Caesar after the battle of Pharsalia, he was again
rewarded with the sovereignty (προστασία τοῦ ἔθνους, Jos. Ant.
xx. 10) in 47 B.C., Antipater of Idumaea, however, being at the
same time made procurator of Judaea. In 41 B.C. he was
practically superseded by Antony’s appointment of Herod and
Phasael to be tetrarchs of Judaea; and in the following year he
was taken prisoner by the Parthians, deprived of his ears that
he might be permanently disqualified for priestly office, and
carried to Babylon. He was permitted in 33 B.C. to return to
Jerusalem, where on a charge of treasonable correspondence
with Malchus, king of Arabia, he was put to death in 30 B.C.
See Josephus (Ant. xiii. 8-10; xiv. 5-13; Bell. Jud. i. 2; i. 8-13).
Also Maccabees, History.
(J. H. A. H.)
HYSSOP (Hyssopus officinalis), a garden herb belonging to the
natural order Labiatae, formerly cultivated for use in domestic
medicine. It is a small perennial plant about 2 ft. high, with
slender, quadrangular, woody stems; narrowly elliptical,
pointed, entire, dotted leaves, about 1 in. long and 1⁄3 in. wide,
growing in pairs on the stem; and long terminal, erect, half-whorled,
leafy spikes of small violet-blue flowers, which are in
blossom from June to September. Varieties of the plant occur
in gardens with red and white flowers, also one having variegated
leaves. The leaves have a warm, aromatic, bitter taste, and are
believed to owe their properties to a volatile oil which is present
in the proportion of ¼ to ½%. Hyssop is a native of the south
of Europe, its range extending eastward to central Asia. A strong
tea made of the leaves, and sweetened with honey, was formerly
used in pulmonary and catarrhal affections, and externally as an
application to bruises and indolent swellings.
The hedge hyssop (Gratiola officinalis) belongs to the natural
order Scrophulariaceae, and is a native of marshy lands in the
south of Europe, whence it was introduced into Britain more
than 300 years ago. Like Hyssopus officinalis, it has smooth
opposite entire leaves, but the stems are cylindrical, the leaves
twice the size, and the flowers solitary in the axils of the leaves
and having a yellowish-red veined tube and bluish-white limb,
while the capsules are oval and many-seeded. The herb has
a bitter, nauseous taste, but is almost odourless. In small
quantities it acts as a purgative, diuretic and emetic when taken
internally. It was formerly official in the Edinburgh Pharmacopoeia,
being esteemed as a remedy for dropsy. It is said to
have formed the basis of a celebrated nostrum for gout, called
Eau médicinale, and in former times was called Gratia Dei.
When growing in abundance, as it does in some damp pastures
in Switzerland, it becomes dangerous to cattle. G. peruviana
is known to possess similar properties.
The hyssop (’ezob) of Scripture (Ex. xii. 22; Lev. xiv. 4, 6;
Numb. xix. 6, 18; 1 Kings v. 13 (iv. 33); Ps. li. 9 (7); John xix.
29), a wall-growing plant adapted for sprinkling purposes, has long
been the subject of learned disputation, the only point on which
all have agreed being that it is not to be identified with the Hyssopus
officinalis, which is not a native of Palestine. No fewer than
eighteen plants have been supposed by various authors to answer
the conditions, and Celsius has devoted more than forty pages to
the discussion of their several claims. By Tristram (Oxford Bible
for Teachers, 1880) and others the caper plant (Capparis spinosa)
is supposed to be meant; but, apart from other difficulties, this
identification is open to the objection that the caper seems to be,
at least in one passage (Eccl. xii. 5), otherwise designated (’abiy-yônah).
Thenius (on 1 Kings v. 13) suggests Orthotrichum saxatile.
211
The most probable opinion would seem to be that found in Maimonides
and many later writers, according to which the Hebrew ’ezob
is to be identified with the Arabic sa’atar, now understood to be
Satureja Thymus, a plant of very frequent occurrence in Syria and
Palestine, with which Thymus Serpyllum, or wild thyme, and
Satureja Thymbra are closely allied. Its smell, taste and medicinal
properties are similar to those of H. officinalis. In Morocco the
sa’atar of the Arabs is Origanum compactum; and it appears probable
that several plants of the genera Thymus, Origanum and others
nearly allied in form and habit, and found in similar localities, were
used under the name of hyssop.
HYSTASPES (the Greek form of the Persian Vishtāspa).
(1) A semi-legendary king (kava), praised by Zoroaster as his
protector and a true believer, son of Aurvataspa (Lohrasp).
The later tradition and the Shahname of Firdousi makes him
(in the modern form Kai Gushtāsp) king of Iran. As Zoroaster
probably preached his religion in eastern Iran, Vishtāspa must
have been a dynast in Bactria or Sogdiana. The Zoroastrian
religion was already dominant in Media in the time of the
Assyrian king Sargon (c. 715 B.C.), and had been propagated
here probably in much earlier times (cf. Persia); the time
of Zoroaster and Vishtāspa may therefore be put at c. 1000 B.C.
(2) A Persian, father of Darius I., under whose reign he was
governor of Parthia, as Darius himself mentions in the Behistun
inscription (2. 65). By Ammianus Marcellinus, xxiii. 6. 32, and
by many modern authors he has been identified with the protector
of Zoroaster, which is equally impossible for chronological and
historical reasons, and from the evidence of the development of
Zoroastrianism itself (see Persia: Ancient History).
(Ed. M.)
HYSTERESIS (Gr. ὑστέρησις, from ὑστέρειν, to lag behind),
a term added to the vocabulary of physical science by J. A.
Ewing, who defines it as follows: When there are two qualities
M and N such that cyclic variations of N cause cyclic variations
of M, then if the changes of M lag behind those of N, we may
say that there is hysteresis in the relation of M to N (Phil. Trans.,
1885, 176, p. 524). The phenomenon is best known in connexion
with magnetism. If an iron bar is subjected to a magnetic
force which is first gradually increased to a maximum and then
gradually diminished, the resulting magnetization of the bar
for any given value of the magnetic force will be greater when
the force is decreasing than when it is increasing; the iron
always tends to retain the magnetic condition which it has
previously acquired, and changes of its magnetization consequently
lag behind changes of the magnetic force. Thus there
is hysteresis in the relation of magnetization to magnetic force.
In consequence of hysteresis the process of magnetizing a piece
of iron to a certain intensity and then restoring it to its original
condition, or of effecting a double reversal of its magnetization,
involves the expenditure of energy, which is dissipated as heat
in the iron. Electrical generators and transformers often
contain pieces of iron the magnetization of which is reversed
many times in a second, and in order to economize power and
to avoid undue heating it is essential that hysteresis should
in such cases be as small as possible. Iron and mild steels
showing remarkably little hysteresis are now specially manufactured
for use in the construction of electrical machinery.
(See Magnetism.)
HYSTERIA, a term applied to an affection which may manifest
itself by a variety of symptoms, and which depends upon a
disordered condition of the highest nervous centres. It is characterized
by psychical peculiarities, while in addition there is often
derangement of the functions subserved by the lower cerebral
and spinal centres. Histological examination of the nervous
system has failed to disclose associated structural alterations.
By the ancients and by modern physicians down to the time
of Sydenham the symptoms of hysteria were supposed to be
directly due to disturbances of the uterus (Gr. ὑστέρα, whence the
name). This view is now universally recognized to be erroneous.
The term “functional” is often used by English neurologists
as synonymous with hysterical, a nomenclature which is tentatively
advantageous since it is at least non-committal. P. J.
Möbius has defined hysteria as “a state in which ideas control
the body and produce morbid changes in its functions.” P.
Janet, who has done much to popularize the psychical origin
of the affection, holds that there is “a limitation of the field
of consciousness” comparable to the contraction of the visual
fields met with in the disease. The hysterical subject, according
to this view, is incapable of taking into the field of consciousness
all the impressions of which the normal individual is conscious.
Strong momentary impressions are no longer controlled so
efficiently because of the defective simultaneous impressions
of previous memories. Hence the readiness with which the impulse
of the moment is obeyed, the loss of emotional control
and the increased susceptibility to external suggestion, which
are so characteristic. A secondary subconscious mental state
is engendered by the relegation of less prominent impressions
to a lower sphere. The dual personality which is typically exemplified
in somnambulism and in the hypnotic state is thus
induced. The explanation of hysterical symptoms which are
independent of the will, and of the existence of which the individual
may be unaware, is to be found in a relative preponderance
of this secondary subconscious state as compared with the
primary conscious personality. An elaboration of this theory
affords an explanation of hysterical symptoms dependent
upon a “fixed idea.” The following definition of hysteria has
recently been advanced by J. F. F. Babinski: “Hysteria is a
psychical condition manifesting itself principally by signs
that may be termed primary, and in an accessory sense others
that we may call secondary. The characteristic of the primary
signs is that they may be exactly reproduced in certain subjects
by suggestion and dispelled by persuasion. The characteristic
of the secondary signs is that they are closely related to the
primary phenomena.”
The causes of hysteria may be divided into (a) the predisposing,
such as hereditary predisposition to nervous disease, sex, age
and national idiosyncrasy; and (b) the immediate, such as
mental and physical exhaustion, fright and other emotional
influences, pregnancy, the puerperal condition, diseases of the
uterus and its appendages, and the depressing influence of injury
or general disease. Perhaps, taken over all, hereditary predisposition
to nerve-instability may be asserted as the most
prolific cause. There is frequently direct inheritance, and cases
of epilepsy and insanity or other form of nervous disease are
rarely wanting when the family history is carefully enquired
into. As regards age, the condition is apt to appear at the
evolution periods of life—puberty, pregnancy and the climacteric—without
any further assignable cause except that first spoken
of. It is rare in young children, but very frequent in girls
between the ages of fifteen and twenty-five, while it sometimes
manifests itself in women at the menopause. It is much more
common in the female than in the male—in the proportion of
20 to 1. Certain races are more liable to the disease than others;
thus the Latin races are much more prone to hysteria than are
those who come of a Teutonic stock, and in more aggravated
and complex forms. In England it has been asserted that an
undue proportion of cases occur among Jews. Occupation,
or be it rather said want of occupation, is a prolific cause. This
is noticeable more especially in the higher classes of society.
An hysterical attack may occur as an immediate sequel to an
epileptic fit. If the patient suffers only from petit mal (see
Epilepsy), unaccompanied by true epileptic fits, the significance
of the hysterical seizure, which is really a post-epileptic phenomenon,
may remain unrecognized.
It is convenient to group the very varied symptoms of hysteria
into paroxysmal and chronic. The popular term “hysterics”
is applied to an explosion of emotionalism, generally the result
of mental excitement, on which convulsive fits may supervene.
The characters of these vary, and may closely resemble epilepsy.
The hysterical fit is generally preceded by an aura or warning.
This sometimes takes the form of a sensation as of a lump in the
throat (globus hystericus). The patient may fall, but very rarely
is injured in so doing. The eyes are often tightly closed, the
body and limbs become rigid, and the back may become so arched
that the patient rests on her heels and head (opisthotonos). This
stage is usually followed by violent struggling movements. There
is no loss of consciousness. The attack may last for half-an-hour
212
or even longer. Hysterical fits in their fully-developed form are
rarely seen in England, though common in France. In the
chronic condition we find an extraordinary complexity of symptoms,
both physical and mental. The physical symptoms are
extremely diverse. There may be a paralysis of one or more
limbs associated with rigidity, which may persist for weeks,
months or years. In some cases, the patient is unable to walk;
in others there are peculiarities of the gait quite unlike anything
met with in organic disease. Perversions of sensation are usually
present; a common instance is the sensation of a nail being
driven through the vertex of the head (clavus hystericus). The
region of the spine is a very frequent seat of hysterical pain.
Loss of sensation (anaesthesia), of which the patient may be unaware,
is of common occurrence. Very often this sensory loss is
limited exactly to one-half of the body, including the leg, arm and
face on that side (hemianaesthesia). Sensation to touch, pain,
heat and cold, and electrical stimuli may have completely disappeared
in the anaesthetic region. In other cases, the anaesthesia
is relative or it may be partial, certain forms of sensation
remaining intact. Anaesthesia is almost always accompanied by
an inability to recognize the exact position of the affected limb
when the eyes are closed. When hemianaesthesia is present,
sight, hearing, taste and smell are usually impaired on that side
of the body. Often there is loss of voice (hysterical aphonia).
It is to such cases of hysterical paralysis and sensory disturbance
that the wonderful cures effected by quacks and charlatans may
be referred. The mental symptoms have not the same tendency
to pass away suddenly. They may be spoken of as inter-paroxysmal
and paroxysmal. The chief characteristics of the
former are extreme emotionalism combined with obstructiveness,
a desire to be an object of interest and a constant craving for
sympathy which is often procured at an immense sacrifice of
personal comfort. Obstructiveness is the invariable symptom.
Hysteria may pass into absolute insanity.
The treatment of hysteria demands great tact and firmness
on the part of the physician. The affection is a definite entity
and has to be clearly distinguished from malingering, with which
it is so often erroneously regarded as synonymous. Drugs are
of little value. The moral treatment is all-important. In severe
cases, removal from home surroundings and isolation, either in
a hospital ward or nursing home, are essential, in order that full
benefit may be derived from psychotherapeutic measures.
Bibliography.—Charcot, Leçons sur les maladies du système
nerveuse (1877); S. Weir Mitchell, Lectures on Diseases of the Nervous
System especially in Women (1885); Buzzard, Simulation of Hysteria
by Organic Nervous Disease (1891); Pitres, Leçons cliniques sur
l’hystérie et l’hypnotisme (1891); Richer, Études cliniques sur la
grande hystérie (1891); Gilles de la Tourette, Traité clinique et
thérapeutique de l’hystérie (1891); Bastian, Hysterical or Functional
Paralysis (1893); Ormerod, Art. “Hysteria,” in Clifford Allbutt’s
System of Medicine (1899); Camus and Pagnez, Isolement et Psychotherapie
(1904).
(J. B. T.; E. Bra.)
HYSTERON-PROTERON (Gr. ὕστερον, latter, and πρότερον,
former), a figure of speech, in which the order of words or phrases
is inverted, and that which should logically or naturally come
last is put first, to secure emphasis for the principal idea; the
classical example is Virgil’s “moriamur et in media arma
ruamus,” “let us die and charge into the thick of the fight”
(Aen. ii. 358). The term is also applied to any inversion in
order of events, arguments, &c.
HYTHE, a market town and watering-place, one of the Cinque
Ports, and a municipal and parliamentary borough of Kent,
England, 67 m. S.E. by E. of London on a branch of the South
Eastern & Chatham railway. Pop. (1901) 5557. It is beautifully
situated at the foot of a steep hill near the eastern extremity
of Romney Marsh, about half a mile from the sea, and consists
principally of one long street running parallel with the shore,
with which it is connected by a straight avenue of wych elms.
On account of its fine situation and picturesque and interesting
neighbourhood, it is a favourite watering-place. A sea-wall
and parade extend eastward to Sandgate, a distance of 3 m.
There is communication with Sandgate by means of a tramway
along the front. On the slope of the hill above the town stands
the fine church of St Leonard, partly Late Norman, with a very
beautiful Early English chancel. The tower was rebuilt about
1750. In a vault under the chancel there is a collection of
human skulls and bones supposed to be the remains of men killed
in a battle near Hythe in 456. Lionel Lukin (1742-1834),
inventor of the life-boat, is buried in the churchyard. Hythe
possesses a guildhall founded in 1794 and two hospitals, that
of St Bartholomew founded by Haimo, bishop of Rochester,
in 1336, and that of St John (rebuilt in 1802), of still greater
antiquity but unknown date, founded originally for the reception
of lepers. A government school of musketry, in which instructors
for the army are trained, was established in 1854, and has been
extended since, and the Shorncliffe military camp is within
2½ m. of the town.
Lympne, which is now 3 m. inland, is thought to have been the
original harbour which gave Hythe a place among the Cinque
Ports. The course of the ancient estuary may be distinctly
traced from here along the road to Hythe, the sea-sand lying
on the surface and colouring the soil. Here are remains of a
Roman fortress, and excavations have brought to light many
remains of the Roman Portus Lemanis. Large portions of the
fortress walls are standing. At the south-west corner is one of
the circular towers which occurred along the line of wall. The
site is now occupied by the fine old castellated mansion of
Studfall castle, formerly a residence of the archdeacons of
Canterbury. The name denotes a fallen place, and is not
infrequently thus applied to ancient remains. The church at
Lympne is Early English, with a Norman tower built by Archbishop
Lanfranc, and Roman material may be traced in the
walls. A short distance east is Shipway or Shepway Cross,
where some of the great assemblies relating to the Cinque Ports
were held. A mile north from Hythe is Saltwood Castle, of very
ancient origin, but rebuilt in the time of Richard II. The castle
was granted to the see of Canterbury in 1026, but escheated
to the crown in the time of Henry II., when the murder of Thomas
à Beckett is said to have been concerted here, and having been
restored to the archbishops by King John remained a residence
of theirs until the time of Henry VIII. It was restored as a
residence in 1882. About 2 m. N.W. of Saltwood are remains
of the fortified 14th-century manor-house of Westenhanger. It
is quadrangular and surrounded by a moat, and of the nine
towers (alternately square and round) by which the walls were
defended, three remain.
The parliamentary borough of Hythe, which includes Folkestone,
Sandgate and a number of neighbouring villages, returns
one member. The town is governed by a mayor, 4 aldermen
and 12 councillors. Area 2617 acres.
Hythe (Heda, Heya, Hethe, Hithe, i.e. landing-place) was
known as a port in Saxon times, and was granted by Halfden,
a Saxon thegn, to Christ Church, Canterbury. In the Domesday
Survey the borough is entered among the archbishop’s lands as
appurtenant to his manor of Saltwood, and the bailiff of the
town was appointed by the archbishop. Hythe was evidently
a Cinque Port before the Conquest, as King John in 1205
confirmed the liberties, viz. freedom from toll, the right to be
impleaded only at the Shepway court, &c., which the townsmen
had under Edward the Confessor. The liberties of the Cinque
Ports were confirmed in Magna Carta and later by Edward I.
in a general charter, which was confirmed, often with additions,
by subsequent kings down to James II. John’s charter to
Hythe was confirmed by Henry IV., Henry V. and Henry VI.
These charters were granted to the Cinque Ports in return for the
fifty-seven ships which they supplied for the royal service, of which
five were contributed by Hythe. The ports were first represented
in the parliament of 1365, to which they each sent four members.
Hythe was governed by twelve jurats until 1574, when it was
incorporated by Elizabeth under the title of the mayor, jurats
and commonalty of Hythe; a fair for the sale of fish, &c., was
also granted, to be held on the feast of St Peter and St Paul.
As the sea gradually retreated from Hythe and the harbour
became choked up with sand, the town suffered the fate of other
places near it, and lost its old importance.
213
I the ninth letter of the English and Latin alphabet, the tenth
in the Greek and Phoenician, because in these the symbol
Teth (the Greek θ) preceded it. Teth was not included in
the Latin alphabet because that language had no sound
corresponding to the Greek θ, but the symbol was metamorphosed
and utilized as the numeral C = 100, which took this form through
the influence of the initial letter of the Latin centum. The name
of I in the Phoenician alphabet was Yōd. Though in form it
seems the simplest of letters it was originally much more complex.
In Phoenician it takes the form 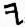 , which is found also in the
earliest Syriac and Palestinian inscriptions with little modification.
Ultimately in Hebrew it became reduced to a very small
symbol, whence comes its use as a term of contempt for things
of no importance as in “not one jot or tittle” (Matthew v. 18).
The name passed from Phoenician to Greek, and thence to the
Latin of the vulgate as iōta, and from the Latin the English
word is derived. Amongst the Greeks of Asia it appears only
as the simple upright I, but in some of the oldest alphabets
elsewhere, as Crete, Thera, Attica, Achaia and its colonies in
lower Italy, it takes the form
, which is found also in the
earliest Syriac and Palestinian inscriptions with little modification.
Ultimately in Hebrew it became reduced to a very small
symbol, whence comes its use as a term of contempt for things
of no importance as in “not one jot or tittle” (Matthew v. 18).
The name passed from Phoenician to Greek, and thence to the
Latin of the vulgate as iōta, and from the Latin the English
word is derived. Amongst the Greeks of Asia it appears only
as the simple upright I, but in some of the oldest alphabets
elsewhere, as Crete, Thera, Attica, Achaia and its colonies in
lower Italy, it takes the form  or S, while at Corinth and
Corcyra it appears first in a form closely resembling the later
Greek sigma Σ. It had originally no cross-stroke at top and
bottom. I being not i but z. The Phoenician alphabet having
no vowel symbols, the value of yōd was that of the English y.
In Greek, where the consonant sound had disappeared or been
converted into h, I is regularly used as a vowel. Occasionally,
as in Pamphylian, it is used dialectically as a glide between i and
another vowel, as in the proper name Δαμάτριιυς. In Latin I
was used alike for both vowel and consonant, as in iugum (yoke).
The sound represented by it was approximately that still assigned
to i on the continent. Neither Greek nor Latin made any
distinction in writing between short and long i, though in the
Latin of the Empire the long sound was occasionally represented
by a longer form of the symbol I. The dot over the i begins in
the 5th or 6th century A.D. In pronunciation the English
short i is a more open sound than that of most languages, and
does not correspond to the Greek and Latin sound. Nor are
the English short and long i of the same quality. The short i
in Sweet’s terminology is a high-front-wide vowel, the long i,
in English often spelt ee in words like seed, is diphthonged,
beginning like the short vowel but becoming higher as it proceeds.
The Latin short i, however, in final syllables was open and
ultimately became e, e.g. in the neuter of i-stems as utile from
utili-s. Medially both the short and the long sounds are very
common in syllables which were originally unaccented, because
in such positions many other sounds passed into i: officio but
facio, redimo but emo, quidlibet but lubet (libet is later); collīdo
but laedo, fīdo from an older feido, istis (dative plural) from an
earlier istois.
or S, while at Corinth and
Corcyra it appears first in a form closely resembling the later
Greek sigma Σ. It had originally no cross-stroke at top and
bottom. I being not i but z. The Phoenician alphabet having
no vowel symbols, the value of yōd was that of the English y.
In Greek, where the consonant sound had disappeared or been
converted into h, I is regularly used as a vowel. Occasionally,
as in Pamphylian, it is used dialectically as a glide between i and
another vowel, as in the proper name Δαμάτριιυς. In Latin I
was used alike for both vowel and consonant, as in iugum (yoke).
The sound represented by it was approximately that still assigned
to i on the continent. Neither Greek nor Latin made any
distinction in writing between short and long i, though in the
Latin of the Empire the long sound was occasionally represented
by a longer form of the symbol I. The dot over the i begins in
the 5th or 6th century A.D. In pronunciation the English
short i is a more open sound than that of most languages, and
does not correspond to the Greek and Latin sound. Nor are
the English short and long i of the same quality. The short i
in Sweet’s terminology is a high-front-wide vowel, the long i,
in English often spelt ee in words like seed, is diphthonged,
beginning like the short vowel but becoming higher as it proceeds.
The Latin short i, however, in final syllables was open and
ultimately became e, e.g. in the neuter of i-stems as utile from
utili-s. Medially both the short and the long sounds are very
common in syllables which were originally unaccented, because
in such positions many other sounds passed into i: officio but
facio, redimo but emo, quidlibet but lubet (libet is later); collīdo
but laedo, fīdo from an older feido, istis (dative plural) from an
earlier istois.
(P. Gi.)
IAMBIC, the term employed in prosody to denote a succession
of verses, each consisting of a foot or metre called an iambus
(ἵαμβος), formed of two syllables, of which the first is short and
the second long ( ). After the dactylic hexameter, the iambic
trimeter was the most popular metre of ancient Greece. Archilochus
is said to have been the inventor of this iambic verse, the
τρίμετρος consisting of three iambic fed. In the Greek tragedians
an iambic line is formed of six feet arranged in obedience to the
following scheme:—
). After the dactylic hexameter, the iambic
trimeter was the most popular metre of ancient Greece. Archilochus
is said to have been the inventor of this iambic verse, the
τρίμετρος consisting of three iambic fed. In the Greek tragedians
an iambic line is formed of six feet arranged in obedience to the
following scheme:—
Much of the beauty of the verse depends on the caesura, which is
usually In the middle of the third foot, and far less frequently
in the middle of the fourth. The English language runs more
naturally in the iambic metre than in any other. The normal
blank verse in English is founded upon an iambic basis, and
Milton’s line—
And swims | or sinks | or wades | or creeps | or flies | —
exhibits it in its primitive form. The ordinary alexandrine of
French literature is a hexapod iambic, but in all questions of
quantity in modern prosody great care has to be exercised to
recollect that all ascriptions of classic names to modern forms of
rhymed or blank verse are merely approximate. The octosyllabic,
or four-foot iambic metre, has found great favour in English verse
founded on old romances. Decasyllabic iambic lines rhyming
together form an “heroic” metre.
IAMBLICHUS (d. c. A.D. 330), the chief representative of Syrian
Neoplatonism, is only imperfectly known to us in the events
of his life and the details of his creed. We learn, however,
from Suidas, and from his biographer Eunapius, that he was born
at Chalcis in Coele-Syria, the scion of a rich and illustrious family,
that he studied under Anatolius and afterwards under Porphyry,
the pupil of Plotinus, that he himself gathered together a large
number of disciples of different nations with whom he lived on
terms of genial friendship, that he wrote “various philosophical
books,” and that he died during the reign of Constantine,—according
to Fabricius, before A.D. 333. His residence (probably)
at his native town of Chalcis was varied by a yearly visit with
his pupils to the baths of Gadara. Of the books referred to by
Suidas only a fraction has been preserved. His commentaries
on Plato and Aristotle, and works on the Chaldaean theology
and on the soul, are lost. For our knowledge of his system we
are indebted partly to the fragments of these writings preserved
by Stobaeus and others, and to the notices of his successors,
especially Proclus, partly to his five extant books, the sections
of a great work on the Pythagorean philosophy. Besides these,
Proclus (412-485) seems to have ascribed to him1 the authorship
of the celebrated book On the Egyptian Mysteries (so-called),
and although its differences in style and in some points of doctrine
from the writings just mentioned make it improbable that the
work was by Iamblichus himself, it certainly emanated from his
school, and in its systematic attempt to give a speculative
justification of the polytheistic cultus of the day, marks the
turning-point in the history of thought at which Iamblichus
stood.
As a speculative theory Neoplatonism (q.v.) had received its
highest development from Plotinus. The modifications introduced
by Iamblichus were the elaboration in greater detail of
its formal divisions, the more systematic application of the
Pythagorean number-symbolism, and chiefly, under the influence
of Oriental systems, the thorough-going mythic interpretation of
what the previous philosophy had still regarded as notional.
It is on the last account, probably, that Iamblichus was looked
upon with such extravagant veneration. As a philosopher he had
learning indeed, but little originality. His aim was to give a
philosophical rendering of the popular religion. By his contemporaries
he was accredited with miraculous powers (which he,
however, disclaimed), and by his followers in the decline of Greek
philosophy, and his admirers on its revival in the 15th and 16th
centuries, his name was scarcely mentioned without the epithet
“divine” or “most divine,” while, not content with the more
modest eulogy of Eunapius that he was inferior to Porphyry only
in style, the emperor Julian regarded him as not even second
to Plato, and said that he would give all the gold of Lydia for one
epistle of Iamblichus.
Theoretically, the philosophy of Plotinus was an attempt
to harmonize the principles of the various Greek schools. At
the head of his system he placed the transcendent incommunicable
one (ἓν ἀμέθεκτον), whose first-begotten is intellect (νοῦς), from
which proceeds soul (ψυχή), which in turn gives birth to φύσις, the
214
realm of nature. Immediately after the absolute one, Iamblichus
introduced a second superexistent unity to stand between it and
the many as the producer of intellect, and made the three succeeding
moments of the development (intellect, soul and nature)
undergo various modifications. He speaks of them as intellectual
(θεοὶ νοεροί), supramundane (ὑπερκόσμιοι), and mundane
gods (ἐγκόσμιοι). The first of these—which Plotinus
represented under the three stages of (objective) being (ὄν),
(subjective) life (ζωή), and (realized) intellect (νοῦς)—is distinguished
by him into spheres of intelligible gods (θεοὶ νοεροί) and
of intellectual gods (θεοὶ νοεροί), each subdivided into triads, the
latter sphere being the place of ideas, the former of the archetypes
of these ideas. Between these two worlds, at once separating
and uniting them, some scholars think there was inserted
by Iamblichus, as afterwards by Proclus, a third sphere partaking
of the nature of both (θεοὶ νοητοὶ καὶ νοεροί). But this supposition
depends on a merely conjectural emendation of the text.
We read, however, that “in the intellectual hebdomad he
assigned the third rank among the fathers to the Demiurge.”
The Demiurge, Zeus, or world-creating potency, is thus identified
with the perfected νοῦς, the intellectual triad being increased to
a hebdomad, probably (as Zeller supposes) through the subdivision
of its first two members. As in Plotinus νοῦς produced
nature by mediation of ψυχή, so here the intelligible gods are
followed by a triad of psychic gods. The first of these is incommunicable
and supramundane, while the other two seem to be
mundane though rational. In the third class, or mundane
gods (θεοὶ ἐγκόσμιοι), there is a still greater wealth of divinities,
of various local position, function, and rank. We read of gods,
angels, demons and heroes, of twelve heavenly gods whose
number is increased to thirty-six or three hundred and sixty,
and of seventy-two other gods proceeding from them, of twenty-one
chiefs (ἡγεμόνες) and forty-two nature-gods (θεοὶ γενεσιουργοί),
besides guardian divinities, of particular individuals and
nations. The world is thus peopled by a crowd of superhuman
beings influencing natural events, possessing and communicating
knowledge of the future, and not inaccessible to prayers and
offerings.
The whole of this complex theory is ruled by a mathematical
formulism of triad, hebdomad, &c., while the first principle is
identified with the monad, νοῦς with the dyad, and ψυχή with
the triad, symbolic meanings being also assigned to the other
numbers. “The theorems of mathematics,” he says, “apply
absolutely to all things,” from things divine to original matter
(ὕλη). But though he thus subjects all things to number, he
holds elsewhere that numbers are independent existences, and
occupy a middle place between the limited and unlimited.
Another difficulty of the system is the account given of nature.
It is said to be “bound by the indissoluble chains of necessity
which men call fate,” as distinguished from divine things which
are not subject to fate. Yet, being itself the result of higher
powers becoming corporeal, a continual stream of elevating
influence flows from them to it, interfering with its necessary
laws and turning to good ends the imperfect and evil. Of evil
no satisfactory account is given; it is said to have been generated
accidentally.
In his doctrine of man Iamblichus retains for the soul the
middle place between intellect and nature which it occupies
in the universal order. He rejects the passionless and purely
intellectual character ascribed to the human soul by Plotinus,
distinguishing it sharply both from those above and those below
it. He maintains that it moves between the higher and lower
spheres, that it descends by a necessary law (not solely for trial
or punishment) into the body, and, passing perhaps from one
human body to another, returns again to the supersensible.
This return is effected by the virtuous activities which the soul
performs through its own power of free will, and by the assistance
of the gods. These virtues were classified by Porphyry as
political, purifying (καθαρτικαί), theoretical, and paradigmatic;
and to these Iamblichus adds a fifth class of priestly virtues
(ἱερατικαὶ ἀρεταί), in which the divinest part of the soul raises
itself above intellect to absolute being.
Iamblichus does not seem ever to have attained to that
ecstatic communion with and absorption in deity which was the
aim of earlier Neoplatonism, and which Plotinus enjoyed four
times in his life, Porphyry once. Indeed his tendency was not so
much to raise man to God as to bring the gods down to men—a
tendency shown still more plainly in the “Answer of Abamon
the master to Porphyry’s letter to Anebo and solutions of the
doubts therein expressed,” afterwards entitled the Liber de
mysteriis, and ascribed to Iamblichus.
In answer to questions raised and doubts expressed by
Porphyry, the writer of this treatise appeals to the innate idea
all men have of the gods as testifying to the existence of divinities
countless in number and various in rank (to the correct arrangement
of which he, like Iamblichus, attaches the greatest importance).
He holds with the latter that above all principles of
being and intelligence stands the absolute one, from whom the
first god and king spontaneously proceeds; while after these
follow the ethereal, empyrean, and heavenly gods, and the
various orders of archangels, angels, demons, and heroes distinguished
in nature, power, and activity, and in greater profusion
than even the imagination of Iamblichus had conceived.
He says that all the gods are good (though he in another place
admits the existence of evil demons who must be propitiated),
and traces the source of evil to matter; rebuts the objection
that their answering prayer implies passivity on the part of gods
or demons; defends divination, soothsaying, and theurgic
practices as manifestations of the divine activity; describes the
appearances of the different sorts of divinities; discusses the
various kinds of sacrifice, which he says must be suitable to the
different natures of the gods, material and immaterial, and to the
double condition of the sacrificer as bound to the body or free
from it (differing thus in his psychology from Iamblichus); and,
in conclusion, states that the only way to happiness is through
knowledge of and union with the gods, and that theurgic practices
alone prepare the mind for this union—again going beyond
his master, who held assiduous contemplation of divine things
to be sufficient. It is the passionless nature of the soul which
permits it to be thus united to divine beings,—knowledge of
this mystic union and of the worship associated with it having
been derived from the Egyptian priests, who learnt it from
Hermes.
On one point only does the author of the De mysteriis seem
not to go so far as Iamblichus in thus making philosophy subservient
to priestcraft. He condemns as folly and impiety the
worship of images of the gods, though his master held that these
simulacra were filled with divine power, whether made by the
hand of man or (as he believed) fallen from heaven. But images
could easily be dispensed with from the point of view of the
writer, who not only held that all things were full of gods (πάντα πλήρη θεῶν, as Thales said), but thought that each man had a
special divinity of his own—an ἴδιος δαίμων—as his guard and
companion.
The following are the extant works of Iamblichus: (1) On the
Pythagorean (Life Περὶ τοῦ Πυθαγορικοῦ βίου), ed. T. Kiessling
(1815), A. Nauck (St Petersburg, 1884); for a discussion of the
authorities used see E. Rohde in Rheinisches Museum, xxvi., xxvii.
(1871, 1872); Eng. trans. by Thomas Taylor (1818), (2) The Exhortation
to Philosophy (Λόγος προτρεπτικὸς εἰς φιλοσοφίαν), ed. T. Kiessling
(1813); H. Piselli (1888). (3) The treatise On the General Science
of Mathematics (Περὶ τῆς κοινῆς μαθηματικῆς ἐπιστήμης), ed. J. G. Friis
(Copenhagen, 1790), N. Festa (Leipzig, 1891). (4) The book On the
Arithmetic of Nicomachus (Περὶ τῆς Νικομάχου ἀριθμητικῆς εἰσαγωγῆς),
along with fragments on fate (Περὶ εἱμαρμένης) and prayer (Περὶ εὐχῆς), ed. S. Tennulius (1688), the Arithmetic by H. Pistelli (1894).
(5) The Theological Principles of Arithmetic (Θεολογούμενα τῆς ἀριθμητικῆς)—the seventh book of the series—by F. Ast (Leipzig,
1817). Two lost books, treating of the physical and ethical signification
of numbers, stood fifth and sixth, while books on music, geometry
and astronomy followed. The emperor Julian had a great admiration
for Iamblichus, whom he considered “intellectually not inferior
to Plato”; but the Letters to Iamblicus the Philosopher which bear
his name are now generally considered spurious.
The so-called Liber de mysteriis was first edited, with Latin
translation and notes, by T. Gale (Oxford, 1678), and more
recently by C. Parthey (Berlin, 1857); Eng. trans. by Thomas
Taylor (1821).
215
There is a monograph on Iamblichus by G. E. Hebenstreit (De
Iamblichi, philosophi Syri, doctrina, Leipzig, 1764), and one of the
De myst. by Harless (Das Buch v. d. ägypt. Myst., Munich, 1858).
The best accounts of Iamblichus are those of Zeller, Phil. d. Griechen,
iii. 2, pp. 613 sq., 2nd ed.; E. Vacherot, Hist. de l’école d’Alexandrie
(1846), ii. 57 sq.; J. Simon, Hist. de l’école d’Alexandrie (1845); A. E.
Chaignet, Histoire de la psychologie des Grecs (Paris, 1893) v. 67-108;
T. Whittaker, The Neo-Platonists (Cambridge, 1901).
(W. R. So.)
1 Besides the anonymous testimony prefixed to an ancient MS. of
Proclus, De Myst. viii. 3 seems to be quoted by the latter as Iamblichus’s.
Cf. Meiners. “Judicium de libro qui de Myst. Aeg. inscribitur,”
in Comment. Soc. Reg. Sci. Gott., vol. iv., 1781, p. 77.
IAMBLICHUS, of Syria, the earliest of the Greek romance
writers, flourished in the 2nd century A.D. He was the author
of Βαβυλωνιακά, the loves of Rhodanes and Sinonis, of which an
epitome is preserved in Photius (cod. 94). Garmus, a legendary
king of Babylon, forces Sinonis to marry him and throws Rhodanes
into prison. The lovers manage to escape, and after many
singular adventures, in which magic plays a considerable part,
Garmus is overthrown by Rhodanes, who becomes king of
Babylon. According to Suidas, Iamblichus was a freedman,
and a scholiast’s note on Photius further informs us that he
was a native Syrian (not descended from Greek settlers); that
he borrowed the material for his romance from a love story told
him by his Babylonian tutor, and that he subsequently applied
himself with great success to the study of Greek. A MS. of the
original in the library of the Escorial is said to have been
destroyed by fire in 1670. Only a few fragments have been
preserved, in addition to Photius’s epitome.
See Scriptores erotici, ed. A. Hirschig (1856) and R. Hercher
(1858); A. Mai, Scriptorum veterum nova collectio, ii.; E. Rohde,
Der griechische Roman (1900).
IANNINA (i.e. “the city of St John”; Gr. Ioannina; Turk
Yaniá; also written Janina, Jannina, and, according to its
Albanian pronunciation, Yanina), the capital of the vilayet of
Iannina, Albania, European Turkey. Pop. (1905) about 22,000.
The largest ethnical groups in the population are the Albanian and
Greek; the purest form of colloquial Greek is spoken here among
the wealthy and highly educated merchant families. The position
of Iannina is strikingly picturesque. At the foot of the grey
limestone mass of Mount Mitzekeli (1500 ft.), which forms part of
the fine range of hills running north from the Gulf of Arta, there
lies a valley (the Hellopia of antiquity) partly occupied by a lake;
and the city is built on the slopes of a slight eminence, stretching
down to the western shore. It has greatly declined from the state
of barbaric prosperity which it enjoyed from 1788 to 1822, when
it was the seat of Ali Pasha (q.v.), and was estimated to have
from 30,000 to 50,000 inhabitants. The fortress—Demir Kule
or Iron Castle, which, like the principal seraglio, was built on a
promontory jutting into the lake—is now in ruins. But the city
is the seat of a Greek archbishop, and still possesses many
mosques and churches, besides synagogues, a Greek college
(gymnasium), a library and a hospital. Sayades (opposite Corfu)
and Arta are the places through which it receives its imports.
The rich gold and silver embroidery for which the city has long
been famous is still one of the notable articles in its bazaar; but
the commercial importance of Iannina has notably declined since
the cession of Arta and Thessaly to Greece in 1881. Iannina had
previously been one of the chief centres of the Thessalian grain
trade; it now exports little except cheese, hides, bitumen and
sheepskins to the annual value of about £120,000; the imports,
which supply only the local demand for provisions, textile goods,
hardware, &c., are worth about double that sum.
The lake of Iannina (perhaps to be identified with the Pambotus
or Pambotis of antiquity) is 6 m. long, and has an area of 24 sq.m.,
with an extreme depth of less than 35 ft. In time of flood it is
united with the smaller lake of Labchistas to the north. There
are no affluents of any considerable size, and the only outlets are
underground passages or katavothra extending for many miles
through the calcareous rocks.
The theory supported by W. M. Leake (Northern Greece,
London, 1835) that the citadel of Iannina is to be identified with
Dodona, is now generally abandoned in favour of the claims of a
more southern site. As Anna Comnena, in describing the capture
of the town (τὰ Ἰοάννινα) by Bohemond in 1082, speaks of the
walls as being dilapidated, it may be supposed that the place
existed before the 11th century. It is mentioned from time to
time in the Byzantine annals, and on the establishment of the
lordship of Epirus by Michael Angelus Comnenus Ducas, it
became his capital. In the middle ages it was successively
attacked by Serbs, Macedonians and Albanians; but it was in
possession of the successors of Michael when the forces of the
Sultan Murad appeared before it in 1430 (cf. Hahn, Alban.
Studien, Jena [1854], pp. 319-322). Since 1431 it has continued
under Turkish rule.
Descriptions of Iannina will be found in Holland’s Travels (1815);
Hughes, Travels in Greece, &c. (1830); H. F. Tozer, Researches in
the Highlands of Turkey (London, 1869). See also Albania and the
authorities there cited.
IAPETUS, in Greek mythology, son of Uranus and Gaea, one
of the Titans, father of Atlas, Prometheus, Epimetheus and
Menoetius, the personifications of certain human qualities
(Hesiod, Theog. 507). As a punishment for having revolted
against Zeus, he was imprisoned in Tartarus (Homer, Iliad, viii.
479) or underneath the island of Inarime off the coast of Campania
(Silius Italicus xii. 148). Hyginus makes him the son of
Tartarus and Gaea, and one of the giants. Iapetus was considered
the original ancestor of the human race, as the father of
Prometheus and grandfather of Deucalion. The name is probably
identical with Japhet (Japheth), and the son of Noah in the
Greek legend of the flood becomes the ancestor of (Noah) Deucalion.
Iapetus as the representative of an obsolete order of
things is described as warring against the new order under Zeus,
and is naturally relegated to Tartarus.
See F. G. Welcker, Griechische Götterlehre, i. (1857); C. H. Völcker,
Die Mythologie des Iapetischen Geschlechtes (1824); M. Mayer,
Giganten und Titanen (1887).
IAPYDES, or Iapodes, one of the three chief peoples of Roman
Illyria. They occupied the interior of the country on the north
between the Arsia (Arsa) and Tedanius (perhaps the Zermanja),
which separated them from the Liburnians. Their territory
formed part of the modern Croatia. They are described by
Strabo as a mixed race of Celts and Illyrians, who used Celtic
weapons, tattooed themselves, and lived chiefly on spelt and
millet. They were a warlike race, addicted to plundering
expeditions. In 129 B.C. C. Sempronius Tuditanus celebrated
a triumph over them, and in 34 B.C. they were finally crushed
by Augustus. They appear to have had a foedus with Rome,
but subsequently rebelled.
See Strabo iv. 207, vii. 313-315; Dio Cassius xlix. 35; Appian,
Illyrica, 10, 14, 16; Livy, Epit. lix. 131; Tibullus iv. 1. 108; Cicero,
Pro Balbo, 14.
IATROCHEMISTRY (coined from Gr. ἰατρός, a physician, and
“chemistry”), a stage in the history of chemistry, during
which the object of this science was held to be “not to make
gold but to prepare medicines.” This doctrine dominated
chemical thought during the 16th century, its foremost supporters
being Paracelsus, van Helmont and de la Boë Sylvius.
But it gave way to the new definition formulated by Boyle,
viz. that the proper domain of chemistry was “to determine
the composition of substances.” (See Chemistry: I. History;
Medicine.)
IAZYGES, a tribe of Sarmatians first heard of on the Maeotis,
where they were among the allies of Mithradates the Great.
Moving westward across Scythia, and hence called Metanastae,
they were on the lower Danube by the time of Ovid, and about
A.D. 50 occupied the plains east of the Theiss. Here, under the
general name of Sarmatae, they were a perpetual trouble to
the Roman province of Dacia. They were divided into freemen
and serfs (Sarmatae Limigantes), the latter of whom had a
different manner of life and were probably an older settled
population enslaved by nomad masters. They rose against them
in A.D. 334, but were repressed by foreign aid. Nothing is
heard of Iazyges or Sarmatae after the Hunnish invasions.
Graves at Keszthely and elsewhere in the Theiss valley, shown
by their contents to belong to nomads of the first centuries A.D.,
are referred to the Iazyges.
(E. H. M.)
IBADAN, a town of British West Africa, in Yorubaland,
Southern Nigeria, 123 m. by rail N.E. of Lagos, and about 50 m.
N.E. of Abeokuta. Pop. 1910 estimated at 150,000. The
town occupies the slope of a hill, and stretches into the valley
216
through which the river Ona flows. It is enclosed by mud walls,
which have a circuit of 18 m., and is encompassed by cultivated
land 5 or 6 m. in breadth. The native houses are all low, thatched
structures, enclosing a square court, and the only break in the
mud wall is the door. There are numerous mosques, orishas
(idol-houses) and open spaces shaded with trees. There are a
few buildings in the European style. Most of the inhabitants are
engaged in agriculture; but a great variety of handicrafts is
also carried on. Ibadan is the capital of one of the Yoruba
states and enjoys a large measure of autonomy. Nominally
the state is subject to the alafin (ruler) of Oyo; but it is virtually
independent. The administration is in the hands of two chiefs,
a civil and a military, the bale and the balogun; these together
form the highest court of appeal. There is also an iyaloda or
mother of the town, to whom are submitted all the disputes of
the women. Ibadan long had a feud with Abeokuta, but on
the establishment of the British protectorate the intertribal
wars were stopped. In 1862 the people of Ibadan destroyed
Ijaya, a neighbouring town of 60,000 inhabitants. A British
resident and a detachment of Hausa troops are stationed at
Ibadan.
IBAGUÉ, or San Bonifacio de Ibagué, a city of Colombia,
and capital of the department of Tolima, about 60 m. W. of
Bogotá and 18 m. N.W. of the Nevado de Tolima. Pop. (1900,
estimate) 13,000. Ibagué is built on a beautiful plain between
the Chipalo and Combeima, small affluents of the Cuello, a
western tributary of the Magdalena. Its elevation, 4300 ft.
above the sea, gives it a mild, subtropical climate. The plain
and the neighbouring valleys produce cacao, tobacco, rice and
sugar-cane. There are two thermal springs in the vicinity, and
undeveloped mines of sulphur and silver. The city has an
endowed college. It is an important commercial centre, being
on the road which crosses the Quindio pass, or paramo, into the
Cauca valley. Ibagué was founded in 1550 and was the capital
of the republic for a short time in 1854.
IBARRA, a city of Ecuador and capital of the province of
Imbabura, about 50 m. N.N.E. of Quito, on a small fertile plain
at the northern foot of Imbabura volcano, 7300 ft. above sea-level.
Pop. (1900, estimate) 5000. It stands on the left bank
of the Tahuando, a small stream whose waters flow north and
west to the Pacific through the Mira, and is separated from
the higher plateau of Quito by an elevated transverse ridge of
which the Imbabura and Mojanda volcanoes form a part. The
surrounding country is mountainous, the valleys being very
fertile. Ibarra itself has a mild, humid climate, and is set in the
midst of orchards and gardens. It is the see of a bishop and
has a large number of churches and convents, and many substantial
residences. Ibarra has manufactures of cotton and
woollen fabrics, hats, sandals (alpargates), sacks and rope from
cabulla fibre, laces, sugar and various kinds of distilled spirits and
cordials made from the sugar-cane grown in the vicinity. Mules
are bred for the Colombian markets of Pasto and Popayan.
Ibarra was founded in 1597 by Alvaro de Ibarra, the president
of Quito. It has suffered from the eruptions of Imbabura, and
more severely from earthquakes, that of 1859 causing great
damage to its public buildings, and the greater one of the 16th
of August 1868 almost completely destroyed the town and
killed a large number of its inhabitants. The village of Carranqui,
1¼ m. from Ibarra, is the birthplace of Atahualpa, the Inca
sovereign executed by Pizarro, and close by is the small lake
called Yaguarcocha where the army of Huaynacapac, the father
of Atahualpa, inflicted a bloody defeat on the Carranquis.
Another aboriginal battle-field is that of Hatuntaqui, near Ibarra,
where Huaynacapac won a decisive victory and added the greater
part of Ecuador to his realm. The whole region is full of tolas,
or Indian burial mounds.
IBERIANS (Iberi, Ἲβηρες), an ancient people inhabiting
parts of the Spanish peninsula. Their ethnic affinities are not
known, and our knowledge of their history is comparatively
slight. It is almost impossible to make any statement in regard
to them which will meet with general agreement. At the same
time, the general lines of Iberian controversy are clear enough
The principal sources of information about the Iberians are
(1) historical, (2) numismatic, (3) linguistic, (4) anthropological.
1. Historical.—The name seems to have been applied by the
earlier Greek navigators to the peoples who inhabited the eastern
coast of Spain; probably it originally meant those who dwelt
by the river Iberus (mod. Ebro). It is possible (Boudard,
Études sur l’alphabet ibérien (Paris, 1852) that the river-name
itself represents the Basque phrase ibay-erri “the country of the
river.” On the other hand, even in older Greek usage (as in
Thuc. vi. 1) the term Iberia is said to have embraced the country
as far east as the Rhone (see Herodorus of Heraclea, Fragm.
Hist. Gr. ii. 34), and by the time of Strabo it was the common
Greek name for the Spanish peninsula. Iberians thus meant
sometimes the population of the peninsula in general and
sometimes, it would appear, the peoples of some definite race
(γένος) which formed one element in that population. Of the
tribal distribution of this race, of its linguistic, social and political
characteristics, and of the history of its relation to the other
peoples of Spain, we have only the most general, fragmentary
and contradictory accounts. On the whole, the historical
evidence indicates that in Spain, when it first became known
to the Greeks and Romans there existed many separate and
variously civilized tribes connected by at least apparent identity
of race, and by similarity (but not identity) of language, and
sufficiently distinguished by their general characteristics from
Phoenicians, Romans and Celts. The statement of Diodorus
Siculus that the mingling of these Iberians with the immigrant
Celts gave rise to the Celtiberians is in itself probable. Varro
and Dionysius Afer proposed to identify the Iberians of Spain
with the Iberians of the Caucasus, the one regarding the eastern,
and other the western, settlements as the earlier.
2. Numismatic.—Knowledge of ancient Iberian language and
history is mainly derived from a variety of coins, found widely
distributed in the peninsula,1 and also in the neighbourhood of
Narbonne. They are inscribed in an alphabet which has many
points of similarity with the western Greek alphabets, and some
with the Punic alphabet; but which seems to retain a few
characters from an older script akin to those of Minoan Crete
and Roman Libya.2 The same Iberian alphabet is found also
rarely in inscriptions. The coinage began before the Roman
conquest was completed; the monetary system resembles that of
the Roman republic, with values analogous to denarii and
quinarii. The coin inscriptions usually give only the name of
the town, e.g. plplis (Bilbilis), klaqriqs (Calagurris), seqbrics
(Segobriga), tmaniav (Dumania). The types show late Greek and
perhaps also late Punic influence, but approximate later to
Roman models. The commonest reverse type, a charging
horseman, reappears on the Roman coins of Bilbilis, Osca,
Segobriga and other places. Another common type is one man
leading two horses or brandishing a sword or a bow. The obverse
has usually a male head, sometimes inscribed with what appears
to be a native name.
3. Linguistic.—The survival of the non-Aryan language
among the Basques around the west Pyrenees has suggested
the attempt to interpret by its means a large class of similar-sounding
place-names of ancient Spain, some of which are
authenticated by their occurrence on the inscribed coins, and to
link it with other traces of non-Aryan speech round the shores
of the Western Mediterranean and on the Atlantic seaboard
of Europe. This phase of Iberian theory opens with K. W.
Humboldt (Prüfung der Untersuchungen über die Urbewohner
Hispaniens vermittelst der waskischen Sprache, Berlin, 1821),
217
who contended that there existed once a single great Iberian
people, speaking a distinct language of their own; that an
essentially “Iberian” population was to be found in Sicily,
Sardinia and Corsica, in southern France, and even in the British
Isles; and that the Basques of the present day were remnants
of this race, which had elsewhere been expelled or absorbed.
This last was the central and the seminal idea of the work, and
it has been the point round which the battle of scholarship has
mainly raged. The principal evidence which Humboldt adduced
in its support was the possibility of explaining a vast number of
the ancient topographical names of Spain, and of other asserted
Iberian districts, by the forms and significations of Basque.
In reply, Graslin (De l’Ibérie, Paris, 1839), maintained that the
name Iberia was nothing but a Greek misnomer of Spain, and
that there was no proof that the Basque people had ever
occupied a wider area than at present; and Bladé (Origine des
Basques, Paris, 1869) took the same line of argument, holding
that Iberia is a purely geographical term, that there was no
proper Iberian race, that the Basques were always shut in by
alien races, that their affinity is still to seek, and that the whole
Basque-Iberian theory is a figment. His main contention has met
with some acceptance,3 but the great current of ethnographical
speculation still flows in the direction indicated by Humboldt.
4. Anthropological.—Humboldt’s “Iberian theory” depended
partly on linguistic comparisons, but partly on his observation
of widespread similarity of physical type among the population
of south-western Europe. Since his time the anthropological
researches of Broca, Thurnam and Davis, Huxley, Busk, Beddoe,
Virchow, Tubino and others have proved the existence in Europe,
from Neolithic times, of a race, small of stature, with long or
oval skulls, and accustomed to bury their dead in tombs. Their
remains have been found in Belgium and France, in Britain,
Germany and Denmark, as well as in Spain; and they bear a
close resemblance to a type which is common among the Basques
as well as all over the Iberian peninsula. This Neolithic race
has consequently been nicknamed “Iberians,” and it is now
common to speak of the “Iberian” ancestry of the people of
Britain, recognizing the racial characteristics of “Iberians”
in the “small swarthy Welshman,” the “small dark Highlander,”
and the “Black Celts to the west of the Shannon,” as well as
in the typical inhabitants of Aquitania and Brittany.4 Later
investigators went further. M. d’Arbois de Jubainville, for
example (Les Premiers habitants de l’Europe, Paris, 1877),
maintained that besides possessing Spain, Gaul, Italy and the
British Isles, “Iberian” peoples penetrated into the Balkan
peninsula, and occupied a part of northern Africa, Corsica and
Sardinia; and it is now generally accepted that a race with
fairly uniform characteristics was at one time in possession of
the south of France (or at least of Aquitania), the whole of Spain
from the Pyrenees to the straits, the Canary Islands (the
Guanches) a part of northern Africa and Corsica. Whether
this type is more conveniently designated by the word Iberian,
or by some other name (“Eur-african,” “Mediterranean,” &c.)
is a matter of comparative indifference, provided that there is
no misunderstanding as to the steps by which the term Iberian
attained its meaning in modern anthropology.
Authorities.—K. W. von Humboldt, “Über die cantabrische
oder baskische Sprache” in Adelung, Mithridates iv. (1817), and
Prüfung d. Untersuchungen ü. die Urbewohner Hispaniens vermittelst
der waskischen Sprache (Berlin, 1821); L. F. Graslin, De l’Ibérie
(Paris, 1838); T. B. G. M. Bory de St Vincent, Essai géologique sur
le genre humain (1838); G. Lagneau, “Sur l’ethnologie des peuples
ibériens,” in Bull. soc. anthrop. (1867), pp. 146-161; J. F. Bladé,
Études sur l’origine des Basques (Paris, 1869), Défense des études, &c.
(Paris, 1870); Phillips, Die Einwanderung der Iberer in die pyren.
Halbinsel (Vienna, 1870), Über das iberische Alphabet (Vienna, 1870);
W. Boyd Dawkins, “The Northern Range of the Basques,” in
Fortnightly Rev. N.S. xvi. 323-337 (1874); W. T. van Eys, “La
Langue ibérienne et la langue basque,” in Revue de linguistique,
pp. 3-15 (1874); W. Webster, “The Basque and the Kelt,” in Journ.
Anthrop. Inst. v. 5-29 (1875); F. M. Tubino, Los Aborigines ibericos
o los Berberos en la peninsula (Madrid, 1876); A. Luchaire, Les
Origines linguistiques de l’Aquitaine (Paris, 1877); W. Boyd Dawkins,
Early Man in Britain (London, 1880); A. Castaing, “Les Origines
des Aquitains,” Mém. Soc. Eth. N.S. 1, pp. 183-328 (1884); G. C. C.
Gerland, “Die Basken und die Iberer” in Gröber, Grundriss d. roman.
Philologie, 1, pp. 313-334 (1888); M. H. d’Arbois de Jubainville,
Les Premiers habitants de l’Europe (1889-1894); J. F. Bladé, Les
Vascons avant leur établissement en Novempopulanie, Agen. (1891);
W. Webster, “The Celt-iberians,” Academy xl. 268-269 (and consequent
correspondence) (1891); J. Rhys, “The Inscriptions and
Language of the Northern Picts,” Proc. Soc. Ant. Scot. xxvi. 263-351
(1892); F. Fita, “El Vascuence en las inscripciones ógmicas,”
Bol. Real. Acad. Hist. Madrid (June 1893), xxii. 579-587; G. v. d.
Gabelentz, “Baskisch u. Berberisch,” Sitz. k. preuss. Akad. Wiss.
593-613 (Berlin, 1893), Die Verwandtschaft der Baskischen mit der
Berber-Sprache Nordafrikas nachgewiesen (Braunschweig, 1894);
M. H. d’Arbois de Jubainville, “Les Celtes en Espagne,” Rev.
celtique, xiv. 357-395 (1894); G. Buschan, “Über die iberische
Rasse,” Ausland, lxvi. 342-344 (1894); F. Olóriz y Aguilera, Distribucion
geografica del indice cefalico en España (Madrid, 1894),
“La Talla humana en España” in Discursos R. Acad. Medicina
xxxvi. 389 (Madrid, 1896); R. Collignon, “La Race basque,”
L’Anthropologie, v. 276-287 (1894); T. de Aranzadi, “Le Peuple
basque, résumé” Bull. soc. d’anth. 510-520 (1894), “Consideraciones
acerca de la raza basca” Euskel-Erria xxxv. 33, 65, 97, 129 (1896);
H. Schuchhardt, Baskische Studien, i. “Über die Entstehung der
Bezugsformen des baskischen Zeitworts”; Denkschriften der K.
Akad. der Wiss., Phil.-Hist., Classe, Bd. 42, Abh. 3. (Wien, 1893);
Ph. Salmon, Rev. mens. Éc. d’anthr. v. 155-181, 214-220 (1895);
R. Collignon, “Anthr. du S.-O. de la France,” Mém. Soc. Anthr.
§ 3. 1. 4. p. 1-129 (1895), Ann. de géogr. v. 156-166 (1896), and with
J. Deniker, “Les Maures de Sénégal,” L’Anthr. vii. 57-69 (1897);
G. Hervé, Rev. mens. Éc. d’anthr. vi. 97-109 (1896); G. Sergi,
Africa: Anthropologia della stirpe Camitica (Turin, 1897), Arii ed
Italici (1898); L. de Hoyos Sainz, “L’Anthropologie et la préhistorique
en Espagne et en Portugal en 1897,” L’Anthropologie,
ix. 37-51 (1898); J. Deniker (see Collignon) “Les Races de l’Europe,”
L’Anthropologie, ix. 113-133 (1898); M. Gèze, “De quelques rapports
entre les langues berbère et basque,” Mém. soc. arch. du Midi de
la France, xiii. See also the works quoted in the footnotes; and the
bibliography under Basques.
(J. L. M.)
1 For the prehistoric civilization of the peninsula as a whole
see Spain.
2 P. A. Boudard’s Études sur l’alphabet ibérien (Paris, 1852).
and Numismatique ibérienne (Béziers, 1859); Aloiss Heiss, Notes
sur les monnaies celtibériennes (Paris, 1865), and Description générale
des monnaies antiques de l’Espagne (Paris, 1870); Phillips, Über das
iberische Alphabet (Vienna, 1870), Die Einwanderung der Iberer in
die pyren. Halbinsel (Vienna, 1870); W. M. Flinders Petrie, Journ.
Anthr. Inst. xxix. (1899) 204, and above all E. Hübner, Monumenta
linguae Ibericae.
3 W. van Eys, for example, “La Langue ibérienne et la langue
basque,” in Revue de linguistique, goes against Humboldt; but
Prince Napoleon and to a considerable extent A. Luchaire maintain
the justice of his method and the value of many of his results. See
Luchaire, Les Origines linguistiques de l’Aquitaine (Paris, 1877).
4 Compare the interesting résumé of the whole question in Boyd
Dawkins’s Early Man in Britain (London, 1880).
IBEX, one of the names of the Alpine wild goat, otherwise
known as the steinbok and bouquetin, and scientifically as Capra
ibex. Formerly the ibex was common on the mountain-ranges
of Germany, Switzerland and Tirol, but is now confined to the
Alps which separate Valais from Piedmont, and to the lofty
peaks of Savoy, where its existence is mainly due to game-laws.
The ibex is a handsome animal, measuring about 4½ ft. in length
and standing about 40 in. at the shoulder. The skin is covered
in summer with a short fur of an ashy-grey colour, and in winter
with much longer yellowish-brown hair concealing a dense fur
beneath. The horns of the male rise from the crest of the skull,
and after bending gradually backwards terminate in smooth
tips; the front surface of the remainder carrying bold transverse
ridges or knots. About 1 yd. is the maximum recorded length
of ibex-horns. The fact that the fore-legs are somewhat shorter
than those behind enables the ibex to ascend mountain slopes
with more facility than it can descend, while its hoofs are as
hard as steel, rough underneath and when walking over a flat
surface capable of being spread out. These, together with its
powerful sinews, enable it to take prodigious leaps, to balance
itself on the smallest foothold and to scale almost perpendicular
rocks. Ibex live habitually at a greater height than chamois
or any other Alpine mammals, their vertical limit being the line
of perpetual snow. There they rest in sunny nooks during the
day, descending at night to the highest woods to graze. Ibex
are gregarious, feeding in herds of ten to fifteen individuals;
but the old males generally live apart from, and usually at
greater elevations than, the females and young. They utter
a sharp whistling sound not unlike that of the chamois, but when
greatly irritated or frightened make a peculiar snorting noise.
The period of gestation in the female is ninety days, after which
she produces—usually at the end of June—a single young one
which is able at once to follow its mother. Kids when caught
young and fed on goat’s milk can be readily tamed; and in the
16th century young tamed ibex were frequently driven to the
218
mountains along with the goats, in whose company they would
afterwards return. Even wild ibex have been known to stray
among the herds of goats, although they shun the society of
chamois. Its flesh is said to resemble mutton, but has a flavour
of game.
 |
| The Ibex (Capra ibex). |
By naturalists the name “ibex” has been extended to embrace
all the kindred species of wild goats, while by sportsmen it is
used in a still more elastic sense, to include not only the
true wild goat (known in India as the Sind ibex) but even the
short-horned Hemitragus hylocrius of the Nilgiris. Dealing
only with species zoologically known as ibex, the one nearest
akin to the European kind is the Asiatic or Siberian ibex (Capra
sibirica), which, with several local phases, extends from the
northern side of Kashmir over an enormous area in Central
Asia. These ibex, especially the race from the Thian Shan, are
incomparably finer than the European species, their bold knotted
horns sometimes attaining a length of close on 60 in. The
Arabian, or Nubian, ibex (C. nubiana) is characterized by the
more slender type of horn, in which the front edge is much
narrower; while the Simien ibex (C. vali) of Central Abyssinia
is a very large and dark-coloured animal, with the horns black
instead of brownish, and bearing only slightly marked front
ridges. The Caucasian ibex (C. caucasica), or tur, is a wholly
fox-coloured animal, in which the horns are still flatter in front,
and thus depart yet further from the ibex type. In the Spanish
ibex (C. pyrenaica) the horns are flattened, with ill-defined
knobs, and a spiral twist. (See Goat.)
(W. H. F.; R. L.*)
IBIS, one of the sacred birds of the ancient Egyptians. James
Bruce identified this bird with the Abu-Hannes or “Father
John” of the Abyssinians, and in 1790 it received from Latham
(Index ornithologicus, p. 706) the name of Tantalus aethiopicus.
This determination was placed beyond question by Cuvier (Ann.
du Muséum, iv. 116-135) and Savigny (Hist. nat. et mythol.
de l’ibis) in 1805. They, however, removed it from the Linnaean
genus Tantalus and, Lacépède having some years before founded
a genus Ibis, it was transferred thither, and is now generally
known as I. aethiopica, though some speak of it as I. religiosa.
No attempt can here be made to treat the ibis from a mythological
or antiquarian point of view. Savigny’s memoir contains a great
deal of matter on the subject. Wilkinson (Ancient Egyptians, ser.
2, vol. ii. pp. 217-224) added some of the results of later research,
and Renouf in his Hibbert Lectures explains the origin of the
myth.
The ibis is chiefly an inhabitant of the Nile basin from Dongola
southward, as well as of Kordofan and Sennar; whence about
midsummer it moves northwards to Egypt.1 In Lower Egypt it
bears the name of Abu-mengel, or “father of the sickle,” from
the form of its bill, but it does not stay long in that country,
disappearing when the Nile has subsided. Hence most travellers
have failed to meet with it there2 (since their acquaintance with
the birds of Egypt is limited to those which frequent the country
in winter), and writers have denied generally to this species a
place in its modern fauna (cf. Shelley, Birds of Egypt, p. 261).
However, in 1864, von Heuglin (Journ. für Ornithologie, 1865,
p. 100) saw a young bird which had been shot in the Delta, and
E. C. Taylor (Ibis, 1878, p. 372) saw an adult which had been
killed near Lake Menzal in 1877. The story told to Herodotus
of its destroying snakes is, according to Savigny, devoid of
truth, but Cuvier states that he discovered partly digested
remains of a snake in the stomach of a mummied ibis.
The ibis is somewhat larger than a curlew, Numenius arquata,
which bird it resembles, with a much stouter bill and stouter
legs. The head and greater part of the neck are bare and black.
The plumage is white, except the primaries, which are black,
and a black plume, formed by the secondaries, tertials and lower
scapulars, and richly glossed with bronze, blue and green, which
curves gracefully over the hind-quarters. The bill and feet are
also black. The young lack the ornamental plume, and in them
the head and neck are clothed with short black feathers, while
the bill is yellow. The nest is placed in bushes or high trees,
the bird generally building in companies, and in the middle of
August von Heuglin (Orn. Nord-Ost-Afrikas, p. 1138) found that
it had from two to four young or much incubated eggs.3 These
are of a dingy white, splashed, spotted and speckled with
reddish-brown.
Congeneric with the typical ibis are two or three other species,
the I. melanocephala of India, the I. molucca or I. strictipennis,
of Australia, and the I. bernieri of Madagascar, all of which
closely resemble I. aethiopica; while many other forms not very
far removed from it, though placed by authors in distinct genera,4
are known. Among these are several beautiful species such as
the Japanese Geronticus nippon, the Lophotibis cristata of
Madagascar, and the scarlet ibis,5 Eudocimus ruber, of America.
The glossy ibis, Plegadis falcinellus, found throughout the West
Indies, Central and the south-eastern part of North America, as
well as in many parts of Europe (whence it not unfrequently
strays to the British Islands), Africa, Asia and Australia. This
bird, believed to be the second kind of ibis spoken of by Herodotus,
is rather smaller than the sacred ibis, and mostly of a
dark chestnut colour with brilliant green and purple reflections
on the upper parts, exhibiting, however, when young none of
the rufous hue. This species lays eggs of a deep sea-green colour,
having wholly the character of heron’s eggs, and it often breeds
in company with herons, while the eggs of all other ibises
whose eggs are known resemble those of the sacred ibis. Though
ibises resemble the curlews externally, there is no affinity between
them. The Ibididae are more nearly related to the storks,
Ciconiidae, and still more to the spoonbills, Plataleidae, with
which latter many systematists consider them to form one
group, the Hemiglottides of Nitzsch. Together these groups
form the sub-order Ciconiae of the order Ciconiiformes. The
true ibises are also to be clearly separated from the wood-ibises,
Tantalidae, of which there are four or five species, by several
not unimportant structural characters. Fossil remains of a true
219
ibis, I. pagana, have been found in considerable numbers in the
middle Tertiary beds of France.6
(A. N.)
1 It has been said to occur occasionally in Europe (Greece and
southern Russia).
2 E. C. Taylor remarked (Ibis, 1859, p. 51), that the buff-backed
heron, Ardea bubulcus, was made by the tourists’ dragomans to do
duty for the “sacred ibis,” and this seems to be no novel practice,
since by it, or something like it, Hasselqvist was misled, and through
him Linnaeus.
3 The ibis has more than once nested in the gardens of the Zoological
Society in London, and even reared its young there.
4 For some account of these may be consulted Dr Reichenow’s
paper in Journ. für Ornithologie (1877), pp. 143-156; Elliot’s in
Proc. Zool. Society (1877), pp. 477-510; and that of Oustalet in
Nouv. Arch. du Muséum, ser. 2, vols. i. pp. 167-184.
5 It is a popular error—especially among painters—that this bird
was the sacred ibis of the Egyptians.
6 The name “Ibis” was selected as the title of an ornithological
magazine, frequently referred to in this and other articles, which
made its first appearance in 1859.
IBLIS, or Eblis, in Moslem mythology the counterpart of the
Christian and Jewish devil. He figures oftener in the Koran
under the name Shaitan, Iblis being mentioned 11 times,
whereas Shaitan appears in 87 passages. He is chief of the
spirits of evil, and his personality is adapted to that of his Jewish
prototype. Iblis rebelled against Allah and was expelled from
Paradise. The Koranic legend is that his fall was a punishment
for his refusal to worship Adam. Condemned to death he was
afterwards respited till the judgment day (Koran vii. 13).
See Gustav Weil, The Bible, the Koran and the Talmud (London,
1846).
IBN ‘ABD RABBIHI [Abū ‘Umar Aḥmad ibn Maḥommed
ibn ‘Abd Rabbihi] (860-940), Arabian poet, was born in Cordova
and descended from a freed slave of Hishām, the second Spanish
Omayyad caliph. He enjoyed a great reputation for learning
and eloquence. No diwan of his is extant, but many selections
from his poems are given in the Yatīmat ud-Dahr, i.
412-436 (Damascus, 1887). More widely known than his poetry
is his great anthology, the ‘Iqd ul-Farīd (“The Precious Necklace”),
a work divided into twenty-five sections, the thirteenth
being named the middle jewel of the necklace, the chapters on
either side of this being named after other jewels. It is an adab
book (see Arabia: Literature, section “Belles Lettres”) resembling
Ibn Qutaiba’s ‘Uyūn ul-Akhbār, from which it borrows
largely. It has been printed, several times in Cairo (1876,
1886, &c.).
(G. W. T.)
IBN ‘ARABĪ [Muḥyiuddīn Abū ‘Abdallāh ibn ul-’Arabī]
(1165-1240), Moslem theologian and mystic, was born in Murcia
and educated in Seville. When thirty-eight he travelled in
Egypt, Arabia, Bagdad, Mosul and Asia Minor, after which he
lived in Damascus for the rest of his life. In law he was a
Zahirite, in theology a mystic of the extreme order, though
professing orthodox Ash’arite theology and combating in many
points the Indo-Persian mysticism (pantheism). He claims to
have had conversations with all the prophets past and future,
and reports conversations with God himself. Of his numerous
works about 150 still exist. The most extensive is the twelve-volume
Futūḥāt ul-Makkīyāt (“Meccan Revelations”), a general
encyclopaedia of Sufic beliefs and doctrines. Numerous extracts
from this work are contained in Sha‘rānī’s (d. 1565) manual of
Sufic dogma (Yawāqīt) published several times in Cairo. A
short account of these works is given in A. von Kremer’s
Geschichte der herrschenden Ideen des Islams, pp. 102-109
(Leipzig, 1868). Another characteristic and more accessible
work of Ibn ‘Arabi is the Fuṣūṣ ul-Ḥikam, on the nature and
importance of the twenty-seven chief prophets, written in 1230
(ed. Bulāq, 1837) and with the Commentary (Cairo, 1891) of
Qāshāni (d. 1350); cf. analysis by M. Schreiner in Journal of
German Oriental Society, lii. 516-525.
Of some 289 works said to have been written by Ibn ‘Arabī 150
are mentioned in C. Brockelmann’s Gesch. der arabischen Litteratur,
vol. i. (Weimar, 1898), pp. 441-448. See also R. A. Nicholson,
A Literary History of the Arabs, pp. 399-404 (London, 1907).
(G. W. T.)
IBN ATHĪR, the family name of three brothers, all famous
in Arabian literature, born at Jazīrat ibn ‘Umar in Kurdistan.
The eldest brother, known as Majd ud-Dīn (1149-1210), was
long in the service of the amir of Mosul, and was an earnest
student of tradition and language. His dictionary of traditions
(Kitāb un-Nihāya) was published at Cairo (1893), and his
dictionary of family names (Kitāb ul-Murassa’) has been edited
by Seybold (Weimar, 1896). The youngest brother, known as
Diyā ud-Dīn (1163-1239), served Saladin from 1191 on, then
his son, al-Malik ul-Afdal, and was afterwards in Egypt,
Samosata, Aleppo, Mosul and Bagdad. He was one of the most
famous aesthetic and stylistic critics in Arabian literature. His
Kitāb ul-Mathal, published in Bulāq in 1865 (cf. Journal of
the German Oriental Society, xxxv. 148, and Goldziher’s
Abhandlungen, i. 161 sqq.), contains some very independent
criticism of ancient and modern Arabic verse. Some of his
letters have been published by D. S. Margoliouth “On the Royal
Correspondence of Diya ed-Din el-Jazari” in the Actes du
dixième congrès international des orientalistes, sect. 3, pp. 7-21.
The brother best known by the simple name of Ibn Athīr
was Abu-l-Ḥasan ‘Izzuddīn Mahommed Ibn ul-Athīr (1160-1234),
who devoted himself to the study of history and tradition.
At the age of twenty-one he settled with his father in Mosul and
continued his studies there. In the service of the amir for many
years, he visited Bagdad and Jerusalem and later Aleppo and
Damascus. He died in Mosul. His great history, the Kāmil,
extends to the year 1231; it has been edited by C. J. Tornberg,
Ibn al-Athiri Chronicon quod perfectissimum inscribitur (14 vols.,
Leiden, 1851-1876), and has been published in 12 vols. in Cairo
(1873 and 1886). The first part of this work up to A.H. 310
(A.D. 923) is an abbreviation of the work of Tabarī (q.v.) with
additions. Ibn Athīr also wrote a history of the Atabegs of
Mosul, published in the Recueil des historiens des croisades (vol.
ii., Paris); a work (Usd ul-Ghāba), giving an account of 7500
companions of Mahomet (5 vols., Cairo, 1863), and a compendium
(the Lubāb) of Sam‘āni’s Kitāb ul-Anṣāb (cf. F. Wüstenfeld’s
Specimen el-Lobabi, Göttingen, 1835).
(G. W. T.)
IBN BATUTA, i.e. Abu Abdullah Mahommed, surnamed Ibn
Batuta (1304-1378), the greatest of Moslem travellers, was born
at Tangier in 1304. He entered on his travels at twenty-one
(1325) and closed them in 1355. He began by traversing the
coast of the Mediterranean from Tangier to Alexandria, finding
time to marry two wives on the road. After some stay at Cairo,
then probably the greatest city in the world (excluding China),
and an unsuccessful attempt to reach Mecca from Aidhab on the
west coast of the Red Sea, he visited Palestine, Aleppo and
Damascus. He then made the pilgrimage to Mecca and Medina,
and visited the shrine of Ali at Mashhad-Ali, travelling thence
to Basra, and across the mountains of Khuzistan to Isfahan,
thence to Shiraz and back to Kufa and Bagdad. After an
excursion to Mosul and Diarbekr, he made the haj a second time,
staying at Mecca three years. He next sailed down the Red Sea
to Aden (then a place of great trade), the singular position of
which he describes, noticing its dependence for water-supply upon
the great cisterns restored in modern times. He continued his
voyage down the African coast, visiting, among other places,
Mombasa and Quiloa (Kilwa). Returning north he passed by
the chief cities of Oman to New Ormuz (Hurmuz), which had
about 15 years before, c. 1315, been transferred to its famous
island-site from the mainland (Old Ormuz). After visiting other
parts of the gulf he crossed the breadth of Arabia to Mecca,
making the haj for the third time. Crossing the Red Sea, he made
a journey of great hardship to Syene, and thence along the Nile
to Cairo. After this, travelling through Syria, he made a circuit
among the petty Turkish states into which Asia Minor was divided
after the fall of the kingdom of Rum (Iconium). He now
crossed the Black Sea to Kaffa, then mainly occupied by the
Genoese, and apparently the first Christian city he had seen,
for he was much perturbed by the bell-ringing. He next
travelled into Kipchak (the Mongol khanate of Russia), and
joined the camp of the reigning khan Mahommed Uzbeg, from
whom the great and heterogeneous Uzbeg race is perhaps named.
Among other places in this empire he travelled to Bolghar
(54° 54′ N.) in order to witness the shortness of the summer
night, and desired to continue his travels north into the “Land
of Darkness” (in the extreme north of Russia), of which wonderful
things were told, but was obliged to forego this. Returning
to the khan’s camp he joined the cortège of one of the Khatuns,
who was a Greek princess by birth (probably illegitimate) and in
her train travelled to Constantinople, where he had an interview
with the emperor Andronikos III. the Younger (1328-1341).
He tells how, as he passed the city gates, he heard the guards
muttering Sarakinu. Returning to the court of Uzbeg, at Sarai
on the Volga, he crossed the steppes to Khwarizm and Bokhara;
thence through Khorasan and Kabul, and over the Hindu Kush
(to which he gives that name, its first occurrence). He reached
220
the Indus, on his own statement, in September, 1333. This
closes the first part of his narrative.
From Sind, which he traversed to the sea and back again, he
proceeded to Multan, and eventually, on the invitation of
Mahommed Tughlak, the reigning sovereign, to Delhi. Mahommed
was a singular character, full of pretence at least to many
accomplishments and virtues, the founder of public charities, and
a profuse patron of scholars, but a parricide, a fratricide, and as
madly capricious, bloodthirsty and unjust as Caligula. “No
day did his palace gate fail to witness the elevation of some abject
to affluence and the torture and murder of some living soul.”
He appointed the traveller to be kazi of Delhi, with a present of
12,000 silver dinars (rupees), and an annual salary of the same
amount, besides an assignment of village lands. In the sultan’s
service Ibn Batuta remained eight years; but his good fortune
stimulated his natural extravagance, and his debts soon amounted
to four or five times his salary. At last he fell into disfavour and
retired from court, only to be summoned again on a congenial
duty. The emperor of China, last of the Mongol dynasty, had
sent a mission to Delhi, and the Moor was to accompany the
return embassy (1342). The party travelled through central
India to Cambay and thence sailed to Calicut, classed by the
traveller with the neighbouring Kaulam (Quilon), Alexandria,
Sudak in the Crimea, and Zayton (Amoy harbour) in China, as
one of the greatest trading havens in the world—an interesting
enumeration from one who had seen them all. The mission
party was to embark in Chinese junks (the word used) and smaller
vessels, but that carrying the other envoys and the presents,
which started before Ibn Batuta was ready, was wrecked totally;
the vessel that he had engaged went off with his property, and he
was left on the beach of Calicut. Not daring to return to Delhi,
he remained about Honore and other cities of the western coast,
taking part in various adventures, among others the capture of
Sindabur (Goa), and visiting the Maldive Islands, where he
became kazi, and married four wives, and of which he has left the
best medieval account, hardly surpassed by any modern. In
August 1344 he left the Maldives for Ceylon; here he made the
pilgrimage to the “Footmark of our Father Adam.” Thence he
betook himself to Maabar (the Coromandel coast), where he
joined a Mussulman adventurer, residing at Madura, who had
made himself master of much of that region. After once more
visiting Malabar, Canara and the Maldives, he departed for
Bengal, a voyage of forty-three days, landing at Sadkawan
(Chittagong). In Bengal he visited the famous Moslem saint
Shaykh Jalaluddin, whose shrine (Shah Jalal at Silhet) is still
maintained. Returning to the delta, he took ship at Sunarganw
(near Dacca) on a junk bound for Java (i.e. Java Minor of Marco
Polo, or Sumatra). Touching the coast of Arakan or Burma, he
reached Sumatra in forty days, and was provided with a junk for
China by Malik al Dhahir, a zealous disciple of Islam, which had
recently spread among the states on the northern coast of that
island. Calling (apparently) at Cambodia on his way, Ibn
Batuta reached China at Zayton (Amoy harbour), famous from
Marco Polo; he also visited Sin Kalan or Canton, and professes
to have been in Khansa (Kinsay of Marco Polo, i.e. Hangchau),
and Khanbalik (Cambaluc or Peking). The truth of his visit to
these two cities, and especially to the last, has been questioned.
The traveller’s history, not least in China, singularly illustrates
the free masonry of Islam, and its power of carrying a Moslem
doctor over the known world of Asia and Africa. On his way
home he saw the great bird Rukh (evidently, from his description,
an island lifted by refraction); revisited Sumatra, Malabar,
Oman, Persia, Bagdad, and crossed the great desert to Palmyra
and Damascus, where he got his first news of home, and heard of
his father’s death fifteen years before. Diverging to Hamath and
Aleppo, on his return to Damascus, he found the Black Death
raging, so that two thousand four hundred died in one day.
Revisiting Jerusalem and Cairo he made the haj a fourth time,
and finally reappeared at Fez (visiting Sardinia en route) on
the 8th of November 1349, after twenty-four years’ absence.
Morocco, he felt, was, after all, the best of countries. “The
dirhems of the West are but little; but then you get more for
them.” After going home to Tangier, Ibn Batuta crossed into
Spain and made the round of Andalusia, including Gibraltar,
which had just then stood a siege from the “Roman tyrant
Adfunus” (Alphonso XI. of Castile, 1312-1350). In 1352 the
restless man started for Central Africa, passing by the oases of
the Sahara (where the houses were built of rock-salt, as Herodotus
tells, and roofed with camel skins) to Timbuktu and Gogo on the
Niger, a river which he calls the Nile, believing it to flow down into
Egypt, an opinion maintained by some up to the date of Lander’s
discovery. Being then recalled by his own king, he returned to
Fez (early in 1354) via Takadda, Haggar and Tuat. Thus ended
his twenty-eight years’ wanderings which in their main lines alone
exceeded 75,000 m. By royal order he dictated his narrative to
Mahommed Ibn Juzai, who concludes the work, 13th of December
1355 (A.D.) with the declaration: “This Shaykh is the traveller of
our age; and he who should call him the traveller of the whole
body of Islam would not exceed the truth.” Ibn Batuta died in
1378, aged seventy-three.
Ibn Batuta’s travels have only been known in Europe during the
19th century; at first merely by Arabic abridgments in the Gotha
and Cambridge libraries. Notices or extracts had been published
by Seetzen (c. 1808), Kosegarten (1818), Apetz (1819), and Burckhardt
(1819), when in 1829 Dr S. Lee published for the Oriental
Translation Fund a version from the abridged MSS. at Cambridge,
which attracted much interest. The French capture of Constantina
afforded MSS. of the complete work, one of them the autograph of
Ibn Juzai. And from these, after versions of fragments by various
French scholars, was derived at last (1858-1859) the standard edition
and translation of the whole by M. Défrémery and Dr Sanguinetti,
in 4 vols. See also Sir Henry Yule, Cathay, ii. 397-526; C. Raymond
Beazley, Dawn of Modern Geography, iii. 535-538. Though there
are some singular chronological difficulties in the narrative, and a
good many cursory inaccuracies and exaggerations, there is no part
of it except, perhaps, certain portions of the journeys in north China,
which is open to doubt. The accounts of the Maldive Islands, and of
the Negro countries on the Niger, are replete with interesting and
accurate particulars. The former agrees surprisingly with that given
by the only other foreign resident we know of, Pyrard de la Val,
two hundred and fifty years later. Ibn Batuta’s statements and
anecdotes regarding the showy virtues and solid vices of Sultan
Muhammad Tughlak are in entire agreement with Indian historians,
and add many fresh details.
(H. Y.; C. R. B.)
IBN DURAID [Abū Bakr Mahommed ibn ul-Ḥasan ibn
Duraid ul-Azdī] (837-934), Arabian poet and philologist, was
born at Baṣra of south Arabian stock. At his native place he was
trained under various teachers, but fled in 871 to Oman at the
time Baṣra was attacked by the negroes, known as the Zanj,
under Muhallabī. After living twelve years in Oman he went to
Persia, and, under the protection of the governor, ‘Abdallāh ibn
Mahommed ibn Mīkāl, and his son, Isma’īl, wrote his chief works.
In 920 he went to Bagdad, where he received a pension from the
caliph Moqtadir.
The Maqsūra, a poem in praise of Ibn Mīkāl and his son, has been
edited by A. Haitsma (1773) E. Scheidius (1786) and N. Boyesen
(1828). Various commentaries on the poem exist in MS. (cf. C.
Brockelmann, Gesch. der ar. Lit., i. 211 ff., Weimar, 1898),
The Jamhara fi-l-Lugha is a large dictionary written in Persian but
not printed. Another work is the Kitāb ul-Ishtiqāq (“Book of
Etymology”), edited by F. Wüstenfeld (Göttingen, 1854); it was
written in opposition to the anti-Arabian party to show the etymological
connexion of the Arabian tribal names.
(G. W. T.)
IBN FARADĪ [Abū-l-Walīd ‘Abdallāh ibn ul-Faradi] (962-1012),
Arabian historian, was born at Cordova and studied law
and tradition. In 992 he made the pilgrimage and proceeded to
Egypt and Kairawān, studying in these places. After his return
in 1009 he became cadi in Valencia, and was killed at Cordova
when the Berbers took the city.
His chief work is the History of the Learned Men of Andalusia,
edited by F. Codera (Madrid, 1891-1892). He wrote also a history
of the poets of Andalusia.
(G. W. T.)
IBN FĀRID [Abū-l-Qāsim ‘Umar ibn ul-Fāriḍ] (1181-1235),
Arabian poet, was born in Cairo, lived for some time in Mecca and
died in Cairo. His poetry is entirely Sufic, and he was esteemed
the greatest mystic poet of the Arabs. Some of his poems are said
to have been written in ecstasies. His diwan has been published
with commentary at Beirūt, 1887, &c.; with the commentaries of
Burīnī (d. 1615) and ‘Abdul-Ghānī (d. 1730) at Marseilles, 1853,
and at Cairo; and with the commentary of Rushayyid Ghālib
221
(19th century) at Cairo, 1893. One of the separate poems was
edited by J. von Hammer Purgstall as Das arabische hohe Lied der
Liebe (Vienna, 1854).
See R. A. Nicholson, A Literary History of the Arabs (London,
1907), pp. 394-398.
(G. W. T.)
IBN GABIROL [Solomon ben Judah], Jewish poet and
philosopher, was born at Malaga, probably about 1021. The
early part of his troublous life was spent at Saragossa, but few
personal details of it are recorded. His parents died while he
was a child and he was under the protection first of a certain
Jekuthiel, who died in 1039, and afterwards of Samuel ha-Nagid,
the well-known patron of learning. His passionate disposition,
however, embittered no doubt by his misfortunes, involved him
in frequent difficulties and led to his quarrelling with Samuel.
It is generally agreed that he died young, although the date is
uncertain. Al Harizi1 says at the age of twenty-nine, and
Moses b. Ezra2 about thirty, but Abraham Zaccuto3 states that
he died (at Valencia) in 1070. M. Steinschneider4 accepts the
date 1058.
His literary activity began early. He is said to have composed
poems at the age of sixteen, and elegies by him are extant on
Hai Gaon (died in 1038) and Jekuthiel (died in 1039), each of
which was written probably soon after the death of the person
commemorated. About the same time he also wrote his ‘Anaq,
a poem on grammar, of which only 97 lines out of 400 are preserved.
Moses ben Ezra says of him that he imitated Moslem
models, and was the first to open to Jewish poets the door of
versification,5 meaning that he first popularized the use of Arabic
metres in Hebrew. It is as a poet that he has been known to
the Jews to the present day, and admired for the youthful
freshness and beauty of his work, in which he may be compared
to the romantic school in France and England in the early 19th
century. Besides his lyrical and satirical poems, he contributed
many of the finest compositions to the liturgy (some of them
with the acrostic “Shelomoh ha-qaṭō”), which are widely
different from the artificial manner of the earlier payyeṭanim.
The best known of his longer liturgical compositions are the
philosophical Kether Malkūth (for the Day of Atonement) and
the Azharōth, on the 613 precepts (for Shebhu‘ōth). Owing to his
pure biblical style he had an abiding influence on subsequent
liturgical writers.
Outside the Jewish community he was known as the philosopher
Avicebron (Avencebrol, Avicebrol, &c.) The credit of
identifying this name as a medieval corruption of Ibn Gabirol
is due to S. Munk, who showed that selections made by Shem
Tōbh Palqera (or Falqera) from the Meqōr Ḥayyīm (the Hebrew
translation of an Arabic original) by Ibn Gabirol, corresponded
to the Latin Fons Vitae of Avicebron. The Latin version, made
by Johannes Hispalensis and Gundisalvi about one hundred years
after the author’s death, had at once become known among the
Schoolmen of the 12th century and exerted a powerful influence
upon them, although so little was known of the author that it
was doubted whether he was a Christian or a Moslem. The
teaching of the Fons Vitae was entirely new to the country of
its origin, and being drawn largely from Neoplatonic sources
could not be expected to find favour with Jewish thinkers. Its
distinctive doctrines are: (1) that all created beings, spiritual or
corporeal, are composed of matter and form, the various species
of matter being but varieties of the universal matter, and
similarly all forms being contained in one universal form; (2)
that between the primal One and the intellect (the νοῦς of
Plotinus) there is interposed the divine Will, which is itself
divine and above the distinction of form and matter, but is the
cause of their union in the being next to itself, the intellect,
in which Avicebron holds that the distinction does exist. The
doctrine that there is a material, as well as a formal, element in
all created beings was explicitly adopted from Avicebron by
Duns Scotus (as against the view of Albertus Magnus and Thomas
Aquinas), and perhaps his exaltation of the will above the
intellect is due to the same influence. Avicebron develops his
philosophical system throughout quite independently of his
religious views—a practice wholly foreign to Jewish teachers,
and one which could not be acceptable to them. Indeed, this
charge is expressly brought against him by Abraham ben David
of Toledo (died in 1180). It is doubtless this non-religious
attitude which accounts for the small attention paid to the Fons
Vitae by the Jews, as compared with the wide influence of the
philosophy of Maimonides.
The other important work of Ibn Gabirol is Iṣlāḥ al-akhlāq (the
improvement of character), a popular work in Arabic, translated
into Hebrew (Tiqqūn middōth ha-nephesh) by Judah ibn Tibbon.
It is widely different in treatment from the Fons, being intended
as a practical not a speculative work.
The collection of moral maxims, compiled in Arabic but best
known (in the Hebrew translation of Judah ibn Tibbon) as
Mibḥar ha-penīnīm, is generally ascribed to Ibn Gabirol, though
on less certain grounds.
Bibliography.—Texts of the liturgical poems are to be found
in the prayer-books: others in Dukes and Edelmann, Treasures
of Oxford (Oxford, 1850); Dukes, Shīrē Shelomoh (Hanover, 1858);
S. Sachs, Shīr ha-shīrīm asher li-Shelomoh (Paris, 1868, incomplete);
Brody, Die weltlichen Gedichte des ... Gabirol (Berlin, 1897, &c.).
“Avencebrolis Fons Vitae” (Latin text) in Clemens Bäumker’s
Beiträge zur Gesch. d. Philosophie, Bd. i. Hefte 2-4 (Münster, 1892);
The Improvement of the Moral Qualities [Arabic and English] ed. by
S. S. Wise (New York, 1901); A Choice of Pearls [Hebrew and
English] ed. by Ascher (London, 1859).
On the philosophy in general: S. Munk, Mélanges (quoted above);
Guttmann, Die Philosophie des Sal.-ibn Gabirol (Göttingen, 1889);
D. Kaufmann, Studien über Sal.-ibn Gabirol (Budapest, 1899);
S. Horovitz, “Die Psychologie Ibn Gabirols,” in the Jahresbericht
des jüd. theol. Seminars Fränckel’scher Stiftung (Breslau, 1900);
Wittmann, “Zur Stellung Avencebrols ...” (in Bäumker’s
Beiträge, Bd. v. Heft 1, Münster, 1905).
(A. Cy.)
1 Jud. Har. Macamæ, ed. Lagarde (Göttingen, 1883), p. 89, l. 61.
2 See the passage quoted by Munk, Mélanges de philosophie arabe
et juive (Paris, 1859), pp. 264 and 517.
3 Liber Juchassin, ed. Filipowski (London, 1857), p. 217.
4 Hebr. Übersetzungen (Berlin, 1893), § 219, note 70; cf. Kaufmann,
Studien über Sal.-ibn Gabirol (Budapest, 1899), p. 79, note 2.
5 See Munk, op. cit. pp. 515-516, transl. on pp. 263-264. Metre
had been already used by Dunash.
IBN HAUKAL, strictly Ibn Hauqal, a 10th century Arabian
geographer. Nothing is known of his life. His work on geography,
written in 977, is only a revision and extension of the
Masālik ul-Mamālik of al-Iṣṭakhrī, who wrote in 951. This
itself was a revised edition of the Kitāb ul-Ashkāl or Ṣuwar
ul-Aqālim of Abū Zaid ul-Balkhī, who wrote about 921. Ibn
Hauḳal’s work was published by M. J. de Goeje (Leiden, 1873).
An anonymous epitome of the book was written in 1233.
See M. J. de Goeje, “Die Iṣṭahrī-Balhī Frage,” in the Zeitschrift
der deutschen Morgenländischen Gesellschaft, xxv. 42 sqq.
IBN ḤAZM [Abū Maḥommed ‘Alī ibn Aḥmad ibn Ḥazm]
(994-1064), Moslem theologian, was born in a suburb of Cordova.
He studied history, law and theology, and became a vizier as his
father had been before him, but was deposed for heresy, and
spent the rest of his life quietly in the country. In legal matters
he belonged first to the Shāfi’ite school, but came to adopt the
views of the Zāhirites, who admitted only the external sense of
the Koran and tradition, disallowing the use of analogy (Qiyās)
and Taqlīd (appeal to the authority of an imām), and objecting
altogether to the use of individual opinion (Ra‘y). Every
sentence of the Koran was to be interpreted in a general and
universal sense; the special application to the circumstances
of the time it was written was denied. Every word of the Koran
was to be taken in a literal sense, but that sense was to be learned
from other uses in the Koran itself, not from the meaning in
other literature of the time. The special feature of Ibn Ḥazm’s
teaching was that he extended the application of these principles
from the study of law to that of dogmatic theology. He thus
found himself in opposition at one time to the Mo‘tazilites, at
another to the Ash‘arites. He did not, however, succeed in
forming a school. His chief work is the Kitāb ul-Milal
wan-Niḥal, or “Book of Sects” (published in Cairo, 1899).
For his teaching cf. I. Goldziher, Die Zahiriten, pp. 116-172
(Leipzig, (1884), and M. Schreiner in the Journal of the German
Oriental Society, lii. 464-486. For a list of his other works
see C. Brockelmann’s Geschichte der arabischen Literatur, vol. i.
(Weimar, 1898), p. 400.
(G. W. T.)
222
IBN HISHĀM [Abū Maḥommed ‘Abdulmalik ibn Hishām ibn
Ayyūb ul-Himyarī] (d. 834), Arabian biographer, studied in
Kufa but lived afterwards in Fostāt (old Cairo), where he gained
a name as a grammarian and student of language and history.
His chief work is his edition of Ibn Isḥāq’s (q.v.) Life of the
Apostle of God, which has been edited by F. Wüstenfeld (Göttingen,
1858-1860). An abridged German translation has
been made by G. Weil (Stuttgart, 1864; cf. P. Brönnle, Die
Commentatoren des Ibn Isḥaq und ihre Scholien, Halle, 1895).
Ibn Hishām is said to have written a work explaining the
difficult words which occur in poems on the life of the Apostle,
and another on the genealogies of the Himyarites and their
princes.
(G. W. T.)
IBN ISHĀQ [Mahommed ibn Isḥāq Abū ‘Abdallāh] (d. 768),
Arabic historian, lived in Medina, where he interested himself
to such an extent in the details of the Prophet’s life that he was
attacked by those to whom his work seemed to have a rationalistic
tendency. He consequently left Medina in 733, and went
to Alexandria, then to Kufa and Hira, and finally to Bagdad,
where the caliph Manṣūr provided him with the means of
writing his great work. This was the Life of the Apostle of God,
which is now lost and is known to us only in the recension of
Ibn Hishām (q.v.). The work has been attacked by Arabian
writers (as in the Fihrist) as untrustworthy, and it seems clear
that he introduced forged verses (cf. Journal of the German
Oriental Society, xiv. 288 sqq.). It remains, however, one of the
most important works of the age.
(G. W. T.)
IBN JUBAIR [Abū-l Ḥusain Maḥommed ibn Aḥmad ibn
Jubair] (1145-1217), Arabian geographer, was born in Valencia.
At Granada he studied the Koran, tradition, law and literature,
and later became secretary to the Mohad governor of that city.
During this time he composed many poems. In 1183 he left
the court and travelled to Alexandria, Jerusalem, Medina,
Mecca, Damascus, Mosul and Bagdad, returning in 1185 by
way of Sicily.
The Travels of Ibn Jubair were edited by W. Wright (Leiden,
1852); and a new edition of this text, revised by M. J. de Goeje,
was published by the Gibb Trustees (London, 1907). The part
relating to Sicily was published, with French translation and notes,
by M. Amari in the Journal asiatique (1845-1846) and a French
translation alone of the same part by G. Crolla in Museon, vi.
123-132.
(G. W. T.)
IBN KHALDŪN [Abū Zaid ibn Maḥommed ibn Maḥommed ibn
Khaldūn] (1332-1406), Arabic historian, was born at Tunis. He
studied the various branches of Arabic learning with great success.
In 1352 he obtained employment under the Marīnid sultan Abū
Inān (Faris I.) at Fez. In the beginning of 1356, his integrity
having been suspected, he was thrown into prison until the death
of Abū Inān in 1358, when the vizier al-Hasan ibn Omar set him
at liberty and reinstated him in his rank and offices. He here
continued to render great service to Abu Salem (Ibrahim III.),
Abū Inān’s successor, but, having offended the prime minister,
he obtained permission to emigrate to Spain, where, at Granada,
he was received with great cordiality by Ibn al Ahmar, who had
been greatly indebted to his good offices when an exile at the
court of Abu Salem. The favours he received from the sovereign
excited the jealousy of the vizier, and he was driven back to
Africa (1364), where he was received with great cordiality by the
sultan of Bougie, Abu Abdallah, who had been formerly his
companion in prison. On the fall of Abu Abdallah Ibn Khaldūn
raised a large force amongst the desert Arabs, and entered the
service of the sultan of Tlemçen. A few years later he was taken
prisoner by Abdalaziz (‘Abd ul ‘Azīz), who had defeated the
sultan of Tlemçen and seized the throne. He then entered a
monastic establishment, and occupied himself with scholastic
duties, until in 1370 he was sent for to Tlemçen by the new
sultan. After the death of ‘Abd ul ‘Azīz he resided at Fez,
enjoying the patronage and confidence of the regent. After
some further vicissitudes in 1378 he entered the service of the
sultan of his native town of Tunis, where he devoted himself
almost exclusively to his studies and wrote his history of the
Berbers. Having received permission to make the pilgrimage
to Mecca, he reached Cairo, where he was presented to the sultan,
al-Malik udh-Dhahir Barkuk, who insisted on his remaining there,
and in the year 1384 made him grand cadi of the Malikite rite
for Cairo. This office he filled with great prudence and probity,
removing many abuses in the administration of justice in Egypt.
At this time the ship in which his wife and family, with all his
property, were coming to join him, was wrecked, and every
one on board lost. He endeavoured to find consolation in the
completion of his history of the Arabs of Spain. At the same
time he was removed from his office of cadi, which gave him
more leisure for his work. Three years later he made the pilgrimage
to Mecca, and on his return lived in retirement in the Fayum
until 1399, when he was again called upon to resume his functions
as cadi. He was removed and reinstated in the office no fewer
than five times.
In 1400 he was sent to Damascus, in connexion with the
expedition intended to oppose Timur or Tamerlane. When
Timur had become master of the situation, Ibn Khaldūn let
himself down from the walls of the city by a rope, and presented
himself before the conqueror, who permitted him to return to
Egypt. Ibn Khaldūn died on the 16th of March 1406, at the
age of sixty-four.
The great work by which he is known is a “Universal History,”
but it deals more particularly with the history of the Arabs of Spain
and Africa. Its Arabic title is Kitāb ul‘Ibar, wa dīwān el Mubtada
wa’l Khabar, fī ayyām ul ‘Arab wa’l’Ajām wa’l Berber; that is, “The
Book of Examples and the Collection of Origins and Information
respecting the History of the Arabs, Foreigners and Berbers.” It
consists of three books, an introduction and an autobiography.
Book i. treats of the influence of civilization upon man; book ii. of
the history of the Arabs and other peoples from the remotest antiquity
until the author’s own times; book iii. of the history of the Berber
tribes and of the kingdoms founded by that race in North Africa.
The introduction is an elaborate treatise on the science of history
and the development of society, and the autobiography contains
the history, not only of the author himself, but of his family and of
the dynasties which ruled in Fez, Tunis and Tlemçen during his
lifetime. An edition of the Arabic text has been printed at Būlāq,
(7 vols., 1867) and a part of the work has been translated by the late
Baron McG. de Slane under the title of Histoire des Berbères (Algiers,
1852-1856); it contains an admirable account of the author and
analysis of his work. Vol. i., the Muqaddama (preface), was published
by M. Quatremère (3 vols., Paris, 1858), often republished in the
East, and a French translation was made by McG. de Slane (3 vols.,
Paris, 1862-1868). The parts of the history referring to the expeditions
of the Franks into Moslem lands were edited by C. J. Tornberg
(Upsala, 1840), and the parts treating of the Banu-l Aḥmar kings
of Granada were translated into French by M. Gaudefroy-Demombynes
in the Journal asiatique, ser. 9, vol. xiii. The Autobiography
of Ibn Khaldūn was translated into French by de Slane in the
Journal asiatique, ser. 4, vol. iii. For an English appreciation of the
philosophical spirit of Ibn Khaldūn see R. Flint’s History of the
Philosophy of History (Edinburgh, 1893), pp. 157-170.
(E. H. P.; G. W. T.)
IBN KHALLIKĀN [Abū-l ‘Abbās Aḥmad ibn Khallikān]
(1211-1282), Arabian biographer, was born at Arbela, the son
of a professor reputed to be ascended from the Barmecides of
the court of Harun al-Rashid. When eighteen he went to Aleppo,
where he studied for six years, then to Damascus, and in 1238
to Alexandria and Cairo. In 1252 he married and became
chief cadi of Syria in Damascus in 1261. Having held this office
for ten years, he was professor in Cairo until 1278, when he again
took office in Damascus for three years. In 1281 he accepted
a professorship in the same city, but died in the following year.
His great work is the Kitab Wafayāt ul-A‘yān, “The Obituaries
of Eminent Men.” It contains in alphabetical order the lives of the
most celebrated persons of Moslem history and literature, except
those of Mahomet, the four caliphs and the companions of Mahomet
and their followers (the Tābiūn). The work is anecdotal and contains
many brief extracts from the poetry of the writers. It was
published by F. Wüstenfeld (Göttingen, 1835-1843), in part by McG.
de Slane (Paris, 1838-1842), and also in Cairo (1859 and 1882).
An English translation by McG. de Slane was published for the
Oriental Translation Fund in 4 vols. (London, 1842-1871). Thirteen
extra biographies from a manuscript in Amsterdam were published
by Pijnappel (Amsterdam, 1845). A Persian translation exists in
manuscript, and various extracts from the work are known. Several
supplements to the book have been written, the best known being
that of Maḥommed ibn Shākir (d. 1362), published at Cairo 1882.
A collection of poems by Ibn Khallikān is also extant.
(G. W. T.)
IBN QUTAIBA, or Kotaiba [Abū Maḥommed ibn Muslim ibn
Qutaiba] (828-889), Arabian writer, was born at Bagdad or
223
Kufa, and was of Iranian descent, his father belonging to Merv.
Having studied tradition and philology he became cadi in
Dinawār and afterwards teacher in Bagdad, where he died.
He was the first representative of the eclectic school of Bagdad
philologists that succeeded the schools of Kufa and Baṣra (see
Arabia: Literature, section “Grammar”). Although engaged
also in theological polemic (cf. I. Goldziher, Muhammedanische
Studien, ii. 136, Halle, 1890), his chief works were directed
to the training of the ideal secretary. Of these five may be said
to form a series. The Adab ul-Kātib (“Training of the Secretary”)
contains instruction in writing and is a compendium of Arabic
style. It has been edited by Max Grünert (Leiden, 1900).
The Kitāb ush-Sharāb is still in manuscript. The Kitāb
ul-Ma’ārif has been edited by F. Wüstenfeld as the Handbuch der
Geschichte1 (Göttingen, 1850); the Kitāb ush-Shi’r
wash-Shu’arāi (“Book of Poetry and Poets”) edited by M. J. de Goeje
(Leiden, 1904).2 The fifth and most important is the ’Uyūn
ul-Akhbār, which deals in ten books with lordship, war, nobility,
character, science and eloquence, asceticism, friendship, requests,
foods and women, with many illustrations from history, poetry
and proverb (ed. C. Brockelmann, Leiden, 1900 sqq.).
For other works (which were much quoted by later Arabian
writers) see C. Brockelmann, Gesch. der arabischen Literatur, vol. i.
(Weimar, 1898), pp. 120-122.
(G. W. T.)
1 Summary in E. G. Browne, A Literary History of Persia (London,
1902), pp. 387 f.
2 The preface was translated into German by Theodor Nöldeke
in his Beiträge (Hanover, 1864), pp. 1-51.
IBN ṢA’D [Abū ‘Abdallāh Maḥommed ibn Ṣa’d ibn Mani’
uz-Zuhrī], often called Kātib ul-Waqidī (“secretary of Waqidī”)
of Baṣra] (d. 845), Arabian biographer, received his training
in tradition from Waqidī and other celebrated teachers. He
lived for the most part in Bagdad, and had the reputation of
being both trustworthy and accurate in his writings, which,
in consequence, were much used by later writers. His work,
the Kitāb ul-Ṭabaqāt ul-Kabīr (15 vols.) contains the lives of
Mahomet, his Companions and Helpers (including those who
fought at Badr as a special class) and of the following generation
(the Followers) who received their traditions from the personal
friends of the Prophet.
This work has been edited under the superintendence of E.
Sachau (Leiden, 1904 sqq.); cf. O. Loth, Das Classenbuch des Ibn
Sa‘d (Leipzig, 1869).
(G. W. T.)
IBN TIBBON, a family of Jewish translators, who flourished
in Provence in the 12th and 13th centuries. They all made
original contributions to philosophical and scientific literature,
but their permanent fame is based on their translations. Between
them they rendered into Hebrew all the chief Jewish writings
of the middle ages. These Hebrew translations were, in their
turn, rendered into Latin (by Buxtorf and others) and in this
form the works of Jewish authors found their way into the learned
circles of Europe. The chief members of the Ibn Tibbon family
were (1) Judah Ben Saul (1120-1190), who was born in Spain
but settled in Lunel. He translated the works of Baḥya, Halevi,
Saadiah and the grammatical treatises of Janaḥ. (2) His son,
Samuel (1150-1230), translated the Guide of the Perplexed
by Maimonides. He justly termed his father “the father of
the Translators,” but Samuel’s own method surpassed his
father’s in lucidity and fidelity to the original. (3) Son of
Samuel, Moses (died 1283). He translated into Hebrew a
large number of Arabic books (including the Arabic form of
Euclid). The Ibn Tibbon family thus rendered conspicuous
services to European culture, and did much to further among
Jews who did not understand Arabic the study of science and
philosophy.
(I. A.)
IBN ṬUFAIL, or Ṭofail [Abū Bakr Maḥommed ibn ‘Abd-ul-Malik
ibn Ṭufail ul-Qaisī] (d. 1185), Moslem philosopher, was
born at Guadix near Granada. There he received a good training
in philosophy and medicine, and is said to have been a pupil of
Avempace (q.v.). He became secretary to the governor of
Granada, and later physician and vizier to the Mohad caliph,
Abu Ya‘qūb Yūsuf. He died at Morocco.
His chief work is a philosophical romance, in which he describes
the awakening and growth of intellect in a child removed from the
influences of ordinary life. Its Arabic title is Risālat Hayy ibn Yaqzān;
it was edited by E. Pococke as Philosophus autodidactus (Oxford,
1671; 2nd ed., 1700), and with a French translation by L. Gauthier
(Algiers, 1900). An English translation by S. Ockley was published
in 1708 and has been reprinted since. A Spanish translation by
F. Pons Boigues was published at Saragossa (1900). Another work
of Ibn Ṭufail, the Kitāb Asrār ul-Hikma ul-mashraqīyya (“Secrets
of Eastern Science”), was published at Bulāq (1882); cf. S. Munk,
Mélanges (1859), pp. 410 sqq., and T. J. de Boer, Geschichte der Philosophie
im Islam (Stuttgart, 1901), pp. 160 sqq. (also an English translation).
(G. W. T.)
IBN USAIBI‘A [Muwaffaquddīn Abū-l-’Abbās Aḥmad ibn
ul-Qāsim ibn Abī Usaibi’a] (1203-1270), Arabian physician, was
born at Damascus, the son of an oculist, and studied medicine
at Damascus and Cairo. In 1236 he was appointed by Saladin
physician to a new hospital in Cairo, but surrendered the appointment
the following year to take up a post given him by
the amir of Damascus in Salkhad near that city. There he
lived and died. He wrote ‘Uyūn ul-Anba‘fī Ṭabaqāt ul-Aṭibba‘
or “Lives of the Physicians,” which in its first edition (1245-1246)
was dedicated to the vizier of Damascus. This he enlarged,
though it is uncertain whether the new edition was made public
in the lifetime of the author.
Edition by A. Müller (Königsberg, 1884).
(G. W. T.)
IBO, a district of British West Africa, on the lower Niger
immediately above the delta, and mainly on the eastern bank
of the river. The chief town, frequently called by the same
name (more correctly Abo or Áboh), lies on a creek which falls
into the main stream about 150 m. from its mouth and contains
from 6000 to 8000 inhabitants. The Ibo are a strong well-built
Negro race. Their women are distinguished by their embonpoint.
The language of the Ibo is one of the most widely spoken
on the lower Niger. The Rev. J. F. Schön began its reduction
in 1841, and in 1861 he published a grammar (Oku Ibo Grammatical
Elements, London, Church Miss. Soc.). (See Nigeria.)
IBRAHĪM AL-MAUṢILĪ (742-804), Arabian singer, was born
of Persian parents settled in Kufa. In his early years his parents
died and he was trained by an uncle. Singing, not study,
attracted him, and at the age of twenty-three he fled to Mosul,
where he joined a band of wild youths. After a year he went to
Rai (Rei, Rhagae), where he met an ambassador of the caliph
Manṣūr, who enabled him to come to Baṣra and take singing
lessons. His fame as a singer spread, and the caliph Mahdī
brought him to the court. There he remained a favourite under
Hādī, while Harūn al-Rashīd kept him always with him until
his death, when he ordered his son (Ma’mūn) to say the prayer
over his corpse. Ibrahīm, as might be expected, was no strict
Moslem. Two or three times he was knouted and imprisoned
for excess in wine-drinking, but was always taken into favour
again. His powers of song were far beyond anything else known
at the time. Two of his pupils, his son Isḥāq and Muḥāriq,
attained celebrity after him.
See the Preface to W. Ahlwardt’s Abu Nowas (Greifswald, 1861),
pp. 13-18, and the many stories of his life in the Kitāb ul-Aghāni,
v. 2-49.
(G. W. T.)
IBRAHIM PASHA (1789-1848), Egyptian general, is sometimes
spoken of as the adopted son of Mehemet Ali, pasha of
Egypt. He is also and more commonly called his son. He was
born in his father’s native town, Kavala in Thrace. During
his father’s struggle to establish himself in Egypt, Ibrahim,
then sixteen years of age, was sent as a hostage to the
Ottoman capitan pasha (admiral), but when Mehemet Ali was
recognized as pasha, and had defeated the English expedition
under General A. M. Fraser, he was allowed to return to Egypt.
When Mehemet Ali went to Arabia to prosecute the war against
the Wahhabis in 1813, Ibrahim was left in command in Upper
Egypt. He continued the war with the broken power of the
Mamelukes, whom he suppressed. In 1816 he succeeded his
brother Tusun in command of the Egyptian forces in Arabia.
Mehemet Ali had already begun to introduce European discipline
into his army, and Ibrahim had probably received some training,
but his first campaign was conducted more in the old Asiatic
224
style than his later operations. The campaign lasted two years,
and terminated in the destruction of the Wahhabis as a political
power. Ibrahim landed at Yembo, the port of Medina, on the
30th of September 1816. The holy cities had been recovered
from the Wahhabis, and Ibrahim’s task was to follow them into
the desert of Nejd and destroy their fortresses. Such training
as the Egyptian troops had received, and their artillery, gave
them a marked superiority in the open field. But the difficulty
of crossing the desert to the Wahhabi stronghold of Deraiya,
some 400 m. east of Medina, and the courage of their opponents,
made the conquest a very arduous one. Ibrahim displayed
great energy and tenacity, sharing all the hardships of his army,
and never allowing himself to be discouraged by failure. By the
end of September 1818 he had forced the Wahhabi leader to
surrender, and had taken Deraiya, which he ruined. On the
11th of December 1819 he made a triumphal entry into Cairo.
After his return he gave effective support to the Frenchman,
Colonel Sève (Suleiman Pasha), who was employed to drill
the army on the European model. Ibrahim set an example
by submitting to be drilled as a recruit. When in 1824 Mehemet
Ali was appointed governor of the Morea by the sultan, who
desired his help against the insurgent Greeks, he sent Ibrahim
with a squadron and an army of 17,000 men. The expedition
sailed on the 10th of July 1824, but was for some months unable
to do more than come and go between Rhodes and Crete. The
fear of the Greek fire ships stopped his way to the Morea. When
the Greek sailors mutinied from want of pay, he was able to
land at Modon on the 26th of February 1825. He remained
in the Morea till the capitulation of the 1st of October 1828
was forced on him by the intervention of the Western powers.
Ibrahim’s operations in the Morea were energetic and ferocious.
He easily defeated the Greeks in the open field, and though the
siege of Missolonghi proved costly to his own troops and to the
Turks who operated with him, he brought it to a successful
termination on the 24th of April 1826. The Greek guerrilla
bands harassed his army, and in revenge he desolated the country
and sent thousands of the inhabitants into slavery in Egypt.
These measures of repression aroused great indignation in Europe,
and led first to the intervention of the English, French and
Russian squadrons (see Navarino, Battle of), and then to
the landing of a French expeditionary force. By the terms of
the capitulation of the 1st of October 1828, Ibrahim evacuated
the country. It is fairly certain that the Turkish government,
jealous of his power, had laid a plot to prevent him and his
troops from returning to Egypt. English officers who saw him
at Navarino describe him as short, grossly fat and deeply marked
with smallpox. His obesity did not cause any abatement of
activity when next he took the field. In 1831, his father’s
quarrel with the Porte having become flagrant, Ibrahim was
sent to conquer Syria. He carried out his task with truly remarkable
energy. He took Acre after a severe siege on the 27th of
May 1832, occupied Damascus, defeated a Turkish army at
Homs on the 8th of July, defeated another Turkish army at
Beilan on the 29th of July, invaded Asia Minor, and finally
routed the grand vizier at Konia on the 21st of December. The
convention of Kutaiah on the 6th of May left Syria for a time
in the hands of Mehemet Ali. Ibrahim was undoubtedly helped
by Colonel Sève and the European officers in his army, but his
intelligent docility to their advice, as well as his personal hardihood
and energy, compare most favourably with the sloth,
ignorance and arrogant conceit of the Turkish generals opposed
to him. He is entitled to full credit for the diplomatic judgment
and tact he showed in securing the support of the inhabitants,
whom he protected and whose rivalries he utilized. After the
campaign of 1832 and 1833 Ibrahim remained as governor in
Syria. He might perhaps have administered successfully, but
the exactions he was compelled to enforce by his father soon
ruined the popularity of his government and provoked revolts. In
1838 the Porte felt strong enough to renew the struggle, and war
broke out once more. Ibrahim won his last victory for his
father at Nezib on the 24th of June 1839. But Great Britain
and Austria intervened to preserve the integrity of Turkey.
Their squadrons cut his communications by sea with Egypt, a
general revolt isolated him in Syria, and he was finally compelled
to evacuate the country in February 1841. Ibrahim spent the
rest of his life in peace, but his health was ruined. In 1846 he
paid a visit to western Europe, where he was received with
some respect and a great deal of curiosity. When his father
became imbecile in 1848 he held the regency till his own death
on the 10th of November 1848.
See Edouard Gouin, L’Égypte au XIXe siècle (Paris, 1847); Aimé
Vingtrinier, Soliman-Pasha (Colonel Sève) (Paris, 1886). A great
deal of unpublished material of the highest interest with regard to
Ibrahim’s personality and his system in Syria is preserved in the
British Foreign Office archives; for references to these see Cambridge
Mod. Hist. x. 852, bibliography to chap. xvii.
IBSEN, HENRIK (1828-1906), Norwegian dramatic and
lyric poet, eldest son of Knud Henriksen Ibsen, a merchant,
and of his wife Marichen Cornelia Altenburg, was born at Skien
on the 20th of March 1828. For five generations the family had
consisted on the father’s side of a blending of the Danish, German
and Scottish races, with no intermixture of pure Norwegian.
In 1836 Knud Ibsen became insolvent, and the family withdrew,
in great poverty, to a cottage in the outskirts of the town. After
brief schooling at Skien, Ibsen was, towards the close of 1843,
apprenticed to an apothecary in Grimstad; here he remained
through seven dreary years of drudgery, which set their mark
upon his spirit. In 1847, in his nineteenth year, he began to
write poetry. He made a gloomy and almost sinister impression
upon persons who met him at this time, and one of his associates
of those days has recorded that Ibsen “walked about Grimstad
like a mystery sealed with seven seals.” He had continued, by
assiduous reading, his self-education, and in 1850 he contrived
to come up as a student to Christiania. In the same year he
published his first work, the blank-verse tragedy of Catilina,
under the pseudonym Brynjolf Bjarme. A second drama,
The Viking’s Barrow, was acted (but not printed) a few months
later; Ibsen was at this time entirely under the influence of the
Danish poet Oehlenschläger. During the next year or two he
made a very precarious livelihood in Christiania as a journalist,
but in November 1851 he had the good fortune to be appointed
“stage-poet” at the little theatre of Bergen, with a small but
regular salary. He was practically manager at this house, and
he also received a travelling stipend. In 1852, therefore, he
went for five months to study the stage, to Copenhagen and to
Dresden. Among many dramatic experiments which Ibsen made
in Bergen, the most considerable and most satisfactory is the
saga-drama of Mistress Inger at Östraat, which was produced in
1855; and printed at Christiania in 1857; here are already
perceptible some qualities of his mature character. Much less
significant, although at the time more successful, is The Feast at
Solhaug, a tragedy produced in Bergen in 1856; here for a
moment Ibsen abandoned his own nascent manner for an
imitation of the popular romantic dramatist of Denmark, Henrik
Hertz. It is noticeable that Ibsen, by far the most original of
modern writers for the stage, was remarkably slow in discovering
the true bent of his genius. His next dramatic work was the
romantic tragedy of Olaf Liljekrans, performed in 1857, but
unprinted until 1898. This was the last play Ibsen wrote in
Bergen. In the summer of the former year his five years’
appointment came to an end, and he returned to Christiania.
Almost immediately he began the composition of a work which
showed an extraordinary advance on all that he had written
before, the beautiful saga-drama of The Warriors in Helgeland,
in which he threw off completely the influence of the Danish
romantic tragedians, and took his material directly from the
ancient Icelandic sources. This play marks an epoch in the
development of Norwegian literature. It was received by the
managers, both in Christiania and Copenhagen, with contemptuous
disapproval, and in the autumn of 1857 Ibsen could
not contrive to produce it even at the new theatre of which he
was now the manager. The Warriors was printed at Christiania
in 1858, but was not acted anywhere until 1861. During these
years Ibsen suffered many reverses and humiliations, but he
persisted in his own line in art. Some of his finest short poems,
225
among others the admirable seafaring romance, Terje Vigen,
belong to the year 1860. The annoyances which Ibsen suffered,
and the retrograde and ignorant conditions which he felt around
him in Norway, developed the ironic qualities in his genius, and
he became an acid satirist. The brilliant rhymed drama, Love’s
Comedy, a masterpiece of lyric wit and incisive vivacity, was
published in 1862. This was a protest against the conventionality
which deadens the beauty of all the formal relations between
men and women, and against the pettiness, the publicity, and
the prosiness of betrothed and married life among the middle
classes in Norway; it showed how society murders the poetry
of love. For some time past Ibsen had been meditating another
saga-drama in prose, and in 1864 this appeared, Kongsemnerne
(The Pretenders). These works, however, now so universally
admired, contained an element of strangeness which was not
welcome when they were new. Ibsen’s position in Christiania
grew more and more disagreeable, and he had positive misfortunes
which added to his embarrassment. In 1862 his theatre became
bankrupt, and he was glad to accept the poorly-paid post of
“aesthetic adviser” at the other house. An attempt to obtain
a poet’s pension (digtergage) was unsuccessful; the Storthing,
which had just voted one to Björnson, refused to do the same for
Ibsen. His cup was full of disillusion and bitterness, and in
April 1864 he started, by Berlin and Trieste, ultimately to settle
in Rome. His anger and scorn gave point to the satirical arrows
which he shot back to his thankless fatherland from Italy in the
splendid poem of Brand, published in Copenhagen in 1866, a
fierce attack on the Laodicean state of religious and moral
sentiment in the Norway of that day; the central figure, the
stern priest Brand, who attempts to live like Christ and is
snubbed and hounded away by his latitudinarian companions,
is one of the finest conceptions of a modern poet. Ibsen had
scarcely closed Brand before he started a third lyrico-dramatic
satire. Peer Gynt (1867), which remains, in a technical sense,
the most highly finished of all his metrical works. In Brand
the hero had denounced certain weaknesses which Ibsen saw in
the Norwegian character, but these and other faults are
personified in the hero of Peer Gynt; or rather, in this figure the
poet pictured, in a type, the Norwegian nation in all the egotism,
vacillation, and lukewarmness which he believed to be characteristic
of it. Ibsen, however, acted better than he preached, and
he soon forgot his abstraction in the portrait of Peer Gynt as
a human individual. In this magnificent work modern Norwegian
literature first rises to a level with the finest European
poetry of the century. In 1869 Ibsen wrote the earliest of his
prose dramas, the political comedy, The Young Men’s League,
in which for the first time he exercised his extraordinary gift
for perfectly natural and yet pregnant dialogue. Ibsen was in
Egypt, in October 1869, when his comedy was put on the stage
in Christiania, amid violent expressions of hostility; on hearing
the news, he wrote his brilliant little poem of defiance, called
At Port Saïd. By this time, however, he had become a successful
author; Brand sold largely, and has continued to be the most
popular of Ibsen’s writings. In 1866, moreover, the Storthing
had been persuaded to vote him a “poet’s pension,” and there
was now an end of Ibsen’s long struggle with poverty. In 1868
he left Rome, and settled in Dresden until 1874, when he returned
to Norway. But after a short visit he went back to Germany,
and lived first at Dresden, afterwards at Munich, and did not
finally settle in Christiania until 1891. His shorter lyrical poems
were collected in 1871, and in that year his name and certain of
his writings were for the first time mentioned to the English
public. At this time he was revising his old works, which were
out of print, and which he would not resign again to the reading
world until he had subjected them to what in some instances
(for example, Mistress Inger at Östraat) amounted to practical
recomposition. In 1873 he published a double drama, each part
of which was of unusual bulk, the whole forming the tragedy of
Emperor and Galilean; this, Ibsen’s latest historical play, has
for subject the unsuccessful struggle of Julian the Apostate to
hold the world against the rising tide of Christianity. The work
is of an experimental kind, and takes its place between the early
poetry and the later prose of the author. Compared with the
series of plays which Ibsen had already inaugurated with The
Young Men’s League, Emperor and Galilean preserves a colour
of idealism and even of mysticism which was for many years to
be absent from Ibsen’s writings, but to reappear in his old age
with The Master-builder. There is some foundation for the
charge that Ibsen has made his romantic Greek emperor needlessly
squalid, and that he has robbed him, at last, too roughly
of all that made him a sympathetic exponent of Hellenism.
Ibsen was now greatly occupied by the political spectacle of
Germany at war first in Denmark, then in France, and he believed
that all things were conspiring to start a new epoch of individualism.
He was therefore deeply disgusted by the Paris commune,
and disappointed by the conservative reaction which
succeeded it. This disillusion in political matters had a very
direct influence upon Ibsen’s literary work. It persuaded
him that nothing could be expected in the way of reform
from democracies, from large blind masses of men moved
capriciously in any direction, but that the sole hope for the
future must lie in the study of personality, in the development
of individual character. He set himself to diagnose the conditions
of society, which he had convinced himself lay sick unto death.
Hitherto Ibsen had usually employed rhymed verse for his
dramatic compositions, or, in the case of his saga-plays, a studied
and artificial prose. Now, in spite of the surprising achievements
of his poetry, he determined to abandon versification, and to
write only in the language of everyday conversation. In the first
drama of this his new period, The Pillars of Society (1877), he
dealt with the problem of hypocrisy in a small commercial centre
of industry, and he drew in the Bernick family a marvellous
picture of social egotism in a prosperous seaport town. There
was a certain similarity between this piece and A Doll’s House
(1879), although the latter was much the more successful in
awakening curiosity. Indeed, no production of Ibsen’s has been
so widely discussed as this, which is nevertheless not the most
coherently conceived of his plays. Here also, social hypocrisy,
was the object of the playwright’s satire, but this time mainly
in relation to marriage. In A Doll’s House Ibsen first developed
his views with regard to the individualism of woman. In his
previous writings he had depicted woman as a devoted and
willing sacrifice to man; here he begins to explain that she
has no less a duty to herself, and must keep alive her own conception
of honour and of responsibility. The conclusion of A
Doll’s House was violently and continuously discussed through
the length and breadth of Europe, and to the situation of Nora
Helmer is probably due more than to anything else the long
tradition that Ibsen is “immoral.” He braved convention still
more audaciously in Ghosts (1881), perhaps the most powerful
of the series of plays in which Ibsen diagnoses the diseases
of modern society. It was received in Norway with a tumult
of ill-will, and the author was attacked no less venomously than
he had been twenty years before. Ibsen was astonished and
indignant at the reception given to Ghosts, and at the insolent
indifferentism of the majority to all ideas of social reform.
He wrote, more as a pamphlet than as a play, what is yet one of
the most effective of his comedies, An Enemy of the People
(1882). Dr Stockmann, the hero of that piece, discovers that
the drainage system of the bathing-station on which the little
town depends is faulty, and the water impure and dangerous.
He supposes that the corporation will be grateful to have these
deficiencies pointed out; on the contrary, they hound him out
of their midst as an “enemy of the people.” In this play occurs
Ibsen’s famous and typical saying, “a minority may be right—a
majority is always wrong.” This polemical comedy seemed
at first to be somewhat weakened by the personal indignation
which runs through it, but it has held the stage. Ibsen’s next
drama, The Wild Duck (1884), was written in singular contrast
with the zest and fire which had inspired An Enemy of the
People. Here he is squalid and pessimistic to a degree elsewhere
unparalleled in his writings; it is not quite certain that he is
not here guilty of a touch of parody of himself. The main
figure of the play is an unhealthy, unlucky enthusiast, who goes
226
about making hopeless mischief by exposing weak places in
the sordid subterfuges of others. This drama contains a figure,
Hjálmar Ekdal, who claims the bad pre-eminence of being the
meanest scoundrel in all drama. The Wild Duck is the darkest,
the least relieved, of Ibsen’s studies of social life, and his object
in composing it is not obvious. With Rosmersholm (1886) he
rose to the height of his genius again; this is a mournful, but
neither a pessimistic nor a cynical play. The fates which hang
round the contrasted lives of Rosmer and Rebecca, the weak-willed
scrupulous man and the strong-willed unshrinking woman,
the old culture and the new, the sickly conscience and the robust
one, create a splendid dramatic antithesis. Ibsen then began
to compose a series of dramas, of a more and more symbolical
and poetic character; the earliest of these was the mystical
The Lady from the Sea (1888). At Christmas 1890 he brought
out Hedda Gabler; two years later The Master-builder (Bygmester
Solnaes), in which many critics see the highest attainment of
his genius; at the close of 1894 Little Eyolf; in 1896 John
Gabriel Borkman; and in 1900 When We Dead Awaken. On
the occasion of his seventieth birthday (1898) Ibsen was the
recipient of the highest honours from his own country and of
congratulations and gifts from all parts of the world. A colossal
bronze statue of him was erected outside the new National
Theatre, Christiania, in September 1899. In 1901 his health
began to decline, and he was ordered by the physician to abandon
every species of mental effort. The evil advanced, and he
became unconscious of the passage of events. After lingering
in this sad condition he died, without suffering, on the 23rd of
May 1906, and was accorded a public funeral, with the highest
national honours.
No recent writer belonging to the smaller countries of Europe
has had so widely spread a fame as that of Ibsen, and although
the value of his dramatic work is still contested, it has received
the compliment of vivacious discussion in every part of the
world. There would, perhaps, have been less violence in this
discussion if it had been perceived that the author does not
pose as a moral teacher, but as an imaginative investigator.
He often and with much heat insisted that he was not called
upon as a poet to suggest a remedy for the diseases of society,
but to diagnose them. In this he was diametrically opposed
to Tolstoi, who admitted that he wrote his books for the healing
of the nations. If the subjects which Ibsen treats, or some of
them, are open to controversy, we are at least on firm ground
in doing homage to the splendour of his art as a playwright.
He reintroduced into modern dramatic literature something
of the velocity and inevitability of Greek tragic intrigue. It is
very rarely that any technical fault can be found with the architecture
of his plots, and his dialogue is the most lifelike that the
modern stage has seen. His long apprenticeship to the theatre
was of immense service to him in this respect. In every country,
though least perhaps in England, the influence of Ibsen has been
marked in the theatrical productions of the younger school.
Even in England, on the rare occasions when his dramas are
acted, they awaken great interest among intelligent playgoers.
The editions of Ibsen’s works are numerous, but the final text is
included in the Samlede Vaerker, with a bibliography by J. B.
Halvorsen, published in Copenhagen, in 10 vols. (1898-1902). They
have been translated into the principal European languages, and
into Japanese. The study of Ibsen in English was begun by Mr
Gosse in 1872, and continued by Mr William Archer, whose version of
Ibsen’s prose dramas appeared in 5 vols. (1890, 1891; new and
revised edition, 1906). Other translators have been Mr C. Herford,
Mr R. A. Streatfield, Miss Frances Lord and Mr Adie. His Correspondence
was edited, in 2 vols., under the supervision of his son,
Sigurd Ibsen, in 1904 (Eng. trans., 1905). Critical studies on the
writings and position of Ibsen are innumerable, and only those
which were influential in guiding opinion, during the early part
of his career, in the various countries, can be mentioned here:
Georg Brandes Ästhetiske Studier (Copenhagen, 1868); Les Quesnel,
Poésie scandinave (Paris 1874); Valfrid Valsenius, Henrik Ibsen
(Helsingfors, 1879); Edmund Gosse, Studies in Northern Literature
(London, 1879); L. Passarge, Henrik Ibsen (Leipzig, 1883); G.
Brandes, Björnson och Ibsen (Stockholm, 1882); Henrik Jaeger,
Henrik Ibsen 1828-1888 (Copenhagen, 1888; Eng. trans., 1890);
T. Terwey, Henrik Ibsen (Amsterdam, 1882); G. Bernard Shaw,
The Quintessence of Ibsen (London, 1892). In France Count Moritz
Prozor carried on an ardent propaganda in favour of Ibsen from
1885, and Jules Lemaître’s articles in his Les Contemporains and
Impressions de théâtre did much to encourage discussion. W. Archer
forwarded the cause in England from 1878 onwards. In Germany
Ibsen began to be known in 1866, when John Grieg, P. F. Siebold
and Adolf Strodtmann successively drew attention to his early
dramas; but his real popularity among the Germans dates from
1880.
(E. G.)
IBYCUS, of Rhegium in Italy, Greek lyric poet, contemporary
of Anacreon, flourished in the 6th century B.C. Notwithstanding
his good position at home, he lived a wandering life, and spent
a considerable time at the court of Polycrates, tyrant of Samos.
The story of his death is thus related: While in the neighbourhood
of Corinth, the poet was mortally wounded by robbers.
As he lay dying he saw a flock of cranes flying overhead, and
called upon them to avenge his death. The murderers betook
themselves to Corinth, and soon after, while sitting in the theatre,
saw the cranes hovering above. One of them, either in alarm or
jest, ejaculated, “Behold the avengers of Ibycus,” and thus
gave the clue to the detection of the crime (Plutarch, De Garrulitate,
xiv.). The phrase, “the cranes of Ibycus,” passed
into a proverb among the Greeks for the discovery of crime
through divine intervention. According to Suidas, Ibycus
wrote seven books of lyrics, to some extent mythical and heroic,
but mainly erotic (Cicero, Tusc. Disp. iv. 33), celebrating the
charms of beautiful youths and girls. F. G. Welcker suggests
that they were sung by choruses of boys at the “beauty competitions”
held at Lesbos. Although the metre and dialect are
Dorian, the poems breathe the spirit of Aeolian melic poetry.
The best editions of the fragments are by F. W. Schneidewin
(1833) and Bergk, Poëtae lyrici Graeci.
ICA (Yca, or Ecca), a city of southern Peru and the capital
of a department of the same name, 170 m. S.S.E. of Lima, and
46 m. by rail S.E. of Pisco; its port on the Pacific coast. Pop.
(1906, official estimate) 6000. It lies in a valley of the foothills
of the Cordillera Occidental, which is watered by the Rio de
Ica, is made highly fertile by irrigation, and is filled with vineyards
and cotton fields; between this valley and the coast is
a desert. The original town was founded in 1563, 4 m.
E. of its present site, but it was destroyed by the earthquake
of 1571, and again by that of 1664, after which the present town
was laid out near the ruins. In 1882 a Chilean marauding
expedition inflicted great damage to private property in the
town and vicinity. These repeated disasters give the place a
partially ruined appearance, but it has considerable commercial
and industrial prosperity. It has a large cotton factory and
there are some smaller industries. Wine-making is one of the
principal industries of the valley, and much brandy, called
pisco, is exported from Pisco. A new industry is that of drying
the fruits for which this region is celebrated. Ica is the seat of
a national college.
The department of Ica lies between the Western Cordillera
and the Pacific coast, and extends from the department of Lima
S.E. to that of Arequipa. Pop. (1906, official estimate) 68,220;
area 8721 sq. m. Ica is in the rainless region of Peru, and the
greater part of its surface is barren. It is crossed by the rivers
Pisco, Ica and Grande, whose tributaries drain the western
slope of the Cordillera, and whose valleys are fertile and highly
cultivated. The valley of the Nasca, a tributary of the Grande,
is celebrated for an extensive irrigating system constructed by
the natives before the discovery of America. The principal
products of the department are cotton, grapes, wine, spirits,
sugar and fruit. These are two good ports on the northern
coast, Tambo de Mora and Pisco, the latter being connected
with the capital by a railway across the desert, 46 m. long.
ICE (a word common to Teutonic languages; cf. Ger. Eis),
the solid crystalline form which water assumes when exposed
to a sufficiently low temperature. It is a colourless crystalline
substance, assuming forms belonging to the hexagonal system,
and distinguished by a well-marked habit of twinning, which
occasions the beautiful “ice flowers” displayed by hoar-frost.
It is frequently precipitated as hoar-frost, snow or hail; and
in the glaciers and snows of lofty mountain systems or of regions
227
of high latitude it exists on a gigantic scale, being especially
characteristic of the seas and lands around the poles. In various
regions, especially in France and Italy, great quantities of ice
form in caves, which, in virtue of their depth below the earth’s
surface, their height above the sea-level, or their exposure to
suitable winds, or to two or more of these conditions in combination,
are unaffected by ordinary climatic changes, so that
the mean annual temperature is sufficiently low to ensure the
permanency of the ice. The temperature at which water
freezes, and also at which ice melts, is so readily determined
that it is employed as one of the standard temperatures in the
graduation of ordinary thermometer scales, this temperature
being the zero of the Centigrade and Réaumur scales, and 32°
of the Fahrenheit (see Thermometry). In the act of freezing,
water, though its temperature remains unchanged, undergoes
a remarkable expansion so that ice at 0° C. is less dense than
water—a fact demonstrated by its power of floating. The
sub-aqueous retention of “ground-ice” or “anchor-ice,”
which forms in certain circumstances at the bottom of streams
or pools in which there are many eddies, is due to the cohesion
between it and the stones or rocks which compose the bed of
the streams or pools. As water expands on freezing, so conversely
ice contracts on melting; and the ice-cold water thus
formed continues to contract when heated until it has reached
its point of maximum density, the temperature at which this
occurs being about 39° Fahr, or 4° C. Above this point water
continuously expands, and at no temperature is it less dense
than ice as is shown by the following table:—
| Density of ice at | 0°C. = .9175 |
| ” water at | 0°C. = .99988 |
| ” ” | 4°C. = 1.00000 |
| ” ” | 10°C. = .99976 |
| ” ” | 100°C. = .95866 |
Under the influence of heat, ice itself behaves as most solids
do, contracting when cooled, expanding when heated. According
to Plücker, the coefficient of cubical dilatation at moderately
low temperatures is 0.0001585. From a series of elaborate
experiments, Person deduced 0.505 as the specific heat of ice,
or about half that of water.
Though no rise of temperature accompanies the melting of
ice, there is yet a definite quantity of heat absorbed, namely,
about 80 calories per gram; this is called the latent heat of
fusion of water (see Fusion). The same amount of heat is
evolved when water becomes ice. That ice can be melted by
increase of pressure was first pointed out by James Thomson
in 1849. He showed that, since water expands on freezing,
the laws of thermodynamics require that its freezing-point
must be lowered by increase of pressure; and he calculated
that for every additional atmosphere of pressure the freezing-point
of water was lowered by 0.0075°. This result was verified
by his brother, Sir William Thomson (Lord Kelvin), in 1850.
The Thomsons and H. L. F. Helmholtz successfully applied
this behaviour of ice under pressure to the explanation of many
properties of the substance. When two blocks of ice at 0° C.
are pressed together or even simply laid in contact, they gradually
unite along their touching surfaces till they form one block.
This “regelation” is due to the increased pressure at the various
points of contact causing the ice there to melt and cool. The
water so formed tends to escape, thus relieving the pressure
for an instant, refreezing and returning to the original temperature.
This succession of melting and freezing, with their accompanying
thermal effects, goes on until the two blocks are cemented
into one.
Ice forms over fresh water if the temperature of the air has
been for a sufficient time at or below the freezing-point; but
not until the whole mass of water has been cooled down to its
point of maximum density, so that the subsequent cooling
of the surface can give rise to no convection currents, is freezing
possible. Sea-water, in the most favourable circumstances,
does not freeze till its temperature is reduced to about −2° C.;
and the ice, when formed, is found to have rejected four-fifths
of the salt which was originally present. In the upper provinces
of India water is made to freeze during cold clear nights by
leaving it overnight in porous vessels, or in bottles which are
enwrapped in moistened cloth. The water then freezes in virtue
of the cold produced by its own evaporation or by the drying
of the moistened wrapper. In Bengal the natives resort to a
still more elaborate forcing of the conditions. Pits are dug
about 2 ft. deep and filled three-quarters full with dry straw,
on which are set flat porous pans containing the water to be
frozen. Exposed overnight to a cool dry gentle wind from the
north-west, the water evaporates at the expense of its own
heat, and the consequent cooling takes place with sufficient
rapidity to overbalance the slow influx of heat from above
through the cooled dense air or from below through the badly
conducting straw.
ICEBERG (from ice and Berg, Ger. for hill, mountain), a
floating mass of ice broken from the end of a glacier or from an
ice-sheet. The word is sometimes, but rarely, applied to the
arch of an Arctic glacier viewed from the sea. It is more commonly
used to describe huge floating masses of ice that drift
from polar regions into navigable waters. They are occasionally
encountered far beyond the polar regions, rising into beautiful
forms with breakers roaring into their caves and streams of
water pouring from their pinnacles in the warmer air. When,
however, they rest in comparatively warm water, melting takes
place most rapidly at the base and they frequently overturn.
Only one-ninth of the mass of ice is seen above water. When
a glacier descends to the sea, as in Alaska, and “advances
into water, the depth of which approaches its thickness, the
ends are broken off and the detached masses float away as
icebergs. Many of the bergs are overturned, or at least tilted,
as they set sail. If this does not happen at once it is likely to
occur later as the result of the wave-cutting and melting which
disturb their equilibrium” (T. C. Chamberlin and R. D. Salisbury,
Geology: Processes and their Results, 1905). These bergs carry
a load of débris from the glacier and gradually strew their load
upon the sea floor. They do not travel far before losing all
stony and earthy débris, but glacial material found in dredgings
shows that icebergs occasionally carry their load far from land.
The structure of the iceberg varies with its origin and is always
that of the glacier or ice-sheet from which it was broken. The
breaking off of the ice-sheet from a Greenland glacier is called
locally the “calving” of the glacier. The constantly renewed
material from which the icebergs are formed is brought down
by the motion of the glacier. The ice-sheet cracks at the end,
and masses break off, owing to the upward pressure of the water
upon the lighter ice which is pushed into it. This is accomplished
with considerable violence. The disintegration of an Arctic ice-sheet
is a simpler matter, as the ice is already floating.
ICELAND (Dan. Island), an island in the North Atlantic
Ocean, belonging to Denmark. Its extreme northerly point
is touched by the Arctic Circle; it lies between 13° 22′ and 24°
35′ W., and between 63° 12′ and 66° 33′ N., and has an area of
40,437 sq. m. Its length is 298 m. and its breadth 194 m., the
shape being a rough oval, broken at the north-west, where a
peninsula, diversified by a great number of fjords, projects
from the main portion of the island. The total length of the
coast-line is about 3730 m., of which approximately one-third
belongs to the north-western peninsula. Iceland is a plateau
or tableland, built up of volcanic rocks of older and younger
formation, and pierced on all sides by fjords and valleys. Compared
with the tableland, the lowlands have a relatively small
area, namely, one-fourteenth of the whole; but these lowlands
are almost the only parts of the island which are inhabited.
In consequence of the rigour of its climate, the central tableland
is absolutely uninhabitable. At the outside, not more than one-fourth
of the area of Iceland is inhabited; the rest consists of
elevated deserts, lava streams and glaciers. The north-west
peninsula is separated from the main mass of the island by the
bays Hunaflói and Breiðifjörðr, so that there are really two
tablelands, a larger and a smaller. The isthmus which connects
the two is only 4¼ m. across, but has an altitude of 748 ft. The
228
mean elevation of the north-west peninsula is 2000 ft. The
fjords and glens which cut into it are shut in by precipitous walls
of basalt, which plainly shows that they have been formed
by erosion through the mass of the plateau. The surface of
this tableland is also bare and desolate, being covered with gravel
and fragments of rock. Here and there are large straggling
snowfields, the largest being Glámu and Drangajökull,1 on the
culminating points of the plateau. The only inhabited districts
are the shores of the fjords, where grass grows capable of supporting
sheep; but a large proportion of the population gain their
livelihood by fishing. The other and larger tableland, which
constitutes the substantial part of Iceland, reaches its culminating
point in the south-east, in the gigantic snowfield of Vatnajökull,
which covers 3300 sq. m. The axis of highest elevation of Iceland
stretches from north-west to south-east, from the head of
Hvammsfjörðr to Hornafjörðr, and from this water-parting the
rivers descend on both sides. The crest of the water-parting
is crowned by a chain of snow-capped
mountains, separated by broad patches of
lower ground. They are really a chain of
minor plateaus which rise 4500 to 6250 ft.
above sea-level and 2000 to 3000 ft. above
the tableland itself. In the extreme east is
Vatnajökull, which is separated from Tungnafellsjökull
by Vonarskard (3300 ft.). Between
Tungnafellsjökull and Hofsjökull lies the broad
depression of Sprengisandr (2130 ft.). Continuing
north-west, between Hofsjökull and the
next snow-capped mountain, Langjökull, lies
Kjölur (2000 ft.); and between Langjökull
and Eiriksjökull, Flosaskard (2630 ft.). To
the north of the jöklar last mentioned there
are a number of lakes, all well stocked with
fish. Numerous valleys or glens penetrate into
the tableland, especially on the north and east,
and between them long mountain spurs, sections
of the tableland which have resisted the action
of erosion, thrust themselves towards the sea.
Of these the most considerable is the mass
crowned by Mýrdalsjökull, which stretches
towards the south. The interior of the tableland
consists for the most part of barren,
grassless deserts, the surface being covered
by gravel, loose fragments of rock, lava, driftsand, volcanic
ashes and glacial detritus.
Save the lower parts of the larger glens, there are no lowlands
on the north and east. The south coast is flat next the sea;
but immediately underneath Vatnajökull there is a strip of
gravel and sand, brought down and deposited by the glacial
streams. The largest low-lying plain of Iceland, lying between
Mýrdalsjökull and Reykjanes, has an area of about 1550 sq. m.
In its lowest parts this plain barely keeps above sea-level,
but it rises gradually towards the interior, terminating in a
ramification of valleys. Its maximum altitude is attained
at 381 ft. near Geysir. On the west of Mount Hekla this plain
connects by a regular slope directly with the tableland, to the
great injury of its inhabited districts, which are thus exposed to
the clouds of pumice dust and driftsand that cover large areas
of the interior. Nevertheless the greater part of this lowland
plain produces good grass, and is relatively well inhabited. The
plain is drained by three rivers—Markarfljót, Thjórsá and
Oelfusá—all of large volume, and numerous smaller streams.
Towards the west there exist a number of warm springs. There
is another lowland plain around the head of Faxaflói, nearly
400 sq. m. in extent. As a rule the surface of this second plain
is very marshy. Several dales or glens penetrate the central
tableland; the eastern part of this lowland is called Borgarfjörðr,
the western part Mýrar.
The great bays on the west of the island (Faxaflói and Breiðifjörðr),2
as well as the many bays on the north, which are
separated from one another by rocky promontories, appear to
owe their origin to subsidences of the surface; whereas the
fjords of the north-west peninsula, which make excellent harbours,
and those of the east coast seem to be the result chiefly of erosion.
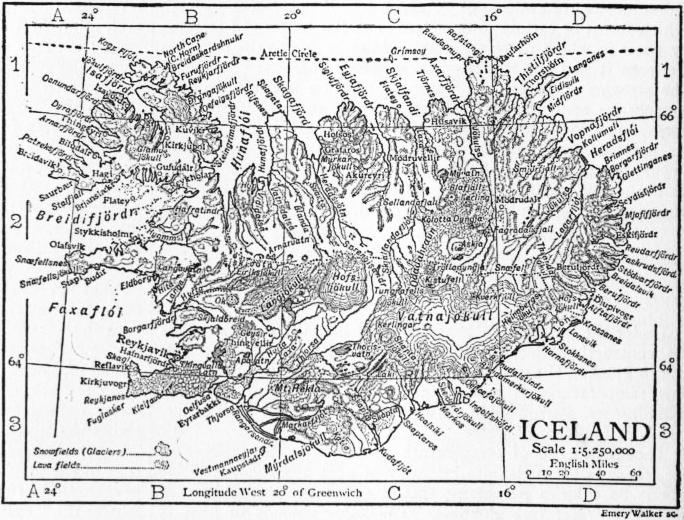
Glaciers.—An area of 5170 sq. m. is covered with snowfields
and glaciers. This extraordinary development of ice and snow
is due to the raw, moist climate, the large rainfall and the low
summer temperature. The snow-line varies greatly in different
parts of the island, its range being from 1300 to 4250 ft. It is
highest on the tableland, on the north side of Vatnajökull, and
lowest on the north-west peninsula, to the south of North Cape.
Without exception the great névés of Iceland belong to the interior
tableland. They consist of slightly rounded domes or billowy
snowfields of vast thickness. In external appearance they bear
a closer resemblance to the glaciers of the Polar regions than
to those of the Alps. The largest snowfields are Vatnajökull
(3280 sq. m.), Hofsjökull (520) Langjökull (500) and Mýrdalsjökull
(390). The glaciers which stream off from these snowfields
are often of vast extent, e.g. the largest glacier of Vatnajökull
has an area of 150 to 200 sq. m., but the greater number are
small. Altogether, more than 120 glaciers are known in Iceland.
It is on the south side of Vatnajökull that they descend lowest;
the lower end of Breidamerkurjökull was in the year 1894 only
30 ft. above sea-level. The glaciers of the north-west peninsula
also descend nearly to sea-level. The great number of streams
of large volume is due to the moist climate and the abundance
of glaciers, and the milky white or yellowish-brown colour of
their waters (whence the common name Hvítá, white) is due to
the glacial clays. The majority of them change their courses
very often, and vary greatly in volume; frequently they are
impetuous torrents, forming numerous waterfalls. Iceland also
possesses a great number of lakes, the largest being Thingvallavatn3
and Thorisvatn, each about 27 sq. m. in area.
Mývatn, in the north, is well known from the natural beauty of
its surroundings. Above its surface tower a great number of
volcanoes and several craters, and its waters are alive with
water-fowl, a multitude of ducks of various species breeding
on its islands. The lakes of Iceland owe their origin to different
causes, some being due to glacial erosion, others to volcanic
subsidence. Mývatn fills a depression between lava streams,
and has a depth of not more than 8¾ ft. The group of lakes
called Fiskivötn (or Veidivötn), which lie in a desolate region
to the west of Vatnajökull, consist for the most part of crater
lakes. The groups of lakes which lie north-west from Langjökull
occupy basins formed between ridges of glacial gravel; and in
229
the valleys numerous lakes are found at the backs of the old
moraines.
Volcanoes.—Iceland is one of the most volcanic regions of
the earth; volcanic activity has gone on continuously from
the formation of the island in the Tertiary period down to the
present time. So far as is known, there have in historic times
been eruptions from twenty-five volcanic vents. Altogether
107 volcanoes are known to exist in Iceland, with thousands of
craters, great and small. The lava-streams which have flowed
from them since the Glacial epoch now cover an area of 4650
sq. m. They are grouped in dense masses round the volcanoes
from which they have flowed, the bulk of the lava dating from
outbreaks which occurred in prehistoric times. The largest
volume of lava which has issued at one outflow within historic
times is the stream which came from the craters of Laki at
Skaptá. This belongs to the year 1783, and covers an area of
218 sq. m., and amounts to a volume represented by a cube each
of whose sides measures 7½ m. The largest unbroken lava-field
in Iceland is Odaðahraun (Lava of Evil Deeds), upon the tableland
north from Vatnajökull (2000 to 4000 ft. above sea-level).
It is the accretion of countless eruptions from over twenty
volcanoes, and covers an area of 1300 sq.m. (or, including all
its ramifications and minor detached streams, 1700 sq. m.), and
its volume would fill a cube measuring 13.4 m. in every direction.
As regards their superficies, the lava-streams differ greatly.
Sometimes they are very uneven and jagged (apalhraun), consisting
of blocks of lava loosely flung together in the utmost
confusion. The great lava-fields, however, are composed of
vast sheets of lava, ruptured and riven in divers ways (helluhraun).
The smooth surface of the viscous billowy lava is further
diversified by long twisted “ropes,” curving backwards and
forwards up and down the undulations. Moreover, there are
gigantic fissures, running for several miles, caused by subsidences
of the underlying sections. The best-known fissure of this
character is Almannagjá at Thingvellir. On the occasion of
outbreaks the fine ashes are scattered over a large portion of
the island, and sometimes carried far across the Atlantic. After
the eruption of Katla in 1625 the ashes were blown as far as
Bergen in Norway, and when Askja was in eruption in 1875
a rain of ashes fell on the west coast of Norway 11 hours 40
minutes, and at Stockholm 15 hours, afterwards. The volcanic
ash frequently proves extremely harmful, destroying the pastures
so that the sheep and cattle die of hunger and disease. The
outbreak of Laki in 1783 occasioned the loss of 11,500 cattle,
28,000 horses and 190,500 sheep—that is to say, 53% of the
cattle in the island, 77% of the horses and 82% of the sheep.
After that the island was visited by a famine, which destroyed
9500 people, or one-fifth of the total population.
The Icelandic volcanoes may be divided into three classes:
(1) cone-shaped, like Vesuvius, built up of alternate layers
of ashes, scoriae and lava; (2) cupola-shaped, with an easy
slope and a vast crater opening at the top—these shield-shaped
cupolas are composed entirely of layers of lava, and their inclination
is seldom steeper than 7°-8°; (3) chains of craters running
close alongside a fissure in the ground. For the most part the
individual craters are low, generally not exceeding 300 to 500 ft.
These crater chains are both very common and often very long.
The chain of Laki, which was formed in 1783, extends 20 m.,
and embraces about one hundred separate craters. Sometimes,
however, the lava-streams are vomited straight out of gigantic
fissures in the earth without any crater being formed. Many
of the Icelandic volcanoes during their periods of quiescence
are covered with snow and ice. Then when an outbreak occurs
the snow and ice melt, and in that way they sometimes give
rise to serious catastrophes (jökulhlaup), through large areas
being suddenly inundated by great floods of water, which bear
masses of ice floating on their surface. Katla caused very
serious destruction in this way by converting several cultivated
districts into barren wastes. In the same way in the year
1362 Oeræfajökull, the loftiest mountain in Iceland (6424 ft.),
swept forty farms, together with their inhabitants and live
stock, bodily into the ocean. The best-known volcano is Hekla
(5108 ft.), which was in eruption eighteen times within the
historic period down to 1845. Katla during the same period
was active thirteen times down to 1860. The largest volcano
is Askja, situated in the middle of the lava-field of Odaðahraun.
Its crater measures 34 sq. m. in area. At Mývatn there are
several volcanoes, which were particularly active in the years
1724-1730. On several occasions there have been volcanic outbreaks
under the sea outside the peninsula of Reykjanes, islands
appearing and afterwards disappearing again. The crater
chain of Laki has only been in eruption once in historic times,
namely, the violent and disastrous outbreak of 1783. Iceland,
however, possesses no constantly active volcano. There are
often long intervals between the successive outbreaks, and many
of the volcanoes (and this is especially true of the chains of
craters) have only vented themselves in a solitary outburst.
Earthquakes are frequent, especially in the districts which
are peculiarly volcanic. Historical evidence goes to show
that they are closely associated with three naturally defined
regions: (1) the region between Skjálfandi and Axarfjörðr
in the north, where violent earth tremblings are extremely
common; (2) at Faxaflói, where minor vibrations are frequent;
(3) the southern lowlands, between Reykjanes and Mýrdalsjökull,
have frequently been devastated by violent earthquake
shocks, with great loss of property and life, e.g. on the 14th-16th
of August 1784, when 92 farmsteads were totally destroyed,
and 372 farmsteads and 11 churches were seriously damaged;
and again in August and September 1896, when another terrible
earthquake destroyed 161 farmsteads and damaged 155 others.
Hot springs are found in every part of Iceland, both singly
and in groups; they are particularly numerous in the western
portion of the southern lowlands, where amongst others is the
famous Geyser (q.v.). Sulphur springs and boiling mud lakes
are also general in the volcanic districts; and in places there
are carbonic acid springs, these more especially on the peninsula
of Snæfellsnes, north of Faxaflói.
Geology.—Iceland is built up almost entirely of volcanic rocks,
none of them older, however, than the middle of the Tertiary period.
The earlier flows were probably contemporaneous with those of Greenland,
the Færoes, the western islands of Scotland and the north-east
of Ireland. The principal varieties are basalt and palagonitic
breccias, the former covering two-thirds of the entire area, the latter
the remaining one-third. Compared with these two systems, all
other formations have an insignificant development. The palagonitic
breccias, which stretch in an irregular belt across the island, are
younger than the basalt. In the north-west, north and east the coasts
are formed of basalt, and rise in steep, gloomy walls of rock to altitudes
of 3000 ft. and more above sea-level. Deposits of clay, with
remains of plants of the Tertiary period, lignite and tree-trunks
pressed flat, which the Icelanders call surtarbrandur, occur in places
in the heart of the basalt formation. These fossiliferous strata are
developed in greatest thickness in the north-west peninsula. Indeed,
in some few places well-marked impressions of leaves and fruit have
been discovered, proving that in Tertiary times Iceland possessed
extensive forests, and its annual mean temperature must have been
at least 48° Fahr., whereas the present mean is 35.6°. The palagonitic
breccias, which attain their greatest development in the south of the
island and on the tableland, consist of reddish, brown or yellowish
rocks, tuffs and breccias, belonging to several different groups or
divisions, the youngest of which seems to be of a date subsequent
to the Glacial epoch. All over Iceland, in both the basalt and breccia
formations, there occur small intrusive beds and dikes of liparite,
and as this rock is of a lighter colour than the basalt, it is visible
from a distance. In the south-east of the island, in the parish of
Lón, there exist a few mountains of gabbro, a rock which does not
occur in any other part of Iceland. Near Húsavik in the north there
have been found marine deposits containing a number of marine
shells; they belong to the Red Crag division of the Pliocene. In
the middle of Iceland, where the geological foundation is tuff and
breccias, large areas are buried under ancient outflows of lava, which
bear evidences of glacial scratching. These lava streams, which are
of a doleritic character, flowed before the Glacial age, or during its
continuance, out of lava cones with gigantic crater openings, such as
may be seen at the present day. During the Glacial epoch the whole
of Iceland was covered by a vast sheet of inland ice, except for a
few small isolated peaks rising along its outer margins. This ice-cap
had on the tableland a thickness of 2300 to 2600 ft. Rocks scored
by glacial ice and showing plain indications of striation, together with
thousands of erratic blocks, are found scattered all over Iceland.
Signs of elevation subsequent to the Glacial epoch are common all
round the island, especially on the north-west peninsula. There are
found strikingly developed marine terraces of gravel, shore lines and
230
surf beaches marked on the solid rock. In several places there are
traces of shells; and sometimes skeletal remains of whales and
walruses, as well as ancient driftwood, have been discovered at
tolerable distances from the present coast. The ancient shore-lines
occur at two different altitudes. Along the higher, 230 to 266 ft. above
the existing sea-level, shells have been found which are characteristic
of high Arctic latitudes and no longer exist in Iceland; whereas
on the lower shore-line, 100 to 130 ft., the shells belong to species
which occur amongst the coast fauna of the present day.
The geysers and other hot springs are due to the same causes as
the active volcanoes, and the earthquakes are probably manifestations
of the same forces. A feature of special interest to geologists in
the present conditions of the island is the great power of the wind
both as a transporting and denuding agent. The rock sculpture is
often very similar to that of a tropical desert.4
Climate.—Considering its high latitude and situation, Iceland
has a relatively mild climate. The meteorological conditions
vary greatly, however, in different parts of the island. In the
south and east the weather is generally changeable, stormy
and moist; whilst on the north the rainfall is less. The climate
of the interior tableland approximates to the continental type
and is often extremely cold. The mean annual temperature is
37.2° F. in Stykkishólmr on Breiðifjörðr, 38.5° at Eyrārbakki in
the south of Iceland, 41° at Vestmannæyjar, 36° at Akureyri in
the north, 36.7° on Berufjörðr in the east, and 30.6° at Mödrudalr
on the central tableland. The range is great not only from year
to year, but also from month to month. For instance, at
Stykkishólmr the highest annual mean for March was 39.7°,
and the lowest 8°, during a period of thirty-eight years. Iceland
lies contiguous to that part of the north Atlantic in which the
shifting areas of low pressure prevail, so that storms are frequent
and the barometer is seldom firm. The barometric pressure
at sea-level in the south-west of Iceland during the period 1878-1900
varied between 30.8 and 27.1 in. The climate of the coasts
is relatively mild in summer, but tolerably cold in winter. The
winter means of the north and east coasts average 31.7° and
31.3° F. respectively; the summer means, 42.8° and 44.6°;
and the means of the year, 33.1° and 35.6°. The winter means
of the south and west coasts average 32° and 31.7° respectively;
the summer means, 48.2° and 50°; the annual means, 37.4° and
39.2°. The rainfall on the south and east coasts is considerable,
e.g. at Vestmannæyjar, 49.4 in. in the year; at Berufjörðr,
43.6 in. On the west coast it is less, e.g. 24.3 in. at Stykkishólmr;
but least of all on the north coast, being only 14.6 in. on the
island of Grimsey, which lies off that coast. Mist is commonly
prevalent on the east coast; at Berufjörðr there is mist on
no fewer than 212 days in the year. The south and west coasts
are washed by the Gulf Stream, and the north coast by an Arctic
current, which frequently brings with it a quantity of drift-ice,
and thus exercises a considerable effect upon the climate of
the island; sometimes it blocks the north coast in the summer
months. On the whole, during the 19th century, the north
coast was free from ice on an average of one year in every four
or five. The clearness of the atmosphere has been frequently
remarked. Thunderstorms occur mostly in winter.
Flora.—The vegetation presents the characteristics of an Arctic
European type, and is tolerably uniform throughout the island,
the differences even on the tableland being slight. At present 435
species of phanerogams and vascular cryptogams are known; the
lower orders have been little investigated. The grasses are of the
greatest importance to the inhabitants, for upon them they are
dependent for the keep of their live stock. Heather covers large
tracts, and also affords pasture for sheep. The development of
forest trees is insignificant. Birch woods exist in a good many places,
especially in the warmer valleys; but the trees are very short,
scarcely attaining more than 3 to 10 ft. in height. In a few places,
however, they reach 13 to 20 ft. and occasionally more. A few
mountain ash or rowan trees (Sorbus aucuparia) are found singly
here and there, and attain to 30 ft. in height. Willows are also
pretty general, the highest in growth being Salix phyllicifolia, 7 to
10 ft. The wild flora of Iceland is small and delicate, with bright
bloom, the heaths being especially admired. Wild crowberries and
bilberries are the only fruit found in the island.
Fauna.—The Icelandic fauna is of a sub-Arctic type. But while
the species are few, the individuals are often numerous. The land
mammals are very poorly represented; and it is doubtful whether
any species is indigenous. The polar bear is an occasional visitant,
being brought to the coast by the Greenland drift-ice. Foxes are
common, both the white and the blue occurring; mice and the brown
rat have been introduced, though one variety of mouse is possibly
indigenous. Reindeer were introduced in 1770. The marine
mammalia are numerous. The walrus is now seldom seen, although
in prehistoric times it was common. There are numerous species of
seals; and the seas abound in whales. Of birds there are over 100
species, more than one-half being aquatic. In the interior the
whistling swan is common, and numerous varieties of ducks are found
in the lakes. The eider duck, which breeds on the islands of Breiðifjörðr,
is a source of livelihood to the inhabitants, as are also the
many kinds of sea-fowl which breed on the sea-cliffs. Iceland
possesses neither reptiles nor batrachians. The fish fauna is abundant
in individuals, some sixty-eight species being found off the coasts.
The cod fisheries are amongst the most important in the world.
Large quantities of herring, plaice and halibut are also taken.
Many of the rivers abound in salmon, and trout are plentiful in the
lakes and streams.
Population and Towns.—The census of 1890 gave a total
population of 70,927, and this number had increased by 1901
to 78,489. The increase during the 19th century was 27,000,
while at least 15,600 Icelanders emigrated to America, chiefly
to Manitoba, from 1872 to the close of the century. The largest
town is Reykjavik on Faxaflói, with 6700 inhabitants, the
capital of the island, and the place of residence of the governor-general
and the bishop. Here the Althing meets; and here,
further, are the principal public institutions of the island (library,
schools, &c.). The town possesses a statue to Thorvaldsen,
the famous sculptor, who was of Icelandic descent. The remaining
towns include Isafjörðr (pop. 1000) on the north-west
peninsula, Akureyri (1000) on the north and Seydisfjörðr (800)
in the east.
Industries.—The principal occupation of the Icelanders is
cattle-breeding, and more particularly sheep-breeding, although
the fishing industries have come rapidly to the front in modern
times. In 1850, 82% of the population were dependent upon
cattle-breeding and 7% upon fishing; in 1890 the numbers
were 64% and 18% respectively. The culture of grain is not
practised in Iceland; all bread-stuffs are imported. In ancient
times barley was grown in some places, but it never paid for the
cost of cultivation. Cattle-breeding has declined in importance,
while the number of sheep has increased. Formerly gardening
was of no importance, but considerable progress has been made
in this branch in modern times, as also in the cultivation of
potatoes and turnips. Fruit-trees will not thrive; but black
and red currants and rhubarb are grown, the last-named doing
excellently. Iceland possesses four agricultural schools, one
agricultural society, and small agricultural associations in nearly
every district. The fisheries give employment to about 12,000
people. For the most part the fishing is carried on from open
boats, notwithstanding the dangers of so stormy a coast. But
larger decked vessels have come into increasing use. In summer
the waters are visited by a great number of foreign fishermen,
inclusive of about 300 fishing-boats from French ports, as well
as by fishing-boats from the Færoes and Norway, and steam
trawlers from England. Excellent profit is made in certain
parts of the island from the herring fishery; this is especially
the case on the east coast. There are marine insurance societies
and a school of navigation at Reykjavik. The export of fish and
fish products has greatly increased. In 1849 to 1855 the annual
average exported was 1480 tons; whereas at the close of the
century (in 1899) it amounted to 11,339 tons and 68,079 barrels
of oil, valued at £276,596.
Commerce.—From the first colonization of the island down
to the 14th century the trade was in the hands of native Icelanders
and Norsemen; in the 15th century it was chiefly in the hands
of the English, in the 16th of Germans from the Hanse towns.
From 1602 to 1786 commerce was a monopoly of the Danish
government; in the latter year it was declared free to all Danish
subjects and in 1854 free to all nations. Since 1874, when Iceland
obtained her own administration, commerce has increased
considerably. Thus the total value of the imports and exports
together in 1849 did not exceed £170,000; while in 1891-1895
the imports averaged £356,000 and the exports £340,000. In
231
1902 imports were valued at £596,193 and exports at £511,083.
Trade is almost entirely with Denmark, the United Kingdom,
and Norway and Sweden, in this order according to value. The
principal native products exported are live sheep, horses, salt
meat, wool and hides, to which must be added the fish products—cod,
train-oil, herring and salmon—eiderdown and woollen
wares. The spinning, weaving and knitting of wool is a widespread
industry, and the native tweed (vaðmal) is the principal
material for the clothing of the inhabitants. The imports consist
principally of cereals and flour, coffee, sugar, ale, wines and
spirits, tobacco, manufactured wares, iron and metal wares,
timber, salt, coal, &c. The money, weights and measures
in use are the same as in Denmark. The Islands Bank in Reykjavik
(1904) is authorized to issue bank-notes up to £133,900
in total value.
Communications.—All land journeys are made on horseback,
and in the remoter parts all goods have to be transported by
the same means. Throughout the greater part of the island
there exist no proper roads even in the inhabited districts, but
only bridle-paths, and in the uninhabited districts not even
these. Nevertheless much has been done to improve such paths
as there are, and several miles of driving roads have been made,
more particularly in the south. Since 1888 many bridges have
been built; previous to that year there was none. The larger
rivers have been spanned by iron swing-bridges, and the Blanda
is crossed by a fixed iron bridge. Postal connexion is maintained
with Denmark by steamers, which sail from Copenhagen and
call at Leith. Besides, steamers go round the island, touching
at nearly every port.
Religion.—The Icelanders are Lutherans. For ecclesiastical
purposes the island is divided into 20 deaneries and 142 parishes,
and the affairs of each ecclesiastical parish are administered
by a parish council, and in each deanery by a district (hjerað)
council. When a living falls vacant, the governor-general of
the island, after consultation with the bishop, selects three
candidates, and from these the congregation chooses one, the
election being subsequently confirmed by the governor-general.
In the case of certain livings, however, the election requires
confirmation by the crown. In 1847 a theological seminary
was founded at Reykjavik, and there the majority of the Icelandic
ministry are educated; some, however, are graduates
of the university of Copenhagen.
Health.—The public health has greatly improved in modern
times; the death-rate of young children has especially diminished.
This improvement is due to greater cleanliness, better dwellings,
better nourishment, and the increase in the number of doctors.
There are now doctors in all parts of the country, whereas
formerly there were hardly any in the island. There is a modern
asylum for leprosy at Laugarnes near Reykjavik, and a medical
school at Reykjavik, opened in 1876. The general sanitary
affairs of the island are under the control of a chief surgeon
(national physician) who lives in Reykjavik, and has superintendence
over the doctors and the medical school.
Government.—According to the constitution granted to Iceland
in 1874, the king of Denmark shares the legislative power with
the Althing, an assembly of 36 members, 30 of whom are elected
by household suffrage, and 6 nominated by the king. The
Althing meets every second year, and sits in two divisions, the
upper and the lower. The upper division consists of the 6
members nominated by the king and 6 elected by the representatives
of the people out of their own body. The lower
division consists of the remaining 24 representative members.
The minister for Iceland, who resided in Copenhagen until
1903, when his office was transferred to Reykjavik, is responsible
to the king and the Althing for the maintenance of the constitution,
and he submits to the king for confirmation the legislative
measures proposed by the Althing. The king appoints a governor-general
(landshöfðingi) who is resident in the island and
carries on the government on the responsibility of the minister.
Formerly Iceland was divided into four quarters, the east, the
south, the west and north. Now the north and the east are
united under one governor, and the south and the west under
another. The island is further divided into 18 sýslur (counties),
and these again into 169 hreppur (rapes) or poor-law districts.
Responsible to the governors are the sheriffs (sýslumenn), who
act as tax gatherers, notaries public and judges of first instance;
the sheriff has in every hreppur an assistant, called hreppstjóri.
In every hreppur there is also a representative committee, who
administer the poor laws, and look after the general concerns
of the hreppur. These committees are controlled by the committees
of the sýslur (county boards), and these again are under
the control of the amtsráð (quarter board), consisting of three
members. From the sheriff courts appeals lie to the superior
court at Reykjavik, consisting of three judges. Appeals may
be taken in all criminal cases and most civil cases to the supreme
court at Copenhagen.
Iceland has her own budget, the Althing having, by the constitution
of 1874, the right to vote its own supplies. As the Althing
only meets every other year, the budget is passed for two years
at once. The total income and expenditure are each about
£70,000 per financial period. There is a national reserve fund
of about £60,000, but no public debt; nor is there any contribution
for either military or naval purposes. Iceland has her own
customs service, but the only import duties levied are upon
spirits, tobacco, coffee and sugar, and in each case the duties
are fairly low.
Education.—Education is pretty widespread amongst the
people. In the towns and fishing villages there are a few elementary
schools, but often the children are instructed at home;
in some places by peripatetic teachers. It is incumbent upon
the clergy to see that all children are taught reading, writing
and arithmetic. The people are great readers; considering the
number of the inhabitants, books and periodicals have a very
extensive circulation. Eighteen newspapers are issued (once and
twice a week), besides several journals, and Iceland has always
been distinguished for her native literature. At Reykjavik
there are a Latin school, a medical school and a theological
school; at Mödruvellir and Hafnarfjörðr, modern high schools
(Realschulen); and in addition to these there are four agricultural
schools, a school of navigation, and three girls’ schools. The
national library at Reykjavik contains some 40,000 volumes
and 3000 MSS. At the same place there is also a valuable
archaeological collection. Amongst the learned societies are
the Icelandic Literary Society (Bokmentafjelag), the society
of the Friends of the People, and the Archaeological Society of
Reykjavik.
Authorities.—Among numerous works of Dr Thorvald
Thoroddsen, see Geschichte der Islands Geographie (Leipzig, 1898);
and the following articles in Geografisk Tidskrift (Copenhagen):
“Om Islands geografiske og geologiske Undersögelse” (1893);
“Islandske Fjorde og Bugter” (1901); “Geog. og geol. Unders.
ved den sydlige Del af Faxaflói paa Island” (1903); “Lavaörkener
og Vulkaner paa Islands Höjland” (1905). See also C. S. Forbes,
Iceland (London, 1860); S. Baring-Gould, Iceland, its Scenes and
Sagas (London, 1863); Sir R. F. Burton, Ultima Thule (Edinburgh,
1875); W. T. McCormick, A Ride across Iceland (London, 1892);
J. Coles, Summer Travelling in Iceland (London, 1882); H. J.
Johnston Lavis, “Notes on the Geography, Geology, Agriculture
and Economics of Iceland,” Scott. Geog. Mag. xi. (1895); W. Bisiker,
Across Iceland (London, 1902); J. Hann, “Die Anomalien der
Witterung auf Island in dem Zeitraume 1851-1900, &c.,” Sitzungsberichte,
Vienna Acad. Sci. (1904); P. Hermann, Island in Vergangenheit
und Gegenwart (Leipzig, 1907). Also Geografisk Tidskrift, and
the Geographical Journal (London), passim. (Th. T.)
History
Shortly after the discovery of Iceland by the Scandinavian,
c. 850 (it had long been inhabited by a small colony of Irish
Culdees), a stream of immigration set in towards it, which lasted
for sixty years, and resulted in the establishment of some 4000
homesteads. In this immigration three distinct streams can be
traced. (1) About 870-890 four great noblemen from Norway,
Ingolf, Ketil Hæng, Skalla-Grim and Thorolf, settled with their
dependants in the south-west of the new found land. (2) In
890-900 there came from the western Islands Queen Aud, widow
of Olaf the White, king of Dublin, preceded and followed by a
number of her kinsmen and relations (many like herself being
232
Christians), Helgi Biolan, Biorn the Eastern, Helgi the Lean,
Ketil the Foolish, &c., who settled the best land in the island
(west, north-west and north), and founded families who long
swayed its destinies. There also came from the Western Islands a
fellowship of vikings seeking a free home in the north. They had
colonized the west in the viking times; they had “fought
at Hafursfirth,” helping their stay-at-home kinsmen against
the centralization of the great head-king, who, when he had
crushed opposition in Norway, followed up his victory by compelling
them to flee or bow to his rule. Such were Ingimund
the Old, Geirmund Hellskin, Thord Beardie (who had wed
St. Edmund’s granddaughter,) Audun Shackle, Bryniulf the
Old, Uni, to whom Harold promised the earldom of the new
land if he could make the settlers acknowledge him as king
(a hopeless project), and others by whom the north-west, north
and east were almost completely “claimed.” (3) In 900-930
a few more incomers direct from Norway completed the settlement
of the south, north-east and south-east. Among them were
Earl Hrollaug (half-brother of Hrolf Ganger and of the first
earl of Orkney), Hialti, Hrafnkell Frey’s priest, and the sons of
Asbiorn. Fully three-quarters of the land was settled from the
west, and among these immigrants there was no small proportion
of Irish blood. In 1100 there were 4500 franklins, i.e. about
50,000 souls.
Table of Icelandic Literature and History.
| | | I. The Commonwealth. 400 years. |
| Heroic Age. |
870- 930 | Poetry of Western Islands. | Settlement by colonists from Western Isles and Norway. |
| 930- 980 | Early Icelandic poets, chiefly abroad. | Constitution worked out—Events of earlier sagas take place. |
| 980-1030 | Icelandic poets abroad. | Christianity comes in—Events of later sagas take place. |
| Saga Telling. |
1030-1100 | First era of phonetic change. | Peace—Ecclesiastical organization. |
| The Literary Age. |
1100-1150 | Ari and his school—Thorodd—Vernacular writing begins. | |
| 1150-1220 | Saga-Writers—Second generation of historians. | First civil wars—1208-22—Rise of Sturlungs. |
| 1220-1248 | Snorri and his school—Biographers. | Second civil wars, 1226-58—Fall of Great Houses. |
| 1248-1284 | Sturla—Second era of phonetic change. | Change of law, 1271—Submission to Norwegian kings. |
| | | II. Medievalism. 250 years. |
| Continental Influence chiefly Norse. |
1284-1320 | Collecting and editing—Foreign romances. | Foreign influence through Norway. |
| 1320-1390 | Annalists—Copyists—New Medieval poetry begins. | Great eruptions, 1362 and 1389—Epidemics—Danish rule, 1380. |
| 1390-1413 | Death of old traditions, &c. | Epidemics—Norse trade—Close of intercourse with Norway. |
| Dark Age. |
1413-1530 | Only Medieval poetry flourishes. | Isolation from Continent—English trade. |
| | | III. Reformation—Absolute Rule—Decay. 320 years. |
| Reformation. |
1530-1575 | Odd—Printing—Third era of phonetic change. | Religious struggle—New organization—Hanse trade. |
| Renaissance. |
1575-1640 | First antiquarians. | Danish monopoly—Pirates’ ravages. |
| 1640-1700 | Hallgrim—Paper copies taken. | |
| | | | Increasing Decay |
| Gradual Decay. |
1700-1730 | Jon Vidalin—Arni Magnusson—MSS. taken abroad. | Smallpox kills one-third population, 1707. |
| 1730-1768 | Eggert Olafsson. | Great famine, 10,000 die, 1759—Sheep plague, 1762—Eruption, 1765. |
| 1768-1800 | Finn Jonsson—Icelandic scholars abroad. | Great eruption, 1783. |
| 1800-1850 | Rationalistic movement—European influences first felt. | Beginnings of recovery—Travellers make known island to Europe—Free constitution in Denmark, 1848. |
| | | IV. Modern Iceland. |
| Recovery of Iceland. |
1850-1874 | Modern thought and learning—Icelandic scholars abroad | Increasing wealth and population—Free trade, 1854—Jon Sigurdsson and home rule struggle |
| 1874 | | Home rule granted. |
The unit of Icelandic politics was the homestead with its
franklin-owner (buendi), its primal organization the hundred-moot
(thing), its tie the goðorð (godar) or chieftainship.
The chief who had led a band of kinsmen and dependants
Organization.
to the new land, taken a “claim” there, and
parcelled it out among them, naturally became their leader,
presiding as priest at the temple feasts and sacrifices of heathen
times, acting as speaker of their moot, and as their representative
towards the neighbouring chiefs. He was not a feudal lord nor
a local sheriff, for any franklin could change his goðorð when
he would, and the rights of “judgment by peers” were in full
use; moreover, the office could be bequeathed, sold, divided
or pledged by the possessor; still the goði had considerable
power as long as the commonwealth lasted.
Disputes between neighbouring chiefs and their clients,
and uncertainty as to the law, brought about the Constitution
of Ulfliot (c. 930), which appointed a central moot for the whole
island, the Althing, and a speaker to speak a single “law”
(principally that followed by the Gula-moot in Norway); the
Reforms of Thord Gellir (964), settling a fixed number of moots
and chieftaincies, dividing the island into four quarters (thus
characterized by Ari: north, thickest settled, most famous;
east, first completely settled; south, best land and greatest
chiefs; west, remarkable for noble families), to each of which
a head-court, the “quarter-court,” was assigned; and the
Innovations of Skapti (ascribed in the saga to Nial) the Law-Speaker
(d. 1030), who set up a “fifth court” as the ultimate tribunal
in criminal matters, and strengthened the community against the
chiefs. But here constitutional growth ceased: the law-making
body made few and unimportant modifications of custom; the
courts were still too weak for the chiefs who misused and defied
them; the speaker’s power was not sufficiently supported to
enable him to be any more than a highly respected lord chief
justice, whereas he ought to have become a justiza if anarchy was
to be avoided; even the ecclesiastical innovations, while they
secured peace for a time, provoked in the end the struggles which
put an end to the commonwealth.
Christianity was introduced c. 1000. Tithes were established in
1096, and an ecclesiastical code made c. 1125. The first disputes
about the jurisdiction of the clergy were moved by Gudmund in the
13th century, bringing on a civil war, while the questions of
patronage and rights over glebe and mortmainland occupied Bishop
Arni and his adversaries fifty years afterwards, when the land
was under Norwegian viceroys and Norwegian law. For the civil
wars broke down the great houses who had monopolized the
chieftaincies; and after violent struggles (in which the
Sturlungs of the first generation perished at Orlygstad, 1238,
and Reykiaholt, 1241, while of the second generation Thord Kakali
was called away by the king in 1250, and Thorgils Skardi slain in
1258) the submission of the island to Norway quarter after
quarter, took place in 1262-1264, under Gizur’s auspices, and the
old Common Law was replaced by the New Norse Code “Ironside” in
1271.
The political life and law of the old days is abundantly
illustrated in the sagas (especially Eyrbyggia, Hamsa-Thori,
Reykdæla, Hrafnkell, and Niala), the two collections of
law-scrolls (Codex Regius, c. 1235, and Stadarhol’s Book, c.
1271), the Libellus, the Liberfragments, and the Landnamabók of
Ari, and the Diplomatarium. K. Maurer has made the subject his
own in his Beiträge, Island, Grágás, &c.
The medieval Icelandic church had two bishoprics, Skalholt (S.,
W., and E.) 1056, and Holar (N.) 1106, and about 175 parishes
(two-thirds of which belonged to the southern bishopric). They
belonged to the metropolitan see of Bremen, then to Lund, lastly
to Nidaros, 1237. There were several religious foundations:
Thingore (founded 1133), Thwera (1155), Hitardale (c. 1166),
Kirkby Nunnery (1184), Stad Nunnery (1296), and Saurby (c. 1200)
were Benedictine, while Ver (1168), Flatey after Holyfell (1172),
Videy (1226), Madderfield Priory (1296), and Skrid Priory (14th
century) were Augustinian. The bishops, elected by the people at
the Althing till 1237, enjoyed considerable power; two, Thorlak
of Skalholt and John of Holar, were publicly voted saints at the
Althing, and one, Gudmund, received the title of “Good” by decree
of the bishop and chapter. Full details as to ecclesiastical
history will be found in the Biskupasögur (edited by Dr
Vigfusson).
Iceland was not agricultural but pastoral, depending upon flocks
Mode of and herds for subsistence, for, though rye and other grain
233
would grow in favoured localities, the hay, self-sown, was the
only regular crop. In some districts the fisheries and fowling
Mode of life.
were of importance, but nine-tenths of the population
lived by their sheep and cattle. Life on each homestead
was regularly portioned out: out door occupations—fishing,
shepherding, fowling, and the hay-making
and fuel-gathering—occupying the summer; while indoor
business—weaving, tool-making, &c.—filled up the long winter.
The year was broken by the spring feasts and moots, the great
Althing meeting at midsummer, the marriage and arval gatherings
after the summer, and the long yule feasts at midwinter.
There were but two degrees of men, free and unfree, though
only the franklins had any political power; and, from the nature
of the life, social intercourse was unrestrained and unfettered;
goði and thrall lived the same lives, ate the same food, spoke
the same tongue, and differed little in clothing or habits. The
thrall had a house of his own and was rather villein or serf
than slave, having rights and a legal price by law. During the
heathen days many great chiefs passed part of their lives in
Norway at the king’s court, but after the establishment of Christianity
in Iceland they kept more at home, visiting the continent,
however, for purposes of state, suits with clergy, &c. Trade was
from the first almost entirely in foreign (Norse) hands.
The introduction of a church system brought little change.
The great families put their members into orders, and so continued
to enjoy the profits of the land which they had given to the
church; the priests married and otherwise behaved like the
franklins around them in everyday matters, farming, trading,
going to law like laymen.
Life in the commonwealth was turbulent and anarchic, but
free and varied; it produced men of mark, and fostered bravery,
adventure and progress. But on the union with
Norway all this ceased, and there was left but a low
Effects of the Union.
dead level of poor peasant proprietors careless of all
save how to live by as little labour as possible, and
pay as few taxes as they could to their foreign rulers. The
island received a foreign governor (Earl, Hirdstjori or Stiptamtsmadr
as he was successively called), and was parcelled out into
counties (sýslur), administered by sheriffs (sýslumadr) appointed
by the king. A royal court took the place of the Althing courts;
the local business of the local things was carried out by the
(hreppstjóri) bailiff, a subordinate of the sheriff; and the goðorð,
things, quarter-courts, trial by jury, &c., were swept away by
these innovations. The power of the crown was increased by
the confiscation of the great Sturlung estates, which were underleased
to farmers, while the early falling off of the Norse trade
threatened to deprive the island of the means of existence;
for the great epidemics and eruptions of the 14th century had
gravely attacked its pastoral wealth and ruined much of its
pasture and fishery.
The union of the Three Crowns transferred the practical
rule of Iceland to Denmark in 1280, and the old Treaty of Union,
by which the island had reserved its essential rights, was disregarded
by the absolute Danish monarchs; but, though new
taxation was imposed, it was rather their careless neglect than
their too active interference that damaged Iceland’s interests.
But for an English trade, which sprang up out of the half-smuggling,
half-buccaneering enterprise of the Bristol merchants,
the island would have fared badly, for during the whole of the
15th century their trade with England, exporting sulphur,
eiderdown (of which the English taught them the value),
wool, and salt stock-fish, and importing as before wood, iron,
honey, wine, grain and flax goods, was their only link with the
outer world. This period of Iceland’s existence is eventless:
she had got peace but with few of its blessings; all spirit seemed
to have died with the commonwealth; even shepherding and
such agriculture as there had been sank to a lower stage;
wagons, ploughs and carts went out of use and knowledge;
architecture in timber became a lost art, and the fine carved
and painted halls of the heathen days were replaced by turf-walled
barns half sunk in the earth; the large decked luggers
of the old days gave way to small undecked fishing-boats.
The Reformation in Iceland wakened men’s minds, but it
left their circumstances little changed. Though the fires of
martyrdom were never lighted in Iceland, the story
of the easily accepted Reformation is not altogether
The Reformation.
a pleasant one. When it was accomplished, the
little knot of able men who came to the front did much in
preserving the records of the past, while Odd and Hallgrim
exhibit the noblest impulses of their time. While there was
this revolution in religion a social and political revolution
never came to Iceland. The Hanse trade replaced the English
for the worse; and the Danish monopoly which succeeded it
when the Danish kings began to act again with vigour was
still less profitable. The glebes and hospital lands were a
fresh power in the hands of the crown, and the subservient
Lutheran clergy became the most powerful class in the island,
while the system of under-leasing at rackrent and short lease
with unsecured tenant right extended over at least a quarter
of the better land.
A new plague, that of the English, Gascon and Algerine
pirates, marked the close of the 16th century and opening of
the 17th, causing widespread panic and some devastation
in 1579, 1613-1616 and 1627. Nothing points
Decadence.
more to the helplessness of the natives’ condition than
their powerlessness against these foes. But the 18th century
is the most gloomy in Iceland’s annals. Smallpox, famine,
sheep disease, and the eruptions of 1765 and 1783 follow each
other in terrible succession. Against such visitations, which
reduced the population by about a fourth, little could be done.
The few literary men, whose work was done and whose books
were published abroad, were only concerned with the past, and
Jon Vidalin is the one man of mark, beside Eggert Olafsson,
who worked and wrote for his own generation.5
Gradually the ideas which were agitating Europe spread
through Scandinavia into Iceland, and its claims were more
respectfully listened to. The continental system,
Modern times.
which, by its leading to the blockade of Denmark,
threatened to starve Iceland, was neutralized by special
action of the British government. Trade and fishery grew a
little brisker, and at length the turn came.
The rationalistic movement, headed by Magnus Stephenson,
a patriotic, narrow-minded lawyer, did little good as far as
church reform went, but was accompanied by a more successful
effort to educate the people. A Useful Knowledge Society
was formed and did some honest work. Newspapers and
periodicals were published, and the very stir which the ecclesiastical
disputes encouraged did good. When free trade came,
and when the free constitution of Denmark had produced its
legitimate effects, the endeavours of a few patriots such as
Jon Sigurdsson were able to push on the next generation a step
further. Questions of a modern political complexion arose;
the cattle export controversy and the great home rule struggle
began. After thirty years’ agitation home rule was conceded
in 1874 (see above, Government).
(F. Y. P.)
Ancient Literature
Poetry.—Iceland has always borne a high renown for song,
but has never produced a poet of the highest order, the qualities
which in other lands were most sought for and admired in
poetry being in Iceland lavished on the saga, a prose epic, while
Icelandic poetry is to be rated very high for the one quality
which its authors have ever aimed at—melody of sound. To
these generalizations there are few exceptions, though Icelandic
literature includes a group of poems which possess qualities of
high imagination, deep pathos, fresh love of nature, passionate
dramatic power, and noble simplicity of language which Icelandic
poetry lacks. The solution is that these poems do not
belong to Iceland at all. They are the poetry of the “Western
Islands.”
It was among the Scandinavian colonists of the British coasts
that in the first generations after the colonization of Iceland
234
therefrom a magnificent school of poetry arose, to which we owe
works that for power and beauty can be paralleled in no Teutonic
language till centuries after their date. To this school, which
is totally distinct from the Icelandic, ran its own course apart
and perished before the 13th century, the following works belong
(of their authors we have scarcely a name or two; their dates
can be rarely exactly fixed, but they lie between the beginning
of the 9th and the end of the 10th centuries), classified into
groups:—
(a) The Helgi trilogy (last third lost save a few verses, but preserved
in prose in Hromund Gripsson’s Saga), the Raising of Anganty
and Death of Hialmar (in Hervarar Saga), the fragments of a Volsung
Lay (Volsungakiraða) (part interpolated in earlier poems, part underlying
the prose in Volsunga Saga), all by one poet, to whom Dr
Vigfusson would also ascribe Völuspá, Vegtamskviða, Þrymskviða,
Grötta Song and Völundarkviða.
(b) The Dramatic Poems:—Flyting of Loki, the För Skirnis, the
Harbarðslioð and several fragments, all one man’s work, to whose
school belong, probably, the Lay underlying the story of Ivar’s
death in Skioldunga Saga.
(c) The Didactic Poetry:—Grímnismál, Vafpruðnismál, Alvíssmal,
&c.
(d) The Genealogical and Mythological Poems:—Hyndluljoð
written for one of the Haurda-Kari family, so famous in the Orkneys;
Ynglingatal and Haustlong, by Thiodolf of Hvin; Rig’s Thul, &c.
(e) The Dirges and Battle Songs—such as that on Hafur-firth
Battle Hrafnsmal, by Thiodolf of Hvin or Thorbjörn Hornklofi, shortly
after 870; Eirik’s Dirge (Eíríksmál) between 950 and 969; the Dart-Lay
on Clontarf Battle (1014); Bíarka-mal (fragments of which we
have, and paraphrase of more is found in Hrolf Kraki’s Saga and in
Saxo).
There are also fragments of poems in Half’s Saga, Asmund Kappa-Bana’s
Saga, in the Latin verses of Saxo, and the Shield Lays
(Ragnarsdrapa) by Bragi, &c., of this school, which closes with the
Sun-Song, a powerful Christian Dantesque poem, recalling some of
the early compositions of the Irish Church, and with the 12th-century
Lay of Ragnar, Lay of Starkad, The Proverb Song (Havamal) and
Krakumal, to which we may add those singular Gloss-poems, the
Þulur, which also belong to the Western Isles.
To Greenland, Iceland’s farthest colony, founded in the 10th
century, we owe the two Lays of Atli, and probably Hymiskvtiða,
which, though of a weirder, harsher cast, yet belong to the Western
Isles school and not to Iceland.
In form all these poems belong to two or three classes:—kviða,
an epic “cantilena”; tál, a genealogical poem; drapa, songs
of praise, &c., written in modifications of the old Teutonic
metre which we know in Beowulf; galdr and lokkr, spell and
charm songs in a more lyric measure; and mál, a dialogue
poem, and liod, a lay, in elegiac measure suited to the subject.
The characteristics of this Western school are no doubt the
result of the contact of Scandinavian colonists of the viking-tide,
living lives of the wildest adventure, with an imaginative and
civilized race, that exercised upon them a very strong and lasting
influence (the effects of which were also felt in Iceland, but in
a different way). The frequent intermarriages which mingled
the best families of either race are sufficient proof of the close
communion of Northmen and Celts in the 9th and 10th centuries,
while there are in the poems themselves traces of Celtic mythology,
language and manners.6
When one turns to the early poetry of the Scandinavian
continent, preserved in the rune-staves on the memorial stones
of Sweden, Norway and Denmark, in the didactic Havamal,
the Great Volsung Lay (i.e. Sigurd II., Fafnis’s Lay, Sigrdrifa’s
Lay) and Hamdismal, all continental, and all entirely consonant
to the remains of Old English poetry in metre, feeling and treatment,
one can see that it is with this school that the Icelandic
“makers” are in sympathy, and that from it their verse naturally
descends. While shrewdness, plain straightforwardness, and
a certain stern way of looking at life are common to both,
the Icelandic school adds a complexity of structure and ornament,
an elaborate mythological and enigmatical phraseology,
and a regularity of rhyme, assonance, luxuriance, quantity
and syllabification, which it caught from the Latin and Celtic
poets, and adapted with exquisite ingenuity to its own main
object, that of securing the greatest possible beauty of sound.
The first generations of Icelandic poets resemble in many
ways the later troubadours; the books of the kings and the
sagas are full of their strange lives. Men of good birth (nearly
always, too, of Celtic blood on one side at least), they leave
Iceland young and attach themselves to the kings and earls
of the north, living in their courts as their henchmen, sharing
their adventures in weal and woe, praising their victories, and
hymning their deaths if they did not fall by their sides—men of
quick passion, unhappy in their loves, jealous of rival poets
and of their own fame, ever ready to answer criticism with a
satire or with a sword-thrust, but clinging through all to their
art, in which they attained most marvellous skill.
Such men were Egil, the foe of Eirik Bloodaxe and the
friend of Æthelstan; Kormak, the hot-headed champion;
Eyvind, King Haakon’s poet, called Skaldaspillir, because
he copied in his dirge over that king the older and finer Eíríksmál;
Gunnlaug, who sang at Æthelred’s court, and fell at the
hands of a brother bard, Hrafn; Hallfred, Olaf Tryggvason’s
poet, who lies in Iona by the side of Macbeth; Sighvat, Saint
Olafs henchman, most prolific of all his comrades; Thormod,
Coalbrow’s poet, who died singing after Sticklestad battle;
Ref, Ottar the Black, Arnor the earls’ poet, and, of those whose
poetry was almost confined to Iceland, Gretti, Biorn the Hitdale
champion, and the two model Icelandic masters, Einar Skulason
and Markus the Lawman, both of the 12th century.
It is impossible to do more here than mention the names of
the most famous of the long roll of poets which are noted in the
works of Snorri and in the two Skalda-tal. They range from the
rough and noble pathos of Egil, the mystic obscurity of Kormak,
the pride and grief of Hallfred, and the marvellous, fluency of
Sighvat, to the florid intricacy of Einar and Markus.
The art of poetry stood to the Icelanders in lieu of music;
scarcely any prominent man but knew how to turn a mocking
or laudatory stanza, and down to the fall of the commonwealth
the accomplishment was in high request. In the literary age
the chief poets belong to the great Sturlung family, Snorri
and his two nephews, Sturla and Olaf, the White Poet, being the
most famous “makers” of their day. Indeed, it is in Snorri’s
Edda, a poetic grammar of a very perfect kind, that the best
examples of the whole of northern poetry are to be found. The
last part, Hattatal, a treatise on metre, was written for Earl
Skuli about 1222, in imitation of Earl Rognvald and Hall’s
Hattalykill (Clavis metrica) of 1150. The second part, Skaldskapar-mal,
a gradus of synonyms and epithets, which contains
over 240 quotations from 65 poets, and 10 anonymous lays—a
treasury of verse—was composed c. 1230. The first part,
an exquisite sketch of northern mythology, Gylfa-ginning, was
probably prefixed to the whole later. There is some of Sturla’s
poetry in his Islendinga Saga, and verses of Snorri occur in the
Grammatical Treatise on figures of speech, &c., of Olaf, which
contains about one hundred and forty quotations from various
authors, and was written about 1250.
Besides those sources, the Kings’ Lives of Snorri and later
authors contain a great deal of verse by Icelandic poets. King
Harold Sigurdsson, who fell at Stamford Bridge 1066, was both
a good critic and composed himself. Many tales are told of him
and his poet visitors and henchmen. The Icelandic sagas also
comprise much verse which is partly genuine, partly the work
of the 12th and 13th century editors. Thus there are genuine
pieces in Nial’s Saga (chaps. 34, 78, 103, 126, 146), in Eyrbyggia,
Laxdæla, Egil’s Saga (part only), Grettla (two and a half stanzas,
cf. Landnamabók), Biorn’s Saga, Gunnlaug’s Saga, Havard’s
Saga, Kormak’s Saga, Viga-Glum’s Saga, Erik the Red’s Saga
and Fostbrædra Saga. In Nial’s, Gisli’s and Droplaug’s Sons’
Sagas there is good verse of a later poet, and in many sagas
worthless rubbish foisted in as ornamental.
To these may be added two or three works of a semi-literary
kind, composed by learned men, not by heroes and warriors.
Such are Konunga-tál, Hugsvinnsmál (a paraphrase of Cato’s
235
Distichs), Merlin’s Prophecy (paraphrased from Geoffrey of
Monmouth by Gunnlaug the monk), Jomsvikinga-drapa (by
Bishop Ketil), and the Islendinga-drapa, which has preserved
brief notices of several lost sagas concerning Icelandic worthies,
with which Gudmundar-drapa, though of the 14th century,
may be also placed.
Just as the change of law gave the death-blow to an already
perishing commonwealth, so the rush of medieval influence,
which followed the union with Norway, completed a process
which had been in force since the end of the 11th century, when
it overthrew the old Icelandic poetry in favour of the rimur.
The introduction of the danz, ballads (or fornkvædi, as they
are now called) for singing, with a burden, usually relating
to a love-tale, which were immensely popular with the people
and performed by whole companies at weddings, yule feasts
and the like, had relegated the regular Icelandic poetry to more
serious events or to the more cultivated of the chiefs. But
these “jigs,” as the Elizabethans would have called them,
dissatisfied the popular ear in one way: they were, like old
English ballads, which they closely resembled, in rhyme, but
void of alliteration, and accordingly they were modified and
replaced by the “rimur,” the staple literary product of the 15th
century. These were rhymed but also alliterative, in regular
form, with prologue or mansong (often the prettiest part of the
whole), main portion telling the tale (mostly derived in early
days from the French romances of the Carlovingian, Arthurian
or Alexandrian cycles, or from the mythic or skrök-sögur), and
epilogue. Their chief value to us lies in their having preserved
versions of several French poems now lost, and in their evidence
as to the feelings and bent of Icelanders in the “Dark Age”
of the island’s history. The ring and melody which they all
possess is their chief beauty.
Of the earliest, Olafsrima, by Einar Gilsson (c. 1350), and the
best, the Aristophanic Skída-rima (c. 1430), by Einar Fostri,
the names may be given. Rimur on sacred subjects was called
“diktur”; of these, on the legends of the saints’ lives, many
remain. The most notable of its class is the Lilia of Eystein
Asgrimsson, a monk of Holyfell (c. 1350), a most “sweet sounding
song.” Later the poems of the famous Jon Arason (b.
1484), last Catholic bishop of Holar (c. 1530), Liomr (“gleam”)
and Píslargrátr (“passion-tears”), deserve mention. Arason
is also celebrated as having introduced printing into Iceland.
Taste has sunk since the old days; but still this rimur poetry
is popular and genuine. Moreover, the very prosaic and artificial
verse of Sturla and the last of the old school deserved the oblivion
which came over them, as a casual perusal of the stanzas scattered
through Islendinga will prove. It is interesting to notice that
a certain number of kenningar (poetical paraphrases) have
survived from the old school even to the present day, though
the mass of them have happily perished. The change in the
phonesis of the language is well illustrated by the new metres
as compared with the old Icelandic drott-kvædi in its varied
forms. Most of the older rimur and diktur are as yet unprinted.
Many of the fornkvædi are printed in a volume of the old Nordiske
Litteralur-Samfund.
The effects of the Reformation was deeply felt in Icelandic
literature, both prose and verse. The name of Hallgrim Petursson,
whose Passion-hymns, “the flower of all Icelandic poetry,”
have been the most popular composition in the language, is
foremost of all writers since the second change of faith. The
gentle sweetness of thought, and the exquisite harmony of wording
in his poems, more than justify the popular verdict. His
Hymns were finished in 1660 and published in 1666, two great
Protestant poets thus being contemporaries. A collection of
Reformation hymns, adapted, many of them, from the German,
the Holar-book, had preceded them in 1619. There was a good
deal of verse-writing of a secular kind, far inferior in every way,
during this period. In spite of the many physical distresses
that weighed upon the island, ballads (fornkvædi) were still
written, ceasing about 1750, rimur composed, and more elaborate
compositions published.
The most notable names are those of the improvisatore
Stephen the Blind; Thorlak Gudbrandsson, author of Ulfar-Rímur,
d. 1707; John Magnusson, who wrote Hristafla, a
didactic poem; Stefan Olafsson, composer of psalms, rimur,
&c., d. 1688; Gunnar Pálsson, the author of Gunnarslag, often
printed with the Eddic poems, c. 1791; and Eggert Olafsson,
traveller, naturalist and patriot, whose untimely death in
1768 was a great loss to his country. His Bunadar-balkr, a
Georgic written, like Tusser’s Points, with a practical view of
raising the state of agriculture, has always been much prized.
Paul Vidalin’s ditties are very naïve and clever.
Of later poets, down to more recent times, perhaps the best
was Sigurd of Broadfirth, many of whose prettiest poems were
composed in Greenland like those of Jon Biarnisson before
him, c. 1750; John Thorlaksson’s translation of Milton’s great
epic into Eddic verse is praiseworthy in intention, but, as
may be imagined, falls far short of its aim. He also turned
Pope’s Essay on Man and Klopstock’s Messiah into Icelandic.
Benedikt Gröndal tried the same experiment with Homer in
his Ilion’s Kvædi, c. 1825. There is a fine prose translation
of the Odyssey by Sweinbjörn Egillson, the lexicographer, both
faithful and poetic in high degree.
Sagas.—The real strength of ancient Icelandic literature is
shown in its most indigenous growth, the “Saga” (see also
Saga). This is, in its purest form, the life of a hero, composed
in regular form, governed by fixed rules, and intended for oral
recitation. It bears the strongest likeness to the epic in all
save its unversified form; in both are found, as fixed essentials,
simplicity of plot, chronological order of events, set phrases used
even in describing the restless play of emotion or the changeful
fortunes of a fight or a storm, while in both the absence of digression,
comment or intrusion of the narrator’s person is invariably
maintained. The saga grew up in the quieter days which followed
the change of faith (1002), when the deeds of the great families’
heroes were still cherished by their descendants, and the exploits
of the great kings of Norway and Denmark handed down with
reverence. Telling of stories was a recognized form of entertainment
at all feasts and gatherings, and it was the necessity of
the reciter which gradually worked them into a regular form,
by which the memory was relieved and the artistic features
of the story allowed to be more carefully elaborated. That
this form was so perfect must be attributed to Irish influence,
without which indeed there would have been a saga, but not
the same saga. It is to the west that the best sagas belong;
it is to the west that nearly every classic writer whose name
we know belongs; and it is precisely in the west that the admixture
of Irish blood is greatest. In comparing the Irish tales
with the saga, there will be felt deep divergencies in matter,
style and taste, the richness of one contrasting with the chastened
simplicity of the other; the one’s half-comic, half-earnest
bombast is wholly unlike the other’s grim humour; the marvellous,
so unearthly in the one, is almost credible in the other;
but in both are the keen grasp of character, the biting phrase,
the love of action and the delight in blood which almost assumes
the garb of a religious passion.
When the saga had been fixed by a generation or two of oral
reciters, it was written down; and this stereotyped the form,
so that afterwards when literary works were composed by
learned men (such as Abbot Karl’s Swerri’s Saga and Sturla’s
Islendinga) the same style was adopted.
Taking first the sagas relating to Icelanders, of which some
thirty-five or forty remain out of thrice that number, they
were first written down between 1140 and 1220, in
the generation which succeeded Ari and felt the
Icelandic sagas.
impulse his books had given to writing, on separate
scrolls, no doubt mainly for the reciter’s convenience; they then
went through the different phases which such popular compositions
have to pass in all lands—editing and compounding
(1220-1260), padding and amplifying (1260-1300), and finally
collection in large MSS. (14th century). Sagas exist showing
all these phases, some primitive and rough, some refined and
beautified, some diluted and weakened, according as their copyists
have been faithful, artistic or foolish; for the first generation
236
of MSS. have all perished. We have also complex sagas put
together in the 13th century out of the scrolls relating to a given
locality, such a group as still exists untouched in Vapnfirdinga
being fused into such a saga as Niala or Laxdæla. Of the authors
nothing is known; we can only guess that some belong to the
Sturlung school. According to subject they fall into two classes,
those relating to the older generation before Christianity and
those telling of St Olaf’s contemporaries; only two fall into a
third generation.
Beginning with the sagas of the west, most perfect in style
and form, the earliest in subject is that of Gold-Thori (c. 930),
whose adventurous career it relates; Hensa-Þorissaga tells of
the burning of Blund-Ketil, a noble chief, an event which led
to Thord Gelli’s reforms next year (c. 964); Gislasaga (960-980)
tells of the career and death of that ill-fated outlaw; it is beautifully
written, and the verses by the editor (13th century) are
good and appropriate; Hord’s Saga (980) is the life of a band
of outlaws on Whalesfirth, and especially of their leader Hord.
Of later subject are the sagas of Havard and his revenge for his
son, murdered by a neighbouring chief (997-1002); of the
Heiðarirgasaga (990-1014), a typical tale of a great blood feud,
written in the most primitive prose; of Gunnlaug and Hrafn
(Gunnlaugssaga Ormstungu, 980-1008), the rival poets and their
ill-starred love. The verse in this saga is important and interesting.
To the west also belong the three great complex sagas
Egla, Eyrbyggia and Laxdæla. The first (870-980), after
noticing the migration of the father and grandfather of the hero
poet Egil, and the origin of the feud between them and the kings
of Norway, treats fully of Egil’s career, his enmity with Eirik
Bloodaxe, his service with Æthelstan, and finally, after many
adventures abroad, of his latter days in Iceland at Borg, illustrating
very clearly what manner of men those great settlers and
their descendants were, and the feelings of pride and freedom
which led them to Iceland. The style is that of Snorri, who
had himself dwelt at Borg. Eyrbyggia (890-1031) is the saga
of politics, the most loosely woven of all the compound stories.
It includes a mass of information on the law, religion, traditions,
&c., of the heathen days in Iceland, and the lives of Eric, the
real discoverer of Greenland, Biorn of Broadwick, a famous
chief, and Snorri, the greatest statesman of his day. Dr Vigfusson
would ascribe its editing and completion to Sturla the Lawman,
c. 1250. Laxdæla (910-1026) is the saga of Romance. Its
heroine Gudrun is the most famous of all Icelandic ladies. Her
love for Kiartan the poet, and his career abroad, his betrayal
by his friend Bolli, the sad death of Kiartan at his hands, the
revenge taken for him on Bolli, whose slayers are themselves
afterwards put to death, and the end of Gudrun, who becomes
an anchorite after her stormy life, make up the pith of the
story. The contrast of the characters, the rich style and fine
dialogue which are so remarkable in this saga, have much in
common with the best works of the Sturlung school.
Of the north there are the sagas of Kormak (930-960), most
primitive of all, a tale of a wild poet’s love and feuds, containing
many notices of the heathen times; of Vatzdælasaga (890-980),
relating to the settlement and the chief family in Waterdale;
of Hallfred the poet (996-1014), narrating his fortune at King
Olafs court, his love affairs in Iceland, and finally his death
and burial at Iona; of Reyk-dæla (990), which preserves the
lives of Askell and his son Viga-Skuti; of Svarf-dæla (980-990),
a cruel, coarse story of the old days, with some good scenes in
it, unfortunately imperfect, chapters 1-10 being forged; of Viga-Glum
(970-990), a fine story of a heathen hero, brave, crafty
and cruel. To the north also belong the sagas of Gretti the
Strong (1010-1031), the life and death of the most famous of
Icelandic outlaws, the real story of whose career is mixed up
with the mythical adventures of Beowulf, here put down to Gretti,
and with late romantic episodes and fabulous folk-tales (Dr
Vigfusson would ascribe the best parts of this saga to Sturla;
its last editor, whose additions would be better away, must
have touched it up about 1300), and the stories of the Ljosvetningasaga
(1009-1060). Gudmund the Mighty and his family and
neighbours are the heroes of these tales, which form a little
cycle. The Banda-manna saga (1050-1060), the only comedy
among the sagas, is also a northern tale; it relates the struggles
of a plebeian who gets a chieftancy against the old families of
the neighbourhood, whom he successfully outwits; Öl-kofra
þattr is a later imitation of it in the same humorous strain. The
sagas of the north are rougher and coarser than those of the
west, but have a good deal of individual character.
Of tales relating to the east there survive the Weapon-firth
cycle—the tales of Thorstein the White (c. 900), of Thorstein the
Staffsmitten (c. 985), of Gunnar Thidrand’s Bane (1000-1008)
and of the Weapon-firth Men (975-990), all relating to the family
of Hof and their friends and kin for several generations—and
the story of Hrafnkell Frey’s Priest (c. 960), the most idyllic
of sagas and best of the eastern tales. Of later times there are
Droplaug’s Sons’ Saga (997-1007), written probably about 1110,
and preserved in the uncouth style of the original (a brother’s
revenge for his brother’s death is the substance of it; Brandkrossa
Þattr is an appendix to it), and the tales of Thorstein
Hall of Side’s Son (c. 1014) and his brother Thidrandi (c. 996),
which belong to the cycle of Hall o’ Side’s Saga, unhappily lost;
they are weird tales of bloodshed and magic, with idyllic and
pathetic episodes.
The sagas of the south are either lost or absorbed in that of
Nial (970-1014), a long and complex story into which are woven
the tales of Gunnar Nial, and parts of others, as Brian Boroimhe,
Hall o’ Side, &c. It is, whether we look at style, contents or
legal and historical weight, the foremost of all sagas. It deals
especially with law, and contains the pith and the moral of all
early Icelandic history. Its hero Nial, type of the good lawyer,
is contrasted with its villain Mord, the ensample of cunning,
chicane, and legal wrong doing; and a great part of the saga
is taken up with the three cases and suits of the divorce, the
death of Hoskuld and the burning of Nial, which are given
with great minuteness. The number and variety of its dramatis
personae give it the liveliest interest throughout. The women
Hallgerda, Bergthora and Ragnhild are as sharply contrasted
as the men Gunnar, Skarphedin, Flosi and Kari. The pathos
of such tragedies as the death of Gunnar and Hoskuld and the
burning is interrupted by the humour of the Althing scenes
and the intellectual interest of the legal proceedings. The plot
dealing first with the life and death of Gunnar, type of the
chivalry of his day, then with the burning of Nial by Flosi,
and how it came about, and lastly with Kari’s revenge on the
burners, is the ideal saga-plot. The author must have been of
the east, a good lawyer and genealogist, and have composed it
about 1250, to judge from internal evidence. It has been
overworked by a later editor, c. 1300, who inserted many spurious
verses.
Relating partly to Iceland, but mostly to Greenland and
Vinland (N. America), are the Floamannasaga (985-990), a
good story of the adventures of Thorgils and of the
struggles of shipwrecked colonists in Greenland, a
Of Greenland and North America.
graphic and terrible picture; and Eirikssaga rauða
(990-1000), two versions, one northern (Flatey-book),
one western, the better (in Hawk’s Book, and AM. 557), the story
of the discovery of Greenland and Vinland (America) by the
Icelanders at the end of the 9th century. Later is the Fostbrædrasaga
(1015-1030), a very interesting story, told in a quaint
romantic style, of Thorgeir, the reckless henchman of King
Olaf, and how his death was revenged in Greenland by his sworn
brother the true-hearted Thormod Coalbrow’s poet, who afterward
dies at Sticklestad. The tale of Einar Sookisson (c. 1125)
may also be noticed. The lost saga of Poet Helgi, of which only
fragments remain, was also laid in Greenland.
Besides complete sagas there are embedded in the Heimskringla
numerous small Þættir or episodes, small tales of Icelanders’
adventures, often relating to poets and their lives at
the kings’ courts; one or two of these seem to be fragments of
sagas now lost. Among the more notable are those of Orm
Storolfsson, Ogmund Dijtt, Halldor Snorrason, Thorstein Oxfoot,
Hromund Halt, Thorwald Tasaldi, Svadi and Arnor Herlingar-nef,
Audunn of Westfirth, Sneglu-Halli, Hrafn of Hrutfiord, Hreidar
237
Heimski, Gisli Illugison, Ivar the poet, Gull-Æsu Thord, Einar
Skulason the poet, Mani the poet, &c.
The forged Icelandic sagas appear as early as the 13th century.
They are very poor, and either worked up on hints given in
genuine stories or altogether apocryphal.
History.—About the year of the battle of Hastings was born
Ari Froði Thorgilsson (1067-1148), one of the blood of Queen
Aud, who founded the famous historical school of Iceland, and
himself produced its greatest monument in a work which can
be compared for value with the English Domesday Book.
Nearly all that we know of the heathen commonwealth may
be traced to the collections of Ari. It was he too that fixed
the style in which history should be composed in Iceland. It
was he that secured and put into order the vast mass of fragmentary
tradition that was already dying out in his day. And
perhaps it is the highest praise of all to him that he wrote in
his own “Danish tongue,” and so ensured the use of that tongue
by the cultured of after generations. Ari’s great works are
Konungabók, or The Book of Kings, relating the history of the
kings of Norway from the rise of the Yngling dynasty down to
the death of Harald Sigurdsson in the year of his own birth.
This book he composed from the dictation of old men such as
Odd Kolsson, from the genealogical poems, and from the
various dirges, battle-songs and eulogia of the poets. It is
most probable that he also compiled shorter Kings’ Books
relating to Denmark and perhaps to England. The Konungabók
is preserved under the Heimskringla of Snorri Sturloson, parts
of it almost as they came from Ari’s hands, for example Ynglinga
and Harald Fairhair’s Saga, and the prefaces stating the plan
and critical foundations of the work, parts of it only used as a
framework for the magnificent superstructure of the lives of
the two Olafs, and of Harald Hardrada and his nephew Magnus
the Good. The best text of Ari’s Konungabók (Ynglinga, and
the sagas down to but not including Olaf Tryggvason’s) is that
of Frisbók.
The Book of Settlements (Landnamabók) is a wonderful performance,
both in its scheme and carrying out. It is divided
into five parts, the first of which contains a brief account of
the discovery of the island; the other four, one by one taking
a quarter of the land, describe the name, pedigree and history
of each settler in geographical order, notice the most important
facts in the history of his descendants, the names of their homesteads,
their courts and temples, thus including mention of 4000
persons, one-third of whom are women, and 2000 places. The
mass of information contained in so small a space, the clearness
and accuracy of the details, the immense amount of life which
is breathed into the whole, astonish the reader, when he reflects
that this colossal task was accomplished by one man, for his
collaborator Kolsegg merely filled up his plan with regard to
part of the east coast, a district with which Ari in his western
home at Stad was little familiar. Landnamabók has reached us
in two complete editions, one edited by Sturla, who brought
down the genealogies to his own grandfather and grandmother,
Sturla and Gudny, and one by Hawk, who traces the pedigrees
still later to himself.
Ari also wrote a Book of Icelanders (Islendingabók, c. 1127),
which has perished as a whole, but fragments of it are embedded
in many sagas and Kings’ Lives; it seems to have been a complete
epitome of his earlier works, together with an account of
the constitutional history, ecclesiastical and civil, of Iceland.
An abridgment of the latter part of it, the little Libellus Islandorum
(to which the title of the bigger Liber—Islendingabók—is
often given), was made by the historian for his friends Bishops
Ketil and Thorlak, for whom he wrote the Liber (c. 1137). This
charming little book is, with the much later collections of laws,
our sole authority for the Icelandic constitution of the commonwealth,
but, “much as it tells, the lost Liber would have been
of still greater importance.” Kristni-Saga, the story of the
christening of Iceland, is also a work of Ari’s, “overlaid” by
a later editor, but often preserving Ari’s very words. This
saga, together with several scattered tales of early Christians
in Iceland before the change of faith (1002), may have made up
a section of the lost Liber. Of the author of these works little
is known. He lived in quiet days a quiet life; but he shows
himself in his works, as Snorri describes him, “a man wise,
of good memory and a speaker of the truth.” If Thucydides
is justly accounted the first political historian, Ari may be fitly
styled the first of scientific historians.
A famous contemporary and friend of Ari is Sæmund (1056-1131),
a great churchman, whose learning so impressed his age
that he got the reputation of a magician. He was the friend of
Bishop John, the founder of the great Odd-Verjar family, and
the author of a Book of Kings from Harald Fairhair to Magnus
the Good, in which he seems to have fixed the exact chronology
of each reign. It is most probable that he wrote in Latin. The
idea that he had anything to do with the poetic Edda in general,
or the Sun’s Song in particular, is unfounded.
The flame which Ari had kindled was fed by his successors
in the 12th century. Eirik Oddsson (c. 1150) wrote the lives
of Sigurd Evil-deacon and the sons of Harold Gille, in his
Hryggiar-Stykki (Sheldrake), of which parts remain in the MSS.
collections of Kings’ Lives, Morkin-skinna, &c. Karl Jonsson,
abbot of Thingore, the Benedictine minister, wrote (c. 1184)
Sverrissaga from the lips of that great king, a fine racy biography,
with a style and spirit of its own. Böglunga-Sögur tell the
story of the civil wars which followed Sverri’s death. They are
probably by a contemporary.
The Latin Lives of St Olaf, Odd’s in Latin (c. 1175), compiled
from original authorities, and the Legendary Life, by another
monk whose name is lost, are of the medieval Latin school of
Sæmund to which Gunnlaug belonged.
Snorri Sturlason (q.v.) was known to his contemporaries as
a statesman and poet; to us he is above all an historian. Snorri
(1179-1241) wrote the Lives of the Kings (Heimskringla), from
Olaf Tryggvason to Sigurd the Crusader inclusive; and we
have them substantially as they came from his hand in the
Great King Olaf’s Saga; St Olaf’s Saga, as in Heimskringla and
the Stockholm MS.; and the succeeding Kings’ Lives, as in
Hulda and Hrokkinskinna, in which, however, a few episodes
have been inserted.
These works were indebted for their facts to Ari’s labours, and
to sagas written since Ari’s death; but the style and treatment
of them are Snorri’s own. The fine Thucydidean speeches,
the dramatic power of grasping character, and the pathos and
poetry that run through the stories, along with a humour such
as is shown in the Edda, and a varied grace of style that never
flags or palls, make Snorri one of the greatest of historians.
Here it should be noticed that Heimskringla and its class
of MSS. (Eirspennil, Jofraskinna, Gullinskinna, Fris-bok and
Kringla) do not give the full text of Snorri’s works. They are
abridgments made in Norway by Icelanders for their Norwegian
patrons, the Life of St Olaf alone being preserved intact, for the
great interest of the Norwegians lay in him, but all the other
Kings’ Lives being more or less mutilated, so that they cannot
be trusted for historic purposes; nor do they give a fair idea
of Snorri’s style.
Agrip is a 12th-century compendium of the Kings’ Lives from
Harald Fairhair to Sverri, by a scholastic writer of the school of
Sæmund. As the only Icelandic abridgment of Norwegian
history taken not from Snorri but sources now lost, it is of worth.
Its real title is Konunga-tal.
Noregs Konunga-tal, now called Fagrskinna, is a Norse compendium
of the Kings’ Lives from Halfdan the Black to Sverri’s
accession, probably written for King Haakon, to whom it was
read on his death-bed. It is an original work, and contains
much not found elsewhere. As non-Icelandic it is only noticed
here for completeness.
Styrmi Karason, a contemporary of Snorri’s, dying in 1245,
was a distinguished churchman (lawman twice) and scholar.
He wrote a Life of St Olaf, now lost; his authority is cited.
He also copied out Landnamabók and Sverri’s Life from his
MSS., of which surviving copies were taken.
Sturla, Snorri’s nephew, wrote the Hakonssaga and Magnussaga
at the request of King Magnus, finishing the first c. 1265, the
238
latter c. 1280. King Haakon’s Life is preserved in full; of the
other only fragments remain. These are the last of the series
of historic works which Ari’s labours began, from which the
history of Norway for 500 years must be gathered.
A few books relating the history of other Scandinavian realms
will complete this survey. In Skioldunga-bok was told the
history of the early kings of Denmark, perhaps derived from
Ari’s collections, and running parallel to Ynglinga. The earlier
part of it has perished save a fragment Sogu-brot, and citations
and paraphrases in Saxo, and the mythical Ragnar Lodbrok’s
and Gongu-Hrolf’s Sagas; the latter part, Lives of Harold Bluetooth
and the Kings down to Sveyn II., is still in existence and
known as Skioldunga.
The Knutssaga is of later origin and separate authorships,
parallel to Snorri’s Heimskringla, but earlier in date. The
Lives of King Valdemar and his Son, written c. 1185, by a
contemporary of Abbot Karl’s, are the last of this series. The
whole were edited and compiled into one book, often quoted
as Skioldunga, by a 13th-century editor, possibly Olaf, the
White Poet, Sturla’s brother, guest and friend of King Valdemar
II. Jomsvikinga Saga, the history of the pirates of Jom, down
to Knut the Great’s days, also relates to Danish history.
The complex work now known as Orkneyinga is made up of
the Earls’ Saga, lives of the first great earls, Turf-Einar, Thorfinn,
&c.; the Life of St Magnus, founded partly on Abbot
Robert’s Latin life of him (c. 1150) an Orkney work, partly on
Norse or Icelandic biographies; a Mirade-book of the same saint;
the Lives of Earl Rognwald and Sveyn, the last of the vikings,
and a few episodes such as the Burning of Bishop Adam. A
scholastic sketch of the rise of the Scandinavian empire, the
Foundation of Norway, dating c. 1120, is prefixed to the whole.
Færeyinga tells the tale of the conversion of the Færeys
or Faroes, and the lives of its chiefs Sigmund and Leif, composed
in the 13th century from their separate sagas by an
Icelander of the Sturlung school.
Biographies.—The saga has already been shown in two forms,
its original epic shape and its later development applied to the
lives of Norwegian and Danish kings and earls, as heroic but
deeper and broader subjects than before. In the 13th century
it is put to a third use, to tell the plain story of men’s lives
for their contemporaries, after satisfying which demand it dies
away for ever.
These biographies are more literary and medieval and less
poetic than the Icelandic sagas and king’s lives; their simplicity,
truth, realism and purity of style are the same. They run in
two parallel streams, some being concerned with chiefs and
champions, some with bishops. The former are mostly found
embedded in the complex mass of stories known as Sturlunga,
from which Dr Vigfusson has extricated them, and for the first
time set them in order. Among them are the sagas of Thorgils
and Haflidi (1118-1121), the feud and peacemaking of two great
chiefs, contemporaries of Ari; of Sturla (1150-1183), the founder
of the great Sturlung family, down to the settlement of his
great lawsuit by Jon Loptsson, who thereupon took his son
Snorri the historian to fosterage,—a humorous story but with
traces of the decadence about it, and glimpses of the evil days
that were to come; of the Önundar-brennusaga (1185-1200), a
tale of feud and fire-raising in the north of the island, the hero
of which, Gudmund Dyri, goes at last into a cloister; of Hrafn
Sveinbiornsson (1190-1213), the noblest Icelander of his day,
warrior, leech, seaman, craftsman, poet and chief, whose life
at home, travels and pilgrimages abroad (Hrafn was one of the
first to visit Becket’s shrine), and death at the hands of a foe
whom he had twice spared, are recounted by a loving friend
in pious memory of his virtues, c. 1220; of Áron Hiorleifsson
(1200-1255), a man whose strength, courage and adventures
befit rather a henchman of Olaf Tryggvason than one of King
Haakon’s thanes (the beginning of the feuds that rise round
Bishop Gudmund are told here), of the Svinefell-men (1248-1252),
a pitiful story of a family feud in the far east of Iceland.
But the most important works of this class are the Islendinga
Saga and Thorgils Saga of Lawman Sturla. Sturla and his
brother Olaf were the sons of Thord Sturlason and his mistress
Thora. Sturla was born and brought up in prosperous times,
but his manhood was passed in the midst of strife, in which his
family fell one by one, and he himself, though a peaceful man
who cared little for politics, was more than once forced to fly
for his life. While in refuge with King Magnus, in Norway,
he wrote his two sagas of that king and his father. After his
first stay in Norway he came back in 1271, with the new Norse
law-book, and served a second time as lawman. The Islendinga
must have been the work of his later years, composed at Fairey
in Broadfirth, where he died, 30th July 1284, aged about seventy
years. The saga of Thorgils Skardi (1252-1261) seems to have
been the first of his works on Icelandic contemporary history;
it deals with the life of his own nephew, especially his career
in Iceland from 1252 to 1258. The second part of Islendinga
(1242-1262), which relates to the second part of the civil war,
telling of the careers of Thord Kakali, Kolbein the Young, Earl
Gizur and Hrafn Oddsson. The end is imperfect, there being
a blank of some years before the fragmentary ending to which
an editor has affixed a notice of the author’s death. The first
part of Islendinga (1202-1242) tells of the beginning and first
part of the civil wars, the lives of Snorri and Sighvat, Sturla’s
uncles, of his cousin and namesake Sturla Sighvatsson, of
Bishop Gudmund, and Thorwald Gizursson,—the fall of the
Sturlungs, and with them the last hopes of the great houses
to maintain the commonwealth, being the climax of the story.
Sturla’s power lies in his faithfulness to nature, minute
observance of detail and purity of style. The great extent
of his subject, and the difficulty of dealing with it in the saga
form, are most skilfully overcome; nor does he allow prejudice
or favour to stand in the way of the truth. He ranks below Ari
in value and below Snorri in power; but no one else can dispute
his place in the first rank of Icelandic writers.
Of the ecclesiastical biographers, an anonymous Skalholt
clerk is the best. He wrote Hungrvaka, lives of the first five
bishops of Skalholt, and biographies of his patron Bishop Paul
(Pálssaga) and also of St Thorlak (Thorlakssaga). They are
full of interesting notices of social and church life. Thorlak
was a learned man, and had studied at Paris and Lincoln, which
he left in 1161. These lives cover the years 1056-1193. The
life of St John, a great reformer, a contemporary of Thorodd,
whom he employed to build a church for him, is by another
author (1052-1121). The life of Gudmund (Gudmundar Saga
Goda), as priest, recounts the early life of this Icelandic Becket
till his election as bishop (1160-1202); his after career must
be sought out in Islendinga. It is written by a friend and
contemporary. A later life by Arngrim, abbot of Thingore,
written c. 1350, as evidence of his subject’s sanctity, tells a good
deal about Icelandic life, &c. The lives of Bishops Arni and
Lawrence bring down our knowledge of Icelandic history into
the 14th century. The former work, Arna Saga Biskups, is
imperfect; it is the record of the struggles of church and state
over patronage rights and glebes, written c. 1315; it now covers
only the years 1269-1291; a great many documents are given
in it, after the modern fashion. The latter, Laurentius Saga
Biskups, by his disciple, priest Einar Haflidason, is a charming
biography of a good and pious man, whose chequered career
in Norway and Iceland is picturesquely told (1324-1331). It
is the last of the sagas. Bishop Jon’s Table-Talk (1325-1339)
is also worth noticing; it contains many popular stories which
the good bishop, who had studied at Bologna and Paris, was
wont to tell to his friends.
Annals.—The Annals are now almost the sole material for
Icelandic history; they had begun earlier, but after 1331 they
got fuller and richer, till they end in 1430. The best are Annales
Regii, ending 1306, Einar Haflidason’s Annals, known as “Lawman’s
Annals,” reaching to 1392, and preserved with others
in Flatey-book, and the New Annals, last of all. The Diplomatarium
Islandicum, edited by Jon Sigurdsson, contains what
remains of deeds, inventories, letters, &c., from the old days,
completing our scanty material for this dark period of the
island’s history.
239
Literature of Foreign Origin.—After the union with Norway
and change of law genuine tradition died out with the great
houses. The ordinary medieval literature reached Iceland
through Norway, and every one began to put it into a vernacular
dress, so neglecting their own classics that but for a few collectors
like Lawman Hauk they would have perished entirely.
The Norwegian kings, Haakon Haakonson (c. 1225), and Haakon
V. (c. 1305), employed Icelanders at their courts in translating
the French romances of the Alexander, Arthur and Charlemagne
cycles. Some forty or fifty of these Riddara-Sögur (Romances
of Chivalry) remain. They reached Iceland and were eagerly
read, many Rimur being founded on them. Norse versions of
Mary of Brittany’s Lays, the stories of Brutus and of Troy, and
part of the Pharsalia translated are also found. The Speculum
Regale, with its interesting geographical and social information,
is also Norse, written c. 1240, by a Halogalander. The computistic
and arithmetical treatises of Stiorn-Odd, Biarni the
Number-skilled (d. 1173), and Hauk Erlendsson the Lawman
(d. 1334), and the geography of Ivar Bardsson, a Norwegian
(c. 1340), are of course of foreign origin. A few tracts on geography,
&c., in Hauk’s book, and a Guide to the Holy Land, by Nicholas,
abbot of Thwera (d. 1158), complete the list of scientific works.
The stories which contain the last lees of the old mythology
and pre-history seem to be also non-Icelandic, but amplified
by Icelandic editors, who probably got the plots from the Western
Islands. Völsunga Saga and Hervarar Saga contain quotations
and paraphrases of lays by the Helgi poet, and Half’s, Ragnar’s
and Asmund Kappabana’s Sagas all have bits of Western poetry
in them. Hrolf Kraki’s Saga paraphrases part of Biarkamal;
Hromund Gripsson’s gives the story of Helgi and Kara (the lost
third of the Helgi trilogy); Gautrek’s Arrow Odd’s, Frithiof’s
Sagas, &c., contain shreds of true tradition amidst a mass of
later fictitious matter of no worth. With the Riddara-Sögur
they enjoyed great popularity in the 15th century, and gave
matter for many Rimur. Thidrek’s Saga, a late version of the
Völsung story, is of Norse composition (c. 1230), from North
German sources.
The medieval religious literature of Western Europe also
influenced Iceland, and the Homilies (like the Laws) were,
according to Thorodd, the earliest books written in the vernacular,
antedating even Ari’s histories. The lives of the Virgin,
the Apostles and the Saints fill many MSS. (edited in four large
volumes by Professor Unger), and are the works of many authors,
chiefly of the 13th and 14th centuries; amongst them are the
lives of SS. Edward the Confessor, Oswald of Northumbria,
Dunstan and Thomas of Canterbury. Of the authors we know
Priest Berg Gunsteinsson (d. 1211); Kygri-Biorn, bishop-elect (d.
1237); Bishop Brand (d. 1264); Abbot Runolf (d. 1307); Bishop
Lawrence’s son Arni (c. 1330); Abbot Berg (c. 1340), &c. A
paraphrase of the historical books of the Bible was made by
Bishop Brand (d. 1264), called Gydinga Sögur. About 1310
King Haakon V. ordered a commentary on the Bible to be made,
which was completed down to Exodus xix. To this Brand’s
work was afterwards affixed, and the whole is known as Stiorn.
The Norse version of the famous Barlaam and Josaphat, made
for Prince Haakon (c. 1240), must not be forgotten.
Post-classical Literature.—The post-classical literature falls
chiefly under three heads—religious, literary and scientific.
Under the first comes foremost the noble translation of the New
Testament by Odd Gottskalksson, son of the bishop of Hólar.
Brought up in Norway, he travelled in Denmark and Germany,
and took upon him the new faith before he returned to Iceland,
where he became secretary to Bishop Ogmund of Skalholt. Here
he began by translating the Gospel of Matthew into his mother-tongue
in secret. Having finished the remainder of the New
Testament at his own house at Olves, he took it to Denmark,
where it was printed at Roskild in 1540. Odd afterwards
translated the Psalms, and several devotional works of the day,
Corvinus’s Epistles, &c. He was made lawman of the north
and west, and died from a fall in the Laxa in Kios, June 1556.
Three years after his death the first press was set up in Iceland
by John Matthewson, at Breidabolstad, in Hunafloe, and a
Gospel and Epistle Book, according to Odd’s version, issued from
it in 1562. In 1584 Bishop Gudbrand, who had brought over a
splendid fount of type from Denmark in 1575 (which he completed
with his own hands), printed a translation of the whole
Bible at Hólar, incorporating Odd’s versions and some books
(Proverbs and the Son of Sirach, 1580) translated by Bishop
Gizar, but supplying most of the Old Testament himself. This
fine volume was the basis of every Bible issued for Iceland till
1826, when it was replaced by a bad modern version. For
beauty of language and faithful simplicity of style the finer
parts of this version, especially the New Testament, have never
been surpassed.
The most notable theological work Iceland ever produced is
the Postill-Book of Bishop John Vidalin (1666-1720), whose
bold homely style and stirring eloquence made “John’s Book,”
as it is lovingly called, a favourite in every household, till in the
19th century it was replaced for the worse by the more sentimental
and polished Danish tracts and sermons. Theological
literature is very popular, and many works on this subject,
chiefly translations, will be found in the lists of Icelandic bibliographers.
The first modern scientific work is the Iter per patriam of
Eggert Olafsson and Biarni Paulsson, which gives an account
of the physical peculiarities—fauna, flora, &c.—of the island
as far as could be done at the date of its appearance, 1772.
The island was first made known to “the world” by this book
and by the sketch of Unno von Troil, a Swede, who accompanied
Sir Joseph Banks to Iceland in 1772, and afterwards wrote
a series of “letters” on the land and its literature, &c. This
tour was the forerunner of an endless series of “travels,” of which
those of Sir W. J. Hooker, Sir G. S. Mackenzie (1810), Ebenezer
Henderson (1818), Joseph Paul Gaimard (1838-1843), Paijkull
(1867) and, lastly, that of Sir Richard Burton, an excellent
account of the land and people, crammed with information of
every kind (1875), are the best.
Iceland is emphatically a land of proverbs, while of folk-tales,
those other keys to the people’s heart, there is plentiful store.
Early work in this direction was done by Jon Gudmundsson,
Olaf the Old and John Olafsson in the 17th century, who all
put traditions on paper, and their labours were completed by
the magnificent collection of Jon Arnason (1862-1864), who
was inspired by the example of the Grimms. Many tales are
but weak echoes of the sagas; many were family legends,
many are old fairy tales in a garb suited to their new northern
home; but, besides all these, there are a number of traditions
and superstitions of indigenous origin.
The Renaissance of Iceland dates from the beginning of the
17th century, when a school of antiquaries arose. Arngrim
Jonsson’s Brevis Commentarius (1593), and Crymogaea (1609),
were the first-fruits of this movement, of which Bishops Odd,
Thorlak and Bryniulf (worthy parallels to Parker and Laud)
were the wise and earnest supporters. The first (d. 1630) collected
much material for church history. The second (d. 1656) saved
Sturlunga and the Bishops’ Lives, encouraged John Egilsson to
write his New Hungerwaker, lives of the bishops of the Dark
Ages and Reformation, and helped Biorn of Skardsa (d. 1655),
a bold and patriotic antiquary (whose Annals continue Einar’s),
in his researches. The last (d. 1675) collected a fine library of
MSS., and employed the famous copyist John Erlendsson,
to whom and the bishop’s brother, John Gizurarsson (d. 1648),
we are indebted for transcripts of many lost MSS.
Torfaeus (1636-1719) and Bartholin, a Dane (d. 1690), roused
the taste for northern literature in Europe, a taste which has
never since flagged; and soon after them Arni Magnusson
(1663-1730) transferred all that remained of vellum and good
paper MSS. in Iceland to Denmark, and laid the foundations
of the famous library and bequest, for which all Icelandic students
are so much beholden. For over forty years Arni stuck to his
task, rescuing every scrap he could lay hands on from the
risks of the Icelandic climate and carelessness, and when he
died only one good MSS. remained in the island. Besides his
magnificent collection, there are a few MSS. of great value at
240
Upsala, at Stockholm, and in the old royal collection at Copenhagen.
Those in the university library in the latter city perished
in the fire of 1728. Sagas were printed at Upsala and Copenhagen
in the 17th century, and the Arna-Magnaean fund has been working
since 1772. In that year appeared also the first volume
of Bishop Finn Jonsson’s Historia Ecclesiastica Islandiae, a work
of high value and much erudition, containing not only ecclesiastical
but civil and literary history, illustrated by a well-chosen
mass of documents, 870-1740. It has been continued by
Bishop P. Peterson to modern times, 1740-1840. The results,
however, of modern observers and scholars must be sought for
in the periodicals, Safn, Felagsrit, Ny Felagsrit and others. John
Espolin’s Arbækr is very good up to its date, 1821.
A brilliant sketch of Icelandic classic literature is given by Dr
Gudbrandr Vigfusson in the Prolegomena to Sturlunga Saga (Oxford,
1879). It replaces much earlier work, especially the Sciagraphia
of Halfdan Einarsson (1777), and the Saga-Bibliotek of Müller.
The numerous editions of the classics by the Icelandic societies,
the Danish Société des Antiquités, Nordiske Litteratur Samfund,
and the new Gammel Nordisk Litteratur Samfund, the splendid
Norwegian editions of Unger, the labours of the Icelanders Sigurdsson
and Gislason, and of those foreign scholars in Scandinavia and
Germany who have thrown themselves into the work of illustrating,
publishing and editing the sagas and poems (men like P. A. Munch,
S. Bugge, F. W. Bergmann, Th. Möbius and K. von Maurer, to name
only a few), can only be referred to here. See also Finnur Jónsson,
Den Oldnorske og Oldislanske Litteraturs Historie (Copenhagen,
1893-1900); R. B. Anderson’s translation (Chicago, 1884) of Winkel
Horn’s History of the Literature of the Scandinavian North; and W.
Morris and E. Magnusson’s Saga Library.
(F. Y. P.)
Recent Literature
The recent literature of Iceland has been in a more flourishing
state than ever before since the 13th century. Lyrical poetry is
by far the largest and the most interesting portion of it. The
great influence of Jónas Hallgrímsson (1807-1845) is still felt,
and his school was the reigning one up to the end of the 19th
century, although then a change seemed to be in sight. The
most successful poet of this school is Steingrímr Thorsteinsson
(b. 1830). He is specially famous for his splendid descriptions
of scenery (The Song of Gilsbakki), his love-songs and his
sarcastic epigrams. As a translator he has enriched the literature
with The Arabian Nights, Sakuntala, King Lear and several
other masterpieces of foreign literature. Equal in fame is
Matthías Jochumsson (b. 1835), who, following another of
Jónas Hallgrímsson’s many ways, has successfully revived the
old metres of the classical Icelandic poets, whom he resembles
in his majestic, but sometimes too gorgeous, language. He is
as an artist inferior to Steingrímr Thorsteinsson, but surpasses
him in bold flight of imagination. He has successfully treated
subjects from Icelandic history Grettisljóð, a series of poems
about the famous outlaw Grettir. His chief fault is a certain
carelessness in writing; he can never write a bad poem, but
rarely a poem absolutely flawless. He has translated Tegnér’s
Frithiofs Saga, several plays of Shakespeare and some other
foreign masterpieces. The great religious poet of Iceland,
Hallgrímr Pétursson, has found a worthy successor in Valdemar
Briem (b. 1848), whose Songs of the Bible are deservedly
popular. He is like Matthías Jochumsson in the copious flow
of his rhetoric; some of his poems are perfect both as regards
form and contents, but he sometimes neglects the latter while
polishing the former. An interesting position is occupied by
Benedict Gröndal (b. 1826), whose travesties of the old
romantic stories,7 and his Aristophanic drama Gandreiðin
(“The Magic Ride”) about contemporary events, are among
the best satirical and humorous productions of Icelandic
literature.
Influenced by Jónas Hallgrímsson with regard to language
and poetic diction, but keeping unbroken the traditions of
Icelandic medieval poetry maintained by Sigurðr Breiðfjörð
(1798-1846), is another school of poets, very unlike the first.
In the middle of the 19th century this school was best represented
by Hjálmar Jónsson from Bóla (1796-1875), a poor farmer
with little education, but endowed with great poetical talents,
and the author of satirical verses not inferior to those of Juvenal
both in force and coarseness. In the last decades of the 19th
century this school produced two poets of a very high order,
both distinctly original and Icelandic. One is Páll Olafsson
(b. 1827). His songs are mostly written in the medieval
quatrains (ferskeytla), and are generally of a humorous and
satirical character; his convivial songs are known by heart
by every modern Icelander; and although some of the poets
of the present day are more admired, there is none who is
more loved by the people. The other is Þorsteinn Erlingsson
(b. 1858). His exquisite satirical songs, in an easy and elegant
but still manly and splendid language, have raised much discussion.
Of his poems may be mentioned The Oath, a series
of most beautiful ballads, with a tragical love-story of the 17th
century as their base, but with many and happy satirical allusions
to modern life; Jörundr, a long poem about the convict king,
the Danish pirate Jörgensen, who nearly succeeded in making
himself the master of Iceland, and The Fate of the Gods and The
Men of the West (the Americans), two poems which, with their
anti-clerical and half-socialistic tendencies, have caused strong
protests from orthodox Lutheran clergy. Near to this school,
but still standing apart, is Grímur Thomsen (b. 1820).
In the beginning of the ’eighties a new school arose—having
its origin in the colony of Icelandic students at the University
of Copenhagen. They had all attended the lectures of Georg
Brandes, the great reformer of Scandinavian literature, and,
influenced by his literary theories, they chose their models in
the realistic school. This school is very dissimilar from the
half-romantic school of Jónas Hallgrímsson; it is nearer the
national Icelandic school represented by Páll Olafsson and
Þorsteinn Erlingsson, but differs from those writers by introducing
foreign elements hitherto unknown in Icelandic literature,
and—especially in the case of the prose-writers—by imitating
closely the style and manner of some of the great Norwegian
novelists. Their influence brought the Icelandic literature into
new roads, and it is interesting to see how the tough Icelandic
element gradually assimilates the foreign. Of the lyrical poets,
Hannes Hafsteinn (b. 1861) is by far the most important.
In his splendid ballad, The Death of Skarphedinn, and in his
beautiful series of songs describing a voyage through some of
the most picturesque parts of Iceland, he is entirely original;
but in his love-songs, beautiful as many of them are, a strong
foreign influence can be observed. Among the innovations
of this poet we may note a predilection for new metres, sometimes
adopted from foreign languages, sometimes invented by himself,
a thing practised rarely and generally with small success by
the Icelandic poets.
No Icelandic novelist has as yet equalled Jón Thóroddsen
(1819-1868). The influence of the realistic school has of late
been predominant. The most distinguished writer of that
school has been Gestur Pálsson (1852-1891), whose short stories
with their sharp and biting satire have produced many imitations
in Iceland. The best are A Home of Love and Captain Sigurd.
Jónas Jónasson (b. 1856), a clergyman of northern Iceland,
has, in a series of novels and short stories, given accurate, but
somewhat dry, descriptions of the more gloomy sides of Icelandic
country life. His best novel is Randiðr from Hvassafell, an
historical novel of the middle ages. Besides these we may
mention Torfhildur Hólm, one of the few women who have
distinguished themselves in Icelandic literature. Her novels
are mostly historical. The last decade of the 19th century
saw the establishment of a permanent theatre at Reykjavik.
The poet Matthías Jochumsson has written several dramas,
but their chief merits are lyrical. The most successful of Icelandic
dramatists as yet is Indrði Einarsson, whose plays, chiefly
historical, in spite of excessive rhetoric, are very interesting
and possess a true dramatic spirit.
In geography and geology Þorvaldr Thoroddsen has acquired
a European fame for his researches and travels in Iceland,
especially in the rarely-visited interior. Of his numerous
writings in Icelandic, Danish and German, the History of
241
Icelandic Geography is a monumental work. In history Páll
Melsteð’s (b. 1812) chief work, the large History of the World,
belongs to this period, and its pure style has had a beneficial
influence upon modern Icelandic prose.
Of the younger historians we may mention Þorkell Bjarnason
(History of the Reformation in Iceland). Jón Þorkelsson (b.
1822), inspector of the archives of Iceland, has rendered great
services to the study of Icelandic history and literature by his
editions of the Diplomatarium Islandicum and Obituarium
Islandicum, and by his Icelandic Poetry in the 15th and 16th
Century, written in Danish, an indispensable work for any student
of that period. A leading position among Icelandic lexicographers
is occupied by Jón Þorkelsson, formerly head of the Latin school
at Reykjavik, whose Supplement til islandske Ordbøger, an
Icelandic-Danish vocabulary (three separate collections), has
hardly been equalled in learning and accuracy. Other distinguished
philologists are his successor as head of the Latin
school, Bjôrn Magnússon Olsen (Researches on Sturlunga, Ari
the Wise, The Runes in the Old Icelandic Literature—the last
two works in Danish); Finnur Jónsson, professor at the University
of Copenhagen (History of the Old Norwegian and Icelandic
Literature, in Danish, and excellent editions of many old
Icelandic classical works); and Valtýr Guðmundsson, lecturer
at the University of Copenhagen (several works on the old architecture
of Scandinavia) and editor of the influential Icelandic
literary and political review, Eimreiðin (“The Locomotive”).
See J. C. Poestion, Islandische Dichter der Neuzeit (Leipzig, 1897);
C. Küchler, Geschichte der isländischen Dichtung der Neuzeit (Leipzig,
1896); Ph. Schweitzer, Island; Land und Leute (Leipzig, 1885);
Alexander Baumgartner, Island und die Faroer (Freiburg im Breisgau,
1889).
(S. Bl.)
1 Jökull, plural jöklar, Icel. snowfield, glacier.
2 Flói, bay; fjörðr, fjord.
3 Vatn, lake.
4 See Th. Thoroddsen, “Explorations in Iceland during the years
1881-1898,” Geographical Journal, vol. xiii. (1899), pp. 251-274,
480-513, with map.
5 For the periods succeeding the union, Danish state papers and
the History of Finn Jonsson are the best authority.
6 Many of these poems were Englished in prose by the translator
of Mallet, by B. Thorpe in his Sæmund’s Edda, and two or three
by Messrs Morris and Magnussen, as appendices to their translation
of Volsunga Saga. Earlier translations in verse are those in Dryden’s
Miscellany (vol. vi), A. Cottle’s Edda, Mathias’s Translations, and
W. Herbert’s Old Icelandic Poetry. Gray’s versions of Darradar-liod
and Vegtamskviða are well known.
7 E.g. “The Battle of the Plains of Death,” a burlesque on the
battle of Solferino.
ICELAND MOSS, a lichen (Cetraria islandica) whose erect or
ascending foliaceous habit gives it something of the appearance
of a moss, whence probably the name. It is often of a pale
chestnut colour, but varies considerably, being sometimes almost
entirely greyish white; and grows to a height of from 3 to 4
in., the branches being channelled or rolled into tubes, which
terminate in flattened lobes with fringed edges. It grows
abundantly in the mountainous regions of northern countries,
and it is specially characteristic of the lava slopes and plains
of the west and north of Iceland. It is found on the mountains
of north Wales, north England, Scotland and south-west
Ireland. As met with in commerce it is a light-grey harsh
cartilaginous body, almost destitute of colour, and having a
slightly bitter taste. It contains about 70% of lichenin or
lichen-starch, a body isomeric with common starch, but wanting
any appearance of structure. It also yields a peculiar modification
of chlorophyll, called thallochlor, fumaric acid, licheno-stearic
acid and cetraric acid, to which last it owes its bitter
taste. It forms a nutritious and easily digested amylaceous
food, being used in place of starch in some preparations of
cocoa. It is not, however, in great request, and even in Iceland
it is only habitually resorted to in seasons of scarcity. Cetraric
acid or cetrarin, a white micro-crystalline powder with a bitter
taste, is readily soluble in alcohol, and slightly soluble in water
and ether. It has been recommended for medicinal use, in doses
of 2 to 4 grains, as a bitter tonic and aperient.
ICE-PLANT, the popular name for Mesembryanthemum
crystallinum, a hardy annual most effective for rockwork. It
is a low-growing spreading herbaceous plant with the fleshy
stem and leaves covered with large glittering papillae which
give it the appearance of being coated with ice. It is a dry-country
plant, a native of Greece and other parts of the Mediterranean
region, the Canary Islands, South Africa and California.
Mesembryanthemum is a large genus (containing about 300
species) of erect or prostrate fleshy herbs or low shrubs, mostly
natives of South Africa, and rarely hardy in the British Isles
where they are mostly grown as greenhouse plants. They bear
conspicuous white, yellow or red flowers with many petals inserted
in the calyx-tube. The thick fleshy leaves are very variable
in shape, and often have spiny rigid hairs on the margin. They
are essentially sun-loving plants. The best-known member of
the genus is M. cordifolium, var. variegatum, with heart-shaped
green and silvery leaves and bright rosy-purple flowers. It is
extensively used for edging flower-beds and borders during the
summer months.
ICE-YACHTING, the sport of sailing and racing ice-boats.
It is practised in Great Britain, Norway and Sweden, to some
extent, and is very popular in Holland and on the Gulf of Finland,
but its highest development is in the United States and Canada.
The Dutch ice-yacht is a flat-bottomed boat resting crossways
upon a planking about three feet wide and sixteen long, to which
are affixed four steel runners, one each at bow, stern and each end
of the planking. The rudder is a fifth runner fixed to a tiller.
Heavy mainsails and jibs are generally used and the boat is
built more for safety than for speed. The ice-boat of the Gulf
of Finland is a V-shaped frame with a heavy plank running
from bow to stern, in which the mast is stepped. The stern or
steering runner is worked by a tiller or wheel. The sail is a
large lug and the boom and gaff are attached to the mast by
travellers. The passengers sit upon planks or rope netting.
The Russian boats are faster than the Dutch.
In 1790 ice-yachting was in vogue on the Hudson river, its
headquarters being at Poughkeepsie, New York. The type was a
square box on three runners, the two forward ones being nailed
to the box and the third acting as a rudder operated by a tiller.
The sail was a flatheaded sprit. This primitive style generally
obtained until 1853, when triangular frames with “boxes” for
the crew aft and jib and mainsail rig were introduced. A heavy,
hard-riding type soon developed, with short gaffs, low sails,
large jibs and booms extending far over the stern. It was over-canvassed
and the mast was stepped directly over the runner-plank,
bringing the centre of sail-balance so far aft that the boats
were apt to run away, and the over-canvassing frequently caused
the windward runner to swing up into the air to a dangerous
height. The largest and fastest example of this type, which
prevailed until 1879, was Commodore J. A. Roosevelt’s first
“Icicle,” which measured 69 ft. over all and carried 1070 sq. ft.
of canvas. In 1879 Mr H. Relyea built the “Robert Scott,”
which had a single backbone and wire guy-ropes, and it became
the model for all Hudson river ice-yachts. Masts were now
stepped farther forward, jibs were shortened, booms cut down,
and the centre of sail-balance was brought more inboard and
higher up, causing the centres of effort and resistance to come
more in harmony. The shallow steering-box became elliptical.
In 1881 occurred the first race for the American Challenge
Pennant, which represents the championship of the Hudson river,
the clubs competing including the Hudson river, North Shrewsbury,
Orange lake, Newburgh and Carthage Ice-Yacht Clubs.
The races are usually sailed five times round a triangle of which
each leg measures one mile, at least two of the legs being to
windward. Ice-yachts are divided into four classes, carrying
respectively 600 sq. ft. of canvas or more, between 450 and
600, between 300 and 450, and less than 300 sq. ft. Ice-yachting
is very popular on the Great Lakes, both in the United States
and Canada, the Kingston (Ontario) Club having a fleet of over
25 sail. Other important centres of the sport are Lakes Minnetonka
and White Bear in Minnesota, Lakes Winnebago and
Pepin in Wisconsin, Bar Harbor lake in Maine, the St Lawrence
river, Quinte Bay and Lake Champlain.
A modern ice-yacht is made of a single-piece backbone
the entire length of the boat, and a runner-plank upon which
it rests at right angles, the two forming a kite-shaped frame.
The best woods for these pieces are basswood, butternut and
pine. They are cut from the log in such a way that the heart of
the timber expands, giving the planks a permanent curve, which,
in the finished boat, is turned upward. The two forward runners,
usually made of soft cast iron and about 2 ft. 7 in. long and 2½
in. high, are set into oak frames a little over 5 ft. long and
5 in. high. The runners have a cutting edge of 90%, though a
V-shaped edge is often preferred for racing. The rudder is a
runner about 3 ft. 7 in. long, worked by a tiller, sometimes made
very long, 7½ ft. not being uncommon. This enables the helmsman
to lie in the box at full length and steer with his feet,
leaving his hands free to tend the sheet. Masts and spars are
242
generally made hollow for racing-yachts and the rigging is
pliable steel wire. The sails are of 10-oz. duck for a boat
carrying 400 sq. ft. of canvas. They have very high peaks,
short hoists and long booms. The mainsail and jib rig is general,
but a double-masted lateen rig has been found advantageous.
The foremost ice-yacht builder of America is G. E. Buckhout
of Poughkeepsie.
An ice-yacht about 40 ft. in length will carry 6 or 7 passengers
or crew, who are distributed in such a manner as to preserve the
balance of the boat. In a good breeze the crew lie out on the
windward side of the runner-plank to balance the boat and
reduce the pressure on the leeward runner. A course of 20 m.
with many turns has been sailed on the Hudson in less than
48 minutes, the record for a measured mile with flying start
being at the rate of about 72 m. an hour. In a high wind,
however, ice-yachts often move at the rate of 85 and even 90 m.
an hour.
Several of the laws of ice navigation seem marvellous to the
uninitiated. Commodore Irving Grinnell, who has made a
scientific study of the sport, says: “The two marked peculiarities
of ice-yachting which cause it to differ materially from
yachting on the sea are: (1) Sailing faster than the wind.
(2) Sheets flat aft under all circumstances.” Mr H. A. Buck,
in the “Badminton Library,” Skating, Curling, Tobogganing,
&c., thus explains these paradoxes. An ice-boat sails faster
than the wind because she invariably sails at some angle to it.
The momentum is increased by every puff of wind striking
the sails obliquely, until it is finally equalled by the increase
of friction engendered. Thus the continued bursts of wind
against the sails cause a greater accumulation of speed in the
ice-yacht than is possessed by the wind itself. When the boat
sails directly before the wind she is, like a balloon, at its mercy,
and thus does not sail faster than the wind. The ice-yacht
always sails with its sheets flat aft, because the greater speed
of the boat changes the angle at which the wind strikes the sail
from that at which it would strike if the yacht were stationary
to such a degree that, in whatever direction the yacht is sailing,
the result is always the same as if the yacht were close-hauled
to the wind. It follows that the yacht is actually overhauling
the wind, and her canvas shivers as if in the wind’s eye. When
eased off her momentum becomes less and less until it drops
to the velocity of the wind, when she can readily be stopped
by being spun round and brought head to the wind. The
latter method is one way of “coming to,” instead of luffing
up in the usual way from a beam wind. In beating to windward
an ice-boat is handled like a water yacht, though she points
more closely.
On the bays near New York a peculiar kind of ice-boat has
developed, called scooter, which may be described as a toboggan
with a sail. A typical scooter is about 15 ft. long with an extreme
beam of 5 ft., perfectly oval in form and flat. It has mainsail
and jib carried on a mast 9 or 10 ft. long and set well aft, and is
provided with two long parallel metal runners. There is no
rudder, the scooter being steered entirely by trimming the sails,
particularly the jib. As the craft is flat and buoyant it sails
well in water, and can thus be used on very thin ice without
danger. A speed of 50 m. an hour has been attained by a scooter
(see Outing for March 1905).
See Ice Sports, in the “Isthmian Library”; Skating, Curling,
Tobogganing, &c. in the “Badminton Library.”
I-CH‘ANG (Yi-ch‘ang, anciently known as Yi-ling), a town
of China in the province of Hu-peh, one of the four ports opened
to foreign trade by treaty in 1877. It is situated in 30° 42′ N.
and (approximately) 111° 20′ E., on the Yangtsze-Kiang, 1000 m.
from Shanghai. Built on the left bank of the river where it
escapes from the ravines and gorges which for 350 m. have
imprisoned its channel, I-ch’ang is exposed to considerable
risk of floods; in 1870 the waters rose 20 ft. in one day, and
the town had many of its houses and about half of its wall swept
away. The first English vessels to ascend the river as far as
I-ch’ang were those of Admiral Sir James Hope’s expedition
in 1861. All cargo to or from Szech’uen is here transhipped
from steamer to junk, or vice versâ. About 10 m. above I-ch’ang
the famed scenery of the Yangtsze gorges begins. Through
these the great river runs in a series of rapids, which make
navigation by vessels of any size extremely difficult. A very
large trade, nevertheless, is carried on by this route between
Chungk’ing and I-ch’ang. As a local centre of distribution this
port is of no great consequence, the transhipment trade with
Szech’uen being almost its sole business. The population is
estimated at 35,000. The number of foreign residents is very
small, trade being carried on by Chinese agents. Before the
anti-opium campaign of 1906 (see China) opium was much
grown. The trade of the port amounted in 1899 to £531,229,
and in 1904 to £424,442, the principal import being cotton
yarn and the principal export opium.
 |
| Egyptian Ichneumon (Herpestes ichneumon). |
ICHNEUMON (Gr. ἰχνεύμων, from ἰχνεύειν, to track out),
the common name of the North African representative of a
number of small weasel-shaped mammals belonging to the
carnivorous family Viverridae; the Indian representatives
of the group being known as mongooses. A large number of
species of the type genus are known, and range over southern
Asia and all Africa, the typical Herpestes ichneumon also occurring
in the south of Spain. The latter is an inhabitant of Egypt
and the north of Africa, where it is known to foreign residents
as “Pharaoh’s rat.” It is covered with long harsh fur of a tawny-grey
colour, darker on the head and along the middle of the
back, its legs reddish and its feet and tail black. It lives largely
on rats and mice, birds and reptiles, and for this reason it is
domesticated. It is, however, fond of poultry and their eggs,
and its depredations among fowls detract from its merits as a
vermin-killer. During the inundations of the Nile it is said
to approach the habitations of man, but at other seasons
it keeps to the fields and to the banks of the river. The Indian
mongoose (H. mungo) is considerably smaller than the Egyptian
animal, with fur of a
pale-grey colour, the
hairs being largely
white-ringed, while
the cheeks and
throat are more or
less reddish. Like
the former it is frequently
domesticated. It is especially serviceable in India as a
serpent-killer, destroying not only the eggs and young of these
creatures, but killing the most venomous adult snakes. The
fact that it survives those encounters has led to the belief
that it either enjoys immunity from the effects of snake
poison, or that after being bitten it has recourse, as the
Hindus maintain, to the root of a plant as an antidote.
It has been found, however, that when actually bitten
it falls a victim to the poison as rapidly as other mammals,
while there is no evidence of its seeking a vegetable antidote. The
truth seems to be that the mongoose, by its exceeding agility
and quickness of eye, avoids the fangs of the snake while fixing
its own teeth in the back of the reptile’s neck. Moreover,
when excited, the mongoose erects its long stiff hair, and it
must be very difficult for a snake to drive its fangs through
this and the thick skin which all the members of the genus possess.
The mongoose never hesitates to attack a snake; the moment
he sees his enemy, “his whole nature,” writes a spectator of one
of those fights, “appears to be changed. His fur stands on end,
and he presents the incarnation of intense rage. The snake
invariably attempts to escape, but, finding it impossible to evade
the rapid onslaught of the mongoose, raises his crest and lashes
out fiercely at his little persecutor, who seems to delight in dodging
out of the way just in time. This goes on until the mongoose
sees his opportunity, when like lightning he rushes in and
seizes the snake with his teeth by the back of the neck close
to the head, shaking him as a terrier does a rat. These tactics
are repeated until the snake is killed.” The mongoose is equally
dexterous in killing rats and other four-footed vermin.
ICHNEUMON-FLY, a general name applied to parasitic
insects of the section Ichneumonoidea (or Entomophaga), order
243
Hymenoptera, from the typical genus Ichneumon, belonging to
the chief family of that section—itself fancifully so called
after the Egyptian mammal (Herpestes). The species of the
families (Ichneumonidae, Braconidae, Evaniidae, Proctotrypidae,
and Chalcididae) are often indiscriminately called “Ichneumons,”
but the “super-family” of the Ichneumonoidea in the classification
of W. H. Ashmead contains only the Evaniidae, the Stephanidae,
and the large assemblage of insects usually included
in the two families of the Ichneumonidae and the Braconidae,
which are respectively equivalent to the Ichneumones genuini
and I. adsciti of older naturalists, chiefly differing in the former
having two recurrent nerves to the anterior wing, whilst the latter
has only one such nerve. The Ichneumonidae proper are one
of the most extensive groups of insects. Gravenhorst described
some 1650 European species, to which considerable subsequent
additions have been made. There are 6 sub-families of the
Ichneumonidae, viz. the Ichneumoninae, Cryptinae, Agriotypinae,
Ophioninae, Tryphoninae and Pimplinae, differing considerably
in size and facies, but united in the common attribute of being,
in their earlier stages, parasitic upon other insects. They have
all long narrow bodies; a small free head with long filiform
or setaceous antennae, which are never elbowed, and have
always more than sixteen joints; the abdomen attached to the
thorax at its hinder extremity between the base of the posterior
coxae, and provided in the female with a straight ovipositor
often exserted and very long; and the wings veined, with perfect
cells on the disk of the front pair. Ashmead proposes to separate
the Agriotypidae (which are remarkable for their aquatic habit,
being parasitic on caddis-worms) from the Ichneumonidae on
account of their firm ventral abdominal segments and spined
scutellum. He also separates from the Braconidae the Alysiidae
as a distinct family; they have peculiar mandibles with out-turned
tips.
Their parasitic habits render these flies of great importance
in the economy of nature, as they serve to check any inordinate
increase in the numbers of injurious insects. Without their
aid it would in many cases be impossible for the agriculturist
to hold his own against the ravages of his minute insect foes,
whose habits are not sufficiently known to render artificial
checks or destroying agents available. The females of all the
species are constantly on the alert to discover the proper living
food for their own larvae, which are hatched from the eggs they
deposit in or on the eggs, larvae or pupae of other insects of all
orders, chiefly Lepidoptera, the caterpillars of butterflies and
moths being specially attacked (as also are spiders). Any one
who has watched insect life during the summer can hardly have
failed to notice the busy way in which the parent ichneumon,
a small four-winged fly, with constantly vibrating antennae,
searches for her prey; and the clusters of minute cocoons round
the remains of some cabbage-butterfly caterpillar must also
have been observed by many. This is the work of Apanteles
(or Microgaster) glomeratus, one of the Braconidae, which in
days past was a source of disquietude to naturalists, who believed
that the life of the one defunct larva had transmigrated into
the numerous smaller flies reared from it. Ichneumon-flies
which attack external feeders have a short ovipositor, but those
attached to wood-feeding insects have that organ of great length,
for the purpose of reaching the haunts of their concealed prey.
Thus a species from Japan (Bracon penetrator) has its ovipositor
nine times the length of the body; and the large species of
Rhyssa and Ephialtes, parasitic on Sirex and large wood-boring
beetles in temperate Europe, have very long instruments (with
which when handled they will endeavour to sting, sometimes
penetrating the skin), in order to get at their secreted victims.
A common reddish-coloured species of Ophion (O. obscurum),
with a sabre-shaped abdomen, is noteworthy from the fact of
its eggs being attached by stalks outside the body of the
caterpillar of the puss-moth (Cerura vinula). Lepidopterists
wishing to breed the latter cut off the eggs of the parasite with
scissors.
The larvae of the ichneumon-flies are white, fleshy, cylindrical,
footless grubs; the majority of them spin silk cocoons before
pupating, often in a mass (sometimes almost geometrically),
and sometimes in layers of different colours and texture.
Authorities.—Among the older works on Ichneumonoidea may
be specially mentioned J. L. K. Gravenhorst, Ichneumonologia
Europaea (Breslau, 1829); A. H. Haliday (Entom. Mag. i.-v., 1833-1838),
and A. Förster (Verhandl. Naturhist. Ver. Rheinl. u. Westph.
xix., xxv., 1862, 1868). Full reference to the systematic literature
of the group will be found in C. G. de Dalla Torre’s Catalogus
hymenopterorum, vols, iii., iv. (Leipzig, 1898-1902), and a comprehensive
summary in W. H. Ashmead’s recent memoir (Proc. U.S.
Nat. Mus. xxiii., 1901). For the British species consult C. Morley,
Ichneumons of Great Britain (Plymouth, 1903), and T. A. Marshall
(Trans. Entom. Soc., 1885-1899).
(G. H. C.)
ICHNOGRAPHY (Gr. ἴχνος, a trace, and γραφή, description),
in architecture, a term defined by Vitruvius (i.2) as “the ground-plan
of the work,” i.e. the geometrical projection or horizontal
section representing the plan of any building, taken at such a
level as to show the outer walls, with the doorways, windows,
fireplaces, &c., and the correct thickness of the walls; the
position of piers, columns or pilasters, courtyards and other
features which constitute the design.























































 and secondary buds
may be produced on the medusa-buds before the latter are set free
as medusae. Each bud arises as a thickening of the epithelium, which
first forms two or three layers (fig. 47, A), and becomes separated into
a superficial layer, future ectoderm, surrounding a central mass, future
endoderm (fig. 47, B). The ectodermal epithelium on the distal side
of the bud becomes thickened, grows inwards, and forms a typical
entocodon (fig. 37, D, E, F). The remaining development of the bud
is just as described above for the indirect method of medusa-budding
(fig. 47, G, H). When the bud is nearly complete, the body-wall of
the parent immediately below it becomes perforated, placing the
coelenteric cavity of the parent in secondary communication with
that of the bud (H), doubtless for the better nutrition of the latter.
and secondary buds
may be produced on the medusa-buds before the latter are set free
as medusae. Each bud arises as a thickening of the epithelium, which
first forms two or three layers (fig. 47, A), and becomes separated into
a superficial layer, future ectoderm, surrounding a central mass, future
endoderm (fig. 47, B). The ectodermal epithelium on the distal side
of the bud becomes thickened, grows inwards, and forms a typical
entocodon (fig. 37, D, E, F). The remaining development of the bud
is just as described above for the indirect method of medusa-budding
(fig. 47, G, H). When the bud is nearly complete, the body-wall of
the parent immediately below it becomes perforated, placing the
coelenteric cavity of the parent in secondary communication with
that of the bud (H), doubtless for the better nutrition of the latter.




































 . β-phenylhydroxyl-amine,
C
. β-phenylhydroxyl-amine,
C
















 , which is found also in the
earliest Syriac and Palestinian inscriptions with little modification.
Ultimately in Hebrew it became reduced to a very small
symbol, whence comes its use as a term of contempt for things
of no importance as in “not one jot or tittle” (Matthew v. 18).
The name passed from Phoenician to Greek, and thence to the
Latin of the vulgate as iōta, and from the Latin the English
word is derived. Amongst the Greeks of Asia it appears only
as the simple upright I, but in some of the oldest alphabets
elsewhere, as Crete, Thera, Attica, Achaia and its colonies in
lower Italy, it takes the form
, which is found also in the
earliest Syriac and Palestinian inscriptions with little modification.
Ultimately in Hebrew it became reduced to a very small
symbol, whence comes its use as a term of contempt for things
of no importance as in “not one jot or tittle” (Matthew v. 18).
The name passed from Phoenician to Greek, and thence to the
Latin of the vulgate as iōta, and from the Latin the English
word is derived. Amongst the Greeks of Asia it appears only
as the simple upright I, but in some of the oldest alphabets
elsewhere, as Crete, Thera, Attica, Achaia and its colonies in
lower Italy, it takes the form  or S, while at Corinth and
Corcyra it appears first in a form closely resembling the later
Greek sigma Σ. It had originally no cross-stroke at top and
bottom. I being not i but z. The Phoenician alphabet having
no vowel symbols, the value of yōd was that of the English y.
In Greek, where the consonant sound had disappeared or been
converted into h, I is regularly used as a vowel. Occasionally,
as in Pamphylian, it is used dialectically as a glide between i and
another vowel, as in the proper name
or S, while at Corinth and
Corcyra it appears first in a form closely resembling the later
Greek sigma Σ. It had originally no cross-stroke at top and
bottom. I being not i but z. The Phoenician alphabet having
no vowel symbols, the value of yōd was that of the English y.
In Greek, where the consonant sound had disappeared or been
converted into h, I is regularly used as a vowel. Occasionally,
as in Pamphylian, it is used dialectically as a glide between i and
another vowel, as in the proper name  ). After the dactylic hexameter, the iambic
trimeter was the most popular metre of ancient Greece. Archilochus
is said to have been the inventor of this iambic verse, the
). After the dactylic hexameter, the iambic
trimeter was the most popular metre of ancient Greece. Archilochus
is said to have been the inventor of this iambic verse, the