Liste aller Werke

2. Die Kunst des Lullus
oder
Eine Maschine, die den »Faust« dichten könnte

Abgekürzte Erkenntniswege – Die ars magna Lulli – Die Begriffs- und Denkmaschine des Lullus – Enttäuschte Hoffnungen – Leibniz und die Rechenmaschine – Laßwitz' Universalbibliothek – Die Theorie der Denkmaschine – Was ist ein Buch? – Etwas von der Kombinatorik – Die Lullische Universal-Druckmaschine – Die Freiheit des Geistes – Gefährdet und gerettet!

Seltsam sind oftmals die Wege, auf denen der menschliche Geist nach Wissen, Weisheit und Erkenntnis strebt, und das Denken aller Zeiten und Völker bietet dafür zahlreiche Beispiele. Besonders das Mittelalter war reich an Erfindungsgabe auf diesem Gebiete, und die Gelehrten aller Fakultäten ließen es sich angelegen sein, Mittel ausfindig zu machen, die schneller und leichter als der bedächtige und mühevolle Weg der logischen Forschung zum Born der Erkenntnis führen und damit zugleich auch den Besitz aller Macht, die Wissen und Weisheit zu verleihen vermögen, mühelos vermitteln sollten.

Einer der merkwürdigsten Versuche, auf beschleunigtem Wege zu Weisheit und Erkenntnis zu gelangen, knüpft sich an den Namen des Raimundus Lullus, der von 1235 bis 1315 in Spanien lebte und sich bis heute den Ruf eines der seltsamsten und ideenreichsten Geister aus jener an solchen Gestalten doch wahrlich nicht armen Zeit gewahrt hat. Seines Zeichens Philosoph, Astrolog und Alchemist – denn das gehörte damals noch zusammen – und seines scholastischen Scharfsinnes wegen hochgeschätzt, wurde er doch vor allem durch die von ihm erfundene Lullische Kunst oder die ars magna Lulli berühmt. Auch diese Kunst war eines jener Mittel, den langen Weg des schritt- und stufenweisen Nachdenkens abzukürzen, und zugleich eines der sonderbarsten Systeme, die je zu diesem Zwecke von spekulativen Köpfen ausgedacht worden sind.

Welche Bewandtnis hatte es mit dieser seltsamen Kunst? Über Studien der Aristotelischen Logik war Lullus zu der Überzeugung gelangt, daß es möglich sein müsse, durch mechanische Kombination aller logischen Begriffe zu allen Erkenntnissen zu gelangen, die überhaupt durch Begriffe auszudrücken seien. Wie er sich das dachte, mag folgendes Beispiel erläutern: Wenn man den Begriff »Gold« mit allen möglichen Farbenbegriffen in Verbindung setzt und etwa die Verbindungen bildet: Gold ist schwarz – Gold ist weiß – Gold ist grün – Gold ist blau – Gold ist gelb – usw., so muß unter allen diesen überhaupt möglichen begrifflichen Verbindungen auch diejenige enthalten sein, die der wirklichen Farbe des Goldes entspricht. Gäbe es also einen Menschen, der weder vom Sehen noch vom Hörensagen wüßte, von welcher Farbe das besagte Edelmetall ist, so würde er in der Reihe jener Kombinationen auch diejenige enthalten finden, die die wirkliche Farbe des Goldes ausdrückt, und könnte dadurch Aufschluß hierüber erhalten. Allerdings müßte nun in der Reihe der möglichen Kombinationen diejenige bestimmt werden, die der Wirklichkeit entspricht. Das ließe sich nun vielleicht durch Bildung einer neuen Kombinationsreihe erreichen, die sich über die nur allein mögliche Farbe des Goldes ausspricht. Durch Verknüpfung und Kreuzung mehrerer solcher Kombinationsreihen würden bestimmte der gebildeten begrifflichen Kombinationen aufgehoben oder negiert werden, so daß schließlich nur noch eine Kombination als einzig mögliche logische und sichere Aussage zurückbliebe, die die Farbe des Goldes der Wirklichkeit entsprechend angibt. So dachte es sich Lullus wenigstens. Das ganze Verfahren besteht also in einer schematischen Kombination der Worte als Symbole der Begriffe zu allen überhaupt möglichen Zusammenstellungen und mußte ihres schematischen Charakters wegen auch durch eine Maschine ausführbar sein. Lullus konstruierte eine solche Maschine. Sie bestand im wesentlichen in einer Anordnung der philosophischen Hauptbegriffe in sieben konzentrischen Kreisen; durch Drehung dieser Kreise wurden alle möglichen Kombinationen der Begriffe bewirkt, und durch diese sollte dann zugleich Aufschluß über alle nur möglichen Fragen und Probleme erreicht werden.

Das also war die Begriffs- und Denkmaschine des Lullus, die schnell und mühelos zur höchsten Stufe der Erkenntnis führen sollte. Mit ihr glaubte ihr Schöpfer zugleich auch das große und von allen Gelehrten jenes Zeitalters ehrfurchtsvoll bestaunte Geheimnis der Kabbala, der Geheimlehre der Orientalen, deren Kenntnis ebenfalls zu allem Wissen über Gott und die Welt führen sollte, ergründet zu haben.

Lullus' Verfahren machte in den Gelehrtenkreisen der ganzen Welt ungeheures Aufsehen. Die hochgespannten Erwartungen und Hoffnungen, die der Urheber dieser merkwürdigen Erfindung selbst auf diese setzte und denen er in begeisterten Worten Ausdruck lieh, wurden ebenso freudig und optimistisch aufgenommen. Allgemein glaubte man, in der Lullischen Kunst und der Lullischen Maschine den Weg gefunden zu haben, der zur schnellen Lösung aller Aufgaben und Probleme und damit zur beschleunigten Erlangung aller Kenntnisse und Erkenntnisse führen müßte. Mit Feuereifer stürzte man sich auf die praktische Anwendung des Verfahrens; Philosophen, Astrologen und Alchemisten suchten durch sie schnellen Aufschluß über die sie bewegenden Fragen zu erlangen; aber auch die Geistlichen und selbst die Päpste befaßten sich mit der ars magna Lulli, die ihren Urheber zu einem der berühmtesten Leute seiner Zeit machte.

Über hundert Jahre hindurch mühte man sich, die Hoffnungen zu verwirklichen, die die Lullische Kunst rege gemacht hatte, suchte man auf diesem Wege den Schatz des Wissens zu vermehren. Dann aber zeigte sich, daß die Denkmaschine leider doch nicht hielt, was sie versprochen hatte. Trotz aller Versuche und trotz aller Anwendungen von Kombinationen und Kombinationsreihen war es nicht möglich, zu wirklich eindeutigen Folgerungen zu gelangen, war es, um auf das oben gegebene Beispiel zurückzugreifen, nicht möglich, in der Reihe der Verknüpfungen, die aus den Begriffen des Goldes und den Farbenbegriffen gebildet werden können, eine einzelne eindeutig zu bestimmen. Die Vieldeutigkeit blieb, und damit war die Möglichkeit genommen, auf diesem immerhin ungewöhnlichen Wege zu sicheren Urteilen und zu neuen Wahrheiten zu gelangen. So sah man sich schließlich doch genötigt, das Lullische Verfahren als unfruchtbar aufzugeben und wieder zu den alten und gewohnten Bahnen des Denkens und Forschens zurückzukehren, auf denen sich die Erkenntnisse zwar langsam, aber doch immerhin mit einer gewissen Sicherheit einzustellen pflegen.

Ganz freilich wurde die Hoffnung auf die Fruchtbarkeit der Lullischen Methode nicht aufgegeben; vereinzelte Anhänger hat diese auch in den folgenden Jahrhunderten gehabt, die sich wohl von dem Gedanken leiten ließen, daß es nur der richtigen Anwendungsweise bedürfe, um die Kunst des Lullus zum Erfolge zu führen, und die daher jenes seltsame Begriffs- und Denkwerk auch weiterhin übten. Zu denen, die hier anzuführen sind, gehört Giordano Bruno (1548-1600), der große Märtyrer der Wissenschaft, der bei seiner sich in die kühnsten und gewagtesten Spekulationen erhebenden Gedankenwelt sich zu der Idee der Lullischen Kunst sehr hingezogen fühlen mußte und sich jedenfalls ernsthaft bemühte, aus dieser Gewinn zu ziehen. Sein Bemühen war jedoch ebenso erfolglos wie das aller seiner Vorgänger. Auch der Philosoph und Mathematiker Athanasius Kircher (1601-1680), ein ebenso bedeutender wie zu wissenschaftlichen Kuriositäten geneigter Geist, dem auch die Erfindung der laterna magica zu danken ist, beschäftigte sich mit der ars magna Lulli, besonders in einem Werk, dem er in Anlehnung an jene Bezeichnung den Namen Ars magna lucis gegeben hat, jedoch ebenfalls nur mit negativem Erfolge. Endlich ist hier noch ein ganz Großer aus dem Reiche des Geistes zu nennen, Gottfried Wilhelm Leibniz, der große deutsche Philosoph und Mathematiker und Miterfinder der Differentialrechnung, der von der Richtigkeit der Lullischen Kunst, wenigstens ihrer Idee nach, durchaus überzeugt war und ihr in seiner »Universalwissenschaft« einen Platz eingeräumt hat. Man hat sich daran gewöhnt, die Beschäftigung Leibnizens mit der Lullischen Kunst als des großen Philosophen nicht recht würdig zu betrachten, und erwähnt sie nicht gern. Aber das ist durchaus unrecht, denn Leibniz gelang es tatsächlich, auf dem Wege der Lullischen Kunst zu einem bedeutsamen Ergebnis zu gelangen, und dieses war – die Rechenmaschine, die bekanntlich von Leibniz erfunden worden ist. Man darf mit Fug und Recht annehmen, daß Leibniz zu dieser Erfindung durch die Lullische Kunst angeregt worden ist, denn bei den Zahlen ist eine solche mechanisch-kombinatorische Verknüpfung mit eindeutigen und zuverlässigen Resultaten, wie sie Lullus und die Lullisten für die allgemeinen Begriffe vergeblich angestrebt hatten, innerhalb gewisser Grenzen tatsächlich möglich; eine Rechenmaschine ist gleichsam die Lullische Maschine ins Arithmetische übertragen. Deswegen ist es durchaus verkehrt, jene Beschäftigung Leibnizens, durch die er der vielverspotteten Lullischen Kunst schließlich doch einen Erfolg abgerungen hat, mit Stillschweigen zu übergehen, denn wenn ein Philosoph schon wirklich einmal etwas Praktisches zustande bringt, soll man ihm das auch nicht schmälern.

Nach Leibniz verhielten sich Philosophen und Logiker, soweit sie sich überhaupt noch mit der Lullischen Kunst befaßten, durchweg kritisch und ablehnend zu dieser, denn die Bedeutung und der Einfluß dieser Kunst auf die Erfindung der Rechenmaschine war nicht bekannt und noch weniger anerkannt. Als dann im vorigen Jahrhundert die spekulative Epoche der Philosophie einsetzte und Hegel aus den Begriffen nach dialektischer Methode alle Erkenntnis über Sein und Sinn der Welt ableiten wollte, da fand auch die Lullische Kunst gelegentlich wieder Erwähnung, aber auch mehr ablehnend oder satirisch als ernsthaft, denn das maschinelle Verfahren des Lullus behagte den Verkündern des absoluten Geistes nicht. Hegel, Herbart und Lotze erwähnen gelegentlich die Lullische Kunst. In dieser Zeit erhielt die kuriose Idee des Lullus auch eine neue Wendung. Man erörterte, ebenfalls mehr humoristisch als ernsthaft, den Gedanken, daß noch besser als durch die Lullische Kombination der Begriffssymbole, also der Wörter, durch die Kombination der Lautsymbole bzw. Lautzeichen, also der Schriftzeichen unseres Alphabets, die Gesamtheit alles Wissens erschöpft werden müsse. Wenn man alle Schriftzeichen zu allen überhaupt möglichen Kombinationen miteinander verknüpft, so muß man auch alle Wörter und auch alle überhaupt möglichen Wortverbindungen und damit schließlich den Inhalt alles Wissens und Denkens aus Vergangenheit, Gegenwart und Zukunft, soweit es überhaupt durch Schrift ausdrückbar ist, erhalten. Bei Gustav Theodor Fechner, einem der eigenartigsten und spekulativsten Denker aus der zweiten Hälfte des vorigen Jahrhunderts, dem Entdecker des psychophysischen Grundgesetzes, der sich gern und viel in solchen vagierenden Gedankengängen bewegte, findet sich jene Wendung der Lullischen Kunst erörtert, und Fechners Schüler und Biograph Kurd Laßwitz hat jene Idee in einer hübschen Novelle mit dem Titel »Die Universalbibliothek« dichterisch ausgeführt, indem er dort eine Bibliothek beschreibt, die alle überhaupt denkbaren Kombinationen unserer Laut- und Schriftzeichen in Buchform umfaßt und damit zugleich alles dem menschlichen Geist überhaupt erreichbare Wissen enthält. Der Umfang einer solchen Universalbibliothek wäre allerdings ein so ungeheurer, daß sie den Weltraum um die Erde herum bis zu den fernsten Sternen ausfüllen würde.

Mit dieser Wendung der Lullischen Idee könnte man nun sogar Prinzip und Theorie einer Maschine angeben, die selbständig denken und dichten könnte, die in ähnlicher Weise wie die Rechenmaschine arithmetische Operationen ausführt, automatisch alle und selbst die höchsten Operationen und Funktionen des menschlichen Geistes vollzieht und mit derselben Leichtigkeit den »Faust« wie die »Kritik der reinen Vernunft« verfassen und überhaupt alles Denken und Wissen, das dem menschlichen Geiste aus Vergangenheit, Gegenwart und Zukunft zugänglich und erreichbar ist, in mechanischer Weise zu produzieren imstande wäre. Mit dieser Wendung wäre dann die Lullische Kunst von der Rechenmaschine zur Denkmaschine fortgeschritten, und mit Wesen, Einrichtung und Funktion einer solchen Denkmaschine wollen wir uns in den nachfolgenden Zeilen noch befassen.

Wir fragen zunächst: Was ist ein Buch? Die Antwort auf diese naive Frage kann natürlich sehr verschieden ausfallen und wird immer richtig sein. Im eigentlichen und ursprünglichsten Sinne aber ist ein Buch, gleichviel ob es der »Faust«, die »Kritik der reinen Vernunft«, das Bürgerliche Gesetzbuch, das Adreßbuch von Kyritz an der Knatter, ein Fachwerk über Flohdressur, der Text einer Oper oder eines Gassenhauers oder sonst ein Erzeugnis menschlicher Gehirn- und Geistestätigkeit in Druckform ist, niemals etwas anderes als eine der möglichen Anordnungen der etwa hundert Schriftzeichen unseres Alphabets auf einige hunderttausend Stellen, denn so viel Letternstellen umfaßt ungefähr ein Buch. Diese etwa hundert alphabetischen Zeichen, die in vielfacher Anordnung und Wiederholung den Raum des Buches füllen, umfassen also die Buchstaben unseres großen und kleinen Alphabets, auch die Zahl- und Interpunktionszeichen, sowie alle weiteren überhaupt vorkommenden graphischen Zeichen, die nötig sind, um Gedachtes oder Geschehenes in Schrift- oder Druckform auszudrücken, nicht zu vergessen auch das Spatium, die Type für den Zwischenraum, der die einzelnen Wörter innerhalb der Druckzeile voneinander trennt. Wir wollen annehmen, daß das alles zusammen gerade hundert Zeichen sind, die also die graphischen Elemente darstellen, vermittels welcher wir alles menschliche Denken in Kunst, Wissenschaft und hoher Politik wie auch in allen sonstigen Regionen geistiger Betätigung graphisch fixieren, in so vielen und verschiedenartigen Möglichkeiten es sich auch äußert. Jedes Denken bewegt sich in irgendeiner der möglichen Anordnungen dieser Elemente, und jedes geistige Erzeugnis, gleichviel welcher Art und in welcher Sprache ersonnen und ausgedrückt, läßt sich durch eine Anordnung jener hundert Laut- oder Schriftzeichen definieren. Die Gesamtheit jener Anordnungen ist daher gleichbedeutend mit der Gesamtheit des menschlichen Denkens und aller überhaupt nur denkbaren geistigen Erzeugnisse der Menschheit selber.

Nehmen wir nun ein Buch an, das gerade aus einer Million Lettern (einschließlich der Spatien) besteht, was ungefähr dem Umfange der »Kritik der reinen Vernunft« oder auch des »Faust« entsprechen dürfte, und suchen wir die Frage zu beantworten, wieviel verschiedene Bücher dieses Umfanges wohl mit jenen hundert Zeichen hergestellt werden könnten. Das ist gleichbedeutend mit der Anzahl der überhaupt möglichen Kombinationen der hundert graphischen Zeichen auf dem Raum eines Buches von dem genannten Umfange, wobei also jede überhaupt mögliche Anordnung der hundert Zeichen unseres Alphabets auf den Raum von einer Million Letternstellen als Buch gelten soll, gleichviel was bei dieser Anordnung herauskommt, ob größter Blödsinn oder höchste Weisheit. Auch der nicht mathematisch geschulte Leser wird überzeugt sein, daß auf diese Weise eine ganz ungeheure Menge solcher Buchstabenkombinationen, also Bücher, hergestellt werden könnte. Schon die Bücherkataloge aller Länder und Nationen geben Ausweis über eine ganz gewaltige Menge von Büchern, die seit Gutenberg gedruckt worden sind (unter »Buch« hier natürlich immer nur der Artbegriff des Druckwerkes, nicht das Einzelexemplar der Auflage verstanden). Aber ob das nun eine Million oder tausend Millionen sind, und selbst wenn es noch millionen- oder gar billionenmal mehr wären, als es in Wirklichkeit der Fall ist, die Zahl, die auf diese Weise herauskommt und die unsere Herren Bibliographen gefälligst selbst feststellen wollen, ist immer nur ein völlig verschwindend kleiner Bruchteil der Menge aller überhaupt möglichen Bücher, die auf solche wie die beschriebene Weise, durch immer verschiedene Kombination der hundert alphabetischen Zeichen im Rahmen eines Buchumfanges, hergestellt werden könnten. Diese Zahl ist ungeheuer viele Male größer, als selbst die ausschweifendste und an den astronomischen Ziffern der Inflationszeit unseligen Angedenkens ausgiebig geschulte Zahlenphantasie unserer Leser sich träumen läßt.

Wir wollen kurz zeigen, wie man zur Berechnung der Anzahl jener Bücher kommt, und das an einem einfachen Beispiel erläutern. Wieviel verschiedene Anordnungen kann man aus zwei verschiedenen Buchstaben, etwa a und b, bilden, wenn jede Anordnung ebenfalls aus zwei Stellen bestehen soll? Die Antwort lautet, daß in diesem Falle vier (2 ²) solcher Anordnungen möglich sind, nämlich aa, ab, ba, bb. Wir könnten aus diesen beiden Buchstaben aber auch Anordnungen aus je drei Stellen bilden, und in diesem Falle wäre die Anzahl der möglichen Anordnungen im ganzen acht (2 ³), nämlich aaa, aab, aba, baa, abb, bab, bba, bbb. Mit der Bildung solcher Anordnungen aus einer gegebenen Zahl von Elementen beschäftigt sich ein besonderer Zweig der Mathematik, die Kombinatorik. Sie nennt solche Anordnungen »Variationen«, und wenn, wie in den angeführten beiden Fällen, in jeder Variation jedes der Elemente auch wiederholt vorkommen kann (wie in aaa oder bb oder aba), so spricht sie von »Variationen mit Wiederholungen«. Bei drei verschiedenen Elementen, etwa a, b, c, die zu Anordnungen von je drei Stellen verbunden werden sollen, wäre die Anzahl der möglichen Variationen mit Wiederholungen bereits 27, also 3 ³, und sollten jene drei Elemente auf Variationen von jedesmal fünf Stellen verteilt werden, so wäre die Zahl der möglichen Variationen in diesem Falle schon 3 ⁵, also 243. Man spricht in dem letztgenannten Falle – der fünf Stellen der Anordnungen wegen – von Variationen 5. Klasse. Aus den vier Elementen a, l, m, t lassen sich bereits über 68 Millionen (nämlich 4 ¹³) Variationen 13. Klasse bilden, und eine dieser Variationen wäre die Wortfolge » Alma malt Malta«, die immerhin schon einen leidlichen Sinn hat. Allerdings haben wir hier der Einfachheit halber es unterlassen, auch das Spatium, das Zwischenraumzeichen zwischen den einzelnen Worten dieser Wortfolge, mit in Rechnung zu stellen; mit diesem wäre die Zahl der möglichen Variationen noch viel größer.

Nunmehr können wir leicht errechnen, wieviel Bücher im Umfange von je einer Million Buchstaben sich vermittels der hundert Zeichen unseres Alphabets herstellen lassen. Ein jedes dieser Bücher ist, wie sich nach unseren Ausführungen ohne weiteres ergibt, im Sinne der Kombinatorik nichts weiter als eine Wiederholungs-Variation der hundert alphabetischen Zeichen in Druckform, und zwar eine Variation der millionsten Klasse. Die Gesamtheit aller dieser Bücher aber ist 100 ^1 000 000, gelesen und gesprochen: Hundert hoch Million, das heißt die Zahl, die wir erhalten, wenn wir den Faktor 100 eine Million mal mit sich selbst multiplizieren. Das wäre zugleich auch die Anzahl der Bücher in der obenerwähnten »Universalbibliothek« von Kurd Laßwitz.

Nunmehr wollen wir noch einen Schritt weitergehen und uns eine Druckmaschine denken, die so konstruiert ist, daß sie in jeder vollständigen Funktion, also in jedem Arbeitsgange ihren Letternvorrat automatisch zu einer anderen Variation zusammenfügt und zum Abdruck bringt. In kleinem Maßstabe geschieht das bereits bei einer Numeriermaschine, wie sie zur Numerierung von Banknoten, Fahrscheinen usw. verwandt wird, die mit jedem Druckgang die Ziffernlettern zu einer neuen Folge bzw. einer neuen Zahl selbständig umsetzt und abdruckt, und auch eine Rechenmaschine könnte mit Leichtigkeit so eingerichtet werden, daß sie die variierenden Ziffernfolgen der Reihe nach selbst einstellt und mit jeder Kurbelumdrehung automatisch eine der möglichen Zahlenoperationen ausführt. Die von uns gedachte Druckmaschine dieser Art soll nun einen Vorrat von einer Million Lettern für jedes alphabetische Zeichen, zusammen also 100 Millionen Lettern, haben, ein Quantum, das gar nicht einmal allzu groß und kaum viel größer als der Letternvorrat etwa einer großen Zeitungsdruckerei wäre. Mit diesem Letternvorrat also soll unsere Maschine in der beschriebenen Weise ans Werk gehen. Dann würde sie mit jedem Druckgange eine jener mit hundert alphabethischen Zeichen auf einer Million Stellen möglichen Anordnungen, also jedesmal eins der Bücher aus jener Gesamtmenge, herstellen. Und in der Gesamtmenge der Bücher, die sie so allmählich zum Drucke bringt, würde sich alles wiederfinden, was menschlicher Geist je erdacht, ersonnen und erschaffen hat. Denn alles, was je erdacht, ersonnen, gedichtet, theoretisiert, politisiert usw. worden ist, ist, in Druckform dargestellt, nur eine unter jenen Hundert hoch Million Variationen und müßte bei unermüdlich fortdauernder Tätigkeit unserer Maschine einmal als Buch oder Teil eines Buches seine Auferstehung in Druckerschwärze erleben. Und so würde in der Gesamtmenge der Bücher, die unsere Maschine produziert, sowohl die Bibel wie Darwins »Entstehung der Arten«, die »Kritik der reinen Vernunft« wie »Die Hosen des Herrn von Bredow«, der »Faust« wie jeder Lieder-, Opern- oder Operettentext, das Evangelium wie die Kriegserklärungen von Anno 1914, die Ilias wie der neueste Fracht- und Eisenbahntarif, die Liebeslieder der Sappho wie Knigges »Umgang mit Menschen«, der Talmud wie die Gebührenordnung der Herren Rechtsanwälte nach der letzten Erhöhung, die philosophischen Systeme der alten Inder wie die weniger tiefsinnigen Fachwerke über Stiefelwichse- oder Marmeladenfabrikation, die Reden des Demosthenes wie die viel weniger unsterblichen Sprechübungen unserer heutigen Parlamentarier, die Dialoge Platos wie der neueste Liebesbriefsteller, der letzte Leitartikel aus dem Lieblingsblatt des Lesers wie das erste Polizeiverbot – alles, alles würde die Universalmaschine mit derselben Wurschtigkeit rein mechanisch als Letternsatz erzeugen und zum Abdruck bringen, ohne eines Autors oder eines Manuskriptes zu bedürfen.

Und noch viel mehr und Erstaunlicheres könnte sie leisten! Nicht nur alles, was je gedacht und an mehr oder weniger bedeutsamen Geisteserzeugnissen geschaffen worden ist, sondern auch alles, was jemals in fernster Zukunft an solchen Erzeugnissen von Menschenhirnen erfunden und erdacht werden könnte in Kunst, Wissenschaft, Dichtung, Wirtschaft, Technik, Politik und sonstigen Gebieten, würde die Maschine fertig zur Kenntnisnahme bringen, denn auch jede künftige Geistesschöpfung, ob groß ob klein, ob nichtig oder wichtig, wäre ja nur als eine jener Variationen aufzufassen. Auch alle Geschichtswerke über die Ereignisse selbst in fernster Zukunft müßten in dieser Menge von Büchern, die unsere Maschine unermüdlich ausspeit, ihren Platz finden, und damit würde sich die Maschine zugleich als Prophetin erweisen, die um Millionen von Jahren die Geschicke der Menschen auf Erden oder die Ereignisse im Weltenraum voraussagen könnte, und ebenso würde sie auch alles in der Vergangenheit Geschehene und Geschaffene, soweit es sich überhaupt in geschriebener Form ausdrücken läßt, mit tödlicher Sicherheit in Druckerschwärze zu Papier bringen. Alle Rätsel der Wissenschaft und Geschichte würde die Maschine lösen und die verwickeltsten Geheimnisse aus Vergangenheit und Zukunft enthüllen. Sie würde an einer Stelle drucken, wer die Eiserne Maske war, und an einer anderen, ob und wann Menschen unserer Erde einmal die Reise nach unserem Nachbarplaneten Mars gelingt; sie würde wissen, wie die Lösung des Fermatschen Problems lautete, die uns leider verlorengegangen ist und trotz alles Forschens unserer Mathematiker seit bald dreihundert Jahren bis heute nicht wiedergefunden werden konnte; sie würde auch in die tiefsten Tiefen der Vergangenheit blicken und uns mitteilen, wann und wo der erste Mensch gelebt und gewohnt hat, und sie würde ebenso prophetischen Blickes in die fernste Zukunft schauen und uns verkünden, wann beim Wohnungsamt einmal eine Wohnung zu haben sein wird.

Damit hätten wir die Grundlagen für die denkende Maschine gewonnen, die jedes Menschenhirn, das je auf Erden dachte oder jemals hier denken wird, an Geistesschärfe und Leistungsfähigkeit ungezählte Male übertrifft, vor der sich unsere Unsterblichen, wie Plato und Archimedes, Kant und Goethe, Shakespeare und Newton, Gauß und Leonardo da Vinci, verstecken müßten, als hätten sie nie gelebt. Eine Mechanisierung des Geistes in höchster nur denkbarer Vollkommenheit würde die Tätigkeit jener Maschine darstellen, und damit würde unseren Philosophen von neuem das Problem erwachsen, ob nicht auch die geistige Funktion, die sie als eine keiner Mechanisierung fähige freie Leistung und Schöpfung des Geistes aufzufassen gewohnt sind, nicht letzten Endes doch nur einen Spezialfall mechanischer Arbeit darstellt, wie die Tätigkeit eines Webstuhls oder einer Dampfmaschine. Und sollten sie selbst trotz aller gelehrten Disputationen über diese Frage zu keiner Entscheidung kommen können, so würden sie sich die Antwort vielleicht am einfachsten von unserer Druckmaschine geben lassen, denn auch über dieses Problem müßte diese sich irgendeinmal auslassen, einschließlich der kritischen Erörterung aller Argumente für und wider, die unsere gelehrten Häupter zu jener Frage überhaupt nur beibringen könnten.

Fast scheint es, als ob wir angesichts der Übergewalt der Tatsachen, die durch eine solche zum mindesten im Prinzip denkbare Dicht- und Denkmaschine repräsentiert wird, auf jeden Gedanken der Freiheit und Autonomie des menschlichen Geistes verzichten müssen, und als ob der krasseste Materialismus recht behielte, der auch im Menschen nichts anderes als eine Maschine und selbst in den feinsten und edelsten geistigen und seelischen Funktionen nur den Ablauf physikalischer und chemischer Prozesse sieht!

Wie also wäre das Problem, das sich an jene Druckmaschine knüpft und das so vernichtende Auspizien für den menschlichen Stolz und den menschlichen Geist zu eröffnen scheint, zu lösen?

Nun, die Lösung stellt sich ein, wenn wir die enorme Produktion unserer Druckmaschine doch einmal kritisch betrachten. Es ist richtig, die Maschine würde alles, was Menschenhirne je einmal erdacht und geschaffen haben oder jemals erdenken und schaffen werden, als Druckwerk produzieren. Aber nicht alles, was sie auf die beschriebene Weise druckt, wären Erzeugnisse von Wert oder auch nur von einem Minimum von Sinn und Verstand. Im Gegenteil, nur auf einen nahezu unendlich kleinen Teil ihrer Druckerzeugnisse würden diese Prädikate zutreffen, denn der aller-allergrößte Teil von diesen wäre nichts weiter als eine völlig sinnlose Zusammenstellung graphischer Zeichen. Schon unter den oben angeführten acht Variationen dritter Klasse aus den beiden Zeichen a und b findet sich keine einzige, die, in der deutschen Sprache wenigstens, Sinn und Verstand hätte, und ob unter den mehr als 68 Millionen von Variationen 13. Klasse aus den vier Zeichen a, l, m, t sich noch weitere als die oben angeführte » Alma malt Malta« befinden, die ebenfalls einen gewissen Sinn haben, ist schwer zu sagen, viele dürften es jedenfalls nicht sein. Und dieses Mißverhältnis zwischen sinnvollen und völlig sinnlosen Buchstabenfolgen nimmt mit der Zahl der Elemente und der Höhe der Klasse der Variationen ungeheuerlich zu. Bei unserer Druckmaschine mit ihren Variationen der millionsten Klasse aus hundert Elementen würde dieses Mißverhältnis in einem Maße angewachsen sein, das es schon rein technisch unmöglich macht, das Sinnvolle von dem Sinnlosen zu scheiden. Hundert Bücher würden beispielsweise nur aus Schriftzeichen einer einzigen Art bestehen, etwa vom ersten bis zum letzten Zeichen nur aaaa … lauten; ungezählte Billionen und Trillionen der Bücher würden ihrem ganzen Inhalte nach nur zwei verschiedene Zeichen des Alphabets aufzuweisen haben. Jede überhaupt herstellbare, im übrigen aber völlig sinnlose Zusammenstellung der alphabetischen Zeichen, auf je eine Million Stellen verteilt, wäre vertreten, und solche absolute graphische Sinnlosigkeiten, für die es in keiner Sprache des Weltalls auch nur eine Spur von Deutung gäbe, würden den weitaus größten Teil aller Bücher füllen, die die Maschine ausspeien würde. Noch nicht der trillionste oder quadrillionste Teil eines Prozentes würde Bücher mit auch nur annähernd sinnvollem Inhalte ergeben. In diesem Wust von Sinnlosigkeit würden solche Bücher, deren Inhalt wenigstens einen gewissen Sinn darstellt oder die gar sinnvoll wären, wie vereinzelte Körnchen in einem ganzen Ozean von Sinnlosigkeit und Wahnsinn herumschwimmen.

Das wird einleuchtend, wenn wir uns über die Menge von Hundert hoch Million Büchern Rechenschaft ablegen. Das ist nämlich eine überaus stattliche Zahl, ein arithmetisches Ungetüm, gegen das selbst die allerhöchsten Ziffernwerte aus der Inflationszeit oder die noch viel größeren Zahlenangaben, mit denen die Astronomie rechnet, wahre Zwerge – was sage ich Zwerge – nur Mücken, Bazillen, Atome wären. In der gewöhnlichen Schreibweise müßte jene Zahl mit einer Eins nebst zwei Millionen Nullen geschrieben werden, und wer sich wagemutig daranmachen würde, diese Zahl zu Papier zu bringen, hätte eine reichliche Woche zu tun, um sie aufzuschreiben, und er würde dazu eines Papierstreifens von der Länge einer reichlichen deutschen Meile benötigen. Mit dem beliebten Suffix »…ion«, mit dem wir unsere Millionen, Billionen, Trillionen und ähnliche arithmetische Kleinigkeiten bilden, könnte jene Zahl überhaupt nicht ausgedrückt werden; das kann eben nur in der konzentrierten Form von »Hundert hoch Million« geschehen. Und diese Zahl würde also die Gesamtmenge der Bücher ergeben, die sich als Variationen aus den hundert Zeichen des Alphabets herstellen lassen. Das gäbe eine sehr stattliche Bibliothek. Wenn Buch an Buch gelegt würde, die ganze Erdoberfläche voll, und dann immer wieder Buch auf Buch, so würde dieser Bücherwall konzentrisch um die Erde herum den Weltraum bis auf unendliche Weiten ausfüllen, nicht nur bis zur Sonne etwa, die doch immerhin schon an zwanzig Millionen Meilen abseits von unserem Wege liegt, sondern sogar bis zu den allerfernsten noch sichtbaren Gestirnen, die um viele Jahrtausende von Lichtjahren von uns entfernt sind, und selbst dann wäre erst der kleinste Teil dieser Riesenbibliothek untergebracht. Und aus diesem unendlichen Wall von Büchern, die, wie dargelegt, zum allergrößten Teil aus völlig sinnlosen Zusammenstellungen graphischer Zeichen beständen, wären nunmehr die Bücher sinngemäßen Inhaltes herauszusuchen. Ein sehr mühsames Geschäft, das uns die Druckmaschine leider nicht ebenfalls besorgen würde. Auf Trillionen oder Quadrillionen von solchen Druckerzeugnissen käme vielleicht erst ein einziges Buch lesbaren Inhaltes, und Billionen von Jahren würde es bedürfen, um ein solches herauszufinden, vergleichbar dem Bemühen, eine Stecknadel zu finden, von der wir nur wissen, daß sie irgendwo auf dem Grunde des Ozeans liegt, aber ohne die nähere Stelle zu kennen, ja sogar noch ungezählte Male mühevoller und länger dauernd als ein solches Unterfangen. Unsere Romandichter bescheren uns, schlecht gerechnet, pro Jahr etwa tausend Romane. Nehmen wir an, daß ein allmächtiger Zauberer unsere Druckmaschine geschaffen und mit ihr die Hundert hoch Million Bücher schon fertig gedruckt hätte; nehmen wir ferner an, daß die Menschen, seit der Erdball überhaupt bewohnt ist, bis auf den heutigen Tag nichts weiter getan hätten, als jene Riesenbibliothek durchzublättern und die Spreu vom Weizen zu sondern, und daß für jedes Buch nur eine einzige Sekunde für diesen Zweck verwandt würde, so hätten sie bis heute aller Wahrscheinlichkeit nach noch nicht einen einzigen lesbaren Roman der Art, von welcher uns unsere Romandichter jährlich tausend Stück liefern, herausgefunden.

Da dürfte es also für uns doch wohl angebrachter sein, bei der bisherigen Art der Romanproduktion zu bleiben. Und was vom Roman gilt, gilt natürlich auch für jede Art anderer von unserer Maschine in Druck gebrachter Geisteserzeugnisse, und damit würde eine solche Druckmaschine für uns jeden Wert verlieren.

Aber damit allein wäre das von uns aufgeworfene Problem, die Frage nämlich, ob die Möglichkeit einer solchen Maschine nicht als ein eklatanter Gegenbeweis gegen die Annahme der Freiheit und Autonomie des menschlichen Geistes zu gelten habe, doch noch nicht entschieden. Wenn eine solche Druckmaschine auch nur in der Idee möglich ist, so würde diese Möglichkeit schon genügen, um jenen Gegenbeweis gegen die Freiheit des Geistes, wenn er nicht noch auf andere Weise widerlegt werden könnte, wenigstens im Prinzip gelten zu lassen. Wir rieten oben unseren Gelehrten, falls sie über die Frage, ob die Freiheit des Geistes durch eine solche wie die beschriebene Druckmaschine als erschüttert zu betrachten sei, nicht ins klare kommen sollten, die Maschine selbst über dieses Problem zu fragen und die Lösung hierüber, die sich ja ebenfalls in der Menge der von ihr erzeugten Druckwerke befinden müßte, nachzulesen. Angenommen nun, unsere Gelehrten hätten sämtliche von der Maschine erzeugten Bücher, die über dieses Thema handeln, bereits fix und fertig zur Hand und sie machten sich an die Lektüre, nun, dann würden sie feststellen, daß sie hierdurch auch keinen Ausweg aus dem Dilemma finden. Denn in den Büchern, die von diesem Gegenstand handeln, würde sich ja nicht nur eine einzige, eindeutige Meinung über das Problem vorfinden, sondern alle überhaupt möglichen Meinungen und Auffassungen. Zu jedem Argument würde sich ein Gegenargument, zu jeder Behauptung ihr Gegenteil, zu jedem Beweis ein Gegenbeweis vorfinden, und damit bliebe es völlig unentschieden, was denn nun eigentlich Wahrheit und welches die alleinige und eindeutige Lösung des in Frage stehenden Problems ist. Statt Eindeutigkeit, wie sie die Wissenschaft erstrebt und die allein Erkenntnis und Wahrheit verbürgt, würde sich eine bis zum Äußersten getriebene Vieldeutigkeit ergeben, die jede Entscheidung über das Problem und seine Lösung ausschließt, genau wie es vor Hunderten von Jahren bei der ursprünglichen Maschine des Lullus der Fall war. Auch unsere Druckmaschine ist ja nichts anderes als ein Lullischer Mechanismus, in welchem das Lullische Prinzip bis zur äußersten Konsequenz durchgeführt worden ist, und sie würde sich, selbst wenn man von der technischen Unmöglichkeit des Apparates und der Ungeheuerlichkeit seiner Produktion absieht, mit der radikalen Vieldeutigkeit der von ihr fabrizierten Meinungen als ein völlig unmögliches Mittel, zu Erkenntnissen zu gelangen, erweisen. Welche von den sämtlichen Meinungen, die die Maschine über das ihr vorgelegte Problem in Druckschrift äußert, die allein wahre und welches die einzig richtige und wahre Lösung des in Frage stehenden Problems ist, das müßten dann die Gelehrten, die sich mit ihrem Problem an die Maschine wandten, also letzten Endes doch selbst entscheiden.

Damit aber wäre die Lösung des in Frage stehenden Problems doch wieder Sache des menschlichen Denkens und der Freiheit des Geistes selbst geworden; und wie die Entscheidung über jenes einzelne Problem, so natürlich auch die über alle Dinge, Fragen und Probleme, über die die Maschine Druckerzeugnisse produziert. Auch eine solche wie die beschriebene Druckmaschine kann trotz der absoluten Universalität ihrer graphischen Produktion nicht denken. Sie kann immer nur Druckerzeugnisse liefern, aber was in diesem Wust von Druckerzeugnissen sinnlosen und was sinnvollen Inhaltes ist, und wie aus der absoluten Vieldeutigkeit des Inhaltes der von ihr gelieferten und selbst als sinnvoll befundenen Druckerzeugnisse die Eindeutigkeit der Wahrheit und Erkenntnis abzuleiten wäre, das zu entscheiden wäre sie nicht imstande. Bedeutung, Sinn, Wert und Inhalt könnten ihre Erzeugnisse immer nur durch den denkenden Geist selbst erhalten, der an ihre Sichtung und Bestimmung herangeht. Die Masse erhält Sinn und Geist erst durch den Geist des denkenden Subjektes selbst. Die kritische Scheidung des Sinnvollen von dem Sinnlosen und die kritische Beurteilung des als sinnvoll Befundenen im Sinne eindeutiger Entscheidung und Erkenntnis, wie sie trotz der universalen Leistungsfähigkeit unserer Druckmaschine immer stattfinden müßte, wenn ihre Produktion überhaupt Sinn und Wert erhalten soll, das ist eine Funktion, die die Maschine selbst nicht leisten könnte. In solcher kritischen Scheidung und Beurteilung besteht die Funktion des Denkens. Sie ist die Funktion des freien Geistes selbst, der sich damit letzten Endes als das einzige Mittel, zu Wahrheit und Erkenntnis zu gelangen, erweist, sich gleichzeitig damit aber auch als von völlig anderer und unendlich höherer Wesenheit als der mechanische Ablauf selbst der kompliziertesten Maschine erweist und niemals durch einen Mechanismus erzeugt oder ersetzt werden kann.

Also die Freiheit und Autonomie des Geistes ist gerettet, und die Lullische Kunst, gleichviel ob in alter oder in modernisierter Form, die Denken und Geist aus dem gebundenen Schematismus oder Mechanismus ableiten und erzeugen will, stellt sich damit als eine Wahnidee heraus, die das Wesen des Geistigen völlig verkennt. Damit erweist sich zugleich auch der bedächtige und mühevolle Weg der geistigen Forschung als der einzige überhaupt mögliche Weg zur Erkenntnis und zur Wahrheit. Keine Art Lullischer Kunst aus alter, aus neuer und aus – heutiger Zeit vermag diesen Weg abzukürzen und zu Erkenntnissen zu führen, und das ist die einzige Wahrheit, die wir der Lullischen Kunst verdanken.

Postskriptum I
Die Lullische Druckmaschine im Minimalformat

Ganz so ungeheuerlich, wie es hier geschildert ist, brauchte übrigens eine solche Universal-Druckmaschine nicht zu sein. Man könnte ja statt eines Buches von einer Million Letternstellen eine Druckseite von rund tausend Stellen zugrunde legen, und auch dann müßte alles menschliche Wissen und Können aus Vergangenheit, Gegenwart und Zukunft in Druckschrift zum Vorschein kommen, wenn auch nicht in Buch-, sondern in Seitenform. Des weiteren könnte auch die Zahl der alphabetischen Zeichen, die in unserem Beispiel mit hundert angenommen ist, ganz bedeutend verringert werden. Die Großbuchstaben könnten gänzlich fortfallen, da sich alles Gedachte mit kleinen Buchstaben ebensogut ausdrücken läßt, auch die Ziffern wären entbehrlich, da sämtliche Zahlenangaben statt durch Ziffern sich auch durch die ausgeschriebenen Worte ausdrücken lassen. Die Zeichen x, y und v, wohl auch noch andere, könnten ebenfalls fortfallen, da sich ihr Lautwert durch andere Zeichen des Alphabets ebensogut wiedergeben läßt. Dadurch könnte die Zahl der notwendigen graphischen Zeichen auf 25 verringert werden, so daß wir auf eine Menge von 25 ¹⁰⁰⁰ Variationen kommen, deren jede eine Druckseite darstellt. Das ist zwar auch noch immer eine gewaltig hohe Zahl (sie wäre mit 1398 Ziffern zu schreiben), aber gegen die Menge von 100 ^1 000 000 Büchern eine verschwindend kleine Menge. Man könnte sogar noch bedeutend weiter einschränken, indem man die Zahl der notwendigen alphabetischen Zeichen nur auf so viel Stellen, als diese Zahl selbst angibt, variiert, also mit den notwendigen 25 alphabetischen Zeichen Variationen 25. Klasse druckweise herstellt. Das ergäbe eine Menge von 25 ²⁵ Druckzeilen, in denen ebenfalls das gesamte dem menschlichen Geiste überhaupt zugängliche Wissen zum Ausdruck kommen müßte. Die Anzahl dieser Druckzeilen wäre 543 420 Quintillionen. Das ergäbe zwar immer noch ein stattliches Konversationslexikon von über 5 Quintillionen Bänden, aber es hielte sich doch in den Grenzen des Vorstellbaren und könnte vielleicht auf unserem Erdballe untergebracht werden, ohne daß die Regale bis zu den fernsten Sternen hinaufgebaut werden müßten.

Postskriptum II
Moderne Lullische Kunst

Die Lullische Kunst hat ein zähes Leben. Die sechs Jahrhunderte seit ihrer Entstehung, in denen der Gedanke an dieses Verfahren der mechanischen Begriffsverknüpfung immer wieder auftauchte und immer wieder mit mehr oder weniger Ernst versucht worden ist, ihm doch eine fruchtbare Seite abzugewinnen, haben das gezeigt. Ja, in einer bestimmten Form ist sie sogar gegenwärtig zu neuem Leben erwacht, nämlich als die sogenannte mathematische Logik. Diese Disziplin, die ursprünglich von englischen Logikern ausging, aber heute im Rahmen der Mathematik Lehrfach an den meisten Universitäten geworden ist, betrachtet die Worte als Zeichen oder Symbole der Sprache; die sprachlichen Operationen sind ihr Instrumente des Denkens und können vermittels eines Systems von Symbolen durchgeführt werden. Auf diese Weise entsteht eine Verknüpfung von Symbolen als Vertretern der Begriffe und Operationen, die nach der Meinung der mathematischen Logiker geeignet sein soll, die Mehr- und Vieldeutigkeit der gewöhnlichen Sprache zu vermeiden und zu eindeutigen Bestimmungen zu gelangen. Die Paradoxien des gewöhnlichen Denkens und insbesondere die Paradoxien der Mengenlehre sollen auf diese Weise beseitigt werden. Daß diese neue Disziplin dieser Aufgabe in vollem Umfange gerecht zu werden vermag, dafür hat sie noch nicht den Beweis erbracht; sie hat zwar eine Reihe von Paradoxien aus der Mengenlehre ausgeschieden, kann aber keine Gewähr bieten, daß solche nicht doch wieder auftreten. In ihrer schematischen Verknüpfung von Symbolen, mit der Kombination der durch Symbole vertretenen Begriffe und Funktionen, erinnert die mathematische Logik stark an den Schematismus der Lullischen Kunst. Ob sie in höherem Maße als diese ein Instrument der Erkenntnis werden kann? Federico Enriques, der ausgezeichnete Mathematiker und Logiker, urteilt in seinem Werk: »Zur Geschichte der Logik« Leipzig 1927, übersetzt von Bieberbach., nachdem er über die Lullische Kunst und ihre Wiederkehr in der Gedankenwelt Leibnizens gesprochen und sie als »einzigartige Vermischung von Wahrheit und Unsinn« bezeichnet hat, darüber in der vielsagenden Frage: »Wieviel von diesem Gedanken lebt wohl noch fort in dem Glauben, den moderne Vertreter der mathematischen Logik in die magische, schöpferische oder heuristische Kraft der Symbole legen?« – Also die Lullische Kunst lebt weiter. Ob in ihrer modernisierten Form mehr herauskommen wird, als es in ihrer früheren bei Lullus und Leibniz der Fall war, kann mit apodiktischer Gewißheit nicht gesagt werden. Vielleicht, daß sie ebenfalls, wie es bei Leibniz der Fall war, zu einem neuen Rechenverfahren führt, wenn auch der »logische Kalkül«, der das Instrument der mathematischen Logik ist, diese Bedeutung noch keinesfalls hat; vielleicht daß bei ihr auch einmal eine Art »Rechenmaschine« der Erfolg der Bemühungen sein wird.

3. Der Streit um die Allmacht
Eine höchst logische Geschichte

Also der Willibald Achtelpfund war gestorben, und es muß gesagt werden – rückhaltlos – ein Guter war er nicht gewesen, beileibe nicht! Ganz gegenteilig, mancherlei erheblichen Anlaß zu gerechtem Ärgernis hatte er den wahrhaft Frommen zeit seines Erdenwallens gegeben. Meint ihr etwa, der hätte sich, als es noch Krieg war, mit den ihm von Amts und Rechts wegen zugestandenen Lebensmittelkarten zur Aufrechterhaltung seines genußsüchtigen Leibes begnügt? Daß ich nicht lache! Hintenherum gekauft hat er vielerlei mit hinterhältigem Geschick und dadurch viele andere, die weniger geschickt waren, in berechtigte Zorneswallungen versetzt. Und glaubt ihr, der hätte, als der Krieg aus war und dafür der Rundfunk eingeführt wurde, seine Antenne sogleich dem Postminister gemeldet? Schwarz gehört hat er, monatelang, unbezahlt und unbestraft! Und nehmt ihr wirklich an, er hätte sich in der Straßenbahn jedesmal, wie es doch in großen Druckbuchstaben weithin sichtbar angeschlagen ist, sogleich beim Schaffner zur Entgegennahme und Zahlung eines Fahrscheines gemeldet? Keineswegs hat er das immer getan, oftmals ist er unabgefertigt bis zu Ende gefahren, und es besteht der dringende Verdacht, daß das nicht gegen seine Absichten geschah. Und wie oft hat er beim Straßenübergang sein Sündenkonto beschwert, indem er statt in dem vorgeschriebenen rechten Winkel in einer völlig eigenmächtigen Kurve das andere Ufer erstrebte und selbst an den Straßenkreuzungen trotz der befehlenden Geste des Schupomannes den weißen Strich, der ihm den rechten Pfad weisen sollte, mißachtete! Und ob er wohl seine Steuererklärungen immer in Gott völlig wohlgefälliger Weise abgefaßt, nichts verschwiegen und nichts hinzugesetzt hat? Gewiß ist, daß er nur den Barbetrag, der ihm kraft seiner Gehaltgruppe zufloß, angegeben hat, weil man das nämlich sehr genau kontrollieren konnte; aber verschwiegen hat er manche Nebeneinnahmen, die er aus nichtamtlicher Anfertigung von Gedichten anläßlich Kindtaufen, Hochzeiten, Beerdigungen und sonstigen Trauerfällen bezog, und hinzugesetzt hat er, zu den Berufsunkosten nämlich, um die er die Besteuerung seiner Einnahmen zu mindern trachtete, mancherlei, was sich nicht kontrollieren ließ, sogar das Fahrgeld für die vielen Straßenbahnfahrten, wo er unabgefertigt bis zum Ende geblieben ist. Ich meine, es hat alles seine Grenzen! Willibald Achtelpfund aber hat sich gegen diese Grenzen oftmals in mehr als üblicher Weise vergangen. Ganz zu schweigen, daß er sich zu Lebzeiten darin gefiel, allerlei unerbauliche Bücher zu lesen, besonders solche von alten Philosophen, die sich Skeptiker oder Scholastiker nannten und darin allerlei bedenkliche Meinungen über Gott und die Welt äußerten. Dem Seelenheil ist das Lesen solcher Druckwerke nie förderlich gewesen, und wenn Willibald Achtelpfund sich durch die außeramtliche Beschäftigung mit solchen gedruckten Bedenklichkeiten verleiten ließ, seinen Witz selbst an den ehrwürdigsten Einrichtungen zu üben und sogar die gewissesten Dinge in Zweifel zu ziehen, so hat er damit sein unsterbliches Teil nur gefährdet.

War es da ein Wunder, daß nunmehr, nachdem Willibald Achtelpfund aus dem irdischen Dasein geschieden war, es um die Art seines jenseitigen Aufenthaltes, ob Hölle oder Himmel, sehr fraglich stand? Das war ihm selber gewiß, als er jetzt im Kreuzverhör vor dem Teufel stand. Denn es besteht in den jenseitigen Bezirken die Vorschrift, daß sich alle nicht ganz einwandfreien Neuankömmlinge zunächst einmal bei dem Höllenfürsten als Vorinstanz zu melden haben, und erst wenn hier die Untersuchung ergibt, daß sich der Prüfling doch nicht genügend Sündenschmalz angemästet habe, um erfolgreich im Fegefeuer schmoren zu können, wird er aus der höllischen Untersuchungshaft entlassen und darf dann sein Glück bei den himmlischen Behörden versuchen. Da mochte also Willibald Achtelpfund mehr Bedrückung empfinden als jemals bei seinem zweifelhaften irdischen Treiben, und ob er auch alle Listen und Ränke durchdachte, so wollte ihm doch nicht einfallen, wie er hier seine Seele mit Anstand und Erfolg für den Himmel salvieren könnte.

Nun und der Herr Urian selbst, wie er so die irdische Führungsliste, die ja bekanntlich für jeden Sterblichen, ohne daß er es merkt, schon bei seinen Lebzeiten von den jenseitigen Behörden geführt wird, durchsah, der lächelte da so recht teuflisch und meinte wohlwollend: »Na, Willibald Achtelpfund, ich glaube, du bist reif für mich und dürftest dich wohl für ein längeres Weekend so von einigen hunderttausend Jährchen in meiner Heißluftsiedlung einrichten!«

»Aber, Euer Hochwohlgeboren,« erwiderte Willibald Achtelpfund mit zaghafter Opposition, »ich meine, so schlimm ist es doch nun gerade nicht gewesen, und wegen dem bißchen da in meinen Ausweispapieren …«

»Ein bißchen, ich höre immer ein bißchen!« höhnte der Teufel. »Das nennen die Herrschaften immer ein bißchen, wenn sie von unten ankommen. Aber wir sind da zumeist sehr konträrer Meinung, und was hier über deine irdische Führung verzeichnet steht, das ist nicht ein bißchen, sondern ein bißchen viel, mein Lieber! Was meinst du denn, wie wir solche Gefräßigkeit beurteilen, die aus deinen vielfachen Zuwiderhandlungen gegen alle amtlichen Lebensmittelkartenverordnungen damals, als noch Krieg war, spricht?«

»Aber man wollte doch schließlich auch damals leben,« verteidigte sich Willibald Achtelpfund kleinlaut, »ich hätte ja wahr und wahrhaftig verhungern müssen, wenn ich mir nicht Zuschuß zu den Karten geschafft hätte.«

»Besser reinen Herzens verhungert, als sich hintenherum sattgegessen«, antwortete ihm streng der Teufel. »So haben es damals die wirklich Guten alle gehalten, ob Fürsten oder Kommerzienräte, und wenn du, wie ich dem Ausdruck deines Sündergesichtes wohl ansehe, diese Versicherung in Zweifel ziehst, so erwirbst du damit höchstens die Aussicht, daß für dich extra die Hölle noch um einige hundert Grad höher temperiert wird. Und was meinst du ferner zu den vielen unabgefertigten Fahrten auf der Straßenbahn? Hier sind alle verzeichnet, und es ist eine hübsche Strecke.«

»Ich bitte,« wandte Willibald Achtelpfund ein, »bei dem Gedränge in den Wagen, wo sie einem die Sachen vom Leibe reißen, da kann man sich oft nicht beim Schaffner melden, obschon man es will.«

»Faule Ausrede, wer will, der kann! Und das Schwarzhören beim Rundfunk, mein Lieber? Da war kein Gedränge!«

»Das freilich nicht,« meinte Willibald Achtelpfund, »aber die Damen und Herren, die da im Rundfunk ihre Sachen erzählen oder ihre Liedeln singen, haben nie dabei gesagt, daß sie dafür etwas bezahlt haben wollen, und da habe ich geglaubt, daß …«

»… das alles umsonst ist!« unterbrach ihn voller Spott der Beherrscher der Hölle. »Das glaubst du doch wohl selber nicht und ein anderer dir nur, wenn du ihn dafür weit über Tarif bezahlst. Aber da dir das Gegenteil nicht nachzuweisen ist, will ich das gelten lassen, und auch daß du an den Straßenkreuzungen so oft gegen den Strich gegangen bist, soll dir nicht weiter angekreidet werden, denn aus den Vorschriften der Verkehrspolizei wird selbst der Teufel nicht klug. Aber –« und hier grinste der Teufel so teuflisch, daß es schon nicht mehr schön war –, »aber nun, mein Bester, was sagst du denn wohl zu deinen ehemaligen Steuerangaben? Haben die etwa immer bis auf den letzten Pfennig gestimmt?«

Da wurde ja nun dem Willibald Achtelpfund schwül und heiß auch schon ohne Fegefeuer, kaum daß er die Entgegnung stottern konnte, sein Amtsgehalt habe er immer redlich angegeben, denn das hätte das Finanzamt ohnehin gekannt, und seine Nebeneinnahmen für die Gedichte – nun, da habe er doch angenommen, daß solche geistige Arbeit steuerfrei sei, wohingegen eine Tätigkeit als Magistratsbeamter, die ja keinerlei Geist erfordere, immer …«

»Keine posthume Vorspiegelung falscher Tatsachen«, unterbrach ihn aber voll Hohn und Heiterkeit der leibhaftige Satan. »Besteuert werden muß alles, ob mit oder ohne Geist. Nein, mein Lieber, ich wiederhole, du bist reif für die heiße Zone, und so bestimme ich denn kraft meiner Allmacht …«

Bei diesem Worte blitzte – im letzten Moment – dem Willibald Achtelpfund ein rettender Gedanke auf.

»Allmacht, Allmacht –«, echote er, »ich höre immer Allmacht!«

»Elender ehemaliger Erdenwurm!« schrie da der Teufel ergrimmt. »Willst du an meiner Allmacht zweifeln? Weißt du auch, daß ich dir für diese Vermessenheit die Hölle doppelt heizen lassen werde, und wenn ich das Dreifache an Koksvorschuß zu bezahlen hätte?« – Nichts konnte nämlich den Teufel mehr kränken, als wenn man ihm seine Allmacht bestritt, durch die er sich für ranggleich mit dem Herrn im Himmel wähnte. Daher seine Wut, wobei er zugleich intensiv mit den Augen rollte.

Aber Willibald Achtelpfund spielte va banque, und deswegen sagte er, zwar innerlich zitternd, aber äußerlich bestimmt: »Und dennoch behaupte ich, daß Euer Hochwohlgeboren nicht allmächtig sind. Das kann ich beweisen, und darauf gehe ich jede Wette ein!«

»Du mit mir wetten, du Schwarzhörer, du unabgefertigter Straßenbahnfahrer, du – du – –!« dem Teufel verschlug es beinahe die Stimme ob solcher Frechheit. »Du willst beweisen und wetten, daß ich nicht allmächtig bin?«

»Jawohl, will ich!« sagte Willibald Achtelpfund mit verzweifelter Entschiedenheit, und berechnend setzte er hinzu: »Mir scheint aber, daß Euer Hochwohlgeboren Bedenken tragen, die Wette anzunehmen.«

Der Teufel schwankte, ob er den Frechling sogleich beim Genick nehmen und ins Fegefeuer, dorthin, wo es am heißesten ist, spedieren oder die Wette wirklich annehmen sollte. Aber da sein kitzligster Punkt berührt war, entschied er sich für letzteres und sagte mit unheimlicher Ruhe: »Gut, wetten wir, der Ausgang ist mir nicht weiter schleierhaft! Also, du wettest, mir beweisen zu können, daß ich nicht allmächtig bin. Vermagst du den Beweis nicht zu führen, so nimmst du seelenlängliches Fegefeuer bei Höchsttemperatur und unter Verzicht auf jedwede Bewährungsfrist, die dir nach Ablauf der ersten hunderttausend Jahre bei guter Führung und dito Wohlverhalten immerhin zustände, auf dich. Einverstanden?«

Dem Willibald Achtelpfund wurde es um diesen Einsatz zwar etwas bange. Dann aber überlegte er, daß zwischen hunderttausend Jahren und seelenlänglich eigentlich kaum ein wesentlicher Unterschied sein dürfte, und sagte darum: »Einverstanden, ich halte die Wette, wenn Sie als Gegeneinsatz für den Fall, daß ich die Wette gewinne, auf meine fernere Anwesenheit in Ihren Territorien verzichten und mir das Visum nach den himmlischen Gefilden ausstellen.«

»Gemacht!« schrie der Teufel, der sich seiner Sache absolut sicher fühlte, und hielt seinen Pferdefuß hin, in den Willibald Achtelpfund mannhaft einschlug. »Und nun heraus mit deinem sogenannten Beweis,« fuhr der Teufel voll Hohn und Ungeduld fort, »und gnade dir meine Frau Urgroßmutter, wenn er dir nicht bis auf das I-Tüpfelchen gelingt!«

Da tat Willibald Achtelpfund einen tiefen Atemzug, soweit das für eine körperlose Seele noch angängig war, und sagte dann: »Also der Beweis wäre folgender: Wenn Sie, Herr Teufel, wirklich allmächtig sind, dann müssen Sie doch alles tun können, was Sie wollen oder was ich von Ihnen verlange, nicht wahr?«

»Selbstverständlich, mein Lieber,« antwortete der Teufel mit unterdrückter Heiterkeit, »kann ich und werde ich!«

»Dann müssen Sie also auch einen Stein schaffen können, so groß wie ich nur will«, fuhr Willibald Achtelpfund fort.

»Nichts leichter als das,« hohnlächelte der Teufel, »so groß, wie du willst, meinetwegen bis ans Ende der Welt oder noch darüber hinaus.«

Da legte Willibald Achtelpfund seinen Zeigefinger an die Nase und sagte mit Betonung: »Dann verlange ich als Zeichen Ihrer Allmacht, daß Sie einen Stein erschaffen, der so groß ist, daß Sie nicht darüberspringen können.«

»Mit denkbar größtem Vergnügen«, frohlockte der Teufel, murmelte eine Zauberformel, die so dunkel und rätselhaft klang wie die berühmte Reichsgerichtsentscheidung über den Begriff der Eisenbahn, und schon stand vor Willibald Achtelpfund ein Stein, der sich in unübersehbare Höhe erstreckte. »Voila, mein Lieber,« grinste der Teufel, »hier ist der Stein!«

»Ist der aber auch wirklich so groß, daß Sie nicht darüberspringen können?« fragte Willibald Achtelpfund.

»Auf Ehrenwort, das mir so heilig ist, wie der Katze der Schwanz«, beteuerte der Teufel feierlich und legte beschwörend den Pferdefuß ans Herz. »Über den Stein kann selbst ich nicht springen.«

»Wenn dem so ist, Herr Teufel,« sagte Willibald Achtelpfund, »dann sind Sie ja nicht allmächtig.«

»Hallo, was soll das heißen?« rief der Teufel erstaunt. »Hier steht der Stein, den du zum Zeichen meiner Allmacht von mir verlangt hast.«

»Aber allmächtig sind Sie darum doch nicht,« erwiderte Willibald Achtelpfund bedachtsam, »denn Sie können nicht alles tun, was Sie wollen, beispielsweise nicht über diesen Stein springen, wie Sie soeben selbst zugegeben haben. Also sind Sie nicht allmächtig.«

»O bitte, ich kann auch sofort einen Stein schaffen, über den ich springen kann«, wandte der Teufel ein.

»Das wäre dann aber nicht der Stein, den ich von Ihnen verlangt habe, denn der soll ja gerade so groß sein, daß Sie nicht darüberspringen können«, setzte Willibald Achtelpfund dem Teufel, der etwas schwer von Begriff war, kühl und sachlich auseinander. »Sie sehen also: wenn Sie über den Stein springen können, so ist das nicht das verlangte Allmachtszeichen; können Sie aber nicht über den Stein springen, so dokumentieren Sie damit einen Mangel an Sprungvermögen. In diesem wie in jenem Falle sind Sie also nicht allmächtig.«

»Teufel,« sagte der Teufel, »mir scheint, da bin ich 'reingefallen!« Und wie er die spitzfindige Logik seines Widerparts auch wandte und drehte, er konnte ihr nicht beikommen. Und daher sagte er schließlich mit Gefaßtheit: »Willibald Achtelpfund, du hast die Scholastiker, wie ich sehe, mit Erfolg studiert; die haben solche Schlußfolgerungen ausgeheckt und sollen darum von jetzt ab von mir noch mehr eingeheizt kriegen. Also ich habe dir mein Ehrenwort gegeben und werde meinen Kanzleisekretär Theophrastus Bombastus Paracelsus von Hohenheim, auch einen von diesen infamen Scholastikern, der noch etliche Zehntausende von Jahren bei mir zu absolvieren hat, beauftragen, dir das Visum nach dem Himmel auszufertigen. Doch, apropos Himmel, da fällt mir ein: wenn es in der Hölle keine Allmacht gibt, dann kann es natürlich im Himmel auch keine geben! Stimmt's?«

»Die Logik gilt für Himmel und Hölle in gleicher Weise«, erwiderte Willibald Achtelpfund vorsichtig.

»Dann ist ja euer lieber Gott im Himmel, von dessen Allmacht immer soviel Wesens gemacht wird, auch nicht allmächtig«, rief der Teufel und wurde plötzlich wieder guter Laune. »Hurra, das wollen wir dem alten Herrn da oben doch gleich einmal zu Gemüte führen. Der hat immer noch viel bestimmter als ich behauptet, allmächtig zu sein; das gibt einen Hauptspaß. Komm, Willibald Achtelpfund, wollen mal gleich bei den himmlischen Herrschaften vorsprechen und ihnen deinen Beweis vorlegen. Was die dazu wohl sagen werden, hahaha!«

Damit packte er Willibald Achtelpfund, dem, so froh er war, der Hölle entrinnen zu können, bei den Absichten des Teufels doch keineswegs ganz geheuer war, beim Genick, murmelte abermals einen Zauberspruch, der so rätselhaft klang wie ein Gedicht von Christian Morgenstern, und im nächsten Augenblick hatten sie beide mit kosmischer Geschwindigkeit das Weltall bis zum andern Ende durcheilt und waren an der Himmelstür angelangt, wo der Teufel kräftig anklopfte. Petrus öffnete, und als er den Höllenfürsten erblickte, sagte er mehr erstaunt als erfreut: »Nanu, Herr Urian, Sie haben sich wohl in der Adresse geirrt? Sie wissen doch, daß hier für Sie permanenter Lokalschluß ist.«

Der Teufel aber ließ sich nicht abweisen. »Es handelt sich um dynastische Interessen von größter Wichtigkeit für Ihren Herrn«, sagte er, schob den verdutzten Himmelspförtner einfach beiseite, und gleich darauf stand er auch schon mit Willibald Achtelpfund vor Gottes Thron.

»Was verschafft mir das zweifelhafte Vergnügen, Eure Infernalische Majestät hier zu sehen?« fragte der liebe Gott, nachdem ihm der Teufel seine Reverenz erwiesen hatte.

»Ich fürchte, Eure Himmlische Majestät werden besagtes Vergnügen sogleich noch zweifelhafter finden, als soeben zart angedeutet wurde«, grinste der Teufel im Vorgefühl seines Triumphes überaus höhnisch. »Es handelt sich, kurz gesagt, darum, daß es mit Ihrer und leider auch mit meiner Allmacht zu Ende ist, wie mir dieser Schubbejack Willibald Achtelpfund unanfechtbar bewiesen hat. Es würde mich nun lebhaft interessieren, zu hören, wie Eure Himmlische Majestät mit diesem Beweis die bisher immer aufs entschiedenste betonte Annahme der Allmacht Eurer Majestät vereinbaren zu können glauben.«

Zu dieser Teufelsrede lächelte der liebe Gott nur milde und mitleidig und sagte dann gelassen: »Wollen Sie mir, bitte, den Beweis demonstrieren.«

»Das ist leicht geschehen, und ich bin erstaunt, daß Eure Himmlische Majestät den Beweis nicht schon selbst kennen, wo doch die himmlische Telegraphenagentur ständig die Meldung verbreitet, daß Eure Majestät allwissend seien«, höhnte der Teufel. »Also hier der Beweis, daß es keine Allmacht gibt, auch seitens Eurer Himmlischen Majestät nicht: Ich verlange als Zeichen Ihrer Allmacht, daß Sie mir einen Stein schaffen, der so groß ist, daß Sie nicht darüberspringen können. Wenn Sie einen solchen Stein nicht schaffen können, sind Sie nicht allmächtig; wenn Sie ihn schaffen, aber nicht darüberspringen können, sind Sie ebenfalls nicht allmächtig, nämlich wegen Mangels an Sprungvermögen. Also sind Sie weder in diesem noch in jenem Falle allmächtig. Voilà!« Voller Triumph und Bosheit wedelte der Teufel mit der Schwanzquaste, die er wie eine Schleppe über den Arm gelegt hatte.

Der liebe Gott aber lächelte nach dieser Rede des Teufels noch milder und freundlicher, daß unten auf der Erde gleich strahlender Sonnenschein aus allen Wolken brach, denn das Wetter auf Erden hängt immer davon ab, ob der Herrgott im Himmel heiter oder ernst gestimmt ist, was aber die Meteorologen und die Zeitungen auf der Erde nicht wissen, weswegen sie auch immer das falsche Wetter prophezeien. »Und damit glauben Sie also den Beweis geliefert zu haben, daß ich nicht allmächtig bin?« fragte der liebe Gott den Teufel sarkastisch.

»Können Sie den Beweis widerlegen? Ich nicht«, meinte dieser.

»Nun, letzteres möchte vielleicht nicht allzuviel besagen,« sagte dazu der liebe Gott. »Aber wir wollen einmal den Fall betrachten. Also Sie verlangen von mir zum Zeichen meiner Allmacht die Erschaffung eines Steines, der so groß ist, daß ich nicht darüberspringen kann. Und wenn ich dann nicht über den Stein springen kann, so legen Sie mir das als einen Mangel an Allmacht aus.«

»Sehr wohl, Eure Himmlische Majestät sind vollkommen im Bilde.«

»Ihre Forderung lautet mit etwas anderen Worten also: Ich soll über einen Stein springen können, über den ich nicht springen kann. Und nur wenn ich dieser Forderung nachzukommen vermag, würden Sie mich für wirklich allmächtig erklären. So ist es doch?«

Der Teufel mußte angestrengt nachdenken, denn Logik war gerade nicht seine starke Seite. Aber schließlich hatte er kapiert und erwiderte mit zustimmendem Nicken: »So ist es, in der Tat, und ich bin begierig, wie Sie diese sich selbst widersprechende Forderung …«

»Diese Forderung besteht also in Wirklichkeit aus zwei getrennten und sich anscheinend widersprechenden Forderungen«, unterbrach ihn jedoch der liebe Gott. »Erstens, ich soll über einen zu erschaffenden Stein springen können, zweitens, ich soll über denselben Stein nicht springen können. Auf diese Formel reduziert sich das Problem.«

»Das dürfte richtig sein«, stimmte nach abermaliger angestrengter Gedankenarbeit der Teufel zu.

»Nun kann ich jederzeit jeden beliebigen Stein erschaffen und darüberspringen, denn das ist ja für unsereinen weiter kein Kunststück«, fuhr der liebe Gott fort. »Damit wäre also die erste Forderung erfüllt.«

»Nun aber die zweite,« rief der Teufel hitzig, »jetzt sollen Sie über denselben Stein auch nicht springen können.«

»Sehr einfach! Ich kann auch über denselben Stein nicht springen.«

»Dann sind Sie nicht allmächtig,« triumphierte Herr Urian, »denn dieses Nichtkönnen bedeutet einen Mangel an Allmacht.«

»Da verwechseln aber Eure Infernalische Majestät wieder einmal ganz gehörig die Begriffe«, unterbrach ihn aber sehr gelassen der liebe Gott. »Ich sagte soeben: Ich kann auch über denselben Stein nicht springen. Das bedeutet und kann nach den Prämissen des Falles nur bedeuten: Ich habe die Macht, den Sprung zu unterlassen. Verneint ist in der zweiten Forderung nämlich nicht das Können, sondern das Springen.«

»Das geht über meinen Horizont«, gestand der Teufel.

»Auf größere Entfernungen scheint der dann gerade nicht eingerichtet zu sein«, meinte dazu der liebe Gott gemütlich. »Ich will Ihnen die Sache daher an einem Beispiel deutlicher zu machen suchen. Ein Mensch kann essen und er kann auch nicht essen, das heißt das Essen unterlassen, also hungern. Das Hungern kann man ihm doch nicht als Mangel an Fähigkeiten auslegen, sondern im Gegenteil gerade als Fähigkeit, von der mancher arme Teufel – entschuldigen Sie den Ausdruck! – mehr als ihm lieb ist, Gebrauch machen muß. Auf Erden lassen sich jetzt ja sogar manche Künstler die Tätigkeit des negativen Essens, also zu hungern, mit Geld bezahlen, und wie ich vernahm, sollen einige dieser Hungerkünstler bereits zu Eurer Infernalischen Majestät in läuternde Behandlung gekommen sein, weil sie trotz des Hungerns dicker wurden. Jedenfalls ist Ihnen klar, daß sich die beiden Fähigkeiten, nämlich zu essen und nicht zu essen, keinesfalls ausschließen. In analoger Weise erledigt sich auch das Problemchen, mit dem Eure Infernalische Majestät mir ein wenig voreilig meine Allmacht bestreiten zu können glaubten. Die Forderung, von der Sie annahmen, daß sie über meine Allmacht geht, hat in der ursprünglichen Form also lediglich die Bedeutung: Ich soll einen Stein erschaffen, der so groß ist, daß ich es unterlassen kann, darüberzuspringen! Das aber ist keinerlei logische Unmöglichkeit, sondern lediglich schlechtes Deutsch. Wo also wäre die Lücke meiner Allmacht?«

»Teufel!« sagte der Teufel nach abermaligem Gedankenwälzen, daß ihm schon der Schweiß von den Hörnern rann, »mir scheint, da bin ich wieder 'reingefallen.« Und ganz kleinlaut setzte er hinzu: »Dann wären wir also doch allmächtig.«

» Wir wäre wohl etwas zuviel gesagt,« meinte der liebe Gott mit feinem Lächeln, »denn Eure Infernalische Majestät haben nicht einmal die Macht gehabt, einen höchst einfachen Sophismus mittelalterlicher Weisheit zu durchschauen, was nach allen Regeln der Logik – und diesmal tatsächlich – einen Mangel an Allmacht in sich schließt. Wenn irgendwelche Menschlein da unten solche Sophismen aushecken und in ihrer Einfalt glauben, damit wunder was gesagt und bewiesen zu haben, nun, so sind das eben arme Teufel, die es nicht besser verstehen. Aber wer sich von solchen Spitzfindigkeiten bluffen läßt und sie für bare Münze nimmt, der scheint mir mehr ein dummer Teufel zu sein!«

Und dabei sah der liebe Gott den Teufel scharf und vielsagend an. In dem kochte es begreiflicherweise vor Wut, und er stotterte, daß solche Zweideutigkeiten doch nicht dem heiligen Orte entsprächen. Dabei fiel sein wutrollendes Auge auf Willibald Achtelpfund, und sein Blick heiterte sich auf: »Na, Willibald Achtelpfund,« sagte er höhnisch, »dann wäre es also nichts mit deinem Beweis, wie du soeben von einer unbestreitbaren Kapazität gehört hast. Dann hast du also deine Wette mit Glanz verloren, wie ich es dir gleich vorausgesagt habe, und du gehörst mir. Komm, mein Lieber, mein Oberheizer wartet schon auf dich!«

Was nun Willibald Achtelpfund anbetraf, so hatte er während der ganzen hier geführten Debatte zitternd und bebend an der untersten Thronesstufe gelegen und nicht gewagt, den streitenden Herren ins Gesicht zu sehen. Um der Wahrheit die Ehre zu geben, hatte er mit seinem Sophismus, den er aus einem uralten Buche herausgelesen hatte, eigentlich nicht beabsichtigt, die Allmacht des lieben Herrgottes in Zweifel zu ziehen, sondern er wollte damit in dem Kreuzverhör mit dem Teufel sich nur aus der Patsche helfen, was ihm schon beinahe gelungen schien. Und nun sollte alles vergeblich gewesen sein? Schon fühlte er voller Kümmernis die böse Faust des Teufels wieder an seinem Genick.

Der liebe Gott hatte natürlich den ganzen Sachverhalt von Anfang an durchschaut, und da erbarmte er sich des zitternden Willibald Achtelpfund, hielt den Teufel, der, mit Willibald Achtelpfund unterm Arm, schon seine Reverenz zum Abschied machte, mit einem Blick zurück und sagte: »Eure Infernalische Majestät sind im Begriff, Ihre Kompetenzen zu überschreiten, was Wir nicht zugeben können. Sie haben den Willibald Achtelpfund einmal aus der Hölle entlassen, und wem das geschehen ist, der ist nach dem Reglement über die Behandlung irdischer Sünder nicht gehalten, ein zweites Mal in die Hölle zurückzukehren. Wir bestimmen daher, daß der Willibald Achtelpfund hierbleibe. Seine Konduite ist allerdings nicht die beste, aber der Mantel der christlichen Nächstenliebe ist nun einmal im Himmel herrschende Mode. Er soll hier geläutert werden. Bei Unserer für Zeit und Ewigkeit ausreichenden Verproviantierung mit Nektar und Ambrosia wird er nicht in Versuchung kommen, sich über seine himmlische Lebensmittelkarte einzudecken; den himmlischen Rundfunk mit täglichem Engelgesang hat er umsonst, und Straßenbahnen, auf denen er unabgefertigt fahren könnte, gibt es hier oben nicht, da die Engel ja bekanntermaßen fliegen können. Seine Steuererklärung aber soll mit Nachsicht geprüft werden, denn bei den Finanzämtern da unten ist auch nicht alles in Ordnung, und besser als die braucht ein steuerzahlender Erdenmensch auch nicht zu sein. Petrus soll sehen, aus dem Willibald Achtelpfund ein brauchbares Mitglied der himmlischen Gesellschaft zu machen. Habe die Ehre, Eure Infernalische Majestät!«

So ging dem Willibald Achtelpfund, der es nach seinem bedenklichen Lebenswandel doch eigentlich anders verdient hätte, seine Beschäftigung mit den spitzfindigen Scholastikern schließlich noch zum Guten aus. Ja, ja, die Zweifelhaften erlangen oft die größten Vorteile über die wahrhaft Guten und Frommen!

4. Heitere Logik

Vom logischen Witz – Die vieldeutige Negation – Der Hörnerbeweis – Die Katze mit den drei Schwänzen – Zweideutigkeiten in alter und neuer Zeit – Der Witz der Zweideutigkeit – Vom Wortwitz

Bei den Ausgrabungen in Babylon hat man große Mengen Draht gefunden und daraus geschlossen, daß die alten Babylonier bereits die Telegraphie gekannt haben; bei den Ausgrabungen in Ninive hat man keinen Draht gefunden und daraus den Schluß gezogen, daß die alten Ninivenser bereits die Telegraphie ohne Draht gekannt haben!

Das ist, wie man zugeben wird, ein ganz hübscher Witz, der sich in manchen Lehrbüchern der Logik als scherzhaftes Beispiel falschen Schlußverfahrens angeführt findet. Woraus wiederum geschlossen werden darf, daß auch im Bereich der Logik, dieser abstraktesten aller Wissenschaften, für die der Laie zumeist keine, aber auch gar keine Sympathie übrig hat, Oasen des Humors vorhanden sind, in denen die Blüte des Witzes ihr Gedeihen findet. Und diese Folgerung ist richtig und kann durch zahllose Beispiele aus allen Zeitaltern des logischen oder auch unlogischen Denkens erhärtet werden.

Der logische Witz ist besonderer Art. Er kleidet sich, freiwillig oder unfreiwillig erzeugt, immer in die Form eines Widerspruches, eines Fehl- oder Trugschlusses oder sonstwie kuriosen gedanklichen Resultates und stellt zugleich die Aufgabe, den Grund des falschen Schlusses zu finden, was auch für Zeitgenossen, die nicht Logiker von Fach sind, oftmals eine amüsante Denkübung ist. Welches ist nun in dem oben angeführten Falle der Grund des merkwürdigen Schlusses? Für den Fall, daß ihn der immer sehr geschätzte Leser nicht schon längst allein herausgefunden haben sollte, sei er ihm neidlos mitgeteilt. Er besteht darin, daß die negative Bestimmung »kein Draht« – wie alle Bestimmungen dieser Art überhaupt – keine bestimmte Schlußfolgerung zuläßt, also auch nicht auf das Vorhandensein von Telegraphie mit oder ohne Draht. Die Negation ist immer vieldeutig, läßt sogar unendlich viele Deutungen und daher mit logischer Sicherheit keine einzige einwandfreie Deutung zu. Ein Butterbrot ist ein eindeutig bestimmter Begriff, an dem nicht zu drehen und zu deuteln ist; ein Brot ohne Butter aber kann ein sehr verschiedenartiges Ding sein: es kann mit Honig, mit Marmelade, mit Schmalz oder sonst einem Aufstrich versehen, es kann auch ein »trockenes«, das heißt ungestrichenes, Brot sein. Es wird in allen diesen Fällen immer dem Begriff »ohne Butter« entsprechen, und von allen möglichen Eigenschaften darf es nur die eine, mit Butter bestrichen zu sein, nicht haben. Gourmets und Gourmands seien auf diese gastronomisch bedeutsame Vieldeutigkeit der Negation verwiesen. Ein Gastwirt aber dachte einstmals anders. Auf der Speisekarte seiner Wirtschaft war verzeichnet: Butterbrot mit Schinken 1 Mark, ohne Schinken 60 Pfennige; Butterbrot mit Käse 75 Pfennige, ohne Käse 50 Pfennige. Also zwei verschiedene Preise für Butterbrot »ohne«. Und als der Wackere von einem Gast um Aufklärung ob solcher Zweideutigkeit der Preisberechnung ersucht wurde, da meinte er achselzuckend, daß Schinken doch überall teurer sei als Käse! Aus dieser Tatsache also hatte er privatim den Schluß gezogen, daß auch ein Butterbrot ohne Schinken teurer sein dürfe als ein solches ohne Käse!

Die Negation verwirrt und verwischt die Begriffe und wird dadurch der Feind des logischen Denkens, ist dadurch die Ursache zahlloser Trugschlüsse, Widersprüche und Paradoxien geworden, an denen sich Logiker und Philosophen oftmals Hunderte von Jahren hindurch die Köpfe zerbrochen haben, wird dadurch aber auch zumeist zum Ausgangspunkt des logischen Humors und Witzes, weswegen wir sie auch trotz alledem in der Logik nicht missen möchten. Mit der Negation kann man die merkwürdigsten Dinge beweisen. Das wußten schon die Logiker des Altertums, insbesondere die Sophisten, die gern mit logischen Spitzfindigkeiten zu brillieren und ihre Zeitgenossen zu bluffen suchten und zu diesem Zweck jene Eigenschaft der Negation weidlich auszunutzen verstanden. Von ihnen beispielsweise stammt der sogenannte Hörnerbeweis. Er lautet: Was man nicht verloren hat, hat man; Hörner hat der Mensch nicht verloren, also hat der Mensch Hörner! Wie man zugeben wird, ein sehr bündiges Verfahren, seinen Mitmenschen Hörner aufzusetzen. Über diesen Sophismus ist schon im Altertum gelacht, noch mehr aber gestritten worden, da besonders kluge Leute dahinter mehr als nur einen Witz wittern zu müssen glaubten. Der Hörnerbeweis ist jedenfalls ein schönes Beispiel für die Begriffsverwirrung durch die Negation. Denn im Vordersatz jenes Sophismus wird als ein Nichtverlorenes im üblichen Sinne etwas gemeint, das man besitzt und zwar verlieren kann, aber noch nicht verloren hat; im Mittelsatz aber wird damit etwas gemeint, was man niemals hatte und daher auch nicht verlieren kann, das also in diesem Sinne unverlierbar ist. Beide so wesentlich verschiedenen Begriffe, das noch nicht Verlorene und das Unverlierbare, werden unter dieselbe negative Begriffsbestimmung »nicht verloren« zusammengefaßt, und diese begriffliche Verschiebung ermöglicht dann den merkwürdigen Schlußsatz, demzufolge jeder Mensch Hörner hat.

Noch berühmter als der Hörnerbeweis ist der Drei-Schwänze-Beweis. Dieser Beweis ist von den mittelalterlichen Scholastikern ausgeheckt worden, die es ihren sophistischen Kollegen aus dem Altertum an Spitzfindigkeit in der Konstruierung merkwürdiger Paradoxa gern gleichzutun liebten, und lautet in der Form des exakten logischen Schlußverfahrens:

Eine Katze hat einen Schwanz mehr als keine Katze;
Keine Katze hat zwei Schwänze;
––––––––––––––––––––––

Eine Katze hat drei Schwänze!

Man irrt sich, wenn man annimmt, daß die Herren Scholastiker sich damit begnügten, diesen bemerkenswerten Schluß einfach als Witz hinzunehmen. Im Gegenteil, es ist lang und viel dieserhalb gestritten und geschrieben worden – erstens, um zu beweisen, daß der Schluß falsch sei; zweitens – welches der Fehler des Schlußverfahrens war; drittens, ob nicht vielleicht doch der Schluß irgendwie Wahrheit sei –, und wer will, kann auch heute noch seinen Scharfsinn an der Aufhellung jenes Paradoxons erproben.

Die Negation ist vieldeutig, ja sie läßt, wie wir sahen, oftmals sogar unendlich viele Deutungen eines Satzes oder einer Aussage zu. Aber schon die Zweideutigkeit genügt in zahllosen Fällen, um den Sinn eines Satzes in sein Gegenteil zu verwandeln oder doch einer Aussage eine Auslegung zu geben, die dem gemeinten Sinn stracks zuwiderläuft, wodurch eine unerschöpfliche Quelle des logischen Witzes und Humors erschlossen wird.

Als der Lydierkönig Krösus, derselbe, dessen Reichtum noch heute sprichwörtlich ist, sich mit der Absicht trug, den Persern den Krieg zu erklären, sandte er, so berichtet die Geschichte, zuvor einen Boten nach dem berühmten Orakel in Delphi, ließ Geschenke, die eines so reichen Königs würdig waren, überreichen und um einen Spruch der Seherin bitten, ob er auf einen glücklichen Ausgang des geplanten kriegerischen Unternehmens rechnen könne. Der Spruch der Pythia lautete: »Wenn Krösus die Perser mit Krieg überzieht, wird er ein großes Reich zerstören!« Diese Antwort dünkte den Lydierkönig eine überaus günstige Prognose, und die Wirklichen und Geheimen Räte seines Hofes waren derselben Meinung. Also begann er den Krieg mit den Persern und – wurde vernichtend geschlagen, gefangengenommen und entging nur mit knapper Not dem Feuertode, den der siegreiche Perserkönig ihm nach der Sitte jener guten alten Zeit zugedacht hatte. Späterhin ließ Krösus dann die Pythia fragen, wie sie ihren Orakelspruch mit dem wirklichen Verlauf der historischen Ereignisse zusammenzureimen gedächte und ob nicht auch sie selbst der Meinung wäre, daß das königliche Honorar, das er ihr für die erbetene Auskunft ehemals gezahlt hatte, mehr für sie selbst als für ihn eine günstige Kapitalsanlage gewesen sei. Die weissagende Dame aber war keinesfalls um die Antwort verlegen; sie ließ ihm sagen, daß ihr Orakelspruch durchaus in Erfüllung gegangen sei, denn durch den Krieg mit den Persern habe er, wie prophezeit, tatsächlich ein großes Reich zerstört, nämlich – sein eigenes! Da mußte Krösus der Prophetin ja wohl recht geben, aber er mag auch zugleich gedacht haben, daß die Erteilung von Orakelsprüchen, wenn sie von solcher Zweideutigkeit begleitet sei, vielleicht eine Kunst, aber gerade kein Kunststück sei.

Es ist eine eigene Sache um die Zweideutigkeiten, und wer sich auf solche versteht, wird immer recht behalten. Wer möchte bestreiten, daß das Verfahren der delphischen Dame für alle die vielen klugen Frauen von heute, die, sei es aus Passion, sei es aus Gründen des Erwerbs, solchen Neugierigen, die nicht alle werden, aus den Handlinien, den Karten, aus Kaffeesatz, Eidotter oder ähnlichen mystischen Substanzen die Zukunft zu enthüllen pflegen, bis auf den heutigen Tag vorbildlich geworden und das geeignete Mittel geblieben ist, um immer recht zu behalten und diese Kunst gleichzeitig geschäftlich vorteilhaft und erfolgreich zu verwerten! Kommt es so, wie die Prophetin verkündete – und etwas wird bei der Vieldeutigkeit ihrer Auskünfte ja meistens »so kommen« –, so ist ihre prophetische Gabe glänzend bewiesen; kommt es anders, dann hat der Klient eben ihre Antwort falsch aufgefaßt, und da es nur so oder anders kommen kann, so behält die kluge Frau eben immer recht. Der noch unvergessene Komiker Bendix, Jahrzehnte hindurch der »Urkomische« der Berliner, ließ in einer Glanzrolle die von ihm virtuos dargestellte Kartenlegerin Krawutschke sagen: »Manchmal trifft's ein, manchmal ooch nich, ja lieber Jott, denn helf' er sich!« und hat mit dieser humorvollen Kennzeichnung des ebenso zweideutigen wie zweifelhaften Geschäftsgebarens der zahllosen Krawutschkes männlichen und weiblichen Geschlechts die Lacher und die – Logik immer auf seiner Seite gehabt.

Noch von einer anderen tüchtigen Persönlichkeit, die sich die Zweideutigkeit geschickt zunutze zu machen verstand, weiß die Sage der Alten zu berichten. Als die Königstochter Dido, die nachmalige Geliebte des homerischen Helden Äneas, vertrieben und heimatlos an die Küste Afrikas gelangte, bat sie den dort herrschenden König, ihr so viel Land zu überlassen, als sie mit einer Stierhaut zu umspannen vermöchte. Diese bescheidene Bitte wurde ihr gern gewährt. Die listige Dido aber nahm eine möglichst große Stierhaut, zerschnitt sie in zahllose dünne Riemen und verknüpfte diese zu einem riesenlangen Riemenbande, mit dem sie ein ganz gehöriges Stück Land umspannen konnte, groß genug, um darauf die berühmte Stadt Karthago zu gründen. Logisch und juristisch hätte sich gegen diese Auslegung des Begriffes »umspannen« ja allerdings manches einwenden lassen, aber der Gegenpart der listigen Dido war der Meinung, daß man auch an eines afrikanischen Königs Wort nicht drehen und deuteln dürfe, auch nicht mit spitzfindigen Begriffszergliederungen, und so kam es vermöge einer Zweideutigkeit zu dem besten Geschäft, das je mit einer Rindshaut gemacht worden ist.

Aber auch eine lustige und erfolgreiche Waffe zu Angriff und Verteidigung kann die Zweideutigkeit werden, und der Tageskampf der Geister liefert dafür unerschöpfliche Beispiele. Glaubte da in einer bayerischen Provinzstadt der Schriftleiter des Lokalblattes Grund zu herber Kritik an den Verhandlungen und Beschlüssen des städtischen Parlamentes zu haben. Also schrieb er einen bitterbösen Leitartikel gegen die Stadtväter und beendete seine mehr polemischen als diplomatischen Auseinandersetzungen mit den mannhaften Worten: »Die Hälfte unserer Stadtverordneten sind Rindviecher!« Darob gerechte Entrüstung bei den Ortsparlamentariern, und der Herr Stadtverordnetenvorsteher setzte sich hin und schrieb namens der hochansehnlichen Versammlung dem Pressemenschen einen kernigen Brief, in welchem er unter Androhung aller möglichen himmlischen und irdischen Strafen die Zurücknahme des zoologischen Vergleichs verlangte. Dieser kategorischen Aufforderung kam der journalistische Schwerverbrecher denn auch nach, indem er in der nächsten Nummer seines Blattes schrieb: »Die erhobene Behauptung nehme ich zurück und erkläre, daß die Hälfte der Stadtverordneten nicht aus Rindviechern besteht!« Da hatten denn die gekränkten Stadtväter ihren Willen, aber ob sie von dem Widerruf sehr erbaut waren, dürfte dennoch fraglich sein. Der Fall, über den viel gelacht wurde, ist ein ebenso drastisches wie humorvolles Beispiel begrifflicher Zweideutigkeit. Jedes Ding, und mithin auch jede Stadtverordnetenversammlung, hat eben zwei Hälften; dadurch wird der Begriff der »Hälfte« ohne weiteren unterscheidenden Zusatz zweideutig, und die für die eine Hälfte abgegebene Ehrenerklärung des Pressesünders ließ noch vollständig offen, was mit der anderen Hälfte los sei. Ähnlich war es auch in folgendem Falle: Von einem bekannten Karikaturisten, der sich zugleich auch als satirischer Schriftsteller betätigt, pflegen seine guten Freunde zu sagen: Die Maler behaupten, X. könne zwar nicht malen, sei aber ein guter Schriftsteller; die Schriftsteller hingegen erklären, er könne zwar nicht schreiben, sei aber ein guter Maler; jeder von beiden hat aber nur zur Hälfte recht! Also auch hier die spitzfindige Zweideutigkeit des Begriffes der Hälfte, der in gleicher Weise dem Logiker wie dem Freunde des Humors Freude macht, dem Gegenstand dieser Zweideutigkeit allerdings wohl erheblich weniger.

Häufiger noch als die begriffliche Zweideutigkeit ist die des Wortausdruckes, die in allen Sprachen auftritt und um so häufiger und witziger zu sein pflegt, je entwickelter und ausdrucksreicher die Sprache ist. Zahllose Anekdoten beruhen auf der Zweideutigkeit des Wortes. Hier eins der vielen Beispiele dieser Art, die mit Bismarck in Verbindung gebracht werden. Eine Dame, die Gattin eines ausländischen Diplomaten, der gerade nicht als überragende Erscheinung seines Berufes galt, ließ sich mit dem Altreichskanzler in ein Gespräch über die deutsche Sprache ein und äußerte, es sei ein Fehler dieser Sprache, daß sie in vielen Fällen mehrere gleichbedeutende Bezeichnungen für einen und denselben Begriff habe, wie etwa »senden« und »schicken«; einer dieser Ausdrücke sei überflüssig, und solche Überflüssigkeiten erschwerten Gebrauch und Verständnis der Sprache, so erklärte sie. Bismarck war anderer Meinung. »Wer Deutsch kennt«, erwiderte er, »weiß, daß solche Bezeichnungen nicht immer gleichbedeutend sind, sondern im Gegenteil dazu dienen, die Feinheiten im Unterschiede der Begriffe auszudrücken. Das gilt auch für ›senden‹ und ›schicken‹. Beispielsweise ist Ihr Herr Gemahl zwar ein Gesandter, aber kein ›Geschickter‹, meine Gnädigste!« Wenn vielleicht auch nicht wahr, so doch ein hübsches Beispiel sprachlicher Zweideutigkeit im Dienste der hohen Diplomatie, die ja überhaupt von dieser Eigenschaft der Begriffsbildung einen ausgiebigen Gebrauch machen soll. Verbürgt ist folgendes kleines Geschichtchen, ebenfalls aus diplomatischen Kreisen. Eine bei Hofe verkehrende ausländische Dame, die doch wohl noch nicht in alle Feinheiten der deutschen Sprache eingedrungen war, wurde von einem Verehrer als eine selten schöne Frau gepriesen. Hinterher äußerte die Dame, Herr X. habe wirklich eine eigene Art, Komplimente zu machen; eine wirklich schöne Frau sei nicht nur »selten« schön, sondern immer schön! Die Dame war erst zufriedengestellt, als man ihr erklärte, daß das Adverb »selten« nicht nur temporale, sondern auch numerische Bedeutung habe, eine Zweideutigkeit, die bei einem Nichtkenner allerdings zu einem solchen heiteren Mißverständnis führen konnte. Als einstmals ernstere diplomatische Verwicklungen drohten, äußerte ein regierender Herr von einer Verwandten im anderen Lande, der er einen Teil der entstandenen Dissonanzen aufs Konto schreiben zu müssen glaubte: »Gott erhalte meine Schwiegermutter – aber möglichst bald!« In vergröberter und vergröbernder Form sind diese und noch zahllose andere Zweideutigkeiten des Wortausdruckes in die Witzblätter übergegangen und werden auch jetzt immer wieder variiert. Überhaupt ist ja die Zwei- und Vieldeutigkeit so vieler Begriffe und Ausdrücke der unerschöpfliche Nährboden des Wortwitzes wohl in allen Sprachen. Die witzige Feinheit entfaltet die Zweideutigkeit allerdings immer nur dort, wo sie ursprünglicherweise aus Rede und Gegenrede fließt, gleichsam erlebt wird. Kommt sie dann als Wortwitz in Umlauf oder in die Witzblätter, so wird sie zumeist vergröbert und entstellt, entbehrt der Unmittelbarkeit und verliert dadurch an Feinheit und Wirkung.

Die Zweideutigkeit der Dinge, der Begriffe und Worte und schließlich der – Menschen selbst ist ein eigenes Kapitel. Sie hat schon manches Übel angerichtet, hat aber auch schon manches zur Erheiterung der Welt beigetragen, und das wird so lange gehen, als noch nicht die Forderung erfüllt ist: Dein Ja sei Ja und dein Nein sei Nein!

5. Trugschlüsse

Fallstricke des Denkens – Der Krokodilsschluß – Der Lügner – Ein verzweifelter Figaro – Logik und Mengenlehre – Die Menge aller Dinge – Von sinnfreien Aussagen – Autonom und Heteronom – Begriffsverwechselungen

Das menschliche Denken geht oft seltsame Wege. Es strebt nach Wahrheit und Erkenntnis und bedient sich zur Erreichung dieses Zieles der Logik, die als Methodenlehre des Denkens bezeichnet wird. Aber gerade die Logik ist es, die das Denken oftmals auf Irrwege führt, es in Fallgruben und Fallstricke stürzt, aus denen es anscheinend dann kein Entrinnen mehr gibt und die alles Streben nach Wahrheit und Erkenntnis zunichte zu machen scheinen.

Diese Fallgruben und Fallstricke des Denkens sind die Trugschlüsse, die Widersprüche und Paradoxien, zu denen die logische Betrachtung der Dinge und Probleme oftmals gelangt, und die wie ein schleppendes Übel das menschliche Denken durch die Jahrhunderte und Jahrtausende seiner Geschichte begleiten und nicht abzuschütteln sind. In dem berühmten Widerspruch von Achilles und der Schildkröte, der seit bald zweieinhalb Jahrtausenden herumspukt und selbst heute noch viele Logiker beschäftigt, haben wir bereits einen jener Fallstricke des Denkens kennengelernt; eine große Zahl anderer solcher und ähnlicher Denkverwirrungen läßt sich ihm zur Seite stellen, die gleich jenem die nachdenkliche Menschheit schon seit Jahrhunderten und Jahrtausenden teilweise peinigen, teilweise belustigen.

In dem Denken der Gegenwart sind diese Widersprüche, nachdem sie eine Zeitlang bereits erledigt und begraben schienen, zu neuem Leben erwacht. Teils hat man die alten Widersprüche und Paradoxien wieder ausgegraben, hat neue Rätselhaftigkeiten in ihnen entdeckt und bemüht sich, den logischen Sezierungsprozeß, mit dem man ihnen auf den Grund zu kommen hofft, fortzusetzen; teils hat man in Philosophie, Logik und Mathematik neue solcher Widersprüche und Paradoxien ausgeheckt und dadurch Stoff zu neuer logischer Sezierungsarbeit gefunden. Man schwelgt heute geradezu in Paradoxien, und es gibt heute bereits Spezialisten für solche, die bemüht sind, immer neue solcher gedanklicher Fehl- und Trugschlüsse ausfindig zu machen, und in diesem Bemühen eine anerkennenswerte Virtuosität erlangt haben.

Nächst dem »Achilleus« ist es besonders der sogenannte Krokodilsschluß gewesen, der, ebenfalls schon aus dem Altertum stammend, den Logikern bis heute zu schaffen gemacht hat. Er besteht in dem folgenden merkwürdigen Problem: Ein Krokodil hatte ein Kind geraubt und die Mutter des Kindes bat flehentlich um dessen Rückgabe. Das Krokodil, anscheinend ein besonders boshaftes und spitzfindiges Exemplar seiner Gattung, das wohl bei den alten (oder auch den modernen) Sophisten in die Schule gegangen war, sagte: »Ich bin bereit, dir das Kind zurückzugeben, wenn du richtig errätst, was ich mit dem Kinde tun werde!« Die Mutter überlegte und sagte dann: »Du wirst mir mein Kind nicht zurückgeben.« Triumphierend erwiderte das Krokodil: »Du hast dein Kind verspielt. Denn wenn du richtig geraten hast, so erhältst du das Kind auf Grund deiner eigenen Aussage nicht zurück; hast du aber falsch geraten, so bekommt du es nicht zurück auf Grund unseres Vertrages.« Aber die Mutter ließ sich nicht beirren und antwortete: »Du mußt mir das Kind auf alle Fälle zurückgeben, und zwar, wenn ich richtig geraten habe, auf Grund unseres Vertrages, wenn ich aber falsch geraten habe, auf Grund deiner eigenen Entschließung!« Keinesfalls durfte die Mutter die Antwort geben: »Du wirst mir mein Kind zurückgeben!«, denn dann hätte das Krokodil behaupten können, daß die Mutter unrichtig geraten und daher ihr Kind verloren habe, und dagegen hätte die Mutter dann kein Argument mehr gehabt. Da gab es nun einen langen Streit über die Frage, wer von den beiden recht hatte, einen Streit, der nicht nur die Hauptbeteiligten, Mutter, Kind und Krokodil, sondern viele Jahrhunderte hindurch auch Sophisten, Juristen und Logiker beschäftigte, und der neuerdings sogar auch den Mathematikern Kopfschmerzen macht, die in dem Krokodilsschluß einen Fall mengentheoretischer Paradoxie sehen.

Und warum kam das so? Weil der zwischen der Mutter und dem Krokodil geschlossene Vertrag nicht eindeutig abgefaßt war und daher überhaupt keine bestimmte logische und rechtliche Folgerung zuließ. Ja, der erwähnte Vertrag hat in dieser Formulierung überhaupt keinen bestimmten Sinn, so daß jeder der Beteiligten aus ihm den Sinn herauslesen kann, der ihm zweckmäßig scheint. Das Dilemma, in das das boshafte Krokodil die Mutter und die gesamte logisch interessierte Menschheit gebracht hat, hätte vermieden werden können, wenn die Mutter dem Krokodil auf seinen Vorschlag geantwortet hätte: »Einverstanden, verehrtes Krokodil, aber wir wollen den Vertrag schriftlich machen. Schreibe hier auf diesen Zettel nieder, was du mit dem Kinde zu tun gedenkst, und dann werde ich raten, was deine Absicht ist.« Bei dieser Form des Vertrages wäre die fatale Vieldeutigkeit oder, was auf dasselbe hinauskommt, die Sinnlosigkeit des Vertrages vermieden worden, denn dann hätte es sich nur noch darum gehandelt, ob die Mutter richtig oder unrichtig geraten hätte, was das Krokodil niedergeschrieben hatte. Hätte sie den formalen Inhalt der Niederschrift erraten, so hätte ihr das Krokodil vertragsgemäß das Kind zurückgeben müssen, und zwar auch dann, wenn der Wortlaut der Niederschrift die entgegengesetzte Absicht des Krokodils ausgedrückt hätte, denn es hätte sich dann nur noch darum gehandelt, den formalen, nicht den materiellen Inhalt der Niederschrift zu erraten. Allerdings hätte die Mutter bei diesem Verfahren auch das Unrichtige erraten können, in welchem Falle sie dann das Kind vertragsgemäß verloren hätte. Auf alle Fälle aber wäre dann die Vieldeutigkeit oder Sinnlosigkeit des Vertrages vermieden worden, und den Logikern dreier Jahrtausende wäre das Kopfzerbrechen darüber erspart geblieben, wer in besagtem Falle recht hatte.

Ein anderes Beispiel, wie das logische Denken in die Sackgasse geraten kann, ist das unter dem Namen »Der Lügner« bekannte Paradoxon, das ebenfalls schon im Altertum von Leuten, die mit anderweitigen Sorgen nicht übermäßig belastet gewesen zu sein scheinen, ausgeheckt worden ist. Der Kreter Epimenides äußerte von seinen Landsleuten einmal: Alle Kreter sind Lügner! Aus dieser Behauptung kann man folgern: Wenn alle Kreter Lügner sind, so ist auch Epimenides, der selbst ein Kreter ist, ein Lügner und die von ihm aufgestellte Behauptung ebenfalls eine Lüge. Dann folgt daraus, daß alle Kreter die Wahrheit sagen und auch die Behauptung des Epimenides Wahrheit ist. Wenn das aber der Fall ist, so sind dieser Behauptung zufolge alle Kreter Lügner; wenn aber alle Kreter Lügner sind, so ist auch die Behauptung des Epimenides Lüge und alle Kreter sprechen die Wahrheit; wenn aber … und so weiter in infinitum! Der angeführte Syllogismus stempelt abwechselnd die Kreter zu Lügnern und zu Wahrheitsaposteln, enthält also einen eklatanten Widerspruch.

Aber auch dieser Widerspruch läßt sich lösen, und sogar leichter und, wie anzunehmen ist, auch überzeugender als der Krokodilsschluß. Der Grund des Widerspruches ist hier darin zu suchen, daß die Behauptung »Alle Kreter sind Lügner« im übertreibenden Sinne ausgelegt und gefolgert wird, daß ein Mensch, der als Lügner gilt, immer lügen müsse und überhaupt niemals die Wahrheit sprechen könne. Das aber ist Unsinn. Auch der lügenhafte Mensch wird sehr oft die Wahrheit sprechen, die meisten seiner Aussagen werden sogar trotz seiner Verlogenheit wahr sein müssen. Wenn also der gute Epimenides, der nota bene sich selbst wohl stillschweigend von dem Verdammungsurteil über seine Landsleute ausgeschlossen wissen wollte, ebenfalls ein Lügner wäre, so könnte die von ihm aufgestellte Behauptung nur den Sinn haben: Für jeden Kreter gilt, daß vieles von dem, was er sagt, Lüge ist! In diesem Sinne aber könnte jene Behauptung eindeutig wahr sein, ohne die Möglichkeit zu bieten, aus ihr das Gegenteil herauszulesen. Würde man aber unter dem Begriff »Lügner« einen Menschen verstehen, der absolut und bei jedem Worte lügt, so wäre der Widerspruch noch viel einfacher zu lösen. Denn wenn ich von einem Menschen weiß, daß absolut jede seiner Behauptungen eine Lüge ist, so wäre das gleichbedeutend, als wenn er absolut die Wahrheit spräche. Ich weiß dann, wenn er behauptet, es sei Regenwetter, daß der Himmel regenlos strahlt, wenn er versichert, reich zu sein, daß er ein armer Schlucker ist usw. Der absolute Lügner wäre gleichbedeutend mit dem absolut die Wahrheit sagenden Menschen; er redet nur in einer anderen Sprache als andere Menschen, indem er mit seinen Worten und Behauptungen gerade die gegenteilige Bedeutung wie diese verknüpft. In diesem Sinne ist also der absolute Lügner eine logische Unmöglichkeit. Es liegt also bei dem angeblichen Trugschluß eine Verwischung des Begriffes »Lügner« vor, indem dieser Begriff einmal im gewöhnlichen Sinne, nämlich im Sinne eines Menschen, der gelegentlich lügt, zum anderen Male im übertreibenden Sinne, also als eines Menschen, der bei jeder einzelnen Behauptung lügt, ausgelegt wird, und nur durch diese begriffliche Verwischung, das heißt letzten Endes dadurch, daß zwei verschiedene Dinge mit demselben Wort bezeichnet werden, kommt der Trugschluß zustande.

Noch ein Widerspruch dieser Art sei erwähnt, der neueren Datums ist. Einem Barbier wird gegen eine große Belohnung die Aufgabe gestellt, alle Männer seines Ortes zu rasieren, die sich nicht selbst rasieren. Wie fängt er es an, um die ausgesetzte Belohnung zu bekommen, und wie hat er sich vor allem hinsichtlich seiner Person selbst zu verhalten? Wenn er sich selbst ebenfalls rasiert, verstößt er gegen die Bedingung des Vertrages, denn er soll ja nur die Männer rasieren, die sich nicht selbst rasieren; wenn er sich aber ausläßt, verstößt er ebenfalls gegen den Vertrag, denn er soll nach diesem alle Männer des Ortes rasieren, die sich nicht selbst rasieren, und zu diesen gehört er dann unzweifelhaft selbst. Also wie er es auch anstellt, er verstößt in jedem Falle gegen den Vertrag oder, anders ausgedrückt: wenn er den Vertrag erfüllt, verstößt er gegen den Vertrag. Und weil er diesen Widerspruch nicht zu lösen vermochte, kam er um die ausgesetzte Belohnung und beging unter feierlichen Verwünschungen gegen die Logik Selbstmord.

Unser Figaro hätte nicht so aus dem Häuschen zu geraten brauchen, denn der Widerspruch hätte sich ohne allzu große Schwierigkeiten lösen lassen, wenn er folgende Betrachtung aufgestellt hätte: Von ihm wurde verlangt, die Männer des Ortes zu »rasieren«. Damit, so hätte er mit Fug und Recht folgern dürfen, war er selbst von den zu Rasierenden ausgeschlossen, denn wenn er die Tätigkeit des Rasierens an sich selbst vorgenommen hätte, so wäre das nicht ein »Rasieren«, sondern ein »Sichrasieren« gewesen. »Rasieren« und »sich rasieren« aber sind begrifflich verschiedene Dinge, wie überhaupt immer die transitive und die reflexive Form eines Verbums begrifflich voneinander zu unterscheiden sind. Der begriffliche Unterschied besteht darin, daß bei der reflexiven Tätigkeit Gegenstand der Tätigkeit der Tätige selbst, bei der transitiven Tätigkeit aber ein anderer Mensch Gegenstand derselben ist. Das genügt vollkommen, um einen Unterschied jener beiden Begriffe festzustellen, und weil in jenem merkwürdigen Vertrag das nicht geschah und die transitive und die reflexive Form des Rasierens sozusagen in einen Topf getan worden waren, kam es zu dem anscheinenden Widerspruch. Der Barbier hätte also den Vertrag erfüllt, wenn er lediglich die anderen Männer des Ortes rasiert hätte, und hätte danach gerechtfertigten Anspruch auf seinen Lohn gehabt. Der angebliche Widerspruch trat nur deswegen in Erscheinung, weil die Sprache bei dem Verbum »Rasieren« die reflexive und die transitive Form der Tätigkeit nur sehr schwach auseinanderhält. In anderen Fällen sind diese beiden Formen der Tätigkeit auch sprachlich bereits genügend unterschieden. Hätte der Barbier beispielsweise den Auftrag bekommen, alle Männer seines Ortes zu ermorden, so wäre er jedenfalls ganz von selbst auf den Gedanken gekommen, daß er diese Tätigkeit nicht auch an sich selbst ausüben solle, und hätte das sehr richtig damit begründet, daß das nicht Ermordung, sondern Selbstmord, eine begrifflich und sprachlich deutlich von der von ihm verlangten Tätigkeit unterschiedene Aufgabe gewesen wäre.

Also auch in diesem Falle führte die sprachliche Ungenauigkeit zur Verwischung der obwaltenden Begriffe, und solche Begriffsverwischungen sind mehr oder weniger deutlich immer die Ursache der logischen Widersprüche und Trugschlüsse. Oftmals ist jene Verwischung der Begriffe allerdings eine ganz unmerkliche, wird von dem logisch naiven Menschen nicht erkannt und bereitet ihm dann erhebliche Schwierigkeiten, die Ursache des Fehlschlusses zu ergründen. Deswegen stellt der Logiker mit Recht an die Spitze seiner Wissenschaft den lapidaren Satz » a = a«, und er will mit dieser Sentenz, die dem Laien so unendlich banal und nichtssagend erscheint, sagen, daß bei allen logischen Operationen die zur Verwendung kommenden Begriffe unverrückbar gleich bleiben und ihrer Bedeutung und ihrem Inhalte nach in allen Phasen des Schlußverfahrens festgehalten werden müssen, und daß dieses Bemühen unter ständiger und stärkster Kontrolle zu erfolgen hat. Wird dieser Forderung Genüge geleistet, so führt die sorgfältige logische Betrachtung immer zur Entdeckung des Denkfehlers, der solchen wie den angeführten Widersprüchen zugrunde liegt, und bietet damit dem menschlichen Denken die ausreichende Gewähr für die Richtigkeit und Zuverlässigkeit seiner Methode.

Aber so leichten Kaufes wollen sich manche Logiker die geliebten Widersprüche älteren und neueren Datums doch nicht rauben lassen, und so sind diese, nachdem sie schon hundertmal totgeschlagen worden sind, in den: Denken der Gegenwart zu neuem fröhlichen Leben erwacht. Das ist besonders in der Mengentheorie, einem noch jungen Zweig der heutigen reinen Mathematik, der Fall gewesen. Sie hat alle jene Widersprüche von neuem aufgegriffen und zum Gegenstand hochnotpeinlicher Untersuchung gemacht, hat ferner aber auch, wie bereits erwähnt, auf eigene Faust neue Antinomien und Paradoxien und damit für ihren logischen Sezierungsprozeß neues und ungeahnt reichhaltiges Material ausfindig gemacht. Mit einigen Erzeugnissen dieser Denkungsweise wollen wir uns noch beschäftigen.

Da ist zunächst das bekannteste Paradoxon der Mengenlehre, der sogenannte Russelsche Widerspruch, zu nennen, der nach seinem geistigen Vater, dem englischen Logiker Bertrand Russel, einem Pionier und Säulenheiligen der modernen Disziplinen des reinen Denkens und Mitbegründers der sogenannten mathematischen Logik, benannt worden ist. Dabei handelt es sich um ziemlich abstrakte Dinge, und wir bitten daher den Leser, das Folgende mit geschärfter Aufmerksamkeit zu verfolgen.

Unter einer »Menge« versteht die Mengentheorie die Zusammenfassung irgendwelcher Dinge zu einer Gesamtheit. Die Einzeldinge werden die »Elemente« der Menge genannt. So ist beispielsweise eine Klasse die Menge ihrer Schüler, und die Schüler sind die Elemente dieser Menge; ein Wald ist eine Menge von Bäumen, diese die Elemente der Menge »Wald« usw. Bei den weitaus meisten Mengen verhält sich nun die Sache so, daß die Menge nicht Element von sich selbst ist. Die Klasse ist nicht Element von sich selbst, denn ihre Elemente sind die Schüler, und ebenso ist der Wald nicht Element von sich selbst. Andererseits aber gibt es auch Mengen, die Element von sich selbst sind. Das wäre beispielsweise der Fall bei der Menge aller abstrakten Begriffe, denn diese Menge ist selbst ein abstrakter Begriff und daher Element von sich selbst; ebenso verhält es sich bei der Menge aller derjenigen Dinge, die »Nicht-Menschen« sind, eine Definition, die auf diese Menge selbst zutrifft, weswegen sie Element von sich selbst sein muß. Schließlich gilt das auch von der Menge aller Dinge; da diese Menge selbst ein Ding – wenn auch nur ein Gedankending – ist, so muß sie als Element in sich selbst enthalten sein.

Nunmehr wollen wir eine Menge, sie werde M genannt, bilden, deren Elemente andere Mengen und zwar alle diejenigen Mengen sein sollen, die sich selbst als Element nicht enthalten. Solche Mengen mögen N genannt werden. Wir stellen uns nun die Frage: Ist diese Menge M als Element in sich selbst enthalten, ist sie also ebenfalls eine Menge N, oder ist das nicht der Fall? Die Antwort erfordert Gedankenkonzentration und besagt: Wenn die Menge M als Element nicht selbst in sich enthalten ist, dann ist sie nach der Definition der Mengen N ebenfalls eine Menge N und muß als solche, gemäß der Definition der Menge M, als Element in sich enthalten sein. Das aber ist ein eklatanter Widerspruch, denn es wird in der Antwort auf unsere Frage gesagt, daß, wenn M nicht als Element in sich enthalten ist, es als Element in sich enthalten sein muß! Es wird eine Eigenschaft und zugleich ihr Gegenteil von demselben Dinge ausgesagt.

Dieser Widerspruch ist in der Mengentheorie von erheblicher Bedeutung geworden. Es muß auch betont werden, daß es sich trotz der nahezu grotesk ausgeklügelten Form keinesfalls um eine jener bloßen »Doktorfragen« handelt, mit denen sich die Gelehrten die Köpfe zu zerbrechen pflegen, wenn sie gerade nichts Besseres vorhaben, sondern es handelt sich hierbei um Grundfragen des Denkens überhaupt, um die Frage nämlich, ob, wie es den Anschein hat, auch das nach allen Regeln des exakten Schlußverfahrens handelnde reine Denken zu Widersprüchen führen kann. War doch zum ersten Male in den Jahrtausenden der Geschichte der Mathematik der Fall zu verzeichnen, daß in dieser exaktesten aller Wissenschaften ein Widerspruch auftrat, allerdings Grund genug, den Ursachen dieser seltsamen Erscheinung nachzugehen und alles zu tun, um den unangenehmen Gast schleunigst wieder loszuwerden.

Wir wollen den Russelschen Widerspruch zunächst in derselben Weise wie die anderen bisher angeführten Widersprüche analysieren. Er läßt sich auf diese Weise ebenfalls lösen, ohne die Grundlagen unseres Denkens zu erschüttern. Die Lösung ergibt sich aus folgender Betrachtung: Das Problem geht aus von dem Begriff einer Menge, die sich selbst als Element enthält. Der Widerspruch steckt bereits in diesem Begriff, denn eine Menge, die sich selbst enthält, ist nicht nur eine reale, sondern auch eine logische Unmöglichkeit. Ein Ding kann sich selbst niemals enthalten. Ein Faß kann Wasser, Sand, Äpfel und alles mögliche sonst noch enthalten, aber es kann niemals sich selbst enthalten, denn sonst wäre es Enthaltendes und Enthaltenes, wäre es Gefäß und Inhalt zugleich, was logisch unmöglich ist. Ebensowenig kann eine Menge sich selbst enthalten, und da damit die Prämisse des Widerspruches fällt, so ist dieser eigentlich bereits gelöst. Gegen diese Deduktion kann von dem Mengentheoretiker allerdings noch folgender Einwand erhoben werden: Wenn, wie eben behauptet worden ist, die Menge M sich nicht als Element enthält oder überhaupt nicht enthalten kann, dann ist sie eben eine Menge N und als solche Element der Menge M, also in sich selbst enthalten; also bleibt der Widerspruch bestehen. Darauf aber ist zu erwidern: Wenn eine Menge M sich überhaupt nicht selbst als Element enthalten kann, so folgt daraus nur, daß die verlangte Menge M, die aus allen Mengen N, die sich selbst als Element nicht enthalten, bestehen soll, überhaupt nicht vollständig gebildet werden kann. Denn zu dieser Menge müßte auch M selbst als Element gehören, und da das nicht möglich ist, so ist auch die Bildung der Menge M selbst eine Unmöglichkeit. Diese Menge M ist also ein Unding und ein Unbegriff zugleich, ein Etwas, das man nur in Worte kleiden kann, dem im übrigen aber weder in der Wirklichkeit noch in der Logik eine Existenz zugeschrieben werden kann. Damit fällt aber auch die Alternative, ob die Menge M Element von sich ist oder nicht, in sich zusammen, wird sinnlos. Diese Sinnlosigkeit der Alternative ist die Ursache des vermeintlichen Widerspruches, der sich somit nur als eine fehlerhafte Denkoperation entpuppt.

Die Mengentheorie hat sich mit dieser rein logischen Behandlung des Problems allerdings nicht begnügt, sondern sie hat – und zwar sehr berechtigterweise – die Frage aufgeworfen, wie es überhaupt zu solchen Widersprüchen kommen kann, wenn alle Vorschriften des logischen Denk- und Schlußverfahrens beachtet werden. Sie hat den Grund dafür in einer nicht genügend scharfen und exakten Fassung ihrer Axiome zu finden geglaubt, und die entstandenen Widersprüche waren daher die Ursache, die axiomatischen Grundlagen der Mengentheorie einer Revision zu unterziehen. Das wichtigste Ergebnis dieser Revision war die Folgerung, daß es außer Sätzen, die wahr oder falsch sind, noch solche gibt, die keines von beiden und als sinnlos oder sinnfrei zu bezeichnen sind. Aussagen wie die von einer Menge, die sich selbst enthält, sind sinnfrei. Solche sinnfreien Aussagen dürfen nicht in das logische Verfahren hineinspielen; geschieht es dennoch, so führen sie zu Antinomien und Paradoxien. Die Erkennung und Ausmerzung solcher sinnfreien Aussagen ist die Aufgabe der mathematischen Logik, und durch die vollkommene Lösung dieser Aufgabe wird das Denken von den Widersprüchen befreit.

In dieser Weise ist es tatsächlich gelungen, die aufgetauchten Widersprüche der Mengentheorie – der Russelsche Widerspruch ist nicht der einzige – dingfest zu machen und auszumerzen; nicht aber ist es auf diese Weise gelungen, absolute Gewähr dafür zu erlangen, daß sich in der so axiomatisch revidierten und gereinigten Mengentheorie an Stelle der alten und ausgemerzten nicht neue und andere Widersprüche einstellen werden. Auch die alten Widersprüche, wie den Krokodilsschluß, den »Lügner« usw., hat man dieser mengentheoretischen Betrachtungsweise unterworfen und auch hier den Grund in sinnlosen oder sinnfreien Aussagen gefunden, die zu jenen Denkverwirrungen führten. Jene Bedingung des Krokodils oder jene Aussage des Kreters Epimenides über die Kreter usw. gehören zu den sinnfreien Aussagen, die keine korrekten Denkoperationen zulassen und von solchen daher ausgeschlossen werden müssen, wenn das Denken sich nicht im Zirkel bewegen und zu Trugschlüssen gelangen soll. Der Hinweis auf die sinnfreien Aussagen und die Rolle, die sie im logischen Denken spielen, ist sicher eine bedeutsame Entdeckung, aber er besagt im Grunde genommen nur das, was wir aus der alten Logik schon lange wissen, daß bei nicht genügend scharfer Formulierung oder bei Verwischung der Begriffe eindeutige Schlüsse nicht zu erwarten sind und sich das Denken in Trug- und Zirkelschlüsse verstrickt, aus denen es sich erst durch genügend scharfe Analyse der stattgefundenen Denkprozesse zu befreien vermag. Jedenfalls ist diese Befreiung, ist die Auflösung entstandener Widersprüche und Paradoxien der alten Logik mit ihren Mitteln und Methoden noch immer gelungen.

Von den verschiedenen anderen Widersprüchen, die in der Mengentheorie erörtert werden, sei noch einer erwähnt, der sich durch seine eigenartige Fassung auszeichnet. Es gibt Worte, die die Eigenschaft, die sie ausdrücken, selbst haben. So ist das Wort »klein« selbst klein, das Wort »deutsch« selbst deutsch usw. Solche Worte seien autonom genannt. Die meisten Worte haben diese Eigenschaft nicht; das Wort »lang« ist nicht selbst lang, das Wort »französisch« nicht selbst französisch usw., und diese Worte, die also die von ihnen bezeichnete Eigenschaft nicht selbst haben, seien heteronom genannt. Zu welcher dieser beiden Arten von Worten gehört nun das Wort »heteronom« selbst? Wenn es autonom ist, so muß es die von ihm bezeichnete Eigenschaft selbst haben, also heteronom sein, und wenn es heteronom ist, darf es diese Eigenschaft nicht selbst haben, ist dann also autonom! In diesem wie in jenem Falle kommt also ein Widerspruch zustande, denn es wird von dem Wort eine Eigenschaft und zugleich ihr Gegenteil ausgesagt. Die Lösung dieses unbestreitbar höchst kniffligen Widerspruches Urheber dieses Widerspruches ist Dr. Kurt Grelling. sehe ich darin, daß hierbei Wort und Begriff verwechselt werden. »Heteronom« als Eigenschaft habendes Ding ist Begriff, als Eigenschaft ausdrückendes Ding dagegen Wort, und hält man das beides in den Deduktionen säuberlich auseinander, so kann man den erwähnten Widerspruch überhaupt nicht konstruieren.

Immer sind es Verwechslungen der Begriffe, die, mehr oder weniger versteckt, Grund und Kern der sogenannten logischen Widersprüche bilden, und alle diese lassen sich lösen, wenn man den Dingen, das heißt hier den Begriffen, mit denen dabei operiert wird, auf den Grund geht. Unlösbare logische Widersprüche gibt es nicht und kann es nicht geben, denn die Logik ist in ihrer Gesamtheit nur das begriffliche Abbild der Wirklichkeit und kann ebensowenig wie diese selbst Widersprüche enthalten. Bei alledem ist die Beschäftigung mit solchen Widersprüchen und das Bemühen, solche dort, wo sie auftauchen, zu lösen und aus der Welt zu schaffen, ein durchaus nützliches und notwendiges Unterfangen, denn es schärft das Vermögen für die Unterscheidung der Begriffe und trägt dazu bei, gedankliche Irrgänge und Fallstricke, die aus Begriffsvermischungen und Begriffsverwirrungen des sprachlichen Ausdrucks erzeugt werden, zu erkennen und zu vermeiden und so zur präzisesten Form des Gedankens und seines sprachlichen Ausdruckes zu gelangen.

II.
Probleme der Linie

1. Mit Zirkel und Lineal

Vier uralte Probleme – Die Bedingungen Platos – Altertum und Mittelalter – Ein Universitätsbeschluß – Eine neue Richtung – Drei Unmöglichkeitsbeweise

Zu den ältesten und reizvollsten Problemen, die die Geschichte des menschlichen Denkens kennt, gehört eine Anzahl geometrischer Aufgaben, bei denen es sich darum handelt, bestimmte geometrische Figuren herzustellen oder bestimmte geometrische Konstruktionen auszuführen und für diesen Zweck lediglich Zirkel und Lineal als Hilfsmittel zu verwenden. Vor allem sind das die folgenden Probleme:

Die Quadratur des Kreises;
Das Delische Problem oder das Problem der Verdoppelung des Würfels;
Das Problem der Dreiteilung des Winkels, auch kurz als Problem der Trisektion bezeichnet;
Das Problem der Kreisteilung.

Diese Probleme haben den menschlichen Geist an zweieinhalb Jahrtausende beschäftigt, ehe es gelang, die ganze ungeheure Schwierigkeit und Tiefe dieser doch so einfach anmutenden Aufgaben auszuschöpfen und das zauberhafte Geheimnis, das sich an sie knüpfte, in vollem Umfange zu lösen. Wie ein Stück Romantik des menschlichen Geistes mutet die Geschichte gerade dieser Probleme und ihrer Lösung an, romantisch einerseits wegen des blendenden Reizes, der gerade jenen Problemen zu eigen war und noch heute zu eigen ist, andererseits aber wegen der ungeheuren Summe von Mühe, Arbeit und unerhörtem geistigen Ringen, das an die Lösung dieser Aufgaben gewandt wurde, ehe es gelang, sie restlos zu bewältigen. Und nicht nur die berufenen Fachleute der exakten wissenschaftlichen Forschung, sondern auch weite Kreise gebildeter Laien haben diese Probleme zu allen Zeiten in ihren Bann gezogen. Das liegt in der Natur dieser Aufgaben begründet, die par excellence Probleme des reinen Denkens sind, zugleich aber auch Probleme, die, wenigstens äußerlich angesehen, einer Behandlung oder sogar Lösung auch durch den, der nicht Fachgelehrter im Reiche der Mathematik ist, zugänglich zu sein scheinen. Einen Kreis in ein Quadrat von gleichem Flächeninhalt zu verwandeln, einen Würfel von dem doppelten Rauminhalt eines gegebenen anderen Würfels zu konstruieren, einen Winkel in drei oder einen Kreis in sieben Teile zu teilen, das schienen Aufgaben, die nur der persönlichen Findigkeit, viel weniger wissenschaftlicher Tiefgründigkeit bedurften, um restlos gelöst werden zu können, und an denen sich daher auch der findige Laie versuchen konnte. Das waren und das sind noch die Gründe für das Interesse, das gerade spekulativ veranlagte Köpfe allgemein jenen Problemen von jeher entgegenbrachten und noch heute entgegenbringen, die Gründe für den Eifer, den gerade auch Laien mit mehr oder weniger unzulänglichen Mitteln an die Ergründung und Lösung jener Aufgaben setzten, und die jenen Problemen sogar eine ausgesprochene Popularität ganz ähnlich derjenigen des Perpetuum mobiles verschafften, das sich ja ebenfalls, wenn es auch keinesfalls auf ein so stattliches Alter wie unsere Aufgaben zurückblicken kann, von jeher der Gunst Berufener und noch mehr Unberufener zu erfreuen hatte. So ist die Geschichte jener vier geometrischen Aufgaben eins der reizvollsten Kapitel in der Geschichte menschlichen Denkens und menschlichen Scharfsinnes geworden, eine Geschichte unermüdlicher Versuche, eine Anzahl merkwürdige Rätsel zu lösen, die Jahrhunderte und Jahrtausende hindurch mit dem ganzen Zauber des Geheimnisvollen und Unergründlichen behaftet waren.

Schon die frühesten Mathematiker des Altertums haben sich mit jenen Problemen beschäftigt und die ganze Eigenart und Schwierigkeit derselben in vollem Umfange erfahren und empfunden. Schon die Pythagoreer, die älteste Mathematikerschule der Griechen, aus deren Schoß die Lösung so mancher mathematischen und geometrischen Aufgabe hervorging, bemühten sich ebenso angestrengt wie vergeblich auch um die Lösung dieser Probleme. Die eingehendste Behandlung und Bearbeitung aber erfuhren diese Probleme in dem Kreise des großen Plato (427-347 v. Chr.), der in seiner Philosophenschule auch die Mathematik aufs eifrigste pflegte und über den Eingang seines Lehrgebäudes schreiben ließ, daß niemand dort eintreten solle, der sich nicht zuvor gründliche mathematische Kenntnisse angeeignet habe. Plato und seine Schüler versuchten mit allem Scharfsinn, den wir an den Gelehrten jener Zeit, vor allem den damaligen Geometern, kennen und bewundern, die Lösung der Probleme zu finden, jedoch mit ebensowenig Erfolg wie ihre Vorgänger, und ebenso wie diese überrascht und ratlos durch die Schwierigkeit dieser Aufgaben, die allen und selbst den raffiniertesten Konstruktionsmethoden, allen den zahllosen Kunstgriffen, die extra für sie erfunden wurden, trotzten. Plato war es aber auch, der jenen Problemen zuerst die strenge präzis wissenschaftliche Formulierung gab, indem er die Forderung aufstellte, daß die verlangten Konstruktionen lediglich vermittels Zirkels und Lineals, unter Ausschluß aller anderen Hilfsmittel, ausgeführt werden dürften. Diese Bedingung, die natürlich nicht nur für unsere vier Probleme, sondern für alle geometrischen Aufgaben und Konstruktionen überhaupt festgelegt wurde, ist seitdem für die Mathematiker bindendes Gesetz geworden. Erst durch diese Bedingung ist die Geometrie auf eine exakt wissenschaftliche Grundlage gestellt worden, erst hierdurch aber sind auch die geometrischen Konstruktionsaufgaben, vor allem unsere vier genannten Probleme, zu der harten Nuß geworden, an der sich so viele die Zähne ausgebissen haben.

Es gelang Plato und seinen Schülern nicht, jene vier Probleme unter den gestellten einschränkenden Bedingungen zu lösen, und die Vergeblichkeit aller ihrer vielfachen Anstrengungen ließ die ganze Schwierigkeit und Tiefe jener Aufgaben in ihnen aufdämmern. Von der Lösbarkeit der Probleme an und für sich aber war man überzeugt und hatte angesichts der großen Erfolge der platonischen Methoden bei der Lösung vieler anderer Konstruktionsaufgaben zu dieser Annahme auch allen Grund. Warum also sollte, was einst dem Pythagoras in so eleganter Weise gelungen und auch bei so vielen anderen geometrischen Problemen erreicht worden war, nämlich Ausführung der verlangten Konstruktion nur mit Zirkel und Lineal, nicht auch bei dem Delischen und dem Winkelteilungsproblem und ebenso bei der Quadratur des Kreises möglich sein? Auf eine oder einige Hekatomben fetter Ochsen sollte es nach dem Vorbild des Pythagoreers gewiß nicht ankommen.

Und von den Mathematikern des Altertums gingen die Probleme auf die Gelehrten des Mittelalters über, nach wie vor behaftet mit dem ganzen aufreizenden Geheimnis ihrer Schwierigkeit und Rätselhaftigkeit. Die merkwürdigsten und kompliziertesten rechnerischen und geometrischen Methoden wurden ersonnen und eine ungeheure Summe von Scharfsinn und Geistesarbeit im Laufe der Jahrhunderte daran gewandt, um die Konstruktionen im Sinne Platos zu verwirklichen. Unzählige Male auch glaubten scharfsinnige Köpfe die Lösung des einen oder anderen der so heißumstrittenen Probleme gefunden zu haben, unzählige vermeintliche Lösungen dieser Art wurden im Laufe der Zeit den wissenschaftlichen Instanzen zur Prüfung unterbreitet, zumeist immer mit großem Triumphgeschrei der glücklichen Entdecker, die schon den Kranz unvergänglichen Lorbeers auf ihren Häuptern sahen; ebensooft aber machte die genauere Untersuchung alle daran geknüpften Hoffnungen und Erwartungen wieder zunichte, und viele hochberühmte Gelehrte blamierten sich nach dieser Hinsicht nicht weniger als wagemutige Laien. Am meisten hatten unter der Popularität jener Probleme die wissenschaftlichen Institute, besonders die Universitäten, zu leiden, die ständig mit Abhandlungen von Gelehrten und Ungelehrten über die angeblich vollkommene Lösung dieser Aufgaben überschüttet wurden. Daher beschloß endlich die Pariser Akademie der Wissenschaften im Jahre 1775, fernerhin Abhandlungen, die sich mit diesen Aufgaben befaßten, überhaupt nicht mehr zur Prüfung anzunehmen, um ihren Mitgliedern ein für allemal die sehr mühevolle und zeitraubende und doch immer vergebliche Arbeit der Prüfung solcher Elaborate zu ersparen, und dem Beispiel dieses berühmtesten und maßgebendsten wissenschaftlichen Institutes jener Zeit folgten auch die meisten anderen Universitäten.

Das aber bedeutete zugleich, daß die Wissenschaft vor dem großen Geheimnis, das sich an die Lösung jener Probleme knüpfte, endgültig kapituliert hatte und keine Hoffnung mehr hegte, die Konstruktion der verlangten Figuren im Sinne der Bedingungen Platos verwirklichen zu können. Mit dieser Kapitulation aber war die mathematische Forschung zugleich zu einer veränderten Stellungnahme zu jenen Problemen gedrängt und vor die Frage gestellt: Welches sind, wenn die Konstruktion jener Figuren im platonischen Sinne unmöglich ist, wie aus den Jahrtausende währenden vergeblichen Versuchen mit Sicherheit geschlossen werden muß, die Gründe dieser Unmöglichkeit? und ferner: Kann vielleicht, da sich die verlangten Konstruktionen als unmöglich erwiesen haben, der Beweis dieser Unmöglichkeit mit wissenschaftlicher Exaktheit erbracht werden? Mit dieser Fragestellung war zugleich auch eine neue Richtung der wissenschaftlichen Forschung zur Aufhellung jener geheimnisvollen Konstruktionen gewiesen. Statt die Versuche zur Konstruktion der verlangten Figuren fortzusetzen, richtete sich nunmehr das Bestreben darauf, den Beweis für die Unmöglichkeit der positiven Lösung dieser Aufgaben zu finden und die hartnäckigen Probleme auf diese Weise zum Abschluß zu bringen. Auch ein solcher Unmöglichkeitsbeweis mußte, wenn er mit voller wissenschaftlicher Exaktheit gelang, eine Lösung bedeuten, wenn auch eine Lösung anderer Art, als man bis dahin die Jahrtausende hindurch angenommen hatte. Seit der Mitte des 18. Jahrhunderts etwa bewegte sich die wissenschaftliche mathematische Forschung in der angedeuteten Richtung, und hier sollte ihr, wenn freilich auch erst nach langem und schwerem Bemühen, schließlich ein voller Erfolg beschieden sein. Kurz vor dem Ende des 18. Jahrhunderts hatte der Student Karl Friedrich Gauß den ganzen Problemkomplex, der sich an die Kreisteilung knüpft, restlos zum Abschluß gebracht und damit ein Rätsel von Jahrtausenden gelöst, und bald nach Beginn des vorigen Jahrhunderts erbrachte derselbe Gauß, der Fürst der Mathematiker, wie ihn die mathematische Mit- und Nachwelt neidlos genannt hat, den Unmöglichkeitsbeweis für das Delische Problem und ebenso für das Problem der Dreiteilung des Winkels. Einige Jahrzehnte dauerte es dann freilich immer noch, ehe es gelang, auf ähnliche Weise auch die härteste Nuß, die es für die Mathematiker jemals zu knacken gab, die Quadratur des Kreises, zu erledigen und auch für dieses am meisten umstrittene Problem den exakten Unmöglichkeitsbeweis zu finden, was im Jahre 1882 dem deutschen Mathematiker Lindemann gelang.

Damit war eine Geistesarbeit von Jahrtausenden zum Abschluß gebracht und der Kampf um die Lösung jener Probleme beendet. Die Probleme sind als gelöst zu betrachten, aber diese Lösung ist negativer Art und besteht in dem Nachweis, daß die verlangten Konstruktionen mit Zirkel und Lineal allein überhaupt nicht ausgeführt werden können. Für die Wissenschaft waren jene Probleme damit erledigt, nicht aber für die Welt der Laien. Diese gaben sich mit einem solchen Ausgang der Sache nicht zufrieden und suchen daher auch heute noch mit heißem Bemühen nach der Lösung jener Aufgaben, sei es, weil sie nicht wissen, zu welcher Auffassung die Wissenschaft inzwischen von diesen Dingen gekommen ist, sei es, weil sie diese Auffassung einfach nicht anerkennen und auf eigene Faust das Verdikt der Wissenschaft umstoßen zu können glauben. Und tatsächlich bieten die hier genannten geometrischen Probleme, wenn sie auch wissenschaftlich als gelöst und erledigt zu betrachten sind, doch dem denkenden Laien auch heute noch so viel des Reizvollen und Interessanten, auch noch immer so viel des Geheimnisvollen, daß man es versteht, wenn von dieser Seite an der Geschichte dieser Probleme noch immer weitergearbeitet wird. Die Lösungsversuche von dieser Seite lassen oft einen großen Scharfsinn und eine gewisse Originalität des Denkens erkennen und sind, wenn sie freilich auch ewig zur Ergebnislosigkeit verurteilt sind, nichtsdestoweniger als ein Geistessport eigener Art aufzufassen, der jedenfalls viel mehr Scharfsinn erfordert als die manchmal höchst banalen Arten des modernen »Denksports«.

Nachdem wir den allgemeinen Charakter jener geometrischen Probleme erörtert haben, wollen wir diese auch noch einzeln betrachten, da erst dadurch die ganze Eigenart dieser Aufgaben erschlossen werden kann.

2. Die Quadratur des Kreises

Die Aufgabe – Quadratur und Rektifikation – Punkt und Linie – Die Monde des Hippokrates – Der Sinn der Platonischen Bedingung – Mittelalterliches – Technische Lösungen – Entdeckerfreuden und –leiden – Die Aufhellung des Geheimnisses – Die Zahl π – Quadratoren von heute

Das älteste und eigenartigste jener geometrischen Probleme, die sich an Zirkel und Lineal knüpfen, ist die Quadratur des Kreises. Es ist die berühmteste und, wenn man so sagen darf, zugleich auch die populärste jener geometrischen Aufgaben, und zwar deswegen, weil an der Lösung dieser Aufgabe die Jahrhunderte hindurch nicht nur die Mathematiker von Fach, sondern in ganz besonderem Maße auch die Laien ihren Scharfsinn erprobt haben. Diese sind es, die auch heute noch gerade an dieses Problem Zeit, Arbeit und Scharfsinn verwenden und dadurch die Aktualität dieser merkwürdigen geometrischen Aufgabe noch immer aufrechterhalten, während diese heute für die Wissenschaft selbst nur noch historische Bedeutung hat.

Rein äußerlich betrachtet, handelt es sich bei der Quadratur des Kreises um die anscheinend sehr einfache Aufgabe, zu einem gegebenen Kreise ein Quadrat zu zeichnen – oder vielmehr zu »konstruieren«, wie sich der Mathematiker ausdrückt –, das denselben Flächeninhalt wie der Kreis hat, wobei zur Konstruktion lediglich Zirkel und Lineal verwandt werden sollen. Aufgaben dieser Art, die man allgemein als »Verwandlungsaufgaben« bezeichnet, sind, sofern es sich nur um geradlinige Figuren handelt, sehr leicht zu lösen. So ist es beispielsweise spielend leicht, irgendein beliebiges Dreieck, Rechteck oder Vieleck in ein Quadrat zu verwandeln oder auch umgekehrt aus einem Quadrat oder Rechteck ein flächengleiches Dreieck zu machen, und im letztgenannten Falle sind sogar unendlich viele solcher Dreiecke möglich. Auch demjenigen, der nur über ganz elementare Kenntnisse in der Geometrie verfügt, sind solche Aufgaben und Konstruktionen geläufig, und daher ist es auch heute noch vielen unbegreiflich, daß das, was bei solchen wie den erwähnten Figuren so leicht und in so einfacher Weise ausgeführt werden kann, bei dem Kreise, diesem schönsten und regelmäßigsten unter allen geometrischen Gebilden, auf unüberwindliche Schwierigkeiten stoßen und daß diese Aufgabe sogar unlösbar sein soll.

Bemerkt sei noch, daß man unter Rektifikation des Kreises die Aufgabe versteht, die Umfangslinie oder Peripherie des Kreises in eine gerade Linie von gleicher Länge zu verwandeln, selbstverständlich ebenfalls nur vermittels Zirkel und Lineal. Beide Probleme stehen in engstem Zusammenhange, sind sogar im Grunde wesensgleich insofern, als mit der Lösung des einen zugleich auch die des anderen Problems gegeben wäre und die Unmöglichkeit der Lösung beider Probleme in derselben Wurzel zu suchen ist. Wir betrachten das Problem im folgenden lediglich von der Seite der Quadratur des Kreises aus.

Schon die Mathematiker des griechischen Altertums, bei denen die Geometrie zuerst ihre exakte Begründung erlangte, kannten das Problem und seine Tücken. Schon Pythagoras, dem der erste Beweis des nach ihm benannten Fundamentalsatzes gelang (um 500 v. Chr.), versuchte sich an der Lösung der Aufgabe, und der Geometer Hippokrates, der ein halbes Jahrhundert später in Athen lehrte, glaubte sogar die Lösung bereits gefunden zu haben, was sich dann aber, wie in so vielen derartigen Fällen, als Irrtum herausstellte. Die strenge präzis wissenschaftliche Formulierung und damit seine ganze Eigenart erhielt das Problem aber erst in der Philosophen- und Mathematikerschule Platos, der, wie für alle geometrischen Aufgaben, so auch für die Quadratur des Kreises die Bedingung aufstellte, daß diese nur mit Zirkel und Lineal ausgeführt werden dürfe. Erst durch diese Bedingung hat das Problem seine Schwierigkeit und seinen rätselhaften Inhalt erlangt. Wenn also der Mathematiker heute die Quadratur des Kreises als unlösbares Problem bezeichnet, so gilt das immer nur für die exakt mathematische Ausführung der verlangten Konstruktion, das heißt unter strikter Einhaltung der Platonischen Bedingung. Unter Zuhilfenahme noch anderer Hilfsmittel und ebenso für die annäherungsweise Ausführung, sogar für eine solche von jeder verlangten Genauigkeit, hingegen gibt es zahlreiche Methoden, und unter diesem Gesichtspunkt betrachtet ist die Quadratur des Kreises niemals ein Problem gewesen. Entsprechendes gilt auch von den erwähnten anderen geometrischen Aufgaben.

Machen wir uns zunächst die Eigenart unseres Problems unter dem Gesichtspunkte der Platonischen Bedingung allgemein klar. Die Konstruktion einer geometrischen Figur unter den genannten Bedingungen geschieht immer, indem man Linien zieht und auf diesen Punkte bestimmt, durch welche wiederum Länge und Richtung anderer Linien und dadurch schließlich die ganze gesuchte Figur bestimmt werden. Wenden wir das Gesagte auf unser Problem der Quadratur des Kreises an. In unserer Abbildung 1 haben wir einen Kreis dargestellt, dem ein Quadrat ABCD umgezeichnet und ein anderes Quadrat abcd eingezeichnet ist. Das umgeschriebene Quadrat hat, wie der Augenschein lehrt, einen größeren, das eingeschriebene Quadrat einen kleineren Flächeninhalt als der Kreis. Welches wäre nun das Quadrat, das denselben Flächeninhalt wie der Kreis hat? Es müßte seiner Größe nach augenscheinlich zwischen dem umgeschriebenen und dem eingeschriebenen Quadrat liegen, und seine vier Seiten müßten zwischen denen jener anderen beiden Quadrate verlaufen, etwa in der Weise wie die gestrichelten Linien in unserer Figur. Die vier Seitenlinien des gesuchten flächengleichen Quadrates müßten dann, wie aus der Zeichnung ohne weiteres hervorgeht, die vier Strecken Aa, Bb, Cc und Dd in je einem Punkte schneiden, und diese vier Punkte müßten dann die Eigenschaft haben, daß die durch sie gelegten vier geraden Linien ein dem vorgezeichneten Kreise flächengleiches Quadrat ergeben.

Abb. 1

Aber wie sind diese vier Punkte zu bestimmen, beispielsweise der Schnittpunkt x auf der Strecke Aa, auf der ja unendlich viele Punkte liegen? In der Abbildung 1 liegt der Punkt x etwa in der Mitte der Strecke Aa. Selbstverständlich ist aber keinesfalls gesagt, daß der Mittelpunkt dieser Strecke der gesuchte Punkt x wäre, und er ist das auch nicht. Ein Punkt in der Geometrie ist immer nur der Schnittpunkt zweier Linien, entweder zweier Geraden oder zweier Kreisbogen oder einer Geraden mit einem Kreisbogen. Das heißt also, um einen Punkt von bestimmten Eigenschaften zu finden, müssen sich aus den Voraussetzungen und Bedingungen der Aufgabe heraus zwei Linien bestimmen lassen, deren Schnittpunkt der Punkt mit den verlangten Eigenschaften ist. Für die Bestimmung des Punktes x ist uns aber leider nur eine gerade Linie gegeben, nämlich die Strecke MA, auf deren äußerem Abschnitt Aa der Punkt x liegen muß. Es gelingt nicht, aus den Voraussetzungen der Aufgabe heraus noch eine weitere gerade oder krumme Linie ausfindig zu machen, die durch den Schnittpunkt mit der Strecke Aa einen Punkt von der verlangten Eigenschaft bestimmt, und solange das nicht möglich ist, ist die Konstruktion des Quadrates, das dem vorgezeichneten Kreise flächengleich ist, mit Zirkel und Lineal unmöglich.

Diese Andeutungen mögen genügen, um den Charakter und die Eigenschaften geometrischer Probleme und Konstruktionen im allgemeinen und unseres hier behandelten Problems im besonderen anschaulich zu machen. Nur eins sei noch erwähnt, das spezielle Bedeutung für das Problem der Quadratur des Kreises hat: Man könnte die Frage aufwerfen, ob es zu einem gegebenen Kreise denn überhaupt ein Quadrat von genau, das heißt im mathematisch-exakten Sinne genau demselben Flächeninhalt gibt. Vielleicht gibt es ein solches überhaupt nicht, und vielleicht ist nur das der Grund der Unlösbarkeit der Aufgabe! Dem ist aber keinesfalls so, und die gestellte Frage ist unbedingt zu bejahen. Zwischen den beiden Quadraten ABCD und abcd in unserer Figur 1 gibt es eine unendliche Reihe von Quadraten, deren Flächeninhalt in stetiger, lückenloser Annäherung von dem Inhalt des kleineren zu dem des größeren aufsteigt, eins der dazwischenliegenden unendlich vielen Quadrate muß also auch von dem Flächeninhalte des gegebenen Kreises sein, dessen Flächeninhalt ja ebenfalls zwischen den Inhalten der bezeichneten beiden Quadrate liegt, denn sonst hätte jener Verlauf eine Lücke aufzuweisen. Das ist eine Folgerung, die durch die Stetigkeitstheorie der modernen Mathematik mit aller Sicherheit bestätigt wird. Also das gesuchte Quadrat, das dem gegebenen Kreise flächengleich sein soll, ist seiner Möglichkeit nach wirklich vorhanden, und die Aufgabe besteht nur darin, es unter den unendlich vielen Quadraten, zwischen denen es liegt, ausfindig zu machen und konstruktiv mit Zirkel und Lineal festzustellen.

Es gelang Plato und seinen Schülern nicht, das Problem unter der gestellten einschränkenden Bedingung zu lösen, und die Vergeblichkeit ihrer vielfachen und mit größtem Aufwand an Scharfsinn ausgeführten Versuche ließ die ganze Schwierigkeit und Tiefe des Problems in ihnen aufdämmern. Von der Lösbarkeit des Problems an und für sich war man überzeugt, und das um so mehr, als bereits damals bekannt war, daß sich in einem ganz bestimmten Falle der Flächeninhalt krummliniger – das heißt durch Kreisbogen begrenzter – Figuren auf den Flächeninhalt einer geradlinig begrenzten Figur zurückführen läßt. Diese Entdeckung rührt von dem bereits erwähnten griechischen Geometer Hippokrates her, der etwa ein Jahrhundert vor Plato in Athen wirkte, und die Figuren, um die es sich hierbei handelt, sind die nach ihrem Entdecker so benannten »Monde des Hippokrates«. Unsere Abbildung 2 veranschaulicht diesen Fall. Hier ist D ein rechtwinkliges Dreieck, über dessen Grundlinie ebenso wie über die beiden Seitenlinien der Halbkreis gezogen ist. Nach dem Verallgemeinerten pythagoreischen Lehrsatz ist der Flächeninhalt des Halbkreises A über der Grundlinie gleich der Summe der beiden Halbkreise B und C über den Seitenlinien, also A = C + B. Lege ich nun den Halbkreis A so, wie es Figur 3 zeigt, über die andere Seite der Grundlinie, so daß er durch die der Grundlinie gegenüberliegende Spitze des Dreieckes gehen muß, so überdeckt der Halbkreis A die beiden Halbkreise B und C zum Teil, so daß der Halbkreis C in die halbmondförmige Figur c und das Segment k, der Halbkreis B ebenso in den Halbmond b und das Segment p zerfällt. Es läßt sich nun leicht zeigen, daß die Summe der beiden Monde c und b gleich dem Dreieck D ist, denn der Halbkreis A ist nach dem Gesagten gleich der Summe b + p + c + k, das Dreieck D aber gleich dem Halbkreis A vermindert um p und k, also gleich b und c. Damit ist bewiesen, daß das Dreieck D den beiden Halbmonden c und b flächengleich ist. In schulmäßig-korrekter Form kommt das durch die folgenden Gleichungen heraus:
A = B + C D = A – p – k = B + C – p – k = B – p + C – k D = b + c

Das Dreieck D aber läßt sich wie jede geradlinige Figur dann mit Leichtigkeit in ein flächengleiches Quadrat verwandeln, und damit ist dann auch zugleich die Quadratur der beiden Monde, also zweier von Kreisbogen begrenzter Figuren, mit aller nur wünschenswerten mathematischen Exaktheit ausgeführt. Diese Monde des Hippokrates haben bei den Geometern des Altertums eine große Rolle gespielt. Hippokrates selbst glaubte durch seine Entdeckung die Quadratur des Kreises wenigstens im Prinzip möglich gemacht zu haben, und diese Auffassung wurde allgemein vorherrschend. War aber in einem Falle die Quadratur von durch Kreisbogen begrenzten Figuren gelungen, so mußte das, so folgerte man, auch bei dem Kreise selbst möglich sein, und so wurde die Entdeckung des Hippokrates ein Ansporn zu unermüdlicher Tätigkeit zur Lösung jenes Problems.

Abb. 2

Abb. 3

Die an die Entdeckung des Hippokrates geknüpften Folgerungen stellten sich schließlich doch als Irrtum heraus; es zeigte sich, daß die Quadratur jener krummlinigen Figuren nur einen Spezialfall darstellt, der bindende Schlüsse für die allgemeine Aufgabe, alle krummlinigen Figuren überhaupt und insbesondere auch den Kreis in flächengleiche Quadrate zu verwandeln, nicht zuläßt, ein Fall, wie er in ähnlicher Weise in der Geschichte der mathematischen Probleme noch sehr oft auftritt. So blieb das Problem der Quadratur des Kreises trotz Hippokrates und trotz aller Versuche der Mathematiker des gesamten Altertums ungelöst, blieb es, was es war: ein vollkommenes Rätsel, dessen Kernpunkt man mit allem Scharfsinn nicht zu ergründen vermochte.

Vom Altertum übernahm das Mittelalter das Problem der Quadratur des Kreises als rätselhafte Erbschaft, die immer von neuem anspornte, die Lösung des Geheimnisses zu erforschen und wohl alle Mathematiker dieser Epoche mehr oder weniger beschäftigt hat. Warum sollte, was einst dem Hippokrates schon gelungen war, nämlich die Quadratur einer von Kreisbogen begrenzten Figur, nicht auch beim Kreise selbst gelingen? Die Geister, die Hippokrates und Plato beschworen hatten, wurden die Mathematiker des Mittelalters nicht los, und weil die Quadratur des Zirkels sich trotz aller Mühen und Methoden nicht finden lassen wollte und immer von neuem Rätsel aufgab, wurde das Problem in der noch sehr auf das Okkulte gerichteten Denk- und Auffassungsweise jener Zeit geradezu zu einer Art Mysterium von ganz derselben Bedeutung wie der Stein der Weisen, ein Geheimnis, hinter dem man den Grund der Dinge vermutete und dessen Lösung übermenschliche Gaben und Fähigkeiten verleihen sollte.

Weil die Lösung des Problems unter der einschränkenden Bedingung Platos nicht gelingen wollte, verlegten sich einzelne Mathematiker darauf, die Quadratur des Kreises wenigstens praktisch unter Zuhilfenahme anderer Hilfsmittel möglich zu machen. Verschiedene Methoden dieser Art wurden erfunden, darunter etliche höchst bemerkenswerte und scharfsinnige. Eine derselben rührt von Leonardo da Vinci, dem großen italienischen Maler, Bildhauer und Ingenieur, der zugleich auch ein vortrefflicher Mathematiker war, her und bestand in der Verwendung einer Walze. Ist nämlich ein Kreis gegeben, so wird eine Walze, deren Radius gleich dem des Kreises und deren Höhe gleich der Hälfte dieses Radius ist, einmal um ihren Umfang abgerollt, ein Rechteck beschreiben, das dem gegebenen Kreise genau flächengleich ist, wie jeder leicht nachprüfen kann, der über die Kenntnis der elementaren Kreisrechnung verfügt. Das Rechteck kann dann leicht in ein flächengleiches Quadrat verwandelt werden, und damit ist dann zugleich auch die Quadratur des ursprünglichen Kreises mit aller nur wünschenswerten Genauigkeit ausgeführt. Aber die hierbei verwandte Walze ist eben kein Hilfsmittel im Sinne der platonischen Bedingung, und solche Verfahren wie das von Leonardo da Vinci sind auch von den Mathematikern des Mittelalters niemals als wirkliche Lösung des Problems betrachtet worden.

Man hat oft die Frage aufgeworfen, ob die Bedingung, die Plato festlegte, nicht eine unnötige, zum mindesten gänzlich willkürliche, Erschwerung des Problems bedeute, und ob diese Bedingung mit dem mathematischen Charakter des Problems überhaupt etwas zu tun habe. Aber jene Bedingung hat ihren tiefen Sinn. Denn was bedeutet denn die Forderung, eine geometrische Konstruktion lediglich mit Zirkel und Lineal auszuführen? Sie bedeutet, daß die Lösung der gestellten Aufgabe eigentlich ohne alle äußeren Hilfsmittel, lediglich durch das Denken selbst, gefunden werden soll. Durch Überlegung werden die Punkte und Linien bestimmt, die die verlangte Konstruktion darstellen, und Zirkel und Lineal dienen dann lediglich als Hilfsmittel, um das durch das reine Denken Gefundene äußerlich zu fixieren. In dieser rein geistigen Methode sah und erkannte Plato das Wesen der Mathematik, und deswegen stellte er für die Lösung geometrischer Aufgaben jene Bedingung, die den Konstruierenden nötigt, die notwendigen Punkte und Linien erst durch reine Überlegung zu finden, ehe er sie graphisch fixieren darf. Indem die Mathematiker seit Plato jene Bedingung zum unverbrüchlichen Gesetz erhoben, haben sie den Charakter der Mathematik als einer reinen Vernunftwissenschaft festgehalten und durchgeführt. Jetzt ist ersichtlich, warum ein Verfahren wie das von Leonardo da Vinci keine Lösung des Problems im exakt wissenschaftlichen Sinne der Mathematik sein konnte; denn hierbei werden die nötigen Punkte und Linien, die die gesuchte Figur bestimmen, nicht durch das reine Denken ermittelt, sondern empirisch durch ein materielles Hilfsmittel, die Walze, gefunden und graphisch fixiert.

So ging der Kampf um das Problem bei Gelehrten und Laien weiter. Denn auch zahllose Laien, die mehr oder weniger mathematischer Bildung bar waren, beteiligten sich mit Feuereifer an der Ergründung des Geheimnisses. Warum sollte, was kein Verstand der Gelehrten sah, nicht in Einfalt das kindliche Gemüt eines Ungelehrten sehen und möglich machen? So kam es, daß die Quadratur des Kreises nicht nur das berühmteste und schwierigste, sondern zugleich auch eins der populärsten Probleme wurde, das mit Ehrfurcht erwähnt und erörtert wurde, wenn man auch sonst nichts weiter davon verstand, und in viele volkstümliche Schriften und Erzählungen, ja auch in Schwänke und Theaterstücke jener Zeit, spielte das Problem hinein. Sehr oft auch wurden erhebliche Geldpreise für die Lösung ausgesetzt, sowohl von wissenschaftlichen Instituten wie auch von für die Geometrie begeisterten Privatleuten, selbstverständlich für zahllose ein weiterer Anreiz, sich um die Lösung des hartnäckigen Rätsels zu bemühen, ohne daß aber jemals einer einen solchen goldenen Vogel abgeschossen hätte. Umgekehrt setzten aber auch oftmals Leute, die die Lösung des Problems gefunden zu haben glaubten, Belohnungen aus für den, der ihnen einen Fehler ihrer Lösung nachweisen könnte. So schrieb ein Franzose, Mathulon mit Namen, einen Preis von 1000 Talern aus für den Fall, daß jemand in seiner Quadratur des Kreises einen Fehler entdecken würde; ein zünftiger Mathematiker wies ihm einen Fehler nach, und Mathulon mußte bezahlen. Ein ähnliches Mißgeschick hatte auch ein polnischer Genieoffizier, der auf diese Weise um 50 Dukaten erleichtert wurde, und ähnliche Fälle gab es noch mehr. Auch durch den Beschluß der Pariser Akademie vom Jahre 1775, Prüfungen von angeblichen Quadraturen überhaupt nicht mehr vorzunehmen Siehe Seite 61., wurde die Problemfreudigkeit der Nichtzünftigen keineswegs gemindert. Die Volkstümlichkeit des Problems und die Bemühungen um seine Lösung erhielten sich nach wie vor.

Die wissenschaftliche Forschung selbst wurde durch die völlige Erfolglosigkeit aller die Jahrhunderte hindurch fortgesetzten Versuche um die Lösung des Problems, wie bereits dargelegt, schließlich zu der Auffassung geführt, daß eine exakte Lösung der Aufgabe überhaupt nicht zu erzielen sei. Damit begann eine neue Epoche in der Geschichte des Problems, die gekennzeichnet ist durch das Bemühen der Mathematiker, den exakten Beweis der Unmöglichkeit der verlangten Konstruktion unter der Platonischen Bedingung zu erbringen. Und auf diesem neuen Wege sollte sich endlich das Geheimnis des Problems dem forschenden Geiste erschließen. Nachdem Gauß schon nach Beginn des vorigen Jahrhunderts den Unmöglichkeitsbeweis für die verwandten Probleme der Dreiteilung des Winkels und des Delischen Problems erbracht hatte, war auch der Weg gewiesen, auf dem die Lösung des Problems der Quadratur des Kreises in diesem Sinne gesucht und gefunden werden mußte. Gauß hatte gezeigt, daß die erwähnten beiden Probleme unter der Bedingung Platos überhaupt nicht zu lösen sind, weil die Aufgaben in dieser einengenden Form auf algebraische Probleme führen, für die es eine Lösung nicht gibt und nicht geben kann, und die algebraische Behandlung der Aufgabe ließ gegen Ende des vorigen Jahrhunderts endlich auch das eigentliche Wesen der Quadratur des Kreises erkennen und ermöglichte es, auch für dieses schwierigste und am meisten umstrittene Problem den exakten Unmöglichkeitsbeweis zu erbringen. Wie bei jenen anderen beiden Problemen war es auch hier ein deutscher Mathematiker, dem dieser Beweis gelang. Im Jahre 1882 unterbreitete Ferdinand Lindemann, Professor der Mathematik in München, der wissenschaftlichen Welt den exakten Beweis der Unmöglichkeit der Quadratur des Kreises mit Zirkel und Lineal. Der Beweis beruht, um das Wesentlichste darüber zu sagen, auf der Eigenart der bekannten Zahl π, also 3,1415926 … usw., die das Verhältnis des Durchmessers eines Kreises zu seinem Umfange angibt. Diese Zahl ist, wie Lindemann nachwies, eine sogenannte transzendente Zahl. Eine solche Zahl hat neben ihren anderen merkwürdigen Eigenschaften auch die, sich nicht konstruieren zu lassen, das heißt, es können mit Zirkel und Lineal nicht zwei Strecken bestimmt werden, deren Längenverhältnis jener merkwürdigen Zahl entspricht, von denen also die eine soviel mal länger ist als die andere, wie der Umfang eines Kreises länger ist als sein Durchmesser Nach der genaueren Definition ist transzendent eine Zahl, die nicht Wurzel einer algebraischen Gleichung mit ganzzahligen Koeffizienten sein kann.. Die Zahl ist die Ursache der Unmöglichkeit der Quadratur des Kreises mit Zirkel und Lineal, sie hatte schuld, daß sich die Menschheit einige Jahrtausende hindurch den Kopf umsonst zerbrochen hat.

Mit dem exakten Beweis der Unmöglichkeit der Quadratur des Kreises im Sinne der Bedingung Platos hatte der Kampf um dieses hartnäckigste und schwierigste aller geometrischen Probleme, mit denen sich die Mathematiker jemals zu beschäftigen hatten, seinen Abschluß, das Problem selbst seine Lösung gefunden. Freilich war die Lösung anderer Art, als man einstmals gedacht hatte; sie war negativer Art und hatte die Alternative, ob die Lösung des Problems möglich oder unmöglich sei, mit dem exakten Beweis der Unmöglichkeit beantwortet, und für die Wissenschaft bedeutete das die vollkommene Entscheidung, an der nicht mehr zu drehen und zu deuteln ist. Der Kampf um das Problem war zu Ende gegangen, aber alles, was Gelehrte und Laien im Laufe vieler Jahrhunderte dazu beigetragen haben, wird für immer eins der eigenartigsten und reizvollsten Kapitel in der Geschichte des Forschens und des Strebens nach wissenschaftlicher Erkenntnis bleiben.

Postskriptum

Quadratoren von heute – Ein Arzt, ein Steinmetz und ein Orgelkünstler – Techniker als Quadratoren – Ein gelehrter Opponent – Die Quadratur des Kreises in der Fliederblüte

Wer über die Quadratur des Kreises schreibt und gemäß der wohlbegründeten Auffassung, zu der die Wissenschaft in dieser Frage gekommen ist, die Lösung dieses Problems als unmöglich bezeichnet, der muß mit Wehmut und Bedauern feststellen, daß die Mathematiker ihren Zeitgenossen unter allem, was da kreucht und fleucht, die vertrauensunwürdigsten Erzeugnisse der Schöpfung zu sein scheinen! Man glaubt ihnen einfach nicht, und ihre Behauptungen über das, was in der Mathematik als richtig und als falsch, als möglich und als unmöglich zu gelten habe, werden mit energischstem Widerspruch, mit mitleidsvollem Achselzucken oder auch mit Spott und Hohn und immer mit der strikten Behauptung, daß gerade das Gegenteil richtig sei, beantwortet. Diese Erfahrungen konnte ich nach einigen Veröffentlichungen über jenes Problem, insbesondere auch nach einem Rundfunkvortrag hierüber, überreichlich machen. Eine Unzahl von Zuschriften ging mir in diesem wie in jenem Falle zu, in denen mir haarscharf nachgewiesen wurde, daß alles, was ich über die Unmöglichkeit der Quadratur des Kreises gesagt und geschrieben hatte, nur eine Vorspiegelung kurioser Tatsachen oder eine Art fixer Idee von mir sei. Und gleichzeitig wurden mir die verschiedenartigsten geometrischen Konstruktionen übersandt, die die absolute Lösung dieses Problems enthalten sollten. Das sind die Quadratoren von heute, die modernen Vertreter jener niemals ausgestorbenen und niemals aussterbenden, nicht unsympathischen Gattung, die auf eigene Faust die Lösung jenes Problems, das der Wissenschaft selbst unüberwindliche Schwierigkeiten bereitete, erzwingen will.

Lassen wir Beispiele sprechen: Ein Dr. med. schrieb mir, er sei jederzeit in der Lage, sowohl die Dreiteilung des Winkels wie auch die Quadratur des Kreises in exakter Weise nur mit Zirkel und Lineal auszuführen. Die Gründe, die die Mathematiker für die angebliche Unmöglichkeit dieser Konstruktion anführten, seien nichts weiter als Verlegenheitsphrasen, um die eigene Unfähigkeit zu verdecken. Er fechte grundsätzlich jede dieser Behauptungen, wo immer er sie finde, an und fordere alle Mathematiker der Welt heraus, seine Beweise nachzuprüfen, aber noch keiner habe den Mut gehabt, seine Forderung anzunehmen! Wie gesagt, das schrieb ein Arzt. Nun sind ja unzweifelhaft Medizin und Mathematik nicht unwesentlich verschiedene Gebiete des Wissens und Könnens, aber darin sollten sie sich doch ähneln, daß die Leidenden hier wie dort dem Fachmann wenigstens das notdürftigste Vertrauen entgegenbringen müssen. Der Herr hat mich dann auch einmal aufgesucht, ein liebenswürdiger älterer, temperamentvoller Herr; sein Geheimnis hat er mir nicht enthüllt, und das Vertrauen, dessen ich zu seiner »Heilung«, das heißt zum Nachweis der Irrigkeit seiner Annahmen und Behauptungen bedurfte, konnte er nicht aufbringen. Er glaubte mir eben nicht.

Ein anderer Fall: Ein wackerer Steinmetzmeister schrieb mir, er begreife absolut nicht, wie man zu der Behauptung komme, daß die Quadratur des Kreises unmöglich sei; er komme durch seinen Beruf täglich in die Lage, diese ausführen zu müssen, und wolle mir gern Unterricht erteilen. Darauf folgte noch die zarte Mahnung, die Rückerstattung des seinerzeit für mich angewandten Schulgeldes zu beantragen, und nachdem der Gute so seine Verachtung aller Wissenschaft noch mit dem üblichen »Hochachtungsvoll« bekräftigt hatte, gab er in einem Postskriptum seinen Gefühlen noch mit den mannhaften Worten Ausdruck: »Die Gelehrten sind eben allens Ochsen!« Ein anderer meiner Leser sandte mir seine Konstruktion zur Quadratur des Kreises ein; ich sandte sie ihm mit dem Hinweis auf die sehr kindlichen Fehler zurück. Schon wenige Tage darauf bekam ich von ihm eine Neubearbeitung mit der Versicherung, daß die begangenen Fehler ausgemerzt seien und diesmal die Lösung unwiderruflich richtig sei. Auch diese Ausarbeitung ging mit den angestrichenen Fehlern an ihren Urheber zurück mit dem Erfolg, daß nach einer knappen Woche eine abermalige Bearbeitung des Unermüdlichen ankam. Nach der sechsten Bearbeitung gab ich das Rennen auf, und seitdem mag mein Kredit als Wissenschaftler bei diesem Forscher von eigenen Gnaden auf dem absoluten Nullpunkt angelangt sein. Aus einer Kleinstadt im Osten unseres Vaterlandes aber kam mir ein Brieflein zu, zwar von zarter Hand, aber voll mannhaften Tones und des Inhaltes, daß die Absenderin meine Veröffentlichung zur Veranlassung nehmen werde, um im Kreisblatt einen Artikel »über den unglaublichen Aberglauben« zu schreiben, der anscheinend noch bei vielen sogenannten Intellektuellen grassiere; denn mit der Quadratur des Kreises habe man sich wohl in früheren dunklen Zeiten beschäftigt und sie damals für unmöglich erklärt, aber heute wisse jeder aufgeklärte Mensch, daß das eben nur ein Aberglauben sei. Ob der vernichtende Leitartikel im Kreisblatt erschienen ist, weiß ich nicht, aber ich habe lange in zitternder Erwartung geschwebt. Ein anderer dieser privaten Forscher, ein wackerer Orgelbauer, aber veröffentlichte in der Fachzeitung seines Gewerbes eine Entgegnung, in der er an einer ebenso kunstvollen wie fehlerhaften Zeichnung bewies, daß es ihm gelungen sei, die Quadratur des Kreises zu finden, und die Redaktion des betreffenden Blattes, die von der Sache wohl geradesoviel verstand wie der geschätzte Mitarbeiter, begleitete dessen Abhandlung mit hoheitsvollen Worten über die Unzulänglichkeit der offiziellen Wissenschaft im allgemeinen und die der Mathematiker im besonderen, die sich hier von einem einfachen, ungelehrten und unstudierten Werkstattechniker beschämen lassen müßten. Ich habe mich lange sehr bedrückt gefühlt!

Man irrt aber, wenn man annimmt, daß die Unmöglichkeit der Quadratur des Kreises oder der Lösung der verwandten geometrischen Probleme etwa nur von Leuten bestritten werde, die es bisher verschmähten, mit der Mathematik nähere Bekanntschaft zu machen. Eine ganze Anzahl solcher wie oben gekennzeichneter Schreiben ging mir auch von Technikern, Diplom- und anderen Ingenieuren zu, also von Leuten, die doch von Berufs wegen mit einem tüchtigen Teil mathematischer Kenntnisse ausgerüstet sind. Sie alle sandten mir auch technische Zeichnungen und umfangreiche Beweise, die die Richtigkeit ihrer Auffassung dartun sollten, und ich gebe gern zu, daß die Beweiskonstruktionen von dieser Seite im allgemeinen schwieriger und interessanter waren als die vieler anderer Quadratoren, die sich die Sache manchmal doch allzu leicht machen. Besonders mit interessanten Kurvenkonstruktionen suchen die Herren von der technischen Fakultät dem Problem gern zu Leibe zu gehen, aber da alle Kurven außer dem Kreise andere Hilfsmittel als Zirkel und Lineal erfordern, so konnte auch niemals einer dieser Versuchskonstruktionen der Preis der Anerkennung zuerteilt werden. Sogar ein Dozent einer Technischen Hochschule war unter den Quadratoren, die meine Veröffentlichung zum Widerspruch, sogar zu einem äußerst geharnischten, herausgefordert hatte. Dieser Opponent schrieb an die Redaktion des Blattes, in dem meine Veröffentlichung erschienen war, einen flammenden Protest, meinte, daß der Verfasser dieser Abhandlung anscheinend nicht über die Kenntnisse eines Obertertianers verfüge, und fügte Zeichnung und Berechnung bei, wie sowohl die Quadratur des Kreises wie die Dreiteilung des Winkels auszuführen sei, Ideen, die bei einem Lehrer einer Technischen Hochschule, der, wenn er auch nicht eigentlicher Mathematiker ist, so doch einem technischen Fachgebiete angehört, als in hohem Maße bemerkenswert anmuten mußten. Der unbekümmerte Ton seines Schreibens führte dann zu einer sehr deutlichen Auseinandersetzung, in deren Verlauf sich mein rabiater Ankläger genötigt sah, der Redaktion des Blattes wie auch mir gegenüber seine merkwürdigen Behauptungen selbst als Irrtum zu bezeichnen, den kränkenden »Obertertianer« reuevoll zurückzunehmen und schließlich noch einen Barbetrag für bereits entstandene gerichtliche Kosten zu bezahlen. Die Person des Beteiligten hat diesen Fall immerhin bemerkenswert gemacht.

Daß der mathematisch gebildete Techniker die von ihm ersonnene Annäherungskonstruktion gern für die vollendete Lösung des Problems zu halten geneigt ist, hat seinen tieferen psychologischen Grund. Der Techniker, der Mann der Praxis, neigt sehr begreiflicherweise dazu, das, was sich mit technischen Hilfsmitteln und Methoden erreichen läßt, auch bei einem mathematischen Problem für die exakte Lösung zu halten, besonders dann, wenn die Konstruktion augenscheinlich einen hohen Genauigkeitsgrad aufzuweisen hat. Aber die Mathematik sieht ihre Probleme mit anderen Augen an. Sie hat mit den Hilfsmitteln und Methoden der Technik nichts zu tun, auch nicht bei der Lösung der mathematischen Probleme, und was dort als richtig und zulässig gilt, ist das noch keineswegs im Gebiet der sogenannten reinen Mathematik, die alle äußeren oder auf der bloßen Erfahrung beruhenden Methoden und Hilfsmittel abweist und durch reines Denken zu ihren Ergebnissen und Beweisen gelangen will. An dieser Unterscheidung gehen selbst viele mathematisch Gebildete vorbei, und daraus ergibt sich dann die heftige Anfeindung der Auffassung der wissenschaftlichen Mathematik gerade seitens dieser Kreise.

Abb. 4
Die Quadratur des Kreises in der Fliederblüte

Eine sehr interessante, wenn natürlich ebenfalls nicht exakte Versuchskonstruktion zur Quadratur des Kreises sei noch erwähnt. Sie stammt von Oberleutnant K., der sie mir zur Prüfung unterbreitete. Er hatte, wie er mir erzählte, als er im Felde war, in Mußestunden Gelegenheit gehabt, die Blüte des Flieders zu studieren, und an dieser war ihm das exakte mathematische Verhältnis aufgefallen, das ihm die Lösung des Problems der Quadratur des Kreises zu sein schien. Die nebenstehende Abbildung zeigt das geometrische Bild der Fliederblüte. Die Konstruktion ist aus der Abbildung ohne weiteres ersichtlich. Verbindet man die vier Punkte, in denen sich die Viertelkreise schneiden, so erhält man ein Quadrat; schlägt man dann um den Mittelpunkt dieses Quadrates einen Kreis, der die Viertelkreise berührt, so sind, wie Herr K. annahm, dieser Kreis und das Quadrat flächengleich. Tatsächlich glaubte er, in dem mathematischen Bild der Fliederblüte die Lösung des uralten Problems der Quadratur des Kreises sehen zu dürfen, von der Erwägung ausgehend, daß die Natur sicherlich doch zustande bringen könne, was dem Scharfsinn der Mathematiker bislang entgangen sei. Die Prüfung ergab dann freilich, daß auch dieses mathematische Naturbild nicht als vollkommene Quadratur bezeichnet werden kann, denn Quadrat und Kreis sind nicht vollkommen flächengleich, wie die analytische Berechnung ihrer Flächeninhalte ohne weiteres ergibt. Wohl aber ist die Verschiedenheit der beiden Flächeninhalte nur eine verhältnismäßig geringe; sie beträgt nur etwa ein Hundertstel des Kreisinhaltes, so daß das Bild der Fliederblüte immerhin als eine ziemlich genaue und auf alle Fälle überaus interessante Annäherungskonstruktion bezeichnet werden darf. Aber selbst wenn die Rechnung absolute Übereinstimmung der beiden Flächeninhalte ergeben hätte, wäre das doch keine exakte Quadratur gewesen, denn bei einer solchen dürfen nur Zirkel und Lineal als Hilfsmittel verwandt werden. Die Natur, die ihre Gebilde auf ihre Weise schafft, hätte also, selbst wenn sie die Quadratur rechnerisch mit absoluter Genauigkeit irgendwo herstellte, sich dabei unzulässiger Hilfsmittel bedient, und das darf auch die Natur nicht, wenn sie den Anforderungen der exakten Mathematiker genügen will!

3. Der geheimnisvolle Würfel
(Das Delische Problem)

Ein Zauberkunststück – Die Forderung des Gottes – Das Rätsel der Würfelverdoppelung – Die Verdoppelung des Quadrates – Die Konstruktion der Quadratwurzel – Der nützliche »Pythagoras« – Die Konstruktion der Kubikwurzel – Ein fehlender Lehrsatz

Bei den Vorführungen vieler Zauberkünstler spielt oftmals ein geheimnisvoller Würfel eine große Rolle. Beispielsweise zaubert der Künstler aus einem solchen hohlen Würfel alle möglichen Dinge hervor, die weder ihrer Größe noch ihrer Zahl nach Platz in dem Würfel zu haben scheinen, oder er überdeckt mit einem solchen Würfel irgendeinen Gegenstand für einen Augenblick, und wenn er den Würfel dann wieder emporhebt, ist der Gegenstand verschwunden, oder es steht ein ganz anderes Ding auf dem Zaubertisch usw. Diese Kunststücke wirken immer sehr verblüffend; geht man der Sache jedoch auf den Grund, oder läßt man sich durch einen Fachmann die rätselhaften Vorgänge erklären, so wird der Würfel seines Geheimnisses freilich gründlich entkleidet, und es stellt sich heraus, daß das ganze Kunststück nur auf einer geschickten Täuschung der Zuschauer beruht. Dagegen gibt es ein anderes Geheimnis, das sich an den Würfel knüpft, dessen positive Lösung aber bis heute weder einem Zauberkünstler noch einem anderen Sterblichen gelungen ist, obwohl sich daran die scharfsinnigsten Forscher seit über zweitausend Jahren die Köpfe zerbrochen haben.

Welcher Art dieses merkwürdige Geheimnis des Würfels ist, darüber gibt schon eine Mitteilung aus dem Altertum Auskunft. Um das Jahr 400 v. Chr. wurde Griechenland von einer verheerenden Pest heimgesucht, die unheimlich lange anhielt, zahllose Opfer forderte und trotz aller Gebete und auch trotz aller ärztlichen Mittel nicht weichen wollte. Schließlich entschloß man sich, eine Abordnung nach dem berühmten Orakel des Gottes Apollo in Delos zu entsenden, die einen Spruch des Gottes erbitten sollte, was zu geschehen habe, um der Seuche Einhalt zu tun. Die Antwort, die der Gott durch den Mund der Pythia erteilte, lautete, die Pest würde zu Ende gehen, wenn man dem Gott einen Altar von dem doppelten Rauminhalt des im Tempel zu Delos stehenden Altars, der die Gestalt eines Würfels hatte, erbauen würde. Das schien sehr einfach, und bald war ein Altar von dem doppelten Rauminhalt des alten und von quaderförmiger Gestalt an Stelle jenes errichtet. Trotzdem aber wütete die Pest weiter, und als man das Orakel nochmals befragte, antwortete es, der neue Altar müsse nicht nur den doppelten Rauminhalt des alten haben, sondern auch wie dieser genau würfelförmig gestaltet sein. Auch das schien nicht schwer, und wiederum machte man sich schleunigst an die Arbeit, die Forderung des Gottes zu erfüllen, also einen Würfel von dem doppelten Rauminhalt des alten Altars zu erbauen. Da aber machte man die merkwürdige Erfahrung, daß die gestellte Aufgabe, die doch so leicht aussah, ganz ungeahnte Schwierigkeiten bereitete. Es gelang den Geometern, die zunächst beauftragt waren, die Längenverhältnisse bzw. die Seitenlänge des zu erbauenden Würfels zu bestimmen, nicht, mit den allein zur Verfügung stehenden geometrischen Hilfsmitteln, nämlich Zirkel und Lineal, die gesuchte Längengröße mit mathematischer Genauigkeit zu ermitteln. Deswegen wandte man sich schließlich an Plato, den berühmten Philosophen und Mathematiker, und bat um Rat, auf welche Art und Weise die gestellte geometrische Aufgabe zur Zufriedenheit des Gottes gelöst werden könnte. Wie sich die Sache mit der Pest weiter entwickelt hat, ist nicht berichtet; sie wird ja wohl einmal aufgehört haben, obwohl es nicht möglich war, der Forderung des Gottes nachzukommen. Denn auch Plato und seine Schüler, die sich mit Feuereifer an die Lösung der Aufgabe machten, waren nicht imstande, diese in völlig exakter, mathematisch absolut genauer Weise zu lösen. Auf keine Art und Weise war es möglich, mit Zirkel und Lineal, den bewährten Hilfsmitteln bei der Lösung aller geometrischen Aufgaben, die Seitenlänge eines Würfels, der den doppelten Rauminhalt eines gegebenen anderen Würfels haben soll, zu bestimmen. Man sah sich vor ein Rätsel gestellt, dessen Kernpunkt man trotz aller höchst scharfsinnigen Versuche und Untersuchungen nicht enthüllen konnte und das als Problem der Würfelverdoppelung oder als Delisches Problem in der Folgezeit, ähnlich wie die Quadratur des Kreises, eine der berühmtesten wissenschaftlichen Aufgaben wurde.

Wir wissen heute, welches der Grund der Unmöglichkeit ist, die verlangte Konstruktion nur mit Zirkel und Lineal auszuführen. Wir müssen, um diesen Grund zu erkennen, die Aufgabe zunächst algebraisch behandeln, das heißt, die geometrische Aufgabe in die Form einer Gleichung bringen. Diese Betrachtung erfordert nur ganz elementare mathematische Kenntnisse, deren sich jeder aus seiner Schulzeit erinnern wird, der dort überhaupt die Elemente der Geometrie und der Algebra kennengelernt hat.

Wir wollen, um den inneren Charakter der Aufgabe der Würfelverdoppelung zu erkennen, zunächst eine andere, ähnliche geometrische Aufgabe betrachten, nämlich die Verdoppelung eines Quadrates. Angenommen, wir haben ein Quadrat, dessen Seite die Länge a hat. Der Flächeninhalt dieses Quadrates ist dann a × a oder, in der üblichen Schreibweise, a ². Ein Quadrat von dem doppelten Flächeninhalt dieses Quadrates wäre dann 2a ² groß, und wir fragen: Wie können wir ein Quadrat von dem Flächeninhalt 2a ² mit Zirkel und Lineal konstruieren? Diese Aufgabe ist auf sehr einfache Art und Weise auszuführen. Um die Seitenlänge des gesuchten Quadrates zu bestimmen, müssen wir aus dem Ausdruck 2a ² die Wurzel ziehen. Bezeichnen wir die Seite des gesuchten Quadrates mit s, so erhalten wir mithin die Gleichung s = √2·a ² oder, wenn wir den Ausdruck unter dem Wurzelzeichen in eine angemessenere Form bringen, s = a√2.

Abb. 5

Das ist also die algebraische Form, in die wir die ursprüngliche geometrische Aufgabe der Verdoppelung eines Quadrates gebracht haben, und die weitere Aufgabe besteht nunmehr nur noch darin, die Größe a√2 zu konstruieren. Das ist sehr einfach. Die Strecke a ist ja gegeben, es handelt sich also nur noch darum, den in jener Größe auftretenden Ausdruck √2, also die quadratische Wurzel aus 2, zu konstruieren. Auch das ist ohne Schwierigkeit möglich, denn wir sind in der Lage, jede Quadratwurzel zu konstruieren, und zwar mit Hilfe des pythagoreischen Lehrsatzes, der bekanntlich besagt, daß in jedem rechtwinkligen Dreieck die Summe der Quadrate über den beiden Katheten gleich ist dem Quadrat über der Hypotenuse. Um die Wurzel aus 2 zu konstruieren, brauchen wir nur einen rechten Winkel zu zeichnen, machen jeden Schenkel = 1 (etwa 1 Zentimeter oder eine sonstige Einheit lang) und verbinden die Spitzen der Schenkel. Dann entsteht das rechtwinklige und gleichseitige Dreieck unserer Figur 5, und bezeichnen wir in dieser die Hypotenuse mit s, so ist nach dem pythagoreischen Lehrsatz s ² = 1 ² + 1 ² oder s ² = 2, mithin s = √2. Die Hypotenuse in unserem Dreieck ist also die geometrische Konstruktion des algebraischen Ausdrucks √2. Ebenso könnten wir auch die Wurzel aus 3 konstruieren mit Hilfe eines neuen rechtwinkligen Dreiecks, dessen Katheten die Längen 1 und √2 haben. Die Hypotenuse des neuen Dreiecks wäre dann die geometrische Konstruktion der Wurzel aus 3. Damit ist die Lösung der Aufgabe selbst ohne weiteres gegeben. Haben wir ein Quadrat mit der Seitenlänge a und ziehen wir in diesem die Diagonale, die wir mit s bezeichnen wollen, so ist, wie wir auseinandergesetzt haben, nach dem Pythagoras s ² = 2a ², mithin s = a√2. Errichten wir nun über dieser Diagonale ein neues Quadrat, dessen Seitenlänge also a√2 ist, so ist der Flächeninhalt des ganzen neuen Quadrates gleich (a√2) ² = 2a ², also gerade doppelt so groß wie das Quadrat mit der Seitenlänge a, von dem wir ausgegangen sind. Um also ein Quadrat zu verdoppeln, brauchen wir nur über der Diagonale desselben ein neues Quadrat zu errichten, und da alle hierbei auftretenden Operationen mit Zirkel und Lineal ausgeführt werden können, so ist die Aufgabe der Verdoppelung eines gegebenen Quadrates damit einwandfrei gelöst.

Nunmehr wollen wir aus dem Gesagten die Nutzanwendung für unser eigentliches Problem, die Verdoppelung des Würfels, ziehen. Angenommen, wir haben einen Würfel von der Kantenlänge a, so ist der Rauminhalt dieses Würfels a × a × a oder in algebraischer Schreibweise, a ³. Ein Würfel von doppeltem Rauminhalt des gegebenen hätte mithin den Inhalt 2a ³, und um einen solchen Würfel zu konstruieren, müssen wir zunächst seine Kantenlänge bestimmen. Diese erhalten wir, wenn wir aus dem Ausdruck 2a ³ die dritte (oder kubische) Wurzel ziehen; bezeichnen wir die Kante des zu konstruierenden Würfels wieder mit s, so ist also s = ∛2a3, oder, in vereinfachter Form, a ∛2.

In diesem Ausdruck a ∛2, auf den uns die algebraische Behandlung unserer Aufgabe geführt hat, tritt also eine Wurzel vom dritten Grade oder eine kubische Wurzel auf, und wir fragen, ob und auf welche Weise wir diesen Ausdruck mit Zirkel und Lineal konstruieren können. Und da müssen wir leider sagen, daß dies auf keine Art möglich ist. Quadratische Wurzeln können wir, wie wir dargelegt haben, sehr leicht konstruieren, kubische Wurzeln aber nicht, und zwar deswegen nicht, weil uns für diesen Zweck nicht ein so bequemer Lehrsatz, wie es der pythagoreische Lehrsatz für die Konstruktion quadratischer Wurzeln ist, zur Verfügung steht. Für die Konstruktion kubischer Wurzeln gibt es einen solchen Lehrsatz nicht, und ein solcher kann auch niemals aufgestellt werden.

Das also ist der Grund, daß die Forderung des Gottes nicht erfüllt werden konnte und wir bis heute noch nicht in der Lage sind, die Aufgabe, die er stellte, mit Zirkel und Lineal allein mathematisch exakt zu lösen.

Selbstverständlich ist die Aufgabe nur in der beschriebenen exakten Form, also mit Zirkel und Lineal als alleinigen Hilfsmitteln, als nichtlösbar zu bezeichnen. In angenäherter Form und mit anderen Hilfsmitteln ist sie auf vielfache Weise, und zwar mit jeder gewünschten Genauigkeit, ausführbar, und in der Technik sind ja Aufgaben dieser Art sehr oft zu lösen. Auf diese technischen und Annäherungsmethoden hier einzugehen, bietet kein Interesse, dagegen werden wir bei dem Problem der Dreiteilung des Winkels sehr interessante und scharfsinnige Methoden dieser Art kennenlernen. Mit diesem Problem wollen wir uns in dem nächsten Aufsatz beschäftigen.

4. Der widerspenstige Winkel
(Das Trisektionsproblem)

Die Entstehung des Problems – Mögliche und unmögliche Winkelteilungen – Vermeintliche Lösungen – Die Einschiebungsmethode – Außenseiter – Die Lösung des Problems

Das dritte jener berühmten geometrischen Probleme, die sich an Zirkel und Lineal knüpfen, und deren Lösung die Wissenschaft viele Jahrhunderte hindurch nachging, ohne sie finden zu können, ist die Dreiteilung des Winkels, auch kurz Trisektionsproblem genannt. Es besteht, wie ja schon die Bezeichnung erkennen läßt, darin, eine Methode anzuwenden oder zu erfinden, durch die unterschiedslos jeder Winkel in drei Teile geteilt werden kann, und hierbei als Hilfsmittel nur Zirkel und Lineal zu benutzen.

Auch über die Eigenart dieses Problems wird uns am besten eine kurze geschichtliche Betrachtung Aufschluß geben. Auch dieses Problem war schon im Altertum bekannt und schon in der Schule der Pythagoreer aufgetaucht. Die hatten sich viel mit Kreisteilungen beschäftigt, das heißt mit der Aufgabe, die Peripherie eines Kreises auf geometrischem Wege in gleiche Teile zu teilen. Man hatte bereits die Drei-, Vier-, Fünf-, Sechs-, Zehn-, Zwölf- und Fünfzehnteilung und ähnliche Teilungen einfacher Zahlenverhältnisse gefunden, während andere Teilungen, wie etwa die Sieben-, Neun- oder Dreizehnteilung, damals auch noch die Siebzehnteilung, sich als nicht möglich erwiesen. Man ging nun weiter und suchte die genannten Teilungen auch auf einem beliebigen Stück eines Kreisbogens auszuführen, bzw. einen beliebigen Winkel (auch der Kreis ist ja nur als ein Winkel von 360 Grad aufzufassen) in ebensolcher Weise zu teilen, wie es beim ganzen Kreise möglich war. Auch für die Lösung dieser Aufgabe galten nur Zirkel und Lineal als zulässige Hilfsmittel. Während nun die Zwei- und demgemäß auch die Vier-, Acht-, Sechzehnteilung usw. eines beliebigen Winkels spielend leicht war, zeigte es sich, daß die Dreiteilung, abgesehen von bestimmten Ausnahmefällen, unüberwindliche Schwierigkeiten bereitete und sich trotz alles darangesetzten Scharfsinnes keine Methode ausfindig machen ließ, die die exakte Lösung jenes Problems bedeutet hätte, vermöge deren es also möglich gewesen wäre, jeden beliebigen Winkel in exakt mathematischer Weise in drei gleiche Teile zu teilen. Damit war ein weiteres geometrisches Rätsel gegeben, das der Quadratur des Kreises wie auch dem Delischen Problem ebenbürtig an die Seite trat und nicht weniger als diese die Ursache ungezählter scharfsinniger Bemühungen der Mathematiker wurde, Bemühungen, die die Jahrhunderte hindurch, das ganze Altertum, seit es überhaupt die exakte Mathematik entdeckt hatte, und ebenso das gesamte Mittelalter, das die Mathematik allerdings mit mehr Eifer als Erfindungsgabe betrieb, hindurch fortgesetzt wurden, aber ebenso wie bei jenen anderen geometrischen Aufgaben immer wieder ergebnislos verliefen.

Abb. 6

Allerdings muß hier eine Einschränkung gemacht werden. Nur die Aufgabe, einen Winkel allgemein mit Zirkel und Lineal zu dreiteilen, erwies und erweist sich als unlösbar. Der Nachdruck liegt dabei auf dem Wörtchen »allgemein«, und das will besagen, daß die verlangte und gesuchte Methode der Trisektion für ausnahmslos alle Winkel in der gleichen Weise anwendbar sein soll. Sehr viele Winkel nämlich sind mit Zirkel und Lineal sehr leicht in drei Teile zu teilen. Um beispielsweise diese Operation bei einem Winkel von 90 Grad auszuführen, schlägt man um den Scheitelpunkt M des Winkel AMB, wie unsere Figur 6 zeigt, einen Kreis. Dann braucht man nur den Radius des so entstandenen Viertelkreises einmal von B und einmal von A aus auf der Peripherie abzutragen und erhält dann die Schnittpunkte E und D, durch welche die Peripherie und damit zugleich der gegebene Winkel in drei Teile geteilt ist, wie sich leicht beweisen läßt. Auf ähnliche einfache Weise läßt sich auch jeder andere Winkel, dessen Gradzahl durch neun teilbar ist, also auch der Winkel von 18, 27, 36, 45 oder auch 135, 180 usw. Grad, in exakt geometrischer Weise in drei Teile teilen, ebenso auch die Hälfte, der vierte, der achte usw. Teil eines solchen Winkels. Auch für gewisse andere Winkel ist jene Operation, wenn auch in anderer und nur sehr komplizierter Weise ausführbar; so kann beispielsweise auch ein Winkel, der durch den siebzehnten Teil des Kreisumfanges dargestellt ist, mit Zirkel und Lineal in drei Teile geteilt werden, eine Tatsache, die allerdings weder dem Altertum noch dem Mittelalter bekannt war, sondern sich erst aus der Entdeckung der Siebzehnteilung des Kreises durch den genialen Gauß ergab. Aber alle diese Fälle, so zahlreich sie auch sein mögen, sind doch nur als Spezialfälle zu betrachten, die keine allgemeine Lösung des Problems, also nicht die Möglichkeit der Dreiteilung eines jeden beliebigen Winkels, bedeuten. Für die weitaus meisten Winkel haben wir keine exakte geometrische Methode der Dreiteilung; Winkel von 10, 20, 30, 40, 50 oder, um auch höhere Grade zu nennen, von 100, 200, 300 Grad usw. sind in exakter Weise nicht in drei Teile zu teilen; nur für Winkel dieser Art bestand und besteht noch das Problem und seine Unlösbarkeit, und nur um Winkel dieser Art drehte sich der ewige Geisteskampf in Altertum und Mittelalter um die Lösung dieser merkwürdigen Aufgabe.

Oftmals freilich glaubten in diesem Geisteskampfe einzelne Geometer die exakte Lösung des Problems, also eine Methode gefunden zu haben, die bei ausnahmslos allen Winkeln die Dreiteilung in exakter Weise mit Zirkel und Lineal möglich zu machen geeignet sein sollte, und die Geschichte des Dreiteilungsproblems zeigt in dieser Hinsicht große Ähnlichkeit mit der der Quadratur des Kreises. Aber die Ähnlichkeit besteht auch darin, daß solche vermeintlichen Lösungen sich immer wieder als verfehlt erwiesen. Immer ergab die genauere Nachprüfung der Lösung, daß der glückliche Entdecker entweder einen Rechen- oder Konstruktionsfehler begangen oder unbemerkt ein unzulässiges Verfahren angewandt und also zu früh triumphiert hatte. Allerdings liegt gerade beim Trisektionsproblem die Gefahr nahe, scheinbare oder annähernde Lösungen für die wirklich exakte Lösung der Aufgabe zu halten, und dieses Mißgeschick ist selbst manchem tüchtigen Geometer widerfahren. Selbst der große Leonardo da Vinci, der ja nicht nur ein hervorragender Maler, Bildhauer und Ingenieur, sondern auch ein ausgezeichneter Mathematiker und überhaupt eins der größten Universalgenies war, die die Geschichte kennt, hat eine solche von ihm gefundene Annäherungslösung für die wirkliche Lösung der Aufgabe gehalten.

Solcher Hilfs- oder Annäherungsmethoden, die von den Mathematikern selbst zur Lösung des Problems ersonnen wurden, entstanden im Laufe der Zeiten sehr viele. Besonders durch die Verwendung von Kurven der verschiedensten Art glaubte man die Lösung doch zu erzielen. Aber so scharfsinnig, geistreich und interessant diese Methoden auch oftmals waren, so konnten sie doch niemals die exakte wissenschaftliche Lösung des Problems bedeuten. Denn die einzige Kurve, die vermittels des Zirkels ausgeführt werden kann, ist eben der Kreis, und die Kreiskurve führte, wie man sich schließlich überzeugte, nicht zur vollen Lösung des Problems. Alle anderen Kurven aber erfordern entweder andere Hilfsmittel als Zirkel und Lineal oder führen immer nur zu Annäherungswerten. Wir wollen die Gefahren des Trisektionsproblems, die darin bestehen, daß manchmal selbst der mathematisch geschulte Geist Annäherungen mit der exakten Lösung verwechseln kann, an einer sehr berühmten und schon aus dem Altertum stammenden Annäherungsmethode, der sogenannten Einschiebung, veranschaulichen. Auf unserer Abbildung 7 ist ein Winkel ABC gezeichnet, der nach dieser Methode in drei Teile geteilt werden soll. Zu diesem Zwecke fällen wir von einem beliebigen Punkte A des einen Schenkels das Lot AL auf den anderen Schenkel und ziehen ferner durch den Punkt A die Parallele zu BC, alles Operationen, die nur Zirkel und Lineal erfordern. Durch den Scheitelpunkt B legen wir dann eine Gerade, die die Parallele zu BC in dem Punkte E trifft und auf ihrem Wege, wie die Abbildung erkennen läßt, das Lot AL in dem Punkte S schneidet. Dieser Schnittpunkt S teilt die Strecke BE in zwei Strecken, nämlich die Teilstrecken BS und SE. Diese Teilstrecken ändern ihre Größe, wenn die ganze Strecke BE um den Punkt B gedreht wird, wie man sich an Hand der Abbildung leicht veranschaulichen kann. Bringe ich durch Drehen und Ausprobieren nun die Strecke BE in eine solche Lage, daß die Teilstrecke SE gerade doppelt so lang wird wie die Strecke BA (unsere Abbildung stellt annähernd diesen Fall dar), so ist der entstandene Teilwinkel EBC der dritte Teil des ganzen Winkels ABC. Der Beweis für diese Behauptung wird dem geometrischen Scharfsinn unserer Leser keine Schwierigkeiten bereiten, weshalb wir ihn übergehen können. Damit ist nun die Aufgabe schon gelöst; denn wenn ich jetzt den anderen Teilwinkel ABE halbiere, was ja mit Zirkel und Lineal leicht erfolgen kann, so ist der ganze Winkel ABC auf diese Weise in drei gleiche Teile geteilt.

Abb. 7

Aber was hindert uns, diese Methode als exakt im wissenschaftlichen oder mathematischen Sinne anzuerkennen? Lediglich der Umstand, daß hierbei die Länge der Strecke SE, die doppelt so lang wie AB sein muß, bzw. der Punkt S, der diese Strecke bestimmt, nicht in exakter Weise durch den Schnittpunkt zweier anderer Linien, die mit Zirkel und Lineal konstruiert werden können, sondern nur durch allmähliches Ausprobieren ermittelt werden kann, was keine Gewähr für völlige Genauigkeit bietet und der Forderung mathematischer Exaktheit widerspricht. Ja, wenn sich die Lage des Punktes S auf dem Lote AL vorher mit Zirkel und Lineal bestimmen ließe, dann wäre damit das Problem der Dreiteilung des Winkels mit aller nur wünschenswerten Exaktheit gelöst, und nicht der gewissenhafteste und pedantischste zünftige Mathematiker könnte an dieser Lösung dann noch etwas auszusetzen haben. So aber bedeutet auch diese Konstruktion nur eine Annäherung, die freilich bis zu jeder gewünschten Genauigkeit durchgeführt werden kann, praktisch also vollkommen ausreicht, aber eben keine Lösung des Problems im exakt mathematischen Sinne ist.

So ging auch hier der Kampf um die Lösung des Problems bei Gelehrten und Ungelehrten weiter. Denn auch hier finden wir die Tatsache zu verzeichnen, daß das Problem außer auf die zünftigen Mathematiker auch auf die Außenseiter, die mit mathematischer Bildung mehr oder weniger unbeschwert waren, eine große Anziehungskraft ausübte, und zwar deswegen, weil die Aufgabe, rein äußerlich betrachtet, so überaus einfach und leicht erscheint. Irgendeinen Winkel mit Zirkel und Lineal in drei Teile zu teilen, das muß doch schließlich möglich sein, da doch viel schwieriger aussehende Teilungsaufgaben im Reiche der Geometrie, wie etwa die Sieben- oder Siebzehnteilung einer Strecke oder die Dreiteilung eines beliebigen Vielecks und ähnliche Aufgaben ohne weiteres lösbar sind, ohne andere Hilfsmittel als Zirkel und Lineal zu verlangen. Diese anscheinende Einfachheit und Leichtigkeit der Trisektion veranlaßte von jeher gerade auch zahlreiche Nichtmathematiker zu dem Versuch, den zünftigen Gelehrten ein Schnippchen zu schlagen und die von diesen als unmöglich bezeichnete Lösung dennoch möglich zu machen, und diese Beliebtheit hat das Problem in der Laienwelt bis auf den heutigen Tag beibehalten.

Der Jahrhunderte hindurch vergeblich um die Lösung der Aufgabe geführte Kampf wurde schließlich durch die genauere Untersuchung des Wesens des Problems beendet. Der große Gauß war es, der, wie bereits erwähnt, im Anfang des vorigen Jahrhunderts diese Untersuchung ausführte und zu dem Ergebnis gelangte, daß wie die Verdoppelung des Würfels so auch die Dreiteilung des Winkels unter der einschränkenden Platonischen Bedingung, also nur mit Zirkel und Lineal, überhaupt nicht ausgeführt werden kann, und er erbrachte den exakten Beweis für die Unmöglichkeit der Lösung dieser Aufgaben. Die Unmöglichkeit besteht wie beim Delischen Problem so auch bei der Trisektionsaufgabe darin, daß die algebraische Behandlung der Aufgabe, die ja der geometrischen Konstruktion vorangehen muß, auf algebraische Probleme führt, für die es eine Lösung nicht gibt. Auch hier führt die algebraische Behandlung der Aufgabe auf eine Gleichung dritten Grades und die geometrische Konstruktion auf die Notwendigkeit, kubische Wurzeln zu konstruieren. Weil es aber keine Methode und auch keinen Lehrsatz gibt, der, ähnlich wie der pythagoreische Lehrsatz für die Konstruktion von Quadratwurzeln, für die Konstruktion kubischer Wurzeln mit Zirkel und Lineal verwendbar wäre, so ist damit die ganze Aufgabe der Dreiteilung des Winkels als unmöglich zu bezeichnen. Allerdings liegt beim Trisektionsproblem die Sache nicht so einfach wie bei der Würfelverdoppelung. Während bei diesem die notwendigen algebraischen Operationen sehr leicht und durchsichtig sind, sind sie bei der Trisektionsaufgabe doch bereits viel schwieriger und komplizierter, und wir wollen darauf verzichten, sie an dieser Stelle durchzuführen. Aber der Grund der Unmöglichkeit ist in beiden Fällen derselbe, die Tatsache nämlich, daß die algebraische Behandlung des Problems auf eine Gleichung dritten Grades führt, deren Wurzeln mit Zirkel und Lineal nicht konstruiert werden können.

Mit dem von Gauß erbrachten Unmöglichkeitsbeweis, der mit zu den hervorragendsten Leistungen dieses unvergleichlichen Genies gehört, war das Jahrhunderte und Jahrtausende alte Ringen um die Lösung des Delischen und des Trisektionsproblems zum Abschluß gebracht werden. Das bis dahin undurchdringliche Geheimnis, das über jenen beiden Problemen lagerte, hatte sich dem forschenden Geist in seinem Wesenskern restlos enthüllt, und zwei der merkwürdigsten wissenschaftlichen Aufgaben hatten ihre Lösung gefunden. Das hat freilich nicht zu verhindern vermocht, daß jene beiden Probleme auch heute noch immer der Gegenstand ungezählter Lösungsversuche von Außenseitern sind. Zumeist ist ihnen die negative Lösung der Probleme, die die Wissenschaft mit dem Unmöglichkeitsbeweis erbracht hat, nicht bekannt, wenn ihnen diese aber bekannt wird, so wird ihre Gültigkeit mit kühner Handbewegung bestritten und ihr werden die Ergebnisse eigener Forschung entgegengesetzt. So bemühen sich also auch heute noch ungezählte Tausende, die Verdoppelung des Würfels wie auch die Dreiteilung des Winkels zuwege zu bringen. Besonders die Dreiteilungsaufgabe, die doch so leicht und mühelos anmutet und äußerlich freilich nichts von der Tiefe und Schwierigkeit dieses Problems verrät, hat noch zahllose Liebhaber, die alljährlich die Welt mit neuen Konstruktionen und Lösungen zur Bezwingung des widerspenstigen Winkels überraschen. Zu allen diesen Bemühungen aber kann nur gesagt werden, daß es heute an dem Delischen wie an dem Dreiteilungsproblem nichts mehr zu lösen gibt, denn diese Probleme sind heute, geradeso wie das der Quadratur des Kreises, als absolut erledigt zu bezeichnen, sind durch den Unmöglichkeitsbeweis endgültig entschieden. Eine andere als die von der Wissenschaft gefundene und anerkannte Lösung könnte nur darin bestehen, den Unmöglichkeitsbeweis für jene beiden Probleme zu widerlegen. Eine solche Widerlegung würde verlangen, eine Methode oder einen Lehrsatz zu finden, der in der Art des pythagoreischen Lehrsatzes die Konstruktion kubischer Wurzeln mit Zirkel und Lineal angibt. Wer also eine solche Methode oder einen solchen Lehrsatz findet, der hätte den Sieg über Plato, über Leonardo da Vinci und über Gauß davongetragen und würde mit einem Schlage zu den Unsterblichen im Reiche der Mathematik zu rechnen sein. Die Wissenschaft freilich sieht solchen Bemühungen mit Lächeln und Gemütsruhe zu; sie weiß, daß eine solche Methode unter der Bedingung Platos nicht möglich ist und hat daher endgültig Abschied genommen auch von diesen beiden Problemen, die aber, ähnlich wie der Kampf um die Quadratur des Kreises, für immer eins der eigenartigsten Kapitel in der Geschichte der mathematischen Forschung füllen.

Postskriptum

Trisektoren von heute – Beweise, die »sich erübrigen« – Der Beweis durch Abrollen – Ein scharfsinniger Jurist – Ein schwerer Fall – Ein guter Witz – Der Brief eines Toten – Die Methode der Hilfskurven – Mathematisch-finanzielle Ideen – Die Sage von dem hohen Preis – Die lockende Lorelei

Die Dreiteilung des Winkels hat es noch immer vielen angetan und zeitigt, wie bereits erwähnt, ununterbrochen eine Fülle von Lösungsversuchen mehr oder weniger sachverständiger Köpfe. Der Verfasser weiß ein Lied davon zu singen. Er hat das Dreiteilungsproblem wiederholt zum Gegenstand populärer Darstellung in Zeitungen und Zeitschriften gemacht; regelmäßig flatterten ihm nach solchen Veröffentlichungen aus nah und fern mehr oder weniger umfangreiche Ausarbeitungen zu, deren Verfasser den widerspenstigen zweischenkligen Gesellen dennoch und trotz des ablehnenden Verdiktes der Mathematiker von Fach, die mit dem Unmöglichkeitsbeweis sozusagen das Rennen um die positive Lösung dieses Problems aufgegeben haben, bezwungen zu haben und die Dreiteilung nach allen Regeln der Kunst ausführen zu können vermeinen. Die Zuschriften dieser Art sind eine überaus reichhaltige und merkwürdige Sammlung und lassen interessante Schlüsse sowohl auf die Denkungsweise wie auch auf die Psychologie ihrer Verfasser zu. Sämtliche bisher bekannten Erdteile sind in dieser Sammlung vertreten. Viele dieser Versuche lassen einen erheblichen Aufwand an Scharfsinn und Findigkeit erkennen, während andere allerdings nur höchst naiver Natur sind. »Gereizt durch den geheimnisvollen Zauber der Aufgabe habe ich mich an die Lösung der Aufgabe gemacht und glaube diese trotz Gauß im positiven Sinne gefunden zu haben –«, so schrieb mir einer dieser Problematiker, der mit diesen Worten dem Seelenzustand vieler anderer jedenfalls sehr schön Ausdruck verlieh. Unverzagtes Herangehen an den Feind, nämlich den widerspenstigen Winkel, völlige Unbeirrtheit von den Ergebnissen und der Auffassung der Wissenschaft, das ist der leicht erkennbare Charakterzug der meisten dieser Problematiker, und aus vielen ihrer Zuschriften liest man förmlich das Achselzucken darüber heraus, daß die Mathematiker die positive Lösung einer anscheinend so einfachen Aufgabe für unmöglich erklärt haben. Oftmals ist es ja tatsächlich keine ganz leichte Aufgabe, den Fehler der vorgelegten Konstruktion ausfindig zu machen, aber gefunden hat er sich schließlich in allen Fällen, womit aber noch durchaus nicht gesagt war, daß sich die Verfasser für besiegt erklärten. Ganz besonders ungläubige Thomasse halten auch trotz des ihnen nachgewiesenen Fehlers nach wie vor an der Meinung fest, daß nicht sie, sondern daß die Wissenschaft sich irre, und finden sie für diese Auffassung keine Zustimmung, so kommt es oftmals zu einem sehr geharnischten »letzten Wort«, in welchem dann auf die üblichen Formen der Höflichkeit kein besonderer Wert mehr gelegt wird. Dagegen kann man nichts machen.

Abb. 8

Etwa die Hälfte dieser Versuche geht dem hartnäckigen Problem in der folgenden naiven Weise zu Leibe: Man schlägt um die Schenkel eines Winkels einen Kreis und verbindet die Schnittpunkte durch eine Gerade, so daß ein gleichschenkliges Dreieck entsteht; dann wird die Verbindungsstrecke auf mehr oder weniger umständliche und kunstvolle Weise in drei Teile geteilt und die Teilpunkte werden mit dem Scheitel des Winkels durch gerade Linien verbunden, die nach der Meinung dieser Konstrukteure dann auch den Winkel in drei Teile teilen. Die Figuren I und II in Abbildung 8 veranschaulichen diesen Lösungsversuch. »Der Beweis erübrigt sich«, schreiben in merkwürdiger Übereinstimmung oftmals die Einsender zu dieser Behauptung. Hierzu ist aber zu bemerken, daß sich der Beweis keinesfalls »erübrigt« und der nonchalante Verzicht auf einen solchen wohl lediglich dem Unvermögen entspringt, diesen Beweis zu erbringen. Denn die Behauptung, daß durch die Dreiteilung der Verbindungslinie auch der Winkel selbst in drei Teile geteilt wird, ist absolut irrig. Bei einem spitzen Winkel scheint es allerdings so zu sein, daß das aber nur Schein ist, ersieht man sofort, wenn man einen stumpfen Winkel in dieser Weise behandelt. Wie die Figur II deutlich erkennen läßt, ist trotz der drei gleichen Teile der Verbindungslinie der hierbei entstehende Mittelwinkel viel größer als jeder der anliegenden, und entsprechend verhält es sich auch bei jedem spitzen Winkel, wenn bei einem solchen der Größenunterschied auch nur sehr gering ist. Gleich groß werden hierbei immer nur die beiden anliegenden Winkel, die aber, wie gesagt, mit dem Mittelwinkel leider nicht übereinstimmen. Das Verfahren dieser Problemlöser ist also sehr einfach, ihre Haupttätigkeit besteht zumeist darin, die Verbindungslinie in drei Teile zu teilen. Das halten sie für das Schwierigste an dem Problem und zu diesem Zweck erfinden sie unnötigerweise die kompliziertesten Methoden, unnötigerweise deswegen, weil jede Strecke in höchst einfacher Weise mit Zirkel und Lineal nicht nur in drei, sondern in jede beliebige Zahl gleicher Teile geteilt werden kann, was schon in den Anfangsgründen der Schulgeometrie gelehrt wird. Manche dieser Forscher aus innerem Drang ließen sich durch die verblüffende Einfachheit, mit der sie die Aufgabe gelöst zu haben glaubten, in ihren Zuschriften daher zu der zarten Andeutung verleiten, daß das angebliche Problem wohl nur in meinem Kopfe spuke oder ich mir nur einen Aprilscherz erlaubt habe, »denn anders kann es einfach nicht sein«, wie mir eine Dame aus Argentinien schrieb, die auch zugleich mitteilte, daß sie das Problem »überraschend schnell gelöst und knapp in einer Nacht die Dreiteilung der Verbindungslinie herausbekommen« habe. Die Konstruktion, die dieser fundamentalen Aufgabe gewidmet war, nahm nahezu einen Quadratmeter Papier ein, bedeckt mit einem schier undurchdringlichen Netz von Linien und Kreisbogen, geradezu eine Hochleistung geometrischen Scharfsinnes; aber die Dreiteilung des Winkels war es dennoch nicht.

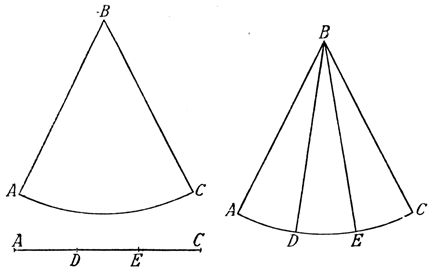
Abb. 9

Nicht ganz so einfach macht es sich eine andere Kategorie von Lösern, die sich von folgendem Gedanken leiten läßt: Man verbindet die Schenkel des Winkels durch einen Kreisbogen, verwandelt diesen dann in eine gerade Linie gleicher Länge und teilt diese in drei gleiche Teile, wie es Abbildung 9 veranschaulicht. Wird diese also geteilte Linie dann wieder in den Kreisbogen zurückverwandelt, so ist dieser und damit der Winkel selbst in drei Teile geteilt. Das wäre an und für sich auch durchaus richtig; die Dreiteilung des Kreisbogens ist tatsächlich gleichbedeutend mit der Dreiteilung des Winkels selbst und damit mit der Lösung des Problems. Aber leider stößt auch dieses so plausibel erscheinende Verfahren auf Tücken und Hindernisse. Denn ein Kreisbogen läßt sich mit Zirkel und Lineal leider auf keine Art und Weise in eine gerade Linie gleicher Länge verwandeln, denn das käme auf die Quadratur bzw. die Rektifikation des Kreises heraus, eine Aufgabe, deren Lösung mit Zirkel und Lineal genau so unmöglich ist wie die Dreiteilung des Winkels. Andere Löser dieser Gattung glauben den Kreisbogen durch »Abrollen« eines Kreissegmentes in eine gerade Linie gleicher Länge verwandeln zu können, wozu aber zu bemerken ist, daß dieses Verfahren im Sinne der Platonischen Bedingung, die nur Zirkel und Lineal zuläßt, eine unzulässige Operation ist; sonst würde es ebenfalls stimmen. Andere Löser wollen den Kreisbogen »nur mit Zirkel und Lineal« durch Ausprobieren in die nötigen drei Teile teilen, was aber an dem Umstande scheitert, daß auch dieses »Ausprobieren« keine zulässige, d. h. keine exakte geometrische, Methode ist, weil für die auf solche Weise ausprobierten Teilpunkte niemals der exakte Beweis erbracht werden kann, daß es auch wirklich die Teilpunkte im geometrischen Sinne sind, denn solche können immer nur durch Schnittpunkte von Linien, geraden oder krummen, erzeugt werden.

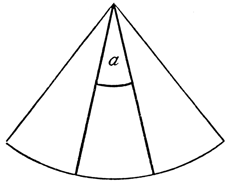
Abb. 10

Einen genialen Einfall hatte ein scharfsinniger Jurist. Er argumentierte folgendermaßen: Ich konstruiere einen beliebigen Winkel a, lege dann an jeden Schenkel dieses Winkels vom Scheitelpunkte an einen Winkel gleicher Größe (Abbildung 10), alles Operationen, die sich mit Zirkel und Lineal ausführen lassen, und erhalte auf diese Weise einen Winkel, der als der Gesamtwinkel der drei anderen in genau drei gleiche Teile geteilt ist, und zwar mit aller nur wünschenswerten mathematischen Exaktheit, selbst Plato hätte es nicht genauer machen können. Das ist absolut richtig; der auf diese Weise konstruierte Winkel besteht ganz zweifellos aus drei gleichen Teilen, und es ist keinerlei Verstoß gegen die Platonische Bedingung erfolgt. Aber leider hat auch diese geniale Konstruktion ihren Haken, denn was hierbei geschehen ist, ist nicht die Dreiteilung eines gegebenen Winkels, sondern die Aneinanderfügung dreier gleicher Winkel zu einem neuen Winkel, das heißt also die Verdreifachung oder die Multiplikation eines Winkels und damit gerade das Gegenteil der verlangten Aufgabe. Also konnte auch diesem scharfsinnigen Logiker trotz der unbestreitbaren Originalität seines Gedankens der Preis nicht zuerkannt werden. Aber einmal konnte ich einem Trisektor doch bestätigen, daß die von ihm konstruierte Dreiteilung eines Winkels als absolut richtig und korrekt zu bezeichnen sei, und zwar vollkommen unter Wahrung der Platonischen Bedingung; nur hatte er leider seinen Versuch an einem Winkel von 90 Grad unternommen, und ein solcher ist, wie überhaupt jeder Winkel, dessen Gradzahl durch 9 teilbar ist, immer in exakter Form in drei Teile zu teilen, und zwar in ganz einfacher Weise und ohne die ungeheuerlich komplizierte und verzwickte Konstruktion, die dieser Problematiker erdacht und ausgeführt hatte, um an das Ziel zu kommen. Für die Dreiteilung eines beliebigen Winkels aber reichte auch diese Konstruktion nicht aus, und so mußte auch hier eine Hoffnung getäuscht werden.

Ein Herr endlich teilte mir sein Verfahren mit, daß nicht nur die Dreiteilung, sondern sogar jede beliebige Teilung eines Winkels mit mathematischer Exaktheit möglich machen sollte. Er hatte, begeistert von seiner Idee, seine Bearbeitung sogar gleich drucken lassen; es war eine stattliche Broschüre geworden, versehen mit sehr vielen und schönen Zeichnungen und einem Vorwort, in welchem sich der Verfasser selbst begeistert als denjenigen pries, dem die Lösung des zweitausendjährigen Rätsels restlos gelungen sei. Natürlich ergab die Prüfung des Beweises auch hier Fehler, mehrere ganz dicke sogar, und mir blieb nur übrig, dem Verfasser, der die Broschüre übrigens siegesbewußt dem Buchhandel übergeben hatte, mitzuteilen, daß es zweckmäßiger gewesen wäre, mir seine Arbeit vor der Drucklegung zu unterbreiten, dann hätte er die mehrere hundert Mark betragenden Kosten der Drucklegung erspart.

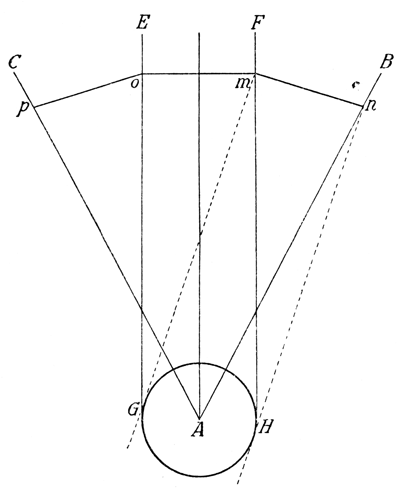
Abb. 11

Viel Vergnügen, aber auch viel Kopfschmerzen, verursachte mir die in der Abbildung 11 wiedergegebene Konstruktion zur Lösung des Problems; Vergnügen, weil es sich um eine äußerst originelle Lösung handelte, Kopfschmerzen aber deswegen, weil ich in Verlegenheit geriet, dem Urheber den Fehler klarzumachen. Der schrieb mir, daß er die Lösung des Problems endlich gefunden habe, und zwar, wie er ausdrücklich betonte, lediglich mit Zirkel und Lineal. Und dem war auch beinahe wirklich so. Zur Dreiteilung des Winkels BAC benötigt der Verfasser dieser Konstruktion eines Lineals und schlägt zunächst um den Scheitelpunkt einen Kreis, dessen Durchmesser geradeso groß wie das Lineal breit ist. Dann legt er das Lineal in der Richtung der Mittellinie des Winkels auf den Kreis und zieht die Linien EG und FH. Dann dreht er das Lineal auf dem Kreise und schiebt es dabei gleichzeitig so weit, bis die Breitseite des Lineals gleichzeitig den Schenkel BA und die Gerade FH berührt, und zieht auf der Breitseite des Lineals die Linie mn. Macht er das auf der anderen Seite des Winkels ebenso, so gewinnt er auf diese Weise die Punkte m, n, o, p. Denken wir uns dann die Punkte o und m noch mit dem Scheitel Averbunden, so ist durch diese Verbindungslinien der Winkel tatsächlich in drei Teile geteilt. Und ebenso tatsächlich sind bei der Konstruktion nur Zirkel und Lineal verwandt, unzweifelhaft eine höchst originelle Methode, der Platonischen Bedingung Genüge zu leisten. Freilich hat die Sache einen kleinen Haken. Denn der Verfasser dieser hübschen Konstruktion hat das Lineal bei der beschriebenen Operation teils als Zirkel benutzt, indem er es auf dem Kreise drehte, teils zum Einschieben der Strecke mn. Das Lineal soll aber lediglich zum Ziehen gerader Linien verwandt werden, und ein solcher weitergehender Gebrauch dieses nützlichen Instrumentes ist eine durchaus unzulässige Verwendung desselben, mit der Plato keinesfalls einverstanden sein würde. Die Einschiebung der Strecke mn in der geschilderten Weise kennzeichnet das Verfahren als Einschiebemethode nach Art der im vorhergehenden Aufsatz beschriebenen Weise. Aber das dem glücklichen Urheber dieser gescheiten Konstruktion klarzumachen, war nicht leicht, und gelungen ist es mir nicht. Auf mein diesbezügliches aufklärendes Schreiben erhielt ich eine geharnischte Antwort: Er habe, wie ich es in meinem Aufsatze als notwendig bezeichnet habe, tatsächlich nur Zirkel und Lineal bei der Konstruktion verwandt, und nun mache ich plötzlich solche Einwendungen; entweder wisse ich selbst nicht, was ich wolle, oder ich wolle ihm die Richtigkeit seiner Konstruktion aus Mißgunst nicht bestätigen. Er werde sich nunmehr an die Universitäten wenden! Da hatte ich nun mein Fett weg, und ich konnte das dem Schöpfer dieser kernigen Worte – sie waren sogar noch etwas betonter – nicht einmal übelnehmen. Mein einziger Trost war, daß, seiner Ankündigung zufolge, sich wohl noch eine ganze Reihe Universitätsmathematiker denselben Anblaser von ihm geholt haben mag.

Herzlich gelacht habe ich über die Mitteilung eines Herrn, der mir schrieb, daß ihm die Lösung des Dreiteilungsproblems restlos gelungen sei. Die Ausführung der Konstruktion erfordere gerade fünf Minuten, und er habe sie bereits einem Professor der Mathematik zur Begutachtung vorgelegt; der habe ihm aber mitgeteilt, daß fünf Minuten für den gedachten Zweck eine viel zu lange Zeit sei! Der Brave hatte nicht gemerkt, daß der Professor, der ein Mann von gutem Humor zu sein scheint, sich mit ihm einen famosen Witz gemacht hatte, denn selbstverständlich hat die Zeit mit der Richtigkeit oder Unrichtigkeit einer geometrischen Konstruktion nicht das geringste zu tun. Sogar von einem – Toten erhielt ich eine Konstruktion zur Winkeltrisektion zugesandt, allerdings nicht von ihm persönlich, denn es ist wohl anzunehmen, daß man im besseren Jenseits über solche und noch zahlreiche andere Fragen einwandfrei im klaren ist, wohl aber von seinen Hinterbliebenen. Ein Ehepaar teilte mir mit, daß der Vater eines der Gatten sich jahrelang mit dem genannten Problem befaßt und die Lösung bestimmt gefunden zu haben geglaubt hatte; kurz vor seinem Tode hatte er die Lösung in Form einer Broschüre veröffentlicht, und es war bis zu seiner letzten Stunde ein Herzensbedürfnis von ihm gewesen, dafür die Anerkennung der Nachwelt zu finden. Man bat daher um Nachprüfung der Arbeit, um gegebenenfalls dem Verstorbenen noch posthum zu der verdienten Anerkennung zu verhelfen. Die übersandte Druckschrift enthielt einen hübschen Versuch von der Art der bereits oben erwähnten Konstruktionen, bei denen die Lösung des Problems durch Rektifizierung eines Kreisbogens angestrebt wird, konnte aber aus den bereits angegebenen Gründen ebensowenig wie jene als eine wirkliche Lösung des Problems gelten. So mußte ich den Übersendern der Arbeit leider schreiben, daß es doch wohl im Interesse des Andenkens des Toten liegen dürfte, wenn die weitere Verbreitung der von ihm verfaßten Arbeit unterbliebe.

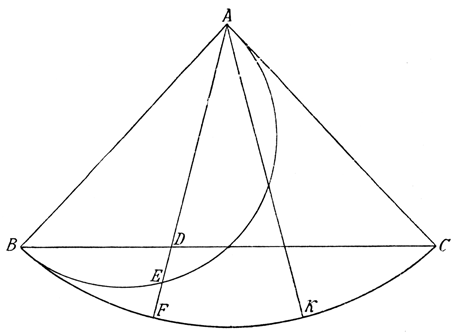
Abb. 12

Abb. 13

Eine Anzahl der mir zugegangenen Lösungsversuche ist jedoch auch wesentlich höher einzuschätzen. Es waren das solche, die auf eine Annäherungsmethode von mehr oder weniger großer Genauigkeit hinausliefen, darunter einige, die einen bemerkenswerten Scharfsinn erkennen ließen. Einen interessanten Versuch dieser Art zeigt Abbildung 12/13. Sie wurde mir von einem mitteldeutschen Großindustriellen übersandt mit humorvoller Schilderung, daß ihm das vertrackte Dreiteilungsproblem manche schlaflose Nacht gekostet habe, bis er zur Lösung gelangt sei. Die Konstruktion ist auch noch aus anderen Gründen bemerkenswert und sei daher kurz erörtert. Angenommen, der Winkel ABC (Abbildung 12) sei durch die Strecken AF und AK in drei Teile geteilt, so schneidet der Radius AF den Halbkreis über AB im Punkte E. Zugleich halbiert der Punkt E, wie leicht zu beweisen ist, den Abschnitt DF des Radius AF. Es kommt also auf die Bestimmung des Punktes E an, durch den die eine der beiden Dreiteilungsstrecken gehen muß. Das erreichte der Einsender durch die in Abbildung 13 dargestellte, von ihm etwas stilisierte Konstruktion. Über der Strecke AB wird der Halbkreis errichtet (der hier nur bis zu der Verbindungslinie BC reicht); dieser ist der eine geometrische Ort für den zu bestimmenden Punkt. Dann werden von dem Scheitelpunkte A aus zahlreiche Radien gezogen. Die Abschnitte dieser Radien, die durch die Verbindungslinie BC und den Kreisbogen BC bestimmt werden, werden sodann halbiert und die Halbierungspunkte verbunden. Die Verbindungslinie dieser Halbierungspunkte der Radiusabschnitte ist der zweite geometrische Ort des zu bestimmenden Punktes E und stellt eine Kurve dar. Derjenige Radiusabschnitt, dessen Mittelpunkt auf den Halbkreis fällt, bestimmt den gesuchten Punkt E, und die durch diesen Punkt gezogene Gerade ist eine Dreiteilungsstrecke. In entsprechender Weise wird natürlich auch die andere Teilungsstrecke bestimmt und durch dieses Verfahren der Winkel in drei Teile geteilt. Es handelt sich also um die Konstruktion der die Mittelpunkte der Radiusabschnitte verbindenden Kurve. Diese Kurve nun ist die Achillesferse des interessanten Lösungsversuchs, denn sie kann nicht, wie es beim Kreise vermittelst des Zirkels möglich ist, in einem Zuge hergestellt bzw. als vollständige Linie gezogen werden, sondern es können immer nur einzelne Punkte der Kurve bestimmt werden, nämlich so viele, als Radien gezogen werden. Dadurch kann aber auch der Schnittpunkt der Kurve mit dem Halbkreis AB nicht genau ermittelt werden, denn die Kurve kann nur punktweise an den Halbkreis herangeführt werden, ohne daß es möglich ist, unter den unendlich vielen Punkten, die selbst in unmittelbarster Nähe des Halbkreises auf der Kurve liegen, exakt den einzigen und alleinigen Punkt E zu bestimmen, der der Schnittpunkt der Hilfskurve mit dem Halbkreis ist. Der Schnittpunkt kann bei diesem Verfahren also nur annäherungsweise ermittelt werden, und die ganze Konstruktion hat daher ebenfalls nur den Wert einer Annäherungskonstruktion. Immerhin ist sie durch die Einfachheit und Durchsichtigkeit der obwaltenden Verhältnisse ein schöner und interessanter Versuch, und das konnte ich ihrem Urheber zum Trost mitteilen, wenn ihm der erhoffte volle Preis für seine schlaflosen Nächte freilich ebenfalls nicht zuerkannt werden konnte.

Abb. 14

Eine andere sehr hübsche und interessante Annäherungskonstruktion dieser Art ist auch die in Abbildung 14 dargestellte, die mir von Oberst v. T. übersandt wurde. Von dem Scheitelpunkt A des Winkels BAC aus werden zahlreiche Kreisbogen über dem Schenkel AB geschlagen. Auf jedem dieser Kreisbogen wird eine beliebige, aber für alle Bogen gleiche Einheitsstrecke dreimal hintereinander abgetragen. Die Verbindung dieser Teilpunkte liefert die drei Kurven I, II und III, die also auf jedem der von ihnen geschnittenen Kreisbogen drei gleiche Teile bestimmen. Ziehe ich nun durch den Punkt E, in welchem die Kurve III den Schenkel AC des gegebenen Winkels schneidet, einen Kreisbogen um A, so wird der Bogen EF und damit der durch ihn bestimmte Winkel EAF, der mit dem Winkel CAB identisch ist, durch die drei Kurven in drei Teile geteilt. Das Verfahren wirkt nahezu überraschend; tatsächlich scheint eine exakte Dreiteilung erreicht zu sein, und solche Methoden machen es erklärlich, daß manchmal selbst mathematisch geschulte Köpfe glaubten, auf diese Weise das Trisektionsproblem restlos gelöst zu haben. Aber der Mangel der Methode liegt, ähnlich wie in der vorbeschriebenen, so auch hier in dem Umstande, daß die nötigen Hilfskurven nicht vollständig, sondern immer nur punktweise konstruiert werden können und daher auch der Schnittpunkt der Kurve III mit dem Winkelschenkel AC nicht mit der nötigen mathematischen Genauigkeit bestimmt werden kann. Wohl aber ist es möglich, auf solche Weise jede gewünschte Annäherungsgenauigkeit zu erzielen.

Die vorbeschriebenen Verfahren sind typisch für die vielen Annäherungskonstruktionen, die mit Hilfskurven die Lösung geometrischer Probleme zu bewirken suchen. Was von der hier beschriebenen Kurve gesagt wurde, gilt von allen solchen Hilfskurven; sie können immer nur punktweise konstruiert werden und ermöglichen daher niemals eine wirklich exakte, sondern immer nur eine annäherungsweise genaue Ausführung der verlangten Konstruktion. In sehr vielen Fällen aber glauben die Erfinder solcher Kurvenmethoden mit diesen die Lösung des Problems wirklich gefunden zu haben, und es ist dann oftmals nicht leicht, ihnen das Zugeständnis des Mangels ihrer Methode abzuringen. Bemerkt sei noch, daß bereits die Geometer des Altertums eine ganze Anzahl solcher Hilfskurven zur Dreiteilung des Winkels erfunden hatten. Vermittels solcher Hilfskurven kann übrigens auch jede andere Winkelteilung, etwa die 5-, 7-, 9-, 11- usw. Teilung bewirkt werden. Beispielsweise brauchten in der Konstruktion der Abbildung 14 auf den einzelnen Kreisbogen nur 5 oder 7 Teile abgetragen zu werden, um auch die 5- oder 7-Teilung des Winkels zu bewirken. Ebenso kann die Methode auch dazu dienen, die Verdoppelung des Würfels und ebenso auch die Quadratur des Kreises auszuführen, selbstverständlich ebenfalls immer nur annäherungsweise. Die Methode der Hilfskurven hat bei Versuchen zur Lösung der berühmten geometrischen Probleme eine große Rolle in der Vergangenheit gespielt und spielt diese bei den heutigen Problematikern dieser Art auch noch.

Unter den Trisektoren sind übrigens nach meinen Erfahrungen in ganz besonderem Maße auch diejenigen Problematiker vertreten, die ihre kühnen Ideen zur Lösung der mathematischen Probleme zugleich mit weittragenden finanziellen Plänen verbinden. Mehr oder weniger werden ja die meisten dieser Experimentatoren den Nebengedanken hegen, wenn möglich mit ihren mühevollen Versuchen auch etwas Geld zu verdienen, was man ihnen auch wirklich nicht verargen kann. Aber bei manchen von ihnen werden diese Nebengedanken doch zu Hauptgedanken und nehmen dann die merkwürdigsten Formen an. So unterbreitete mir ein heller Sachse ein Projekt zur finanziellen Ausbeutung seiner angeblich todsicheren Lösung sowohl des Dreiteilungs- wie auch des Delischen Problems. Er schlug vor, nach Art der Rennwetten einen Totalisator für oder gegen die Richtigkeit seines Lösungsversuchs zu veranstalten, und gab der Hoffnung Ausdruck, daß sich ungezählte Tausende gern mit Einsätzen an einem solchen mathematischen Match beteiligen würden. Ferner ließe sich, wie er glaubte, auch eine erhebliche Einnahmequelle schaffen, wenn seine Lösung der genannten Probleme in Form einer Broschüre in allen Weltteilen gedruckt und über den ganzen Erdball vertrieben würde. Man sieht, Genialität und Geschäftstüchtigkeit brauchen nicht immer getrennt voneinander zu wohnen.

Gerade von dem Trisektionsproblem wird von sehr vielen Leuten angenommen, daß für seine Lösung irgendwo und von irgendwem hohe Preise ausgesetzt seien. Dazu aber ist zu bemerken, daß alle solche Erwartungen vollkommen unberechtigt sind, denn für die Lösung von Problemen, die nachgewiesenermaßen nicht gelöst werden können, werden weder von den wissenschaftlichen noch von sonstigen Instituten Preise ausgesetzt, und ob vielleicht irgendein privater Querkopf einen solchen Preis ausgesetzt hat, wie es in der Geschichte jener Probleme ja oft vorgekommen ist und übrigens bei anderen wissenschaftlichen Aufgaben auch jetzt noch vorkommt, entzieht sich meiner Kenntnis. Das Gerücht von irgendwelchen hohen Preisen für die Lösung des Dreiteilungsproblems jedenfalls erhält sich hartnäckig. So teilte mir ein Herr, der mir seine Trisektion zur Prüfung übersandt hatte, gleichzeitig folgendes mit: Er habe gehört, daß auf der Bank von England ein Preis von 50 000 Pfund für die Lösung jenes Problems deponiert sei, und habe auch dieserhalb an die Bank geschrieben; diese habe ihm jedoch mitgeteilt, daß ihr von einem solchen Depot nichts bekannt sei. Nun wolle er sich, wenn, was er mit Bestimmtheit annehme, die Prüfung die Richtigkeit seiner Lösung ergäbe, sich »behufs Erlangung eines dem Weltproblem entsprechenden Preises« an die berühmteste Universität Amerikas wenden, da bei dem verarmten Deutschland auf einen solchen Preis doch kaum zu rechnen sei. Die Richtigkeit seiner Lösung konnte ich ihm nicht bestätigen, was aber nicht ausschließt, daß er seine energischen Bemühungen um die Erlangung eines »Weltpreises« bei den Engländern oder Amerikanern fortsetzt. Es ist übrigens bemerkenswert, welche hochgespannten Erwartungen solche Problematiker für ihre Bemühungen auf das reiche Amerika setzen. Die merkwürdigsten Optimisten habe ich nach dieser Hinsicht kennengelernt. Buchstäblich wahr ist folgender Fall: Ein Herr, von Beruf Arzt und außerdem eine der bekannten problematisch-mathematischen Naturen, überbrachte mir seine Lösungen etwa eines Dutzends der berühmtesten und schwierigsten mathematischen Probleme: außer dem der Quadratur, der Dreiteilung und Würfelverdoppelung auch das des Gesetzes der Primzahlen, der Teilbarkeit der Zahlen, des Fermatschen Problems usw. Seine Überzeugung von der absoluten Richtigkeit seiner Lösungen konnten ihm auch meine Einwände nicht erschüttern, und nebenbei erzählte er mir, er wolle sich zur besseren Verwertung seiner Entdeckungen an die Amerikaner wenden; die schmissen ja für solche Dinge nur so mit den Milliarden, und er hoffe mit Bestimmtheit, auf diese Weise so viel Geld zu bekommen, um damit alle Kriegsschulden Deutschlands bezahlen zu können; das Geld werde er zu besagtem patriotischen Zweck dann Hindenburg bringen und für sich nur eine Kleinigkeit, etwa eine oder einige Millionen, behalten! Auch ich solle dann für meine Prüfung, wenn sie auch nicht zu einem mit seiner Auffassung übereinstimmenden Ergebnis gekommen sei, nicht vergessen und entsprechend honoriert werden. Ich habe keine Hoffnung darauf gesetzt, auf diese Weise zu einem ungeahnt glänzenden Honorar zu kommen, denn ich glaube, daß die kühl und nüchtern denkenden Yankees ihre Milliarden für alles andere eher als für die ausgefallenen Probleme der Mathematik anwenden werden. Solche Dinge sind nur so recht etwas für deutsche »Sinnierer«, die dauernd unerreichbaren Sphären nachstreben, wenn sie auch, wie die erwähnten Beispiele zeigen, allmählich anfangen, das Ideale mit dem finanziell Nützlichen zu verbinden, aber natürlich gleich in der unpraktischsten Weise weltentrückter Optimisten. Zur Psychologie solcher Problematiker ist dieser mammonistische Optimismus immerhin ein wertvoller Beitrag.

Das ist nur eine kleine Auslese aus der stattlichen Sammlung von Versuchen aus Laienkreisen, die Lösung eines Problems zu erzwingen, die nachgewiesenermaßen nicht möglich ist. Sie vermehrt sich noch ununterbrochen und hat manche heitere Blüte aufzuweisen. Der »geheimnisvolle Zauber des Problems« lockt wie der Sang der Lorelei und findet immer wieder seine Opfer, und das wird wohl auch noch für geraume Zeit so bleiben. Nochmals sei daher betont, daß das vielumstrittene Problem heute durch den wissenschaftlichen Unmöglichkeitsbeweis als absolut gelöst zu betrachten ist, wenn diese Lösung dem Nichtmathematiker auch nicht einleuchtet und sich ihm gefühlsmäßig die Ansicht immer wieder aufdrängt, daß eine, rein äußerlich betrachtet, so einfache Aufgabe sich dennoch in der verlangten Weise positiv lösen lasten müsse. So unmöglich es ist, aus zweimal zwei fünf zu machen, so unmöglich ist es, die Dreiteilung des Winkels mit Zirkel und Lineal auszuführen. An dieser exakt bewiesenen Unmöglichkeit müssen alle gegenteiligen Versuche scheitern. Vielleicht tragen diese Zeilen dazu bei, der so verlockenden und aufreizenden Macht, die das merkwürdige Problem noch immer auf so viele ausübt, Abbruch zu tun und die noch immer zahlreichen Problematiker dieser Art von der Vergeblichkeit ihrer Versuche zu überzeugen Unmittelbar vor Toresschluß, d. h. vor Drucklegung dieses Werkes, meldet sich noch ein Rufer im Streite um das Trisektionsproblem zum Wort. Es ist Herr De Sauerhering, der in einer Broschüre mit dem geheimnisvollen Titel »Paracaidas« sich speziell meine Wenigkeit aufs Korn nimmt und mit von keinerlei Sachkenntnis gedämpfter Energie gegen einen Aufsatz meiner Feder über die Unmöglichkeit der Winkeldreiteilung zu Felde zieht. Für Herrn De S. gibt es eine solche Unmöglichkeit nicht; er unterbreitet der staunenden Mitwelt gleich drei Methoden zur unwiderruflich richtigen Lösung des Problems und spricht mit hohem Selbstgefühl von »meiner nach 2300 Jahren erfolgten Entdeckung der, wie es Plato verlangte, nur mit Lineal und Zirkel zu vollziehenden Dreiteilung jeden Winkels«. Bedrückt widmet man sich der Lektüre der vollen 27 Druckseiten, die alle bisherigen Mathematiker in den Schatten stellen und vernichten sollen. Aber man atmet sehr bald auf. Die vorgeführten Konstruktionen und »Beweise« wimmeln von groben Fehlern, zeigen auch keinerlei Scharfsinn, der ihre Wiedergabe lohnte, sondern sind lediglich grob falsch. Ein großer Aufwand an Arbeit und Druckkosten war wiederum einmal schmählich vertan, und übrig bleibt nur ein höchst komischer Beitrag zu dem Kapitel unfreiwilligen Humors in der Mathematik..

5. Das Problem der Kreisteilung

Noch ein Kreisgeheimnis – Vom 3- und 6-Eck, vom 5-, 10- und 15-Eck – Der Drudenfuß – Die heilige Sieben – Ein altes Problem und ein junger Student – Die Entdeckung der 17-Teilung des Kreises – Die Gaußschen Kreisteilungszahlen – Ohne Lineal

In der Quadratur des Kreises haben wir das bekannteste und berühmteste Problem kennengelernt, das sich an die Kreisfigur knüpft. Aber die Quadratur ist keineswegs das einzige Geheimnis des Kreises. Ein anderes und kaum weniger reizvolles Problem dieser Art ist auch die Kreisteilung, das heißt die Aufgabe, die Kreislinie, gelehrt als Peripherie bezeichnet, mit Zirkel und Lineal in eine Anzahl gleicher Teile zu teilen. Dieses Problem ist in Laienkreisen viel weniger bekannt als das der Quadratur, obwohl sich auch an diese Aufgabe eine lange und inhaltreiche Geschichte und eine Fülle überaus interessanter Konstruktionen und Einzelfragen knüpft.

Abb. 15
Die 3-, 6- und 12-Teilung des Kreises

Sehr viele Fälle der Kreisteilung sind leicht und einfach auszuführen, und solche Fälle werden bereits in der Schulgeometrie gelehrt. Das Problematische dieser Konstruktionen steckt vielmehr in bestimmten Einzelfällen, für die es unter der Platonischen Bedingung keine Lösung gibt. Betrachten wir zunächst kurz die möglichen Fälle der Kreisteilung. Um beispielsweise einen Kreis in zwei Teile zu teilen, braucht man nur durch den Mittelpunkt des Kreises eine gerade Linie zu ziehen, deren Schnittpunkte mit der Peripherie diese in zwei gleiche Teile teilen. Errichtet man dann auf diesem Durchmesser im Mittelpunkte nach beiden Seiten eine lotrechte Linie, so wird hierdurch der Kreis in vier gleiche Teile geteilt, und verbindet man die erhaltenen vier Teilungspunkte durch gerade Linien, so erhält man ein regelmäßiges Viereck oder Quadrat. Auch die Sechsteilung ist überaus einfach und geschieht, indem man den Radius oder Halbmesser des Kreises von irgendeinem Punkte der Kreislinie an hintereinander auf dieser abträgt; das sechste Teilstück hört dann dort auf, wo das erste anfing, und damit ist die Konstruktion ausgeführt. Durch Verbindung dieser Teilungspunkte erhält man das regelmäßige Sechseck, bei dem also alle Seiten und Winkel gleich groß sind, eine sehr schöne geometrische Figur, die in der Mythologie, in Sitte und Glauben, allerdings auch im Aberglauben vieler Völker eine große Rolle gespielt hat. Die Entdeckung der Sechsteilung des Kreises und die Konstruktion des regelmäßigen Sechseckes in dieser Weise soll bereits den alten Babyloniern gelungen sein. Selbstverständlich kann in leichter Weise der Beweis geführt werden, daß durch diese Operation die Kreislinie auch wirklich mit mathematischer Exaktheit in sechs Teile geteilt wird. Verbindet man je zwei der sechs Teilungspunkte, indem man immer einen Punkt übergeht, so teilen die übrigen drei Punkte die Kreislinie in drei gleiche Teile, und man erhält das regelmäßige oder gleichseitige Dreieck, wie es unsere Abbildung 15 veranschaulicht. Ferner können wir, wenn eine bestimmte Teilung gelungen ist, leicht und einfach eine Teilung der Kreislinie von der doppelten Teilungszahl bewirken. Wenn wir beispielsweise in unserer Figur 15 die Seite des regelmäßigen Sechseckes, das die stark gezeichneten Linien darstellen, halbieren und durch diesen Halbierungspunkt eine gerade Linie vom Mittelpunkte des Kreises bis zur Peripherie legen, so ist hierdurch das Bogenstück über der Seite des Sechseckes ebenfalls in zwei Teile geteilt, und führen wir diese Operation bei allen sechs Seiten aus, so ist hierdurch der Kreis in zwölf gleiche Teile geteilt, und durch Verbindung dieser Teilungspunkte ergibt sich das regelmäßige Zwölfeck. Auf entsprechende Weise können wir dann auch die 24-, die 48-, die 96- usw. Teilung des Kreises ausführen, ebenso aus der 2- oder 4-Teilung auch zu der 8-, der 16-, der 32-, der 64- usw. Teilung gelangen und die entsprechenden regelmäßigen Vielecke konstruieren, alles Operationen, bei denen wir lediglich Zirkel und Lineal benötigen. Auf diese Weise erhalten wir also bereits eine überaus große Anzahl von Kreisteilungen.

Abb. 16.
Die 10-Teilung des Kreises

Etwas verwickelter, aber auch noch sehr einfach ist die 10-Teilung des Kreises. Sie wird in mathematischer Weise ausgeführt, indem man, wie es unsere Abbildung 16 zeigt, durch den Mittelpunkt des gegebenen Kreises zunächst zwei aufeinander senkrechte Durchmesser legt, dann um den Mittelpunkt eines der so erhaltenen Halbmesser einen Kreis schlägt und den Mittelpunkt dieses kleinen Kreises mit dem Punkte A verbindet, in welchem die zu teilende Kreislinie sich mit dem anderen Durchmesser schneidet. Diese Verbindungslinie schneidet den kleinen Kreis in dem Punkte C, und trägt man die so erhaltene Strecke AC von irgendeinem Punkte der Kreislinie, also etwa von A an, auf dieser ab, so wird die Kreislinie hierdurch in zehn gleiche Teile geteilt. Durch Verbindung dieser Teilpunkte erhalten wir dann das regelmäßige Zehneck. Durch Überspringen je eines Teilpunktes gelangt man dann auch zur Fünfteilung und durch Verbindung dieser Teilungspunkte zur Konstruktion des regelmäßigen Fünfeckes.

Abb. 17
Der Drudenfuß

Ein anderes Fünfeck zeigt unsere Abbildung 17. Es entsteht, indem man bei der Verbindung der Teilpunkte immer einen Punkt überspringt; der letzte Verbindungszug kehrt dann zum Ausgangspunkt zurück; das Mittelstück dieser ebenfalls sehr interessanten Figur zeigt dann wieder ein kleines regelmäßiges Fünfeck. Diese Figur, Pentagramm oder – volkstümlicher – Drudenfuß genannt, nimmt im Glauben und Aberglauben einen noch größeren Raum als das bereits erwähnte Sechseck ein. Diese Figur sollte, auf der Schwelle ausgezeichnet, Teufel, Hexen und böse Geister vom Hause fernhalten. »Das Pentagramma macht dir Pein?« fragt in diesem Sinne Faust spöttisch Mephisto, der sich in einer solchen Figur gefangen hat und nun nicht wieder heraus kann.

Abb. 18
Die 15-Teilung des Kreises

Von der Zehnteilung gelangen wir durch Halbierung dann auch zur 20-, 40-, 80- usw. Teilung des Kreises und zur Konstruktion der entsprechenden Vielecke. Endlich können wir in dieser Weise, also nur mit Zirkel und Lineal, auch noch die 15-Teilung ausführen. Sie geschieht, indem man von irgendeinem Punkte A der Peripherie erst den sechsten Teil, der dem Bogen AB entspricht (Abb. 18), dann von demselben Punkte aus den zehnten Teil des Kreisumfanges (Bogen AC) abträgt. Die Differenz zwischen diesen beiden Bogenstücken, in unserer Figur also der Bogen BC, ist der fünfzehnte Teil des Gesamtumfanges des Kreises, denn es ist ¹/ ₆ – ¹/ ₁₀ = ¹/ ₁₅. Durch Halbierung gelangen wir dann auch zur 30-, 60-, 120- usw. Teilung und den entsprechenden regulären Vielecken.

Damit sind aber auch die Möglichkeiten der Kreisteilung in der geschilderten elementaren Weise erschöpft. Zwar können auf diese Weise zahlreiche Teilungen ausgeführt, noch viel mehr aber nicht ausgeführt werden. Beispielsweise fehlen unter den angegebenen Teilungen die 7-, 9-, 11-, 13- usw. Teilung und ebenso, um auch einige höhere Teilungszahlen zu nennen, die 35-, 70-, 86-, 87-, 88-, 90- usw. Teilung, und ebenso auch die entsprechenden regelmäßigen Vielecke. Diese Teilungen und Konstruktionen also konnten mit Zirkel und Lineal nicht bewirkt werden, soviel man auch forschte und so viele verschiedenartige Methoden man für diesen Zweck auch ersann. Sind die 2-, 3- und 5-Teilung und die hieraus durch Halbierung und Kombination abgeleiteten Teilungen und Konstruktionen die einzigen oder sind noch andere möglich? Das war die Frage, die sich den Mathematikern aufdrängte und die Antwort von ihnen heischte.

Auch dieses Problem hat schon die ältesten Geometer beschäftigt, ja in seiner einfachsten Form ist es sogar älter als die Quadratur des Kreises. Denn Kreisteilungen und Vieleckskonstruktionen waren von jeher für die verschiedensten praktischen, technischen und wissenschaftlichen, besonders auch astronomischen Zwecke notwendig, und das führte naturgemäß schon in frühester Zeit zu Versuchen und Methoden, auch alle übrigen Kreisteilungen auszuführen. Schon Ägypter und Babylonier suchten diese Probleme zu lösen, angeregt vor allem durch die Beschäftigung mit der Astronomie, die besonders bei den Babyloniern bereits in hoher Blüte stand, und von diesen Völkern ging die Beschäftigung mit den Problemen der Kreisteilung dann auch auf die Griechen über, bei denen diese, wie die gesamte Geometrie überhaupt, ihre präzis wissenschaftliche Formulierung erhielten, vor allem durch die Bedingung Platos, die auch für die Lösung dieser Probleme und die Ausführung der entsprechenden Konstruktionen Zirkel und Lineal als einzig zulässige Hilfsmittel festsetzte. Unter diesen einengenden Bedingungen aber gelang die Ausführung weiterer Teilungsarten als der genannten nicht, soviel Scharfsinn und Arbeit die Geometer seit Pythagoras' Zeiten auch diesen Problemen zuwandten. Insbesondere auf die Siebenteilung des Kreises wurde die Jahrhunderte hindurch sehr viel Arbeit und Scharfsinn verwandt, denn die Sieben galt von jeher als heilige Zahl, und daher war die Siebenteilung des Kreises und die Konstruktion des regelmäßigen Siebenecks mit Zirkel und Lineal ein besonders eifrig verfolgtes Ziel der Geometer. In den engeren Kreisen der Mathematiker spielte die Siebenteilung kaum eine geringere Rolle als die Quadratur des Kreises.

Auch hier ging es wie bei den anderen großen Problemen, die sich an Zirkel und Lineal knüpfen. Die Mathematiker des Altertums wie des Mittelalters versuchten sich ebenso eifrig wie vergeblich auch an diesem Problem, und zahlreiche Methoden wurden erdacht, die aber alle nicht zum befriedigenden Ziele führten. Bei alledem müssen wir uns auch hier vor Augen halten, daß die verlangten Teilungen und Konstruktionen eben nur unter der einschränkenden Platonischen Bedingung, also nur, wenn Zirkel und Lineal als einzige Hilfsmittel zur Verfügung kommen sollen, unmöglich sind. Bei Verwendung anderer Hilfsmittel sind ausnahmslos alle Teilungsarten und die Konstruktion aller regelmäßigen Vielecke, wenn auch nur in angenäherter Form, möglich. Die erreichbare Annäherung reicht für alle überhaupt in Betracht kommenden Zwecke in Technik und Wissenschaft vollkommen aus und kann bis zu jedem beliebigen Genauigkeitsgrade geführt werden. Schon die ältesten Kulturvölker haben uns zahlreiche Darstellungen von Vielecken hinterlassen. Das regelmäßige Siebeneck kommt in diesen Darstellungen sehr oft vor, und die Wagenbauer der ältesten Zeit verstanden sich schon darauf, Wagenräder mit sieben Speichen zu konstruieren, müssen also schon Annäherungsmethoden von ausreichender Genauigkeit gekannt haben.

Für die Wissenschaft der Mathematik freilich waren solche Annäherungsmethoden, selbst die genauesten, keine Lösung des Problems. Für diese bestand eben das Problem darin, die verlangte Teilung und Konstruktion lediglich mit Zirkel und Lineal auszuführen, und unter dieser Bedingung spottete das Problem allen Lösungsversuchen. Wie bei der Quadratur des Kreises, beim Delischen und beim Winkelteilungsproblem, sah man sich auch hier vor ein Geheimnis gestellt, das unergründlich schien. Und weil dem so war und alle Lösungsversuche immer wieder mit Mißerfolgen endeten, neigten viele Gelehrte der Ansicht zu, daß weitere als die obenerwähnten Kreisteilungen, die sich aus den Grundteilungszahlen 2, 3 und 5 ergeben, überhaupt unmöglich seien, ohne allerdings den Beweis für diese Ansicht, der also ein Unmöglichkeitsbeweis gewesen wäre, erbringen zu können, und diese Sachlage blieb bis gegen Ende des 18. Jahrhunderts unverändert bestehen.

Daher mußte es gewaltiges Aufsehen nicht nur bei den Mathematikern, sondern in der gesamten wissenschaftlichen Welt überhaupt erwecken, als im Jahre 1796 ein blutjunger Student bewies, daß die Reihe der Kreisteilungen mit den erwähnten Arten doch noch nicht abgeschlossen und beispielsweise auch die 17-Teilung des Kreises und dementsprechend auch die Konstruktion des regelmäßigen 17-Ecks mit Zirkel und Lineal möglich ist. Dieses jugendliche Genie, das mit dieser Tat die über zweitausend Jahre alte Lehre von der Kreisteilung mit einem Schlage zu neuem Leben und neuer Entwicklung brachte, war der damals neunzehnjährige Karl Friedrich Gauß. Die krumme Zahl 17, an die man in der Geschichte der Kreisteilung wohl nur höchst selten gedacht haben mag, gelangte plötzlich zu ungeahnter Bedeutung und wurde eingereiht unter jene auserwählten Zahlen, für die die Kreisteilung in mathematisch exakter Weise möglich ist. Die Mathematiker standen Kopf, und mit ihnen noch viele andere Leute. Ja, wenn es wenigstens noch die heilige 7 gewesen wäre, aber ausgerechnet 17!

Doch es blieb bei der krummen 17! Die Methode, die der junge Gauß für die 17-Teilung des Kreises entdeckt und mit der er die Mathematik zweier Jahrtausende in den Schatten gestellt hatte, erwies sich als unanfechtbar und allen Anforderungen an mathematische Exaktheit gewachsen. Gleichzeitig schuf der junge Entdecker aber auch eine abschließende Theorie der Kreisteilung, die das so lange und heiß umstrittene Problem mit einem Schlage bis in seine letzten Wurzeln erhellte. Auf Grund dieser Theorie ergab sich, daß jede Kreisteilung mit Zirkel und Lineal möglich ist, wenn die Teilungszahl eine Primzahl von der Form 2 ⁿ + 1 ist. Bei einer Primzahl dieser Form muß der Exponent n selbst wieder eine Potenz von 2, also eine der Zahlen 1, 2, 4, 8, 16, 32, 64 usw. sein. Setzen wir diese Zahlenwerte in den Ausdruck 2 ⁿ + 1 ein, so erhalten wir

2 ¹ + 1 = 3, also die 3-Teilung,
2 ² + 1 = 5, also die 5-Teilung,
2 ⁴ + 1 = 17, also die 17-Teilung,
2 ⁸ + 1 = 257, also die 257-Teilung,
2 ¹⁶ + 1 = 65 537, also die 65 537-Teilung.

Außer der 17-Teilung kamen also auch noch die 257- und die 65 537-Teilung, da diese Zahlen ebenfalls Primzahlen sind, zu den bis dahin bekannten Teilungsmöglichkeiten, ebenfalls alles höchst unglaubwürdige Zahlen, von denen bis dahin kein Mensch angenommen hätte, daß sie jemals in der Kreisteilung eine Rolle spielen würden. Aus der 17-Teilung ergab sich dann auch die 34-, 68- usw. Teilung, Entsprechendes für die anderen neuen Kreisteilungszahlen, und damit war man in der Lage, die Möglichkeit der Kreisteilung gewaltig zu bereichern und bis zu den fernsten Regionen der Zahlenreihe auszudehnen.

Allerdings haben die neuen Teilungsarten nur theoretisches Interesse. Schon die 17-Teilung mit Zirkel und Lineal ist eine höchst umständliche und mühevolle Arbeit und erfordert zu ihrer Ausführung bedeutende mathematische Kenntnisse; die 257-Teilung ist schon eine umfangreiche und in höchstem Maße komplizierte und zeitraubende Aufgabe, an die nur selten ein Gelehrter geht, und die 65 537-Teilung endlich ist bisher nur ein einziges Mal ausgeführt worden, und zwar von dem Mathematiker Hermes, der dafür nicht weniger als zehn voll Jahre brauchte. Die Ausführung dieser Konstruktion stellt ein gewaltiges Manuskript dar, das eine ganze große Kiste füllt und im Mathematischen Seminar der Universität Göttingen aufbewahrt wird.

Bemerkt sei noch, daß die Behandlung des Problems der 17-Teilung übrigens noch einen gewissen Fortschritt erreicht hat, und zwar insofern, als es gelungen ist, diese Konstruktion mit dem Zirkel allein, also mit Fortlassung des Lineals, auszuführen. Dem Franzosen L. Gerard gelang als erstem im Jahre 1896 diese Konstruktion, die also noch über die Platonische Bedingung hinausgeht.

Die Entdeckung der 17-Teilung des Kreises ist, wenn vielleicht auch nicht die bedeutendste, so doch zweifellos die genialste Leistung des unvergleichlichen Gauß. Er selbst hat diese Leistung wohl auch in dieser Weise eingeschätzt und den Wunsch geäußert, daß einst die symbolische Darstellung der 17-Teilung des Kreises seinen Grabstein schmücken möge. Dieser Wunsch ist erfüllt worden; auf dem Denkmal, das dem »Fürsten der Mathematiker« in seiner Geburtsstadt Braunschweig auf dem Gaußberg gesetzt worden ist, ist die 17-Teilung des Kreises plastisch dargestellt, um Kunde zu geben von der Tat eines jugendlichen Genies, die in ihrer Art völlig vereinzelt in der Geschichte der Wissenschaften dasteht und für immer ein Markstein in der Entwicklung der Mathematik und der Geschichte ihrer Probleme sein wird.

Postskriptum

Problematisch-mathematische Naturen – Der Kampf um die Siebenteilung – Eine Beinahe-Lösung – Entdeckerrausch – Ein winziger Unterschied – Enttäuschte Hoffnung – Eine kühne Analogie – Eine kleine Geschichte

Die Mathematik züchtet problematische Naturen! Freilich sind diese anderer Art als die Gestalten in Friedrich Spielhagens vielgelesenem Roman. Es sind das vielmehr jene Naturen, die, ohne zu den zünftigen Mathematikern zu gehören, dennoch Freude an den Problemen der so vielgeschmähten und doch so reizvollen Mathematik empfinden und den unbezähmbaren Trieb in sich spüren, das, was diese Wissenschaft für unmöglich erklärt, dennoch möglich zu machen. Die Quadratoren und Trisektoren gehören zu diesen Naturen, und zu ihnen gesellten sich, seit ich in einer weitverbreiteten Wochenschrift eine ähnliche wie die vorangegangene Abhandlung über die Kreisteilung veröffentlicht hatte, auch noch die Kreisteilungsproblematiker. Während über die Quadratur des Kreises und die Dreiteilung des Winkels, wohl auch über das Delische Problem, in den Zeitungen und Zeitschriften des öfteren geschrieben wird – notabene oftmals total Falsches und geradezu Unsinniges – werden die Probleme der Kreisteilung journalistisch so gut wie nicht ausgebeutet. Daher fand mein Aufsatz bei solchen wie den genannten problematischen Naturen einen ungeahnten Widerhall. Es war dort ausgeführt worden, daß es zwar viele Kreisteilungen gibt, die mit Zirkel und Lineal ausgeführt werden können, aber noch viel mehr andere, wie die Sieben-, Neun-, Elf-, Dreizehnteilung usw., bei denen das nicht der Fall ist, Konstruktionen, von denen die Mathematiker sogar behaupten, daß ihre exakte Ausführung unmöglich sei. Dieses »Unmöglich« erweckte das Problematische in der Natur vieler Leser, und viele, die sich, wenn auch widerstrebend, schon zu dem Zugeständnis durchgerungen hatten, daß man in der Frage der Quadratur des Kreises, der Dreiteilung des Winkels und der Verdoppelung des Würfels den Mathematikern, die diese Dinge für unmöglich erklären, vielleicht recht geben müsse, lehnten es ganz entschieden ab, dieses Zugeständnis auch auf die ihnen bekannt gewordene neue Unmöglichkeit auszudehnen. Schließlich können sich auch die Gelehrten irren, und selbst Mathematikern, sogar sehr bedeutenden, sind schon Irrtümer untergelaufen. Nur der eigene Versuch wirkt überzeugend, und viele, viele schrieben mir, aus In- und Ausland, daß sie durch eigene Versuche einen Irrtum der zünftigen Wissenschaft festgestellt und die für unmöglich erklärten Kreisteilungen mit mathematischer Exaktheit und nur mit Zirkel und Lineal möglich gemacht hätten, und sie sandten mir mehr oder weniger umfangreiche und komplizierte Konstruktionen, um mich von der Richtigkeit solcher kühnen Behauptung zu überzeugen. Da bekam ich reichlich zu tun, um die Mathematik gegen die Anfechtungen der problematischen Naturen zu verteidigen.

Die große Mehrzahl jener Versuche und Konstruktionen hatte es auf die Siebenteilung abgesehen, jenes uralte Problem, an dem schon die Geometer der alten Babylonier und Griechen ihren Scharfsinn erprobt hatten. Und in der Tat, es gibt eine Anzahl von Konstruktionen, die beinahe – aber freilich nur beinahe – die exakte Lösung dieses Problems sein könnten und meinen Widersachern recht zu geben schienen. Eine dieser Konstruktionen, die in dieser oder ähnlicher Form zur größeren Hälfte unter den mir übersandten Lösungsversuchen vertreten war, ist folgende: In einem Kreis wird, wie es die nebenstehende Figur 19 zeigt, ein Halbmesser halbiert und in dem Mittelpunkt desselben das Lot errichtet, alles Operationen, die mit Zirkel und Lineal wunderschön ausgeführt werden können. Wenn man dann die Strecke vom Fußpunkt des Lotes bis zur Kreislinie, also in unserer Figur die Strecke a, in den Zirkel nimmt und von einem beliebigen Punkte der Kreislinie an auf dieser hintereinander abträgt, so wird auf diese Weise die Kreislinie haarscharf in sieben Teile geteilt. Wer den Versuch mit der nötigen Genauigkeit macht, wird das Gesagte bestätigt finden. Der siebente auf diese Weise gefundene Zirkelpunkt fällt immer mit dem Ausgangspunkt zusammen, und selbst dem schärfsten Auge wird es kaum möglich sein, eine Abweichung zu konstatieren. Das ganze Verfahren erinnert natürlich an die Sechsteilung des Kreises, bei der durch Abtragung des Radius auf dem Kreisumfange dieser mit anerkannt mathematischer Exaktheit in sechs Teile geteilt wird.

Daher war es kein Wunder, daß viele Leser, die die beschriebene Konstruktion entdeckt hatten, damit die Lösung des Problems der Siebenteilung gefunden zu haben glaubten und in der felsenfesten Überzeugung von der Richtigkeit ihrer Konstruktion in ihren Briefen den ganzen Triumph der Entdecker ausströmen ließen. »An der Richtigkeit meiner Lösung ist nicht zu zweifeln!« schrieb mir in diesem Sinne ein Leser siegesbewußt. »Es ist mir am 9. Januar d. J., 12 Uhr nachts, gelungen, das Problem restlos zu lösen!« schrieb ein anderer, überzeugt, gut daran getan zu haben, daß er für etwaige spätere Forschungsarbeiten über den Werdegang seiner Entdeckung beizeiten das Datum dieser Großtat bis auf die Stunde genau fixierte. Ein anderer Leser und Löser sandte mir seine Photographie mit längerem Lebenslauf und dem höflichen, aber bestimmten Ersuchen, beides mitsamt seiner Lösung des Problems in der Zeitschrift, in der mein Aufsatz erschienen war, zu veröffentlichen, und für die Gewährung dieser Publikation hatte er sich ein beträchtliches Honorar ausbedungen. Andere meiner Problematiker hielten es aus Gründen der Vorsicht nicht für angebracht, mir ihre Lösungen mitzuteilen, sondern begnügten sich damit, mir die Tatsache ihrer Entdeckung zur Kenntnis zu bringen, und fragten gleichzeitig an, ob und wo und in welcher Höhe Preise auf die Lösung des Problems ausgesetzt seien, um die sie sich zu bewerben wünschten. Eine der übersandten Lösungskonstruktionen aber war mit drei verschiedenen Unterschriften unterzeichnet. Das hieß zu gut deutsch: Laß dir ja nicht einfallen, alter Freund, uns um die dir hiermit anvertraute Entdeckung zu bemausen und diese etwa als dein eigenes Geisteskind auszugeben; wir sind drei gegen einen und schwören dich nötigenfalls in Grund und Boden! Ein Schüler einer technischen Lehranstalt endlich sandte mir seine Konstruktion ein, versehen mit einem unterschriebenen und gestempelten Zeugnis des Leiters der Anstalt und des Inhaltes, daß die beifolgende Konstruktion zur Siebenteilung des Kreises mit dem Mikrometerzirkel nachgeprüft und ihre absolute Genauigkeit einwandfrei festgestellt sei! Man sieht, was die problematisch-mathematischen Naturen tun, das tun sie gründlich.

Abb. 19

Abb. 20

Aber dieser Entdeckerrausch mußte gedämpft werden. Es tat mir beinahe leid, soviel Hoffnung zerstören zu müssen, aber die Wissenschaft über alles! Nun, die erwähnte Konstruktion zur Siebenteilung ist trotz ihrer anscheinenden Genauigkeit und trotz ihrer Ähnlichkeit mit der Sechsteilung doch keine wirklich genaue, sondern nur eine annähernde, sozusagen eine Beinahe-Lösung und war als solche auch den zünftigen Mathematikern keineswegs unbekannt. Die konstruierte Strecke a auf Abbildung 19 ist nämlich die mathematisch exakte Konstruktion der halben Seite des regelmäßigen Dreiecks. Wir hatten in der vorhergehenden Abhandlung bereits eine Konstruktion des regelmäßigen Dreiecks angegeben. Eine andere ist die folgende: Wenn auf dem Mittelpunkt des Kreisradius nach beiden Seiten eine Senkrechte errichtet wird und dann die beiden Schnittpunkte dieser Strecke mit der Kreislinie, so wie es Figur 20 zeigt, mit dem gegenüberliegenden Schnittpunkt des Durchmessers verbunden werden, so ist die so entstandene Figur das regelmäßige Dreieck, nach allen Regeln der Kunst mit Zirkel und Lineal ausgeführt und daher die mathematisch exakte Konstruktion desselben darstellend. Der Vergleich der beiden Figuren zeigt deutlich, daß die Strecke, mit der unsere Problematiker die Siebenteilung des Kreises gefunden zu haben glaubten, genau die Hälfte der Seite des regelmäßigen Dreiecks ist. Und diese Strecke ist zwar beinahe, aber doch nicht völlig gleich der Seite des regelmäßigen Siebenecks. Der Unterschied ist freilich nur ein ganz minimaler und beträgt, wie sich durch Rechnung ziemlich einfach feststellen läßt, nur etwa 17 Zehntausendstel des Radius des Kreises, also bei einem Kreise, dessen Halbmesser 1 Meter lang ist, nur 1,7 Millimeter, bei so kleinen Kreisen hingegen, wie man sie zu geometrischen Experimenten auf Papier zeichnet, nur etwa den zehnten oder hundertsten Teil eines Millimeters, und diese verschwindende Differenz war allen unseren siegesfrohen Problematikern entgangen, die hatte sich selbst mit dem Mikrometerzirkel nicht feststellen lassen.

Aber vorhanden ist diese Differenz, wie die Rechnung mit unumstößlicher Gewißheit ergibt, und selbst wenn sie noch millionmal kleiner wäre, so verhinderte sie dennoch, jene Konstruktion als mathematisch exakte Lösung anzuerkennen. Denn so klein auch jenes Stückchen ist, um das die wirkliche Seite des Siebenecks von der in obiger Weise konstruierten Strecke abweicht, so enthält sie doch immer noch unendlich viele Punkte, und es ist auf keine Art und Weise möglich, unter diesen den alleinigen und einzigen Punkt zu bestimmen, der die wirkliche Seite des Siebenecks begrenzt. Die Ausmessung mit dem Zirkel, auch mit dem Mikrometerzirkel, ist kein Beweis, denn der Zirkel soll lediglich zum Ziehen von Kreislinien dienen, ist aber kein Meß- und kein Beweisinstrument, und mikroskopisch kleine Abweichungen können wir selbst mit den schärfsten Meßapparaten nicht feststellen. Der exakte Beweis für die Richtigkeit einer solchen Behauptung oder Konstruktion kann eben immer nur erbracht werden, indem man die Behauptung auf die bekannten Grund- und Lehrsätze der Geometrie zurückführt, genau in der Weise, wie man etwa die Kongruenz von Dreiecken und daraus die Gleichheit von Seiten oder Winkeln beweist. Unsere Problematiker aber hatten sich durchweg mit dem Augenschein begnügt, der ihnen eine absolute Genauigkeit ihrer Konstruktion vortäuschte, einen wirklich einwandfreien Beweis hatte keiner von ihnen auch nur versucht. Das war ihre große Sünde gegen den Geist der Geometrie gewesen, die sie mit der Enttäuschung ihrer hochgeschwellten Erwartungen bezahlen mußten. »Grausame Ironie des Schicksals, das so große Annäherungen an die genaue Teilstrecke zuläßt, aber die ganz genaue Teilung verhindert!« so schrieb mir in diesem Sinne ein Leser, der mir seine Konstruktion zur Prüfung übersandt hatte, auf meinen Hinweis auf die bewußten siebzehn Zehntausendstel Differenz resigniert zurück.

Ein merkwürdiges Verfahren, um die Richtigkeit einer vorgenommenen Siebenteilung zu beweisen, hatte übrigens ein Problematiker weiblichen Geschlechtes, die Gattin eines Apothekers, angewandt. Die Dame hatte den geteilten Kreis mit möglichster Genauigkeit in sieben Sektoren zerschnitten und diese auf der Apothekerwaage ihres Gatten ausgewogen. »Die Wägung ergab absolute Gleichheit aller sieben Teile, und damit ist wohl der Beweis geliefert, daß mein Teilungsverfahren allen Anforderungen genügt!« schrieb mir dieser praktische Geometer. Dieser Schlußfolgerung konnte ich mich nun allerdings nicht anschließen, und weil das der Fall war und ich der Dame schrieb, daß die Waage, selbst die allerfeinste, kein Beweisinstrument für mathematische Zwecke sei und auch niemals Unterschiede von Millionstel oder Billionstel anzugeben imstande sei, bekam ich eine sehr deutliche Erwiderung, in der mir ob solcher »Haarspalterei« ganz gehörig der Text gelesen und für die Zukunft die unverhohlene Verachtung aller Mathematik ausgedrückt wurde.

Außer der beschriebenen wurden noch verschiedene andere Konstruktionen der Siebenteilung übersandt, und auch an der 9-, der 11- und der 13-Teilung versuchten sich viele Leser und Löser mit Scharfsinn und Verstand, aber natürlich alle ohne Erfolg. In allen Fällen ließ sich der Fehler, wenn er auch noch so minimal war, durch Rechnung mit unumstößlicher Gewißheit nachweisen, und damit wurden auch diese Hoffnungen zuschanden. Einem Leser jedoch konnte ich mit viel Freude die absolute Richtigkeit und Exaktheit seiner Konstruktion bestätigen. Er hatte in ähnlicher Weise, wie aus der 6- und der 10-Teilung des Kreises die 15-Teilung abgeleitet wird (im vorhergehenden Aufsatz ist das eingehend beschrieben), die 85-Teilung des Kreises gefunden. Und diese Konstruktion war vollkommen exakt und einwandfrei, nicht nur annäherungsweise. Aber, so mußte ich diesem Problematiker mitteilen, Neues hatte er mit seiner Entdeckung nicht zuwege gebracht. Denn die 85-Teilung ist aus der 5- und der 17-Teilung des Kreises ableitbar, in ähnlicher Weise auch die 51-Teilung aus der 3- und der 17-Teilung, was sich aus der Theorie der Kreisteilung ergibt. Wohl aber konnte ich diesem Leser zu dem Scharfsinn, den er bei der selbständigen Neuentdeckung dieser Teilungsart bewiesen hatte, meinen aufrichtigen Glückwunsch aussprechen.

Manche der Problematiker bekunden ihre Naturveranlagung übrigens auch in der Konstruktion kühner Analogien. Ist ihnen der Fehler ihres Lösungsversuches nachgewiesen, so kündigen sie alsbald neue an, die angeblich absolut fehlerlos sein sollen, und dem Einwand, daß Konstruktionen wie die 7- oder 11-Teilung des Kreises in exakter Weise nicht möglich seien, begegnen sie dann, indem sie sich für die Berechtigung ihres Strebens auf – Gauß berufen. Denn auch dieser habe die 17-Teilung des Kreises, die doch über zweitausend Jahre hindurch als unmöglich angesehen worden sei, schließlich dennoch möglich gemacht, warum sollte so Ähnliches nicht auch bei der angeblich unmöglichen 7- oder 11-Teilung gelingen?! Manche verwenden dieses Argument sogar, um auch für die Quadratur des Kreises oder die Dreiteilung des Winkels oder das Delische Problem noch Lösungsmöglichkeiten behaupten zu können. Man fühlt sich in der Verfolgung jener Probleme also als zweiter Gauß! Diese Analogie ist jedoch nur eine sehr oberflächliche. Denn wenn auch bis zu Gauß die 17-Teilung des Kreises nicht gelungen war, so hatte man doch auch keinen schlüssigen Beweis dafür aufgestellt, daß die Lösung dieser Aufgabe unmöglich wäre; das Problem war bis zu Gauß' Wirken durchaus in der Schwebe. Für die Quadratur des Kreises, die Dreiteilung des Winkels und die Verdoppelung des Würfels aber ist die Unmöglichkeit erwiesen, und zwar im wesentlichen durch die Arbeiten desselben Gauß, auf den sich jene Problematiker berufen. Ebenso hat die von Gauß aufgestellte Theorie der Kreisteilung, die zur Entdeckung der 17-Teilung führte, zugleich den Beweis der Unmöglichkeit für alle Teilungsarten erbracht, die, wie die 7-, 9-, 11- usw. Teilung, nicht der angegebenen Formel der Kreisteilungszahlen entsprechen. Also Vorsicht mit der Berufung auf Gauß!

Noch von einer kleinen hübschen Geschichte möchte ich erzählen, die sich an den obenerwähnten Aufsatz knüpft, wenn sie allerdings auch nur indirekt mit der Kreisteilung zu tun hat. Schrieb mir da auf diesen Aufsatz auch ein Leser, seines Zeichens Obertertianer vom Gymnasium in D., er habe meine Abhandlung über die Kreisteilung gelesen und daraus die Hoffnung und Überzeugung gewonnen, daß ich vielleicht auch imstande sei, ihn bei einer kniffligen mathematischen Aufgabe über den Kreis, die ihm sein Mathematiklehrer als Hausaufgabe zudiktiert habe, auf den rechten Weg zu bringen. Er komme nicht zustande damit, ob ich ihm daher nicht ein bißchen helfen wolle, und er bäte doch sehr darum, denn die Sache wäre für die kommende Versetzung von Entscheidung.

Nun, edel sei der Mensch, hilfreich und gut, und warum soll man einem bedrängten Obertertianer in Versetzungsnöten nicht ein wenig unter die Arme greifen? Erinnerungen an die eigene Tertianerzeit werden wach und bestärken den menschenfreundlichen Entschluß. Also schrieb ich ihm, gab ihm zwar nicht die Lösung der mitgeteilten Aufgabe selbst, wohl aber bestimmte Andeutungen, um den Charakter der Aufgabe und den Weg der Lösung zu erkennen.

Und der Erfolg solcher guten Tat? Nach drei Wochen hielt ich über ein Dutzend Briefe von Schülern des Gymnasiums in D. in Händen, aus allen Klassen von Tertia an aufwärts, und alle baten um freundlichen Beistand bei der Lösung der mitfolgenden mathematischen Aufgaben. Selbst zwei Herren Oberprimaner hatten mich mit ihrem Vertrauen beehrt zwecks Lösung einiger verwickelter stereometrischer Aufgaben. Da mußte ich nun freilich stoppen, denn erstens hätten es die mathematischen Kollegen vom Gymnasium in D. mit Recht wohl sehr übel vermerkt, wenn ihnen in solcher Weise in den geregelten Lehrplan hineingepfuscht worden wäre – natürlich vorausgesetzt, daß sie es herausgekriegt hätten, aber die Mathematiker kriegen ja bekanntlich alles heraus –, und zweitens hätte ich zu erwarten gehabt, daß, wenn sich die Sache weiter herumsprechen würde, alsbald weitere Gaue der gymnasialen deutschen Jugend mir ihr Vertrauen zuwenden würden und dann für den Rest meines Daseins meine Zeit und Arbeitskraft mit mathematischem Hilfsdienst vollkommen ausgefüllt worden wäre. Also mußte ich meinen jungen Freunden abschreiben, mit einem nassen und einem heiteren Auge, und ich hoffe, daß sie die angegebenen Gründe gewürdigt haben.

III.
Probleme der Zahl

1. Geheimnisse der Zahlenreihe

Pythagoras und die Zahl – Die Zahlenreihe – Primzahlen – Teilbarkeitsregeln – Das Sieb des Eratosthenes – Die größte Primzahl – Die Konstruktion von Primzahlen – Ein Irrtum Fermats – Der Beweis der unendlichen Anzahl der Primzahlen

Die Zahl ist das Wesen der Dinge!« – so lautet ein Ausspruch des großen griechischen Philosophen und Mathematikers Pythagoras, desselben, der einstmals hundert Ochsen opferte aus Freude über die Auffindung des Beweises des nach ihm benannten Lehrsatzes, was wiederum zur Folge gehabt haben soll, daß seitdem alle Ochsen vor der Entdeckung neuer Wahrheiten eine heillose Angst haben. Der griechische Weise wollte mit jenem Satz wohl ausdrücken, daß die Erscheinungen und Gesetze der Natur wie überhaupt alles Seins und Geschehens zahlenmäßig bestimmt seien. Er hat auf diese Weise viele Dinge und Tatsachen in höchst scharfsinniger Weise zu deuten gesucht und beispielsweise den Rhythmus der Töne sehr richtig aus den Zahlenverhältnissen der schwingenden Saiten abgeleitet. Vieles allerdings haben Pythagoras und seine Schüler aus den Zahlen herauszulesen oder in sie hineinzuinterpretieren gesucht, das mehr Phantasie und Mystik als wissenschaftliche Erkenntnis war. Aber die Geheimnisse und Probleme der einfachen Zahlen sind ihnen schon in vollem Umfange aufgegangen, und vielleicht hat gerade das Rätselvolle der Zahlenreihe dem Begründer der Schule zu seinem Ausspruch Veranlassung gegeben. Und wie schon zu Pythagoras' Zeiten, so gehören die Eigenschaften und Rätsel der Zahlen noch heute mit zu den schwierigsten und eigenartigsten, zugleich aber auch reizvollsten Problemen des menschlichen Denkens überhaupt, Probleme, die nicht nur den Fachmann, den Mathematiker bzw. Zahlentheoretiker in ihrem Bann halten, sondern auch auf den denkenden Laien eine große Anziehungskraft ausüben, zumal die naive Beschäftigung mit den Zahlen und selbst mit zahlentheoretischen Begriffen und Problemen auch ohne tiefere mathematische Fachkenntnis geschehen kann und jedem leidlich Gebildeten geläufig ist. Viele Probleme der Zahlen sind seit der Zeit der Pythagoreer entdeckt, viele auch gelöst worden, aber dafür sind neue von ungeahnter Tiefe und Schwierigkeit entstanden.

Die Rätsel der Zahlen stecken in der »Zahlenreihe«, also in der Folge, in der wir, wenn wir zählen, die Zahlen aneinanderreihen nach dem Prinzip, daß jede Zahl immer um eine Einheit größer ist als die vorhergehende. Dabei unterscheiden wir bekanntlich die Primzahlen von den zusammengesetzten Zahlen. Als Primzahl bezeichnen wir eine Zahl, die durch keine andere Zahl teilbar ist, oder die, wie der Zahlentheoretiker, der alle Begriffe haarspalterisch genau auseinanderhält, zu sagen pflegt, nur durch die Zahl 1 und sich selbst teilbar ist, was natürlich auf dasselbe hinauskommt. Die Zahlen 1, 2, 3, 5, 7, 11 usw. oder, um auch einige größere zu nennen, 113, 1093, 3 628 811 usw. sind sämtlich Primzahlen, die also nicht weiter in andere Faktoren geteilt oder zerlegt werden können. Die Zahlen 4, 6, 8, 15, 63, 9287, 14 443 usw. sind zusammengesetzte Zahlen. Die Primzahlen nun sind es in erster Linie, die dem Zahlentheoretiker noch heute eine Reihe ungelöster Rätsel aufgeben; sie sind seine liebsten, aber zugleich auch seine Schmerzenskinder, an die sich eine ganze Reihe der tiefsten und schwierigsten Probleme knüpft. Schon die Feststellung, ob eine Zahl Primzahl ist oder nicht, macht bei großen Zahlen Schwierigkeiten, die im allgemeinen um so größer sind, je größer die fragliche Zahl ist, und die bei ganz großen Zahlen, abgesehen von ganz wenigen Ausnahmefällen, überhaupt nicht zu entscheiden ist, da es leider keine allgemeine Regel gibt, die hier Aufschluß geben könnte. Für einfache Fälle gibt es ja allerdings eine Reihe von Faustregeln. So ist jede Zahl, deren Endziffer eine gerade Zahl oder 0 ist, ebenfalls eine gerade Zahl, d. h. durch 2 teilbar, und ebenso ist jede auf 5 oder 0 endigende Zahl selbst durch 5 teilbar. Ferner ist jede Zahl, deren Quersumme (d. h. die Summe ihrer einzelnen Ziffern) durch 3 teilbar ist, ebenfalls durch 3 teilbar, und Entsprechendes gilt auch für die 9. Es gibt noch eine ganze Reihe solcher Regeln, die sich jedoch alle nur auf die Teilbarkeit mit den niedrigsten Primzahlen beschränken oder doch nur in solchen Fällen von Wert sind. Für die größeren Primteiler gibt es leider so einfache Regeln nicht, und um beispielsweise festzustellen, ob eine vorliegende große ungerade Zahl etwa durch 97 teilbar ist, bleibt nichts anderes übrig, als die Division der gegebenen Zahl mit 97 auszuführen. Bei den ganz großen Zahlen gehört die Feststellung ihrer Teilbarkeit mit zu den umständlichsten und schwierigsten Aufgaben der Zahlentheorie, die auch nur in wenigen Fällen zu einer Lösung führt. Gelänge es, eine Regel zu finden, vermittels deren man jeder und selbst der größten vorgelegten Zahl ansehen könnte, ob sie eine Primzahl ist oder nicht, so wäre damit der Wissenschaft von den Zahlen ein ungeheuer großer Dienst erwiesen.

Wenn es eine solche wie die genannte Regel nun auch noch nicht gibt, so gibt es doch ein Verfahren, um in der Zahlenreihe diejenigen Zahlen, die Primzahlen sind, ausfindig zu machen, ein Verfahren, das ebenso einfach wie geistreich ist und von dem griechischen Mathematiker Eratosthenes, der um das Jahr 250 v. Chr. in Alexandrien lebte und lehrte, herrührt. Das Verfahren, das auch für den Laien von großem Reiz ist, ist folgendes: Man schreibt zunächst die Zahlen, mit 1 beginnend, in ihrer natürlichen Reihenfolge auf, und zwar ein möglichst langes Stück der Zahlenreihe hinauf. Dann durchstreicht man, von der 2 ausgehend, jede zweite Zahl, läßt die 2 selbst aber ungestrichen stehen. Die nächste ungestrichene Zahl nach der 2 ist dann die 3; von dieser ausgehend durchstreicht man dann jede dritte Zahl, wiederum die 3 selbst ungestrichen lassend, wobei man zugleich auf eine große Anzahl vorher schon durchstrichener Zahlen stoßen wird, die jedoch alle mitgezählt werden. Darauf setzt man das Verfahren fort, indem man von der nächsten hinter der 3 stehenden ungestrichenen Zahl ausgeht, die die 5 sein wird, dann von der abermals nächsten ungestrichenen Zahl, der 7, dann der 11 usw. Immer bleibt die erste Zahl der neuen Reihe selbst ungestrichen stehen, und nur die ausgezählten Vielfachen der Anfangszahl werden durchstrichen. Auf diese Weise bleiben nur die Primzahlen ungestrichen stehen, alle zusammengesetzten Zahlen aber werden durchstrichen. Bei diesem Verfahren werden also die Primzahlen aus der Menge der gesamten Zahlen überhaupt gleichsam ausgesiebt, weswegen man das Verfahren auch als das Sieb des Eratosthenes bezeichnet. Die Ausführung des Verfahrens nach der gegebenen Anleitung ist jedem Leser leicht möglich, und es wird ihm viel Vergnügen bereiten, auf diese Weise eine möglichst große Anzahl Primzahlen auszusieben.

Je weiter man das Verfahren fortsetzt, um so mehr Primzahlen wird man naturgemäß erhalten. Leider wird das Verfahren bei weiterem Fortschreiten rein technisch immer schwieriger und umständlicher, so daß auch der Ausfindigmachung der Primzahlen auf diese Weise eine Grenze gesetzt ist. Immerhin sind auf Grundlage dieses Verfahrens sogenannte Primzahlentafeln hergestellt worden, die weit hinauf bis in die Millionen der Zahlenreihe reichen. Die größte bisher hergestellte Primzahlentafel ist von dem amerikanischen Mathematiker Lehmer hergestellt worden und von dem Carnegie-Institut in Washington herausgegeben; sie enthält die Primzahlen aus den ersten zehn Millionen der Zahlenreihe. Darüber hinaus hat man nur in vereinzelten Fällen und vermittels sehr komplizierter mathematischer Methoden Primzahlen bestimmen können. Die größte bisher bekannte Primzahl ist die Zahl 2 ¹²⁷ – 1. Hierbei sei bemerkt, daß man sehr große Zahlen einfacher als durch ihre Ziffernfolge durch ihre Potenzen, d. h. durch die Multiplikation einer angenommenen Grundzahl mit sich selbst, ausdrückt. Der Ausdruck 2 ¹²⁷ bedeutet die Zahl, die man erhält, wenn man die Zahl 2 hintereinander 127mal mit sich selbst multipliziert bzw., genauer ausgedrückt, 127mal als Faktor setzt. Die Zahl 2 ¹²⁷ – 1 war bis vor kurzem nur in der Potenzform bekannt, jetzt ist sie jedoch auch zahlenmäßig ausgerechnet worden, und für Freunde von Zahlenlesen sei die Ausrechnung hier angeführt; es ist die 39ziffrige Zahl 170 141 183 460 469 231 731 687 303 715 884 105 727 gelesen: 170 Sextillionen 141 183 Quintillionen 460 469 Quartillionen 231 731 Trillionen 687 303 Billionen 715 884 Millionen hundertfünftausendundsiebenhundertsiebenundzwanzig. Selbst Lesern, die noch die Erinnerung an die Inflationszeit unseligen Angedenkens bewahrt haben, dürfte die angeführte Zahl noch immer einigermaßen imponieren, denn gegen diese sind selbst die größten Ziffern der Inflationszeit winzige Zwerge.

Wie es keine Regel gibt, um allgemein eine jede gegebene Zahl als Prim- oder als zusammengesetzte Zahl zu erkennen, so gibt es auch kein Verfahren oder keine Formel, um beliebig Primzahlen zu konstruieren, etwa in der Art, daß Zahlen von einer bestimmten Bildung oder Zusammensetzung immer Primzahlen sein müßten. Auch nach dieser Hinsicht sind schon viele Versuche unternommen worden, die bisher aber immer fruchtlos geblieben sind. Pierre Fermat, der große französische Mathematiker (1601-1664), der geradezu als der Vater der modernen Zahlentheorie bezeichnet werden kann und besonders auch den Problemen der Primzahlen viel Arbeit gewidmet hat, glaubte in dem Ausdruck 2 ^{(2 ⁿ
)} + 1, in welchem also der Exponent der Potenz selbst wieder eine Potenz von 2 ist, ein Gesetz für die Bildung von Primzahlen gefunden zu haben, demzufolge jede Zahl von dieser Form also eine Primzahl sein sollte. Einen Beweis allerdings konnte er für diese Mutmaßung nicht erbringen, und diese hat sich in der Folge denn auch als unrichtig erwiesen. Setzen wir für n die aufeinanderfolgenden Werte, so erhalten wir

für n = 0 2 ¹ + 1 = 3
für n = 1 2 ² + 1 = 5
für n = 2 2 ⁴ + 1 = 17
für n = 3 2 ⁸ + 1 = 257
für n = 4 2 ¹⁶ + 1 = 65 537

Bis dahin sind die auf solche Weise erhaltenen Zahlen tatsächlich sämtlich Primzahlen, aber schon bei dem nächsthöheren Wert für n erleidet die Fermatsche Behauptung Schiffbruch, denn für n = 5, also für 2 ³² + 1, erhalten wir die Zahl 4 294 967 297, und diese Zahl ist, wie der noch größere Leonhard Euler (1707-1782) nachwies, keine Primzahl, sondern durch 641 teilbar. Die Auffindung einer allgemeinen Zahlenform, die immer eine Primzahl ergibt und ebenfalls von großer Wichtigkeit für die Wissenschaft von den Zahlen wäre, ist ebenfalls ein noch ungelöstes Problem.

Eine andere Frage, die sich uns bei der Betrachtung der Zahlenreihe und der in diese eingebetteten Primzahlen aufdrängt, ist die, ob die Anzahl der Primzahlen begrenzt oder aber unendlich ist. Dieses Problem hat ebenfalls schon die Mathematiker vor Tausenden von Jahren beschäftigt und hat, wie gleich bemerkt sein mag, im Gegensatz zu vielen anderen Zahlenproblemen schon vor über zwei Jahrtausenden seine restlose Lösung gefunden. Die gewöhnliche Zahlenreihe ist natürlich unendlich, das heißt, wir können auf der Zahlenreihe fortschreitend immer neue Zahlen bilden, ohne jemals zu einer letzten zu kommen; das geht aus der Art unseres Zählsystems, des Dezimalsystems, ohne weiteres hervor und bedarf keines Beweises. Für die Primzahlen aber ist diese Frage keinesfalls so leicht zu entscheiden, denn diese folgen nicht so gesetz- und regelmäßig aufeinander wie die Zahlen überhaupt. Die Zahlenreihe fängt zunächst gleich mit drei hintereinanderliegenden Primzahlen, 1, 2 und 3, an, ein Fall, der in der ganzen unendlichen Zahlenreihe nie wieder auftreten kann; dann folgen als nächste Primzahlen 5 und 7, die, weil sie nur durch eine Zahl getrennt sind, als Primzahlpaar bezeichnet werden. Dann folgt nach einem Zwischenraum von drei zusammengesetzten Zahlen die 11, die mit der 13 wiederum ein Primzahlpaar bildet; als nächste Primzahlen kommen dann 17, 19, 23, dann erst nach einem Zwischenraum von fünf zusammengesetzten Zahlen 29. Wer in dieser Weise die Aufeinanderfolge der Primzahlen weiter untersucht, wird feststellen, daß die Zwischenräume zwischen den Primzahlen im allgemeinen immer größer werden. Im ersten Hundert der Zahlenreihe gibt es 26, im ersten Tausend 168, und in den ersten beiden Tausenden zusammen 303, innerhalb der ersten Million der Zahlenreihe aber 78 499 Primzahlen, und diese Angaben lassen die abnehmende Häufigkeit der Primzahlen bereits deutlich erkennen, denn wenn diese mit derselben Häufigkeit wie im ersten Hundert die ganze Zahlenreihe hindurch sich fortpflanzen würden, so müßte es innerhalb der ersten Million der Zahlenreihe rund 260 000 Primzahlen geben, also über dreimal soviel als es in Wirklichkeit der Fall ist. Daher könnte es durchaus möglich sein, daß die Primzahlen, die in die Zahlenreihe so vereinzelt eingebettet sind wie die Rosinen in den Kuchen, einmal ganz aufhören. Dann müßte es also eine letzte und größte Primzahl geben, und nach dieser würden dann keine weiteren solcher Zahlen in der Zahlenreihe auftreten. So selten nun aber auch die Primzahlen mit dem Fortschreiten der Zahlenreihe werden, so wissen wir doch mit absoluter Bestimmtheit, daß die Primzahlen in der Zahlenreihe niemals aufhören und ihre Anzahl unendlich ist. Der Beweis für diese Behauptung ist schon von Euklid, dem großen Mathematiker der Griechen, um das Jahr 300 v. Chr. erbracht worden und ist in seiner klassischen Schönheit und Einfachheit einer der berühmtesten und schönsten Beweise der ganzen Mathematik überhaupt. Wir wollen daher diesen Beweis, der auch dem, der nicht Mathematiker von Fach ist, durchaus verständlich ist, kurz vorzuführen.

Angenommen, es stellte jemand die Behauptung auf, die Anzahl der Primzahlen wäre begrenzt und es gäbe eine letzte und größte Primzahl, die wir, weil wir nicht wissen, welche Zahl es ist, mit einem Buchstaben, sagen wir als die Zahl z, bezeichnen wollen, wie es die Mathematiker in solchen Fällen zu tun pflegen. Dann machen wir, um jene Behauptung zu widerlegen, folgendes: Wir bilden das Produkt aller Primzahlen von 1 bis z, also 1 × 2 × 3 × 5 × 7 × 11 × 13 × … und so weiter bis … × Z. Dieses Produkt ist dann eine neue, und zwar zusammengesetzte Zahl, die natürlich ungeheuer viel größer als z ist, und diese neue Zahl wollen wir mit P bezeichnen. Zu dieser Zahl P fügen wir dann noch die Zahl 1 hinzu und erhalten somit die Zahl P + 1. Für diese neue Zahl kommen nun zwei Möglichkeiten in Betracht: entweder sie ist eine Primzahl oder sie ist keine. Betrachten wir jeden dieser beiden Fälle einzeln. Erster Fall: Ist P + 1 eine Primzahl, dann ist sie natürlich ungeheuer viel größer als die Zahl z, von der wir ausgegangen sind, und die aufgestellte Behauptung, daß z die größte Primzahl sei, wäre damit widerlegt. Zweiter Fall: Ist P + 1 keine Primzahl, sondern eine zusammengesetzte Zahl, so muß sie bestimmte Primzahlen als Teiler enthalten. Von diesen kann dann aber kein einziger unter den Primzahlen von 1 bis z vorkommen, denn jede dieser Zahlen würde bei der Division in P + 1 den Rest 1 lassen, wie ohne weiteres ersichtlich ist, kann also kein Teiler von P + 1 sein. Dann müssen also die Primteiler, aus denen P + 1 besteht, andere sein als die Zahlen von 1 bis z und müssen größer sein als jede dieser Zahlen und auch größer als z selbst. Damit ist dann auch für den zweiten Fall bewiesen, daß es größere Primzahlen als z geben muß. In diesem wie in jenem Falle ist also die Behauptung, daß z die größte Primzahl sei, widerlegt, und da wir hierbei z so groß annehmen können wie wir wollen, so ist damit zugleich gesagt, daß es Primzahlen über jede noch so groß angenommene Zahl geben muß, daß es also überhaupt keine größte und letzte Primzahl geben kann und mithin die Anzahl der Primzahlen unendlich ist.

Das ist der berühmte Beweis der Unendlichkeit der Primzahlen. Der in mathematischen Dingen wenig geübte Leser wird vielleicht immer noch einige Mühe haben, sich vollständig in den Beweis hineinzulesen und zum völligen Verständnis desselben zu gelangen; hat er das aber erreicht – und er kann das auf alle Fälle erreichen –, so empfindet er dann auch in vollem Maße den unvergleichlichen Genuß, der immer mit der Aneignung gerade der mathematischen Erkenntnisse verknüpft ist. Bemerkt sei noch, daß es noch einige andere Beweise für die Unendlichkeit der Primzahlen gibt, aber keiner reicht an die Klarheit, Einfachheit und Schönheit des Beweises Euklids heran.

Postskriptum I

Die Primzahl 1 – Teilbarkeitsregeln – Ein fehlerhafter Beweis.

Man kann die Frage aufwerfen, ob die Zahl Eins zu den Primzahlen zu rechnen ist oder nicht. Nach der hier gegebenen Definition, die wohl noch immer von den meisten Zahlentheoretikern beibehalten wird, ist eins als Primzahl aufzufassen. Manche Zahlentheoretiker definieren die Primzahl jedoch anders, etwa als Zahl, die nicht mehr aber auch nicht weniger als zwei voneinander verschiedene Teiler (nämlich sich selbst und die Einheit) hat. Das geschieht, um die Eins aus der Reihe der Primzahlen zu streichen, wodurch sich manche zahlentheoretischen Sätze einfacher ausdrücken lassen und in manchen Teilen der Zahlentheorie eine größere Verallgemeinerung erreicht wird. Für andere Sätze oder Teile der Zahlentheorie aber ist es einfacher, die Eins als Primzahl gelten zu lasten. Ob man sich so oder so entscheidet, ist also eine Frage der Willkür oder der Zweckmäßigkeit, ohne daß man die eine Auffassung als falsch oder richtig gegenüber der anderen bezeichnen könnte. Das Natürlichere aber ist es zweifellos, die Eins als Primzahl gelten zu lassen.

(Zu Seite 110)

An und für sich kann für jede Primzahl eine Teilbarkeitsregel gebildet werden, aber das Rechnen mit diesen Regeln ist bei den größeren Zahlen so umständlich, daß es keinerlei Vorteil gegenüber der Ausführung der Division in der gewöhnlichen Weise bietet. Eine sehr hübsche und leicht zu handhabende Regel für die Division durch 11 sei noch erwähnt. Bezeichnen wir in irgendeiner Zahl die erste, die dritte, die fünfte usw. Ziffer als ungeradstellig, die zweite, vierte, sechste usw. als geradstellig, so gilt die Regel, daß, sofern die Quersumme der geradstelligen Ziffern, vermindert um die Quersumme der ungeradstelligen, gleich 0 oder durch 11 teilbar ist, dann die ganze Zahl durch 11 teilbar ist. Beispielsweise ist in der Zahl 78 364 die Quersumme der geradstelligen Ziffern (8 und 6) = 14, ebenso groß ist auch die Quersumme der ungeradstelligen Ziffern (7, 3 und 4); die Differenz beider Quersummen ist also 0 und daher die Zahl durch 11 teilbar. In der Zahl 82 947 051 ist die Quersumme der geradstelligen Ziffern – 7, die der ungeradstelligen – 29, die Differenz beider – 22, also durch 11 teilbar und daher die ganze Zahl ebenfalls durch 11 teilbar. Die hübsche Regel ist leicht anwendbar und erleichtert bei Divisionen durch 11 das Rechnen sehr erheblich.

(Zu Seite 114)

Es muß ausdrücklich darauf hingewiesen werden, daß der vorgeführte Beweis erst dann vollständig und wirklich richtig und überzeugend ist, wenn jene beiden Fälle, die es für P + 1 gibt, also sowohl für den Fall P + 1 ist eine Primzahl, wie auch für den Fall P + 1 ist keine Primzahl, behandelt werden. Darauf hinzuweisen ist deswegen notwendig, weil der zweite dieser beiden Fälle selbst von mathematisch Gebildeten, wenn sie sich mit jenem Beweis befassen oder ihn anderen vorführen, übersehen oder ausgelassen wird, womit dann ein böser Fehler in das Beweisverfahren gelangt. So ist kürzlich ein Buch erschienen, das Mathematik in populärer Form darstellt, aber leider die notwendige Genauigkeit vermissen läßt, die von jedem mathematischen Werk, auch dem populär gehaltenen, unbedingt verlangt werden muß. Hinsichtlich des Beweises für die Unendlichkeit der Anzahl der Primzahlen verfährt der Verfasser jenes Werkes einfach folgendermaßen: Angenommen z wäre die größte Primzahl, so ist das Produkt aller Primzahlen von 1 bis z, vermehrt um 1, also 1 × 2 × 3 × 5 × 7 × … [+] × z + 1, bestimmt wieder eine Primzahl, weil sie durch keine der Primzahlen von 1 bis z ohne Rest teilbar ist. – In dieser Form ist der Beweis falsch, denn die Zahl 1 × 2 × 3 × 5 × 7 × … × z + 1 kann, wenn sie auch durch keine der Primzahlen von 1 bis z teilbar ist, doch andere, größere Primteiler haben und brauchte durchaus keine Primzahl sein. Nach dem Verfasser des erwähnten Werkes müßte beispielsweise die Zahl 1 × 2 × 3 × 5 × 7 × 11 × 13 + 1 eine Primzahl sein; das ist aber durchaus nicht der Fall, denn die so erhaltene Zahl, nämlich 30 031, ist durch 59 und 509 teilbar. Also so einfach und klar der Euklidische Beweis der unendlichen Anzahl der Primzahlen auch ist, so muß er doch mit der nötigen Genauigkeit durchdacht und durchgeführt werden, wenn nicht ein böser Trugschluß herauskommen soll.

Postskriptum II

Ein Zahlenwettbewerb und seine Folgen – Die Berechnung der größten Primzahl – Keine »Kleinigkeit« – Die Wettbewerber – Rechenkünstler – Zahlenungeheuer – Wie der Mathematiker mit den Zahlen rechnet – Der Dr. hon. causa math. – Ein resoluter Besucher – »Entdeckungen« – Fallstricke der Zahlen

Die Zahl 2 ¹²⁷ – 1, die die bisher bekannte größte Primzahl darstellt, war, wie bereits gesagt, bis vor kurzem noch nicht berechnet worden. Ihre Berechnung erfolgte auf originelle Weise, und zwar auf Anregung des Verfassers. Ich hatte in einer weitverbreiteten Unterhaltungszeitschrift einen Aufsatz veröffentlicht, der sich in allgemeinverständlicher Form mit den Eigenschaften und Geheimnissen der Zahlen, besonders der Primzahlen, beschäftigte und darauf hingewiesen, daß die größte Primzahl durch den Ausdruck 2 ¹²⁷ – 1 dargestellt werde, dieser Ausdruck aber noch nicht ziffernmäßig berechnet worden sei. Daran hatte ich scherzhaft die Bemerkung geknüpft, daß ein Leser, der sich der Aufgabe unterziehen würde, den genannten Zahlenausdruck ziffernmäßig zu berechnen, sich dadurch den Dank der Wissenschaft verdienen und – vielleicht – zum Lohn dafür zum Doctor honoris causa mathem. ernannt werden könnte.

Dieser Scherz, insbesondere der Wink mit dem Dr. h. c., hatte eine unerwartete Folge. Ein gewaltiges Rechnen hub in dem Leserkreise des Blattes an, und die Folge war, daß in den folgenden Wochen sowohl bei der Schriftleitung des Blattes wie auch bei mir selbst eine wahre Flut von Berechnungen der großen Primzahl eingingen, eine wahre Massendemonstration von Zahlen, wie ich sie nie erlebt habe. Aus allen Gegenden des deutschen Vaterlandes, dann aber auch aus dem Auslande und in der weiteren Folge schließlich aus sämtlichen Erdteilen gingen die Zahlenbataillone ein, auf Postkarten, gewöhnlichen und eingeschriebenen Briefen, Eilbriefen und Telegrammen, und bei einem Teilnehmer an diesem kuriosen Zahlenwettbewerb hatte die Ausrechnung mit allem Drum und Dran sogar Umfang und Gewicht eines rechtschaffenen Postpaketes angenommen. Und das Motiv, das aus vielen der Begleitbriefe heraussprach, war: Wie, die Herren Mathematiker, die sich auf ihre Rechenkünste soviel einbilden, haben es bisher noch nicht einmal zuwege gebracht, jene Zahl auszurechnen? Denen wollen wir zeigen, was eine Harke im Zahlengarten ist! Her mit dem Doktorhut, wenn er dafür wirklich zu haben sein sollte!

Angesichts jener arithmetischen Hochflut hatte ich mich natürlich selbst auch schleunigst an die Berechnung der Zahl gemacht und konnte mein Ergebnis mit den einlaufenden Berechnungen vergleichen. Es ergab sich, daß von den im ganzen eingegangenen etwa 300 Berechnungen über die Hälfte zu dem gleichlautenden Ergebnis gekommen war, das mithin als das richtige zu bezeichnen war, während der große Rest der hiervon abweichenden Berechnungen falsche Lösungen darstellte. So war die bisher bekannte größte Primzahl, die bis dahin nur in der Potenzform existierte, plötzlich ziffernmäßig berechnet und als die 39stellige Zahl 170 141 183 460 469 231 731 687 303 715 884 105 727 festgestellt worden. Versuchen wir zunächst, uns die Größe dieser Riesenzahl an einigen Beispielen zu veranschaulichen, denn die trockene und langatmige Zahlenfolge allein gibt uns hiervon noch keinen Begriff. Nehmen wir an, es hätte jemand so viel Pfennige, wie jene Riesenzahl ausdrückt, so könnte er damit den ganzen Erdball, wenn dieser aus Gold bestände, bar bezahlen und nicht nur einen, sondern sogar rund eine volle Milliarde solcher Goldplaneten kaufen; wäre die Erde aber ein einziger großer Diamant, so würde der millionste Teil seines Barvermögens genügen, um diesen stattlichen Edelstein für seine Krawattennadel zu erstehen. Eine Teilnehmerin an jenem Zahlenwettbewerb gab zugleich folgende hübsche Veranschaulichung der Größe der von ihr richtig berechneten Zahl: Nehmen wir an, daß eine Milliarde Mikroben (Bazillen, Bakterien u. ä.) nur die Länge von zusammen einem Zentimeter hat und daß so viele solcher Kleinlebewesen, wie die berechnete Zahl angibt, sich hintereinander, Stück an Stück gereiht, in einer Linie befinden, dann würde das Licht, das bekanntlich in einer Sekunde 300 000 Kilometer zurücklegt und für den Weg von der Erde bis zum Monde keine anderthalb Sekunden braucht, etwa 200 Milliarden Jahre benötigen, ehe es diese lange Linie durcheilt hätte. Also die größte bekannte Primzahl ist wirklich keine »Kleinigkeit«.

Manche der Einzelheiten aus jenem Zahlenwettbewerb sind von heiterem arithmetisch-psychologischen Interesse. Nahezu alle Altersklassen waren unter den Teilnehmern vertreten; der jüngste war ein zwölfjähriger Schüler, der ein falsches, der älteste ein fast achtzigjähriger Geistlicher im Ruhestand, der das richtige Ergebnis mitgeteilt hatte. Studenten, Akademiker aller vier Fakultäten, viele Techniker und Ingenieure, Staats-, städtische und Bankbeamte, Angehörige der kaufmännischen Berufe und des Handwerks usw. waren darunter vertreten. Auch Damen hatten sich, wenn auch nur mit einer Minderheit, an dem Wettbewerb beteiligt und hatten, was bemerkenswert ist, durchweg richtige Berechnungen gesandt; die Falschlösungen kamen durchweg auf das Konto männlicher Rechner, dafür hatten aber mehrere männliche Teilnehmer an die Berechnung der Zahl noch auf eigene Faust weitergehende Berechnungen geknüpft. Auch ein veritabler Rechenkünstler befand sich unter den Teilnehmern, der nach seinen Mitteilungen mit den Millionen und Milliarden zu jonglieren und Quadrat- und Kubikwurzeln jedes gewünschten Umfanges im Handumdrehen zu ziehen gewohnt war. Seine Kunst in Ehren – aber seine Berechnung der größten Primzahl war falsch. Einzelne Einsender hielten Vorsicht für angebracht, um nicht durch leichtfertige Preisgabe ihres Ergebnisses um ihr geistiges Eigentum gebracht zu werden, und gaben nur die Anfangs- und Endziffern ihrer Resultate bekannt, andere nannten nur die Quersumme der Zahl, die 154 beträgt. Ein Leser hatte sich, bevor er sich zur Bekanntgabe seiner Ergebnisse entschloß, dieses notariell beglaubigen lassen; seine Vorsicht war überflüssig, denn seine Berechnung war falsch, sogar total falsch.

Auch die Schwierigkeit der Berechnung scheint bei den verschiedenen Teilnehmern sehr verschieden empfunden worden zu sein. Einige haben nach ihren Angaben Tag und Nacht gebraucht, ehe sie zum fertigen Endergebnis kamen, andere die Rechnung in wenigen Stunden durchgeführt, und eine gute Stunde dürfte wohl das Minimum an Zeit sein, das die Rechnung verlangt. Einzelne Teilnehmer des Zahlenwettbewerbs hatten für die Ausführung ihrer Rechnungen an Schreibmaterial nur ein bescheidenes Folioblatt benötigt, bei anderen hatte sich dieses zu einem stattlichen Buch von vielen Blättern ausgewachsen (einschließlich der Nachprüfungen). Ein Teilnehmer schickte mir eine Abschlagszahlung; er war nur bis 2 ¹⁰⁰ gekommen und strich dann die Segel, weil, wie er schrieb, ihm die Zahlen von dem vielen Rechnen schon Charleston vor den Augen tanzten. Ein Teilnehmer hatte sich an 2 ¹²⁷ nicht genügen lassen und nicht nur diese doch immerhin recht stattliche Zahl berechnet, sondern die Berechnung sogar bis zur Potenz 2 ²⁶⁰ durchgeführt und mir das Resultat übermittelt. Es ist das eine 79stellige Zahl, die mit 1 Tredezillion und 852 673 Duodezillionen beginnt und gegen die unsere Zahl mit ihren 127 Potenzen und ihren doch immerhin 39 Stellen sich verhält wie ein Atom zum Erdball. Um diese Zahl zu erhalten, muß man unsere Zahl 2 ¹²⁷ zunächst einmal mit sich selbst multiplizieren und das Produkt dann noch mit 2 ⁶ = 64 multiplizieren. Noch übertroffen aber wurde dieser Rechenkünstler von einem anderen Teilnehmer an dem Zahlenwettbewerb, dem 76jährigen Herrn P. aus Breslau, der nicht nur die große Primzahl richtig berechnete, sondern sich dadurch auch veranlaßt sah, die Potenzen 2 ³⁹⁸, 3 ²⁵¹, 5 ¹⁷¹, 7 ¹⁴¹ und 11 ¹¹⁵ ziffernmäßig auszurechnen. Die Werte dieser Zahlenungeheuer sind Vigintillionen, d. h. Zahlen mit über 120 Stellen, und dürften vielleicht die größten Zahlenwerte sein, die jemals ziffernmäßig berechnet worden sind. Logarithmisch konnte ich sowohl die Richtigkeit der Stellenzahl wie auch die der sechs Anfangsziffern der mir mitgeteilten berechneten Zahlen nachprüfen und bestätigen und dem greisen Rechenkünstler zu seiner zumal in Anbetracht seines hohen Alters geradezu staunenswerten Rechenfähigkeit meine größte Hochachtung und meinen herzlichsten Glückwunsch aussprechen. Denn wenn es sich hierbei auch an und für sich um keine komplizierte Rechenarbeit handelt, so doch um eine unendlich mühsame und langwierige Rechnerei, die, wenn sie korrekt und fehlerfrei durchgeführt werden soll, ganz gewaltige Anforderungen an Ausdauer und Spannkraft stellt. Sich die Größe der erwähnten Riesenzahlen an ähnlichen Beispielen wie den obenangeführten zu veranschaulichen, überlasse ich der Rechenkunst und Phantasie des Lesers.

Eine Anzahl von Lesern gab übrigens ihrer Verwunderung darüber Ausdruck, daß die Ausrechnung der Primzahl 2 ¹²⁷ – 1 nicht schon längst von den Mathematikern selber ausgeführt worden sei, und einige vermuteten sogar, daß ich mir mit meiner diesbezüglichen Angabe nur einen unziemlichen Scherz geleistet habe. Dazu ist folgendes zu bemerken: Tatsächlich war die genannte Zahl bis dahin noch nicht berechnet, aber natürlich wäre die Berechnung für die Mathematiker selbst auch nicht schwerer als für die Teilnehmer an jenem Zahlenwettbewerb gewesen. Wenn sie das dennoch bis dahin nicht getan hatten, so aus dem einfachen Grunde nicht, weil für sie keinerlei Bedürfnis dazu vorlag. Denn für den Mathematiker oder Zahlentheoretiker ist eine Zahl in der Form ihrer Potenz, also in unserem Falle der Ausdruck 2 ¹²⁷ – 1, viel wichtiger und interessanter als ihre ziffernmäßige Darstellung, denn dieser Ausdruck besagt ihm viel mehr über Charakter und Eigenschaften der Zahl als die berechnete Ziffernfolge. Das große Kunststück, das nur dem Mathematiker von Fach geläufig war, bestand ja nicht darin, jene Zahl ziffernmäßig auszurechnen, sondern festzustellen und zu beweisen, daß diese Zahl eine Primzahl ist. Diese Feststellung erforderte die kompliziertesten Hilfsmittel und Methoden der mathematischen Forschung und war eine Arbeit von gewaltiger Schwierigkeit, aber der ziffernmäßigen Darstellung der Zahl bedurfte es zu diesem Zweck nicht. Denn mit ganz anderen Mitteln, als der Nichtfachmann kennt und ahnt, geht der Mathematiker solchen Riesenzahlen in der Form der Potenz auf den Grund. Betrachten wir, um ein Beispiel anzuführen, etwa die Zahl 2 ²⁵⁶ – 1. Dieser Wert stellt eine ungeheuer viel größere Zahl als 2 ¹²⁷ – 1 dar, denn er ergibt, ziffernmäßig ausgerechnet, eine Zahl von 88 Stellen, an die keine menschliche Vorstellungsfähigkeit auch nur im entferntesten heranreicht, und die Berechnung würde selbst den geübtesten Rechner zum mindesten mehrere Stunden in Anspruch nehmen. Der Mathematiker aber sieht aus der Potenzform dieser Zahl, ohne der ziffernmäßigen Ausrechnung der Zahl zu bedürfen oder auch nur die Anzahl ihrer Ziffern zu kennen, daß diese Zahl niemals eine Primzahl sein kann, sondern daß sie durch 3, durch 5, durch 17 und auch durch 257 teilbar sein muß. Also wenn die Mathematiker sich die ziffernmäßige Ausrechnung solcher Zahlenausdrücke wie 2 ¹²⁷ – 1 schenken oder das gern anderen überlassen, so geschieht das wirklich weniger aus Mangel an rechnerischer Begabung als aus Mangel an Interesse für die Ziffernfolge des Zahlenwertes. Das erklärt, warum auch unsere Primzahl bis dahin von den Mathematikern nicht berechnet worden war. Also ein wissenschaftliches Novum, wenn auch gerade kein solches weltbewegender Art, ist aus dem geschilderten Zahlenwettbewerb, der wohl einzig in seiner Art dastehen dürfte, immerhin hervorgegangen und die berechnete Zahl ist seitdem auch in die mathematische Literatur aufgenommen worden.

Noch eine weitere Folge jenes Zahlenwettbewerbes wollen wir erwähnen, sie zeigt, wie auch bei der Beschäftigung mit den Zahlen der Humor manchmal auf seine Rechnung kommt. Eine ganze Anzahl der Teilnehmer berief sich auf die erwähnte scherzhafte Versprechung, daß der Berechner jener größten Primzahl sich – vielleicht – Anrecht auf den Dank der Wissenschaft und auf eine entsprechende akademische Ehrung erwerben würde, und begleitete die Übersendung ihrer arithmetischen Forschungsergebnisse mit dem energischen Ruf: her mit dem Doctor honoris causa! Da kam ich nun allerdings in einige Verlegenheit, denn daß der Scherz so ernsthaft aufgenommen würde, hatte ich nicht geahnt. Beschwichtigend mußte ich daher jenen Kandidaten auf den Doktorhut auseinandersetzen, daß die Berechnung der bewußten großen Primzahl, wenn sie sicher auch Schweiß und Mühe gekostet hatte, sich doch immerhin in den Grenzen normaler Rechenbefähigung gehalten hatte, was besonders aus dem Umstande ersichtlich war, daß sich mehrere Hunderte von Freiwilligen zur Berechnung jener Zahl gefunden und die größere Hälfte von diesen die Zahl auch richtig berechnet hatte. Bei einer solchen Massenleistung wird der Wert der Einzelleistung naturgemäß gedrückt, so daß die Universitäten doch wohl Bedenken tragen dürften, für eine solche den Doktorhut zu verleihen. Also bat ich jene Teilnehmer, sich mit dem Lohn, den die Beschäftigung mit den Dingen der Wissenschaft in sich selbst trägt, zufrieden zu geben und nicht mich persönlich für die entgangene akademische Ehrung verantwortlich zu machen. Diesen Argumenten zeigten sich denn auch die meisten der Doktorhut-Aspiranten zugänglich, und nur einige sehr Enttäuschte machten ihrem Herzen nachdrücklich und in ziemlich ungewählten Worten Luft. Übrigens konnte konstatiert werden, daß die weitaus meisten, die so erpicht auf den Doktorhut waren, zu den – Falschlösern gehörten und schon deswegen keinen Anspruch auf das genannte akademische Bekleidungsstück hatten. Das war auch der Fall bei einem besonders energischen Teilnehmer aus Halle an der Saale. Dieser hatte mir telegraphiert: »Größte Primzahl berechnet; komme heute persönlich!«, und schon einige Stunden später, noch ehe ihn meine abratende Rückantwort erreicht haben konnte, stand er in Lebensgröße vor mir, unterbreitete mir seine umfangreiche Berechnung der großen Primzahl und erkundigte sich diskret nach seinen Aussichten für den Dr. h. c. Mir war recht unerfreulich zumute, denn der resolute Hallenser war von gut durchtrainierter Preisboxerfigur und sah aus, als ob er enttäuschten Hoffnungen sehr gesetzwidrigen Ausdruck geben könnte. Doch als ich die Berechnung prüfte, da war sie – gottlob – falsch, und mit bedauerndem Achselzucken konnte ich meinen Besucher darauf hinweisen, daß eine ganze Anzahl falscher Ziffern in seinem Resultat ihn um den erstrebten Erfolg seiner arithmetischen Bemühungen gebracht hatte.

Eine ganze Anzahl von Lesern jenes Aufsatzes endlich, der ungefähr den Inhalt unseres Kapitels über die Primzahlen hatte, versuchte sich an der Ergründung der anderen darin erwähnten mathematischen Probleme. Wohl ein Dutzend Herren teilte mir mit, daß sie den Beweis für die unendliche Anzahl der Primzahlpaare gefunden hätten, und baten um Prüfung ihres Beweises. Mehrere andere glaubten sogar das Gesetz der Primzahlen gefunden zu haben und erboten sich, dafür den Beweis zu erbringen. Die Nachprüfung ergab jedoch in allen Fällen die völlige Unzulänglichkeit der vorgebrachten Beweise, die auch durch wiederholte nachträgliche Verbesserungen und Redaktionen seitens ihrer Urheber nicht zur Bedeutung mathematischer Wahrheiten gedeihen konnten. Ein Leser endlich glaubte, daß er in der Lage sei, den Beweis für die Unrichtigkeit des Euklidischen Beweises der Unendlichkeit der Anzahl der Primzahlen, der ebenfalls in jenem Aufsatz angeführt worden war, zu erbringen, und bot der Redaktion des betreffenden Blattes die Veröffentlichung seines Beweises gegen Honorar an. Die Schriftleitung entschloß sich jedoch, dem gesicherten Ergebnis der mathematischen Forschung zweier Jahrtausende ihr Vertrauen vorderhand nicht zu entziehen und lehnte daher die Veröffentlichung jenes revolutionären Gegenbeweises ab.

So leicht sind die mathematischen Geheimnisse denn doch nicht zu enthüllen, ebensowenig aber auch die mathematischen Wahrheiten zu erschüttern, und wenn sich die Mathematiker von Fach an einer solchen harten Nuß schon seit Jahrhunderten die Zähne ausgebissen haben, dann kann der Laie, der im Handumdrehen zur Lösung dieser Probleme gelangt zu sein glaubt, sicher sein, daß sein Ergebnis oder sein Beweis falsch, die von ihm angefeindete Ansicht der Mathematiker selbst aber richtig ist. Gerade auf dem Gebiete des abstrakten mathematischen Wissens tut der Laie gut, rückhaltlos den Ergebnissen der Wissenschaft Vertrauen entgegenzubringen, denn diese sind in keinem Wissensgebiet gesicherter und unangreifbarer als gerade in diesem. Aber auch nirgends sind so viele und verborgene Fallstricke ausgelegt wie im Reich der Zahlen, Fallstricke, über die oftmals selbst der Fachmann stolpert, die aber den Uneingeweihten mit Sicherheit zu Fall bringen und die Ergebnisse seiner Forschungstätigkeit auf diesem Gebiete, den Wert seiner Entdeckungen und Beweise völlig illusorisch machen.

2. Das Gesetz der Primzahlen

Ein uraltes Zahlenproblem – Eine Doktorfrage? – Primzahllücken und Primzahlpaare – Eine Annäherungsformel

Nächst der Frage nach der Endlichkeit oder Unendlichkeit der Anzahl der Primzahlen, die durch den Euklidischen Beweis schon vor über zweitausend Jahren restlos gelöst worden ist, tritt ein anderes Problem an den Zahlenforscher heran, und zwar ein solches von ungleich größerer Tiefe und Schwierigkeit, nämlich die Frage nach dem Gesetz der Primzahlen. Befolgen die Primzahlen, die in die Menge der allgemeinen Zahlen eingestreut sind wie die Rosinen in den Kuchen, in ihrer Aufeinanderfolge innerhalb der Zahlenreihe eine bestimmte Gesetzmäßigkeit und welches ist, wenn das der Fall ist, dieses Gesetz? Diese Frage beschäftigte die Mathematiker, solange sie sich überhaupt mit den Eigenschaften und Gesetzen der Zahlen befassen, und ist im wesentlichen heute noch so unbeantwortet wie im Altertum, ist seit Jahrtausenden ein ungelöstes Rätsel und das schwierigste und tiefste Problem, das uns die Zahlenreihe aufgibt.

Betrachten wir, um dem Rätsel auf die Spur zu kommen, die Aufeinanderfolge der Primzahlen innerhalb der Zahlenreihe. Sie läßt nirgends eine irgendwie ausdrückbare Regelmäßigkeit oder Gesetzmäßigkeit erkennen, obwohl auf die Entdeckung einer solchen Gesetzmäßigkeit seit Jahrhunderten von den Mathematikern aller Länder eine enorme Summe von Arbeit und Scharfsinn verwandt worden ist und vielleicht jeder Mathematiker, zum mindesten jeder Zahlentheoretiker, wohl schon seinen Scharfsinn an dieser Aufgabe erprobt hat. Es handelt sich hierbei auch nicht etwa nur um eine bloße »Doktorfrage«, die mehr aus wissenschaftlicher Neugier geboren als imstande ist, unsere Erkenntnis zu vermehren, sondern die Kenntnis jenes Gesetzes wäre für die mathematische Forschung von größter Wichtigkeit und würde auf eine ganze Reihe anderer Probleme aus dem Gebiet der Zahlenkunde ein aufhellendes Licht werfen. Wir erwähnten bereits, daß die Lücken zwischen den Primzahlen innerhalb der Zahlenreihe, also die nur aus zusammengesetzten Zahlen bestehenden Zahlenfolgen, immer größer werden. Eine Lücke von fünf zusammengesetzten Zahlen kommt zum ersten Male zwischen den Primzahlen 23 und 29 vor; zwischen den Primzahlen 89 und 97 findet sich eine solche von sieben und zwischen 113 und 127 bereits eine Lücke von 14 Zahlen, von denen keine eine Primzahl ist. Auf große Lücken folgen dann auch wieder kleinere, selbst solche, die nur aus einer einzigen Zahl bestehen, aber im allgemeinen befolgen die Lücken die Tendenz, immer größer zu werden. Es kann leicht bewiesen werden, daß diese Lücken sogar einmal jede beliebige Größe annehmen müssen, daß, wenn auch erst in unabsehbar fernen Regionen der Zahlenreihe, einmal Lücken von tausend, Million und Billion Zahlen auftreten müssen, von denen keine einzige eine Primzahl ist. Die größte bekannte Primzahllücke befindet sich unter den Zahlen der fünften Million zwischen 4 652 353 und 4 652 507 und umfaßt 153 zusammengesetzte Zahlen. Die Primzahlen werden also immer seltener in der Zahlenreihe. Zugleich aber wissen wir, daß die Anzahl der Primzahlen unendlich ist, daß wir in der Zahlenreihe niemals zu einer letzten oder größten Primzahl gelangen können, daß sich vielmehr hinter jeder noch so fernen und entlegenen Primzahl immer weitere und immer wieder unendlich viele Primzahlen befinden, wie sich aus dem Euklidischen Beweis der Unendlichkeit der Anzahl der Primzahlen ergibt. Das Zusammenbestehen dieser beiden Tatsachen, also einerseits die immer größer werdende Seltenheit der Primzahlen innerhalb der Zahlenreihe, andererseits die unendliche Anzahl der Primzahlen, das ist eins der großen Wunder, das die Zahlenreihe für den Mathematiker in sich schließt, ein Problem, für das sich bisher noch keine befriedigende Lösung hat finden lassen.

Wie die Primzahlen selbst, so werden auch die Primzahlpaare, also je zwei Primzahlen, die nur durch eine zusammengesetzte Zahl getrennt sind, wie 17 und 19 oder 101 und 103 usw., immer seltener. Aber auch hier hat man immer wieder Primzahlpaare festgestellt, wenn auch hier die Lücken zwischen den einzelnen Paaren immer größer werden. Es ist mit hoher Wahrscheinlichkeit anzunehmen, daß auch die Anzahl der Primzahlpaare unendlich groß ist, aber leider hat sich für diese Annahme ein so schlüssiger und eleganter Beweis wie der für die Unendlichkeit der Primzahlen nicht erbringen lassen; auch dieser Beweis harrt noch seines Entdeckers.

In den letzten Jahren glaubte man allerdings, dem Gesetz der Primzahlen wenigstens annäherungsweise auf die Spur gekommen zu sein. Für den Leser, der die Formelsprache der Mathematik noch nicht ganz vergessen hat, sei die Formel, die diese Annäherung ausdrückt, mitgeteilt; sie lautet (das heißt x geteilt durch logarithmus naturalis x), und dieser Ausdruck bedeutet, daß in jedem Zwischenraum auf der Zahlenreihe von 1 bis x (wo also x eine beliebige Zahl ist) die Anzahl der Primzahlen so groß ist, wie durch jene Formel ausgedrückt wird. Aber der Wert, den die Formel angibt, ist nur ein Annäherungswert und entbehrt der absoluten Exaktheit und Genauigkeit, die Kennzeichen und Bedingung aller mathematischen Deduktionen sind. Er wird um so genauer, je größer x angenommen wird, aber ein wirklich genauer Wert ist es, wie gesagt, nicht, und damit ist das Problem der Gesetzmäßigkeit der Primzahlen nach wie vor als ungelöst zu bezeichnen.

3. Das Goldbachsche Problem

Ein einfacher Satz – Erfahrung und Beweis – Tiefen des Zahlenreiches

In engem Zusammenhange mit jenem Problem der Zahlenwelt, das wir als die Frage nach dem Gesetz der Primzahlen kennengelernt haben, steht noch ein weiteres zahlentheoretisches Problem, das als der Goldbachsche Satz bezeichnet wird. Es hat das eigentümliche, daß es in seiner Fassung von der denkbar größten Einfachheit, jedem Kinderverstande sozusagen faßbar ist und dennoch die größten Schwierigkeiten birgt, Schwierigkeiten, die eine Lösung dieses Problems bisher unmöglich gemacht haben.

Das Problem ist benannt nach dem Königsberger Mathematiker Christian Goldbach, der bis 1764 lebte. Er war zwar keiner der überragend Großen seiner Wissenschaft, hat dafür aber den Mathematikern als Erbschaft eine harte Nuß hinterlassen, indem er den Satz aufstellte, daß jede gerade Zahl als Summe zweier Primzahlen dargestellt werden könne. So ist 6 = 1 + 5, 18 = 7 + 11 oder = 5 + 13, 100 = 3 + 97 oder = 17 + 83 oder = 59 + 41 usw. Der Inhalt des Satzes ist also überaus einfach und leichtverständlich. Aber Goldbach hat sich damit begnügt, den Satz aufzustellen, hat aber keinen Beweis dafür aufgestellt, und den Beweis für diesen einfachen Satz zu erbringen, das ist die böse crux des Problems. Er hat sich allen Bemühungen der Zahlentheoretiker bisher standhaft entzogen. Man hat den Satz zwar bei allen geraden Zahlen, die man nach dieser Richtung hin untersucht hat, bestätigt gefunden und sogar feststellen können, daß eine solche Zahl, je größer sie ist, auf um so mehr Arten die Summe zweier Primzahlen zu sein pflegt, wie auch die angeführten Beispiele erkennen lassen, und hat sehr weit ausgedehnte Untersuchungen bis hoch in die Zahlenreihe hinein ausgeführt. Aber naturgemäß ist man nicht in der Lage, alle überhaupt möglichen geraden Zahlen daraufhin zu untersuchen, schon deswegen nicht, weil ja die Anzahl der geraden Zahlen unendlich ist. Eine endgültige Bestätigung des Satzes könnte daher wieder nur durch einen allgemeinen Beweis erbracht werden, und diesen Beweis konnte weder Goldbach selbst noch einer der vielen Mathematiker nach ihm liefern. Der Goldbachsche Satz hat mithin zunächst nur die Bedeutung eines Erfahrungssatzes, das heißt solange nicht der exakte Beweis für die allgemeine Richtigkeit des Satzes erbracht worden ist, muß immer noch mit der Möglichkeit gerechnet werden, daß er eben nicht allgemein und ausnahmslos gilt und sich vielleicht irgendwo in hohen Regionen der Zahlenreihe einmal eine gerade Zahl findet, die nicht die Goldbachsche Regel befolgt und auf keine Weise als Summe zweier Primzahlen dargestellt werden kann. Also auch dieses Problem harrt noch seiner Lösung, und diese würde wahrscheinlich zugleich auch das Problem des Gesetzes der Primzahlen seiner Lösung um ein gutes Stück näherbringen.

Wahrlich, die Reihenfolge der Zahlen, die sich so nüchtern und nichtssagend ausnimmt, wenn man sie hinschreibt oder abliest, sie birgt einen unendlich tiefen Inhalt, birgt die tiefsten und schwierigsten Probleme, die zugleich auf denjenigen, der sich mit ihnen beschäftigt, den ganzen Reiz des Geheimnisvollen und Ungelösten ausüben. Mit Geheimnissen beladen und belastet ist sie. Und sollten die bisher bekannten Probleme einmal gelöst werden, so werden dafür andere auftauchen, denn die Tiefe und der Inhalt der Zahlenreihe ist das nie erschöpfbare Meer der Unendlichkeit. Auch für den denkenden Laien ist die Beschäftigung mit den Zahlen und ihren Geheimnissen oftmals von hohem Reiz, und da er ja, um sich auf diesem Gebiete betätigen zu können, keinerlei umständlicher und kostspieliger Apparate wie bei anderen Experimenten, sondern eigentlich nur eines Bleistiftes und eines Stückes Papier bedarf, so wagt auch er sich gern in jene Tiefen hinein, jongliert rechnerisch mit den Zahlen, sucht Entdeckungen zu machen und die Geheimnisse der Zahlen zu enträtseln. Und da er für dieses Jonglieren und Grübeln ja keinerlei mathematischer Fachbildung bedarf, so stürzt er sich gern in die verwegensten arithmetischen Abenteuer. Viele wertvolle und neue Entdeckungen im Gebiet der Zahlen sind auf diese Weise schon von Laien gemacht worden, allerdings mit der Einschränkung, daß die wertvollen Entdeckungen, die auf solche Weise zustande kommen, nicht neu, sondern schon immer seit vielen Jahrhunderten bekannt, die neuen aber nicht wertvoll, d. h. nicht richtig waren. Aber das schadet nichts, die Freude an der Beschäftigung mit den Zahlen ist auch etwas wert und wird jedem zuteil, der sich den Zahlen und ihren Geheimnissen mit Liebe und Ausdauer naht.

4. Das Fermatsche Problem

Der Vater des Problems – Potenzen und Potenzsummen – Das Problem – Weil der Rand zu knapp war – Der Kampf um den Beweis – Teilerfolge – Der Wolfskehlpreis und seine Folgen – Ein Irrtum Fermats?

Die Geschichte des menschlichen Forschens ist reich an Problemen, die jahrhunderte-, ja sogar jahrtausendelang die Köpfe der Gelehrten beschäftigt und gewaltige Summen von Geistesarbeit gekostet haben, ehe die Wissenschaft zu einer befriedigenden und abschließenden Auffassung kam. Die Quadratur des Kreises, das Perpetuum mobile, die Dreiteilung des Winkels und viele andere noch, das waren solche Aufgaben, deren jede ein eigenes Kapitel in dem Geisteskampfe um wissenschaftliche Erkenntnis füllt. Die eben genannten Probleme können heute als gelöst und erledigt betrachtet werden, zu denjenigen Problemen aber, die bisher allem Scharfsinn getrotzt und sich trotz der Arbeit und Versuche von Jahrhunderten bisher ihrer Lösung standhaft entzogen haben, gehört das sogenannte Fermatsche Problem, das in gleicher Weise wegen der unergründlichen Schwierigkeit wie auch wegen der eigenartigen Geschichte, die sich daran knüpft, berühmt ist.

Das Fermatsche Problem entstammt dem Boden der wissenschaftlichen Zahlenkunde. Der Franzose Pierre Fermat (1601 bis 1665), der von Beruf zwar Jurist und Parlamentsrat, außerberuflich aber einer der hervorragendsten Mathematiker seiner Zeit war, hat seiner Wissenschaft das genannte Problem als berühmte Erbschaft hinterlassen. Bevor wir auf den Kernpunkt des Problems selbst eingehen, wollen wir zuvor kurz einen sehr einfachen mathematischen Begriff erläutern, an den es anknüpft, nämlich den Begriff der Potenz, deren sich viele unserer Leser aus der Schulzeit noch erinnern werden. Als Potenz bezeichnet der Mathematiker die Multiplikation einer Zahl mit sich selbst, wie etwa 5 × 5 oder 7 × 7 usw. Solche wie diese beiden Multiplikationsprodukte, bei denen also der gegebene Faktor zweimal auftritt, bezeichnet man dieserhalb als zweite Potenzen oder Potenzen zweiten Grades und schreibt statt 5 × 5 lieber 5 ² bzw. 7 ²; man liest diesen Ausdruck: »fünf hoch zwei«. Die untenstehende Grundzahl, also in unserem Falle 5 bzw. 7, heißt die Basis, die rechts oben angeführte Ziffer, also hier 2, der Exponent der Potenz. Ebenso kann man Potenzen mit höheren Exponenten bilden, wie etwa 3 × 3 × 3 × 3 = 3 ⁴ (gelesen: »drei hoch vier«), ein Ausdruck, dessen Zahlenwerte natürlich 81 ist, oder 5 × 5 × 5 × 5 × 5 × 5 = 5 ⁶, was, wie sich leicht ausrechnen läßt, 15 625 ist. Auf diese Weise kann man natürlich Potenzen mit beliebig hohem Exponenten oder, wie man zu sagen pflegt, Potenzen vom nten Grade bilden, wo also n irgendeine beliebige Zahl bedeutet. Die Werte der Potenzen werden mit steigendem Exponenten bald sehr hohe, wie der Leser sehr leicht feststellen kann, wenn er vielleicht einige solcher Potenzen mit hohen Exponenten, etwa 2 ⁶⁴ oder 12 ³⁰ usw. auszurechnen versucht.

Unter den Potenzen nehmen nun diejenigen des zweiten Grades, also wie 5 ² oder 13 ², in vielfacher Hinsicht eine besondere Stellung in der Zahlentheorie ein, unter anderem auch dadurch, daß die Summe zweier solcher Potenzen zweiten Grades wieder die zweite Potenz einer ganzen Zahl sein kann. So ist beispielsweise 3 ² + 4 ² = 5 ², was, wenn wir die Potenzen durch ihre Zahlenwerte ersetzen, auf die Gleichung 9 + 16 = 25 herauskommt; ebenso ist 5 ² + 12 ² = 13 ² oder 20 ² + 48 ² = 52 ² usw. Wohlgemerkt ist nicht immer die Summe zweier Potenzen zweiten Grades wieder eine solche Potenz; beispielsweise ist 5 ² + 6 ² = 61, die Zahl 61 aber kann nicht als zweite Potenz einer ganzen Zahl dargestellt werden. Wohl aber gibt es sehr viele, ja sogar unzählig viele Zahlenpaare, die die besondere Eigenschaft zeigen, daß die Summe ihrer zweiten Potenzen wieder die zweite Potenz einer ganzen Zahl ist. Diese Eigenschaft der zweiten Potenzen spielt in der Zahlentheorie wie auch noch in anderen Gebieten der Mathematik eine hervorragende Rolle; beispielsweise führt auch der bekannte pythagoreische Lehrsatz über das Verhältnis der Seiten im rechtwinkligen Dreieck auf eine solche wie die obenerwähnte Beziehung der Potenzen zweiten Grades.

Es liegt nun die Frage sehr nahe, ob etwa Ähnliches wie bei den zweiten Potenzen auch bei Potenzen höheren Grades möglich ist, also etwa auch die Summe zweier Potenzen dritten Grades wieder dritte Potenz einer ganzen Zahl sein kann. Diese Frage hat Fermat in den letzten Jahren seines Lebens zum Gegenstand seiner zahlentheoretischen Untersuchungen gemacht und ist dabei zu dem Resultat gekommen, daß immer nur die Summe zweier Potenzen zweiten Grades wieder eine Potenz gleichen Grades sein, Entsprechendes bei Potenzen höheren Grades aber niemals der Fall sein kann. Diese Behauptung wird für gewöhnlich in der Weise ausgedrückt, daß in der Gleichung a ⁿ + b ⁿ = c ⁿ , wenn a, b und c ganze Zahlen sind, der Exponent n niemals größer als 2 sein kann. Fermat hat diese Behauptung auf den Rand eines Blattes in einem mathematischen Lehrbuch niedergeschrieben und hinzugefügt, daß er für seine Behauptung einen bewunderungswürdigen Beweis habe, daß aber der Rand des Blattes zu knapp sei, um ihn an dieser Stelle niederzuschreiben. Auch sonst hat er den Beweis nicht veröffentlicht und ist gestorben und hat sein Geheimnis mit ins Grab genommen. Den Beweis für die von Fermat aufgestellte Behauptung zu finden, das ist das Fermatsche Problem.

Als nach Fermats Tode dessen Sohn den Nachlaß des großen Mathematikers herausgab, wurde auch der von ihm aufgestellte Satz den Mathematikern bekannt. Leider aber fehlte der Beweis. Man suchte den Beweis von neuem zu finden, von der Meinung ausgehend, daß das, was Fermat gelungen sei, auch anderen Mathematikern gelingen müsse, mußte aber bald feststellen, daß der Beweis trotz aller darangesetzten scharfsinnigen Untersuchungen nicht zu erbringen war. Damit war ein ganz einzigartiger Fall in der Geschichte der Mathematik gegeben: ein Mathematiker hatte einen Satz aufgestellt und nach seiner Behauptung den Beweis dafür gefunden, der sich hinterher von keinem anderen von neuem entdecken ließ. Das reizte natürlich die Nachfolger Fermats ganz gewaltig und veranlaßte fast alle Mathematiker zu dem Versuch, den verlorenen Beweis von neuem zu entdecken, ohne daß aber die diesbezüglichen Bemühungen zum Erfolge geführt hätten. So war die Sachlage und so ist sie seit bald dreihundert Jahren im wesentlichen bis auf den heutigen Tag geblieben. Die meisten und hervorragendsten Mathematiker nach Fermat haben sich an der Lösung des Problems versucht; Euler, Legendre, der große Gauß, Abel, Cauchy, Kummer, Kronecker, Dirichlet usw., alle widmeten sie dem hartnäckigen Problem umfangreiche und tiefgründige Untersuchungen, ohne die Lösung finden zu können, und es blieb die Tatsache bestehen, daß ein von einem Mathematiker einmal entdeckter Beweis von den hervorragendsten Köpfen der mathematischen Wissenschaft, die zum Teil sogar viel bedeutendere Leistungen als Fermat aufzuweisen hatten, nicht nochmals entdeckt werden konnte. Niemals hatten die Mathematiker eine härtere Nuß zu knacken gehabt.

Allerdings wurden gewisse Teilerfolge erzielt. So hatte Leonhard Euler, einer der Größten in der Geschichte der Mathematik (1707-1783), die Nichtigkeit des Fermatschen Satzes für die 3. und 4. Potenz bewiesen, also den exakten Beweis geliefert, daß die Summe zweier Potenzen dritten Grades niemals wieder eine dritte Potenz sein kann und Entsprechendes für die vierten Potenzen, und der Mathematiker Dirichlet hat den Satz für die 5. Potenz bewiesen. Das meiste aber hat auf diesem Gebiete der hervorragende Mathematiker Eduard Kummer (1810-1893), eine Zierde der Berliner Universität, geleistet. Er hat die Nichtigkeit des Satzes von Fermat für alle Fälle bis zur 100. Potenz bewiesen. Aber alle diese Teilerfolge bedeuten keine vollständige Lösung des Problems, bedeuten noch nicht den notwendigen allgemeinen Beweis, daß der Satz von Fermat für alle überhaupt möglichen Potenzen, die ja ins Unendliche gehen, richtig ist. Dieser allgemeine Beweis steht immer noch aus. Solange das aber der Fall ist, muß immer noch mit der Möglichkeit gerechnet werden, daß sich vielleicht in sehr hohen Zahlenregionen Zahlen finden, die sich anders verhalten, als es der Fermatsche Satz wahr haben will. Kummer glaubte übrigens einmal, den vollständigen und allgemeinen Beweis gefunden zu haben, mußte sich jedoch von seinem Fachkollegen Dirichlet einen Fehler nachweisen lassen, durch den die Allgemeingültigkeit seines Beweises illusorisch wurde. An vierzig Jahre seines Lebens hat Kummer auf die Lösung des Problems verwandt, und die Tatsache, daß er bei allen glänzenden Einzelleistungen doch nicht bis zur vollständigen Lösung des Problems durchdringen konnte, ist bis an sein Lebensende eine Quelle gramvoller Resignation des großen Mathematikers gewesen. Auch nach Kummer haben sich die Mathematiker weiter um die Lösung des Problems bemüht, ohne jedoch weiterzukommen. Zahllose Male ist das Problem von den Universitäten als Preis- und Stipendienaufgabe ausgeschrieben worden, ungezählte Dissertationen und sonstige gelehrte Schriften sind darüber geschrieben worden, das Problem blieb, was es war, ungelöst und geheimnisvoll in seiner doppelten Rätselhaftigkeit.

Eine höchst merkwürdige Wendung in der weiteren Geschichte des Problems trat durch den folgenden Umstand ein: Im Jahre 1906 setzte der Mathematiker Wolfskehl in Darmstadt, der sich ebenfalls lange und vergeblich um den Beweis des Fermatschen Satzes bemüht hatte, einen Preis von hunderttausend Mark für die Lösung des Problems aus. Damit war – ein gänzliches Novum in der Geschichte der Mathematik – mit dieser Wissenschaft auf einmal Geld, sogar viel Geld, zu verdienen, und das bewirkte, daß das Fermatsche Problem mit einem Schlage und in völlig ungeahnter Weise auch das Interesse der Laienkreise auf sich lenkte und damit eine Popularität erlangte, wie sie kaum jemals ein mathematisches Problem zuvor aufzuweisen hatte. Ungeahnt viele, die bis dahin die Mathematik nur aus spärlichen Schulerinnerungen kannten, entdeckten plötzlich den Beruf zur Lösung schwierigster mathematischer Probleme in sich und machten sich wagemutig und hoffnungsvoll daran, den verlangten Beweis zu finden. Die Folge war, daß bei der Göttinger Gesellschaft der Wissenschaften, die Wolfskehl mit der Ausführung seines Willens betraut hatte, bald eine ungeheure Flut vermeintlicher Lösungen des Problems einging, zumeist mit dem ebenso höflichen wie dringenden Ersuchen um baldige Auszahlung des ausgesetzten Hunderttausendmarkpreises verbunden. Leute aus allen Gesellschafts-, Berufs- und Bildungskreisen hatten im Handumdrehen das schwierige Problem, an dem sich seit zweieinhalb Jahrhunderten die besten Mathematiker vergeblich die Köpfe zerbrochen hatten, restlos gelöst. Aber keiner schoß den goldenen Vogel ab, den Wolfskehl hatte auffliegen lassen, keiner der Fachleute und keiner der anderen; nur für einzelne Arbeiten, die die Lösung des Problems zwar auch nicht erbracht, wohl aber zu wertvollen Resultaten in anderer Richtung geführt hatten, wurden aus den Zinsen des Legates Teilpreise vergeben. Die Geister, die Wolfskehl gerufen hatte, wurde die Göttinger Gesellschaft erst wieder los, als der Hunderttausendmarkpreis durch die Inflation vollkommen entwertet worden war. Seitdem ist es bedeutend stiller um das Fermatsche Problem geworden.

Aber auch die unverdrossene Arbeit der Fachleute hat das Problem bis heute nicht der Lösung zugeführt, und der Beweis, von dem Fermat sprach, konnte trotz aller ungeheuren darauf verwandten Mühen und Untersuchungen nicht entdeckt werden. Und weil dem so ist, neigen heute manche Mathematiker zu der Vermutung, daß Fermat sich geirrt habe und der Satz überhaupt nicht allgemein richtig und daher auch nicht allgemein zu beweisen sei. Tatsache ist, daß Fermat bei allem Bedeutenden, das er für die Zahlentheorie geleistet hat, sich doch auch wiederholt geirrt und Sätze aufgestellt hat, die hinterher von anderen Mathematikern als falsch nachgewiesen wurden. Möglich also, daß auch der »bewunderungswürdige Beweis«, den er für den nach ihm benannten Satz gefunden haben wollte, doch nicht ganz hieb- und stichfest gewesen ist, und wäre dem so gewesen, dann müßten allerdings alle Bemühungen um den Beweis für immer vergeblich sein. Aber dann müßte es gelingen, den Beweis für die Unrichtigkeit des Satzes zu erbringen. Auch das wäre eine Lösung des Problems, eine negative zwar, aber doch eine vollkommene Lösung, durch die der Kampf um das hartnäckige Problem genau so wie im entgegengesetzten Falle zum Abschluß gebracht werden würde. Aber dieser Unrichtigkeitsbeweis konnte bisher ebenfalls nicht erbracht werden, obwohl manche Mathematiker schon seit langem Untersuchungen nach dieser Richtung hin angestellt haben.

So ist das Problem wie seit zweieinhalb Jahrhunderten auch heute noch ungelöst, ist es nach wie vor die harte Nuß, an der sich allem Anschein nach noch weitere Generationen von Mathematikern und Nichtmathematikern die Zähne ausbeißen werden. Denn auch letztere lassen nicht locker, und von Zeit zu Zeit gehen immer wieder Mitteilungen durch die Presse über die endliche und wirkliche Lösung des Problems, Mitteilungen, die zumeist schon durch die Art der Abfassung erkennen lassen, daß sie von Unberufenen ausgehen, bei denen der Wunsch der Vater des Gedankens war.

Der Kampf um das Fermatsche Problem geht weiter. Gold ist zwar, nachdem der Wolfskehl-Preis durch die Inflation zu Wasser geworden ist, mit der Lösung heute nicht mehr zu verdienen. Aber wem die Lösung des Problems glückt, gleichviel ob im Sinne der Richtigkeit oder der Unrichtigkeit des Fermatschen Satzes, der wird sich einen dauernden Ehrenplatz in der Geschichte der Mathematik erworben haben, und sollte der Glückliche wirklich aus den Reihen der Nichtzünftigen stammen, dann würden ihn zehn Universitäten gern und freudig als Dr. honoris causa in ihre Reihen aufnehmen zum Dank dafür, daß er die Wissenschaft von einem der seltsamsten Rätsel befreit hat, das wie eine unergründliche Sphinx bisher aller gespottet hat, die es bezwingen wollten.

5. Vom Sinn und Unsinn der Zahlen

Der Streit um den Sinn der Zahlen – Die Richardsche Antinomie – Nichtabzählbare Mengen – Größer als unendlich – Das Diagonalverfahren – »Putschisten« und Formalisten in der Mathematik – Ein Bevölkerungsproblem und seine Lösung – Auch ein Problematiker

»Vom Sinn der Zahlen« hat Oswald Spengler das erste Kapitel seines vielgelesenen Werkes über den Untergang des Abendlandes überschrieben. Hier setzt er sich mit den Begriffen und Methoden der heutigen Mathematik, die ja für die Denkungsweise der heutigen exakten Wissenschaft überhaupt in vielfacher Hinsicht maßgebend sind, auseinander und übt scharfe Kritik an ihnen. Der Erfolg dieses Bemühens war ein verblüffender, für Spengler nämlich. Eine ganze Anzahl berufener Fachleute trat für die bedrängte Mathematik auf den Plan, zerzauste die mathematischen Ideen des Untergangspropheten mit aller nur wünschenswerten Gründlichkeit und wies nach, daß diese kaum höher einzuschätzen sind als die Argumente jener Problematiker, die heute noch immer die Quadratur des Kreises möglich machen oder ähnliche Probleme lösen wollen, die von den Mathematikern schon längst erledigt sind. Die schwerste Abfuhr hat ihm wohl der bald danach leider verstorbene ausgezeichnete Mathematiker Gerhard Hessenberg erteilt. Der hat in einer kleinen, ebenso wie jenes Kapitel des Spenglerschen Buches betitelten Schrift mit gründlichster Sachkenntnis und zugleich – eine überaus große Seltenheit in der mathematischen Literatur – mit famosem Humor, überzeugend für jeden, der überhaupt etwas von der Sache versteht, dargelegt, daß die Begriffe und Ideen, die Spengler von den Dingen der Mathematik hegt, den Sinn der Zahlen – gelinde gesagt – in sein Gegenteil verkehren. Kein Zweifel, daß die mathematischen Ausführungen Spenglers der weitaus schwächste und angreifbarste Teil seines Werkes sind, und wenn seine Argumente auf anderen Gebieten nicht stichhaltiger sind, so kann man für den Bestand des Abendlandes wohl bis auf weiteres ohne Sorgen sein.

Freilich, es ist ein eigenes Ding um den Sinn der Zahlen. Um den streiten sich gegenwärtig die Mathematiker selbst so heftig, daß sie sich gegenseitig, wenn auch nicht gleich Diebe und Mörder, so doch Formalisten und – Putschisten nennen. Wie ja Vernunft überhaupt Unsinn werden kann, so auch die Zahl, was immer dann der Fall ist, wenn ein zahlenmäßig errechnetes Ergebnis bei aller äußeren formalen Richtigkeit mit der Wirklichkeit der Dinge in mehr oder weniger krassen Widerspruch gerät. Die berühmten Trugschlüsse und Paradoxien in mathematischem Gewande, wie etwa der »Achilleus«, in welchem haarscharf bewiesen wird, daß ein Schnelläufer niemals eine Schildkröte einholen kann, sofern diese einen Vorsprung vor ihm hat, sind ebenso überzeugende wie erheiternde Beweise des Gesagten, und wenn wir uns vergegenwärtigen, daß die rechnende Menschheit Jahrhunderte und Jahrtausende gebraucht hat, um aus diesem selbstgeschaffenen Irrgarten der Zahlen wieder herauszufinden, so wird damit zur Genüge erhärtet, daß sich der Sinn der Zahlen auch anderwärts noch in sein Gegenteil verkehren kann.

Aber nicht nur die Zahlenkunst der Alten, auch die heutige Mathematik hat Beispiele geschaffen dafür, daß man über den Sinn der Zahlen manchmal zum mindesten sehr verschiedener Ansicht sein kann. Auch sie hat Trugschlüsse und Antinomien nach Art des »Achilleus« ausgeheckt, die den heutigen Zahlengelehrten nicht weniger Kopfschmerzen bereitet haben wie den Sophisten zu Zenos Zeiten die ihrigen. Ein Beispiel dieser Art ist die sogenannte Richardsche Antinomie, bei der es sich um die Definierbarkeit der Zahlen handelt. Diese Antinomie wird in einfachster Form in folgender Weise dargestellt: Jede Zahl läßt sich durch eine endliche Anzahl von Worten in eindeutiger Weise definieren. Beispielsweise kann die Zahl 1 definiert werden als »die kleinste aller positiven ganzen Zahlen«, die Zahl 2 etwa als »die einzige gerade Primzahl«, die Zahl 97 als »die größte Primzahl unter Hundert«, die Zahl 1000 als »die kleinste vierstellige Zahl« usw., und jede dieser Definitionen besteht aus einer endlichen Anzahl von Worten. Wir wollen nunmehr die Gesamtheit derjenigen ganzen Zahlen ins Auge fassen, von denen keine mit nur zwölf Worten zu definieren ist. Unter diesen Zahlen muß es eine kleinste Zahl geben, sie werde x genannt. Diese Zahl x können wir dann definieren als »die kleinste ganze Zahl, die nicht mit zwölf Worten definiert werden kann«. Wenn wir uns aber diesen Satz ansehen, so finden wir, daß er gerade aus zwölf Worten besteht. Der Satz ist also einerseits eine eindeutige, aus zwölf Worten bestehende Definition der Zahl x, besagt andererseits aber zugleich, daß diese Zahl mit zwölf Worten nicht definiert werden kann. Das ist ein merkwürdiger Widerspruch, und es hat ganz den Anschein, als ob die eindeutige Definition der Zahlen eine höchst zweideutige Sache sei. Die Mengentheoretiker haben sich mit diesem Widerspruch jedenfalls eingehend beschäftigt.

Die Auflösung dieses Widerspruches ist jedoch in derselben Weise wie bei den bereits früher behandelten Paradoxien, etwa dem Krokodilsschluß, dem »Lügner«, der Russischen Antinomie von der Menge, die sich selbst enthält usw. möglich. Wie bei jenen Paradoxien finden wir auch hier den Grund in einer Verschiebung oder Verwechslung der bei der angegebenen gedanklichen Operation verwandten Begriffe. Es werden hierbei »Definition«, und »Bezeichnung« verwechselt. Der inkriminierte Satz über die Zahl x ist keine Definition, sondern nur eine Bezeichnung oder Benennung dieser Zahl. Definiert ist lediglich eine Klasse von Zahlen, nämlich diejenigen, die nicht mit höchstens zwölf Worten bezeichnet werden können; der inkriminierte Satz aber ist keine neue Definition, sondern nur eine Bezeichnung einer einzelnen Zahl aus jener Klasse. Die Bezeichnung eines Dinges aber kann niemals einen Widerspruch zur Definition jenes Dinges enthalten. Angenommen, wir haben eine Definition für den Begriff der Farbe, so ist der Ausdruck »die rote Farbe« keinesfalls eine neue Definition, sondern lediglich die Bezeichnung eines einzelnen unter den verschiedenen Dingen, die unter jenen Begriff fallen. So wenig wie die gewählte Bezeichnung »die rote Farbe« einen Widerspruch gegen den Begriff der Farbe enthalten kann, so wenig ist das bei der angeführten Bezeichnung der Zahl x der Fall. Ist auch die begriffliche Verwechslung, die in der Darstellung der Richardschen Antinomie obwaltet, eine sehr versteckte, so ist sie doch nachweisbar und löst den Widerspruch restlos auf. Die Mengentheorie selbst sucht allerdings diesen Widerspruch in derselben Weise wie die anderen mengentheoretischen Paradoxien dadurch zu lösen, daß sie die Eigenschaft, die jener Satz aussagt, als »nicht definit«, d. h., als nicht eindeutig bestimmt, erklärt, wodurch der ganze Satz sinnlos wird. Das Verfahren kommt auf dasselbe wie die Analyse nach den Methoden der alten Logik heraus.

Von ungleich größerer Tiefe und Schwierigkeit ist ein anderes und höchst eigenartiges Problem, bei dem es sich ebenfalls um den Sinn der Zahlen handelt, aber diesmal nicht in Form eines mehr oder weniger kuriosen Widerspruches oder Trugschlusses, sondern einer sehr gründlichen und tiefen Überlegung. Wir wollen versuchen, dieses Problem auch dem Nichtmathematiker verständlich zu machen.

Auf unserer Zahlenreihe 1, 2, 3, 4, 5 … usw. liegt immer eine gerade Zahl neben einer ungeraden. Wir fragen: Gibt es in der Zahlenreihe mehr gerade oder ungerade Zahlen? Die Antwort ist leicht und lautet, daß es ebensoviel gerade wie ungerade Zahlen geben muß. Denn ich kann jeder geraden Zahl immer eine danebenliegende ungerade Zahl zuordnen oder umgekehrt jeder ungeraden Zahl eine danebenliegende gerade, und da ich das mit jeder geraden oder ungeraden Zahl machen kann, so muß es eben von jeder der beiden Zahlenarten genau soviel geben wie von der anderen. Nunmehr fragen wir: Ist die Anzahl aller Zahlen vielleicht größer als die Anzahl aller derjenigen Zahlen, die durch 3 teilbar sind? Diese Frage wird vielleicht einiges Nachdenken erfordern und dann zu folgender Argumentation führen: Innerhalb eines bestimmten Bereiches der Zahlenreihe, etwa in dem Zahlenraum von 1 bis 1 000 000, ist selbstverständlich die Anzahl aller Zahlen überhaupt größer als diejenige der durch 3 teilbaren Zahlen, und Entsprechendes gilt für jeden und auch den größten Zahlenraum. Aber wir fragten nicht nach der Anzahl solcher Zahlen innerhalb eines bestimmten, wenn auch noch so groß angenommenen Bereiches, sondern innerhalb der gesamten unendlichen Zahlenreihe selbst. Wie verhält es sich also in dieser? Darauf ist zu antworten: Innerhalb der unendlichen Zahlenreihe selbst kann ich zu jeder beliebigen Zahl immer eine solche ausfindig machen oder konstruieren, die dreimal größer ist als jene, und da das, wie gesagt, bei jeder Zahl möglich ist, so kann innerhalb der unendlichen Zahlenreihe selbst die Menge aller Zahlen überhaupt nicht größer sein als die Menge der durch 3 teilbaren Zahlen. Von diesen wie von jenen gibt es eben unendlich viele und damit von jeder Art gleich viele, denn zwischen Unendlichkeiten gibt es keine Unterschiede.

Nun aber stellen wir die Kardinalfrage, um die es sich bei unserem Problem handelt: Kann es wohl in der Welt irgendeine Menge von Dingen, konkreter oder abstrakter, also greifbar wirklicher oder nur gedachter, Dinge, geben, die noch größer ist als die Menge der Zahlen in der unendlichen Zahlenreihe? Die also so groß wäre, daß es nicht genug Zahlen gäbe, um sie abzuzählen? Nach angestrengtem Nachdenken, dessen diese Frage wert ist, wird der Leser jedenfalls auch diese entschieden verneinen. Denn da die Menge der Zahlen selbst unendlich groß ist, muß sie auch zum Abzählen jeder noch so großen Menge von Dingen ausreichen. Größer als unendlich groß kann auch eine solche Menge von Dingen nicht sein, also auch nicht größer als die unendliche Menge der Zahlen, die daher auch zum Abzählen jeder anderen nur denkbaren Menge von Dingen ausreichend sein muß. Diese Folgerung erscheint auch dem kritisch geschärften Verstande als absolut sicher und einwandfrei.

Aber dieser Folgerung stimmt die moderne Mathematik nicht zu. Sie kennt Mengen oder glaubt doch solche ausfindig gemacht zu haben, die noch größer als unendlich sind und für die die unendliche Zahlenreihe, um solche Mengen abzuzählen, nicht ausreicht d. h. nicht genug Zahlen hat. Solche Mengen werden als nichtabzählbare Mengen bezeichnet. Beispielsweise ist nach dieser Auffassung die Menge aller reellen Zahlen eine solche nichtabzählbare Menge und viel größer als die Menge der ganzen Zahlen innerhalb der Zahlenreihe. Zu der Menge aller reellen Zahlen gehören außer den ganzen Zahlen selbst noch alle überhaupt möglichen periodischen und nichtperiodischen Dezimalbrüche, die wir ja in beliebiger, sogar unendlicher Anzahl immer zwischen je zwei ganze Zahlen einschalten können. Zu jeder der unendlich vielen ganzen Zahlen gehört also eine Unendlichkeit von periodischen und nichtperiodischen Dezimalbrüchen, und die Gesamtheit aller dieser Unendlichkeiten, die die Menge aller reellen Zahlen überhaupt darstellt, also soll noch größer als unendlich sein. Während wir, wie dargelegt, jeder durch 3 teilbaren Zahl eine von ihr verschiedene ganze Zahl aus der Zahlenreihe zuordnen oder auch umgekehrt jeder ganzen Zahl der Zahlenreihe eine von ihr verschiedene durch 3 teilbare Zahl zuordnen und damit beweisen können, daß die Menge dieser gleich der Menge jener, nämlich unendlich, ist, ist nach der dargelegten Auffassung zwischen der Menge der ganzen Zahlen unserer Zahlenreihe einerseits und der Menge aller reellen Zahlen überhaupt andererseits eine solche eindeutige Zuordnung nicht möglich; es gibt nicht genügend ganze Zahlen, um jeder der reellen Zahlen eine eigene ganze Zahl zuzuordnen. Die Menge der reellen Zahlen ist von einer anderen, viel mächtigeren Art der Unendlichkeit als die Menge der ganzen Zahlen. Zu dieser Folgerung führt die Mengentheorie, der jüngste Zweig der modernen Mathematik, der aber trotzdem von grundlegender Bedeutung für die gesamte mathematische Wissenschaft geworden ist. Der Beweis für jene Folgerung oder Behauptung, daß also die Menge der reellen Zahlen von einer größeren Art der Unendlichkeit ist als diejenige der nur ganzen Zahlen, wird vermittels einer eigentümlichen arithmetischen Operation geführt, die als Diagonalverfahren bezeichnet wird und in der Mengentheorie eine große Rolle spielt.

Das sind nun freilich Folgerungen und Begriffe, die mit keiner menschlichen Vorstellung vereinbar scheinen. Der Normalmensch wird vielleicht geneigt sein anzunehmen, daß Mengen, die noch größer als unendlich sein sollen, wiederum einen der Fälle darstellen, wo sich der Sinn der Zahlen in sein Gegenteil verkehrt. So wenig die Menge aller ganzen Zahlen größer sein kann als die Menge aller durch drei teilbaren Zahlen, so wenig kann irgendeine Menge, also auch die Menge aller reellen Zahlen, mehr Elemente enthalten als die Menge der unendlich vielen ganzen Zahlen, – das scheint eine unabweisliche Forderung selbst des kritisch geschärften Verstandes zu sein. Aber gegen diese Forderung operiert die Mengentheorie zur Begründung und Stützung ihrer gegenteiligen Auffassung mit bestimmten Tatsachen und Folgerungen, die nicht weniger unabweisbar zu sein scheinen. So liegt hier denn ein Problem vor, das zu den tiefsten und schwierigsten, allerdings auch zu den umstrittensten Fragen der heutigen Mathematik gehört. Denn auch viele Mathematiker lehnen den Begriff von Mengen, die von noch größerer Mächtigkeit als die Unendlichkeit selbst sein sollen, ab, weil mit solchen Mengen ein Sinn überhaupt nicht mehr verbunden werden kann, ebenso wie sie auch das Diagonalverfahren als nicht genügend beweiskräftig ablehnen. Heute herrscht gerade über diese Fragen ein großer Streit unter den Mathematikern, und die Opposition gegen die Mengentheorie war es, die vor einiger Zeit bei Gelegenheit eines Mathematikerkongresses Professor David Hilbert, den gegenwärtig wohl bedeutendsten Mathematiker der Welt, den »Neuen Euklid«, wie man ihn ehrend bezeichnet hat, veranlaßte, jene schnöden Oppositionsgeister temperamentvoll als »Putschisten« zu stigmatisieren, als Umstürzler, die gegen alles Bestehende in der Mathematik Sturm laufen. So ist auch hier der Streit über Sinn oder Unsinn der Zahlen in vollem Gange, und der Temperamentsausbruch des genannten berühmten Gelehrten ist dafür ein ebenso drastisches wie bezeichnendes Beispiel, das bereits mit Betonung und Behagen in die Geschichte der Mathematik eingetragen wurde.

Weniger vom Geiste hoher Wissenschaftlichkeit und Gedankentiefe durchtränkt, sondern mehr ein scherzhaftes Beispiel dafür, daß Sinn und Unsinn der Zahlen manchmal dicht beieinander wohnen können, ist ein Trugschluß neueren Datums, dessen geistiger Vater unbekannt ist. Auch läßt er sich ohne Schwierigkeiten restlos lösen, mag aber dennoch manchem Kopfzerbrechen bereiten. Es handelt sich um ein Bevölkerungsproblem in arithmetischem Gewande. Die Anzahl der heute lebenden Menschen wird mit rund 1,8 Milliarden angegeben. Stellt man die Frage, ob heute mehr Menschen leben als zur Zeit der Geburt Christi oder umgekehrt, so wird jeder wohl ohne weiteres das numerische Übergewicht unserer Zeit über jene betonen. Denn aus allen geschichtlichen Mitteilungen können wir entnehmen, daß früher die Menschheit viel dünner gesät gewesen sein muß als heute, und um so dünner, je weiter wir in der Geschichte zurückgehen. Berlin, heute eine Viermillionenstadt, hat zur Zeit Friedrichs des Großen noch keine hunderttausend Einwohner gezählt und ganz Preußen damals nur etwa so viel Köpfe wie seine Hauptstadt heute. Wie mag es da also erst bei Beginn unserer Zeitrechnung mit der Anzahl der Menschen ausgesehen haben! Außerdem weist die Statistik nach, daß innerhalb einer Generation immer mehr Menschen geboren werden als sterben, und der generationsweise Zuwachs läßt sichere Schlüsse auf die viel geringere Bevölkerungsdichte auf unserem Erdball in früheren Jahrtausenden zu, selbst wenn wir Krieg und Pestilenz, ja den Untergang ganzer Völker in Rechnung stellen. Also zur Zeit Christi hat es zweifellos weniger, sogar viel weniger Menschen als heute auf dem Erdenrund gegeben.

Aber gegen diese Behauptung kann der Mathematiker die folgende Gegenrechnung aufmachen: Irgendein Zeitgenosse, sagen wir Herr X., hat, wie jeder normale Mensch, zwei Eltern; von diesen hatte jeder auch zwei Eltern, also hatte Herr X vier Großeltern oder, wie wir es ausdrücken wollen, in der zweiten Generation vor ihm 2 ² Ahnen. Da auch jeder der Großeltern mit einem Elternpaar gesegnet sein muß, hat Herr X. in der dritten Generation vor ihm 2 ³ = 8 Ahnen, in der nächstfrüheren Generation kann er bereits 2 ⁴, dann 2 ⁵ usw. Ahnen zählen. Mit jeder Generation weiter zurück verdoppelt sich die Zahl seiner Ahnen. Rechnen wir nun, daß seit Christi Geburt rund zweiunddreißig Generationen verflossen sind, so beträgt die Zahl der Ahnen unseres Herrn X. aus jener Zeit 2 ³². Das aber gibt die stattliche Anzahl von 4 ¹/ ₃ Milliarden, also weit über das Doppelte der heutigen Menschheitsziffer. Wenn also schon der einzelne Herr X. weit mehr als das Doppelte der heutigen Bevölkerungsziffer an Ahnen zur Zeit Christi zählen kann, dann muß es damals doch wohl auf alle Fälle viel, viel mehr Menschen als heute gegeben haben. Quod erat demonstrandum! Da staunt der Laie, und selbst der Fachmann stutzt, und mit dieser Rechnung soll einst ein Kandidat der Mathematik, der sich in Volkswirtschaft als Nebenfach prüfen ließ und über das besagte Bevölkerungsproblem Auskunft geben sollte, den Examinator so schachmatt gesetzt haben, daß der den Examinanden auf der Stelle mit glänzender Note entließ, nur um den unheimlichen Rechner, der alle Volkswirtschafts- und Bevölkerungstheorien über den Haufen schmiß, schleunigst loszuwerden.

Aber selbstverständlich hat der Bevölkerungstheoretiker recht und jene mathematische Potenzrechnung ein Loch, durch das sie in einen leicht zu durchschauenden Widerspruch mit der Wirklichkeit der Abstammungsverhältnisse gerät. Sie macht nämlich implizite die Annahme, daß die männlichen und weiblichen Vorfahren des Herrn X. in jeder Generation vollständig blutsfremd gewesen seien. Diese Annahme aber ist falsch und mit der Wirklichkeit sogar unverträglich. Schon die Eltern unseres Herrn X. könnten Cousin und Cousine gewesen sein, die von einem gemeinsamen Großelternpaare abstammten, so daß unser Herr X., von dem wir ausgingen, in der betreffenden Generation nicht acht Urgroßeltern gehabt hätte, wie es nach jener Potenzrechnung der Fall hätte sein müssen, sondern nur sechs. Wenn nun auch Heiraten unter Enkelkindern noch verhältnismäßig selten sind, so nehmen sie doch unter den Nachkommen früherer Ahnenstufen immer mehr zu; wenn auch die Blutsverwandtschaft dabei immer dünner wird, verschwindet sie natürlich doch niemals ganz. Unter den vielen Tausenden von Nachkommen eines Ehepaares in der zehnten Ahnenstufe würden schon zahlreiche Heiraten stattfinden, ohne daß die Verheirateten von der gemeinsamen Abkunft und ihrer Blutsverwandtschaft überhaupt noch etwas wüßten. Während also jene Potenzrechnung infolge ihrer falschen Annahme zu der Folgerung führt, daß mit jeder früheren Generation die Zahl der Ahnen unseres Herrn X. wächst, wird diese gerade umgekehrt von einer bestimmten Ahnenstufe an immer geringer und führt schließlich auf ein einziges Ahnenpaar in der letzten Generationsstufe. Verfolgen wir die Rechnung in umgekehrter Reihenfolge, so könnten von einem Ehepaar X. senior, das zur Zeit der Geburt Christi lebte, heute Millionen Nachkommen vorhanden sein; unser Herr X. junior und seine Eltern, Großeltern, Urgroßeltern und die Ahnen noch vieler weiterer Generationsstufen gehörten zu diesen Nachkommen, ohne daß bei allen diesen noch die geringste Kenntnis der gemeinsamen Abstammung vorhanden gewesen sein müßte, zumal sie über alle Länder und Erdteile zerstreut gewesen sein könnten und das zum großen Teil auch sein würden. Tatsächlich führt so der Baum der Abstammung nach anfänglicher Verbreiterung der Baumkrone zu einer sich immer mehr verengenden Spitze und schließlich zu einem letzten Ahnenpaar als Gipfelpunkt. Die Potenzrechnung der dauernd blutsfremden Ahnen steht also mit der Wirklichkeit in klaffendem Widerspruch, und aus ihr folgt mit Gewißheit nur das eine, daß wir Menschen hier auf Erden, so fremd wir uns auch nach Familie, Ursprung und Rasse gegenüberstehen mögen, doch alle miteinander irgendwie blutsverwandt sind. Denn wäre es anders, so hätte jene Potenzrechnung recht, und dann hätten zu Christi Zeit viel mehr Menschen als heute vorhanden gewesen sein müssen. Ob allerdings die ganze Menschheit letzten Endes nur von einem einzigen Ahnenpaare oder mehreren oder vielen abstammt, darüber sind sich die Gelehrten noch nicht ganz einig.

Noch zahlreiche andere Beispiele und Fälle ließen sich anführen, wo, bald scherzhaft, bald ernstgemeint, sich Sinn und Unsinn der Zahlen begegnen. Auch die große Zahl rechnerischer oder mathematischer Scherzaufgaben, bei denen sich die Wirklichkeit der Verhältnisse immer als wesentlich anders herausstellt, als es nach dem rein rechnerischen Ergebnis der Aufgabe sein dürfte, gehört hierher, und an anderer Stelle dieses Buches werden wir dem Leser eine Anzahl solcher Scherzaufgaben unterbreiten, in denen die Zwiespältigkeit von Sinn und Unsinn zum Humor der Zahlen wird. Als Beitrag zu diesem Kapitel sei noch der folgende Fall angeführt. Mich ersuchte schriftlich einmal ein Herr, der sich als Bauingenieur bezeichnete, mir ein mathematisches Problem unterbreiten zu dürfen, mit dem er sich seit über fünfzig Jahren beschäftigt habe und dessen Lösung ihm jetzt endlich geglückt sei. Er bat um eine gutachtliche Äußerung über Wert und Richtigkeit der Lösung, um diese gegebenenfalls einer mathematischen Zeitschrift zur Veröffentlichung zu übergeben. Und um was handelte es sich bei dem Problem? Um die Frage – man höre und staune – warum eine 6 umgekehrt eine 9 ergebe! Das war das Problem, das den Ärmsten seit fünfzig Jahren nicht schlafen ließ. Das Schreiben war keinesfalls scherzhaft gemeint, sondern verriet vollen Ernst des Absenders, der nach seinem Beruf ja auch ein Mann von wissenschaftlicher Bildung sein mußte. Ich muß gestehen, daß ich zunächst längere Zeit verblüfft war, ehe ich mich entschloß, den Fall in jenes Kapitel einzureihen, in dem sich Sinn und Unsinn der Zahlen friedlich mischen. Ich schrieb dem Fragesteller zurück, daß die Lösung des Problems über meine Kraft gehe, und verwies ihn an die Adresse eines Universitätslehrers der Mathematik an seinem Wohnort. Ob der die Sache anders beurteilt hat, weiß ich nicht. Der Fall lehrt, daß die Zahlen manchen Köpfen auch dort Rätsel aufgeben, wo wirklich keine vorhanden sind, daß aber selbst in solchen Fällen der Sinn der Zahlen sich in sein Gegenteil verwandeln kann.

IV.
Vom Humor der Zahl

3 + 3 = 11

Ein Druckfehler? – Die Sprache der Arithmetik – Vom Stellenwert der Ziffer – Ein genialer Einfall – Verschiedene Zahlensysteme – Ein Ehemann, der seit 11 001 Jahren verheiratet ist

»Eine etwas kühne Behauptung!« wird mancher Leser, der die anscheinend höchst unarithmetische Überschrift dieses Essais zur Kenntnis genommen hat, denken; und dann wird er vielleicht die Frage wälzen, ob hier wieder einmal der Druckfehlerteufel seine Hand im Spiel hatte, und wie es kam, daß ein solches haarsträubendes typographisches Versehen unbemerkt bleiben konnte. Daß der Verfasser die sonderbare Gleichung etwa für richtig halten sollte, wird der Leser nicht annehmen; denn wenn er auch allem Gedruckten, kritisch, wie er veranlagt ist, nur ein sehr bedingtes Zutrauen entgegenbringt, wird er im allgemeinen doch nicht abgeneigt sein, den Leuten, die Bücher schreiben, wenigstens eine annähernd zutreffende Kenntnis des kleinen Einmaleins immerhin zuzugestehen.

Allen solchen und ähnlichen Meditationen gegenüber sei aber festgestellt, daß weder Setzer noch Druckfehlerteufel für die Überschrift verantwortlich zu machen sind, und daß die befremdliche Gleichung 3 + 3 = 11 tatsächlich und alles Ernstes für richtig gelten soll.

Nachdem das homerische Gelächter, das diese Behauptung an manchen Stellen vielleicht erweckt hat, verklungen ist, sei es gestattet, den korrekten, mathematisch exakten Beweis dafür zu erbringen. Zu diesem Zweck wird zunächst um die Beantwortung einer Vorfrage gebeten: Wie heißt das Säugetier, dessen Füße man mit Hufeisen beschlägt und das man zum Reiten sowie zum Ziehen von Wagen verwendet? Der durch Kreuzworträtselentzifferung intellektuell trainierte Leser wird auf »Pferd« raten. Stimmt, aber wie kommt es dann, daß der Franzose dasselbe Tier mit » cheval«, der Engländer mit » horse« bezeichnet? Sehr einfach, weil der Franzose oder Engländer eine andere Sprache spricht; nur im Deutschen ist die Bezeichnung »Pferd« für den besagten Quadrupeden richtig, in anderen Sprachen wäre das falsch. Sehr richtig, und ebenso ist die Gleichung 3 + 3 = 11, die in der uns allein geläufigen mathematischen Sprache, nämlich dem Dezimalsystem, so absonderlich aussieht, in einer anderen Sprache dieser Art, das heißt in einem anderen Zahlensystem, vollkommen richtig. »Aha,« denkt jetzt der scharfsinnige Leser, »Einstein, alles relativ, also auch die mathematischen Lehrsätze und Behauptungen!« Worauf aber zu erwidern ist, daß das, was hier soeben über die Richtigkeit oder Unrichtigkeit der Gleichung 3 + 3 = 11 gesagt wurde, mit der Theorie Einsteins nichts zu tun hat, sondern in der Natur der Zahlen und Zahlensysteme begründet ist. Steigen wir also einmal ein wenig hinab in die Tiefen des Zahlenreiches, wo man ja immer viel des Überraschenden und Merkwürdigen erleben kann.

Unser herrschendes Zahlensystem, in welchem 3 + 3 nicht 11, sondern korrekterweise 6 ist, ist nur eins unter zahllosen möglichen Systemen dieser Art. Es wird als Dezimalsystem oder Zehnersystem bezeichnet, und zwar deshalb, weil es auf der Zahl Zehn als Grundzahl zum Aufbau des Zählens und aller rechnerischen Ausdrücke beruht. Wir kennen und verwenden in unserm Rechenverfahren lediglich zehn Zahlenzeichen, nämlich die Ziffern 1 bis 9 und außerdem die 0. Aus diesen zehn Ziffern bilden wir durch geeignete Kombination alle und selbst die größten Zahlenausdrücke. Die Zahlenwerte von 1 bis 9 werden durch einmaliges Setzen der entsprechenden Ziffern selbst dargestellt, alle höheren Zahlenwerte hingegen drücken wir durch mehrere solche nebeneinandergestellte Ziffern aus, wobei wir jeder Ziffer außer ihrem Grundwert noch einen besonderen Stellenwert beilegen, der immer eine Potenz von 10 ist. In dem Ausdruck 34 hat die 4 ihren Grundwert, die 3 dagegen das Zehnfache ihres Grundwertes, und der ganze Ausdruck stellt sich mithin dar als die Summe 3 × 10 + 4, den unser Rechensystem in der ungleich einfacheren und übersichtlicheren Form 34 auszudrücken gestattet. In derselben Weise drücken wir auch die größten Zahlenwerte durch die Stellenwerte der Grundziffern aus. In der Zahl 98 734 beispielsweise ist die 9, die an fünfter Stelle von hinten steht, durch diese Stellung gleichzeitig mit 10 000 = 10 ⁴, die 8 mit 1000 = 10 ³, die 7 mit 100 = 10 ², die 3 mit 10 multipliziert zu denken, und nur die 4, die erste Ziffer von hinten, repräsentiert durch diese Stellung lediglich ihren Grundwert. Die ganze Zahl stellt sich also dar als die Summe 9 × 10 ⁴ + 8 × 10 ³ + 7 × 10 ² + 3 × 10 + 4. Auf diese Weise können wir unendlich weit zählen, ohne jemals anderer als der zehn Grundziffern zu bedürfen, können wir die ganze unendliche Menge der Zahlen und selbst die denkbar größten Zahlenwerte vermittels jener arithmetischen Grundzeichen leicht und übersichtlich ausdrücken. Festhalten wollen wir für das Weitere hierbei, daß unser Zahlensystem, eben weil es ein Zehnersystem ist, auch nur zehn Grundziffern bedarf, nämlich der eigentlichen Zahlenzeichen 1 bis 9, die also alle kleiner sind als die Grundzahl selbst, und des Zeichens 0, das kein eigentliches Zahlzeichen ist, sondern nur den Stellenwert nach jedem Intervall von zehn Zahlen ausdrückt.

Machen wir uns klar, was es bedeuten würde, wenn uns nicht ein so einfaches Zahlensystem, das den Wert der Zahlen durch den Stellenwert der Ziffern ausdrückt, zur Verfügung stände. Dann müßten wir nicht nur für die Grundzahlen 1 bis 9, sondern für jede Zahl überhaupt ein eigenes Ziffernzeichen und ein eigenes Wort haben. Dann aber würde bald jedes Rechnen mit höheren Zahlen zur Unmöglichkeit werden, weil angesichts der Unendlichkeit der Zahlen sowohl der Wortschatz wie auch die Möglichkeit des ziffernmäßigen Ausdruckes binnen kurzem erschöpft sein müßte. Das Rechnen würde in Wort und Ziffer eine ganz ungeheuerliche Vielgestaltigkeit der Ausdrucksweise annehmen, der kein menschliches Gehirn gewachsen wäre. Nur für Rechnungen, die etwa bis zu 1000 oder allerhöchstens einigen Tausenden gehen, würde die Leistungsfähigkeit unseres Gedächtnisses ausreichen, darüber hinaus aber total versagen. Unser ganzes Geistesleben wäre dann in seinen Anfängen steckengeblieben. Es war einer der allergenialsten und fruchtbarsten Einfälle des menschlichen Geistes, die unendliche Menge der Zahlen in ein System von wenigen Grundziffern zu bringen, ein Einfall, auf dem ein gut Teil unserer gesamten Kultur beruht, von dem wir noch heute zehren und so lange zehren werden, als es überhaupt rechnende Menschen geben wird.

Wie sind wir nun aber gerade auf die Zehn als Grundzahl unseres Zahlensystems gekommen? Ganz zweifellos durch die zehn Finger, die im Beginn der arithmetischen Entwicklung des Menschen diesem als naturgegebene Rechenmaschine dienten. An der Reihe seiner Finger zählte er zunächst bis zehn, und hatte er höhere Zahlen zu bilden, so mußte er an derselben Fingerreihe eben von vorn beginnen. Durch diese naturgemäße Wiederholung und Vervielfachung der Zahl seiner Finger wurde er ganz von selbst auf das Zahlensystem geführt, dessen vollkommene Ausbildung allerdings erst auf sehr fortgeschrittener Stufe der geistigen und rechnerischen Entwicklung erfolgte. Diese Vorstellung von der Entstehung unseres Dezimalsystems führt zugleich aber auch zu der Folgerung, daß auch ein Zahlensystem mit der Fünf als Grundzahl sehr wohl möglich gewesen wäre. Der Mensch hätte, statt die Finger beider Hände zu verwenden, auch an den Fingern einer Hand zählen können. Dann hätte er immer von 1 bis 5 gezählt und dann wieder von vorn begonnen, und durch die immer erneute Wiederholung und Vervielfachung der Fünf als Grundzahl wäre es so zu einem regelrechten Fünfersystem gekommen, das ebenfalls, wenn auch in etwas anderer Form, den einfachen und übersichtlichen Ausdruck aller Zahlenwerte möglich gemacht hätte. Wir dürfen auch annehmen, daß ein solches Fünfersystem wirklich einmal bestanden hat, wenn allerdings auch nur in beschränktem Umfange. Reste eines solchen Zahlensystems sind noch heute erkennbar. Die Zahl Sechs, die wir heute mit einer einzigen Ziffer schreiben, wird mit römischen Ziffern zweizifferig, in der Form VI, geschrieben, also mit den nebeneinandergestellten Zahlenzeichen V und I, und entsprechend werden die folgenden Zahlen VII und VIII geschrieben. Also schon nach den ersten fünf Zahlen beginnt hier in der schriftlichen Darstellung die Wiederholung der Grundzahl, was als Überbleibsel eines früher einmal vorhanden gewesenen Fünfersystems sehr wohl gedeutet werden kann. Bei den Griechen im Homerischen Zeitalter bedeutete ferner das Wort für rechnen ( pempazein) seiner Ableitung und seinem ursprünglichen Sinne nach soviel wie »fünfern«, was ebenfalls darauf schließen läßt, daß die Fingerzahl nur einer Hand den ursprünglichen arithmetischen Bedürfnissen genügt haben mag. Die Ziffernsysteme der Griechen und Römer entbehrten übrigens noch der Null als Stellenzeichen, weswegen auch die Schreibweise in römischen Ziffern noch nicht vollkommen derjenigen unseres Dezimalsystems entspricht, das noch wesentlich einfacher und jenem daher technisch noch bedeutend überlegen ist.

Untersuchen wir nun einmal, wie die Zahlenwerte in einem Fünfersystem, das nach Art unseres Dezimalsystems gestaltet ist, auszudrücken wären. Ein solches bedürfte nur der vier Zahlenzeichen 1, 2, 3 und 4 und ferner der 0 als Stellenzeichen. Mit der Zahl Fünf begänne bereits die zweizifferige Schreibweise, diese Zahl müßte dann also 10, die Zahl Sechs entsprechend 11 geschrieben werden. Die Stellenwerte dieser und aller weiteren Zahlen wären nach Potenzen von 5 geordnet. In dem Zahlenausdruck 11 hätte die voranstehende 1 den Stellenwert 1 × 5, die dahinterstehende dagegen nur ihren Grundwert; der Ausdruck würde also die Summe 1·× 5 + 1 darstellen. Die Zahlenwerte unterhalb fünf würden einzifferig durch die entsprechenden Ziffern, der Zahlenwert drei also durch 3 ausgedrückt. Dann müßte also die Gleichung, die in unserem Dezimalsystem 3 + 3 = 6 geschrieben wird, im Fünfersystem 3 + 3 = 11 geschrieben werden. Quod erat demonstrandum!

Wohlgemerkt, der Zahlenwert der Summe 3 + 3 ist natürlich auch im Fünfersystem derselbe wie in unserem Dezimalsystem, also 6. Die Zahlenwerte der Rechenoperationen sind in allen Systemen dieselben, aber sie werden in den verschiedenen Systemen ziffernmäßig sehr verschieden ausgedrückt. Zwischen Zahlenwert und Zahlenausdruck ist also sehr genau zu unterscheiden. In diesem Sinne, also als ziffernmäßiger Ausdruck in einem von dem unsrigen abweichenden Zahlensystem, hat die Gleichung 3 + 3 = 11 ihre volle Richtigkeit.

Aber noch andere Zahlensysteme wären möglich. Wenn der Mensch zu den zehn Fingern auch noch die zehn Zehen hinzunahm, so kam er zu einem Zahlensystem mit der Grundzahl Zwanzig. Ein solches Zahlensystem, in welchem also auch die Stellenwerte nach Potenzen von 20 geordnet wären, hat, wie wir wissen, bei einer ganzen Anzahl früherer Völkerschaften bestanden und findet sich vollkommen ausgebildet beispielsweise bei den Azteken, den Ureinwohnern Mexikos, und noch anderen Stämmen. In den Sprachen dieser Völker finden sich eigene Worte für 20, 400, 8000 und die weiteren Potenzen der Grundzahl Zwanzig. Aber auch bei europäischen Völkerschaften ist, wie die Sprachforschung ergeben hat, das Zwanzigersystem einmal vorhanden gewesen, so bei den Kelten, und aus der Sprache dieser sind Reste des alten Zwanzigersystems auch auf einzelne der heutigen Kulturvölker übergegangen. Beispielsweise wird noch heute im Französischen die Zahl Achtzig durch quatre-vingt, also viermal zwanzig, ausgedrückt, und das ältere Französisch kennt noch mehr solcher vigesimaler Überbleibsel, wie six-vingt, quinze-vingt usw. Auch im Dänischen finden sich noch Reste eines Zwanzigersystems. Die Sprachforschung hat hier ein reichhaltiges Material zusammengetragen, das uns zugleich einen interessanten Blick auf die Vorstufen unseres heutigen Zahlensystems tun läßt. In dem Zwanzigersystem wäre die Gleichung 3 × 8 = 14 ziffernmäßig richtig. Es ist sehr einfach, die Zahlenwerte aus unserem Zehnersystem in das Fünfer- oder Zwanzigersystem, wie überhaupt in jedes andere Zahlensystem, zu übersetzen; der Leser, der das nach den gegebenen Andeutungen unternimmt, wird sehr bald auf den richtigen Weg kommen und damit zugleich zu einer überaus interessanten und geistreichen arithmetischen Beschäftigung gelangen, die ihm manche Eigenart der Zahlenwelt erschließt.

Fünfer-, Zehner- und Zwanzigersystem können auf Grund ihrer Herleitung von den natürlichen Organen des Menschen selbst als natürliche Zahlensysteme bezeichnet werden. Aber auch gänzlich andere Faktoren können zur Bildung von Zahlensystemen geführt haben. Bei den Neuseeländern war ein Elfersystem vorhanden, und Reste eines Zwölfersystems finden sich noch in vielen Sprachen, auch im Deutschen, wo das Dutzend, ferner auch die Rute, die zwölf Fuß zu je zwölf Zoll mißt, als Überbleibsel eines solchen Systems zu gelten haben. Ein Zwölfersystem hätte sogar große Vorteile gegenüber unserem Zehnersystem, denn die Zwölf ist durch mehr Zahlen als die Zehn, durch 2, 3, 4 und 6, teilbar, die Zehn nur durch 2 und 5, ein Umstand, der für unser ganzes Rechenwesen von großem Vorteil gewesen wäre. Vom arithmetischen Standpunkte aus also wäre es entschieden besser gewesen, wenn der Mensch zwölf Finger gehabt und dadurch das Zwölfersystem herrschend gemacht hätte. Ein Zwölfersystem ist neben dem herrschenden Zehnersystem auch bei den alten Babyloniern seitens der Priester und Gelehrten in Anwendung gewesen. Diese bauten dieses Zahlensystem noch aus und erweiterten es zu einem System mit der Zahl 60 als Grundzahl. Dieses Sechzigersystem ist für die gesamte Kulturentwicklung von größter Wichtigkeit geworden, denn die babylonischen Astronomen machten es zur Grundlage ihrer mathematischen Berechnungen und astronomischen Bestimmungen. Von ihnen stammt die Einteilung des Kreises in 6 × 60 = 360 Grade, die bis auf den heutigen Tag in der Mathematik herrschend geblieben ist, ebenso auch die Einteilung des Tages in 24 Stunden und des Jahres in 12 Monate, alles Bestimmungen, die auf das ehemalige Zwölfersystem zurückgehen.

Sogar ein Zahlensystem mit der Zwei als Grundzahl wäre möglich, und der Philosoph und Mathematiker Leibniz glaubte sogar die Spuren eines solchen bei den Chinesen entdeckt zu haben. Ein solches binäres Zahlensystem würde sogar sehr große Vorteile für uns haben, denn es würde nur die beiden Zahlzeichen 0 und 1 aufweisen, und alle Rechenoperationen wären nur mit den entsprechenden beiden Zahlenwerten auszuführen. Das Rechnen nach diesem System wäre also sehr leicht. Doch hätte es auch den großen Nachteil, daß alle Zahlenwerte, selbst die kleinen, verhältnismäßig große Ziffernausdrücke und sehr viele Stellen verlangen würden, was durch die Kleinheit der Grundziffer bewirkt würde. Die Stellenwerte der Ziffern wären nach Potenzen von 2 geordnet, und demgemäß würden die ersten zehn Zahlen unseres Zehnersystems in dem Zweiersystem geschrieben werden: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010. Ein Herr Lehmann, der in der Xstraße 75, vorn 4 Treppen wohnt, im Jahre 1879 geboren, jetzt also 50 Jahre alt, und seit 25 Jahren verheiratet ist, 6 Kinder und ein Einkommen von 10 000 Mark hat, würde, wenn wir seine Personalien im Zweiersystem ausdrücken, in der Xstraße Nr. 1 001 011, vorn 100 Treppen wohnen; er ist im Jahre 11 101 010 111 geboren; der Ärmste ist seit 11 001 Jahren verheiratet und hat 110 Kinder zu ernähren, wofür ihm allerdings das stattliche Jahreseinkommen von 10 011 100 010 000 Reichsmark zur Verfügung steht.

2. Von Zinsen und Zinseszinsen

Eine günstige Kapitalsanlage – Wie man Milliardär werden kann – Verzinsung und Vermehrung – Die Fortpflanzung, ein Vermehrungsprozeß – Zinseszins in der Natur – über kontinuierliche Verzinsung – Die Zahl e – Der Mensch als Anlagekapital

Jeder kennt die berühmte Geschichte von dem Pfennig, der, wenn er bei der Geburt Christi zinstragend angelegt worden wäre, sich in der Zwischenzeit durch die Summierung von Zinsen und Zinseszinsen zu einer ungewöhnlich günstigen Kapitalsanlage entwickelt hätte. Dieser Pfennig würde sich – um den Fall kurz zu rekapitulieren – bis Ende des Jahres 1926 zu einem Bankkonto ausgewachsen haben, das mit einer Zahl von 39 Ziffern zu schreiben wäre, genauer ausgedrückt mit einem Saldo von über 646 Sextillionen Reichsmark zugunsten des glücklichen Kontoinhabers abgeschlossen hätte. Ford, Morgan, die Rothschilds und alle übrigen sogenannten »reichsten Leute der Welt« hätten zusammen noch nicht den billionsten Teil dieser Summe an Vermögen, sogar der Besitz der gesamten Menschheit an Geld und Geldeswert würde nicht diesen bescheidenen Bruchteil ergeben. Und wenn die Erdkugel vollständig aus purem Gold bestände, würde ihr Wert noch bei weitem nicht an jene Riesensumme heranreichen, sondern erst etwa siebentausend solcher Goldplaneten würden ein entsprechendes Äquivalent sein. Jener Krösus hätte auch die Inflation unseligen Angedenkens mit Gemütsruhe über sich ergehen lassen können, denn selbst die Entwertung aller Geldwerte auf den billionsten Teil, wie sie im Höhepunkt der Inflation zur grausamen Wirklichkeit wurde, hätte ihm von seinem Vermögen noch so viel übriggelassen, daß er noch immer ungezählte millionenmal reicher gewesen wäre als die gesamte übrige Menschheit zusammen. Und das alles hätte durch seine Verzinsung der einzige Pfennig getan!

In der Theorie wenigstens hätte er das zuwege gebracht, in der Praxis wäre es ja wohl kaum so glatt gegangen, schon deswegen nicht, weil sich in jener apostolischen Zeit wohl so wenig wie heute eine Bank oder ein Bankier bereit gefunden hätte, einen Pfennig zinstragend in Depot zu nehmen. Also braucht auch niemand Groll auf seine Vorfahren aus jener Zeit zu werfen, daß sie nicht mit einer so bescheidenen Bareinlage mühelos für ihre Nachkommen im zwanzigsten Jahrhundert vorgesorgt haben. In kleinerem Umfange dagegen ist die unverhältnismäßige Vermehrung eines deponierten Kapitals durch Zinseszins sehr wohl möglich und schon oft dagewesen. Wenn man Zeitungsnachrichten trauen darf, soll kürzlich ein Amerikaner, angeregt durch das Beispiel des berühmten Pfennigs, einen Betrag von taufend Dollar bei einer Bank deponiert haben mit der Bestimmung, daß diese tausend Dollar so lange liegenbleiben sollen, bis sie durch Zinsen und Zinseszinsen auf eine volle Milliarde Dollar angewachsen sind, die dann an seine dereinstigen Nachkommen verteilt werden sollen. Bei einem Zinsfuß von fünf Prozent würde dieses Ziel in rund 284 Jahren erreicht werden, also immerhin eine Möglichkeit, in absehbarer Zeit, wenn auch nur posthum, Milliardär zu werden. Die Franzosen endlich behaupten, daß die Kriegsentschädigung, deren Zahlung Deutschland durch den Versailler Frieden auferlegt worden ist, lediglich die Rückzahlung der Kriegsentschädigung von 4 Milliarden Mark, die sie selbst nach dem Kriege von 1870/71 an Deutschland zu zahlen hatten, zuzüglich Zins und Zinseszins, darstelle. Das stimmt aber nicht ganz; denn jene 4 Milliarden Mark würden in den in Betracht kommenden 48 Jahren bei fünfprozentiger Verzinsung auf etwa 41,6 Milliarden Goldmark angewachsen sein, während der Versailler Vertrag Deutschland weit größere finanzielle Opfer auferlegt.

Das Wesen der Zinseszinsen besteht bekanntlich darin, daß die Zinsen, die ein Kapital trägt, jeweils nach Ablauf eines Jahres zum Kapital geschlagen und von da an ebenfalls verzinst werden. Das so vermehrte Kapital bringt dadurch im nächsten Jahre einen entsprechend größeren Zinsertrag, um den das Kapital wiederum vermehrt wird, und so wachsen Kapital und Zinsertrag automatisch von Jahr zu Jahr. Bei gewöhnlicher Verzinsung hingegen werden die auflaufenden Zinsen nicht zum Anfangskapital geschlagen, dieses bleibt also unverändert, wie lange es auch ansteht, und ebenso bleibt auch der jährliche Zinsertrag unverändert derselbe. Ein Kapital von einer Million Mark bringt bei fünf Prozent gewöhnlicher Verzinsung Jahr für Jahr 50 000 Mark Zinsen und würde sich mithin in zwanzig Jahren verdoppeln; auf Zinseszins angelegt, würde die Verdoppelung dagegen schon in 14½ Jahren erfolgen. Zu jener unheimlich vermehrenden Wirkung, bei der sich das Anfangskapital nicht nur verdoppelt, sondern um ein Vielfaches vermehrt, gelangen die Zinseszinsen allerdings auch erst innerhalb eines Zeitraumes von mehreren Jahrzehnten. Eine Einlage von 100 Mark wächst bei fünf Prozent gewöhnlicher Verzinsung in hundert Jahren auf 600 Mark, bei Zinseszins aber würde sie in dieser Zeit auf 13 150 Mark anwachsen, also sich um mehr als das 131fache vermehren, bei einem Zinsfuß von sechs Prozent würden in jener Zeit aus den anfänglichen 100 Mark sogar 34 000 Mark werden, sie sich also auf das 340fache vermehren. Allgemein steigert sich die vermehrende Wirkung der Zinseszinsen mit dem Wachsen des Zeitraumes in einem Maße, daß sie schließlich jede wirtschaftliche und finanzielle Möglichkeit überschreitet. Das hat schon zeitig dazu geführt, Zinseszinsen beim Schuldverhältnis aus Darlehen zum Schutze des Schuldners gesetzlich zu verbieten. Im alten Rom freilich, wo ja Zinswucher das beliebte Geschäft selbst der Vornehmsten war, waren auch die Zinseszinsen geheiligte Tradition seitens aller, die sich überhaupt mit dem Geschäft des Geldausleihens befaßten, eine Tradition, die zur Auspowerung ganzer Gesellschaftskreise führte und der erst durch den Kaiser Justinian, unter dem das Römische Reich reformiert wurde und das Corpus juris entstand, ein für allemal ein Ende gemacht wurde. Seitdem ist die Erhebung von Zinseszinsen bei Darlehensschulden in wohl allen Kulturstaaten verboten, und selbst ausdrückliche Vereinbarungen dieser Art gelten, von bestimmten Ausnahmen abgesehen, als nichtig. Für die verzinslichen Geldeinlagen bei Sparkassen, Banken und ähnlichen Instituten gelten diese Bestimmungen natürlich nicht; diese gewähren den Einlegern vielmehr Zinseszinsen in der Weise, daß sie automatisch am Schlusse eines jeden Jahres die bis dahin entstandenen Zinsen zum Kapital schreiben. Bei solchen Anstalten ist denn auch der Fall nicht vereinzelt, daß Einlagen, die infolge irgendwelcher Umstände Jahrzehnte hindurch nicht abgehoben wurden, sich vervielfachen und, wenn sich die Berechtigten schließlich melden, zu großen Vermögen angewachsen sind, vorausgesetzt, daß keine – Inflation dazwischengekommen ist. Bemerkt sei noch, daß die Berechnung der Zinseszinsen in exakter Weise nur auf mathematischem Wege erfolgen kann; die Banken und sonstigen Geldinstitute verwenden jedoch für diesen Zweck Tabellen mit vorgerechneten Zinseszinsen für alle praktisch vorkommenden Fälle und reichen mit diesem Verfahren auch vollkommen aus.

Das Anwachsen von Kapital durch Zinseszins stellt einen Vermehrungsprozeß dar, bei dem, wie die angeführten theoretischen und praktischen Beispiele zeigen, selbst kleinste Größen bis zu den größten Betrügen anwachsen können. Solche Vermehrungsprozesse sind aber nicht nur im Geldwesen möglich, sondern finden in noch viel ausgedehnterer Weise in der Natur statt, und zwar vollkommen nach den Gesetzen der Zinseszinsrechnung. Stellt doch die Fortpflanzung von Mensch und Tier, die Entwicklung einer winzigen Samenzelle, die nur den kleinsten Bruchteil eines Milligramms Masse hat, zu dem ausgebildeten Lebewesen immer einen solchen Vermehrungsprozeß dar, bei dem die figurierenden Größen zu Anfang und Ende des Prozesses vergleichsweise ebenso differieren wie in dem Fall des berühmten Zinspfennigs. Das Wachsen und Werden der Samenzelle zum ausgewachsenen Individuum ist, arithmetisch betrachtet, durchaus als ein Vermehrungsprozeß nach Art der Kapitalsvermehrung durch Zinseszins aufzufassen, und ebenso ist das der Fall bei der numerischen Vermehrung der Menschheit selbst. Hier wie dort wird das Produkt der Vermehrung immer wieder selbst zum Vermehrungsfaktor, der zum ununterbrochenen Anwachsen der Vermehrungssubstanz beiträgt, wodurch diese schließlich Beträge erreicht, die die Ausgangssubstanz viele millionenmal übersteigen. Die Bibel berichtet, daß nach der Sintflut nur drei Paar Menschen am Leben waren, die aber ein sehr hohes Alter erreichten und sich dadurch in zweihundert Jahren zu einer vollen Million vermehrten. Nach den Regeln der Zinseszinsrechnung würde das eine jährliche Vermehrung der jeweils vorhandenen Menschenzahl um 6½ Prozent darstellen. Die Bibel, die ja gern in hohen anthropologischen Ziffern schwelgt, besonders was Lebensalter und Fruchtbarkeit der biblischen Menschen anbelangt, hat freilich auch den Prozentsatz der jährlichen Vermehrung der Menschheit viel zu hoch angenommen, denn wenn jenes Vermehrungstempo seitdem dauernd stattgefunden hätte, so wäre die Menschheit heute zu einer Bevölkerungsziffer angewachsen, für die, selbst wenn Mann an Mann gestellt würde, nicht einmal auf sämtlichen Planeten unseres Sonnensystems, die Sonne miteinbegriffen, geschweige denn auf unserem Erdenball, Platz wäre. In Wirklichkeit beträgt der Prozentsatz der jährlichen Vermehrung der Menschheit seit geschichtlicher Zeit bis heute nur einen sehr kleinen Bruchteil eines Prozentes, und wäre es anders, so wäre die Wohnungsnot schon längst viel drückender geworden, als es gegenwärtig schon ohnedies der Fall ist. Größer wird dieser Prozentsatz, wenn man die Bevölkerungsvermehrung eines abgeschlossenen Bevölkerungsbereiches, also etwa eines einzelnen Landes, innerhalb eines bestimmten Zeitraumes betrachtet. Für Deutschland liegen diesbezügliche statistische Nachweise für das vorige Jahrhundert vor, die erkennen lassen, daß die jährliche Bevölkerungsvermehrung während dieser Zeit um ein Prozent herum schwankte; kleiner war sie in Frankreich, größer in Rußland. Gegenwärtig weisen die Vereinigten Staaten von Amerika den hohen jährlichen Bevölkerungszuwachs von etwa 2,2 Prozent auf, noch größer aber ist dieser in den Ländern Australiens, wo er bis zu 4 Prozent hinaufgeht, sich also sehr dem Bevölkerungszuwachs nähert, der nach dem erwähnten biblischen Bericht damals stattgefunden haben soll. Freilich wird selbst die stärkste Vermehrung in der Natur übertroffen von den Vermehrungsmöglichkeiten theoretischer Rechnung, wie ja schon der mehrfach erwähnte Zinspfennig beweist.

Betrachten wir die Vermehrungsvorgänge in der Natur, also Fortpflanzung, Wachstum und Bevölkerungszuwachs, von dem Gesichtspunkt der Zinseszinsrechnung aus, so ist gegenüber der finanziellen Zinseszinsrechnung doch ein bemerkenswerter Unterschied festzustellen. Die Natur arbeitet bei ihren Vermehrungsprozessen im allgemeinen mit einem größeren Prozentsatz und betreibt überdies die Vermehrung der Substanz auch in intensiveres und konzentrierterer Weise, als es im Geldgeschäft der Fall ist, und zwar dadurch, daß bei ihr die Vermehrung der vorhandenen Substanz nicht wie dort nur nach bestimmten zeitlichen Zwischenräumen, sondern kontinuierlich erfolgt. Hieran knüpft sich ein überaus interessantes Problem der Zinsrechnung, auf das wir noch kurz eingehen wollen.

Für gewöhnlich findet im Geldwesen der Zuschlag der Zinsen zum vorhandenen Kapital nur von Jahr zu Jahr statt. Ein Kapital von 1 Million Mark, zu 5 Prozent auf Zinseszins angelegt, trägt hierbei im ersten Jahre 50 000 Mark Zinsen und vermehrt sich also nach dieser Frist auf 1 050 000 Mark, die in dieser Höhe dann weiter verzinst werden. Es hätte aber auch vereinbart werden können, daß die Zinsen immer bereits halbjährlich zum Kapital geschlagen werden und schon von diesem Zeitpunkte an an der weiteren Verzinsung teilnehmen. Dieser Modus wäre für den Einleger des Kapitals günstiger. Nach einem halben Jahre hätte sein Kapital zunächst 25 000 Mark Zinsen getragen, so daß dann für die zweite Hälfte des Jahres ein Kapital von 1 025 000 Mark weiter zu verzinsen gewesen wäre, das in dieser Zeit 25 625 Mark gebracht hätte. Dann hätte also das Anfangskapital nach Ablauf des ersten Jahres im ganzen 50 625 Mark Zinsen getragen, also 625 Mark mehr als bei jährlichem Zinszuschlag, immerhin schon ein hübscher Mehrbetrag, der selbst einem Millionär die halbjährliche statt der jährlichen Zinsberechnung lohnend erscheinen lassen dürfte. Tatsächlich werden auch für manche Geldeinlagen Vereinbarungen auf halbjährlichen Zinszuschlag getroffen. Noch höher wäre, wie ohne weiteres ersichtlich ist, der Ertrag des Kapitals, wenn die Zinsen immer schon von Monat zu Monat zum Kapital geschlagen würden, wodurch sich Kapital und Zinsertrag noch intensiver vermehren. In diesem Sinne kann man die Rechnung weiter fortsetzen – theoretisch wenigstens, denn die Banken würden sich jedenfalls für ein solches Verfahren schönstens bedanken – und die Annahme machen, daß die Zinsen täglich, stündlich, ja sogar von Sekunde zu Sekunde und schließlich, da ja auch eine Sekunde rechnerisch noch beliebig weiter teilbar ist, in jedem kleinsten Bruchteil einer Sekunde, also in jedem überhaupt denkbaren Zeitpunkt, das heißt kontinuierlich, zum Kapital geschlagen werden sollen. Es entsteht hierbei die überaus interessante Frage, um wieviel sich ein Kapital bei diesem Verzinsungsmodus innerhalb eines Jahres vermehren würde. Zunächst könnte es den Anschein erwecken, daß bei diesem Verfahren, bei dem also innerhalb einer gegebenen Zeit unendlich viele Zinszuschläge zu dem gegebenen Kapital erfolgen, sich dieses auch innerhalb dieser Zeit ins Unendliche vermehren müßte, sicher eine sehr interessante Perspektive für alle Depotinhaber. Dem ist nun aber durchaus nicht so; es läßt sich vielmehr mathematisch berechnen – das Tabellenverfahren der Banken würde hier allerdings versagen –, daß selbst bei absolut ununterbrochenem Zinszuschlag die Kapitalsvermehrung niemals über eine bestimmte Grenze hinausgehen kann, die sogar nicht einmal sehr erheblich die Kapitalsvermehrung bei jährlichem Zinszuschlag überschreitet. Wir wollen die Rechnung hier nicht ausführen, sondern nur das Resultat mitteilen, und das besagt, daß bei einem solchen Verfahren, also bei kontinuierlicher Verzinseszinsung, beispielsweise ein Kapital, das zu 5 Prozent auf Zinseszins steht, sich jährlich um 5,27 Prozent vermehrt, also nicht erheblich mehr als bei jährlich einmaligem Zinszuschlag. Immerhin würde bei diesem Verfahren eine Million Mark, die bei jährlichem Zinszuschlag 50 000 Mark, bei halbjährlichem Zinszuschlag, wie bereits errechnet, 50 625 Mark Zinsen bringt, doch 52 700 Mark, also 2700 Mark mehr Zinsen als bei dem üblichen Verfahren des Zinszuschlages tragen. Angenommen, es stände ein Kapital zu 100 Prozent zur Verzinsung, so würde dieses sich bei jährlichem Zinszuschlag nach Jahresfrist verdoppeln, bei einem solchen wie beschriebenen kontinuierlichen Zinszuschlag sich in dieser Zeit dagegen 2,71828mal um sich selbst vermehren. Die Leser, die noch die Erinnerung an die mathematischen Studien ihrer Schulzeit aufbewahrt haben, werden die angeführte Zahl kennen; es ist die berühmte Zahl e (2,718 281 828 5 … usw.) die die Basis der natürlichen Logarithmen ist und auch für die Theorie der Zinseszinsrechnung eine große Rolle spielt.

Unsere Banken begnügen sich, wie gesagt, mit jährlichem Zinszuschlag. Anders in der Natur. Bei den natürlichen Wachstums- und Vermehrungsprozessen im Menschen-, Tier- und Pflanzenreich, die ja, arithmetisch betrachtet, Vermehrungsprozesse nach Art der Kapitalsvermehrung durch Zins und Zinseszins darstellen, findet tatsächlich eine kontinuierliche Vermehrung statt. Denn die Natur macht keine Sprünge, auch bei den Wachstumsprozessen nicht, die daher nicht, wie die finanzielle Kapitalsvermehrung, in zeitlichen Intervallen, sondern in jedem kleinsten Augenblick, also kontinuierlich, nach geometrischer Progression auf Grund der Zahl e vonstatten gehen. Nehmen wir an, daß ein Mensch bei seiner Geburt 8 Pfund wog, mit 25 Jahren ausgewachsen ist und damit sein Normalhöchstgewicht von 160 Pfund erreicht hat – von überflüssigem Fettansatz der späteren Jahre sei abgesehen –, so bedeutet das unter dem Gesichtspunkte des jährlichen Vermehrungszuschlages einen Prozentsatz der Vermehrung von 12,7 Prozent, unter dem Gesichtspunkt der kontinuierlichen Vermehrung betrachtet, wie sie bei einem solchen Wachstumsprozeß in Wirklichkeit stattfand, gerade 12 Prozent kontinuierlicher Substanzvermehrung, in diesem wie in jenem Falle eine höchst anständige »Verzinsung« des Anlagekapitals, die erkennen läßt, daß die Natur in des Wortes buchstäblichem Sinne mit ihren »Pfunden« zu wuchern versteht, andererseits aber auch alle ihr gemachten »Anlagen« mit reichlichem Zinseszins heimzahlt.

3. Rothschild und der Bettler

Ein vorsichtiger Wohltäter – Etwas von den geometrischen Reihen – Die harmonische Reihe – Ein unvorsichtiger König

Es wird berichtet: Zu Rothschild kam eines Tages ein Bettler und bat um eine milde Gabe. Rothschild war gut aufgelegt und schenkte ihm 20 Mark. Das war für den Petenten ein lohnendes Geschäft, das ihn veranlaßte, am nächsten Tage seinen Besuch und seine Bitte zu wiederholen. Diesmal beschränkte sich Rothschild auf eine Spende von 10 Mark, und als der verschämte Arme sich auch am nächsten Tage wieder einstellte, auf 5 Mark. Und so ging die Sache weiter. Der Bettler kam jeden Tag wieder, und Rothschild gab ihm jedesmal die Hälfte des Betrages vom vorhergehenden Tage. Nun fragen wir: Wieviel hat Rothschild, nachdem sich die beschriebene finanzielle Aktion ein volles Jahr hingezogen hatte, dem Bettler in dieser Zeit im ganzen geschenkt? Der in dieser Art von Rechnungen unbewanderte Leser wird vielleicht den Eindruck erhalten, daß hierbei doch wohl ein ganz ansehnlicher Betrag von wenigstens 100 Mark oder auch noch mehr herauskommen müsse; denn er rechnet, daß die Spenden in den ersten drei Tagen bereits den Betrag von 35 Mark ergeben, dann müßten doch also wohl die Gaben nach einigen Wochen oder gar Monaten, wenn sie auch immer kleiner werden, insgesamt die ersten 100 Mark erreichen. Aber das ist ein Irrtum. Die Gesamtheit aller in dieser Welt halbierten Beträge wird nach Verlauf eines Jahres noch nicht einmal ganz das Doppelte der Gabe vom ersten Tage, also noch nicht ganz 40 Mark, betragen, und selbst wenn die Schenkungen in dieser Weise zehn oder hundert oder selbst Millionen von Jahren fortgesetzt würden, so würde doch niemals ein voller Gesamtbetrag von 40 Mark erreicht werden können. Die Summe aller Einzelbeträge würde sich zwar 40 Mark immer mehr nähern, sie aber niemals vollkommen erreichen, kleine Bruchteile eines Pfennigs würden immer daran fehlen. Also die Großmut Rothschilds hätte sich trotz der imponierenden Spende vom ersten Tage bei diesem Werke der Nächstenliebe doch nur in sehr mäßigen Grenzen gehalten und mag nach Ablauf des ersten Jahres in dem Bettler sehr gemischte Gefühle erweckt haben.

Man bezeichnet eine solche oder ähnliche wie die beschriebene Summe von Größen, bei der jeder Summand aus dem vorhergehenden durch dieselbe Multiplikation oder Division hervorgeht (in unserem Falle durch die Division durch 2 oder, was dasselbe ist, durch die Multiplikation mit ½) in der Mathematik als eine geometrische Reihe. Betrachten wir in dem Falle unserer Erzählung die am ersten Tage, sozusagen als Anfangsglied in der Reihe der Spenden geschenkten 20 Mark als Einheit, so entwickelt sich die Gesamtheit aller Gaben rechnerisch zu der Reihe 1 + ¹/ ₂ + ¹/ ₄ + ¹/ ₈ + ¹/ ₁₆ + ¹/ ₃₂ + … usw., und diese Reihe kann, soweit und solange man sie auch fortsetzt, niemals das Doppelte des Anfangsgliedes, also niemals den vollen Wert 2 erreichen, was in unserem Falle bedeutet, daß die Gesamtheit aller Beträge, die Rothschild dem Bettler schenkte, niemals volle zwei Zwanzigmarkstücke betragen kann. Der Leser, der diese Behauptung vielleicht anzweifelt, wird den überzeugenden Beweis dafür finden, wenn er sich der Mühe unterzieht, eine beliebige große Anzahl von Summanden der angeführten Reihe nach den gewohnten Regeln der Bruchrechnung zu addieren; er wird niemals auf den vollen Wert 2 kommen. Der Mathematiker bezeichnet 2 als den Grenzwert dieser Reihe, der, mathematisch gesprochen, erst im Unendlichen, das heißt auf gut deutsch niemals, erreicht wird.

Die Reihen spielen in der Mathematik eine große Rolle, und viele von ihnen sind auch für den Laien von Interesse, weil sie zu sehr interessanten rechnerischen Überlegungen und Folgerungen führen. Wir wollen eine andere, ähnliche Reihe betrachten, die das Gesagte bestätigen wird. Unsere Erzählung von Rothschild und dem Bettler hat nämlich noch eine Fortsetzung. Als der Bettler nach Abschluß des ersten Jahres Bilanz gemacht und dabei festgestellt hatte, daß bei dem geschilderten Verfahren nach Maßgabe der geometrischen Reihe für ihn doch recht herzlich wenig herausgekommen sei, bat er Rothschild um eine kleine Änderung des Verfahrens. Er bat, das Gabenspiel nochmals von vorn zu beginnen, ihm also zunächst wieder 20 Mark, am nächsten Tage die Hälfte, am dritten Tage den dritten, am vierten Tage den vierten, am fünften Tage den fünften Teil dieses Anfangsbetrages zu schenken und das Verfahren in dieser leicht erkennbaren Weise fortzusetzen. Rothschild überschlug im Kopfe ungefähr die Rechnung, kam zu der Überzeugung, daß auch bei diesem Verfahren die Mildtätigkeit in erträglichen Grenzen bleiben werde, und ging gutgelaunt auf den Vorschlag ein. Wie stellte sich nun bei diesem Verfahren die Sache nach Verlauf eines Jahres dar? Wenn wir wieder den Anfangsbetrag von 20 Mark als Einheit setzen, so ergibt sich, wie ohne weiteres ersichtlich ist, die Reihe 1 + ¹/ ₂ + ¹/ ₃ + ¹/ ₄ + ¹/ ₅ + ¹/ ₆ + ¹/ ₇ … usw. In dieser Reihe ist also der Nenner eines jeden Bruches immer um 1 größer als der vorhergehende Nenner. In der Mathematik wird diese Reihe ihrer numerisch gleichmäßigen Entwicklung wegen als harmonische Reihe bezeichnet.

Wir fragen nun, zu welchem Werte diese Reihe, beliebig lange fortgesetzt, führen wird. Es mag dem Laien wiederum scheinen, daß auch diese Reihe nicht zu wesentlich höheren Werten führen könnte als die zuerst betrachtete geometrische Reihe. Aber das ist wiederum falsch. Die harmonische Reihe kann vielmehr, sofern sie nur lange genug fortgesetzt wird, zu allen und selbst den größten Werten führen. Der Beweis für diese Behauptung ist ebenso einfach wie interessant, und da er auch keinerlei eigentliche mathematische Kenntnisse voraussetzt, wollen wir ihn unseren Lesern nicht vorenthalten. Wir wollen zu diesem Zweck die harmonische Reihe in einer gewissen Weise in Gruppen einteilen. Das erste und zweite Glied der Reihe lassen wir ungeändert stehen, dann aber fassen wir die nächsten zwei Glieder zu einer Gruppe zusammen, indem wir diese Glieder in Klammern setzen; dann werden die nächsten vier Glieder, dann die nächsten acht, dann die folgenden sechzehn Glieder zu je einer Gruppe zusammengefaßt und in Klammern gesetzt, und dieses Verfahren fortgesetzt. Immer enthält eine jede Gruppe doppelt soviel Glieder wie die vorhergehende Gruppe, so daß sich also unsere harmonische Reihe in folgender Form darstellt:

1 + ¹/ ₂ + ( ¹/ ₃ + ¹/ ₄) + ( ¹/ ₅ + ¹/ ₆ + ¹/ ₇ + ¹/ ₈) + ( ¹/ ₉ + ¹/ ₁₀ + … ¹/ ₁₆) … Um nun den Wert dieser Reihe besser berechnen zu können, wollen wir sie ein wenig verändern, wodurch ihr Wert etwas verkleinert wird. Wir bringen die Brüche in den einzelnen Gruppen sämtlich auf den Wert des größten Nenners in der Gruppe, ersetzen also in der ersten Gruppe den Wert ¹/ ₃ durch ¹/ ₄, ebenso in der nächsten Gruppe alle Werte durch ¹/ ₈ und setzen dieses Verfahren in allen Gruppen fort. Dann präsentiert sich diese so veränderte Reihe in der Form 1 + ¹/ ₂ + ( ¹/ ₄ + ¹/ ₄) + ( ¹/ ₈ + ¹/ ₈ + ¹/ ₈ + ¹/ ₈) + ( ¹/ ₁₆ + ¹/ ₁₆ + … ¹/ ₁₆) usw. Durch dieses Verfahren ist der Wert jedes der veränderten Brüche etwas verringert, denn der Wert eines Bruches wird bekanntlich um so kleiner, je größer sein Nenner wird; also ist hierdurch auch der Wert der einzelnen Gruppen und damit der ganzen Reihe etwas verkleinert. Der Wert jeder einzelnen Gruppe aber ist jetzt, wie ohne weiteres ersichtlich ist, = ¹/ ₂, und wenn wir diesen Wert für die einzelnen Gruppen einsetzen, so wird der Wert der ganzen Reihe 1 + ¹/ ₂ + ¹/ ₂ + ¹/ ₂ + ¹/ ₂ + … Diese Reihe aber muß, genügend lange fortgesetzt, zu jedem beliebigen und selbst dem größten Werte führen, wie wohl ebenfalls ohne weiteres klar ist. Wenn also schon die verkleinerte Reihe zu jedem beliebigen Wert führt, dann natürlich erst recht die ursprüngliche harmonische Reihe, aus der jene hervorgegangen ist und die ja noch einen etwas größeren Wert darstellt. Damit ist also bewiesen, daß die harmonische Reihe, genügend lange fortgesetzt, zu jedem beliebigen und selbst den größten Werten führen kann, ein Beweis, der durch seine Einfachheit und Schlüssigkeit das Herz des Mathematikers ebenso wie des interessierten Laien erfreut.

Wenden wir das gewonnene Ergebnis nun auf das Beispiel in unserer Erzählung an. Der Bettler hätte bei dem von ihm vorgeschlagenen Verfahren, das eine harmonische Reihe darstellt, bereits am vierten Tage den Betrag von vollen zwei Zwanzigmarkstücken, also 40 Mark, erhalten (sogar noch etwas mehr), am achten Tage wäre bereits der Betrag von 50 Mark überschritten, am sechzehnten Tage der von 60 Mark usw. Am Ende des ersten Jahres würde sich der Gesamtbetrag der innerhalb dieser Zeit dem Bettler geschenkten Einzelbeträge auf etwa 105 Mark belaufen, also doch immerhin wesentlich mehr als bei dem zuerst betrachteten Falle der geometrischen Reihe. Dann allerdings würde das weitere Anwachsen des jeweiligen Wertes der Reihe nur sehr langsam weitergehen; erst nach etwa sechs Jahren wäre ein Gesamtbetrag von 130 Mark, nach vollen fünfundzwanzig Jahren erst ein solcher von 150 Mark erreicht. Denn die harmonische Reihe wächst, wenn sie auch theoretisch zu jedem und selbst dem größten Werte führen kann, praktisch doch nur ganz langsam und nur nach einer unverhältnismäßig großen Anzahl von Gliedern an. Beispielsweise würde es in dem Falle unserer Erzählung ganz unberechenbar langer Zeiträume bedürfen, ehe bei dem betrachteten Verfahren zwischen Rothschild und dem Bettler die Reihe der einzelnen Zahlungen auf den Gesamtbetrag von 1000 Mark angewachsen wäre, selbst in Millionen von Jahren würde das noch nicht der Fall sein. Also auch bei der harmonischen Reihe brauchte Rothschild nicht sehr tief in seinen Tresor zu greifen, und der Bettler hatte abermals mit der Mathematik ein schlechtes Geschäft gemacht.

Wiederum eine geometrische Reihe erhalten wir in der Form 1 + 2 + 4 + 8 + 16 + … usw., bei der also jedes Glied doppelt so groß ist wie das vorhergehende. Diese Reihe hat, sehr im Gegensatz zu der harmonischen Reihe, die Eigenschaft, daß sie schon binnen kurzem zu ganz ungeheuren Werten führt. Auch darüber gibt es eine hübsche Erzählung. Der König Scheheran von Indien wollte dem weisen Sissa, der das Schachspiel erfunden hatte, eine Belohnung für diese geistvolle Erfindung gewähren und verhieß ihm die Erfüllung eines Wunsches. Der bescheidene Sissa erbat sich für das erste Feld des Schachbrettes ein Weizenkorn, für das zweite Feld zwei, für das dritte Feld vier, für das vierte Feld acht Körner und dieses Verfahren fortgesetzt bis zum vierundsechzigsten Felde des Schachbrettes, für jedes Feld also immer die doppelte Anzahl von Weizenkörnern wie für das vorhergehende. Die Höflinge lachten über diesen armseligen Wunsch, aber als man daranging, diesen zu erfüllen, da stellte sich heraus, daß – etwa vom vierzigsten Felde des Schachbrettes an – ganz ungeheure Mengen von Getreide nötig wurden, um die Ansprüche Sissas zu erfüllen, ja daß schließlich das ganze ungeheure Reich Indien nicht genug Getreide für diesen Zweck aufzutreiben imstande war. Zu spät rechneten die Hofgelehrten nach, daß die Summe der Getreidekörner, die bei der Fortsetzung des Verfahrens bis zum letzten Felde des Schachbrettes herauskommt, über 18 Trillionen beträgt, und daß das mehr Getreide ist, als die gesamte Erde, selbst wenn alles feste Land angebaut würde, in hundert Jahren produzieren könnte. Da mag König Scheheran wegen der Erfüllung seines Versprechens zunächst einmal ziemlich konsterniert gewesen sein, wenn er nicht auf einen sehr naheliegenden Ausweg verfallen ist. Er hätte dem listigen Schachspielerfinder ruhig die Erfüllung seines Wunsches gewähren können, hätte aber gleichzeitig, wozu er nach der getroffenen Vereinbarung durchaus berechtigt war, zur Bedingung machen können, daß Sissa sich die berechnete Menge Weizenkörner selbst abzählen solle, kein Korn zuviel und keins zuwenig. Bis jener damit zu Ende gekommen wäre, wären einige Billionen Jahre ins Land gegangen, und bis dahin hätte König Scheheran den Ausgang der Angelegenheit wohl unbesorgt abwarten können. Woraus erfolgt, daß manchmal der gesunde Menschenverstand selbst über die verwegensten Rechenkünste hinausgeht.

4. Heitere Rechenkunst

Vom Humor der Rechenaufgabe – Die Schneckenaufgabe – Theorie und Wirklichkeit – Eine Eisenbahnaufgabe – Kleinprobleme – Eine pädagogische Regel – Die Aufgaben.

Die Wissenschaften, die sich mit den Zahlen beschäftigen, also Rechenkunst und Mathematik, sind im allgemeinen eine todernste Angelegenheit, und beim Lösen von Rechen- oder mathematischen Aufgaben hat der Mensch zumeist, wie der Berliner zu sagen pflegt, »nichts zu lachen«. Dennoch blüht auch auf diesem Gebiete dem Humor eine Stätte, und es ist sogar ein sehr origineller Humor, der hier zu seinem Rechte kommt, nämlich der Humor der logischen Finessen, der allerdings anderer Art ist als der manchmal ein wenig gequälte Humor unserer Witzblätter. Rechnen oder Mathematik treiben heißt ja immer nur, aus den Bedingungen oder Voraussetzungen einer Aufgabe das Resultat logisch erschließen. Wie es aber in der reinen Logik oftmals zu Widersprüchen, zu Trugschlüssen oder Paradoxien kommen kann, die immer einen mehr oder weniger humoristischen Charakter haben und oftmals dem Scharfsinn des ausgepichtesten Logikers ein Schnippchen schlagen, so auch bei den Zahlenoperationen. Auch eine Rechenaufgabe kann nicht nur schwer oder leicht, sondern sie kann auch lustig sein, was immer dann der Fall zu sein pflegt, wenn sie ein logisches (oder auch unlogisches) Element enthält, das bewirkt, daß das Ergebnis der Aufgabe ganz anders ausfällt, als es der Wirklichkeit der Dinge entspricht. In anderen Fällen bewirkt der logische Charakter der Aufgabe, daß die Lösung, nach den Regeln der Rechenkunst bearbeitet, sehr umständlich ist und große Schwierigkeiten bereitet, dagegen auf anderem Wege, nämlich durch logische Betrachtung der Bedingungen und Verhältnisse der Wirklichkeit, sehr schnell und leicht zu lösen ist, so daß es sich der exakte Rechenkünstler gefallen lassen muß, ausgelacht zu werden, weil er mit der Kanone des schweren arithmetischen Rüstzeuges nach einem kleinen Spatzen schießt, der auf viel mühelosere Weise zur Strecke gebracht werden kann. Machen wir das an einigen Beispielen klar.

Eine Aufgabe der ersterwähnten Art, bei der also Wirklichkeit und Rechenergebnis in einen heiteren Widerspruch geraten, ist die folgende, die manchen unserer Leser bereits bekannt sein wird. Eine Schnecke will eine 28 Meter hohe Mauer hinaufklettern. Am Tage legt sie immer 7 Meter auf der Mauer zurück, in der Nacht gleitet sie aber jedesmal um 5 Meter wieder herunter. Am wievielten Tage wird die Schnecke oben angelangt sein? Diese Aufgabe wird dem Leser, der sie noch nicht kennt, geradezu lächerlich einfach erscheinen. Denn, so rechnet er, die Schnecke legt an einem vollen Tage immer 7 – 5 = 2 Meter zurück, also wird sie die 28 Meter hohe Mauer in genau vierzehn Tagen erklommen haben. Und dennoch ist diese Lösung falsch, wie sich aus der folgenden sehr einfachen Überlegung ergibt: die Schnecke legt, da sie an jedem vollen Tage um 2 Meter vorwärtskommt, in elf Tagen unzweifelhaft eine Strecke von 22 Metern zurück; klettert sie dann am nächsten Tage noch 6 Meter weiter empor, so – ist sie oben! Also schon in zwölf Tagen statt in vierzehn führt die Kletterpartie die Schnecke ans Ziel entgegen dem rein rechnerischen Ergebnis. Stimmt es oder stimmt es nicht? Gerade an diesem harmlosen Beispiel sehen wir, daß sich die Dinge in der Wirklichkeit manchmal doch anders gestalten, als es nach den Regeln der Rechenkunst der Fall sein müßte, und daß bei der rein rechnerischen Behandlung einer Aufgabe oder eines Vorganges manchmal gewisse Wirklichkeitsverhältnisse unberücksichtigt bleiben, woraus sich dann immer ein sehr heiter anmutender Widerspruch zwischen Rechenkunst und Wirklichkeit ergibt. Selbstverständlich kann die vorliegende Aufgabe, wie es auch bei allen Aufgaben dieser Art der Fall ist, in eine solche Form gebracht werden, daß das rechnerische Ergebnis mit der Wirklichkeit übereinstimmt; dann aber ist die dazu notwendige rechnerische Operation zumeist doch etwas komplizierter, der »Ansatz« der Gleichung ist schwieriger und führt erst nach einem mehr oder weniger großen Umwege an das richtige Ziel.

Eine Aufgabe der anderen Art ist folgende: Um 12 Uhr mittags fährt ein Eisenbahnzug von Berlin nach Hamburg, und zwar mit einer Stundengeschwindigkeit von 70 Kilometern. Anderthalb Stunden später, also um 13½ Uhr, fährt von Hamburg ein Zug auf derselben Strecke nach Berlin, jedoch nur mit einer Geschwindigkeit von 55 Kilometern die Stunde. Die Strecke Berlin-Hamburg werde mit 430 Kilometern angenommen. Zu einem bestimmten Zeitpunkte müssen sich dann die beiden Züge treffen. Welcher der beiden Züge ist in diesem Zeitpunkte weiter von Berlin entfernt, der von Berlin nach Hamburg oder der von Hamburg nach Berlin fahrende? Demjenigen Leser, dessen Geistesstärke vielleicht mehr in Religion als im Kopfrechnen besteht, werden sich schon beim Lesen dieser Aufgabe die Haare zu Berge sträuben, so schwer und kompliziert sieht sie aus, und wenn er sich der guten Sache wegen dennoch wagemutig daranmacht, eine Gleichung aufzustellen und diese nach allen Regeln der Algebra zu lösen, so wird das eine lange und mühevolle Rechenarbeit werden. Und doch ist die Aufgabe spielend leicht, erfordert sogar nicht einmal die einfachste Rechenoperation, sondern ist ohne Bleistift und Papier sofort zu lösen, wenn – ja wenn man die Aufgabe nicht nur von der arithmetischen, sondern zunächst einmal von der logischen Seite betrachtet. Denn wenn sich die beiden Züge treffen, so ist es doch selbstverständlich, daß sie beide gleich weit von Berlin entfernt sein müssen, gleichviel wo der Treffpunkt liegt und gleichviel zu welchem Zeitpunkte sie sich treffen! Das bedarf überhaupt keiner Berechnung, sondern ergibt sich aus der logischen Folgerung, daß zwei Dinge an einem Punkte stets gleich weit von jedem anderen Punkte, also auch gleich weit von Berlin, entfernt sein müssen. Der Hinweis auf den Zeitpunkt des Treffens sowie auch die Angabe der Stundengeschwindigkeiten, Streckenlänge, überhaupt alle Zahlenangaben sind vollständig überflüssig und dienten in der Aufgabe nur dazu, den Rätselrater auf ein falsches Geleise zu schieben, was ja bei einer Eisenbahnaufgabe seine Berechtigung haben dürfte. Es ist immer ein heiteres Schauspiel, wenn ein Rechner, der die logische Pointe der Aufgabe nicht erkennt, sich daranmacht, sie als Gleichung zu behandeln und nach mehr oder weniger langer Zeit und mehr oder weniger großem Aufwand an Rechenarbeit an Hand des Ergebnisses seiner arithmetischen Operationen haarscharf beweist, daß die Züge gleich weit von Berlin entfernt sind, und ich kenne so manchen tüchtigen Arithmetiker, der bei dieser Aufgabe mit Kanonen nach dem Spatz geschossen hat.

Solcher heiterer Aufgaben in rechnerischem oder mathematischem Gewande gibt es zahllose. Nahezu alle Völker und Zeiten, soweit sie überhaupt zur Kunst des Rechnens beigetragen haben, haben auch heitere Rechenaufgaben dieser Art erfunden, die schon im hohen Altertum den Menschen Vergnügen bereiteten. Man soll den Wert solcher Kleinprobleme nicht unterschätzen. Ihre Lösung erfordert geistige Konzentration und logische Überlegung und schärft den Blick für die Wirklichkeit der Verhältnisse, Umstände, die solche Aufgaben im besten Sinne des Wortes zu Intelligenzprüfungen oder, noch besser, zu Intelligenzübungen stempeln, die ganz zweifellos auch von praktischem Wert sind. Die berühmtesten Rechenkünstler und die bedeutendsten Mathematiker haben es nicht verschmäht, auch an Aufgaben dieser Art ihren Scharfsinn zu erproben oder auch selbst solche Aufgaben zum Nutzen und zur Erheiterung der rechnenden Mit- und Nachwelt zu ersinnen. Groß ist die Literatur, die sich mit dieser heiteren Seite der Rechenkunst befaßt, und besonders im deutschen Bücherschatz gibt es eine ganze Reihe trefflicher Werke, die diese heitere Wissenschaft zu ihrem Gegenstand gemacht haben und nicht nur für den rechnenden Normalmenschen, sondern unter Umständen auch für den Mathematiker von Interesse sind. Hat doch die heitere Rechenkunst unter der Bezeichnung »Unterhaltungsmathematik« selbst in der wissenschaftlich-mathematischen Fachliteratur ihren Platz erhalten.

Mit diesen amüsanten Regionen der Rechenkunst wollen wir unsere Leser in den nachfolgenden Zeilen etwas vertrauter machen, indem wir ihnen eine Reihe solcher Aufgaben unterbreiten und sie bitten, an diesen ihren Scharfsinn zu erproben. Eine Anzahl der Aufgaben sind noch neu und an dieser Stelle zum ersten Male veröffentlicht, andere werden von manchen Lesern als gute Bekannte wiedererkannt werden, diese wie jene aber haben das gemein, daß sie weniger an die rechnerischen Fähigkeiten als an das logische Überlegungsvermögen appellieren, wie es ja immer bei Aufgaben dieser Art der Fall zu sein pflegt. Eins sei noch verraten: Der Schein trügt bei solchen Scherzaufgaben, wie die Leser aus den vorgesetzten beiden Kostproben bereits ersehen haben werden, sehr oft. Er trügt auch hinsichtlich der Schwierigkeit der Aufgabe, denn zumeist sind die Aufgaben, die ganz leicht scheinen, viel schwieriger als sie aussehen, und umgekehrt jene, die große Schwierigkeiten zu bieten scheinen, mit einiger Überlegung sehr leicht und schnell zu lösen. Ich kenne einen Mathematiker, einen vortrefflichen Pädagogen, der, wenn er seinen Sekundanern oder Primanern eine so recht knifflige mathematische Aufgabe versetzt hat, zugleich zwei Regeln nennt, um solche Aufgaben schnell und mühelos zu lösen, und diese Regeln lauten: 1. Man sieht sich die Aufgabe an; 2. Man freut sich darüber! Hat man beides in ausreichendem Maße getan, so pflegt man bald auf den richtigen Weg zur Lösung der Aufgabe zu kommen, wobei es dem erwähnten mathematischen Pädagogen allerdings auch passiert ist, daß seine Untertanen auf der Schulbank die zweite jener beiden Regeln so lange und anhaltend befolgten, daß sie vor lauter »Freude« an der Aufgabe nicht zum Rechnen kamen. So weit braucht man die Konsequenz nicht treiben. Aber sich erst einmal das Ding stillvergnügt betrachten, dann kommt man am ersten dahinter, wo des Pudels Kern zu suchen und zu finden ist. Und nun also ans Werk!

Aufgabe 1. König Midas wurde bekanntlich von den Göttern für seine Dummheit in Gold verwandelt. Nehmen wir an, daß die sagenhafte Majestät 75 Kilogramm schwer war und daß damals 1 Kilogramm Gold ebensoviel wie heute, nämlich 2800 Mark, kostete; was war dann König Midas nach seiner Verwandlung wert?

Aufgabe 2. Zu einem Juwelier kam ein Herr, der ein Armband zu kaufen wünschte. Der Juwelier legte ihm mehrere Stücke zur Auswahl vor, und der Herr entschied sich schließlich für ein Armband im Preise von 60 Mark. Zur Bezahlung gab er dem Juwelier einen Hundertmarkschein. Der Juwelier hatte kein Kleingeld in der Kasse und schickte daher den Lehrling mit dem Hundertmarkschein zum Nachbar mit der Bitte, den Schein zu wechseln. Der Lehrling kam mit dem Wechselgeld zurück, der Juwelier packte dem Käufer das Armband ein, gab ihm auf die gezahlten 100 Mark noch 40 Mark heraus, und der Käufer verließ den Laden. Nach einer Stunde kam jedoch der Nachbar, der den Hundertmarkschein gewechselt hatte, aufgeregt zu dem Juwelier, behauptete, daß der Hundertmarkschein falsch wäre und verlangte Ersatz. Der Juwelier überzeugte sich von der Richtigkeit der Behauptung und mußte dem Nachbar schweren Herzens 100 Mark zurückzahlen. Wie groß war der gesamte Schaden, den der Juwelier bei dem Geschäft gehabt hatte?

Aufgabe 3. Was ist größer, die Summe 1 + 2 + 3 oder das Produkt 1 × 2 × 0 × 3?

Aufgabe 4. Zehn Freundinnen hielten einmal einen Kaffeeklatsch ab. Beim Abschiednehmen gab jede der Damen jeder anderen einen Kuß. Wieviel Küsse wurden im ganzen gegeben?

Aufgabe 5. Um 12 Uhr mittags fährt von Berlin nach München ein Eisenbahnzug, und zwar mit einer Geschwindigkeit von 50 Kilometern die Stunde. Um genau dieselbe Zeit fährt auf derselben Strecke ein Zug von München nach Berlin, und zwar ebenfalls mit 50 Kilometern Stundengeschwindigkeit. Die Strecke Berlin-München werde mit rund 800 Kilometern Länge angenommen. Dem von Berlin abfahrenden Zuge fliegt nun eine Taube voraus, die eine Geschwindigkeit von 60 Kilometern in der Stunde entfaltet und ihren Flug so lange fortsetzt, bis sie den von München kommenden Zug erreicht hat. Ist das geschehen, so kehrt sie um und fliegt dem Berliner Zug entgegen; nachdem sie diesen erreicht hat, fliegt sie wieder dem Münchener Zug entgegen und setzte dieses Hin- und Herfliegen so lange fort, als noch eine Entfernung zwischen den beiden Zügen besteht. Welche Strecke wird die Taube, die bei ihrem Fluge immer im Gebiet der betreffenden Strecke bleibt, im ganzen zurücklegen?

Aufgabe 6. Auf einem Schachbrett befinden sich lediglich ein schwarzer und ein weißer Turm, also auch kein König. Wieviel verschiedene Stellungen können die beiden Türme zueinander einnehmen?

Aufgabe 7. Es gibt bei der Eisenbahn eine besondere Art von Wagen, deren Laderaum einen großen Zylinder darstellt und die zum Transport von Gas dienen. Das Gewicht eines solchen Wagens betrage rund 100 Zentner, der Laderaum sei 50 Kubikmeter. Der Wagen wird mit Wasserstoff gefüllt, von dem ein Kubikmeter rund 100 Gramm wiegt. Um wieviel ist der Wagen in vollständig beladenem Zustande schwerer als in unbeladenem?

Aufgabe 8. Ein Flugzeug braucht zur Fahrt von Berlin nach Hamburg 1 Stunde 20 Minuten, zur Rückfahrt auf derselben Strecke und mit derselben Geschwindigkeit jedoch nur 80 Minuten. Wie kommt das?

Aufgabe 9. Ein halbvolles Glas Bier kann unzweifelhaft auch als halbleer bezeichnet werden. Daher können wir nach den Regeln der Gleichungslehre die Gleichung aufstellen:

½ leeres Glas Bier = ½ volles Glas Bier.

Multiplizieren wir jetzt diese Gleichung mit 2, so ergibt sich, wiederum nach den Regeln der Gleichungslehre, das merkwürdige Resultat:

1 leeres Glas Bier = 1 volles Glas Bier.

Ist diese Rechnung richtig? Und wenn nicht, welches ist dann der Fehler, der zu diesem sonderbaren und für alle Freude des edlen Gerstentrankes höchst erschreckenden Resultat führt?

Aufgabe 10. In einer Gesellschaft wurde eine Dame gefragt, ob sie einen ebenfalls dort anwesenden Herrn näher kenne. Sie antwortete: Dieses jungen Mannes Mutter ist meiner Mutter einziges Kind! In welcher Beziehung standen die beiden?

Aufgabe 11. Hauptmann X. macht mit seiner Kompanie eine Felddienstübung. Die Kompanie wird außer von ihm noch befehligt von drei Leutnants und zwölf Unteroffizieren; die Zahl der Untergebenen war zehnmal so groß wie die der Vorgesetzten. Aus wieviel Personen bestand die ganze Kompanie?

Aufgabe 12. Die Operationen des Hauptmanns X. richteten sich gegen die Kompanie des Hauptmanns Y. Bei dieser war die Zahl der Mannschaften zehnmal so groß wie die der Vorgesetzten, und die Zahl der Untergebenen betrug 164. Welches war die Zahl der Vorgesetzten in dieser Kompanie?

Aufgabe 13. Nachdem beide Kompanien ihre kriegerischen Übungen beendet hatten, zogen sie zusammen friedlich heim. Eine Anzahl Unteroffiziere und Mannschaften war aber zurückgeblieben, um eine Feldwache zu beziehen. Die Heimziehenden beider Kompanien zählten zusammen 310 Personen, und die Zahl der Untergebenen war bei beiden zusammen elfmal so groß wie die der Vorgesetzten. Wieviel Mannschaften zählten beide Kompanien zusammen?

Aufgabe 14. Als sie die Stadt erreicht hatten, trennten sich die beiden Kompanien wieder, da sie in verschiedenen Kasernen lagen. An Leutnants und Unteroffizieren befanden sich bei jeder Kompanie 13 Personen, und die Zahl der Untergebenen war um 140 größer als die der Vorgesetzten. Wieviel Köpfe zählte jede der heimkehrenden Kompanien?

Aufgabe 15. An dem runden Stammtisch zum »Goldenen Löwen« saßen, wie alle Abend, die zehn Honoratioren des Ortes in der gewohnten Reihenfolge beisammen. Nachdem alle politischen und sozialen Fragen wieder einmal durchgegangen und dafür der Unterhaltungsstoff ausgegangen war, kam man auf den Gedanken, einmal die gewohnte Sitzordnung zu ändern, dann nochmals und abermals eine neue Reihenfolge zu bilden. Schließlich machte man sich daran, auf diese Weise alle überhaupt möglichen Reihenfolgen auszuprobieren. Angenommen nun, daß zur Bildung einer neuen Reihenfolge immer eine Minute Zeit benötigt wird, wie lange wird es dauern, bis die zehn Herren alle überhaupt möglichen Reihenfolgen absolviert haben?

Aufgabe 16. Es gibt in der Mathematik sogenannte Minima- und Maxima-Aufgaben, in denen es sich darum handelt, die kleinsten bzw. die größten Werte zu berechnen, die den Bedingungen einer Aufgabe genügen. Solche Aufgaben gibt es auch in der heiteren Rechenkunst. Beispielsweise: Eine Gesellschaft bestand aus zwei Herren, ferner der Frau, der Schwägerin, dem Bruder und dem Schwager eines jeden der Herren. Wieviel Personen müssen das mindestens gewesen sein?

Aufgabe 17. Welches ist die größte Zahl, die sich mit zwei Ziffern schreiben läßt?

Aufgabe 18. Welches ist die größte Zahl, die sich mit drei Ziffern schreiben läßt?

Aufgabe 19. Welches ist die kleinste ganze Zahl, die sich mit zwei Ziffern schreiben läßt?

Aufgabe 20. Ein Milchmädchen bringt 8 Liter Milch zur Stadt. Die Kundin will aber diesmal nur 4 Liter haben; leider hat sie kein Litermaß im Haus, wohl aber ein Gefäß, das 5 Liter, und ein weiteres, das 3 Liter Inhalt hat. Durch mehrfaches Umfüllen wird erreicht, daß schließlich in einem der Gefäße 4 Liter Milch zurückbleiben. Auf welche Weise kommen die beiden hierbei am schnellsten zum Ziel?

Aufgabe 21. In eine Konditorei kommt ein Herr und bestellt ein Stück Apfelkuchen mit Schlagsahne. Als der Käufer das Gewünschte bringt, sagt der Herr: »Ich habe mir die Sache überlegt; geben Sie mir für den Apfelkuchen mit Sahne lieber einen Kognak, der ebensoviel kostet!« Der Kellner nimmt den Kuchen mit Schlagsahne zurück und bringt einen Kognak, den sich der Gast gut schmecken läßt. Darauf will er das Lokal verlassen, der Kellner hält ihn jedoch zurück und sagt: »Verzeihung, mein Herr, Sie haben den Kognak noch nicht bezahlt.« – »Dafür habe ich Ihnen ja den Apfelkuchen mit Schlagsahne zurückgegeben«, erwiderte der Gast. – »Den haben Sie aber ebenfalls nicht bezahlt«, wendet der Kellner ein. – »Den habe ich ja auch nicht gegessen!« antwortete darauf der Gast. Das leuchtete dem Kellner ein, so daß er den Gast ziehen ließ. Hinterher kamen ihm allerdings einige Bedenken über die Richtigkeit der Rechnung. Wo mag diese ein Loch haben?

Aufgabe 22. Einen unfreiwilligen Beitrag zur heiteren Rechenkunst lieferte kürzlich ein Witzblatt. Dort war folgender Scherz erwähnt: In einer Gesellschaft äußerte eine Dame, von der allgemein bekannt war, daß sie mit der Wahrheit auf Kriegsfuß lebte, nichtsdestoweniger renommistisch: »Ich habe in meinem Leben erst dreimal gelogen.« Worauf ein Herr ihr antwortete: »Dann haben Sie jetzt, meine Gnädige, das viertemal gelogen!« Der Sinn des notabene sehr mäßigen Witzes war natürlich der, daß der Herr durch seine Antwort der Dame zu verstehen geben will, daß sie schon öfter als dreimal gelogen hat. War dann aber seine Antwort logisch richtig?

Aufgabe 23. Wenn ich eine Zigarre restlos aufrauche, um wieviel sind dann Asche und Rauch, in die die Zigarre verwandelt worden ist, leichter als die ursprüngliche Zigarre?

Aufgabe 24. Von zwei Vätern schenkte der eine seinem Sohn 150 Mark, der andere gab seinem Sohn 100 Mark. Es stellte sich dabei heraus, daß beide Söhne zusammen hierbei nur in den Besitz von 150 Mark gekommen waren. Wie war das möglich?

Aufgabe 25. Eine Flasche mit Kork kostet 1,10 Mark; die Flasche allein kostet 1 Mark mehr als der Kork. Was kostet der Kork?

Aufgabe 26. Ein Mantel, ein Spazierstock und ein Hut kosten zusammen 140 Mark; der Mantel kostet 90 Mark mehr als der Stock und Stock und Mantel kosten zusammen 120 Mark mehr als der Hut. Was kostet jeder der drei Gegenstände?

Aufgabe 27. Punkt 12 Uhr mittags verläßt Herr Schwarz in Berlin seine Wohnung, um ein Telegramm an Mr. White in New York aufzugeben. Er braucht für den Weg bis zum Schalter des Postamtes fünf Minuten; das Doppelte dieser Zeit dauert es, bis das Telegramm aufgegeben ist; das Doppelte der ganzen seit dem Abgang des Herrn Schwarz aus seiner Wohnung verstrichenen Zeit Zeit dauert es dann, bis das Telegramm in dem New-Yorker Postamt angelangt ist, und nochmals das Doppelte der ganzen bis dahin verstrichenen Zeit, bis das Telegramm an Mr. White ausgeliefert wurde. Als Mr. White das Telegramm erhielt, sah er gerade nach der Uhr. Welche Zeit zeigte diese?

Aufgabe 28. Schon die Alten befaßten sich mit Rätseln in arithmetischem Gewande; eine Probe ihrer Kunst auf diesem Gebiete ist das folgende Epigramm, das auf Euklid, den berühmten Begründer unserer Geometrie, zurückgeht und in deutscher Übersetzung lautet:

Esel und Maultier schritten mit Säcken beladen des Weges,
Unter dem Drucke der Last stöhnt schwer und seufzte der Esel.
Jenes bemerkt das und sprach zu dem kummerbeladnen Gefährten:
»Alterchen,« spricht es, »was weinst du und jammerst grad wie ein Mägdlein?«
Doppelt soviel als du grad' trüg' ich, gäbst du einen Sack mir,
Nähmst du mir einen jedoch, dann trügen wir beide dasselbe.«
Zahlenkundiger, sprich, wieviel sie beide getragen.

Aufgabe 29. Der berühmte Mathematiker Diophant aus Alexandrien, nach dem die Diophantischen Aufgaben benannt sind, lebte und wirkte im 4. Jahrhundert. Über sein Leben sind wir nur durch ein Epigramm auf seinem Grabstein unterrichtet, das folgendermaßen lautet:

Hier das Grabmal deckt Diophant. Schauet das Wunder!
Durch des Entschlafenen Kunst lehret sein Alter der Stein.
Knabe zu sein gewährte ihm Gott ein Sechstel des Lebens;
Noch ein Zwölftel dazu sproß auf der Lippe der Bart.
Dazu ein Siebentel noch, da schloß er das Bündnis der Ehe,
Nach fünf Jahren entsproß aus der Verbindung ein Sohn.
Wehe, das Kind, das vielgeliebte, die Hälfte der Jahre
Hatt' es des Vaters erreicht, als es dem Schicksal erlag.
Drauf vier Jahre hindurch, durch der Zahlen Betrachtung den Kummer
Von sich scheuchend kam auch er an das irdische Ziel.

Welches sind nach diesen Angaben die genaueren Lebensdaten Diophants?

Aufgabe 30. Auch die »Brunnenaufgabe«, die auf den berühmten griechischen Mathematiker und Physiker Hero von Alexandrien zurückgeht, sei hier noch angeführt. Sie lautet:

Vier Springbrunnen es gibt; die Zisternen anfüllet der erste
Täglich. Der andere braucht zwei Tage dazu, und der dritte
Drei und der vierte gar vier. Welche Zeit nun brauchen zugleich sie?

Das wären also dreißig Aufgaben aus dem Reiche der heiteren Rechenkunst, die den Lesern, soweit sie nicht geborene Rechen- oder Denkgenies sind, immerhin für einige Stunden Kopfzerbrechen bereiten dürften. Einige harte Nüsse sind jedenfalls darunter, an denen man sich leicht einen Geisteszahn ausbrechen kann, und ob viele Leser sein werden, die sämtliche der dreißig Aufgaben irrtumslos zur Strecke bringen, dürfte nicht ganz wahrscheinlich sein. Um dem Leser Gelegenheit zu geben, festzustellen, wie oft er den Nagel auf den Kopf getroffen hat, folgen nunmehr die Lösungen der Aufgaben. Doch raten wir ihm sehr, die Lösungen nicht vorwegzunehmen, sondern sie eben nur zur Kontrolle seiner eigenen Ergebnisse zu benutzen; er würde sich um einen großen Teil der Anregung und des Vergnügens bringen, die ihm die heitere Rechenkunst sonst gewähren kann. Bemerkt sei noch, daß die vorstehenden Aufgaben von dem Verfasser bereits anderweitig, in Zeitungen und Zeitschriften, veröffentlicht wurden. Bei einer ganzen Anzahl der Aufgaben kam es zu heiteren Auseinandersetzungen zwischen dem Verfasser und solchen Lesern, die zu anderen Ergebnissen gekommen waren oder sich aus anderen Gründen zu äußern wünschten. Diese Dispute sind eine sehr hübsche Ergänzung zu dem Kapitel der heiteren Rechenkunst, weswegen wir in den »Lösungen« auf einige solcher »Äußerungen aus dem Leserkreis« näher eingehen.

5. Lösungen und Löser der »Heiteren Rechenkunst«

Der goldene König – Der geheimnisvolle Hundertmarkschein – Was ist ein Kuß? – Eisenbahn und Rechenkunst – Schach dem Turm! – Das gerettete »volle Glas Bier« – Mathematik am Stammtisch – Flasche und Kork

Aufgabe 1. Die Lösung dieser Aufgabe sieht sehr leicht aus, dennoch ist zu befürchten, daß sich eine Anzahl der Leser die Sache noch leichter gemacht hat, als sie ist, indem sie einfach 75 × 2800 Mark = 210 000 Mark als Resultat der Aufgabe errechnet haben. Aber so billig wäre König Midas, nachdem er in pures Gold verwandelt worden war, doch nicht zu haben gewesen. Im Normalzustande, als er noch aus Fleisch und Bein bestand, wog er 75 Kilogramm, nach seiner Verwandlung in Gold aber wog er 19mal mehr, denn das spezifische Gewicht des Goldes ist 19mal größer als das durchschnittliche spezifische Gewicht der Körpersubstanz des Menschen. Also bezifferte sich der Wert des Gold gewordenen Königs auf 75 × 2800 × 19 = 3 990 000 Mark, ein Resultat, das wohl nicht jeder Löser der Aufgabe errechnet hat.

Gegen diese Lösung ist wiederholt der Einwand erhoben worden, daß bei der Verwandlung des Körpers Seiner Majestät des Königs Midas das angegebene Gewicht von 75 Kilogramm durchaus erhalten bleibe, wenn mit der Verwandlung zugleich auch eine Verringerung des Körpervolumens auf den neunzehnten Teil stattfinde, und eine solche Verringerung besage die Aufgabe implizite. Dem kann aber mit guten Gründen widersprochen werden. Der Begriff der Verwandlung enthält keinesfalls zugleich den der Volumenverringerung, und die meisten Leser und Löser werden sich zweifellos den in Gold verwandelten König auch nach seiner Verwandlung in voller Lebensgröße vorgestellt haben. Es kam bei der Aufgabe darauf an, das Moment des spezifischen Gewichtes, das die Aufgabe selbst nicht erwähnt, zu entdecken und in die Rechnung miteinzubeziehen; für eine Volumenverringerung lag nach Sinn und Wortlaut der Aufgabe keine Veranlassung vor.

Aufgabe 2. Der Schaden des Juweliers beträgt 100 Mark. Denn er selbst hat bei dem Geschäft zunächst 100 Mark eingenommen, nämlich die 100 Mark, die ihm der gefällige Nachbar für den falschen Hundertmarkschein gab, hat selbst aber fortgegeben das Armband im Werte von 60 Mark, die 40 Mark, die er dem faulen Kunden bei dem Kauf noch bar herausgab, und endlich die 100 Mark, die er dem Nachbar erstatten mußte, zusammen 200 Mark, so daß er bei dem Geschäft 100 Mark eingebüßt hat, nicht mehr und nicht weniger. Trotzdem wird der Schaden des Juweliers oftmals auch anders angegeben, und nach einer Veröffentlichung dieser Aufgabe in einem Unterhaltungsblatt erhielt ich mehrere Dutzend von Zuschriften, in denen die mitgeteilte Lösung für falsch erklärt wurde. Mit merkwürdiger Übereinstimmung rechneten die meisten der Einsender mir vor: Wert des gelieferten Armbandes 60 Mark; herausgegebenes Wechselgeld 40 Mark; Einlösung des falschen Hundertmarkscheines 100 Mark, macht zusammen 200 Mark! Wer hat also recht? Nun, der Widerspruch ist ohne Schwierigkeit zu lösen. Alles, was in jener Gegenrechnung angeführt worden ist, stimmt, nur haben die Herren Kritiker vergessen, die 100 Mark in Rechnung zu stellen, die der Juwelier von dem gefälligen Nachbarn für den falschen Schein erhalten hatte. Diese 100 Mark von dem eben berechneten Betrage von 200 Mark in Abzug gebracht, bleiben wiederum nur 100 Mark Schaden des Juweliers übrig; es wird beim besten Willen nicht mehr. In ähnlicher Weise rechnen andere Opponenten immer einen Posten zuwenig oder zuviel. Der Direktor einer Aktiengesellschaft rechnete mir haarscharf vor, daß der Schaden des Juweliers 140 Mark betrage, und ein Einsender gab das Höchstgebot mit 360 Mark angeblichen Schadens des Juweliers ab. Man kann übrigens die Lösung der Aufgabe auch gänzlich ohne Rechnung, auf rein logischem Wege, finden, wenn man sich folgendes vergegenwärtigt: Wäre der Hundertmarkschein echt gewesen, so hätte der Juwelier natürlich überhaupt keinen Schaden gehabt, also kann sein Schaden natürlich nur so groß sein wie der Nominalbetrag des falschen Hundertmarkscheins. Oder man kann auch schließen: Der diebische Käufer hat bei der Sache gerade 100 Mark, nämlich das Armband von 60 Mark und 40 Mark bar, ergattert, und mehr als dieser durch Betrug sich angeeignet hat, kann natürlich der Schaden des Betrogenen nicht sein. Manche Unzufriedene endlich halten der Lösung noch entgegen, daß der Schaden des Juweliers weniger als 100 Mark betragen habe, weil davon der Verdienst, der in dem Verkaufspreis von 60 Mark für das Armband eingerechnet ist, in Abzug gebracht werden müsse. Auch dieser Einwand ist nicht stichhaltig, denn der Juwelier hat durch den Diebstahl nicht nur das, was ihm das Armband selbst gekostet hat, sondern natürlich auch den Verdienst verloren, den er bei regulärem Verkauf des Stückes erzielt haben würde. Also, es bleibt bei den 100 Mark Schaden!

Aufgabe 3. Die Summe 1 + 2 + 3 beträgt 6, das Produkt 1 × 2 × 0 × 3 aber ist = 0, denn jedes Produkt, in dem auch nur ein Faktur Null ist, ist im ganzen Null. Den Glauben an die Richtigkeit dieses Resultates konnte einst ein Einsender nicht aufbringen, der mir schrieb: Wenn ich jemandem erst einmal, dann zweimal, dann dreimal und schließlich noch nullmal hinter die Ohren haue und der Verhauene mich dann bei Gericht anzeigt, glauben Sie, daß mich dann das Gericht freisprechen wird mit der Begründung, daß ich den anderen überhaupt nicht verhauen habe!? Hierzu wurde dem Zweifler geantwortet: Nein, Verehrtester, Sie werden wegen körperlicher Mißhandlung nach Recht und Rechenkunst verknackt; denn Sie haben dem anderen eine und zwei und drei Ohrfeigen, zusammen sechs Ohrfeigen, versetzt. Sie haben die Ohrfeigen addiert und nicht multipliziert, und auf die Addition hat die Null keinen Einfluß, auch beim Ohrfeigengeplänkel nicht. Aber vielleicht bekommen Sie wegen arithmetischer Unkenntnis Bewährungsfrist, wenn die Sache nicht mit Geld abzumachen ist!

Aufgabe 4. Die Lösung dieser Aufgabe wird zumeist mit 100 oder 90 Küssen angegeben, was aber beides falsch ist. Beim Abschied gibt zunächst die erste Dame jeder der anderen neun einen Kuß, gibt also 9 Küsse, und geht, wie wir der besseren Veranschaulichung wegen annehmen wollen, aus dem Zimmer. Von den zurückbleibenden neun Damen gibt wiederum eine den übrigen acht je einen Kuß, gibt also 8 Küsse; die nächste kann nur noch 7 Küsse vergeben, und so kommt eine Summe von 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 Küsse heraus, keiner mehr, aber auch keiner weniger.

An die Veröffentlichung dieser Aufgabe in einer weitverbreiteten Wochenschrift schloß sich einst eine sehr heitere Polemik an über die Richtigkeit des Resultates. Reichlich zwei Dutzend Leser, und zwar durchweg Damen, schrieben mir dieserhalb und bestritten die Richtigkeit des Resultates, das nach ihrer Meinung mit 90 Küssen anzugeben sei. Das Argument der einen Partei war: Damen küssen sich gegenseitig nur auf die Wangen, nicht auf die Lippen, und bei dieser Art des Küssens kommen 90 Küsse heraus, da hierbei ein gegebener Kuß von dem Empfänger immer an den Spender zurückgegeben wird. Das wäre an und für sich richtig, gilt aber eben nur für Wangenküsse; in der Aufgabe ist aber von Küssen schlechtweg, nicht von Wangenküssen, die Rede, und wenn man von Küssen ohne weiteren Zusatz redet, so ist nach allgemeinem deutschen Sprachgebrauch immer der Lippenkuß gemeint, und damit ist die Anzahl der 45 Küsse, die bei jener Prozedur herauskommt, gerechtfertigt. Schwieriger war ein anderes Argument, das übereinstimmend von einer ganzen Anzahl der Einsenderinnen zu diesem Thema in folgender Form vorgebracht wurde: Wie Druck immer Gegendruck erzeugt, so ein Kuß auch immer einen Gegenkuß; wenn sich also zwei Menschen einen Kuß geben, so sind das in Wirklichkeit zwei Küsse, denn es gibt hierbei nicht nur der eine dem anderen, sondern auch der andere dem ersten einen Kuß. Auf diese Weise kämen dann 90 Küsse statt der berechneten 45 heraus. Über diese Frage, also ob ein Kuß, den sich zwei Menschen geben, in Wirklichkeit zwei Küsse seien – und über diese Frage läßt sich von logischen Gesichtspunkten aus durchaus und mit Recht streiten –, konnten die feindlichen Parteien trotz wiederholter Replik und Duplik lange Zeit hindurch nicht zu einer Einigung gelangen, bis sich schließlich die Anhängerinnen der Zwei-Kuß-Theorie folgender vergleichender Argumentation beugten: Wenn das Ehepaar Meier ein Kind hat, so kann man sagen: Herr Meier hat ein Kind und Frau Meier hat ein Kind; das ist aber doch nur ein Kind, denn das Kind, das Herr Meier hat, ist dasselbe Kind, das Frau Meier hat. Ebenso ist es, wenn sich das Ehepaar Meier einen Kuß gibt. Dann kann man auch sagen, Herr Meier gibt Frau Meier einen Kuß, und Frau Meier gibt Herrn Meier einen Kuß. Das sind aber doch nicht zwei Küsse, denn der Kuß, den Herr Meier der Frau Meier gibt, ist derselbe Kuß, den Frau Meier Herrn Meier gibt, ist also nur ein Kuß. Gegen diese »Meierei« war nicht anzukämpfen, weder logisch noch arithmetisch, und so verblieb es bei den 45 Küssen.

Aufgabe 5. Diese Aufgabe wird voraussichtlich von vielen der Leser als schwer empfunden worden sein, vielleicht sogar als schwerer, als es dem Charakter der heiteren Rechenkunst entspricht. Die Mathematiker unter den Lesern werden die Aufgaben vielleicht sogar in die Form einer unendlichen Reihe gebracht haben, zu der sie ihrer Art nach allerdings sehr geeignet zu sein scheint. Aber das ist durchaus überflüssig, denn die Aufgabe ist, rein rechnerisch betrachtet, spielend leicht und kaum schwieriger als die andere Eisenbahnaufgabe, die wir als Probebeispiel angeführt hatten, nur muß sie ebenfalls logisch richtig angefaßt werden, was dann zu der folgenden sehr einfachen Folgerung führt: Da die beiden Züge zu derselben Zeit abfahren und auch die gleiche Geschwindigkeit haben, müssen sie sich gerade in der Mitte der Strecke, also nach 400 Kilometern Fahrt, treffen. Da sie mit 50 Kilometer Geschwindigkeit fahren, erreichen sie den Treffpunkt gerade in acht Stunden. Ebenso lange hat aber nach der Aufgabe die Taube zu fliegen, und da diese in der Stunde 60 Kilometer zurücklegt, so hat sie im ganzen 480 Kilometer zu fliegen. Was sehr einfach zu beweisen war.

Die Lösung dieser Aufgabe ist bisher nicht beanstandet, dagegen konnte sich ein Einsender mit der Lösung der anderen, als Beispiel gegebenen Eisenbahnaufgabe, die von den beiden Zügen handelt, die gleich weit von Berlin entfernt sind, wenn sie sich treffen, nicht einverstanden erklären, und er schrieb ironisch, daß ich mich hierbei gehörig »verdacht« habe. Zum Beweise dessen sandte er eine Zeichnung, ein Doppelgleis darstellend, auf dem die beiden Züge so weit einander genähert sind, daß die Stirnlinien der Lokomotiven eine Linie bilden. Bei dieser Stellung wäre tatsächlich der eine Zug um eine volle Zuglänge von irgendeinem in der Gleisrichtung liegenden Punkte weiter entfernt als der andere. Aber wie kann man denn bei einer solchen Stellung der beiden Züge von einem »Treffen« derselben reden? Es treffen sich hierbei lediglich die Stirnlinien der Lokomotiven, während von einem wirklichen Treffen der beiden Züge erst dann gesprochen werden kann, wenn die Züge sich ihrer ganzen Ausdehnung nach auf den beiden Gleisen gegenüberstehen, also ihre Mittelpunkte zusammenfallen oder doch auf einer Linie, senkrecht zum Gleise, liegen. Dann aber sind beide Züge von jedem Ort auf der Gleisstrecke gleich weit entfernt, und davon beißt keine Maus einen Faden ab.

Aufgabe 6. Das Schachbrett hat bekanntlich 64 Felder. Steht nun der weiße Turm auf irgendeinem Felde, so kann der schwarze Turm auf 63 anderen Feldern stehen. Auch zu jeder anderen Stellung des weißen Turmes kann der schwarze Turm jedesmal 63 verschiedene Stellungen einnehmen. Da der weiße Turm nun im ganzen auf 64 verschiedenen Feldern stehen kann, so können beide Türme im ganzen 64 × 63 = 4032 verschiedene Stellungen zueinander einnehmen. Die Richtigkeit dieser Lösung wird manchmal angezweifelt; es wird behauptet, daß von den angegebenen 4032 Stellungen alle diejenigen in Abzug zu bringen seien, in denen nach den Regeln des Schachspiels der eine Turm den anderen schlagen könne. Dazu ist zu bemerken, daß in der Aufgabe lediglich nach der Zahl der möglichen Stellungen der beiden Türme zueinander gefragt worden ist. Dazu gehören aber auch die Schlagstellungen, denn auch diese sind nach den Schachregeln möglich und kommen überdies in jeder Partie vor. Es liegt also keinerlei Veranlassung vor, diese Stellungen aus der Zahl der möglichen Stellungen auszuscheiden.

Aufgabe 7. Der Eisenbahnwagen wird durch die Ladung nicht schwerer, sondern – leichter. Denn um den Wagen mit dem Wasserstoffgas füllen zu können, muß zunächst die Luft aus ihm entfernt werden. 50 Kubikmeter Luft aber wiegen etwa 50 Kilogramm, die 50 Kubikmeter Wasserstoffgas aber nach der Angabe der Aufgabe nur etwa 5 Kilogramm, so daß der Wagen nach der Füllung um 45 Kilogramm leichter ist als vorher. Hier liegt also der Fall vor, wo, im eisenbahntechnischen Sinne wenigstens, ein Wagen im beladenen Zustande leichter ist als im unbeladenen.

Aufgabe 8. Daß das Fahrzeug für dieselbe Strecke und bei gleicher Geschwindigkeit einmal 1 Stunde 20 Minuten, das andere Mal nur 80 Minuten benötigt, erklärt sich daraus, daß 1 Stunde 20 Minuten = 80 Minuten ist, ein Faktum, das, so banal es ist, nichtsdestoweniger durch die Art, wie die Aufgabe gestellt wird, oftmals übersehen wird, weil wir immer im Dezimalsystem zu denken und zu rechnen gewohnt sind und 1,20 etwas anderes ist als 0,80. Gerade Leute, die viel rechnen, fallen deswegen mit Vorliebe auf diese Scherzaufgabe herein und geben die merkwürdigsten Gründe für den angeblichen Unterschied an, während mehr naiv veranlagte Gemüter den Scherz sofort durchschauen.

Aufgabe 9. Wir hoffen, daß denjenigen unserer Leser, die Freunde eines guten Glases Bier, notabene eines vollen Glases, sind, der Schreck über die merkwürdige Gleichung, derzufolge zwischen einem vollen und einem leeren Glas Bier eigentlich kein Unterschied ist, nicht allzusehr in die Glieder gefahren ist. Es sei ihnen allen zum Troste gesagt, daß jene sonderbare Rechnung gottlob einen Fehler enthält, zwar keinen Rechenfehler, wohl aber einen Denkfehler, der obendrein nicht einmal ganz leicht ausfindig zu machen ist. Ein »halbvolles« Glas Bier ist nämlich etwas ganz anderes als ½ volles Glas Bier. Jenes ist ein ganzes Bierglas, das nur zur Hälfte gefüllt ist und tatsächlich ebensogut als halbleer bezeichnet werden kann; ½ volles Glas Bier hingegen ist die mit Bier gefüllte Hälfte eines ehemals ganzen Bierglases, also etwa eines Glases, das in mittlerer Höhe quer durchgeschnitten ist, und ½ leeres Glas ist ein solches halbiertes Bierglas in leerem Zustande. Also darf ich aus der Tatsache, daß ein halbvolles Glas Bier auch als halbleer bezeichnet werden kann, keinesfalls die Gleichung herleiten ½ volles Glas Bier = ½ leeres Glas Bier, womit das erschreckende Resultat in nichts verfliegt. Es lag also in der Rechnung eine Verwechslung der sehr verschiedenen Begriffe »Glas Bier« und »Bierglas« vor. Zu diesem Ergebnis schrieb mir einmal ein Leser sehr launig, daß er doch schwere Bedenken gegen diese Lösung der Aufgabe habe und er es für seine Person vorziehe, um der Sache ordentlich auf den Grund zu gehen, längere Zeit hindurch einmal volle und halbvolle Gläser auszuprobieren, um sich wirklich zu überzeugen, daß leer und voll nicht dasselbe seien. Manchmal scheine ihm das wirklich so zu sein, aber das läge wohl nur daran, daß die Wirte jetzt das Bier so furchtbar »schnitten«, so daß man zwischen leer und voll schon gar nicht mehr unterscheiden könne. Zu diesem mannhaften Entschluß habe ich dem gewissenhaften Forscher meinen unbedingten Beifall ausgesprochen; nur Erfahrung verschafft unumstößliche Gewißheit.

Aufgabe 10. Die Dame ist die Mutter des Herrn. Diese Aufgabe ist überhaupt nicht rechnerischer Natur, sondern erfordert lediglich die logische Vergegenwärtigung des nach den Bedingungen der Aufgabe allein möglichen Verwandtschaftsverhältnisses, das aber zumeist immer erst nach längerem Raten richtig festgestellt wird. Zumeist kommt die Mutter in den Verdacht, die Tante des jungen Mannes zu sein.

Aufgabe 11. Eine ganze Reihe von Lösern wird – zunächst wenigstens – den Personenbestand der Kompanie mit 160, andere mit 176 oder auch 177 errechnet haben, wenigstens sind diese Ergebnisse in Zuschriften an mich am häufigsten genannt worden. Sie sind jedoch falsch, wie folgende Rechnung erweist: Es sind 16 Vorgesetzte vorhanden (1 Hauptmann, 3 Leutnants, 12 Unteroffiziere), und da die Zahl der Untergebenen zehnmal so groß ist, so beträgt diese 160. Zu diesen gehören auch die Leutnants und die Unteroffiziere, die zwar Vorgesetzte, zugleich aber auch Untergebene, nämlich des Hauptmanns, sind, daher im Personenbestand der Kompanie nicht extra berechnet werden dürfen. Der einzige innerhalb der Kompanie, der nicht Untergebener ist, ist der Hauptmann; dieser und die 160 Untergebenen ergeben zusammen einen Bestand der Kompanie von 161 Personen.

Aufgabe 12. Die Personenzahl dieser Kompanie ist 165 (164 Untergebene und der Hauptmann). Von diesen sind ¹⁰/ ₁₁ = 150 Mannschaften und ¹/ ₁₁ = 15 Vorgesetzte.

Aufgabe 13. Beide heimkehrenden Kompanien zusammen zählen 2 Hauptleute und 308 Untergebene. Daraus ergibt sich die Zahl aller Vorgesetzten mit 28 und die der Mannschaften (310 – 28) mit 282.

Aufgabe 14. Die einzelne Kompanie zählt zusammen 154 Untergebene und den Hauptmann, also 155 Personen. Wer diese Zahl als Lösung berechnet hat, hat dennoch falsch gerechnet, denn in dieser Aufgabe ist nicht nach der Personenzahl, sondern nach der Kopfzahl der Kompanie gefragt worden, und da der Hauptmann seine Kompanie stets zu Pferde führt, so ist in diesem Falle noch ein Pferdekopf mitzurechnen. Also zählt jede der heimkehrenden Kompanien 157 Köpfe. Als diese vier Aufgaben seinerzeit in einem Unterhaltungsblatte aufgegeben worden waren, hat nach Bekanntgabe der Lösungen damals ein erheblicher Teil der deutschen Heeresmacht, unterstützt durch ansehnliche Truppenteile der Randstaaten, gegen mich in zahlreichen Zuschriften mobil gemacht mit der Begründung, daß, wenn das Pferd des Hauptmanns mitgezählt werden solle, das auch bereits in den drei vorhergehenden Aufgaben geschehen müsse; also seien entweder die Lösungen dieser oder die Lösung der letzten Aufgabe falsch. Darauf ist abermals zu erwidern, daß in den drei vorhergehenden Aufgaben nur nach der Personenzahl gefragt wurde, ein Pferd aber ist keine »Person«, sondern nur ein Mittel der Kriegstechnik, wie etwa die Feldküche oder ein Geschütz; einen Kopf hat ein Pferd aber dennoch, und deshalb mußte dieser bei der Kopfzahl mitgerechnet werden.

Aufgabe 15. Wenn die zehn Herren im »Goldenen Löwen« ihre Absicht wirklich ausführen und bis zur letzten der möglichen Reihenfolgen ausharren wollten, so müßten sie eine Dauersitzung von nahezu sieben Jahren veranstalten, denn so lange würde es dauern, bis bei den angegebenen Bedingungen sämtliche möglichen Reihenfolgen absolviert wären. Denn die Zahl der möglichen Reihenfolgen beträgt bei zehn Personen 3 628 000, und diese Zahl Minuten ergibt den genannten stattlichen Zeitraum. Da viele Leser diesen erstaunlichen Angaben nicht ganz trauen werden, wollen wir kurz zeigen, wie das Resultat herauskommt. Zwei Personen, nennen wir sie a und b, können unzweifelhaft nur zwei Reihenfolgen bilden, nämlich die Reihen ab und ba. Kommt noch eine dritte Person c hinzu, so kann diese in jeder der genannten beiden Reihen an drei Stellen stehen, nämlich vorn, in der Mitte oder hinten, so daß jetzt 2 × 3 = 6 Reihenfolgen gebildet werden können, nämlich die 3 Reihen cab, acb, abc und ferner die 3 Reihen cba, bca, bac. Wir merken uns, daß bei 3 Personen 1 × 2 × 3 = 6 Reihen gebildet werden können. Kommt eine vierte Person hinzu, so kann diese in jeder der vorhandenen 6 Reihen 4 Stellungen einnehmen, wie leicht nachgeprüft werden kann, so daß jetzt 1 × 2 × 3 × 4 = 24 Reihenfolgen gebildet werden können. Fahren wir in dieser Weise fort, so finden wir, daß von 10 Personen 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 verschiedene Reihenfolgen gebildet werden können, und dieses lange Produkt ergibt die obengenannte große Zahl, wie man leicht nachrechnen kann. Wir bemerken noch, daß man das Produkt aller Zahlen von 1 an bis zu einer Zahl n als n! bezeichnet, und man liest diesen Ausdruck: » n Fakultät«. Das Produkt der Zahlen von 1 bis 10 ergibt also 10! (gelesen: »zehn Fakultät«). In dieser Weise lassen sich natürlich auch die Fakultätswerte aller weiteren Zahlen berechnen, und der Leser wird finden, daß diese Werte bald ganz gewaltig ansteigen. Leicht läßt sich dann auch ausrechnen, wieviel Reihenfolgen von 11 oder 12 oder gar 20 Personen usw. gebildet werden könnten, nämlich 11! bzw. 12! bzw. 20!. Die Fakultätswerte spielen in der Mathematik eine sehr große Rolle.

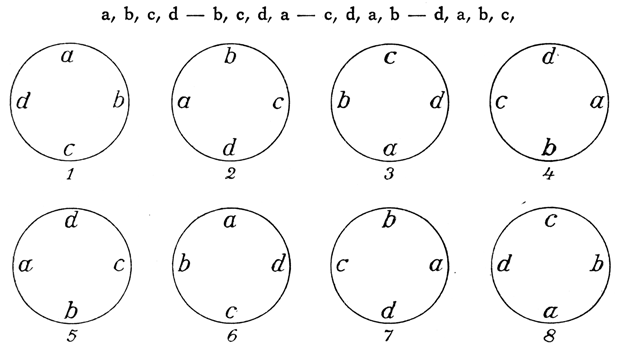
Abb. 21

Gegen die Lösung dieser Aufgabe wurde wiederholt der Einwand erhoben, daß diese nur dann zutreffe, wenn die zehn Personen in gerader Linie nebeneinander sitzen, nicht aber, wenn sie, wie es die Aufgabe vorsieht, um einen runden Tisch gruppiert sind. Durch diesen Umstand, so schrieb mir einst ein Schul- und Oberregierungsrat vom Rhein, wird die Zahl der Reihenfolgen doch erheblich eingeschränkt. Denn es sind, um ein Beispiel anzuführen, in einer Gesellschaft von 4 Herren, wenn diese als a, b, c, d bezeichnet werden, die vier Folgen

a, b, c, d – b, c, d, a – c, d, a, b – d, a, b, c,

für einen runden Tisch offenbar die gleichen, weil hierbei in allen vier Folgen jeder der vier Teilnehmer immer zwischen denselben Nachbarn sitzt. Aber auch die Umkehrungen,

d, c, b, a – a, d, c, b – b, a, d, c – c, b, a, d,

führen nicht zu anderen Folgen, auch hier sitzt wieder jeder zwischen denselben Nachbarn wie bei den ersten Folgen. Das wird anschaulich, wenn wir die genannten acht Folgen bildlich darstellen, wie es in Abbildung 21 geschieht. In allen 8 Folgen sitzt jeder Teilnehmer zwischen denselben Nachbarn. Je 8 Kombinationen führen also nach der Auffassung des Genannten immer zu derselben Folge, so daß bei 4 verschiedenen Personen an einem runden Tisch in Wirklichkeit nur 3 verschiedene Reihenfolgen möglich sind. Entsprechend wären nach seiner Auffassung in einer Gesellschaft von 5 Personen an einem runden Tisch nur 12 verschiedene Reihenfolgen möglich, und für 10 Personen rechnet er unter derselben Bedingung nur 3024 Reihenfolgen aus. Aber dieser Rechnung kann doch nicht zugestimmt werden. Zwar sitzt in den 8 Folgen unserer Abbildung 21 jedesmal jeder zwischen denselben Nachbarn, aber nicht auf denselben Plätzen bzw. denselben Stühlen. Nehmen wir an, daß auf dem Platz, den in der 1. Sitzfolge unserer Abbildung der Teilnehmer a einnimmt, das Präsidium des Tisches ist, so zeigt die Abbildung ohne weiteres, daß bei jeder der Folgen 1 bis 4 ein anderer der Herren das Präsidium innehat und jeder jedesmal auf einem anderen Stuhl sitzt. In den Folgen 5 bis 8 wiederholen sich zwar die Folgen 1 bis 4, aber nun in umgekehrter Richtung. Zwar sitzt auch jetzt wieder jeder zwischen denselben Nachbarn wie in den Folgen 1 bis 4, aber der rechte Nachbar von vordem ist jetzt sein linker und der linke von vordem jetzt sein rechter Nachbar geworden. Dieselbe Reihenfolge, bei der jeder der Teilnehmer auf demselben Platze bzw. demselben Stuhl sitzt wie in der ersten Folge, kehrt erst nach 24- bzw. 4!-maligem Platzwechsel wieder, und Entsprechendes gilt natürlich auch von einer Runde von 10 Teilnehmern, bei der erst nach 101 Änderungen der Reihenfolge die erste Folge wiederkehrt, bei der jeder Teilnehmer auf demselben Stuhl wie in jener sitzt. Damit ist auch dieser sonst durchaus scharfsinnige Einwand gegen die Lösung der Aufgabe ausreichend widerlegt. Die Mathematik macht auch am runden Stammtisch keine Ausnahme.

Aufgabe 16. Die Bedingung der Aufgabe kann mit einer Mindestzahl von vier Personen erfüllt werden, und zwar ist das dann der Fall, wenn die Gesellschaft aus zwei Brüdern besteht, die zwei Schwestern geheiratet haben.

Aufgabe 17 und 18. Die größte zweiziffrige Zahl ist natürlich nicht 99, denn der Ausdruck 9 ⁹, gelesen: »neun hoch neun«, also eine Potenz, in der sowohl die Basis als der Exponent 9 ist bzw. ein Produkt, in welchem die 9 als Faktor neunmal gesetzt ist, ist eine ungleich größere Zahl. Ebensowenig ist 999 die größte dreiziffrige Zahl, denn die ebenfalls dreiziffrigen Ausdrücke 99 ⁹, 9 ⁹⁹ stellen ungeheuer viel größere Zahlenwerte dar. Von diesen beiden ist der letztgenannte der weitaus größere. Die größte Zahl jedoch, die mit drei Ziffern gebildet werden kann, ist, wie schon Gauß erwähnt, der Ausdruck 9 ^{9 ⁹}, also eine Potenz mit der Basis 9, deren Exponent wieder eine Potenz von 9 ist. Dieser Ausdruck stellt, ziffernmäßig berechnet, eine Zahl dar, die mit 233 beginnt und mit über 369 Millionen Ziffern zu schreiben wäre. Der Ausdruck ist ein schönes Beispiel dafür, wie durch die symbolische Schreibweise der Mathematik selbst die allergrößten Zahlenwerte vermittels einiger weniger Zeichen ausgedrückt werden können. Man könnte auf diese Weise sogar noch viel größere Zahlenwerte mit zwei bzw. drei Ziffern bilden. Denn wie wir bereits aus der Lösung der 15. Aufgabe ersehen haben, stellt im allgemeinen jede Zahl, wenn sie mit dem Fakultätszeichen versehen wird, einen vielmal größeren Wert dar, als sie selbst hat, nämlich das Produkt aller Zahlen von 1 bis zu der fraglichen Zahl. Demgemäß könnte die größte zweiziffrige Zahl mit 9 ⁹! und die größte dreiziffrige mit 9 ^{9 ⁹}! angegeben werden. Diese Zahlen sind unendlich viele Male größer als die obenerwähnten und entsprechen ganz unvorstellbar großen Zahlenwerten.

Aufgabe 19. Die kleinsten zweiziffrigen ganzen Zahlen sind nicht etwa 11, 12 usw., sondern ²/ ₂, ³/ ₃, ⁴/ ₄ usw. usw. bis ⁹/ ₉. Jeder dieser Ausdrücke = 1. Wir können diese Zahlenwerte sogar noch etwas knapper ausdrücken und den Bruchstrich ersparen, nämlich in der Form 2 ⁰, 3 ⁰, 4 ⁰ usw. Diese Ausdrücke entsprechen an Wert den genannten Brüchen, und jeder von ihnen ist ebenfalls = 1, da jede Potenz mit dem Exponenten 0 den Wert 1 hat. Falsch dagegen sind die mir wiederholt mitgeteilten Lösungen ¹/ ₂, ¹/ ₃, ¹/ ₄ usw. Diese Zahlenwerte sind zwar noch kleiner als 1, aber es sind keine ganzen Zahlen, wie es die Aufgabe erfordert.

Aufgabe 20. Es sind zunächst in dem größten Gefäß 8 Liter Milch, in jedem der anderen Gefäße 0 Liter enthalten. Durch Umgießen bekommen die drei Gefäße nacheinander die folgenden Inhalte:

8-Liter-Gefäß	5-Liter-Gefäß	3-Liter-Gefäß
3	5	0
3	2	3
6	2	0
6	0	2
1	5	2
1	4	3

Jetzt sind in dem mittleren Gefäß 4 Liter enthalten, womit die Aufgabe gelöst ist. Die Lösung kann auch noch durch andere Umgießungen erreicht werden.

Aufgabe 21. Das Loch, das die Rechnung hat, besteht in der Behauptung des Gastes, daß er für den Kognak den Apfelkuchen »zurückgegeben«, d. h. in dem Sinne, wie er es aufgefaßt haben will, an Zahlungs Statt gegeben, habe. Das ist aber keineswegs der Fall gewesen. Er hat vielmehr, als er statt des Apfelkuchens den Kognak verlangte, nur die Annahme des Apfelkuchens verweigert und die Bestellung geändert. Er hatte also den Apfelkuchen noch nicht erhalten und konnte ihn daher auch nicht als Zahlung für etwas anderes geben. Zu dieser Aufgabe schrieb mir einst ein Fachmann, Oberkellner in einer Konditorei, daß er eine zweckdienlichere und einfachere Lösung der Aufgabe kenne: er würde einem Gast, der ihm mit einer so merkwürdigen Rechnung käme, mit einer Gegenrechnung dienen, nämlich ihm fünfe ins Gesicht dividieren; dann würde der Gast wohl wissen, was er zu bezahlen habe! Stimmt, und ist wieder ein Beweis, daß die Praxis der Wirklichkeit über Logik und Rechenkunst hinausgeht.

Aufgabe 22. Die Antwort des Herrn war natürlich logisch unrichtig. Denn er wollte doch – das war der Sinn des Witzes – durch seine Worte der Dame zu verstehen geben, daß ihre Behauptung, sie habe erst dreimal gelogen, unwahr sei. Dann mußte nach seiner Meinung die Dame also schon vor jener Bemerkung mehr als dreimal, also zum mindesten viermal, gelogen haben, und ihre Bemerkung wäre zum mindesten die fünfte Lüge gewesen. Also auch in einem Witzblatt können unfreiwillige Witze gemacht werden, und ich gestehe, daß ich mich über die Entdeckung dieses Falles viel mehr gefreut habe als über den höchst mäßigen Witz selber.

Aufgabe 23. Rauch und Asche sind zusammen nicht leichter, sondern schwerer als die Zigarre, aus der sie entstanden sind. Denn beim Verbrennen verbindet sich der Kohlenstoff in der Zigarre mit Sauerstoff aus der Luft; das Verbindungsprodukt beider ist der Rauch, der also den Kohlenstoff der Zigarre und überdies noch ein Quantum Sauerstoff enthält, das vordem nicht in der Zigarre enthalten war. Um das Gewicht des aufgenommenen Sauerstoffs müssen also die Verbrennungsprodukte, Rauch und Asche, schwerer sein als die ursprüngliche Zigarre. Die Richtigkeit dieser Aufgabe wurde nur ein einziges Mal bestritten, und zwar von einem Herrn, der mir seine Kompetenz, den Fall besser und richtiger beurteilen zu können – er behauptete, Asche und Rauch müßten ein geringeres Gewicht als die Zigarre haben –, damit nachzuweisen suchte, daß er sich mir als Realschullehrer und Verfasser eines weitverbreiteten Schulbuches für den Unterricht in Physik und Chemie legitimierte. Ich antwortete ihm: Bedauernswerte Schüler!

Aufgabe 24. Die beteiligten Personen waren Großvater, Vater und Sohn, wodurch das Ergebnis zustande kam.

Aufgabe 25. Viele Leser werden – wenigstens auf Anhieb – den Wert des Korkes mit 10 Pfennigen berechnet haben. Das ist aber falsch, denn dann würde die Flasche 1 Mark kosten und wäre nur 90 Pfennige teurer als der Kork. Der Kork kostet vielmehr 5 Pfennig, die Flasche 1,05 Mark, und damit stimmt die Rechnung. So einfach die Aufgabe ist, so verführen doch die Angaben zunächst meistens zu der angegebenen falschen Lösung. Ein Leser schrieb mir einst nach Veröffentlichung der Aufgabe eine Postkarte sehr ungehaltenen Inhaltes, ob ich die Leute denn für kleine Kinder halte, daß ich mit solchen lächerlichen Aufgaben komme. Einen Tag später aber ließ er einen längeren Brief folgen, in welchem er sich selbst mit sehr starken Ausdrücken aus der Zoologie belegte und mitteilte, daß er wieder und immer wieder herumgerechnet habe, was denn an der Aufgabe daran sei, bis ihm im Bette die Erleuchtung kam. Darauf folgten wieder längere Betrachtungen der Selbsterkenntnis mit reichlichem zoologischen Einschlag und das Versprechen, in Zukunft gerade bei den anscheinend leichten Aufgaben alle Geisteskräfte mobil zu machen.

Aufgabe 26. Der Hut kostet 10, der Stock 20 und der Mantel 110 Mark.

Aufgabe 27. Genau 2¼ Stunde, nachdem Herr Schwarz seine Wohnung verlassen hat, ist das von ihm aufgegebene Telegramm in die Hände des Mr. White in New York gelangt. Wer aber daraus den Schluß ziehen würde, daß die Uhr des Mr. White bei Empfang des Telegramms auf ¼3 bzw. ¼15 stand, hätte sich sehr geirrt. Denn die New-Yorker Zeit geht gegen die Berliner bzw. die mitteleuropäische Zeit gerade sechs Stunden nach. Die Uhr des Mr. White zeigte daher, als das Telegramm anlangte, ¼9 vormittags. Nach dem beiderseitigen Uhrenstande berechnet, hätte also Mr. White das Telegramm früher bekommen, als es abgesandt worden war.

Aufgabe 28. Der Esel trug 5, das Maultier 7 Säcke.

Aufgabe 29. Die Aufgabe stellt eine einfache Gleichung mit einer Unbekannten dar, aus der sich ergibt, daß Diophants Knabenzeit mit 14 Jahren beendet war, daß ihm mit 21 Jahren der Bart sproß, daß er mit 33 Jahren heiratete, mit 38 Jahren einen Sohn bekam und mit 84 Jahren starb, nachdem schon vier Jahre vorher sein Sohn im Alter von 42 Jahren gestorben war.

Aufgabe 30. Die vier Springbrunnen füllen vereint die Zisterne in ¹²/ ₂₅ Tagen = 11 Stunden 31 Minuten 12 Sekunden.

6. Heitere Geometrie

Aus dem Kuriositätenkabinett der Mathematik – Apfelsine und Erdkugel – Ein merkwürdiges Ergebnis – Anschauung und Denken – Das Möbiussche Blatt – Die Aufgaben

Wie die Wissenschaft von den Zahlen ihre heitere Seiten hat, so auch jenes Gebiet der Mathematik, das von den räumlichen Größen handelt, also die Geometrie. Auch hier gibt es vieles, das selbst den geschworenen Feind der Mathematik interessant und humorvoll anmutet und ihn zur Beschäftigung reizen kann, und ebenso entbehrt auch dieses Gebiet nicht zahlreicher Scherzaufgaben, die auf Trugschlüsse oder Paradoxien hinauslaufen und einen manchmal recht erheblichen Grad von Scharfsinn erfordern, wenn es gelingen soll, auf den Kern des Problems zu kommen. Meistens verhält es sich bei den Kuriositäten in geometrischem Gewande übrigens so, daß der humorvoll anmutende Charakter nur die äußere Seite eines im übrigen durchaus ernsten und eigenartigen Problems darstellt, ohne daß der Liebhaber solcher Aufgaben das immer vollständig erfaßt. Gerade die Geometrie liefert viele und überaus interessante Beiträge zu dem Kuriositätenkabinett der Mathematik, die zwar ein gewisses Verständnis für die Welt der räumlichen Größen verlangen, im übrigen aber aus dem Rahmen der üblichen Schulgeometrie sehr herausfallen. Die nachfolgenden Beispiele werden das Gesagte vollauf bestätigen.

Zunächst wollen wir uns mit einer höchst merkwürdigen Eigenschaft der Kugel befassen, von der keiner unserer Leser etwas in der Schule gehört hat, denn sie ist sogar manchen Mathematikern von Fach nicht bekannt. Zu diesem Zweck wollen wir das folgende Gedankenexperiment machen. Wir denken uns eine Apfelsine (die wir ja als annähernd kugelförmig betrachten können) und um diese festanliegend ein Band herumgelegt. Dann verlängern wir dieses Band um einen Meter, knüpfen es an den Enden zusammen und legen es konzentrisch, das heißt wie einen Kreis, um die Apfelsine. Zwischen Kugeloberfläche und Kreisband wird dann ein gewisser Abstand vorhanden sein, der schätzungsweise etwa 16 Zentimeter beträgt, was der Leser leicht feststellen kann, denn das Experiment kann ja ohne weiteres ausgeführt werden. Nun wollen wir in Gedanken dasselbe Experiment auch mit der riesengroßen Erdkugel anstellen. Wir denken uns also zunächst wieder ein Band festanliegend um den Erdball gelegt; dieses Band hat eine Länge von 40 Millionen Meter. Dann verlängern wir auch dieses Band um einen einzigen Meter, was angesichts der ungeheuren Länge des Bandes natürlich nur eine ganz winzige Verlängerung bedeutet. Das so verlängerte Band denken wir uns dann wieder konzentrisch um die Erdkugel herumgelegt. Auch in diesem Falle wird das so verlängerte Band einen gewissen Abstand von der Oberfläche der Erdkugel haben, und wir stellen unseren Lesern nunmehr die Frage: Wie groß wird in diesem Falle der Abstand des Bandes von der Kugeloberfläche sein? Wird dieser Abstand so groß sein, daß man vielleicht den kleinen Finger zwischen Band und Kugel hindurchstecken kann? Ausgeschlossen! wird die Antwort lauten. Oder könnte dann vielleicht eine Mücke hindurchkriechen? Auch noch ausgeschlossen! wird man sagen, denn bei der ungeheuren Größe des Erdumfanges bzw. bei der Länge des Bandes von 40 Millionen Meter kann eine Verlängerung um einen einzigen Meter keinen überhaupt merkbaren Abstand zwischen Kugel und Band bewirken. Aber vielleicht könnte wenigstens ein Bazillus da hindurchkriechen, denn ein solches Lebewesen soll ja nur den millionsten oder milliardsten Teil eines Millimeters dick sein? Der könnte vielleicht zwischen Band und Kugel hindurchkriechen, vorausgesetzt, daß er sich sehr dünn macht und sich nicht beschwert, wenn er etwas gequetscht werden sollte! so wird man nach einiger Überlegung vielleicht antworten.

Denjenigen unserer Leser, die in dieser oder ähnlicher Weise die gestellte Frage beantworten, müssen wir aber erwidern, daß ihre Antworten total falsch sind. Denn der Abstand des Bandes von der Kugeloberfläche ist auch im Falle der Erdkugel groß genug, um nicht nur den kleinen Finger, sondern auch die ganze Faust, ja sogar eine ganze Katze in Lebensgröße hindurchzulassen, denn er ist genau so groß wie im Falle der Apfelsine und beträgt wie in diesem Falle etwa 16 Zentimeter. Diese Behauptung wird den meisten unserer Leser, die das Gedankenexperiment mitgemacht haben, als einfach lächerlich oder total unglaubwürdig erscheinen, zum mindesten wird es eine sehr große Überraschung bedeuten. Und nicht nur Laien, selbst Mathematiker, denen das Experiment unbekannt ist, werden durch das Ergebnis in vielen Fällen verblüfft sein. Denn unsere Anschauung scheint dem mitgeteilten Ergebnis völlig zu widersprechen und läuft immer wieder darauf hinaus, daß bei der ungeheuren Länge eines Bandes von 40 Millionen Meter die Verlängerung um die verhältnismäßig ganz winzige Größe von einem einzigen Meter unmöglich einen solchen großen Abstand bewirken kann. Bei der Apfelsine ist die Verlängerung von einem Meter mehrmals so groß wie das ursprüngliche Band selbst, bei der Erdkugel beträgt sie nur den 40millionsten Teil des ursprünglichen Bandes, da kann doch unmöglich in beiden Fällen derselbe Abstand herauskommen! Und dennoch ist es so. Die Anschauung trügt in diesem Falle, oder wir verbinden sie irrtümlicherweise mit unserem Gedankenexperiment. Denn der Abstand ist von der Größe der Kugel vollständig unabhängig und beträgt in allen Fällen dieselben ungefähren 16 Zentimeter, gleichviel ob wir das Experiment mit einer Apfelsine oder mit der Erdkugel oder selbst mit einer noch millionenmal größeren Kugel, etwa der Sonnenkugel, anstellen.

Dem Leser, der sich mit unserer Behauptung nicht abfinden kann, raten wir, zu seiner Überzeugung das Experiment praktisch an Kugelkörpern oder Kreisen von verschiedener Größe anzustellen, zuerst also an einer Apfelsine, dann etwa an einem Kürbis oder Globus, auch ein Faß oder eine kreisrunde Tischplatte, die ja immerhin schon einen zwanzig- oder dreißigmal größeren Durchmesser als eine Apfelsine haben, können dazu herhalten, und wer will, kann sich auf dem Erdboden einen beliebig großen Kreis aufzeichnen. In allen Fällen wird er nach Verlängerung des ersten Bandes um einen Meter feststellen können, daß der Abstand jedesmal der gleiche ist, und dann wird er jedenfalls schon eher geneigt sein, dieses Ergebnis auch für den Fall der Erdkugel gelten zu lassen. Denjenigen unserer Leser jedoch, die aus ihrer Schulzeit her noch über die Kenntnis der Kreisrechnung verfügen, können wir in leichterer Weise die Überzeugung von der Richtigkeit jener Behauptung vermittels des mathematischen Beweises verschaffen. Der Umfang eines Kreises oder einer Kugel ist bekanntlich abhängig von dem Radius ( r) und beträgt immer 2 × r × π (wo π die bekannte Zahl 3,1415 … usw. ist). Die Länge des festanliegenden Bandes ist also in allen Fällen 2 × r × π Meter. Verlängere ich dieses Band um 1 Meter und lege dieses dann konzentrisch um die Kugel, so erhalte ich einen neuen Kreis von 2 × r × π + 1 Meter Umfang. Der Radius dieses neuen Kreises aber beträgt dann Meter.

Der Unterschied zwischen dem Radius des ersten Kreises und dem des Kreises mit vergrößertem Umfang beträgt also in allen Fällen ¹/ _2π Meter, was ungefähr 16 Zentimeter ausmacht, und dieser Unterschied stellt immer den Abstand des verlängerten Bandes von der Kugeloberfläche dar. Wir sehen aber zugleich auch, daß die Größe ¹/ _2π konstant, das heißt in allen Fällen dieselbe und von dem Radius der Kugel vollständig unabhängig ist, denn dieser kommt in dem Ausdruck ¹/ _2π ja überhaupt nicht vor. Für den Mathematiker ist damit der Fall bewiesen, aber selbst die so gewonnene theoretische Überzeugung verhindert nicht, daß man sich kopfschüttelnd fragt, wieso die Anschauung diesem Ergebnis zunächst immer so entschieden Widerspruch leistet. Unser Gedankenexperiment mit der Kugel erweist sich dadurch, daß es in dem naiven Bewußtsein immer eine so völlige Diskrepanz zwischen der Anschauung und dem wirklichen Sachverhalt bewirkt, als eine der eigenartigsten Proben aus dem Kuriositätenkabinett der Mathematik.

Noch ein anderes Kugelexperiment wollen wir anstellen. Kork ist bekanntlich eine sehr leichte Substanz und ein Flaschenkork beispielsweise wiegt, wie man zu sagen pflegt, »so gut wie nichts«. Wie schwer wird dann wohl eine Korkkugel von vier Metern Höhe, also etwa Zimmerhöhe, sein? Als Antwort auf diese Frage wird das Gewicht einer solchen Korkkugel zumeist mit 20 bis 30 Pfund angegeben. Vorsichtige Leute allerdings äußern sich, daß eine solche Kugel doch nicht so leicht sein könne, wie es den Anschein habe, und raten auf einen oder einige Zentner Gewicht. In Wirklichkeit aber wiegt eine solche wie die angegebene Korkkugel rund 10 000 Kilogramm, also volle 200 Zentner, was dem Ladegewicht eines Güterwagens entspricht. Auch hier geraten Anschauung und Wirklichkeit zunächst in einen Widerstreit. Das Bewußtsein, daß Kork eine ganz leichte Substanz ist, verführt dazu, auch einer Korkkugel von der genannten Größe nur ein verhältnismäßig niedriges Gewicht zuzuschreiben. Es wird jedenfalls, wenn es eben nur geschätzt und nicht exakt berechnet wird, immer viel zu niedrig angegeben. Auch hier führt erst die Berechnung des Kubikinhaltes der Kugel, der rund 33 Kubikmeter beträgt, und die Berücksichtigung des spezifischen Gewichtes des Korks (0,3) zu dem richtigen Ergebnis, das dann auch immer eine Überraschung bedeutet.

Abb. 22

Ein höchst eigenartiges Experiment geometrischer Natur ist ferner auch das folgende: Wir nehmen einen Hohlkörper, etwa einen Zylinder, den wir uns aus Papier leicht herstellen können (mit oder ohne Deckflächen) und schneiden an irgendeiner Stelle dieses Zylinders mit der Schere hinein. Wenn wir den Schnitt jetzt so führen, daß er zu seinem Ausgangspunkte zurückkehrt, so wird der Zylinder natürlich in zwei Teile geteilt. Dasselbe ist der Fall, wenn wir das Experiment mit irgendeinem anderen Hohlkörper, etwa einer Kugel, einem Würfel oder sonstigem Gebilde, anstellen. Immer wird der Körper durch einen solchen vollständigen, das heißt zu seinem Ausgangspunkt zurückführenden Schnitt in zwei getrennte Teile geteilt; ebenso verhält es sich auch bei einem Blatt Papier, wenn wir auf diesem einen solchen Schnitt vollführen, und unserer Anschauung nach muß das bei jedem Körper der Fall sein, mit dem wir ein solches Experiment anstellen. Fragen wir nun, ob sich der Leser vielleicht einen Körper denken kann, der dieser Behauptung widerspricht, der also durch einen vollständigen Schnitt nicht in zwei voneinander getrennte Teile zerfallen würde, so wird die Antwort jedenfalls nein lauten, und das war lange Zeit auch die Ansicht der Mathematiker. Daher war es eine große Überraschung, als in der Mitte des vorigen Jahrhunderts der Mathematiker Möbius ein geometrisches Gebilde bekanntgab, bei dem jenes Experiment zu einem anderen Ausfall führt. In unserer Abbildung 22 ist ein Rechteck gezeichnet mit den Seiten AB und CD. Der Leser möge sich ein solches Rechteck aus Papier schneiden und die beiden Ränder so aufeinanderkleben, daß die Ecke A auf D und die Ecke B auf C fällt, was durch eine Verdrehung des Papierstreifens möglich ist. Es wird dann ein Gebilde von der Form der Abbildung 23 entstehen.

Abb. 23

Wird nun von irgendeiner Stelle des Streifeninnern aus ein Schnitt in der Längsrichtung des Streifens so geführt, daß er zu seinem Ausgangspunkt zurückkehrt (die gestrichelte Linie in der Figur zeigt die Richtung eines solchen Schnittes), so wird man die merkwürdige Entdeckung machen, daß der Streifen trotzdem nicht in zwei Teile zerfällt, sondern nach wie vor ein einziges zusammenhängendes Band darstellt. Auch der Ausfall dieses Experimentes scheint aller Anschauung zu widersprechen und wirkt dadurch höchst verblüffend. Als dieses Gebilde – es heißt nach seinem Entdecker das Möbiussche Blatt – und dessen merkwürdige Eigenschaften bekannt wurden, bedeutete das für die Mathematiker selbst eine Überraschung. Bis dahin hatte es gleichsam als ein Axiom gegolten, daß ein jeder Flächenkörper durch einen vollständigen Schnitt in zwei Teile zerfallen müsse, und das Bekanntwerden des Möbiusschen Blattes nötigte, den hierauf bezüglichen geometrischen Sätzen eine veränderte Fassung zu geben.

Wir erwähnten bereits, daß auch die Geometrie Scherzaufgaben kennt, die zu Trugschlüssen oder Paradoxien führen oder auch in anderer Hinsicht überraschende Resultate ergeben. Einige solcher Kleinprobleme heiterer Geometrie wollen wir nunmehr folgen lassen. Sie setzen (mit Ausnahme der Aufgabe 5) keine eigentlichen geometrischen Kenntnisse voraus, sondern verlangen nur etwas Scharfsinn und die Fähigkeit zur Veranschaulichung einfacher räumlicher Verhältnisse oder Vorgänge und überraschen dann durch die Eigenart ihrer Resultate.

Abb. 24

Abb. 25

Aufgabe 1. Vermittels der beiden Figuren 24 und 25 kann bewiesen werden, daß 8 × 8 = 65 ist. Die Figur 24 stellt ein Quadrat von 8 Zentimeter Seitenlänge dar (es ist hier in verkleinertem Maßstabe wiedergegeben), sein Flächeninhalt ist also 8 × 8 = 64 Quadratzentimeter. Wir zerschneiden nun das Quadrat in der in der Figur durch die starken Striche angedeuteten Weise in vier Einzelteile, also in die beiden Trapeze A und B sowie die beiden Dreiecke C und D. Diese Einzelteile lassen sich zu der Figur 4 zusammenlegen; die Art der Zusammenlegung ist auch hier aus den starken Strichen ersichtlich. Diese Figur aber stellt ein Rechteck mit einer Seite von 13 und einer von 5 Zentimeter Länge dar; der Inhalt dieser Figur ist also 5 × 13 = 65 Quadratzentimeter. Es stellt sich also das überraschende Ergebnis heraus, daß lediglich durch Zerschneiden der Figur der Quadratinhalt derselben vermehrt worden ist oder daß 8 × 8, das nach Figur 24 = 64 ist, nach der anders zusammengelegten Figur = 65 ist. Wie ist das möglich?

Aufgabe 2. In einem Bücherregal stehen nebeneinander Band I und Band II eines wissenschaftlichen Werkes. Es sind zwei stattliche Folianten, jeder über 1000 Seiten stark und jeder gerade 10 Zentimeter dick. Die Stärke des Umschlagdeckels werde dabei mit je 2 Millimeter angenommen. Ein Bücherwurm, d. h. ein richtiger aus dem Insektenreich, hat sich von der ersten Seite des ersten Bandes bis zur letzten Seite des zweiten Bandes in gerader Linie durchgebohrt. Wie groß ist die Strecke, die er durchbohrt hat?

Aufgabe 3. Wir betrachten an einem Wagenrad den tiefsten Punkt des Rades; das ist der Punkt, mit dem das Rad den Erdboden berührt. Was für eine Linie beschreibt dieser Punkt, wenn sich der Wagen in Bewegung setzt?

Abb. 26

Aufgabe 4. Es kann bewiesen werden, daß alle Kreise gleichen Umfang haben, wie groß auch ihr Durchmesser sei. Zu diesem Zwecke betrachten wir die Figur 26, die eine kreisrunde Scheibe A darstellt, auf der eine kleinere Scheibe B sitzt. Der Mittelpunkt beider Scheiben ist der gemeinsame Punkt M, beide Scheiben sind fest miteinander verbunden. Wir lassen nunmehr die Scheibe A einmal auf der Linie AA abrollen; die Strecke AA ist dann natürlich gleich dem Umfang des Kreises A. Gleichzeitig mit der Scheibe A dreht sich dann auch die Scheibe B, und hat A, auf der rechten Seite angelangt, hier eine volle Umdrehung vollzogen, so hat das auch die Scheibe B getan. Die Linie BB ist dann die Roll-Linie der Scheibe B, die also dem Umfang von B entsprechen muß. Die Strecke BB aber ist, wie aus der Figur ohne weiteres ersichtlich ist, genau so lang wie die Strecke AA, und damit ergibt sich, daß die beiden Kreisscheiben A und B trotz ihres verschiedenen Durchmessers den gleichen Umfang haben. Stimmt es oder stimmt es nicht?

Abb. 27

Aufgabe 5. Der wichtigste Fundamentalsatz der ebenen Geometrie, der jedem Schüler schon in den ersten Wochen der Beschäftigung mit dieser schönen Wissenschaft haarscharf bewiesen und nachdrücklichst eingeprägt wird, lautet, daß die Summe der Winkel in jedem Dreieck gleich zwei rechten Winkeln ist. Auf diesem Satz baut sich ein großer Teil der gesamten ebenen Geometrie überhaupt auf, und seine Erschütterung wäre geradezu eine Katastrophe für die Mathematik und noch mehr für die Mathematiker. Trotzdem sind wir in der Lage, ein Dreieck anzugeben, bei dem die Summe der Winkel größer als zwei Rechte ist. Zu diesem Zweck betrachten wir die Figur 27, zu deren Verständnis lediglich die elementarsten Kenntnisse aus der Geometrie erforderlich sind. Sie stellt zwei Kreise dar, die sich zum Teil überschneiden. Von dem einen der beiden Schnittpunkte, A, aus legen wir die Durchmesser AD und AE durch die Mittelpunkte der beiden Kreise; dann verbinden wir die Punkte D und E durch eine Gerade, die die beiden Kreise in den Punkten B und C schneidet. B und C verbinden wir dann noch mit A, wodurch das Dreieck ABC entsteht. Dann ist nach dem Satz des Thales der Winkel bei B ein rechter Winkel, weil er Peripheriewinkel im Halbkreise ABE ist, und ebenso ist auch der Winkel bei C ein rechter als Peripheriewinkel im Kreise ACD. Dann hat also das Dreieck ABC bei B und C je einen rechten Winkel und überdies noch bei A einen kleinen spitzen Winkel. Die Summe seiner Winkel ist mithin um den kleinen Winkel A größer als zwei rechte. Quod erat demonstrandum! Diese Aufgabe ist ein besonderer Leckerbissen für Freunde der Geometrie. Wer unternimmt es, die drohende katastrophale Erschütterung der Geometrie, die aus dem merkwürdigen Dreieck ABC spricht, abzuwenden?

Abb. 28

Abb. 29

Aufgabe 6. Wo haben die gebogenen Querlinien der Figur 28 und ebenso die der Figur 29 ihren größten Abstand? In der Mitte oder an den Seiten?

Abb. 30

Aufgabe 7. Die Figur 30 soll in einem Linienzug gezeichnet werden, selbstverständlich ohne unerlaubte Hilfsmittel wie doppelten Bleistift o. ä. und ohne ein Linienstück doppelt zu ziehen.

Abb. 31

Aufgabe 8. Die Figur 31, die etwa eine Schnalle darstellen könnte, soll in drei Zügen gezeichnet werden, selbstverständlich ebenfalls ohne eine Linie doppelt zu ziehen. Wer die Aufgabe 7 gelöst und die Figur 30 nach Vorschrift herausbekommen hat, wird vielleicht der Meinung sein, daß die soviel einfachere Figur 31, für die überdies drei Züge zulässig sind, doch keinerlei besondere Schwierigkeiten verursachen kann. Er wird sein blaues Wunder erleben, wenn er sich an die Lösung dieser Aufgabe macht. Auf die korrekte Lösung dieser Aufgabe war vor Jahren einmal ein hoher Preis ausgesetzt.

Mit diesen acht Aufgaben wollen wir es genug sein lassen des interessanten Spiels mit den Gesetzen der Geometrie. Sie dürften den Lesern ausreichende Beschäftigung und zugleich die Möglichkeit scharfsinniger und teilweise nicht ganz leichter Untersuchungen über räumliche Beziehungen und Vorgänge darbieten. Wir lassen die Lösungen der Aufgaben folgen, doch raten wir auch in diesem Falle, die Lösungen keinesfalls vorwegzunehmen, sondern sie erst nach erfolgten eigenen Lösungsversuchen mit den gefundenen Ergebnissen zu vergleichen.

7. Lösungen und Löser der »Heiteren Geometrie«

Nochmals: Apfelsine und Erdkugel – Anschauung und Denken – Fröhliche Wetten – Eine lustige Stammtischgeschichte – Die Korkkugel und der Athlet – Die Lösungen der Aufgaben – Der ordnungsgemäße Bücherwurm – Das Geheimnis der Schnalle – Eine überraschende Lösung

Auch die in dem vorangegangenen Aufsatz angeführten Fälle und Aufgaben aus dem Gebiet der Heiteren Geometrie sind von dem Verfasser mehrfach in Unterhaltungszeitschriften veröffentlicht worden. Die zahlreichen darauf erfolgten Zuschriften aus dem Leserkreis dieser Blätter sind ein hübscher Beitrag zu dieser heiteren Wissenschaft, weshalb einige dieser Zuschriften auch an dieser Stelle ehrenvolle Erwähnung finden sollen.

Zunächst war es jenes als Paradigma heiterer Geometrie angeführte Gedankenexperiment mit Apfelsine und Erdkugel, das den Forschungstrieb und – den Widerspruch vieler Leser weckte. Ein um die riesengroße Erdkugel gelegtes Band soll nach der Verlängerung um einen einzigen Meter denselben Abstand von der Kugeloberfläche ergeben wie das entsprechende Experiment mit einer Apfelsine. Diese Behauptung stieß, trotz der erläuternden Bemerkungen, in meinem Aufsatz, bei sehr vielen Lesern auf entschiedenen Unglauben. Die Anschauung der Leser konnte sich mit einem solchen merkwürdigen Verhalten der Kugel nicht einverstanden erklären und geriet zunächst mit den Behauptungen der Mathematik in einen unheilbaren Widerspruch. Unmöglich kann sich ein Band von einer Länge von 40 Millionen Metern ebenso verhalten wie ein Band von wenigen Zentimeter Länge, das war der Gedankengang, den jener Aufsatz bei allen diesen Lesern ausgelöst hatte und der sie veranlaßte, der Wahrheit durch das eigene Experiment auf den Grund zu gehen. Die Sache läßt sich ja ohne große Schwierigkeiten ausprobieren. Man braucht ja nicht gleich die Erdkugel selbst zu dem Experiment verwenden, sondern kann sich mit irgendwelchen größeren kreisrunden Gegenständen begnügen. Also ist damals, wie aus den Zuschriften meiner Leser hervorging, von ihnen viel praktische Kreisgeometrie getrieben worden, an Apfelsinen, an runden Tischen, an Schwung- und Wagenrädern, an Wasser- und sonstigen Türmen, und ein findiger Heidelberger hat sogar, wie er mitteilte, seine geometrischen Untersuchungen an dem weltberühmten großen Faß seiner Vaterstadt vorgenommen. Und zum Erstaunen aller Experimentatoren stimmte die bewußte Behauptung immer. Immer ergab sich der Abstand von 16 Zentimetern, wie klein oder wie groß auch das zu der Untersuchung verwandte Kreisgebilde war. Da mußte man ja schließlich jener Behauptung wohl Glauben schenken.

Aber freilich, ganz einleuchtend ist so manchem die Sachlage auch durch den Ausfall seines Experimentes nicht geworden, restlos war der Widerspruch zwischen Anschauung und mathematischem Ergebnis auch hierdurch nicht zu beseitigen. Daher wollen wir noch ein Vergleichsbeispiel anführen, das geeignet sein dürfte, die letzten leisen Zweifel zu beseitigen. Wir legen um ein Brett von – sagen wir – 10 Meter Länge ein Band in der Längsrichtung fest anliegend einmal herum. Dieses Band wird dann, wenn wir von der Dicke des Brettes absehen, eine Länge von 20 Metern haben. Verlängern wir dieses Band um einen Meter und legen es dann, zu einer Schleife verknüpft, wieder in der Längsrichtung des Brettes gleichmäßig um dieses herum, so wird das Band an jedem Ende des Brettes um % Meter überragen. Ohne weiteres einleuchtend ist es nun, daß es ganz gleichgültig ist, ob ich zu diesem Experiment ein Brett von 10 oder 1000 oder 1 000 000 Meter Länge verwende. Der Überschuß muß in allen Fällen dasselbe ¼ Meter betragen, und damit haben wir endlich auch anschaulich den Beweis, das bei solchen Bandexperimenten der Überschuß des um 1 Meter verlängerten Bandes von der Größe des verwandten Versuchskörpers vollständig unabhängig ist. Und wenn man sich in ähnlicher Weise die Sache auch noch an einer Kiste veranschaulicht – die entsprechenden Maßgrößen lassen sich leicht berechnen –, so wird endlich auch dem hartnäckigsten Zweifler in anschaulichster Weise klar werden, daß sich in unserem Gedankenexperiment die Erdkugel genau so, wie angegeben, verhalten muß und sich gar nicht anders verhalten kann.

Eine Reihe von Lesern, die sich auf solche Weise schließlich von der Richtigkeit des Gesagten überzeugt hatte, hat dann die so gewonnene Erkenntnis schnöderweise benutzt, um höchst erfolgreiche Wetten abzuschließen, natürlich mit Leuten, denen die Sache noch nicht bekannt war und die jene Behauptung absolut nicht glauben wollten. Wenn dann die angestellten Meßexperimente die Richtigkeit jener Behauptung ergaben, gab es immer einen fröhlichen Gewinner und einen sehr überraschten Verlierer. So schrieb mir Dr. Z. in Dresden, daß er auf solche Weise von einem ungläubigen Patienten einen vollen Korb Sekt gewonnen habe, und Fräulein v. R. schrieb freudestrahlend, daß sie auf ähnliche Weise dem Herrn Papa, der absolut nicht an die Richtigkeit jener geometrischen Behauptung glauben wollte und erst durch umständliche Meßversuche an dem kreisrunden Gartenbeet zu ihrer Anerkennung veranlaßt werden konnte, endlich das bis dahin immer vergeblich gewünschte funkelnagelneue Fahrrad abgewonnen habe und seitdem eine begeisterte Anhängerin der Geometrie geworden sei. Herr Hotelbesitzer M. im Oldenburgischen aber gewann auf diese Weise von einem befreundeten Gutsbesitzer drei Sack Kartoffeln; aber der Verlierer rächte sich und schickte dem Gewinner die größten Kartoffeln, die auf drei Meilen im Umkreise aufzutreiben waren, mit entsprechenden begleitenden Zeilen ins Haus! Wer wollte da noch an dem Humor der Mathematik zweifeln?

Zu katastrophalen Folgen aber hätte unser Gedankenexperiment beinahe in der guten Stadt P. geführt. Dort hatte ein Stammtischgenosse die Geschichte von der Erdkugel und der Apfelsine gelesen und den übrigen Mitgliedern der Runde zum Besten gegeben. Entschiedener Widerspruch gegen die Richtigkeit des Gehörten wurde ringsum laut. Also mußte die Probe auf das Exempel gemacht werden. Eine Apfelsine brachte der Stammtischwirt bald zur Stelle, und mit einem Bindfaden ward die Messung vorgenommen. Dann wurde das Experiment an dem kreisrunden Stammtisch ausgeführt und schien die Richtigkeit des Versuchs zu ergeben. Aber einige Genossen der Runde waren auch jetzt noch nicht ganz bekehrt. Dazu müßte, so meinten sie, der Versuch noch an einem weiteren und viel größeren runden Körper vorgenommen werden. Aber woher einen solchen nehmen? Da erinnerte man sich des kreisrunden Brunnenbeckens auf dem Marktplatz, das wohl an zehn Meter im Durchmesser haben mochte, und alsbald machte sich die ganze Stammtischrunde auf den Weg, um sich trotz der vorgerückten Stunde am Brunnen Wahrheit und Gewißheit zu holen. Mit dem großen Bindfadenknäuel und mit Hallo und Gelächter machte man sich an die Ausmessung des Brunnenbeckens. Dieses ungewohnte nächtliche Tun aber erweckte den Argwohn des beamteten Wächters der Nacht, der in einer Haustürnische gerade den gewohnten Mitternachtsschlaf zu halten gedachte, nunmehr aber voller Mut und Amtseifer sich wie ein Indianer an die mit dem langen Bindfaden experimentierende Gesellschaft heranschlich. In strengem Ton heischte er Aufklärung über das nächtliche Tun, worauf man ihm einen längeren Vortrag über die geometrischen Beziehungen zwischen einer Apfelsine und dem Erdball hielt. Sei es aber, daß das Auge des Gesetzes die Geschichte mit der Apfelsine für eine Verulkung der hohen Obrigkeit hielt, sei es, daß er die Apfelsine, die einer der Herren noch immer krampfhaft in der Hand hielt, für eine Bombe mit anarchistischem Daseinszweck ansah, kurz und gut, er erklärte, die Hand griffbereit an der polizeilichen Waffe, die gesamte fidele Stammtischrunde für verhaftet und ersuchte stramm und streng, ihm auf die Wache zu folgen. Mit Wonne kamen die Stammtischler der freundlichen Aufforderung nach in dem erhebenden Gefühle, daß sich hier ein Spaß von ungeahnten Dimensionen vorbereite. Nun, und auf der Polizeiwache löste sich die Sache denn auch bald in Wohlgefallen auf. Die Apfelsine wurde seziert und erwies sich als harmlose Südfrucht und keine Bombe; der Aufsatz über das Experiment mit Erde und Apfelsine wurde vorgelesen und damit bewiesen, daß das angestellte Experiment tatsächlich nur der Erforschung der Wahrheit dienen sollte und keinerlei staatsgefährlichen Charakter hatte. Also trennte man sich schließlich mit Lachen und Händeschütteln von dem Orte des Gesetzes und hielt dann im Stammlokal noch einen längeren Nachtschoppen. Zwei Tage daraus aber stand im Lokalblatt ein Artikel mit geheimnisvollen Andeutungen über ein beabsichtigtes Attentat auf den Marktbrunnen mit Bomben in Apfelsinenformat; die Attentäter seien bekannt und die Polizei entfalte die bekannte fieberhafte Tätigkeit. Der Stammtisch aber hatte wochenlang Stoff zum Lachen und hat mir die Geschichte zum Dank dafür getreulich berichtet.

Dann hat auch die in dem vorangegangenen Aufsatz ebenfalls zu einem Gedankenexperiment verwandte Korkkugel von 4 Meter Durchmesser damals den Lesern Stoff zu heiteren Untersuchungen über die Geometrie gegeben. Eine ganze Anzahl von Lesern schrieb, daß nicht nur sie selbst über das Gewicht von 10 000 Kilogramm einer solchen Kugel im höchsten Maße verblüfft waren, sondern auch viele ihrer Bekannten in den gleichen Zustand der Verblüffung versetzt hätten. Zumeist wurde immer auf ein Gewicht von »etwa einem halben Zentner« oder höchstens einem Zentner geraten, und auch hier hat der wirkliche Tatbestand mehrfach zu lustigen Wetten Anlaß gegeben. So teilte mir ein Leser aus München mit, daß er einem Freunde, einem bekannten Amateurathleten, eine Wette angeboten habe, daß dieser eine Korkkugel von der bezeichneten Größe nicht zu heben vermöge. Der starke Mann habe die Wette hohnlachend angenommen und sich anheischig gemacht, besagte Korkkugel mindestens ein dutzendmal zu stemmen. Als er dann das Nettogewicht einer solchen Kugel erfahren habe, sei er allerdings zunächst stumm vor Staunen gewesen, aber geistesgegenwärtig habe er sich auf den Standpunkt gestellt, daß die Wette nur in der Weise wirklich ausgetragen werden könne, daß zunächst einmal eine Korkkugel jener Dimension beschafft würde. Darauf hätten sich die Herren an eine Korkwarenfabrik gewandt, die auch durchaus bereit gewesen sei, eine solche Kugel herzustellen, aber zunächst einmal eine Anzahlung von fünfundzwanzigtausend Mark gewünscht habe, und weil der Wettgegner dieses Kapital nicht investieren wollte, so habe er trotz der Richtigkeit seiner Behauptung die Wette verloren und für den ganzen Athletenverein den Silvesterpunsch bezahlen müssen.

Lassen wir nunmehr die Lösungen der im vorangegangenen Aufsatz angeführten Aufgaben folgen.

Abb. 32

Aufgabe 1. Die Verwandlung einer Fläche von 64 Quadratzentimeter Inhalt durch bloßes Zerschneiden in eine solche von 65 Quadratzentimeter ist natürlich nur scheinbar und beruht auf einer allerdings raffinierten Ungenauigkeit. Die vier Teile, in die die Figur 24 zerschnitten worden ist, lassen sich nämlich nicht ganz so exakt, wie es die Figur 25 zeigt, aneinanderlegen. Die schräge Linie von A ist nicht die genaue geradlinige Verlängerung der schrägen Linie von C, sondern die beiden Linien bilden zusammen einen stumpfen Winkel, dessen beide Schenkel eine zwar nahezu, aber doch nicht genau gerade Linie bilden, und dasselbe gilt auch von B und D. Die nebenstehende Figur 32, die die Teile in exakt aneinandergelegter Form zeigt, läßt das gut erkennen; an den Stellen der beiden Kreisbogen liegen die stumpfen Winkel. Die beiden Schräglinien von A und C bzw. B und D bilden daher nicht die genaue Diagonale des Rechteckes, sondern diese vier Linien schließen einen leeren Raum in Form eines langgestreckten Parallelogramms ein, dessen Inhalt gerade das eine Quadratzentimeter darstellt, um das die Figur 25 größer ist als die Figur 24, aus der sie entstanden war. Die Ungenauigkeit ist allerdings nur eine ganz geringe, und wer das interessante Experiment anstellt, ist zunächst geneigt, die Ungenauigkeit auf eine solche des Scherenschnittes zurückzuführen. Erst wenn die Figur ganz genau gezeichnet wird und die vier Teile ebenso genau geschnitten und aneinandergelegt werden, tritt die Ursache der absonderlichen Inhaltsvermehrung in Erscheinung.

Aufgabe 2. Viele Leser werden die Länge der Bohrstrecke mit 20 Zentimeter angegeben haben; wer vorsichtiger war, hat noch 4 Millimeter für zwei Buchdeckel in Abzug gebracht und ist auf 19,6 Zentimeter gekommen. Beide Angaben sind aber falsch; der Bücherwurm hat vielmehr nur die geringe Strecke von 4 Millimeter durchbohrt, um zu seinem Ziele zu kommen. Denn bei zwei ordnungsmäßig nebeneinanderstehenden Büchern liegt die erste Seite des Bandes neben der letzten Seite des zweiten Bandes, und beide Seiten sind nur durch die beiden Umschlagdeckel voneinander getrennt, wie jedermann an irgend zwei nebeneinanderstehenden Bänden feststellen kann. Der Bücherwurm hatte daher nur die beiden trennenden Buchdeckel zu durchbohren, die zusammen 4 Millimeter stark sind.

Auch die Lösung dieser Aufgabe hat einer Anzahl kritischer Leser zu denken gegeben. Ihre Richtigkeit wurde beanstandet mit der Begründung, daß die Bohrstrecke nur unter der Voraussetzung 4 Millimeter betrage, daß die Bücher in der Reihenfolge von links nach rechts aufgestellt werden; werden die Bücher dagegen von rechts nach links aufgestellt, so habe sich der Bohrwurm durch die ganze Dicke der beiden Bücher durchzufressen, und es sei nicht einleuchtend, daß eine solche Aufstellung der Bücher nicht auch »ordnungsgemäß« sei. Darauf ist zu bemerken, daß wir, wie wir von links nach rechts schreiben, so auch die Zahlen von links nach rechts folgen lassen und daher auch bei der Einrichtung unserer Bibliotheken die numerierten Bände in dieser Reihenfolge anordnen müssen. Nur eine Bücherordnung nach diesem Prinzip kann daher Anspruch auf das Prädikat »ordnungsgemäß« erheben. Ein Leser schrieb, daß er sich tatsächlich entschlossen habe, seine umfangreiche Bibliothek umzuordnen, weniger um den Bücherwürmern zu imponieren, sondern weil nach seiner Meinung eine Bibliothek nur dann »ordnungsgemäß« eingerichtet sei, wenn die letzte Seite jedes Bandes sich neben der ersten des folgenden Bandes befinde. Nun, man soll die Konsequenz nicht übertreiben und auch dem Bücherwurm weiterhin sein verblüffendes Kunststück gönnen.

Abb. 33

Aufgabe 3. Die Lösung dieser Aufgabe erfordert ein gewisses Vermögen der Veranschaulichung, wenn sie richtig ausfallen soll. Oft wird eine Art zurücklaufender Schleifenlinie oder auch eine Schlangenlinie als der Weg bezeichnet, den der fragliche Punkt zurücklegt. Das ist jedoch nicht richtig. Stellt in der nebenstehenden Figur 33 der Kreis den Umfang eines Wagenrades dar, und ist P der Punkt, dessen Weg festgestellt werden soll, so beschreibt dieser beim Fahren eine Reihe von Bogenlinien in der Form und Aufeinanderfolge, wie es die Figur veranschaulicht. Diese Bogenlinie, die also an keiner einzigen Stelle zurückläuft, heißt Radlinie oder Zykloide und spielt in der höheren Geometrie eine sehr wichtige Rolle. Auch diesen Vorgang kann man experimentell ausführen, indem man eine kreisrunde Pappscheibe vor einer Wand auf einer Kante rollen läßt und dabei an der Wand den Weg, den ein bestimmter Punkt am Umfang der Scheibe zurücklegt, markiert.

Aufgabe 4. Diese Aufgabe ist etwas kniffliger Natur und erfordert zu ihrer Lösung eine genaue Betrachtung des Falles, die dann den Widerspruch der aufgestellten Behauptung klarlegt. Wenn die Scheibe A sich einmal vollständig abrollt, dann ist die Strecke AA so lang wie der Umfang der Scheibe A. Gleichzeitig mit A rollt auch die Scheibe B auf der Strecke BB ab. Die Länge dieser Strecke ist aber nicht gleich dem Umfang der Scheibe B, denn diese führt bei ihrer Bewegung von links nach rechts auf der Strecke BB nicht nur eine Roll-, sondern gleichzeitig auch eine Gleit- oder Schleifbewegung aus. Soviel als die Strecke BB größer ist als der Umfang der Scheibe BB, kommt hierbei auf Rechnung der Gleitbewegung. Deutlich wird das, wenn wir uns die Bewegung des Mittelpunktes M der Scheiben veranschaulichen. Dieser hat natürlich überhaupt keinen Umfang und legt dennoch bei vollständiger einmaliger Abrollung der Scheibe A eine Strecke zurück, die ebenfalls so groß ist wie AA oder BB. Der Punkt M führt also überhaupt keine Roll-, sondern nur eine Gleitbewegung aus. Die Scheibe A macht nur eine Rollbewegung; alle Scheiben bzw. alle Kreise, die kleiner als A sind, vollführen gleichzeitig eine Roll- und eine Gleitbewegung, so daß also die zurückgelegte Strecke nur in dem Falle der Scheibe A so lang wie der Umfang der Scheibe ist.

Aufgabe 5. Diese Aufgabe ist geeignet, selbst Mathematiker stutzig zu machen, denn die Anwendung der erwähnten Lehrsätze ist durchaus korrekt. Durch bloßes Nachdenken über die Anwendung jener Lehrsätze wird man, wenn man diese Dinge nicht sehr perfekt beherrscht, den Fehler kaum finden, sondern erst, wenn man dazu übergeht, die ganze Konstruktion der Figur nochmals genau mit Zirkel und Lineal zu wiederholen. Dann stellt sich heraus, daß die Figur eine Ungenauigkeit enthält. Die Strecken AE und AD gehen nämlich in Wahrheit nicht durch die Mittelpunkte der beiden Kreise, sondern sind etwas verschoben. Bei korrekter Ausführung der Konstruktion geht die Verbindungslinie DE durch den unteren Schnittpunkt der beiden Kreise, so daß dann überhaupt kein Dreieck mehr entsteht, also auch keins mit einer Winkelsumme von mehr als zwei rechten Winkeln. Die vorgenommene kleine Schiebung wird zumeist nicht sofort bemerkt, besonders dann nicht, wenn man die Aufgabe vorführt und dabei die Kreise mit freier Hand zeichnet, die Konstruktion also nur andeutet, wobei man die kleine Ungenauigkeit sehr geschickt verhüllen kann.

Aufgabe 6. Die Querlinien in den Figuren 28 und 29 sind überhaupt nicht gebogen, sondern sind gerade und parallel und haben überall gleichen Abstand. Sie stellen einen sehr interessanten Fall optischer Täuschung dar; ihre Biegung wird durch die eingezeichneten Strahlenbündel vorgespiegelt.

Aufgabe 7. Die Aufgabe wird gelöst, indem man beispielsweise an dem obersten Punkte der Figur beginnt, nach links geht und jedesmal, bevor man ein Dreieck schließt, zum nächstfolgenden übergeht. Man kommt dann zu einem Punkte, von dem aus man die Schließung der einzelnen Dreiecke vornehmen kann. Nach einiger Übung wird die Lösung gelingen. Die Aufgabe ist nicht schwer und dient eigentlich nur zur Vorbereitung auf die

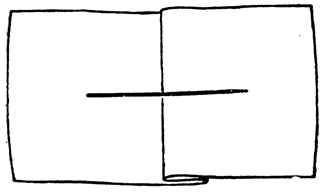
Abb. 34

Aufgabe 8. Diese Aufgabe dürfte von allen diejenige gewesen sein, die unseren Lesern und Lösern am meisten zu schaffen gemacht hat, denn sie ist ihrer ganzen Natur nach dazu angetan, einen Menschen stundenlang zu beschäftigen. Pfundweise Papier kann man mit dem Versuche, die Aufgabe zu lösen, vollzeichnen, und die merkwürdigsten Konstruktionen und Hilfsmittel, wie doppelte Bleistifte, Bleistifte mit doppelter Spitze usw., werden ersonnen, um auf des Pudels Kern zu kommen, der sich aber dennoch dem Scharfsinn selbst der ausdauerndsten Löser entzieht. Nach mehr oder weniger langem vergeblichen Bemühen kommt man dann meist zu der Überzeugung, daß die Lösung der Aufgabe unmöglich sei. Dem kann jedoch nicht ganz zugestimmt werden. Die Lösung der Aufgabe ist möglich, allerdings nur durch einen kleinen »Kniff«, und Zwar durch einen Kniff in des Wortes buchstäblichstem Sinne. Man knifft nämlich das Blatt, auf dem die Zeichnung ausgeführt werden soll, doppelt, wie es die nebenstehende Abbildung 34 veranschaulicht, und zieht dann über die Knifflinie einen geraden Strich. Faltet man das Blatt dann auseinander, so teilt sich der ursprüngliche, in einem Zug hergestellte Strich in zwei einzelne, in gleicher Richtung liegende Striche. Mit zwei weiteren Zügen ist dann die vollständige Zeichnung herzustellen, wie es die Abbildung 35 veranschaulicht, bei der die Verbindungslinien absichtlich ungeschlossen geblieben sind, um den Weg der Züge zu zeigen. Die Aufgabe ist ein ganz vorzügliches Unterhaltungsspiel und geeignet, ganze Gesellschaften stundenlang zu beschäftigen. Meist ertönt schon sehr bald nach Inangriffnahme der Freudenruf: »Ich hab's!«, darauf aber immer sehr bald und kleinlaut der Enttäuschungslaut: »Ach nein!«, weil sich herausgestellt hat, daß doch noch ein kleines Stück an der verlangten Zeichnung fehlt. Und so pflegt das stundenlang zu gehen, jedesmal fehlt immer gerade noch ein kleines Stück. Auf andere als die hier angegebene Weise ist die Aufgabe nicht zu lösen. Ob freilich die Lösung mit dem »Kniff« eine ganz korrekte ist, sei der Beurteilung des Lesers anheimgestellt. Maßgebende Instanzen bestreiten es leider, und deswegen konnte auch der oben erwähnte Preis, der auf die korrekte Lösung der Aufgabe einstmals ausgesetzt war, nicht gewonnen werden.

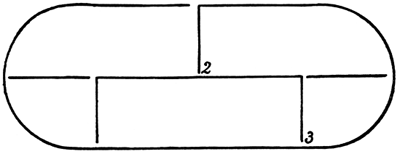
Abb. 35

Die Schnallenaufgabe dürfte jedenfalls unseren Lesern viel Stoff zu geometrischen Versuchen geliefert haben und hat auch nach einer früheren Veröffentlichung unter allen geometrischen Kuriositäten den Vogel abgeschossen, nach Zahl und Inhalt der damals eingegangenen Zuschriften zu schließen. Der Versuch, die Aufgabe zu lösen, hat zu tiefgründigen geometrischen Forschungen angeregt. Mit doppeltem und ausgezacktem Bleistift, mit Pauspapier und Zaubertinte ist man dem Ding zu Leibe gegangen, und eine Reihe von Lesern hat die angegebene Lösung auch selbständig gefunden. Viele andere freilich, denen die Lösung nicht geglückt war, haben dann, als die Lösung bekanntgegeben worden war, aus ihrem Herzen keine Mördergrube gemacht und mir mehr nachdrücklich als liebenswürdig bestätigt, daß ich allen Anlaß habe, hinsichtlich dieser Aufgabe und ihrer Lösung ein schlechtes Gewissen zu haben. Ein Leser hat sogar klar und deutlich »Schieber« geschrieben, dann aber versöhnend hinzugesetzt, daß ihm die Sache riesigen Spaß gemacht habe. Denn er habe die Aufgabe der bei ihm am Silvesterabend versammelten Freundesrunde beiderlei Geschlechts aufgegeben. Mit Feuereifer habe man sich an die Lösung gemacht, stundenlang daran gearbeitet und beinahe darüber vergessen, zur Mitternachtsstunde auf das neue Jahr anzustoßen. Noch weit ins neue Jahr hinein habe man an der Figur »herumgeknobelt« und eine Unmasse Papier und Bleistift verbraucht; erst in früher Morgenstunde des neuen Jahres habe man erschöpft den Kampf um die Lösung aufgegeben und sich unter feierlichen Verwünschungen des Urhebers der heiteren Geometrie getrennt. Ich habe das deutlich gemerkt, denn gerade um jene Zeit hat mein rechtes Ohr wie eine Weckeruhr geklingelt.

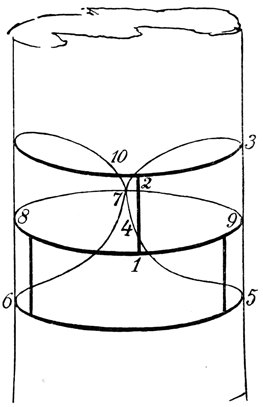
Abb. 36

Eine sehr hübsche und überraschende Lösung der Aufgabe aber hat ein Leser gefunden, der die Schnalle mit Kreide auf ein – Ofenrohr gezeichnet hatte, und zwar derart, daß die beiden seitlichen Enden der Schnallenfigur sich berühren, was auf der gekrümmten Fläche des Ofenrohres möglich ist. Es entsteht dann die nebenstehende Figur (Abbildung 36), die unsere Schnalle in perspektivischer Zeichnung auf dem Ofenrohr darstellt. Auf diese Art ist es möglich, die ganze Figur mit Ausnahme der beiden unteren vertikalen Striche in einem Zuge zu zeichnen, etwa indem man den Linienzug in der durch die Zahlen in der Figur angedeuteten Weise beginnt und weiterführt. Die beiden unteren Vertikalstriche erfordern dann noch zwei Züge, und damit ist die ganze Figur in drei Zügen hergestellt. Freilich, ganz korrekt ist auch diese Lösung nicht, aber sie ist eine neue und originelle Note unter den zahllosen Lösungsversuchen, die mir im Laufe der Jahre unterlaufen sind, und macht den Scharfsinn ihres Erfinders alle Ehre.

V.
Das Problem der Dimensionen

1. Gibt es eine vierte Dimension?

Die Bedeutung des Problems – Der Begriff der Dimension – Augenschein und Denken – Kant, Fechner, Helmholtz – über zweidimensionale Wesen – Entstehen und Verschwinden

Das Problem, das sich an den Begriff der vierten Dimension knüpft, ist eins der eigenartigsten und meistumstrittenen im Bereich des modernen Denkens überhaupt. Freilich herrschen nur über wenig Begriffe so verschiedenartige und verworrene Vorstellungen wie über den der vierten Dimension. Die große Menge selbst der Gebildeten kennt diesen Begriff zumeist nur aus den Theorien und Schriften der Spiritisten, die sich jenen Begriff zunutze gemacht haben, um damit das Vorhandensein einer Geisterwelt und die sogenannten okkulten Erscheinungen, die bei spiritistischen Sitzungen auftreten sollen, plausibel zu machen. Dadurch ist der Begriff der vierten Dimension nun allerdings überaus bekannt und populär, gleichsam zu einem Schlagwort für die Welt der Geister und Gespenster, geworden, hat dadurch jedoch auch in den Augen vieler, die von jenem Begriff eben nichts weiter als die erwähnte okkulte Bedeutung kennen, einen gewissen komischen Beigeschmack erhalten. Aber ganz abgesehen von solchen mehr oder weniger vagen Spekulationen, mit denen wir uns auch noch auseinandersetzen werden, ist der Begriff der vierten Dimension Gegenstand eines hochernsten und schwierigen wissenschaftlichen Problems, das den Philosophen und Erkenntnistheoretiker ebensosehr beschäftigt wie den Mathematiker und Physiker und das fortgesetzt im Mittelpunkte wissenschaftlicher Kontroversen steht, ein Problem, das gerade in der Geistesforschung der letzten Jahrzehnte eine überaus große Rolle gespielt hat und noch spielt. Ist doch, um nur ein Beispiel anzuführen, der Begriff der vierten Dimension ein wesentlicher Faktor der Relativitätstheorie, dieser neuesten Richtung der exakten wissenschaftlichen Betrachtung des Naturgeschehens; für diese hat die vierte Dimension eine höchst konkrete physikalische Bedeutung, die mit spiritistischen Spekulationen nichts, aber auch rein gar nichts zu tun hat.

Welche Bewandtnis hat es also mit jenem vielumstrittenen und eigenartigen Problem, das sich hinter der Frage nach dem Vorhandensein, nach Möglichkeit oder Unmöglichkeit einer vierten Dimension verbirgt? Suchen wir, um zu dieser Frage Stellung nehmen zu können, uns zunächst einmal über den Begriff der Dimension selbst klarzuwerden.

Wir verstehen unter »Dimensionen« die in bestimmter Weise gerichteten Ausdehnungsweisen des Raumes und der räumlichen Gebilde, die uns in der Welt der Erscheinungen entgegentreten. Drei solcher gerichteten Ausdehnungsweisen oder Dimensionen nehmen wir an den im Raume vorhandenen Körpern wahr, die wir gewohntermaßen als Höhe, Breite und Tiefe (oder Länge) bezeichnen. An der Gestalt eines Würfels oder Quaders, etwa einer Zigarrenkiste, können wir diese drei Dimensionen am besten verfolgen, denn von jeder Ecke des Würfels oder Quaders gehen drei Kanten aus, von denen jede auf den anderen beiden senkrecht steht, und deren jede Verlauf und Richtung einer der Ausdehnungsweisen des Raumes darstellt. Die drei Dimensionen sind also bestimmt durch die drei geraden Linien, die in jedem Punkte des Würfels wie überhaupt jeden Körpers aufeinander senkrecht stehen können. Innerhalb einer Fläche, etwa der Ebene auf einem Blatt Papier oder an der Seite des Würfels, können in einem Punkte nur zwei gerade Linien aufeinander senkrecht stehen, und deshalb ist für uns die Ebene zweidimensional. An einer Linie endlich, dargestellt etwa durch einen Strich, den wir mit Bleistift auf ein Stück Papier zeichnen, oder an der Kante unseres Würfels können wir nur eine einzige Ausdehnungsweise oder Dimension unterscheiden. Fläche und Linie sind keine selbständigen räumlichen Gebilde; sie stellen nur die Begrenzungsformen der Körper dar, sind also gleichsam nur Eigenschaften oder Attribute solcher. Die Dreidimensionalität des räumlich vollständigen Gebildes, also des Körpers, ist also definiert durch die Dreizahl der in jedem Punkte des Körpers aufeinander senkrecht stehenden Geraden.

Mehr als drei Dimensionen nehmen wir an keinem Gebilde, keinem Gegenstand oder Körper wahr und können wir uns auch auf keine Weise sinnlich vorstellen oder veranschaulichen. Eine solche Vorstellung käme, gemäß der eben gegebenen Definition der Dimensionen, auf das Problem heraus, in einem Punkte vier aufeinander senkrecht stehende gerade Linien zu errichten oder uns wenigstens vorzustellen, und eine solche Vorstellung widerspricht unserem Anschauungsvermögen vollkommen. Unsere sinnfällige Anschauung der Welt ist vollkommen auf den dreidimensionalen Raum und nur auf diesen eingestellt; keinem menschlichen Geiste ist die anschauliche Vorstellung eines vierdimensionalen Dinges möglich, und alle Veranschaulichungsversuche, die man zu diesem Zweck unternommen hat, laufen immer nur auf Analogien, auf Vergleiche von mehr oder weniger Wert und Deutlichkeit hinaus.

Dennoch aber hat sich der denkende und forschende Geist des Menschen in der Frage nach dem Vorhandensein oder der Möglichkeit einer vierten Dimension nicht mit der Wahrnehmung allein begnügt. Er traut dem Augenschein und überhaupt dem menschlichen Vorstellungsvermögen allein nicht ganz und hat schon oft die Frage aufgeworfen, ob es nicht dennoch eine vierte Dimension geben könne, wenn uns auch die Sinneswahrnehmung eine solche nicht zeigt oder sich als zu einer solchen Vorstellung unfähig erweist. Mit dem Wahrnehmungsbilde, das uns unsere Sinne liefern, ist ja die Welt sicherlich noch nicht erschöpft, und es gibt unzweifelhaft zahllose Dinge, von denen uns keinerlei Wahrnehmung durch unsere Sinnesorgane zukommt, und die dennoch existieren. Noch kein Mensch hat jemals die Elektrizität durch seine Sinne unmittelbar wahrgenommen, noch kein Forscherauge je Atome wirklich gesehen, und dennoch sind wir von der Existenz dieser wie jener überzeugt, weil wir aus bekannten Erscheinungen und Vorgängen, also indirekt, auf das Vorhandensein dieser Realitäten schließen müssen. Und ebenso ist es uns jederzeit eine ohne Schwierigkeit mögliche Vorstellung, daß selbst in jenen Regionen des Weltraumes, in die wir selbst vermittels der größten und schärfsten Fernrohre nicht zu dringen vermögen und vielleicht auch niemals dringen werden, dennoch Weltkörper, Fixsterne, Planeten und Trabanten, ja auch von intelligenten Lebewesen bewohnte Weltkörper vorhanden sein können. Also die Welt ist mit unserem unmittelbaren Wahrnehmungsbilde noch nicht erschöpft und nicht zu Ende, das ist sichere Erkenntnis.

Daher hat sich der forschende Verstand denn auch oftmals geneigt gezeigt, trotz des Fehlens der unmittelbaren Wahrnehmung einer vierten Dimension die aufgeworfene Frage nach dem Vorhandensein oder der Möglichkeit einer vierten Dimension nichtsdestoweniger zu bejahen, selbstverständlich gänzlich unabhängig von den Spekulationen der Okkultisten und lange, bevor diese sich den Begriff der vierten Dimension für ihre Zwecke und Theorien nutzbar zu machen begannen. Kein anderer als der große Kant war es, der sowohl in seinem Hauptwerk, der »Kritik der reinen Vernunft«, wie allerdings noch mehr in seinen vorkritischen Schriften, in denen er sich gerade mit den Problemen von Raum und Zeit vielfach beschäftigt hat, auch die Frage nach der vierten Dimension unter die kritische Lupe nahm und das Problem zuerst auf eine wissenschaftliche Grundlage gestellt hat. Kant hat so manche Tatsachen und Erscheinungen angeführt, die ihm für die Möglichkeit einer vierten Dimension zu sprechen schienen, wenn er letzten Endes allerdings die Lösung der Frage in der Schwebe gelassen hat. Der gewaltige Impuls, den der große Königsberger dann dem gesamten wissenschaftlichen Denken nach ihm gegeben hat, äußerte sich auch darin, daß seitdem das Problem der vierten Dimension von zahlreichen und hervorragenden Forschern aufgegriffen wurde und bis heute nicht aus dem Forschungsbereiche verschwunden ist. Halb im Scherz, halb im Ernst hat Gustav Theodor Fechner, einer der tiefgründigsten und zugleich originellsten Vertreter des wissenschaftlichen philosophischen Denkens aus der zweiten Hälfte des vorigen Jahrhunderts, die Frage aufgeworfen, warum denn die Natur im Dimensionalen nur bis drei solle zählen können. Und der hervorragendste Physiker des vorigen Jahrhunderts, Hermann Helmholtz, hat dem Problem seine volle Aufmerksamkeit zugewandt und ihm eine Reihe von Abhandlungen gewidmet, die zu dem wissenschaftlich Wertvollsten auf diesem schwierigen und abstrakten Gebiete gehören. Eine große Anzahl von Namen hervorragender Forscher aus den verschiedensten Wissensgebieten könnte noch angeführt werden, die alle über jenes eigenartige Problem zur Klarheit zu gelangen suchten.

Welches waren nun aber die Gründe, die solche wie die genannten Forscher veranlaßten, zum mindesten die Möglichkeit einer vierten Dimension in Rechnung zu ziehen? Diese Frage und die Antwort auf diese muß der Ausgangspunkt bei der Betrachtung und Beurteilung des Problems sein. Denn da wir, wie bereits betont, uns eine unmittelbare sinnfällige Anschauung von der vierten Dimension oder von vierdimensionalen Dingen nicht machen können, so muß es doch wohl irgendwelche Erscheinungen geben, die auf das Vorhandensein einer vierten Dimension hinzudeuten scheinen, wenn überhaupt die Beschäftigung mit dieser Frage einen zureichenden Grund haben soll. An der bloßen vagen Spekulation, die keinerlei konkreten Anhalt in der Welt der Erscheinungen hat, können wir uns nicht genügen lassen, weder zur Beschäftigung mit der Frage noch zur Beantwortung dieser. Solche Erscheinungen nun, die also im Sinne der vierten Dimension gedeutet werden könnten und jedenfalls die Frage nach der Möglichkeit einer solchen nahelegen und rechtfertigen, gibt es allerdings. Welcher Art diese Erscheinungen sind, wollen wir uns an einem Exkurs in das zweidimensionale Gebiet wenigstens vergleichsweise klarzumachen suchen, indem wir betrachten, wodurch, durch welche Vorgänge und Erscheinungen sich innerhalb einer zweidimensionalen Welt das Vorhandensein einer dritten Dimension bemerkbar machen würde.

Nehmen wir an, es gäbe auf einer zweidimensionalen Fläche auch eine Art zweidimensionaler Lebewesen. Der Erdboden und die Schatten, die sich auf diesem bewegen, könnten uns als Bilder einer solchen Welt und solcher Lebewesen zweier Dimensionen dienen. Wir machen also für den Augenblick die Annahme, daß solche Schattenwesen leben, daß sie Wahrnehmungen haben und denken können. Schattenwesen dieser Art würden nur solche Dinge und Vorgänge, die in ihrer Ebene selbst vorhanden sind oder sich in dieser abspielen, wahrnehmen können, denn sie sind in ihren Wahrnehmungen und ihrem Wahrnehmungsvermögen auf die zwei Dimensionen der Ebene, die ihre Welt ist, eingestellt und können über diese sozusagen nicht hinausgucken, haben kein Wahrnehmungsvermögen für die Dinge und Vorgänge in der dritten Dimension. Daher würden sie die Existenz solcher Dinge und Vorgänge wie überhaupt das Vorhandensein einer dreidimensionalen Welt in Zweifel ziehen. Nehmen wir nun weiter an, ein Mensch, der das Leben und Treiben solcher Schattenwesen auf dem Erdboden betrachtet, würde plötzlich einen Stock auf den Erdboden, mitten hinein in die Welt jener lebenden Schatten, stellen. Diese würden dann den Stock nur so weit wahrnehmen, als er sich mit dem Erdboden berührt, würden also nur den untersten Querschnitt des Stockes, und zwar nur als ein zweidimensionales Ding, wie alle anderen Dinge in ihrer Welt, wahrnehmen. Aber dieses Ding, als welches ihnen der hineingestellte Stock erscheint, wäre ganz urplötzlich in ihrer Welt aufgetaucht, wie ein durch Zauberkraft plötzlich erschienener Gegenstand, der vordem nicht in ihrer Welt war. Würde jener Mensch dann den Stock wieder emporheben, so würde damit jenes plötzlich erschienene Ding ebenso plötzlich aus der zweidimensionalen Welt unserer Schattenwesen wieder verschwinden. Es hätte also ein plötzliches Erscheinen und Verschwinden von Dingen stattgefunden, das durch die Bedingungen einer zweidimensionalen Welt allein nicht zu erklären wäre und die Bewohner dieser Welt geradezu wie ein Zauberspuk anmuten müßte.

Wie könnten und würden sich unsere Schattenwesen solche rätselhaften Vorgänge nun erklären? Nur durch die Annahme einer dritten Dimension! Sie würden sich sagen: Vollständig aus der Welt verschwunden oder in Nichts zerronnen kann das Ding, das wir soeben noch gesehen haben, nicht sein, denn das würde allen Denk- und Naturgesetzen widersprechen; wenn wir es also in unserer zweidimensionalen Welt nicht mehr vorfinden, so muß es notwendigerweise noch eine uns nicht wahrnehmbare dritte Dimension geben, in die das verschwundene Ding hineingeraten ist. Das plötzliche Erscheinen und Verschwinden von Dingen innerhalb einer zweidimensionalen Welt würde also für Lebewesen dieser zweidimensionalen Welt mit Notwendigkeit auf das Vorhandensein einer dritten Dimension hindeuten.

Die Schlußfolgerung nun, die jene erdichteten zweidimensionalen Wesen aus dem plötzlichen Erscheinen und Verschwinden von Dingen innerhalb ihrer Welt ziehen müßten, können wir nun auch für unsere Frage nach dem Vorhandensein einer vierten Dimension verwerten. Auch in unserer dreidimensionalen Welt müßte das plötzliche Erscheinen oder Verschwinden von Gegenständen auf das Vorhandensein noch einer weiteren Dimension, die unserer Wahrnehmung entzogen ist, schließen lassen, nur durch eine solche vierte Dimension wären derartige Vorgänge zu erklären, und zwar aus ganz analogen Gründen, wie in jenem anderen Falle auf das Vorhandensein einer dritten Dimension geschlossen werden müßte. Ja wir können sagen, daß, falls jemals wirklich einwandfrei und mit absoluter Sicherheit das Erscheinen oder Verschwinden von Gegenständen festgestellt würde, damit zugleich auch ein unbedingter Beweis für das Vorhandensein einer vierten Dimension gegeben wäre.

Die Frage ist also, ob wirklich schon jemals das Erscheinen oder Verschwinden von Dingen mit Sicherheit festgestellt worden ist. Die Spiritisten sagen ja, und sie haben sich die Theorie der vierten Dimension mit Begeisterung und Nachdruck als Beweismittel für ihre Ideen zunutze gemacht. In der vierten Dimension, so argumentieren sie, halten sich die Seelen der Toten, die Geister und Gespenster auf, und von hier aus wirken sie, von uns selbst nicht wahrgenommen, mehr oder weniger störend und aufregend auf die irdische dreidimensionale Welt ein, wie jener Mann mit seinem Spazierstock auf die Welt der Schatten einwirkt; sie erscheinen und verschwinden und lassen ebenso andere Dinge erscheinen und verschwinden. Damit glaubt man dann alle die merkwürdigen Dinge, die in den spiritistischen Sitzungen tagtäglich vorkommen sollen, die Geistermanifestationen, das Erscheinen und Verschwinden von Blumen, Büchern, Tellern, Kochlöffeln und ähnlichen Gegenständen des täglichen Bedarfs, auf höchst einfache und natürliche Weise erklärt und dem Spiritismus eine wissenschaftliche Unterlage gegeben zu haben. Erscheinen und Verschwinden von Geistern und Körpern wären hiernach ebenso einfach und natürlich erklärt wie in dem analogen Vergleichsfalle das Erscheinen und Verschwinden des Spazierstockes innerhalb der zweidimensionalen Welt, wo dieser Stock seinen Ursprung in der dritten Dimension hat.

Tatsächlich wirkt diese Analogie und die hierauf gegründete Beweisführung äußerst bestechend. Selbst mancher kritische Kopf ist ihr zum Opfer gefallen, und selbst so ausgezeichnete Naturforscher wie Zöllner und Crookes, die Hervorragendes auf ihren wissenschaftlichen Spezialgebieten geleistet haben, sind auf Grund jener Argumentation zu überzeugten Spiritisten geworden. Was Wunder also, wenn jene Beweisführung noch viel stärker auf die große Masse derjenigen einwirken muß, die wissenschaftlicher Schulung und kritischen Denkens mehr oder weniger bar sind! In Wirklichkeit ist aber noch niemals das Erscheinen oder Verschwinden von Gegenständen wirklich einwandfrei festgestellt worden, und jene geheimnisvollen Erscheinungen und Vorgänge bei spiritistischen Veranstaltungen sind, wenn sie unter wissenschaftliche Kontrolle gestellt wurden, bisher noch immer und ausnahmslos auf höchst einfache und natürliche Weise, nämlich als Täuschung oder Betrug, erklärt worden. Der exakte Beweis für das Vorhandensein einer vierten Dimension auf Grund von Erscheinen oder Verschwinden von Gegenständen steht also noch vollkommen aus, und alle bisherigen Erfahrungen mit spiritistischen Medien sind viel mehr als Beweis gegen als für die Möglichkeit solcher Vorgänge aufzufassen.

In der folgenden Abhandlung wollen wir weitere für und gegen Vorhandensein oder Möglichkeit einer vierten Dimension vorgebrachten Beweise der Betrachtung unterziehen, um zu einer Beurteilung des eigenartigen Problems zu gelangen.

2. Beweise und Gegenbeweise

Räumliche Erscheinungen und ihre Deutung – Kongruente Dreiecke – Ein Widerspruch? – Das Kantsche Beispiel – Drehung im Raume – Scheinbare und wirkliche Kongruenz – Vom »Richtungssinn« der Figuren – Die Beweiskraft der Anschauung – Der Mangel der Analogie

Die bisher angeführten Argumente, die für die Möglichkeit oder das Vorhandensein einer vierten Dimension geltend gemacht werden, sind ihrer Natur nach mehr Überlegungs- und Analogiebeweise als Tatsachen der Wirklichkeit, denen letzten Endes doch die größere Beweiskraft zukommt. Man hat aber auch gewisse räumlich-geometrische Erscheinungen, die in unserer dreidimensionalen Welt zu konstatieren sind, und denen in höherem Maße als jenen der Wert von Tatsachen- und Wirklichkeitsbeweisen zuzukommen scheint, im Sinne einer vierten Dimension zu deuten gesucht. Wiederum wollen wir uns das Wesen dieser Erscheinungen zunächst durch analoge Verhältnisse der zweiten Dimension zu veranschaulichen suchen.

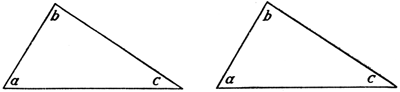
Abb. 37

Abb. 38

In unserer Abbildung 37 sind zwei Dreiecke gezeichnet, die in Winkeln und Seiten vollkommen übereinstimmen. Solche Dreiecke werden bekanntlich als kongruent bezeichnet und haben die Eigenschaft, daß sie zu vollkommener Deckung gebracht werden können. Das geschieht bei den Dreiecken der Abbildung 37 in der Weise, daß man das eine Dreieck über das andere innerhalb der Ebene, in der sich beide befinden, hinweggeschoben denkt, bis die entsprechenden Seiten aufeinanderfallen. In der Abbildung 38 sind dieselben Dreiecke nochmals vorgeführt, diesmal jedoch nicht wie in Abbildung 37 in Parallel-, sondern in Gegen- oder Spiegelstellung; hier ist also das eine Dreieck gleichsam das Spiegelbild des anderen. Diese beiden Dreiecke nun können durch Verschiebung innerhalb der Ebene auf keine Weise zur Deckung gebracht werden, wie sich der Leser leicht überzeugen kann, wenn er die beiden Figuren ausschneidet und gegeneinander verschiebt. Obwohl also die Dreiecke der Abbildung 38 ebenfalls kongruent sind, ebenfalls in Seiten und Winkeln vollkommen übereinstimmen (es sind ja dieselben Dreiecke wie in Abbildung 37, nur in anderer Stellung), ist es doch unmöglich, diese Dreiecke ebenso wie jene anderen beiden durch bloße Verschiebung innerhalb der Ebene zur Deckung zu bringen. Nur auf eine Weise können auch diese Dreiecke zur Deckung gebracht werden, indem man nämlich eins der Dreiecke aus der Ebene herausgehoben denkt (etwa durch Ausschneiden aus dem Papier), es im dreidimensionalen Raume um seine Achse dreht und es dann so auf das andere Dreieck legt, daß die entsprechenden Seiten und Winkel aufeinanderfallen. Hier liegt also der Fall vor, daß zwei kongruente räumliche Gebilde innerhalb der Dimension, der sie selbst angehören, nicht zur Deckung gebracht werden können, daß das vielmehr nur durch Zuhilfenahme einer weiteren Dimension, in unserem Falle der dritten, möglich gemacht werden kann. Hier scheint also ein Widerspruch vorzuliegen, der Widerspruch nämlich, daß es unter denselben gegebenen Bedingungen einmal möglich, das andere Mal aber unmöglich ist, dieselben räumlichen Gebilde zur Deckung zu bringen.

Ganz ähnliche Erscheinungen wie hier in der zweidimensionalen Ebene und an zweidimensionalen geometrischen Gebilden gibt es nun auch im dreidimensionalen Raume. Es gibt Körper, die selbst bei vorhandener vollkommener Kongruenz ihrer Seiten und Winkel doch nicht zur Deckung gebracht werden können. Ein Tetraeder ist ein von vier Dreiecksseiten begrenzter Körper, ist gleichsam das dreidimensionale Gegenstück zum zweidimensionalen Dreieck. Zwei kongruente Tetraeder in Parallelstellung können jederzeit zur Deckung gebracht werden, zwei kongruente Tetraeder in Spiegelstellung dagegen, wenn sie nicht gleichzeitig symmetrisch gebaut sind, niemals. Allgemein kann ein unsymmetrischer Körper, d. h. ein Körper, der nicht in zwei kongruente Hälften geteilt werden kann, niemals mit seinem Spiegelbild zur Deckung (wenn auch nur in Gedanken) gebracht werden, obgleich natürlich jeder Körper mit seinem Spiegelbild vollkommen kongruent ist. Auf solche Erscheinungen hat schon Kant hingewiesen und die Frage aufgeworfen, ob diese im Sinne einer vierten Dimension zu deuten wären. Von ihm stammt das berühmte Beispiel der rechten und linken Hand, die, selbst wenn sie beide vollkommen gleich gebildet sind, dennoch niemals zur Deckung gebracht werden können; oder der Handschuh der einen Hand läßt sich nicht ohne Verzerrung, d. h. ohne Veränderung seiner geometrischen Form, auf die andere Hand ziehen. Hier scheint also ein Widerspruch vorzuliegen. Unser Denken verlangt, daß sich Körper, die kongruent sind, zur Deckung bringen lassen, und dennoch ist das bei solchen wie den erwähnten Körpern auf keine Weise möglich.

Diese Erscheinungen und der Widerspruch, den man in ihnen sehen zu müssen glaubte, boten die Möglichkeit einer Erklärung durch Annahme einer vierten Dimension. Wie die beiden Dreiecke in Spiegelstellung (Abbildung 38), also kongruente Figuren der zweiten Dimension, die trotz vollkommener Kongruenz von Seiten und Winkeln durch bloße Verschiebung innerhalb der zweidimensionalen Ebene nicht zur Deckung gebracht werden können, sich vermittels der dritten Dimension zur Deckung bringen lassen, so werden sich vielleicht, so folgerte man, analogiegemäß auch solche wie die erwähnten kongruenten dreidimensionalen Gebilde vermittels einer vierten Dimension zur Deckung bringen lassen. Jene kongruenten Körper müßten also gleichsam aus dem dreidimensionalen Raume heraus und in die vierte Dimension hineingebracht werden und in dieser, analog dem Vorgang mit den Dreiecken, eine Art Drehung erfahren. Wir können uns zwar von einer solchen Drehung in der vierten Dimension ebensowenig wie von einer vierten Dimension überhaupt eine Vorstellung machen, aber das allein brauchte kein Grund zu sein, eine solche Annahme abzuweisen; zweidimensionale Lebewesen könnten sich auch keine sinnfällige Vorstellung von der Drehung machen, durch welche die Dreiecke der Abbildung 38 zur Deckung gebracht werden können. Wiederum hat auch diese Analogie etwas ungemein Bestechendes; sie bietet eine überraschend einfache Erklärung jener Erscheinungen, und der in diesen Erscheinungen erblickte Widerspruch schien nunmehr geradezu ein Argument für das Vorhandensein einer vierten Dimension zu sein, das sowohl für Philosophen wie auch für Mathematiker und Physiker ein starker Beweis zum mindesten für die Möglichkeit einer vierten Dimension wurde und lange Zeit hindurch diese Rolle gespielt hat.

Heute ist jedoch auch diese Argumentation zugunsten einer vierten Dimension erschüttert, und zwar auf Grund einer schärferen Betrachtung jener geometrischen Verhältnisse. Es hat sich herausgestellt, daß der Widerspruch, den man in dem Verhalten solcher wie der angeführten geometrischen Gebilde sehen zu müssen glaubte, – um es kurz zu sagen – nur ein scheinbarer ist. Gehen wir zum Beweis des Gesagten zunächst nochmals auf die Dreiecke unserer Abbildungen 37 und 38 zurück. Die Dreiecke in Abbildung 38 sind im Schulsinne kongruent, das heißt sie stimmen in Seiten und Winkeln überein und lassen sich dennoch nicht durch Verschiebung innerhalb der Ebene zur Deckung bringen, wie es bei den kongruenten Dreiecken der Abbildung 37 ohne weiteres der Fall ist. Sind denn aber die Dreiecke der Abbildung 38 wirklich und vollkommen kongruent, das heißt: stimmen sie wirklich in allen räumlichen Beziehungen überein? Das ist nicht der Fall, denn Seiten und Winkel sind zwar in beiden Dreiecken gleich, aber sie sind in entgegengesetzter Richtung angeordnet. Die eingezeichneten Pfeilkreise lassen das deutlich erkennen. Bei dem linken Dreieck verlaufen Seiten und Winkel in der Richtung a, b, c, also von links nach rechts, in derselben Richtung wie ein Uhrzeiger, bei dem anderen Dreieck aber in der entgegengesetzten Richtung c, b, a, entgegen der Uhrzeigerrichtung. Die beiden Dreiecke unterscheiden sich also in einer sehr wesentlichen räumlichen Beziehung, durch die Anordnung ihrer Teile, oder durch den »Richtungssinn«, wie der Fachausdruck lautet. Sie sind also keineswegs völlig kongruent, und deswegen können sie auch nicht innerhalb der Ebene, durch bloße Verschiebung, zur Deckung gebracht werden, weil sie bei dieser Operation immer entgegengesetzten Richtungssinn beibehalten.

Entsprechendes wie hier von ebenen Figuren gilt auch von Körpern, also Gebilden dreier Dimensionen, die, wie rechte Hand und linke Hand, wie Original und Spiegelbild unsymmetrischer Körper überhaupt, selbst bei völliger Kongruenz von Seiten und Winkeln dennoch nicht zur Deckung gebracht werden können. Auch solche Körper sind nicht völlig kongruent, unterscheiden sich ebenfalls immer durch die entgegengesetzte Anordnung ihrer Teile, also den Richtungssinn. Sie ermangeln also in Wirklichkeit der völligen räumlichen Übereinstimmung, wodurch die Unmöglichkeit, solche Körper zur Deckung zu bringen, einwandfrei erklärt ist. Bei wirklich völliger Kongruenz, die also auch gleichen Richtungssinn einschließt, also bei Parallelstellung wie bei den Dreiecken in Abbildung 37, sind alle geometrischen Gebilde, gleichviel ob Flächen oder Körper, stets zur Deckung zu bringen, ohne daß es einer weiteren Dimension bedarf, um diese Operation auszuführen. Die Schuldefinition der Kongruenz hat lange Zeit das Moment des »Richtungssinnes« übersehen und damit der Spekulation eine Veranlassung zur Annahme einer vierten Dimension als Erklärungsweise gegeben. Die Aufdeckung des Richtungssinnes als Faktor der Kongruenz beseitigte den erwähnten Widerspruch und enthebt uns jeder Notwendigkeit, zur Erklärung der Erscheinungen, in denen man einen solchen Widerspruch sehen zu müssen glaubte, eine vierte Dimension anzunehmen. Abermals ist dieser Annahme ein Hauptargument entzogen.

Wir kommen also zu der vorläufigen Zusammenfassung: Ein unmittelbarer Beweis für das Vorhandensein einer vierten Dimension durch Erscheinen oder Verschwinden von Körpern ist noch niemals erbracht worden; das Argument für die Möglichkeit einer vierten Dimension, das bislang in der Unmöglichkeit gesehen wurde, bestimmte Körper, die im Schulsinne kongruent sind, zur Deckung zu bringen, ist entkräftet durch die einwandfreie andersartige Erklärung der Erscheinungen, von denen dieses Argument ausging.

Zugleich aber erhebt sich ein Argument von stärkster Beweiskraft gegen Vorhandensein oder Möglichkeit einer vierten Dimension, und dieses besteht in der vollkommenen Unmöglichkeit einer sinnfälligen Vorstellung einer vierten Dimension oder vierdimensionaler Gebilde. Nicht daß wir eine vierte Dimension nirgends finden oder wahrnehmen, wäre ein unbedingter Gegenbeweis gegen eine solche, denn wie bereits betont, sind wir von der Existenz vieler Dinge, wie der Atome, der Elektrizität usw., überzeugt, die wir nicht wahrnehmen und noch niemals wahrgenommen haben, aller Wahrscheinlichkeit nach auch niemals unmittelbar wahrnehmen werden; daß aber dem menschlichen Geiste überhaupt jede Möglichkeit fehlt, sich von vierdimensionalen Gebilden eine Vorstellung zu machen, darin sehe ich allerdings ein Argument von stärkster Beweiskraft gegen Vorhandensein und Möglichkeit einer vierten Dimension überhaupt. Die Atome, ihre Gestalt, Konstitution, Bewegung und Wirkungsweise, wie es die wissenschaftliche Theorie verlangt, können wir uns ohne Mühe vorstellen, eine Vorstellung, die bis zur Ausarbeitung konkreter Atommodelle gelangt ist; ebenso können wir uns von der Beschaffenheit und Wirkungsweise der Elektrizität eine sehr exakte Vorstellung machen, wie noch von zahllosen anderen Dingen, die es nach der Theorie gibt, ohne daß wir sie wahrnehmen können. Auf keine Weise aber ist einem Menschen eine sinnfällige Vorstellung einer vierten Dimension möglich, und damit verneint der menschliche Geist allen Theorien und Hypothesen zum Trotz in seinem Grunde selbst Möglichkeit und Vorhandensein einer vierten Dimension. Es müßten sich zum mindesten in unseren Vorstellungen und unserer Vorstellungsweise Andeutungen oder Übergänge finden lassen, die wir als Annäherungen an vierdimensionale Gebilde oder Vorgänge deuten könnten, aber nicht auch nur die geringsten Spuren solcher Art sind in unserem anschauenden und vorstellenden Bewußtsein zu finden. Die Psychologie des Menschen weist jede solche Möglichkeit ab. Für diese absolute Unmöglichkeit der sinnfälligen Vorstellung von Gebilden und Gestaltungen von mehr als drei Dimensionen aber kann ich keinen anderen Grund ausfindig machen als den, daß die Dreizahl der Dimensionen eine Naturkonstante ist, an die jedes menschliche oder sonstige Vorstellen auf diesem wie auf jedem anderen Planeten gebunden ist. Und wenn Fechner, wie bereits erwähnt, halb scherzhaft, halb ernst die Frage stellt, warum denn die Natur im Dimensionalen nur bis drei solle zählen können, so kann ihm darauf erwidert werden, daß noch in vielen anderen Beziehungen das Zählungsvermögen der Natur an ganz bestimmte Grenzen oder Konstanten gebunden ist. Es gibt nur fünf platonische Körper und kann nicht mehr als fünf geben; nur einmal sind in der unendlichen Zahlenreihe drei hintereinanderfolgende Primzahlen möglich, und die Zahl von 424 Meterkilogramm als Wärmeäquivalent ist nach unserer gesamten naturwissenschaftlichen Auffassung ebenfalls als eine Naturkonstante zu betrachten, die für das ganze Universum Geltung hat.

Damit erledigt sich auch die oft gebrauchte Analogie der zweidimensionalen Lebewesen, die sich zwar selbst keine sinnfällige Vorstellung einer dritten Dimension zu machen imstande sind, dennoch aber durch irgendwelche Erscheinungen auf das Vorhandensein einer solchen dritten Dimension schließen könnten, die ja, wie wir dreidimensionalen Menschen wissen, in Wirklichkeit vorhanden ist. Vielleicht wäre daher auch die menschliche Unfähigkeit, sich eine Vorstellung von der vierten Dimension zu machen, noch kein Beweis gegen die Möglichkeit oder das Vorhandensein einer solchen. Darauf ist zu erwidern, daß zweidimensionale Lebewesen nur eine Fiktion, nur eine begriffliche Erdichtung ohne Wirklichkeitswert sind, an die wir daher auch keinerlei Schlüsse für die Wirklichkeitswelt knüpfen können. Wir kennen Leben und Denken nur als Erscheinungen an selbständigen körperhaften, dreidimensionalen Wesen; Lebewesen zweier Dimensionen sind eine Unmöglichkeit, und daher kann auch das fiktive Denken und Vorstellen solcher fiktiven Wesen keinerlei Argumentation für die Wirklichkeitswelt ergeben, wenn wir jene zweidimensionalen Lebewesen auch zu Analogiezwecken verwenden.

Die Analogie mit den zweidimensionalen Lebewesen und ihrer zweidimensionalen Anschauungs- und Vorstellungsweise hat in den Untersuchungen und Theorien über die vierte Dimension eine große Rolle gespielt; Helmholtz hat diese Fiktion sehr ausgiebig für seine diesbezüglichen Untersuchungen benutzt, kam aber schließlich doch zu der Überzeugung, daß sich aus dieser Analogie keinerlei Schlüsse für die Möglichkeit oder Wirklichkeit einer vierten Dimension ziehen lassen, und ist daher bei dem dreidimensionalen Raume als Form der Wirklichkeitswelt geblieben.

3. Die Lösung des Problems

Neue Gründe – Die vierte Dimension in der Mathematik – Die Relativitätstheorie und die vierte Dimension – Ein »mystischer Schauer« – Nochmals: Anschauung und Denken – Ein unheilbarer Widerspruch? – Eine neue Betrachtung – Das dreidimensionale Kontinuum von Raum, Zeit und Stoff – Die Beseitigung einer Antinomie

Die bisher angeführten Argumente hatten eine ausreichende oder überzeugende Beweiskraft für Möglichkeit oder Vorhandensein einer vierten Dimension – das darf wohl gesagt werden – nicht zu entfalten vermocht. Die Tatsachenbeweise hatten sich nur als scheinbare Beweise oder als ein Operieren mit nur scheinbaren Tatsachen herausgestellt, den Analogiebeweisen aber fehlte die Eindeutigkeit und Zuverlässigkeit des überzeugenden Argumentes vollständig.

Eine neue Stütze schien die Hypothese der vierten Dimension aber durch die Denkrichtung in gewissen Zweigen der heutigen Wissenschaft, vor allem in der Mathematik und der theoretischen Physik, zu erhalten. Mit den hieraus hergeleiteten Argumenten wollen wir uns noch auseinandersetzen. Wir werden sehen, daß gerade die Argumentation gegen die theoretischen Deduktionen dieser Disziplinen den Weg deutet, auf dem die Lösung des vielumstrittenen Problems gesucht und gefunden werden kann.

In der modernen Mathematik spielt der Begriff der vierten Dimension eine sehr bedeutsame Rolle. Die Mathematik rechnet ohne Bedenken mit dem Begriff der vierten Dimension, operiert mit vierdimensionalen Räumen und Gebilden und bestimmt die mathematischen Beziehungen und Verhältnisse in solchen. Und nicht nur die vierte, sondern auch die fünfte, sechste, siebente usw. Dimension ist Gegenstand der mathematischen Betrachtung und Untersuchung. Der Mathematiker ist also in der Annahme dimensionaler Möglichkeiten äußerst großzügig, für ihn sind in dimensionaler Hinsicht sozusagen der Wohltätigkeit überhaupt keine Grenzen gesteckt. Aber zwischen dem Begriff der Dimension im mathematischen Sinne und dem, was in der Welt der Wirklichkeit als Dimension gilt, ist ein erheblicher Unterschied. Für den Mathematiker hat der Begriff der Dimension nur eine rein abstrakt-zahlenmäßige Bedeutung. Er sieht von einer solchen wie oben angeführten Definition, die auf die konkreten Möglichkeiten der Dinge und Beziehungen gerichtet ist und die »Dimension« durch die Zahl der Geraden bestimmt, die in einem Punkte senkrecht aufeinander stehen können, ab. Vielmehr heißt eine Linie für ihn eindimensional, weil es zur Bestimmung einer solchen in einem Koordinatensystem nur einer Zahl bedarf; eine Ebene benötigt zu ihrer Bestimmung zweier Zahlen, weswegen sie als zweidimensional gilt, und ein Körper endlich gilt dem Mathematiker deswegen und nur deswegen als dreidimensional, weil es dreier Zahlen zur Bestimmung eines solchen Gebildes bedarf. Nichts hindert den Mathematiker, in dieser Weise fortzufahren, also rein begrifflich auch geometrische Gebilde von vier, fünf, sechs und sogar beliebig vielen Bestimmungszahlen anzunehmen und dementsprechend mit geometrischen Gebilden und Räumen von vier, fünf, sechs und beliebig vielen Dimensionen zu operieren. Diese n-dimensionalen Räume und Gebilde sind also nur Fiktionen, und der Mathematiker fragt nicht und braucht nicht danach zu fragen, ob diesen rein begrifflich definierten Räumen von mehr als drei Dimensionen irgendeine Wirklichkeitsbedeutung zukommt. Ihm genügt die formale Widerspruchslosigkeit seiner Annahmen, um mit solchen Räumen zu rechnen, als ob es solche Räume gäbe, und keinesfalls fällt ihm ein, auf Grund seiner arithmetischen Fiktionen zu folgern, daß es nun auch in Wirklichkeit eine vierte, fünfte usw. Dimension gäbe oder auch nur geben könne. Die Mathematik rechnet ja vielfach mit wirklichkeitsfremden Größen, den sogenannten imaginären Größen, wie etwa den Wurzeln aus negativen Zahlen usw., also Größen, die nur rechnerische Bedeutung haben, denen aber keinerlei Wirklichkeitsbedeutung zukommt, was dem Mathematiker auch höchst gleichgültig ist und sein kann, denn die Welt der Mathematik ist nicht die Welt der Wirklichkeit. Eine ebensolche nur imaginäre Bedeutung hat im Sinne des Mathematikers auch der Begriff von Räumen von mehr als drei Dimensionen; auch diese vieldimensionalen Räume sind nur imaginäre Rechengrößen, von denen wir irgendwelche Schlüsse auf die dimensionale Beschaffenheit der Wirklichkeitswelt keinesfalls ziehen dürfen, ebensowenig wie das der Mathematiker selbst tut. Bemerkt sei noch, daß wir jene neuartigen »überdimensionalen« Geometrien, die also mit mehr als drei Dimensionen rechnen, als »Nicht-Euklidische Geometrien« bezeichnen zum Unterschied von der Geometrie des alten Euklid, die wir in der Schule gelernt haben und die nur mit dem dreidimensionalen Raume rechnet.

Neuerdings endlich hat das Problem der vierten Dimension erneute Bedeutung erlangt, und zwar durch die Relativitätstheorie, die das wissenschaftliche Denken der Gegenwart ja in weitem Umfange in ihren Bann gezogen hat. Die Relativitätstheorie geht in ihren Deduktionen über die drei Dimensionen unserer Wahrnehmung entschlossen hinaus. Die Relativierung des Zeitbegriffes, dieser Kerngedanke der Relativitätstheorie, nötigte, auch der Zeit die Bedeutung und Wirksamkeit einer Dimension für die gegenständliche Erscheinung und Gestaltung der Welt zuzuschreiben. Die Zeit ist für sich allein etwas Eindimensionales; sie hat nur die einzige Art der Erstreckung, die wir eben als Zeitverlauf wahrnehmen. Diese eindimensionale Zeit ist aber nicht nur Zeitverlauf, sondern verknüpft sich nach der Relativitätstheorie mit den drei Dimensionen des Raumes zu einer vierdimensionalen Einheit, die das eigentliche Weltkontinuum darstellt. Freilich können wir diese vierte Dimension innerhalb des Weltkontinuums nicht unmittelbar wahrnehmen, sondern wir erschließen sie aus der Rechnung auf Grund gewisser Erscheinungen. Andere Relativitätstheoretiker sind dann in der dimensionalen Umgestaltung der Welt noch weiter gegangen, indem sie auch die Materie als dimensionalen Faktor werteten und so zur Auffassung einer fünfdimensionalen Beschaffenheit des Weltganzen gelangten. Das ist gegenwärtig sogar die herrschende Auffassung der Relativitätstheoretiker. Nach dieser haben wir also die uns umgebende Welt, das »Weltkontinuum«, als fünfdimensional zu denken, als eine Union des dreidimensionalen Raumes mit Zeit und Stoff, welch letzteren der Geltungswert je einer Dimension zukommt. Während also die Mathematik mit den von ihr definierten vieldimensionalen Räumen eine Wirklichkeitsvorstellung nicht verknüpft, ist im Gegensatz hierzu im Sinne der Relativitätstheorie das von dieser postulierte vier- oder fünfdimensionale Kontinuum die eigentliche Wirklichkeitswelt, wenn wir uns auch von einer solchen Beschaffenheit der Welt keinerlei sinnfällige Vorstellung machen können. Diese Auffassung ist den Relativitätstheoretikern selbst bereits so in Fleisch und Blut übergegangen, das Einstein, der Vater der heutigen Relativitätstheorie, den »mystischen Schauer«, der sich manchen Zeitgenossen in Erinnerung an die vierdimensionale Spuk- und Geisterwelt der Spiritisten aufdrängt, mit den Worten verspottet, es sei »keine Aussage banaler als die, daß unsere gewohnte Welt ein vierdimensionales Kontinuum ist«.

Aber auch gegen diese theoretisch erschlossene Auffassung einer vier- oder fünfdimensionalen Beschaffenheit der Welt erhebt sich das bereits betonte Argument der völligen Unvorstellbarkeit solcher begrifflichen Gebilde. Dieses Argument halten wir auch gegenüber der Relativitätstheorie aufrecht. Die Tatsache besteht, daß keinem menschlichen Geiste eine solche vier- oder fünfdimensionale Welt auch nur andeutungsweise vorstellbar ist, daß unser Sinnes- und Anschauungsvermögen und unser ganzes erkennendes Seelenvermögen überhaupt jede Möglichkeit einer solchen Vorstellung abweist. Dürfen wir die Daten, die Aussagen und Möglichkeiten unserer naturgegebenen Anschauung der theoretischen Spekulation zuliebe einfach in den Wind schlagen? Unmöglich! Alles Denken und Forschen geht von den Tatsachen und Gegebenheiten der sinnfälligen Erfahrung aus, die auch dann nicht erschüttert werden, wenn das theoretische Denken zu Ergebnissen kommt, die mit jenen Tatsachen in Widerspruch stehen. Die drei und nur drei Dimensionen, die mir die Anschauung zeigt, und die für jeden menschlichen Geist bestehende absolute Unmöglichkeit, sich Gebilde von mehr als drei Dimensionen vorzustellen, müssen für unsere Auffassung von der dimensionalen Beschaffenheit der Welt als ein rocher de bronze gelten.

Gewiß, die Sinne können trügen, und wir sind Irrtümern der Wahrnehmung, Sinnestäuschungen, Halluzinationen usw. vielfach ausgesetzt; andererseits aber ist die sinnfällige Wahrnehmung auch die Quelle absoluter Gewißheiten, über die kein Streit bestehen kann. Wenn ich drei Menschen vor mir sehe, so ist die mir damit vermittelte Dreizahl in jener Vorstellung eine absolute Gewißheit, und es hat überhaupt keinen Sinn, an dieser Gewißheit zu zweifeln. Und wenn ich an den Körpern nur drei Dimensionen wahrnehme und jede Vorstellung eines mehr als dreidimensionalen Ausgedehntseins für jedes menschliche Gehirn eine absolute Unmöglichkeit ist, so ist damit auch das Vorhandensein von drei und nur drei Dimensionen und die Unmöglichkeit des Vorhandenseins einer vierten Dimension in der Welt eine ebenso absolute Gewißheit. Sowenig mir überzeugend nachgewiesen werden kann, daß jene drei Menschen, die ich leibhaftig vor mir sehe, eigentlich vier oder fünf Menschen seien, sowenig kann irgendeine Theorie den Geltungswert der naturgegebenen Anschauung, die mir nur drei Dimensionen zeigt, erschüttern und aus diesen drei Dimensionen vier oder fünf machen. Der »mystische Schauer« vor der vierten Dimension, über den Einstein spottet, ist auch gegenüber den exakten mathematischen Deduktionen der Relativitätstheorie berechtigt und ist die verständliche Abneigung des normal denkenden Menschen, ohne weiteres eine Theorie zu akzeptieren oder theoretische Spekulationen als Wirklichkeit hinzunehmen, die an jedes menschliche Vorstellungsvermögen absolut unerfüllbare Anforderungen stellen. Die Vorstellbarkeit oder Unvorstellbarkeit aber einfach als quantité négligeable zu behandeln, die für Wert und Kritik einer Theorie völlig bedeutungslos sei (wie es die Auffassung der Relativitätstheoretiker ist), ist ein erkenntnistheoretisch absolut unzulässiges Verfahren und nur ein Beweis dafür, daß die Theorie hier über ein ihr widersprechendes Faktum nicht hinwegzukommen vermag. Die vier- oder fünfdimensionale Welt der Relativitätstheorie muß als genau so imaginär, als ebenso wirklichkeitsfremd wie die vieldimensionalen Räume der Mathematik bezeichnet werden. Tatsache ist, daß die Forscher, die die Relativitätstheorie ablehnen, ihre Gegnerschaft in erster Linie mit der völligen Unmöglichkeit begründen, die Forderungen und Annahmen dieser Theorie, vor allem die Annahme von mehr als dreidimensionalen Raumgebilden, mit unserer naturgegebenen Vorstellungs- und Anschauungsweise in Einklang zu bringen.

Es ist also folgendes festzustellen: Denken und Anschauen, diese beiden einzigen Quellen aller menschlichen Erkenntnis, sind innerhalb der Relativitätstheorie, wenigstens in der Fassung, in der sie uns gegenwärtig vorliegt, in einen, wie es zunächst scheint, unheilbaren Widerspruch geraten. Auf der einen Seite führen die Deduktionen der theoretischen Physik mit unabweisbarer Folgerichtigkeit dazu, auch Zeit und Stoff als Dimensionen zu werten, wodurch die Theorie, indem sie diese beiden als dimensionale Faktoren mit den drei Dimensionen des Raumes verknüpft, zur Forderung und Auffassung eines fünfdimensionalen Weltkontinuums gelangt. Auf der anderen Seite aber läßt uns das naturgegebene Anschauen der Welt nur drei Dimensionen erkennen und weist jede Möglichkeit der Vorstellung von Gebilden von mehr als drei Dimensionen absolut zurück, ein Faktum von nicht geringerem Geltungswert als die Forderungen und Folgerungen des reinen Denkens. Damit tut sich eine Antinomie, ein Widerspruch zwischen Denken und Anschauung auf, der überhaupt keiner Lösung fähig scheint.

Und dennoch gibt es – vielleicht – eine Lösung. Der Verfasser hat gerade das Problem der Dimensionen, insbesondere auch die Auffassung der Relativitätstheorie über die dimensionale Beschaffenheit der Welt, zum Gegenstand eigener Untersuchung gemacht, und es sei ihm gestattet, die Lösung jenes Widerspruches, die er gefunden zu haben glaubt, auch an dieser Stelle wenigstens in ihren Grundzügen zu skizzieren.

Es ist eine Lösung von größter Einfachheit und Natürlichkeit, die sich ganz ungezwungen darbietet. Gewiß sind auch Zeit und Stoff als dimensionale Faktoren zu werten, die ebenso wie der Raum zu der dimensionalen Wirklichkeitsgestaltung der Welt beitragen. Deswegen sind wir aber doch nicht genötigt, das jeder Anschaulichkeit und Vorstellung spottende Unding eines vier- oder fünfdimensionalen Kontinuums gelten zu lassen. Denn wie Zeit und Stoff den Geltungswert nur je einer Dimension haben, so hat auch der Raum, den wir bisher als das Kontinuum von drei Dimensionen aufzufassen gewohnt sind, in Wirklichkeit nur Funktion und Bedeutung einer Dimension. Das Kontinuum um uns herum ist dreidimensional, wie es uns die naturgegebene Anschauung lehrt; aber es ist nicht ein lediglich räumliches Kontinuum, sondern ein räumlich-zeitlich-stoffliches Kontinuum, in welchem dem Raum, der Zeit und dem Stoff die Bedeutung und Wirksamkeit je einer Dimension zukommt. In dem dreidimensionalen Kontinuum der Um- und Körperwelt, das wir als »Raum« bezeichnen, ist das Räumliche in Wirklichkeit nur eine Komponente von der Bedeutung einer einzigen Dimension, die sich mit den anderen beiden Komponenten, Zeit und Stoff, zu der dreidimensionalen Union der Wirklichkeitswelt zusammenfindet.

Das ist die Lösung, die uns selbst bei vollkommener Anerkennung der dimensionalen Wirksamkeit von Zeit und Stoff jeder Notwendigkeit enthebt, das Weltkontinuum als vier- oder fünfdimensional aufzufassen. Die theoretische Deduktion, die verlangt, auch Zeit und Stoff als Dimensionen in der Welt- und Wirklichkeitsgestaltung gelten zu lassen, ist mit der naturgegebenen Anschauung, die uns drei und nur drei Dimensionen zeigt und die Vorstellung von mehr als dreidimensionalen Gebilden zu einer absoluten Unmöglichkeit für jeden menschlichen Geist macht, in vollkommene Übereinstimmung gebracht. Die Antinomie zwischen Anschauung und Denken ist vollkommen und in natürlichster und ungezwungenster Weise beseitigt.

Diese Lösung bedeutet keinen Widerspruch gegen die Relativitätstheorie. Ganz im Gegenteil! Sie läßt insbesondere den genialen Grund- und Hauptgedanken Einsteins, die Relativität der Zeit, vollkommen unangefochten; aber sie stellt die Theorie in jenen Teilen, wo sie zu Konsequenzen führt, die jeder menschlichen Vorstellungsfähigkeit widersprechen, auf eine natürliche Basis, auf der die Forderungen der theoretischen Deduktion mit den Tatsachen und Forderungen der naturgegebenen Anschauungsweise in vollkommene Übereinstimmung gebracht werden. Sie befreit die Theorie von einem Widerspruch, der ihr in ihrer heutigen Fassung unzweifelhaft anhaftet und ihr, solange dieser Widerspruch besteht, den Stempel des Imaginären und Wirklichkeitsfremden aufdrückt.

Das Problem der Dimensionen ist nicht identisch mit den Problemen der Relativitätstheorie. Es hat lange bestanden, bevor die Relativitätstheorie aufgestellt wurde, und umfaßt wesentliche Gesichtspunkte, die von neuem aufgerollt und durch den Streit, der sich an jene Theorie heftet, von neuem Gegenstand der Betrachtung von den verschiedensten Gesichtspunkten aus geworden sind. Daß auch die Spiritisten bereits versucht haben, die Relativitätstheorie für ihre vagen Spekulationen über die vierte Dimension in Anspruch zu nehmen, soll der Komik wegen nicht unerwähnt bleiben. So nimmt das Problem nach wie vor im Denken unserer Zeit, in dem Ringen nach Wahrheit und nach Gewinnung eines Wirklichkeitsbildes, eine hervorragende Stelle ein als eine der eigentümlichsten Fragen, die den menschlichen Geist beschäftigen, umbraust vom Streit der Meinungen, Gegenstand der verschiedensten Spekulationen und nach wie vor seiner endgültigen Lösung und Entscheidung harrend.

Postskriptum

Der Grundgedanke, der in der Frage nach der dimensionalen Beschaffenheit der Welt die Forderungen der Relativitätstheorie mit den Forderungen unserer naturgegebenen Anschauung in Einklang bringen zu können glaubt, konnte hier nur angedeutet werden. Wer seine ausführlichere Darstellung und genauere Begründung kennen lernen will, wird diese in des Verfassers Schrift »Das Problem der Dimensionen« Berlin 1926, Verlag Arthur Collignon. finden, in der das Gesamtproblem, nicht nur die relativitätstheoretische Seite desselben, zum Gegenstand der Untersuchung gemacht worden ist und noch von anderen Gesichtspunkten aus die Dreiheit der Dimensionen als Naturkonstante der Weltwirklichkeit nachzuweisen gesucht wird. Der Verfasser glaubt, mit jenem neuartigen Gedanken, der auch dem Raum nur Wert und Wirkungsweise einer Dimension zuerkennt, das vielumstrittene Problem der dimensionalen Beschaffenheit der Welt zum wenigsten auf eine neue Grundlage gestellt zu haben, die eine Lösung des Problems bringen kann.

VI.
Probleme des Metaphysischen

1. Das Problem der Willensfreiheit

Die älteste und schwierigste Frage der Philosophie – Der naive Mensch und sein Argument – Die Kausalität des Geschehens – Zwei Lager – Anhänger und Gegner in der Geschichte der Philosophie – Die Auffassung Kants: die intelligible Freiheit – Das Denken der Gegenwart – Das Fatum – Buridans Esel und Fullertons Hund – Stellungnahme – Die Lösung: Wahlfreiheit – Das Gefühl der Willensfreiheit und sein Wert

Keine Frage von größerer und folgenschwererer Bedeutung für die Beurteilung alles Menschlichen kann es geben als die Frage: Ist der Mensch willensfrei? Ist er in seinem Tun und Lassen abhängig und bestimmt von den Kräften und Mächten, die die Bewegungen und Erscheinungen der unbelebten und nur passiv tätigen Natur bedingen und regeln, oder aber bestimmt er seine Handlungen aus sich selbst heraus, aus inneren Regungen und Motiven, die, unabhängig von dem Kausalnexus von Ursache und Wirkung im mechanischen Naturgesetz, ein Teil seines Seelenlebens und seines ureigensten Seins und Wesens selbst sind und damit sein Tun und Lassen zu einem freien Handeln seines Willens stempeln, für das er und nur er allein verantwortlich ist? Ist auch er eine wenn auch noch so komplizierte Maschine und als solche nur ein mechanisch funktionierendes und daher willenloses Glied in dem nach Raum und Zeit unendlichen Zusammenhang des mechanischen Naturgeschehens, oder ist er ein frei waltender Geist, für den jener Kausalnexus zum mindesten nicht in zwingender Form besteht, sondern der sich die Motive und Gesetze seines Handelns selbst, nach freier, abwägender Überlegung gibt, so wie sich jenes in seinem Bewußtsein widerspiegelt?

Seit der Mensch überhaupt zum Denken über sich selbst und seine Stellung innerhalb des Naturganzen vorgedrungen ist, hat sich ihm auch diese Frage aufgedrängt. Schon die einfache Tatsache, daß er überhaupt dazu kam, jene Frage aufzuwerfen, ist ein Beweis dafür, daß er hier ein Rätsel, ja mehr: ein Problem vorfand, das ihn in einen ausgesprochenen Gegensatz zu der unbelebten und nur mechanisch bewegten Natur und ebenso zu den Bewegungsmechanismen mehr oder weniger komplizierter Art, die er selber herstellt, brachte. Die Frage nach der Willensfreiheit seiner selbst war das erste und älteste Problem, das sich mit dem Erwachen der philosophischen Überlegung einstellte, sie war die erste, die wichtigste und schwierigste Frage der Philosophie von allem Anbeginn und hat diese Bedeutung bis auf den heutigen Tag beibehalten.

Und wie schon in den philosophischen Schulen des Altertums, so stehen sich auch noch in der heutigen Philosophie in der Beantwortung dieser Frage Ja und Nein schroff gegenüber. Wir sind, um es gleich vorwegzunehmen, in der Auffassung und Entscheidung dieser Frage seit den Tagen der alten indischen oder griechischen Philosophen bis heute kaum einen Schritt vorwärtsgekommen, höchstens daß die neuere Philosophie zwischen jene Gegenpole, das entschiedene Ja und das radikal ablehnende Nein, noch eine dritte, vermittelnde Auffassung und Antwort einzuschalten gesucht hat. Die ungeheure Wichtigkeit des Problems aber wird ersichtlich, wenn wir uns vergegenwärtigen, daß von der Auffassung und Entscheidung darüber die Frage der sittlichen Verantwortung des Menschen abhängig ist, insbesondere auch die Frage der strafrechtlichen Verantwortung. Die Frage nach der Willensfreiheit ist zugleich auch das Grundproblem der rechtlichen Überlegung. Wenn der Mensch nicht willensfrei handelt, sondern sein Tun und Lassen unter dem Zwange naturgesetzlicher Kräfte steht, so ist er für seine Handlungen, wenn diese auch Vergehen oder Verbrechen darstellen, ebensowenig verantwortlich zu machen wie etwa eine Dampfmaschine, die einen sich ihr unvorsichtig nähernden Menschen ergreift, in ihr Getriebe hineinzieht und zerschmettert. Und wenn man kürzlich in einem Zoologischen Garten einen Elefanten erschossen hat, weil dieser bereits den zweiten Wärter getötet hatte, so geschah das – nebenbei gesagt sehr im Widerspruch mit den tierliebenden Kreisen der Stadt – nur aus Zweckmäßigkeitsgründen und um weiteren Fällen dieser Art vorzubeugen, nicht etwa auf Grund strafwürdiger Verantwortung des Dickhäuters, denn für das Tier gibt es eine sittlich-rechtliche Verantwortung auf Grund freier Willenstätigkeit nicht. Der Elefant ist nicht »bestraft«, sondern aus dem Wege geräumt worden, wenn das auch de facto auf dasselbe hinauskommt. Die Rechtspflege kann ihren Anspruch auf Bestrafung, durch die sie den Täter zur moralischen Verantwortung für seine Handlung zieht, nur aus dem Postulat der Willensfreiheit desselben herleiten, und der Streit darüber, ob und wieweit dieses Postulat zu Recht besteht, beherrscht die Rechtsphilosophie der Gegenwart nicht minder als die zeitgenössische Philosophie überhaupt.

Der naiv denkende Mensch freilich, der nicht von der Gedankenblässe philosophischer Problematik angekränkelt ist, ist zunächst sehr erstaunt, daß die Frage nach seiner Willensfreiheit überhaupt aufgeworfen wird. Denn für ihn gibt es da überhaupt kein Problem; für ihn ist es absolut selbstverständlich, daß er willensfrei ist und handelt. Denn – und das ist sein natürliches Argument – ich habe doch bei jeder meiner Handlungen das klare Bewußtsein meines freien Willens als Motiv meines Handelns, das deutliche Gefühl, daß sie aus freiem persönlichen Willen heraus geschieht. Ich habe so gehandelt, weil ich so gewollt habe, und hätte anders und genau entgegengesetzt handeln können, wenn ich es gewollt hätte. Wie kann da die Freiheit meines Wollens und Handelns also überhaupt noch in Zweifel gezogen werden? Tatsächlich ist auf diesem Standpunkte des Denkens das Bewußtsein oder das Gefühl der Willensfreiheit das alleinige und überzeugende Argument für die Wirklichkeit der Freiheit und Unabhängigkeit des Willens.

Aber gegen diese Auffassung erhebt sich, und zwar schon auf früher Stufe der philosophischen Reflexion, ein Gegenargument, und das lautet: Jedes Geschehen hat eine Ursache und ist ohne solche überhaupt nicht denkbar. Das Fallen eines Steines, der Lauf der Gestirne, das Wachsen der Organismen, Tod und Leben, überhaupt alles Geschehen in der Natur erfolgt als Wirkung auf vorangegangene Ursachen, und nie beobachten wir einen Vorgang, der von diesem unverbrüchlichen Gesetz eine Ausnahme macht oder auch nur machen könnte. Die Handlungen des Menschen sind aber auch nur Erscheinungen des Naturgeschehens, und für diese gilt daher jenes Gesetz in demselben Maße wie für jeden Vorgang, den wir an der unbelebten Materie wahrnehmen können. Das menschliche Denken erfordert jenen Zusammenhang von Grund und Folge, von Ursache und Wirkung für ausnahmslos alles Geschehen und kann sich ein ursachloses Geschehen oder ein Handeln »aus sich selbst«, d. h. aus dem Nichts, ebensowenig vorstellen wie die Entstehung von körperlichen Dingen aus dem Nichts. Beobachtung, Experiment und Forschung haben noch immer jene Forderung des Denkens, das alles Handeln und Geschehen in den Zusammenhang von Grund und Folge, von Ursache und Wirkung setzt, bestätigt. Das gilt auch für alle menschlichen Handlungen, und daher muß das Gefühl der Willensfreiheit, das sich an diese knüpft, als Irrtum oder Täuschung bezeichnet werden, als eine Gefühlstäuschung, ähnlich den Sinnestäuschungen oder Halluzinationen, denen wir ja vielfach ausgesetzt sind und die uns zu falschen Folgerungen verführen.

Freilich liegen beim menschlichen Handeln die bestimmenden Ursachen nicht so frei zutage wie bei den Vorgängen der unbelebten Natur, sondern sie liegen versteckt, und zwar einerseits in der physischen Konstitution des Menschen, andererseits in den physischen Bedingungen der Umwelt, in die er gestellt ist, des »Milieus«, und müssen aus diesen Komplexen heraus gesucht und gefunden werden. Ein Beispiel: Der Mensch, der Nahrung zu sich nimmt, tut das nicht aus absolut freiem Willen heraus, sondern weil er Hunger hat; der Hunger aber ist eine Folge des augenblicklichen physiologischen, also physikalisch-chemischen Zustandes seines Körpers, also eine Folge physischer Faktoren, und somit sind diese die Ursachen des Hungers und damit zugleich auch der Nahrungsaufnahme. Allerdings kann der Mensch trotz des Hungers auf das Essen verzichten mit der einfachen Begründung »Nun gerade nicht!« Aber auch in diesem Falle, so wird eingewendet, handelt er keinesfalls willensfrei, sondern die Ursache seines Handels ist dann eben sein Trotz, also eine Charaktereigenschaft, die wiederum aus der physischen Veranlagung seines Organismus zu erklären ist. Und wenn ein Märtyrer in den Hungertod gegangen ist oder ein Hungerkünstler sich trotz wütenden Hungers wochenlang der Nahrung enthält, so sind auch in solchen Fällen die Ursachen des Handelns immer im Charakter und in den Verhältnissen der Daseinsweise zu suchen. Immer lassen sich physische Faktoren als Beweggründe ausfindig machen, die auch in solchen Fällen besonderer Willensenergie das Tun und Lassen bestimmen oder »determinieren«, wie es gelehrt heißt. Immer ist der unverbrüchliche Kausalnexus, der Zusammenhang von Ursache und Wirkung in allen menschlichen Handlungen festzustellen, der die Willensfreiheit als Täuschung und Illusion kennzeichnet.

Mit dieser Gegenüberstellung der Argumente sind die beiden großen Richtungen gekennzeichnet, die, seit überhaupt das Problem der Willensfreiheit in den Gedankenkreis der Menschheit eingetreten ist, die Stellungnahme zu diesem bestimmen: einerseits der Determinismus, eben jene Auffassung, die wie alles Geschehen so auch alle menschlichen Handlungen als durch äußere Faktoren bestimmt und bedingt bezeichnet und damit dem Menschen die Willensfreiheit abspricht; andererseits der Indeterminismus, der den Menschen aus der Kette des physischen Geschehens und dem natürlichen Zusammenhang von Ursache und Wirkung herausnimmt und ihn als willensfrei handelndes Wesen allen übrigen Erscheinungen und Vorgängen der Natur gegenüberstellt. Die Begründungen beider Standpunkte scheinen gleich richtig und evident, und so scheint es, als ob das Problem der Willensfreiheit einer eindeutigen Entscheidung in dem einen oder anderen Sinne überhaupt nicht fähig wäre.

Und dieser Zwiespalt der Auffassungen des Problems zieht sich durch die ganze Geschichte des menschlichen Denkens. Aristoteles war Indeterminist; für ihn war der Mensch die »Quelle seiner Taten« und das freie Handeln der Ausdruck seiner bewußten Selbstbestimmung; die Willensfreiheit ist für ihn etwas Selbstverständliches, das Bewußtsein davon der genügende und überzeugende Beweis ihres Vorhandenseins und ihrer Wirklichkeit. Aber schon unmittelbar nach dem Tode des Aristoteles vertrat die Schule der Stoiker den entgegengesetzten Standpunkt. Sie waren es, die vor allem auf den allumfassenden, unauflöslichen und lückenlosen Zusammenhang allen Geschehens nach dem Gesetz von Ursache und Wirkung hinwiesen, einen Zusammenhang, der keine Ausnahme duldet und auch das menschliche Handeln einbegreift. Denn der Mensch ist ein Sinneswesen, dessen Handeln in jedem Falle durch Reize ausgelöst wird, die wiederum durch die Verhältnisse und Faktoren der physischen Außenwelt bewirkt werden; also kann es auch für den Menschen keine Willensfreiheit geben, denn eine solche würde den Kausalzusammenhang der Natur stören und das Chaos in den kausal geordneten Kosmos tragen. Und nicht nur das augenblickliche oder gegenwärtige, sondern auch das zukünftige Handeln des Menschen ist durch diesen Kausalnexus determiniert. Die Stoiker waren von der Vorherbestimmung allen Geschehens, auch des menschlichen Tuns, überzeugt; daher kann es nach ihrer Auffassung gegen das Walten der Naturgesetze, in denen das unerbittliche Schicksal selbst zum Ausdruck kommt, keine Willensfreiheit und keine Auflehnung geben, sondern nur weise Ergebung, eine Auffassung, deren Konsequenz die stoische Lebensauffassung ist, die sich populär am besten mit den Worten ausdrücken läßt: »Mir ist alles Wurst!«

Und dieser Zwiespalt der Auffassungen für oder gegen die Willensfreiheit zieht sich weiterhin durch die ganze Geschichte des philosophischen Denkens. In allen seinen Phasen standen Determinismus und Indeterminismus einander gegenüber. Nach der Kirchenlehre des Mittelalters kann der Mensch keine Willensfreiheit haben, denn sonst wäre er in der Lage, gegen den Willen Gottes zu handeln, der allein Selbstbestimmung und absolute Willensfreiheit besitzt, wie es der Begriff der göttlichen Allmacht erfordert. Viele Vertreter der mittelalterlichen Scholastik aber waren Indeterministen, wie etwa der berühmte Duns Scotus, der im 13. Jahrhundert lebte und lehrte und dem menschlichen Willen die Fähigkeit zusprach, auch ohne bestimmende Gründe seine Entscheidungen zu vollziehen. Mit dem Beginn der neueren Philosophie, die durch den Franzosen Descartes eingeleitet wird, scheiden sich die Geister abermals. Descartes selbst nahm unbedingte Willensfreiheit an, die für ihn so gewiß und selbstverständlich wie nur irgendein anderer der uns angeborenen Begriffe ist. Descartes' großer Nachfolger Spinoza aber war ebenso entschiedener Determinist und sah in dem Menschen nichts weiter als ein Glied in der Gott-Natur, deren Walten er untertan ist, und in dieser Auffassung stimmte ihm auch der große und universale Denker Leibniz bei, sonst der erbittertste Gegner Spinozas, der aber auf Grund der Prädestination, der Vorherbestimmung, dem Menschen die Fähigkeit zu eigenem und unabhängigen Handeln absprechen mußte und in dem Willen nicht die Ursache des Handelns, sondern nur die Wirkung der individuellen Qualitäten und Neigungen des Menschen sah.

Einen neuen und tiefgehenden Gesichtspunkt trug Kant an das Problem heran. Auch er sieht in dem Menschen als physischem Wesen nur ein Glied in der Kette der Erscheinungen, für das alle Gesetze von Ursache und Wirkung gelten. Aber der Mensch ist nach Kant nicht nur ein Wesen der physischen Erscheinungswelt; seiner innersten Natur nach gehört er dem Reiche des rein Geistigen an und als solcher ist er dem Ursachengesetz der physischen Natur entrückt und hat die Fähigkeit, einen Ablauf des Geschehens ursachlos zu beginnen. Als Vorgang der Erscheinungswelt betrachtet, ist dieser Geschehensverlauf durch Naturgesetze bedingt und bewirkt, als Akt des Intelligiblen ist er ein Erzeugnis der Selbständigkeit der praktischen Vernunft und daher ursachlos. Dieses Vermögen der ursachlosen Selbstbestimmung ist die intelligible Freiheit, die sich im Bewußtsein als Willensfreiheit bekennt und dem Menschen zur untrüglichen Gewißheit wird. Man hat Kant diese Dualität, diese Zweiseitigkeit seiner Auffassung in der Frage der Willensfreiheit, oft zum Vorwurf gemacht und darin eine Doppeldeutigkeit und Zwiespältigkeit sehen wollen, die das Problem selbst völlig unentschieden läßt, und Kants Nachfolger, die Fichte, Schelling und Hegel, suchten, entsprechend ihrer völlig idealistischen Denkungsweise, auch in dieser Frage über ihren Meister hinauszugelangen und sprachen daher dem Menschen eine absolute Willensfreiheit zu, die ihm eine Sonderstellung in der einzigen und einheitlichen Natur des physischen und geistigen Geschehens gibt.

Diese Phase des reinen Denkens führte zu einem Zusammenbruch der Philosophie, durch welchen die rein idealistischen Gedankensysteme hohn- und spottbeladen in der Versenkung verschwanden und mit ihnen die extreme Auffassung des absolut freien Willens. Das entgegengesetzte Extrem der Auffassungsweise griff Platz, das rein naturwissenschaftliche Denken bemächtigte sich des Problems der Willensfreiheit. Materialismus und Monismus, in denen diese Denkungsweise ihren radikalsten Ausdruck fanden, sahen im Menschen nur ein Naturerzeugnis, nur einen Mechanismus nach Art einer Maschine und in seinen Funktionen, physischen wie geistigen, nur Bewegungsvorgänge dieser Maschine, die völlig der naturgesetzlichen Kausalität unterliegen. Der Mensch ist eine Maschine –! Mit dieser Parole, die schon vorher der Enzyklopädist de la Mettrie aufgestellt und in extremster Weise ausgebaut hatte, war jeder Gedanke an Willensfreiheit unvereinbar. Diese Denkungsweise bildet den Höhepunkt und die radikalste Ausprägung des Determinismus, der Jahrzehnte hindurch die Auffassung über die Frage der Willensfreiheit in den Kreisen der Gebildeten beherrschte.

Erst mit dem Wiedererwachen des philosophischen Geistes, der sich darauf besann, daß die Welt mit Kraft und Stoff allein nicht zu erklären sei, trat auch eine neue und entschiedene Betonung zugunsten der indeterministischen Auffassung des Problems wieder mehr in den Vordergrund. Die Philosophie der Gegenwart vertritt im wesentlichen eine vermittelnde Auffassung des Problems, die als relativer oder auch als psychologischer Determinismus bezeichnet wird, aber ebensogut auch als relativistischer Indeterminismus bezeichnet werden könnte. Nach dieser Auffassung wird das menschliche Handeln sowohl durch äußere wie auch durch innere Ursachen bestimmt und bedingt. Soweit äußere Faktoren auf den Menschen einwirken und sein Handeln bestimmen, ist er dem naturgesetzlichen Ursachenzwang unterworfen, soweit er jedoch nach inneren, aus geistiger Veranlagung, das heißt seinem Charakter entspringenden Motiven handelt, ist und handelt er frei, soweit unter Freiheit die Möglichkeit der Willensentscheidung unabhängig von äußerem Zwange, nur auf Grund innerer seelischer und intellektueller Neigungen, zu verstehen ist. Keinesfalls aber ist diese Freiheit gleichbedeutend mit völlig ursachlosem Handeln, wie sie etwa Kant für die intelligible Welt gelten ließ. Der Mensch ist und handelt frei innerhalb der Grenzen und Möglichkeiten seines Charakters, das ist im wesentlichen die Quintessenz des psychologischen Determinismus, der nach verschiedenen Vorgängern und Variationen in Deutschland besonders von Wilhelm Wundt vertreten und systematisch ausgestaltet worden ist, der für das Handeln des Menschen, soweit es nicht naturgesetzlich bedingt ist, eine Art geistiger Kausalität gelten lassen will, die nicht dem Zusammenhange von Ursache und Wirkung unterliegt. Wie man sieht, hat diese vermittelnde Auffassung des Problems Elemente aus beiden Seiten entnommen, die sie in die Form einer höheren Einheit überzuführen sucht. Ob ihr das gelungen ist und ob insbesondere hierdurch eine befriedigendere Auffassung des Problems oder gar eine Lösung desselben erreicht worden ist, muß freilich sehr dahingestellt bleiben.

Dieses kaleidoskopartige Bild läßt, so skizzenhaft und unvollständig es auch sein mag, doch die Tiefe und die ungeheure Bedeutung des Problems der Willensfreiheit für die Entwicklung der Erkenntnis und Selbsterkenntnis im Verlaufe des menschlichen Denkens erkennen. Aber das Problem hat nicht nur theoretisch-spekulative Bedeutung gehabt. Oft hat gerade die Auffassung über diese Frage das praktische Handeln der Menschheit tiefgehend beeinflußt. Besonders die deterministische Auffassung, die alles menschliche Tun und Lassen wie alles Geschehen innerhalb der Natur in den Zusammenhang von naturgegebenen Ursachen und Wirkungen stellt, hat im geistigen, politischen und kulturellen Leben, in Krieg und Frieden, oft zu bedeutungsvollen Konsequenzen geführt. Als Mohammed seine Scharen gegen Asien und Europa führte, da war der von ihm gelehrte und gepredigte Glaube an das Fatum, die Lehre, daß jedem Menschen sein Schicksal vorherbestimmt ist und er diesem so wenig entgehen kann wie etwa die Gestirne den vorausberechneten Konstellationen, ein treibendes Element von größter Gewalt, mit dem er seine Kämpfer zu Todesverachtung und alles vergessender Kampfbravour hinriß. Denn, so folgerte jene Lehre, begreiflich und verständlich auch für den einfachsten Soldatenverstand, ob der Kämpfer für Allah feige oder tapfer ist, ob er sich mit Todesverachtung in die feindlichen Reihen stürzt oder um sein Leben besorgt die Flucht ergreift und sich hinter den eigenen Reihen verbirgt, sein Schicksal steht unverrückbar fest. Wenn er fallen soll, so wird ihn dieses Schicksal erreichen, selbst wenn er sich in den geheimsten Schlupfwinkel verkriecht; ist ihm aber bestimmt zu leben, so kann ihm auch das furchtbarste Schlachtengetümmel und die todesverachtende Kühnheit nichts anhaben. Also kämpfe wie ein Löwe zu Ehren Allahs! Mit diesem Fatalismus riß Mohammed seine Heerscharen zum Siege fort, und Jahrhunderte war diese Lehre das geistige Bollwerk des Islam, von dem aus der Prophet und seine Nachfolger den Schrecken in alle Lande trugen. Der Fatalismus, diese radikale Konsequenz des Determinismus war ein Faktor von weltgeschichtlicher Bedeutung geworden. Freilich steckte gerade in diesem Determinismus ein gut Stück Demagogie. Mit derselben Logik, mit der jene Lehre die Kämpfer zu todesverachtender Kühnheit anspornte, hätte jeder einzelne Kämpfer auch folgern können, daß den Heeren Allahs, sofern ihnen der Sieg bestimmt sei, dieser auch dann nicht entgehen könne, wenn jeder einzelne der Streiter sich in ein Mauseloch verkröche! Warum also sich Gefahren aussetzen? Diese nicht minder berechtigte Folgerung, die sich aus dem Fatalismus ergibt, hat man allerdings wohlweislich verschwiegen. Die völlige Einseitigkeit und damit zugleich die Unzulänglichkeit des Determinismus aber kommt in jener Gegenüberstellung aufs beste zum Ausdruck. Jene fatalistische Argumentation zur Anfeuerung des soldatischen Mutes hat sich übrigens keinesfalls auf die Mohammedaner beschränkt, sondern ist mehr oder weniger wohl immer herangeholt worden, wo es galt, die Kriegsscharen zu begeistern, und wo sich zwei Heere gegenüberstanden, da wurde noch immer auf dieser wie jener Seite verkündet, daß »Gott mit unserer gerechten Sache« sei, eine durchaus deterministische, ja sogar fatalistische Parole.

Von grundlegender ethischer Bedeutung ist die Auffassung über das Problem der Willensfreiheit für Rechtspflege und Rechtsphilosophie geworden, und die gegenwärtige Rechtsauffassung sucht sich in stärkster Weise an jenem Problem zu orientieren. Es herrscht hier heute eine stark deterministische Neigung vor, die die Handlungen des Täters vor allem aus den sozialen und wirtschaftlichen Verhältnissen der Umwelt wie auch aus der persönlichen Veranlagung, Vererbung usw. begreifen will und die Frage zu entscheiden sucht, wieweit solche Faktoren bei Begehen der Tat als verursachende Momente im Spiel waren und die freie Willensentscheidung des Täters verminderten.

Man hat sich aber nicht immer mit der theoretischen Erörterung des Problems begnügt, sondern gelegentlich versucht, dieses sozusagen bei den Hörnern zu ergreifen und durch praktische Veranschaulichung oder gar durch Experimente zu lösen. Solche Veranstaltungen haben meist einen gewissen humoristischen Beigeschmack. Das berühmteste Beispiel dieser Art hat wohl der französische Philosoph Jean Buridan gegeben, der im 14. Jahrhundert lebte und mehr als durch seine zahlreichen philosophischen und theologischen Schriften durch das von ihm ersonnene Beweisbeispiel für den Determinismus, nämlich den berühmten Esel Buridans, bekannt geworden ist. Ein hungriger Esel sei zwischen zwei Bündel Heu gestellt, die auf ihn die gleiche Anziehungskraft ausüben; weil er also nicht weiß und sich nicht entscheiden kann, welchem der beiden Bündel er sich zuerst zuwenden soll, muß er elend verhungern. Damit wollte Buridan veranschaulichen, daß es keine ursachlose Willensentscheidung bei Tier oder Mensch gäbe und das Bewußtsein der Willensfreiheit nur eine Täuschung sei. Tiefen Eindruck hat das Argument bei Gegnern und Anhängern der Willensfreiheit gerade nicht gemacht, aber viel gelacht ist darüber worden, und Buridans Esel hat damit sich und seinen geistigen Vater auf die Nachwelt gebracht. Aber was Buridan immerhin nur als Gedankenexperiment angestellt hat, das hat späterhin einmal ein amerikanischer Gelehrter, der Psychologe Fullerton, in praxi auszuführen versucht, um auf diese Weise die ewig umstrittene Frage nach der Willensfreiheit zur Entscheidung zu bringen. Zu diesem Zweck stellte er einen Hund, der darauf dressiert war, seine Nahrung nur auf Zuruf zu nehmen, zwischen zwei Würste. Die Würste waren nach Größe, Form und Füllung und allen sonstigen Eigenschaften, durch die sie auf ein Hundegemüt wirken konnten, von genau gleicher Beschaffenheit, auch waren sie in genau gleichem Abstande von dem Hunde hingelegt und auch alle übrigen Bedingungen, soweit es nur möglich war, auf völlige Symmetrie eingestellt. Und dann gab der Experimentator dem Hunde das Zeichen. Nun, der Hund tat das Gescheitste, was er tun konnte, er fraß erst die eine Wurst und dann die andere, und hat mit diesem bündigen Verfahren vielleicht einen Mangel an philosophischer Reflexion, aber zugleich auch einen überzeugenden Beweis dafür gegeben, daß eine Hundeseele sich durch solche wie die geschilderten Umweltfaktoren jedenfalls nicht in ihrer Willensentscheidung beirren läßt.

Heute ist das Problem der Willensfreiheit noch genau so umstritten wie nur je. Determinismus und Indeterminismus haben ihre Anhänger, und zwischen beiden sucht der psychologische Determinismus zu vermitteln, ohne daß es ihm aber gelungen wäre, einen herrschenden oder entscheidenden Einfluß auf die Auffassung zu dem Problem zu gewinnen. Als eine »Aporie«, eine Denkschwierigkeit, zu deren Beseitigung sich kein Weg finden zu lassen scheint, stellt sich das Problem dem grübelnden Menschengeiste dar und spottet aller Bemühungen seitens Gelehrter und Ungelehrter, zu einer eindeutigen Auffassung zu gelangen. Jedem einzelnen bleibt es überlassen, sich im Streite der Meinungen auf die eine oder die andere Seite zu stellen und darin einen persönlichen Standpunkt zu gewinnen und zu begründen.

Suchen auch wir zu einer bestimmten Auffassung zu dem Problem zu gelangen, so glauben wir jedenfalls die rein deterministische Auffassung mit guten Gründen ablehnen zu können. Zweifellos das stärkste Argument, das der Determinismus für die Verneinung des willensfreien Handelns vorbringt, besteht in dem Hinweis auf das Kausalitätsgesetz, den Zusammenhang zwischen Ursache und Wirkung, den wir überall in der Natur waltend vorhanden sehen und den unser Denken für alles physische Geschehen unzweifelhaft fordert. Aber auch nur für dieses, nur für das physische Geschehen der unbelebten Materie wird diese Forderung erhoben und nur für dieses kann sie erhoben werden. Keine Berechtigung aber haben wir zu der Annahme, daß auch das geistige Geschehen, wie es sich im seelischen und intellektuellen Leben, im Fühlen und Empfinden, Denken und Wollen des Menschen abspielt, demselben Gesetz von Ursache und Wirkung unterworfen sei. Das Geistige ist anderer Art als das Physische, und die völlige Heterogenität dieser beiden Wesenheiten schließt es aus, daß die eine auf die andere zwangsläufig wirken könnte wie etwa die Erde vermöge ihrer Anziehungskraft auf den Stein, der zu ihr herabfällt. Damit ist aber auch zugleich gesagt, daß die Willensentscheidung, die immer ein Akt rein geistiger Natur ist, nicht physisch kausiert sein kann, und damit ist zugleich dem Determinismus sein Hauptargument entzogen.

Aber auch der psychologische Determinismus bedeutet keine Möglichkeit befriedigender Auffassung des Problems. Im Gegenteil, sein Vermittelungsversuch zwischen den beiden Hauptlagern ist doch nur ein Schwanken zwischen den Argumenten beider, bei dem ein fester Standpunkt nicht erreicht wird. Er ist letzten Endes doch nur ein verbrämter Determinismus, und seine Art, teils innere geistige, teils äußere physische Ursachen als Triebfedern des Willens und Handelns gelten zu lassen, dieses teils für frei, teils für unfrei zu erklären, bietet mit dieser völlig unbestimmten Haltung am ehesten das Bild jener berühmten deterministischen Figur, des Buridanschen Esels selbst, der nicht weiß, für welche der beiden Seiten er sich entschließen soll und – zur Spottfigur wird. Gerade in der Frage der Willensfreiheit kann es nur ein Ja oder Nein geben, und ein Drittes ist nach allen logischen Gesetzen gerade in diesem Problem der Erkenntnis ausgeschlossen.

Damit rücken wir in unserer Stellungnahme von selbst auf die Seite des Indeterminismus, und wir glauben mit diesem, daß der menschliche Wille als geistige Wesenheit in den von ihm inaugurierten Handlungen unabhängig ist von den Gesetzen der physischen Natur, daß er insbesondere dem Kausalgesetz des zwangsläufigen physischen Geschehens nicht unterliegt und in diesem Sinne frei ist. Aber freilich, völlig grundlos, völlig aus sich selbst heraus, wie Kant die intelligible Freiheit des Willens interpretierte, kann der Wille den Ablauf des Geschehens nicht inaugurieren. Aber die Gründe seiner Entscheidungen und seines Handelns sind nicht physischer Natur, sondern Motive geistiger Art, die der freien Beurteilung des denkenden und wollenden Subjektes für seine Willenshandlungen unterliegen. Gewiß, ich esse, weil ich Hunger habe, oder ich unterlasse das Essen trotz des Hungers, wenn mich andere Motive zu dieser Art des Handelns veranlassen; ob ich dies oder jenes tue und welchem von den vielen dabei waltenden Motiven ich mich schließlich zuwende, das ist ein Akt freien Wählens zwischen den Motiven auf Grund der freien und vernünftigen Überlegung. Ein Wollen und Handeln völlig ohne Motive gibt es nicht und kann es nicht geben, aber die Motive sind mit dem Sein und Dasein des Willens immer zugleich gegeben. Der Wille ist nicht nur triebhafter Urinstinkt im Sinne Schopenhauers, sondern wo er zum Handeln gelangt, ist er ein bewußt denkendes Handeln nach Motiven. Die Vielheit der Motive ist zugleich mit allem Wollen und Denken gegeben. In der Wahl der Motive ist der Wille, ist der handelnde Mensch frei und autonom, entscheidet und handelt er lediglich nach den Gründen seiner Überlegung. Die Freiheit des Willens ist also Wahlfreiheit.

Den stärksten Beweis für die Wirklichkeit der Willensfreiheit aber sehen wir in dem Gefühl und Bewußtsein der Freiheit, das mit allen unseren Entschlüssen und Handlungen untrennbar verknüpft ist, selbst. Jenes Gefühl, das schon dem naiv denkenden und philosophisch noch völlig unverbildeten Menschen die Freiheit seines Willens zu einer ganz selbstverständlichen Tatsache macht, ist ein Argument, das auf keine Weise hinwegdisputiert oder erschüttert werden kann, so wenig wie die Aussage oder der Gegenstand eines anderen Gefühls oder einer Vorstellung hinwegdisputiert werden kann, etwa die Vorstellung des Himmels. Was der »Himmel« ist, darüber mag unser Denken, mögen Astronomen und Theologen zu sehr verschiedenen Ansichten kommen, aber daß ich die Vorstellung und Wahrnehmung des Himmels habe und daß ein Ding vorhanden ist, das Gegenstand dieser Vorstellung und Wahrnehmung ist, das ist ein Faktum, das für kein Denken aus der Welt geschafft werden kann.

Damit kehren wir zu dem ursprünglichsten Argument für die Willensfreiheit als notwendigen Ausgangspunkt aller Spekulationen über dieses Problem zurück und erkennen es in vollem Umfange als berechtigt an. Ich habe doch bei jeder meiner Handlungen das Bewußtsein, das deutliche Gefühl, daß sie aus freiem persönlichen Willen heraus erfolgt; ich habe so gehandelt, weil ich so gewollt habe und hätte ebensogut anders und genau entgegengesetzt handeln können; wie sollte ich da also an der Freiheit meines Willens zweifeln? Tatsächlich, in dieser ursprünglichen und naiven Argumentation steckt letzten Endes alle Wahrheit und Weisheit über das so unendlich vielerörterte Problem der Willensfreiheit. Der Determinimus glaubt allerdings den Wert und die Beweiskraft dieses Arguments mit der Behauptung abtun zu können, daß jenes Gefühl der Willensfreiheit trügerisch sei. Aber demgegenüber muß betont werden, daß es absolut keinen Sinn hat, ein Gefühl als trügerisch zu bezeichnen. Das Gefühl der Willensfreiheit ist ein Erlebnis von ursprünglicher und unmittelbarer Gewißheit, genau so wie irgendein Gefühl von Lust oder Unlust oder eine Farb- oder Tonempfindung oder sonst irgendein unmittelbares seelisches Erlebnis. Hat es überhaupt einen Sinn, zu sagen, ich sei in einer Täuschung begriffen, wenn mir der Wein angenehm schmeckt, wenn ich froh gestimmt bin, wenn ich das Blatt des Baumes als grün empfinde oder wenn ich den Himmel sehe? Sowenig das der Fall sein kann, sowenig kann es Sinn haben, den Wahrheitswert des Freiheitsgefühls in Zweifel zu ziehen. Über solche unmittelbaren seelischen Erlebnisse ist überhaupt kein Zweifel möglich. Irren kann immer nur das Denken, das sich an solche Erlebnisse knüpft; irren beispielsweise kann man in der Spekulation darüber, was der Himmel ist, oder in der Reflexion, die man an das Gefühl der Willensfreiheit knüpft, wenn man annehmen zu können glaubt, dieses Gefühl könnte trügerisch sein. Das Gefühl der Willensfreiheit hat denselben Erlebniswert wie irgendeine Sinneswahrnehmung und gibt mir für die Freiheit meines Handelns denselben Grad von Gewißheit, wie die Wahrnehmung, daß Achilles die Schildkröte einholt, mir Gewißheit über die Tatsächlichkeit dieses Vorganges verschafft gegenüber der rechnerischen Reflexion, die zu dem Schluß kommt, daß der Schnelläufer die Schildkröte niemals einholen könne. Daß man in diesem wie in jenem Falle dem spekulativen Denken größeren Wahrheitswert beimaß als dem eindeutigen unmittelbaren Erlebnis selbst, stempelt auch das Problem der Willensfreiheit und allen geistigen Aufwand, der an dieses im Laufe der Jahrhunderte vertan wurde, zu einem Wettlauf mit der Schildkröte.

2. Sternenlauf und Menschenschicksal

Krieg und Okkultismus – Das Horoskop des »Gebildeten« – Allgemeinwirkung und Einzelschicksal – Kepler und Newton – Die Mathematik des Astrologen – Die Kunst der Deutung – Eine unbeantwortete Frage – Ein »wissenschaftlicher« Astrolog – Des Schicksals Sterne

Der Okkultismus aller Richtungen und Schattierungen hat gegenwärtig Hochkonjunktur! Das ist eine Folge des Weltkrieges, die in allen Ländern, die überhaupt an diesem größten und erschütterndsten Völkerringen beteiligt waren, zu verzeichnen ist und wohl noch lange anhalten wird. Die seelische Aufwühlung und Verwirrtheit, die das schwere Erlebnis des Krieges bei ungezählten Hunderttausenden bewirkt hat, ist noch lange nicht verwunden. Und diese Erschütterung des Seelenlebens ist es, die, ohne geradezu pathologisch gewertet werden zu müssen, doch geeignet ist, den Blick selbst des gebildeten und intelligenten Menschen für die Wirklichkeit und Natürlichkeit der Dinge und des Geschehens zu trüben, ihn für die mancherlei Irrgänge des Denkens und Glaubens empfänglich zu machen und seine Neigung und Sehnsucht zum Transzendenten, zum Überirdischen und übernatürlichen zu verstärken. Sie ist es auch, die allen jenen dunklen und verworrenen Denkweisen, in denen sich der Okkultismus bewegt, dem Mystizismus jeglicher Art, dem Geister- und Gespensterglauben und ebenso auch der Wahrsagerei in ihren vielen alten und auch noch in einigen neuen Formen, einen fruchtbaren Nährboden geschaffen hat, auf dem das intellektuelle Unkraut üppig gedeiht und die sonderbarsten Blüten treibt.

Das gilt in besonderem Maße auch für die Astrologie, die Kunst, die angeblich aus den Gestirnen und deren Konstellationen das Schicksal des Menschen zu prophezeien vermag. In ungeahntem Maße hat gerade dieser Zweig des Mystizismus seit der Zeit des Krieges von der Depression und Verwirrtheit der Gemüter profitiert, und in einem Maße, wie es vielleicht seit einem Jahrhundert nicht mehr zu konstatieren war, sich Jünger, Freunde und begeisterte Anhänger selbst in jenen Kreisen zu schaffen gewußt, die sich zu den »Gebildeten« rechnen und den übrigen Erscheinungsarten des Okkultismus und Aberglaubens mehr oder weniger kritisch und ablehnend gegenüberstehen. Viele von diesen, die für die Künste der Kartenlegerinnen, der Chiromanten, Traumdeuter und Geisterbeschwörer nur ein mitleidiges Lächeln übrig haben, bringen doch der nicht minder wie jene zweifelhaften Kunst, das Horoskop zu stellen, ein erhebliches Maß von Zutrauen entgegen, wie auch das Anschwellen der astrologischen Literatur beweist.

Der Grund für diese immerhin bemerkenswerte Tatsache darf wohl darin gesehen werden, daß es die Astrologie mehr als die anderen Gebiete der okkulten Betätigung versteht, sich ein Mäntelchen von Wissenschaftlichkeit umzuhängen, das auch dem »Gebildeten« imponiert, dessen Bildung und Kenntnisse ja zumeist auf einem ganz anderen Gebiete als dem der exakten Naturforschung und der kritischen Naturbetrachtung liegen, auf dem einzig und allein der Geltungsanspruch der Astrologie auf Wissenschaftlichkeit zu prüfen wäre. Eine solche Prüfung zerzaust dann allerdings die angebliche wissenschaftliche Gewandung, mit der sich die Astrologen von heute mit Vorliebe zu umhüllen pflegen, mit aller nur wünschenswerten Gründlichkeit.

Daß die Gestirne für alles Leben auf Erden von maßgebendem Einfluß sind, ist eine banale Weisheit. Der Sonne verdanken wir Licht und Wärme und damit die Möglichkeit allen Lebens überhaupt; der Mond übt seinen mächtigen Einfluß in der Regelung von Ebbe und Flut, und auch die Planeten, gewissermaßen die »Hauptpersonen« in dem System astrologischer Prophezeiungen, wirken, wenn auch viel weniger stark und bemerkbar, auf das Dasein unserer Mutter Erde ein. Aber alles das sind lediglich allgemeine Einwirkungen der Gestirne auf Erde und Menschen. Für die Annahme einer Einwirkung der Gestirne auf das individuelle Einzelschicksal, das sich im Rahmen jener allgemeinen Wirkung der Himmelskörper vollziehen soll, insbesondere für die Annahme eines vorbestimmten Einflusses der Gestirne auf den Lebensgang des einzelnen Erdenmenschen, und ganz besonders für das Dogma der Astrologie, daß sich in der Geburtsstunde des Menschen dessen Lebensschicksal vom ersten Lebenstage bis zum Todestage aus der Konstellation der Gestirne in jener Stunde vorherbestimmen lasse, fehlt dem wissenschaftlichen Denken jede Möglichkeit eines Zusammenhangs.

Bei der Beweisführung für die Richtigkeit dieses Dogmas ist freilich von Wissenschaft nicht viel zu spüren. In merkwürdiger Übereinstimmung berufen sich die astrologischen Größen in ihren Schriften und Vorträgen zunächst immer auf die hohe Schätzung, deren sich die Astrologie bei den Kulturvölkern des Altertums, besonders bei Ägyptern und Babyloniern, zu erfreuen hatte. Als ob ehrwürdiges Alter allein einer Denkweise Wahrheit und Beweiskraft schaffen und Grund dafür sein könnte, Irrtümer vergangener Jahrtausende auch heute noch aufrechtzuerhalten! Dann folgt der Hinweis auf die Astronomen des Mittelalters, die alle zugleich auch Astrologen waren, und als Kronzeuge gar wird regelmäßig der große Kepler angeführt, der Astrolog Wallensteins und des Kaisers Rudolf, dem Schiller die Gestalt des Astrologen Seni im »Wallenstein« gegeben hat. Und gewiß, Kepler, der geniale Mathematiker und Astronom, hat, wie viele andere Himmels- und Naturforscher seiner Zeit, lange die Kunst des Horoskops mit Hingebung gepflegt. Dennoch aber fehlt den heutigen Astrologen jede Berechtigung, sich auf diesen Großen zu berufen. Kepler hatte die drei nach ihm benannten Gesetze des Umlaufs der Planeten um die Sonne gefunden und konnte trotz dieser wissenschaftlichen Großtat die Anschauungen der Astrologie mit seinem Denken vereinbaren. Er hatte jene Gesetze auf dem Erfahrungswege gefunden; den inneren Grund für diese Gesetze kannte er noch nicht, und so sah er in ihnen zunächst nur die Schönheitsgesetze, die nach seiner Auffassung dem Kosmos von dem Schöpfer zugrunde gelegt worden waren. Diese Auffassung brauchte für den Glauben an die Astrologie kein Hindernis sein. Als aber Newton das Gesetz der Gravitation gefunden hatte, das die mathematische Grundlage für die Mechanik und die Bahnen der Himmelskörper wurde, und als er damit auch den inneren Grund für die Keplerschen Gesetze lieferte, da war zugleich auch die Unvereinbarkeit zwischen mathematisch-astronomischem und astrologischem Denken ein für allemal festgestellt. Die Planetenkonstellationen werden von Höherem bestimmt und die Himmelskörper haben Wichtigeres und Größeres zu tun, als auf die Geburt eines Erdenmenschleins aufzupassen und für dieses Orakel zu spielen –, das war die Folgerung, die sich aus dem Gravitationsgesetz Newtons ergab und mit der die Astronomie die reinliche Scheidung zwischen sich und der Astrologie vollzog. So war Kepler der letzte Astrolog unter den Astronomen. Vielleicht lesen die Astrologen von heute einmal, was Wilhelm Foerster, der ehemalige Direktor der Berliner Sternwarte, in seiner heute noch mehr als je lesenswerten kleinen Schrift »Himmelskunde und Wahrsagung« über Kepler als Astrologen geschrieben hat. Sie werden dann erfahren, daß ihnen alle Ursache fehlt, sich auf Kepler zu berufen, der letzten Endes seinen Irrtum erkannt und schließlich sehr herbe Worte über die »astrologischen Pfuscher, die mit der Leichtgläubigkeit der Menschen spielen«, gefunden hat.

Nach Kant kann jede wissenschaftliche Disziplin nur so weit als exakte Wissenschaft gelten, als Mathematik in ihr steckt, und die heutige Wissenschaft hat diese Begriffsbestimmung des großen Königsbergers vollkommen übernommen. Mit Nachdruck berufen sich die heutigen Astrologen auf diese Definition, denn – so behaupten sie – das Verfahren, das Horoskop zu stellen, beruhe auf exakt mathematischer Grundlage. Es verlohnt sich, das Verfahren der Astrologie daraufhin nachzuprüfen, inwieweit jene kühne Behauptung zutrifft.

Die Methode besteht darin, die sogenannte »Nativität« aufzustellen, das heißt die »Himmelsfigur«, oder das Horoskop, anzufertigen. Das geschieht auf Grundlage des Geburtsdatums, das bis auf fünf Minuten Genauigkeit angegeben werden soll, sowie der geographischen Länge und Breite des Geburtsortes des in die Sprechstunde des Astrologen kommenden Klienten. Dann wird der Kulminationspunkt des Äquators für die Stunde der Geburt und des weiteren das gerade aufsteigende Tierkreiszeichen sowie der Stand von Sonne, Mond und Planeten vermittels trigonometrischer Rechnung berechnet, wie sie auch von den Astronomen angewandt wird, um den Stand der Gestirne zu einem Zeitpunkt der Vergangenheit zu ermitteln. Bis hierhin ist das Verfahren also tatsächlich exakt mathematisch und einwandfrei –, es kann wenigstens so sein, denn ob alle Astrologen sich auf die wirklich exakte Ausführung solcher ziemlich schwierigen mathematischen Berechnungen verstehen, darf bezweifelt werden. Dann aber fängt das Unsinnige des Verfahrens an. Der Horizont um die Erde herum wird in zwölf sphärische Zweiecke geteilt, welche die Astrologen »Häuser« nennen; der Stellung der Tierkreisbilder zu diesen »Häusern« wird eine bestimmte, aber natürlich völlig unbegründete und willkürliche Bedeutung (gut oder schlecht, günstig oder ungünstig) beigelegt, und daraus werden entsprechende Schlüsse für den Lebensgang des Auskunft Heischenden in Gegenwart und Zukunft gezogen. Ebensolche willkürliche Bedeutungen werden den Konstellationen der Planeten zugesprochen, die überdies noch einzeln in völlig willkürlicher anthropomorphischer Weise mit bestimmten guten und schlechten Eigenschaften ausgestattet sind, die glückliches oder unglückliches Schicksal künden. Venus und Jupiter gelten als Glückspender, als »Wohltäter« des geborenen Menschleins; Merkur nimmt eine sehr zweifelhafte Stellung ein; Saturn, Mars und Uranus gelten in bezug auf das menschliche Schicksal als feindlich Gesinnte und »Übeltäter«; Neptun ist bald freundlich, bald übel gelaunt. Der gute Mond aber bedeutet für das männliche Horoskop die zukünftige Ehegattin, für das Horoskop feminini generis aber den dereinstigen Herrlichsten von allen. In ähnlicher Weise werden aus Konstellation und Eigenschaften der Gestirne auch die Tage besonderen Glücks oder Unglücks, großer Unternehmungen oder Ereignisse, der Tag der Verheiratung und schließlich sogar der Todestag prophezeit.

Und was ist nun der Unterschied zwischen diesem angeblich exakt wissenschaftlichen System und der sonstigen Wahrsagerei, etwa Kartenlesen oder Chiromantie? Keiner! In diesem wie in jenem Falle handelt es sich um dasselbe; nur die Ausführung ist jeweils äußerlich verschieden. Gegeben ist immer eine bestimmte Anzahl von Elementen, die eine große Zahl von Kombinationen ermöglichen; diese Elemente und deren Kombinationen werden in völlig willkürlicher Weise für Charakter oder Schicksal des Suchenden gedeutet. Beim Kartenlesen sind die gegebenen Elemente die 32 Spielkarten, die Kombinationen ergeben sich aus der Reihenfolge, in der die Karten hingelegt werden. Die Anzahl der möglichen Reihenfolgen ist ungeheuer groß und beträgt 32!, lies: zweiunddreißig Fakultät, d. h. das Multiplikationsergebnis sämtlicher Zahlen von 1 bis 32, was eine unvorstellbar große Zahl von ungezählten Billionen und Trillionen ergibt. Die sich in solcher ungeheuren Mannigfaltigkeit ergebenden Kombinationsmöglichkeiten der Karten aber werden nach alten Regeln, für die noch kein Kartenleger den Grund hat glaubhaft machen können, als gut oder schlecht, als Lotteriegewinn, Beinbruch, glückliche Reise, Erfolg, Pleite, Verlobung, Heirat oder Tod usw. gedeutet, und – das Orakel ist fertig und wird anstandslos bezahlt. In der Chiromantie wird in entsprechender Weise die ungeheure Mannigfaltigkeit, die der Verlauf der Handlinien aufweist, willkürlich ausgelegt, und beim Bleigießen zu Silvester werden die zahllosen verschiedenen Formen, in denen ein wenig geschmolzenes und dann in kaltes Wasser gegossenes Blei erscheinen kann, halb humoristisch, halb gläubig zur Deutung für das kommende Jahr benutzt.

Und wie ist's mit der Astrologie? Hier sind die Elemente Tierkreisbilder, Planeten, Sonne und Mond, die ungezählt viele Kombinationen sowohl untereinander wie auch zu den zwölf »Häusern« bilden können. Diese Konstellationen werden tatsächlich mathematisch berechnet, aber ihre Deutung geschieht nach ebenso überlieferungsgemäß willkürlichen Regeln und also in ebenso sinnloser Weise wie beim Kartenlegen oder bei der Tätigkeit jener alten Damen, die aus Kaffeesatz oder Eidotter die Zukunft herausorakeln. Solche Kombinations- und Wahrsagesysteme kann man im Handumdrehen fabrizieren, und wer an den bestehenden noch nicht genug haben sollte, dem sei gleich ein weiteres mitgeteilt. Man nehme ein Schachspiel und lasse eine Person bei verbundenen Augen die Figuren auf das Schachbrett stellen. Aus der sich so ergebenden Stellung von König, Dame, Türmen, Springern, Läufern und Bauern, der feindlichen und freundlichen Figuren, aus dem Vorhandensein von Angriff und Verteidigung usw. lassen sich alle nur möglichen Bedeutungen und Ereignisse für das Schicksal des Spielers herauslesen, und bei der ausgesprochen aufs Menschliche übertragenen Bedeutung aller Figuren und Stellungen im Schachspiel und bei der unerschöpflichen Mannigfaltigkeit der Stellungen und Zusammenhänge erschließt sich hier ein neues System der Prophetie, dem unzweifelhaft ebensoviel oder ebensowenig Wahrheit und Wahrscheinlichkeit zukommt wie der Astrologie.

Also die mathematische Begründung der Astrologie versagt, solange die Astrologen nicht auch mathematisch begründen können, warum Venus eine »Wohltäterin«, Mars ein »Übeltäter« im Schicksal des Geborenen ist, mit welcher Berechtigung sie dem guten Mond die Rolle des Ehekupplers zuweisen und sich überhaupt die ganze übrige anthropomorphische Willkür an den Gestirnen und deren Konstellationen erlauben. An einer anderen kleinen Berechnung aber gehen die Astrologen merkwürdigerweise still vorüber. Sie bestimmen das Menschenschicksal nach der Konstellation der Gestirne zur Geburtsstunde. Aber in ein und derselben Stunde werden unter ein und demselben Längen- und Breitengrad nicht nur einer, sondern immer eine ganze Anzahl von Menschen geboren, die also nach astrologischer Logik alle dasselbe Lebensschicksal haben müßten. In Deutschland werden zu jeder Stunde etwa 250 Menschen geboren, in Berlin oder im Bereich des Längen- und Breitengrades von Berlin 15 bis 20 Menschen, für die alle also das gleiche Horoskop gültig ist, gleichviel, ob der einzelne von ihnen im Palast oder in der Hütte geboren ist, ob er als Kretin oder mit der Anlage zum Genie auf die Welt gekommen ist. Warum hat es dann nur einen Goethe gegeben, obwohl doch in der Stunde seiner Geburt sicher noch einige andere Frankfurter zum Lebenslicht erwacht sind, warum hat es nur einen Bismarck, nur einen Kant, nur einen Raffael gegeben und warum stand uns im Weltkrieg nur ein Hindenburg zur Verfügung? Die Antwort dürfte auch ohne die Fähigkeit, sphärische Zwei- und Dreiecke zu berechnen, nicht schwerfallen.

In einem Buch, das sich »Mathematisch-instruktives Lehrbuch der Astrologie« nennt, leistet sich der Verfasser den hübschen Sophismus, es sei natürlich selbstverständlich, daß neben Millionen richtiger astrologischer Prophezeiungen zu allen Zeiten auch Fehlschlüsse vorgekommen seien! Uns scheint die Folgerung logischer: Wenn auf Millionen falscher astrologischer Prophezeiungen auch mal einige Zufallstreffer kamen, so kann das noch lange kein Beweis für die Daseinsberechtigung der Astrologie in unserer Zeit sein. »Manchmal trifft's ein, manchmal ooch nich, ja lieber Gott, dann helf er sich!« wie der Komiker Bendix zu sagen pflegte, goldene Worte, die auch den Wahrheitswert des Horoskopes treffend kennzeichnen dürften. In demselben Standardwerk der Astrologie werden auch die kühnsten Hypothesen über die Physik der Gestirne aufgestellt, und aus den Ergebnissen der Höhenstrahlenforschung der letzten Jahre wird der Schluß gezogen, daß mit den entdeckten Höhenstrahlen, die nach der gegenwärtigen Auffassung ihren Ursprung in der radioaktiven Tätigkeit ferner Weltkörper haben, der Zusammenhang dieser Weltkörper mit der Erde im astrologischen Sinne bewiesen sei. Man ist mit solchen »Beweisen« zugunsten der Astrologie schnell bei der Hand, während es für den Naturforscher selbstverständlich ist, daß jene Strahlen, die uns aus fernen Welten zukommen, für unsere Erde nur eine allgemeinphysikalische Bedeutung, wie irgendeine andere Strahlung, etwa das Licht, das uns jene Weltkörper zusenden, haben können, daß niemals aber ein Zusammenhang solcher Strahlen mit dem individuellen Einzelschicksal der Erdenbürger im Sinne astrologischer Vorausbestimmung zu konstruieren ist. Welche Bewandtnis es mit der Deutung physikalischer Phänomene seitens solcher astrologischer Wissenschaftler und überhaupt mit ihrer Auffassung von den Naturkräften und dem Naturgeschehen hat, dafür mag angeführt werden, daß in dem erwähnten astrologischen Werk als Beweis des Einflusses des Mondes auf die Dinge und Schicksale auf Erden allen Ernstes behauptet wird, daß ein scharfgeschliffenes Messer, das eine Nacht hindurch dem Licht des Vollmondes ausgesetzt gewesen sei, stumpf werde und nie wieder scharf geschliffen werden könne! Das sind ja höchst merkwürdige physikalische Tatsachen, die sich den Physikern selbst allerdings bisher so raffiniert zu entziehen gewußt haben, daß ein solcher bislang ein derartiges Phänomen noch niemals festzustellen vermochte. Auf dieser Höhe der physikalischen Erkenntnis stehen die Argumentation, die Behauptungen und die Beweisführung der »wissenschaftlichen« Astrologie allgemein und durchweg. Kann angesichts eines solchen physikalischen Aberglaubens noch ein Unterschied zwischen dieser Afterlehre und dem Metier, aus den Karten, aus Kaffeegrund oder den Fingernägeln die Zukunft zu prophezeien, gemacht werden?

Das menschliche Lebensschicksal wird in seinem individuellen Verlauf viel mehr als durch die Gestirne am Himmel durch die Verhältnisse und Bedingungen auf Erden und immer noch mit am meisten durch das eigene Tun und Lassen eines jeden einzelnen selbst bestimmt. »In deiner Brust sind deines Schicksals Sterne«, sagt in diesem Sinne der Dichter, und er warnt damit alle die vielen, die sich heute mehr oder weniger gläubig das Horoskop stellen lassen, vor einer Spekulation, die trotz aller wissenschaftlichen Bemäntelung nur als Geistesverwirrung und unwürdiger Aberglaube einzuschätzen ist.

Postskriptum

Astrologische Kritiker und astrologische Beweisführung – Astrologie und Politik – Ein Lehrstuhl für Astrologie?

Der vorstehende Aufsatz war – in etwas kürzerer Form – seinerzeit in einer weitverbreiteten Berliner Tageszeitung erschienen. Die Folge war, daß mir ein reichliches Hundert von Zuschriften aus dem astrologischen Lager zuging, in denen mir mit mehr oder weniger Liebenswürdigkeit (zumeist mit weniger) der Text über die »empörende Schmähung einer der ältesten, ehrwürdigsten und wahrsten Wissenschaften des Menschengeschlechtes«, wie sich ein Einsender ausdrückte, gelesen wurde. Die merkwürdigsten Geister warfen sich da mit den merkwürdigsten Argumenten zur Verteidigung der Kunst des Horoskopes auf. Beispiel: Einer begründete seine Kompetenz, über solche Dinge ungleich richtiger urteilen zu können, mit dem Hinweis darauf, daß er »anerkannte Autorität in der Fingernagellesekunst« – eine mir damals allerdings noch ganz neue Wissenschaft – sei, und daß die Ergebnisse dieser Kunst regelmäßig mit den astrologischen Aussagen und Prophezeiungen übereinstimmten. Also müssen sie beide richtig sein! Scharfsinniger war ein anderer meiner Korrespondenten, ein Jurist, der meinen Hinweis, warum es nur einen Newton, einen Goethe, einen Bismarck usw. gegeben habe, obwohl doch in der Geburtsstunde jedes dieser Genies noch andere Menschen unter demselben astrologischen Zeichen geboren seien, damit zu widerlegen suchte, daß eben diese Prämisse falsch sei und solche auserwählten Geister nur vereinzelt geboren würden. In der Stunde und unter dem Zeichen, unter dem Goethe geboren worden ist, wurde kein weiterer Mensch geboren. Zu einfach ist dieser hübsche Sophismus, um bewiesen werden zu können. Auch politische Momente spielten in die Debatte hinein. Ein Briefschreiber gab seiner Auffassung dahin Ausdruck, daß Ton und Inhalt meines Aufsatzes keines deutschen Mannes und keines Herrenmenschen würdig sei und nur die proletenhafte Neigung des Verfassers verrate, das Erhabene in den Schmutz zu ziehen. Gerade entgegengesetzt meinte ein anderer, daß mein Aufsatz nur den anmaßenden Hochmut der Leute, »die sich mehr als andere dünken«, erkennen lasse und außerdem das Bestreben, dem Volke die Wissenschaft vorzuenthalten; die Astrologie sei eine echt demokratische Wissenschaft und deswegen nur erfolgten solche gehässigen Angriffe gegen sie! Da bin ich nun an mir selbst irre geworden und weiß nicht, ob ich mich zu den Herrenmenschen oder zu den Proleten zu rechnen habe, will das auch nicht weiter entscheiden. Ein anderer endlich hielt mir in einem langen Sündenregister die vielen »Fehler« und »Irrtümer« meines Aufsatzes vor, berichtigte jeden einzeln und verlangte dann auf Grund des Paragraphen 11 des Preßgesetzes kategorisch von mir Widerruf meines Aufsatzes in der betreffenden Zeitung. Ich war so verstockt, ihm den Gefallen nicht zu tun. Bei alledem war zu konstatieren – und das war das Bedauerliche – daß die Mehrzahl der Schreiber nach Beruf, Titel und Schreibweise unzweifelhaft zur Klasse der »Gebildeten« zu rechnen war, war doch etwa ein Viertel von ihnen Akademiker. Und dennoch diese Kritiklosigkeit einer Afterwissenschaft gegenüber! Ein trauriges und beschämendes Zeichen für die Oberflächlichkeit und Einseitigkeit unserer sogenannten »Bildung«, ein trauriges und beschämendes Zeugnis auch dafür, daß der hochtrabende Begriff »Bildung« in den Augen nur Allzuvieler mit jedem Mangel gesicherter Kenntnisse vereinbar zu sein scheint.

Freilich bekommt man ja über den Wert der modernen Aufklärungs- und Bildungsbestrebungen eigenartige Begriffe angesichts der Tatsache, daß selbst ein so anerkanntes Volksbildungsinstitut wie die Lessing-Hochschule in Berlin ein Semester lang die Astrologie in ihr Vorlesungsprogramm ausgenommen hatte, nicht etwa nur im geschichtlichen oder referierenden Sinne, sondern die waschechte »wissenschaftliche Astrologie« mit Horoskopstellen und allem sonstigen Zauberspuk dieser zweifelhaften Kunst. Wenn dergleichen schon am grünen Holze geschieht, wenn ein Institut, das seiner Tradition und seinem Zwecke nach doch in erster Linie dazu berufen sein sollte, den Kampf gegen den astrologischen Aberglauben zu führen, diesen Kampf geradezu sabotiert, indem es quasi offiziell die Astrologie zum Volksbildungs- und Vorlesungsgegenstand erhebt, dann ist es vielleicht verständlich, wenn der wissenschaftlich bemäntelte astrologische Unfug und Aberglaube auch in den Kreisen unserer mehr oder weniger Intellektuellen solche verheerenden Erfolge erzielen konnte. Nicht unerwähnt mag bleiben, daß man seitens der Astrologen sogar auch Anstrengungen gemacht hat, einen Universitätslehrstuhl zu erlangen, aber gottlob wenigstens von dieser Seite eine ebenso deutliche wie entschiedene Abfuhr erhielt. Bisher wenigstens!

3. Der Goldene Schnitt

I

Zahl und Kunst – Das Buchformat und sein Streckenverhältnis – Zweck und Form – Die Konstruktion des Goldenen Schnittes – Major und Minor – Ein interessantes psychologisches Experiment

Eine der eigenartigsten Erscheinungen, in denen sich das Wirken der Zahl bekundet, ist jene Beziehung, die als der Goldene Schnitt bezeichnet wird. Eigenartig und merkwürdig ist diese Beziehung deswegen, weil hier die Zahl, die wir sonst nur in der unbelebten Natur und dem Ablauf der mechanisch wirkenden und daher zahlenmäßig bestimmbaren Naturgesetze vorfinden, ihr Walten in einem Gebiete bekundet, das mit mechanischer Gesetzmäßigkeit nichts zu tun hat, sondern seinem ganzen Wesen nach gerade das Gegenteil einer solchen ist, im Gebiete der Kunst. Die Kunst aber ist ein aus freiem seelischen und geistigen Leben geborenes Tun, und ihre Schöpfungen sind Äußerungen und Erzeugnisse des frei waltenden Geistes, der sich über die mechanische Zwangsmäßigkeit erhebt, mit der sich die Naturgesetze erfüllen, und wenn wir dennoch in den Schöpfungen der Kunst die Wirksamkeit der Zahl verfolgen können, so manifestiert sich hier die Zahl in besonders eigenartiger Weise als das Wesen der Dinge.

Daß Zahl und Kunst keine Gegensätze sind, dafür ist uns die ursprünglichste aller Künste, die Musik, Beweis. Der Rhythmus der Töne beruht auf dem zahlenmäßigen Zusammenhang der Tonintervalle, der Terz, Quarte, Oktave usw., und läßt erkennen, daß der seelische Akt, der sich in dem Empfinden des Schönen ausdrückt, wenigstens im Reich der Töne von der zahlenmäßig gebundenen Form bedingt wird. Diesen Zusammenhang zwischen Rhythmus und Zahl in der Musik hatten schon die alten Pythagoreer erkannt, und deswegen wandelten sie nur die Bahnen einer bereits vertrauten Auffassung, als sie einen ähnlichen Zusammenhang auch in anderen Gebieten der Kunst, in der Malerei, der Plastik und Baukunst, finden und nachweisen zu können glaubten. Sie fanden, daß die künstlerische Formgebung, wie es gerade an den hervorragendsten Erzeugnissen der genannten Künste erweisbar ist, in ausgesprochenem Maße ein ganz bestimmtes, zahlenmäßig ausdrückbares Verhältnis der Längen und Strecken bevorzugt und daß auch die Natur in ihren Formen, wenigstens denen der lebenden Naturschöpfungen, mit Vorliebe dasselbe Streckenverhältnis befolgt, ein Prinzip der Formgebung, das insbesondere immer da zu konstatieren ist, wo wir ein Kunstwerk oder eine Naturgestalt als besonders schön empfinden.

Dieses Streckenverhältnis ist der Goldene Schnitt.

Die alten Philosophen haben dieser merkwürdigen Beziehung ihre volle Aufmerksamkeit gewidmet und glaubten, in dieser das Gesetz der künstlerischen Formgebung gefunden zu haben, das zugleich auch das Gesetz der schönheitlichen Formgebung in der Natur sei, glaubten so die Zahl auch in der Welt des Schönen, der Naturschönheit wie der Schönheit der künstlerischen Schöpfung, waltend und wirkend wiedergefunden zu haben.

Befassen wir uns zunächst damit, jenes Streckenverhältnis, das der Goldene Schnitt genannt wird, genauer zu bestimmen. Wenn wir irgendein Buch zur Hand nehmen, so werden wir regelmäßig feststellen können, daß es die Form eines Rechteckes aufweist, ein Format also, bei dem die eine Seite länger ist als die andere. Ferner ist es auch nicht ein beliebiges Rechteck, sondern fast immer ein solches, bei dem die Längs- zur Breitseite in einem ganz bestimmten zahlenmäßigen Verhältnis steht. Ich nehme ein Buch aus meiner Bibliothek heraus, messe die Länge der beiden Seiten und finde, daß die eine Seite 13, die andere 21 Zentimeter lang ist. Letztere ist also l,6mal so lang wie die andere, oder die Längen der beiden Seiten stehen, wie man zu sagen pflegt, in dem Verhältnis 1: 1,6. Ich nehme ein anderes Buch, messe wiederum und finde diesmal die Längen der Seiten mit 15 und 24 Zentimeter; wiederum ist die längere Seite gerade l,6mal so lang wie die andere, wiederum ist das Streckenverhältnis 1: 1,6 zu konstatieren. Dann nehme ich ein kleines Notizbuch zur Hand; die Seiten sind 8 und 13 Zentimeter lang, und bei einem kleinen Notizkalender von Westentaschenformat finde ich 5 und 8 Zentimeter als Seitenlängen. Auch in diesen beiden Fällen ist jedesmal das bereits angegebene Streckenverhältnis vorhanden. Nach jenen Buchzwergen greife ich endlich auch zu einem Folianten großen Formates. Es ist ein lateinisches Geschichtswerk aus dem 16. Jahrhundert. Die Ausmessung ergibt genau 20 und 32 Zentimeter Seitenlänge, und auch diese entsprechen jenem Streckenverhältnis. Also schon vor dreihundert Jahren haben Buchdrucker und Buchbinder das Buchformat bevorzugt, bei dem die eine Seite l,6mal so lang ist wie die andere. Die Versuche und Messungen mit den verschiedenartigsten anderen Büchern aus heutiger wie vergangener Zeit führen immer zu ähnlichen Resultaten, und nur selten zeigt sich eine erheblichere Abweichung. So groß oder so klein auch das Format der Buchwerke sein mag, in den meisten Fällen finden wir ein Längenverhältnis der Seiten von etwa 1: 1,6 oder, wenn wir dieses Verhältnis in ganzen Zahlen ausdrücken wollen, was empfehlenswert ist, ein Verhältnis von 5: 8.

Diese Regelmäßigkeit in dem Längenverhältnis der Bücherformate ist eine überaus eigenartige Erscheinung. Es bestand für Buchdrucker und Buchbinder niemals ein Zwang, gerade die Formate von dem genannten Längenverhältnis in so ausgesprochener Weise zu bevorzugen, und wenn wir fragen, warum sie es dennoch taten, so finden wir keine andere Antwort als die, daß diese Formate dem Form- und Schönheitsgefühl der Bücherverfertiger wie der Büchergebraucher von jeher am meisten zusagten. Das Buchformat mit dem Längenverhältnis 5: 8 erzeugt in uns eine gewisse Befriedigung, ein gewisses Schönheitsgefühl, es entspricht am meisten unserem »Geschmack«. Wie sehr das der Fall ist, wird deutlich, wenn wir ein Buch mit einem von dem genannten stark abweichenden Format auf uns wirken lassen. Ein Buch von quadratischem Format beispielsweise macht auf uns einen ausgesprochen unschönen Eindruck; dasselbe gilt auch Von einem Buchformat, das ein sehr langgestrecktes Rechteck darstellt, bei dem etwa die eine Seite doppelt so lang ist wie die andere. Manchmal kommen Bücher solcher abweichenden Formate auf den Markt, doch gehört das zu den Seltenheiten, die auch, wie die Erfahrung regelmäßig lehrt, niemals Anklang bei den Gebrauchern oder Käufern der Bücher findet.

Das Buchformat ist nur ein einzelnes Beispiel für die bevorzugte Anwendung des Streckenverhältnisses 5 : 8. Bei zahllosen anderen Dingen und Gegenständen der Gebrauchswelt finden wir es angewandt, und zwar mit einer Häufigkeit und Regelmäßigkeit, daß wir hier nicht mehr von einem Zufall sprechen können, sondern auf einen tiefer liegenden Grund schließen müssen. Und als diesen Grund können wir nennen, daß die Paarung von Zweckmäßigkeit und wohlgefälliger Form, die wir gerade an den Dingen des täglichen Gebrauchs wünschen, jenen Dingen also, mit denen wir die Umwelt unserer häuslichen Daseinsweise herstellen, durch die Proportionen nach dem Goldenen Schnitt in besonderem Maße gewährleistet wird. Das Buchformat mit dem Seitenverhältnis 5 : 8 ist das zweckmäßigste für den Gebrauch, und zugleich empfinden wir es als das wohlgefälligste. Zweck und Form stehen in einem engen Kausalnexus und bedingen sich gegenseitig. Der Gegenstand, gleichviel ob es sich um ein einzelnes Stück oder um die ganze Anordnung unserer Umgebung, die Gestaltung und Einrichtung von Wohnung und Haus handelt, soll nicht nur nützlich, sondern auch gefällig sein und zur Verschönerung unserer Umwelt und unserer Daseinsweise beitragen. Diese Verbindung des Zweckmäßigen mit dem Gefälligen und Schönen in der äußeren Gestaltung und Formgebung herzustellen ist, soweit es die Dinge unseres Gebrauches betrifft, insbesondere die Aufgabe des Kunstgewerbes, das am Gebrauchsgegenstand dasselbe Gesetz der Formgebung zum Ausdruck bringt, das die reine Kunst in der Form und Gestaltung ihrer rein idealen Schöpfungen befolgt. Das Buchformat stellt nur ein einzelnes, aber überaus sprechendes und beweiskräftiges Beispiel des Formengesetzes des Goldenen Schnittes im Kunstgewerbe dar.

Abb. 39
Die Konstruktion des Goldenen Schnittes

Die Teilung einer Strecke nach dem Goldenen Schnitt ist eine geometrische Aufgabe, die mit der Lehre vom Kreis, dieser schönsten und gleichmäßigsten aller geometrischen Figuren, im Zusammenhang steht und in folgender einfachen Weise zu lösen ist: Angenommen, die Strecke AB in unserer Abbildung 39 soll nach dem Goldenen Schnitt geteilt werden, so errichten wir auf dem einen Endpunkte der Strecke, in unserer Abbildung in B, eine senkrechte Strecke BM, die wir genau halb so lang machen wie die Strecke AB. Um M schlagen wir dann mit der Strecke BM als Halbmesser einen Kreis und verbinden dann die Punkte M und A durch eine gerade Linie, die den Kreis in dem Punkte P schneidet. Die Strecke AP tragen wir dann vermittels des Zirkels auf der Strecke AB ab und erhalten so auf der letzteren einen Teilpunkt C, der die ganze Strecke AB in die beiden Teilstrecken AC und CB teilt. Dann ist die ganze Strecke AB durch den Punkt C nach dem Goldenen Schnitt geteilt. Zugleich steht dann aber auch die ganze Strecke AB zu ihrem größeren Abschnitt, der Strecke AC, im Verhältnis des Goldenen Schrittes, d. h. nicht nur die Strecke AC ist 1,6mal so lang wie die Strecke CB, sondern zugleich ist auch die ganze Strecke AB 1,6mal so groß wie ihr größerer Abschnitt AC. Wenn wir ferner die kleinere Strecke CB auf der größeren AC abtragen, so steht auch der hierbei entstehende kleinere Teil zu der Strecke CB im Teilungsverhältnis des Goldenen Schnittes. Immer wenn wir die beiden Teile einer nach dem Goldenen Schnitt geteilten Strecke aufeinander abtragen oder wenn wir den größeren Teil einer solchen Strecke an die ganze Strecke ansetzen, so entsteht zwischen den beiden Teilen das Teilungsverhältnis des Goldenen Schnittes.

Die mathematische Begründung für diese Behauptungen wollen wir übergehen und nur erwähnen, daß die Konstruktion des Goldenen Schnittes mit der geometrischen Aufgabe der Zehnteilung des Kreises in engem Zusammenhange steht Die in Abbildung 16 (Seite 95) dargestellte 10-Teilung des Kreises läßt die Übereinstimmung mit der Konstruktion des Goldenen Schnittes deutlich erkennen. Die Sehne des regelmäßigen Zehnecks ist der größere Abschnitt des nach dem Goldenen Schnitt geteilten Radius des Umkreises.. Bemerkt sei noch, daß der jeweils größere Abschnitt einer nach dem Goldenen Schnitt geteilten Strecke als »Major« (die erste Silbe ist zu betonen!), der kleinere Abschnitt als »Minor« bezeichnet wird. In dieser Weise hat schon Euklid, der griechische Mathematiker und »Vater der Geometrie«, um das Jahr 300 die Konstruktion des Goldenen Schnittes gelehrt und damit das Verfahren angegeben, um auf geometrischem Wege zu jeder beliebigen Strecke eine andere zu finden, die zu jener in dem Längenverhältnis des Goldenen Schnittes steht.

Abb.40 Format des Goldenen Schnittes

In Abbildung 40 sind die Streckenverhältnisse oder »Proportionen«, wie sie sich bei der Teilung nach dem Goldenen Schnitt ergeben haben, zu einer Formgebung verwandt worden. Wir haben hier ein Rechteck vor uns, dessen Längsseite AB der ganzen Strecke AB unserer Abbildung 39, die Schmalseite des Rechteckes der Strecke AC der Abbildung 39 entspricht. Die Figur gibt die Seitenverhältnisse des üblichen Buchformates wieder, das wir hier also geometrisch hergeleitet haben. Aber auch die beiden Teilstrecken AC und BC der Abbildung 39, die ja ebenfalls Proportionen des Goldenen Schnittes darstellen, sind zu einem Format verwandt worden, und zwar zu dem eingezeichneten kleineren Rechteck mit den Seiten AC und BC. Dieses kleinere Format weist in seinen Seiten dasselbe Streckenverhältnis wie das größere Rechteck auf, stellt also ebenfalls ein Format von besonderer Wohlgefälligkeit dar. Die schönheitliche Wirkung, die die geeignete Verbindung dieser beiden Formate gerade beim Buch erzeugt, finden wir deutlich in unserer Abbildung 41 wieder, die eine Seite aus einem alten englischen Kunstdruckwerk mit reichem Buchschmuck darstellt. Hier finden wir jene beiden Formate, das Format des ganzen Druckblattes und das Format des inneren Drucksatzes, miteinander in harmonische Verbindung gebracht, die einen ästhetisch hervorragend befriedigenden Eindruck erzeugt und in so ausgezeichneter Weise durch kaum eine andere Anordnung von Blatt und Druck erreicht werden könnte.

Abb. 41
Buchformat im Goldenen Schnitt

Bemerkt sei noch, daß der Goldene Schnitt auch Gegenstand der experimentellen Psychologie geworden ist. Durch eingehende wissenschaftliche Versuche ist eine ausgesprochene Bevorzugung der Formate, die dem Teilungsverhältnis des Goldenen Schnittes entsprechen, vor anderen Formaten festgestellt worden. Man hat Versuchspersonen der verschiedensten Bildungsgrade und Altersstufen eine große Reihe verschiedener Vierecksformate vorgelegt mit der Aufforderung, diejenigen zu bezeichnen, die ihnen am meisten gefallen. In den weitaus meisten Fällen wurden immer diejenigen Formate, die dem Teilungsverhältnis des Goldenen Schnittes entsprachen, als die schönsten bezeichnet, auch schöner als die genau quadratischen Formate, die im übrigen bei solchen Versuchen immer an zweiter Stelle genannt wurden.

II

Die Antike und der Goldene Schnitt – »Apoxyomenos« und »Doryphoros« – Der Kanon – Der Goldene Schnitt im Mittelalter – Maler und Mathematiker – Albrecht Dürer – Adolf Zeising und seine Lehre

Die Bevorzugung des Teilungsverhältnisses des Goldenen Schnittes in der Formgebung und den Proportionen der Werke und Erzeugnisse können wir nahezu durch die ganze Geschichte der bildenden Künste und ebenso des Kunstgewerbes verfolgen; sie ist eine weitgehende Bestätigung jenes Gesetzes der schönheitlichen Formgebung in Kunst und Natur, das schon vor über zweitausend Jahren von den Philosophen und Mathematikern des Altertums entdeckt worden ist. Besonders in den Bild- und Malwerken der antiken Künstler, die bis auf den heutigen Tag die unübertroffenen Vorbilder der künstlerischen Harmonie und Formgebung geblieben sind, können wir die Regel vom Goldenen Schritt mit überraschender Häufigkeit und Regelmäßigkeit nachweisen. Überraschend vor allem deswegen, weil wir annehmen müssen, daß jene Künstler wohl niemals bewußt nach jener Regel arbeiteten, ja diese überhaupt noch nicht kannten, sondern sie gleichsam nur unbewußt, den unbewußten Gesetzen eines inneren Bildungstriebes folgend, zur Anwendung brachten, wie es für das intuitive Schaffen des echten Künstlers kennzeichnend ist. Gerade der Naturcharakter jenes Formengesetzes bekundet sich in dieser intuitiv–unbewußten Anwendung seitens des schaffenden Künstlers, der in der äußeren Form und den Proportionen seines Werkes gleichzeitig das Prinzip der größten Zweckmäßigkeit zum Ausdruck und Zweck und Form zu jener Paarung bringt, die sich in ihrer schönheitlichen Wirkung auf uns äußert. Unsere Abbildung 42 zeigt uns eins der berühmtesten Werke der antiken Bildhauerkunst, an dem wir das Gesagte mit besonderer Deutlichkeit veranschaulichen können. Die Abbildung stellt ein Werk des berühmten griechischen Bildhauers Lysippos aus Sikyon dar, der von 360 bis 316 v. Chr. lebte und wirkte, und eine große Zahl von Bildwerken in Metall und Stein geschaffen hat, die dem Künstler nicht nur bei seinen Zeitgenossen größten Ruhm erwarben, sondern ihn auch heute noch als einen der hervorragendsten Vertreter der plastischen Kunst aller Zeiten erweisen. Das Werk ist die Statue eines Athleten, der sich nach beendetem Ringkampf vermittels eines Gerätes gerade den Staub und Schweiß vom Körper abstreift, weswegen die Statue in der Kunstgeschichte als der »Apoxyomenos«, d. h. der Abstreifer, bezeichnet wird, ein hochberühmtes Kunstwerk, das uns in einer sehr guten Nachbildung erhalten geblieben ist, die sich jetzt im Vatikan in Rom befindet. In unserer Abbildung ist die geschaffene Gestalt in Verbindung mit dem Teilungsschema des Goldenen Schnittes dargestellt. Die Größe der ganzen Figur entspricht der ganzen Strecke AB, die in dem Punkte C nach dem Goldenen Schnitt geteilt ist. Der Major dieser ganzen Strecke, also die Teilstrecke BC, reicht von der Sohle bis zum Gürtel und teilt hier die ganze Gestalt in Unter- und Oberkörper. Die Strecke BC ist wiederum nach dem Goldenen Schnitt geteilt und bestimmt die Proportionen des Unterkörpers, deren eine der Länge der Beine von der Sohle bis zum Knie, die andere dem Körperteil vom Knie bis zur Hüfte entspricht. Die Strecke AC hingegen bestimmt in ihrer Unterteilung die Proportionen des Oberkörpers. Der Major dieser Strecke, also Cd, bestimmt den Oberkörper von der Hüfte bis zum Hals, der Minor, also die Strecke Ad, die Höhe des Kopfes.

Abb. 42
Der »Apoxyomenos«

Damit ist die vollendete Harmonie der Körpergestalten, die wir an den Schöpfungen der antiken Plastik bewundern, auf die Regel vom Goldenen Schnitt zurückgeführt, die sich am Apoxyomenos in besonders deutlicher und exakter Weise ausprägt. An zahllosen anderen Werken der antiken Kunst können wir gleichsam handgreiflich das Geltungsgesetz des Goldenen Schnittes in ebensolcher Weise feststellen. Natürlich haben die Künstler jene Regel keinesfalls immer mit absoluter geometrischer Genauigkeit, sondern immer nur mit mehr oder weniger großer Annäherung befolgt, die aber auch durchaus hinreichend ist, um den Eindruck des Schönen und Harmonischen bei der Formgebung nach jenem Teilungsverhältnis hervorzurufen. Auch ist ja ein gewisser Spielraum in der Anwendung jenes Teilungsverhältnisses bei der künstlerischen Formgebung nötig, um die geometrische Gleichförmigkeit der geschaffenen Gestalten zu vermeiden, die sich ja auch in der Natur niemals findet. Aber unter Berücksichtigung dieses notwendigen Spielraumes läßt sich die Geltung jenes Naturgesetzes der Formgebung an den Werken der bildenden Kunst und gerade an den hervorragendsten Werken aus der Geschichte der Malerei, Bildhauerkunst und Architektur aufs deutlichste nachweisen, zeigt es sich, daß die Empfindung des Schönen und Harmonischen, die das dargestellte Werk in uns auslöst, in hohem Maße durch die Anwendung der Regel vom Goldenen Schnitt bewirkt wird.

Abb. 43
»Doryphoros«

Als Gegenstück zu dem Apoxyomenos führen wir unseren Lesern in Abbildung 43 noch eine weitere Figur der griechischen Bildhauerkunst vor, die ebenso wie jene gerade wegen ihrer idealen Proportionen berühmt ist, nämlich den »Doryphoros« oder »Speerträger« des griechischen Bildhauers Polyklet aus Sikyon, der im 5. Jahrhundert, v. Chr. lebte und Zeitgenosse und Nebenbuhler des allerdings noch größeren Phidias, des berühmtesten Meisters der antiken Plastik überhaupt, war. Auch die Gestalt des Speerträgers läßt die Proportionen des Goldenen Schnittes aufs deutlichste erkennen und ist dieser idealen Verhältnisse wegen geradezu das Vorbild für die gesamte spätere Plastik bei der Darstellung des menschlichen Körpers geworden. Ein derartiges Vorbild wird als »Kanon« bezeichnet, und der Speerträger, der in mehrfachen Nachbildungen erhalten ist und eine der bedeutendsten Gestaltungen der antiken Plastik darstellt, ist der berühmteste Kanon, der seiner idealen Formgebung wegen ungezählten Generationen von bildenden Künstlern als Vorbild gedient hat und diesem Zwecke noch heute dient. Der sehr bedeutende deutsche Bildhauer Johann Gottfried Schadow, der nicht nur eine große Reihe berühmter plastischer Werke geschaffen, sondern auch eine Anzahl literarischer Werke über die Bildhauerkunst geschrieben hat, benannte eines der letzteren, das sich speziell mit den Proportionen des menschlichen Körpers befaßt, nach dem Schöpfer des berühmtesten Kanons als »Polyklet«.

Abb. 44
Luca Pacioli, dem Maler Barbari den Goldenen Schnitt demonstrierend

Auch im Mittelalter befaßten sich Maler, Mathematiker und Philosophen mit dem Problem des Goldenen Schnittes, der sectio aurea, wie sie es gelehrt nannten, oder auch der sectio divina, des Göttlichen Schnittes. Bekannt geworden ist ein Werk des Minoritenfraters und Mathematikers Luca Pacioli mit dem Titel » De divina proportione«, d. h. »über das göttliche Teilungsverhältnis«, aus dem Jahre 1509, in welchem der Verfasser eingehende Betrachtungen über den Goldenen Schnitt als Schönheitsprinzip anstellt, das seiner Meinung nach sowohl Gott bei der Erschaffung der Welt angewandt habe, wie es auch von allen bildenden Künstlern infolge göttlicher Eingebung bei ihren Schöpfungen befolgt werde. Auch gibt er eine eingehende Darstellung der Lehre und Konstruktion vom Goldenen Schnitt, der nach seiner Meinung die mathematische Grundlage aller Künste sein soll. Luca Pacioli trat auch mit vielen der berühmtesten Maler und Künstler seinerzeit in Verbindung, so mit dem berühmten Maler und Ingenieur Leonardo da Vinci, dessen Studien für Kunst und Technik hierdurch wesentlichen Einfluß erfuhren. Dem Maler Jacopo de Barbari erteilte Pacioli Unterricht in der Lehre vom Goldenen Schnitt, und aus Dankbarkeit malte Barbari ein Bild, auf dem er sich selbst und seinen Lehrmeister darstellte. Unsere Abbildung 44 gibt dieses Bild wieder. Wir sehen hier Pacioli damit beschäftigt, dem hinter ihm stehenden Barbari die Lehre vom Goldenen Schnitt auf einer Tafel zu demonstrieren; neben dem Maler steht rechts ein eigentümlicher geometrischer Körper, ein Dodekaeder, einer der sogenannten platonischen Körper, der aus zwölf Seiten, deren jede ein regelmäßiges Fünfeck ist, besteht, und an dem das Teilungsverhältnis des Goldenen Schnittes körperlich zur Erscheinung kommt. In der linken oberen Ecke hat der Maler einen weiteren seltsamen Körper dargestellt, einen riesigen Kristall, der in seiner Gestaltung und Abmessung ebenfalls die Proportionen des Goldenen Schnittes erkennen läßt. Das ganze Bild ist erfüllt mit jenem mystischen Nimbus, der charakteristisch für so viele künstlerische Schöpfungen des Mittelalters ist und der natürlich auch niemals fehlte, wo es sich um angeblich so geheimnisvolle Dinge wie den Goldenen oder Göttlichen Schnitt handelte.

Auch der berühmteste Vertreter der Geschichte der deutschen Malerei, Albrecht Dürer (1471-1528), der als Sohn eines Goldschmiedes aus dem Kunstgewerbe hervorgegangen ist und dessen Studien grundlegend waren für die weitere Entwicklung des Kunstgewerbes der gesamten nachfolgenden Zeit, hat sich viel und eingehend mit den Formenverhältnissen des menschlichen Körpers befaßt und – ein Vorgänger Schadows auch nach dieser Hinsicht – ein großes Werk über diesen Gegenstand verfaßt. Die Lehre vom Goldenen Schnitt selbst scheint Dürer jedoch nicht gekannt zu haben, wenigstens erwähnt er diese nicht. Dennoch aber zeigen sich seine Ideen und Vorschriften und ebenso auch die von ihm geschaffenen Bildwerke so erfüllt von dem Prinzip des Goldenen Schnittes, daß wir auch hier ein Beispiel sehen für die Tatsache, daß der wahre Künstler auch ohne bewußte Kenntnis der inneren Gesetze der Formgebung diese dennoch unbewußt in sich trägt und in seinen Werken zur Anwendung bringt.

Dann blieb die Lehre vom Goldenen Schnitt lange Zeit hindurch unbeachtet; bei den meisten Künstlern nach Dürer war sie sogar nahezu völlig in Vergessenheit geraten, und auch die Mathematiker bekümmerten sich nicht viel darum. Erst in der Mitte des vorigen Jahrhunderts erfuhr die Theorie des Goldenen Schnittes und ihre Anwendung für die Formgebung in Kunst und Kunstgewerbe eine Neubelebung, und zwar durch die Arbeiten des Professors Adolf Zeising in München, der in einer Reihe von Schriften seine gründlichen theoretischen und praktischen Studien auf diesem eigenartigen Forschungsgebiete veröffentlichte und dadurch von neuem die Aufmerksamkeit sowohl der Wissenschaftler, insbesondere der Philosophen und der Mathematiker, wie auch der Künstler und Kunstgewerbler auf die Bedeutung des Goldenen Schnittes als Prinzip der Formgebung lenkte. Zeisings Arbeiten und Schriften, insbesondere sein Hauptwerk, das den Titel führt »Neue Lehre von den Proportionen des menschlichen Körpers aus einem bisher unbekannt gebliebenen, die ganze Natur und Kunst durchdringenden morphologischen Gesetz«, machte beträchtliches Aufsehen und führte dazu, daß sich nunmehr wieder weitere Kreise mit der Lehre von den Proportionen nach der Regel vom Goldenen Schnitt und vor allem ihrer Anwendung für Kunst und Kunstgewerbe zuwandten. Zeising selbst nahm die Gültigkeit des Goldenen Schnittes, wie es Jahrhunderte vor ihm schon Luca Pacioli getan hatte, als ein Gesetz für die ganze Welt an und suchte dessen Gültigkeit nicht nur für die menschliche Gestalt, sondern auch für das Tier- und Pflanzenreich, ja sogar auch für das Mineralreich zu erweisen, indem er hier wie dort die Formen der Naturerzeugnisse und Naturgestalten aus dem Goldenen Schnitt abzuleiten versuchte, der nach seiner Auffassung überall nachzuweisen ist, wo sich in den natürlichen Formen und Gestalten Zweckmäßigkeit und Schönheit miteinander gepaart finden. Selbst für den Himmel und den Lauf der Gestirne nahm Zeising die Gültigkeit dieses Gesetzes an, indem er die Bahnen und Abstände der Gestirne auf die Proportionen des Goldenen Schnittes zurückzuführen suchte, womit er sich übrigens der Auffassung der alten griechischen Naturphilosophen näherte, die das ganze Weltall als nach bestimmten Ordnungs- und Schönheitsprinzipien gebaut erklärt und es deswegen »Kosmos«, d. h. Schönheit im Sinne geordneter Harmonie, genannt hatten. Seit Zeisings Arbeiten ist die Lehre vom Goldenen Schnitt noch weiter ausgebaut und ein überaus wichtiger Bestandteil der praktischen Ästhetik, der angewandten Schönheitslehre für die Formgebung in Kunst und Kunstgewerbe, geworden.

III

Das Gesetz der Formgebung in der Natur – Ernst Kapp – Der Goldene Schnitt in der Technik – Philosophie des Goldenen Schnittes – Tier und Pflanze im Goldenen Schnitt – Zweck und Stil – Haus und Möbel – Form und Schönheit

Zeisings Forschungen und Schriften über den Goldenen Schnitt wurden die Veranlassung, das Walten dieses Gesetzes in der Formgebung der Natur, das schon die Alten festgestellt und studiert hatten, von neuem zu untersuchen. Können wir doch gerade an denjenigen Naturerzeugnissen, deren Form und Gestaltung wir als besonders wohlgefällig oder schön empfinden, sei es die menschliche Gestalt selbst, seien es Gestaltungen aus dem Tier- und Pflanzenreiche, ja sogar an solchen aus dem Mineralreiche, die Proportionen des Goldenen Schnittes mit besonderer Häufigkeit feststellen, und gerade hier tritt uns der eigentliche Naturcharakter dieses Formengesetzes entgegen. Während der Künstler in den von ihm geschaffenen idealisierten Menschengestaltungen, wie wir es besonders an den Plastiken der antiken Bildhauer verfolgen konnten, gleichsam unbewußt zum Interpreten der Natur und ihres Formengesetzes wird, spricht hier die Natur in der Formgebung ihrer Schöpfungen selbst.

Abb. 45.
Die weibliche Normalfigur in den Proportionen des Goldenen Schnittes

Nicht nur an der von Künstlerhand geschaffenen idealisierten Menschengestalt, sondern auch am normalen menschlichen Körper selbst wie an den Formen der lebenden Natur überhaupt, suchte man jenes Gesetz der Formgebung wiederzufinden. Ein Schüler Zeisings, Johannes Bocheneck, ist auf diesem Gebiete erfolgreich tätig gewesen und hat die Gültigkeit des Naturgesetzes des Goldenen Schnittes an einer großen Anzahl von Normalgestalten aus dem Menschen-, Tier- und Pflanzenreiche nachzuweisen versucht. Unsere Abbildung 45 zeigt Bochenecks Darstellung der weiblichen Normalfigur nach den Maßverhältnissen des Goldenen Schnittes. Die Figur ist, wie sich aus dem beigegebenen Schema ergibt, zunächst durch eine das Becken schneidende Mittellinie in zwei Hälften geteilt. Die Unterteilung beider Körperhälften läßt die Proportionen des Goldenen Schnittes ohne weiteres erkennen und bestimmt die Größenverhältnisse der einzelnen Körperteile.

Abb. 46
Der Goldene Schnitt am Kopf

Abb. 47.
Der Goldene Schnitt am Arm

Abb. 48
Die Hand im Goldenen Schnitt

Noch ein anderer deutscher Gelehrter, der Professor Ernst Kapp aus Düsseldorf, hat gegen Ende des vorigen Jahrhunderts auf die Wirksamkeit des Goldenen Schnittes an den Naturformen, insbesondere der menschlichen Gestalt, hingewiesen und hierüber überaus interessante Studien gemacht. Unsere Abbildung 46 zeigt die besonderen Proportionen des menschlichen Kopfes nach Maßgabe des Goldenen Schnittes in der Darstellung Kapps. Die ganze Kopfhöhe ist hier durch die Strecke ab angegeben, die im Punkte c nach dem Goldenen Schnitt geteilt ist. Der Major umfaßt die Kopfhöhe bis zur Stirn, der Minor die Gesamthöhe von Stirn und Schädeldecke. Major und Minor sind ihrerseits wieder geteilt und bestimmen die Proportionen der einzelnen Teile und Organe des Kopfes, wie aus dem beigegebenen Konstruktionsschema deutlich ersichtlich ist. So entspricht die Nase dem Minor ce der Strecke ac; die Höhe der Oberlippe, von der Lippenlinie bis zur Nasenwurzel reichend, ist wiederum dem Minor der Strecke ce entsprechend, und in ähnlicher Weise bestimmt die Unterteilung die weiteren Proportionen in der Formgebung des menschlichen Hauptes. Die Maßverhältnisse des menschlichen Armes hingegen zeigt die Abbildung 47. Die Länge des ganzen Armes, von der Spitze des ausgestreckten Fingers bis zur Schulterhöhe reichend, ist im Punkte c nach dem Goldenen Schnitt geteilt. Der Major der Strecke ab bestimmt den Unterarm, der Minor den Oberarm, und der Teilungspunkt c fällt genau mit dem natürlichen Teilungspunkte des Armes, dem Ellbogengelenk, zusammen. Die Länge der Hand, von der Handwurzel bis zum ausgestreckten Finger reichend, entspricht wiederum dem Minor der Strecke ac. Die Normalgestalt der menschlichen Hand nach den Proportionen des Goldenen Schnittes veranschaulicht noch einmal Abbildung 48. Im Punkt d ist hier die natürliche Hauptteilung der Hand in Mittelhand und Vorderhand gekennzeichnet, und die Unterteilung bestimmt die Maßverhältnisse der einzelnen Fingerglieder.

Abb. 49
Arm und Werkzeug im Goldenen Schnitt

Eine überaus interessante Beziehung nach der Regel des Goldenen Schnittes zeigt Abbildung 49. Sie zeigt den männlichen Arm in Verbindung mit der Axt, dem nächst dem Hammer ursprünglichsten und wichtigsten Werkzeug, beide in den Maßverhältnissen des Goldenen Schnittes dargestellt. An dem Arm sind durch die Proportion des Goldenen Schnittes zunächst in derselben Weise wie in unserer Abbildung 47 Oberarm, Unterarm und Hand bestimmt, und diesen Maßverhältnissen entspricht die Form der Axt, deren Stil in der doppelten Biegung ebenfalls das Teilungsprinzip des Goldenen Schnittes befolgt. So passen sich Arm und Werkzeug harmonisch aneinander an, und es hat sich herausgestellt, daß diese Form des Axtstieles die weitaus zweckmäßigste ist und die größte Arbeitsleistung bewirkt, beispielsweise eine größere, als es bei einer Axt mit geradem Stiel der Fall ist. Hier bekundet sich also die Wirksamkeit des Goldenen Schnittes in der Form der größten technischen Zweckmäßigkeit eines Werkzeuges. Gerade auf diesen Zusammenhang zwischen Goldenem Schnitt und Technik, auf die Wirksamkeit dieses Formengesetzes auch in der technischen Formgebung, hat Kapp mit besonderer Betonung hingewiesen, und er hat diesen Zusammenhang sogar zu einer eigenen »Philosophie der Technik« erweitert und in einem so betitelten Werke genauer dargelegt. An einer großen Anzahl von Beispielen sucht Kapp dort die Wirksamkeit des Goldenen Schnittes auch an anderen technischen Hilfsmitteln, Werkzeugen, Apparaten, Maschinen usw. nachzuweisen und so die Ansicht zu erhärten, daß wie am natürlichen menschlichen Körper so auch an den von dem Menschen geschaffenen künstlichen Hilfsmitteln und Vorrichtungen die technisch zweckmäßigste Form sich oftmals in den Proportionen des Goldenen Schnittes manifestiert, so oft, daß vielleicht auch der Techniker Veranlassung hätte, bei seinen Konstruktionen und Gestaltungen jenes Gesetz der Formgebung zu Rate zu ziehen. Gerade an den technischen Maßverhältnissen suchte Kapp den Beweis zu erbringen, daß die Maßverhältnisse des Goldenen Schnittes, die unserem Empfinden von Wohlgefälligkeit und Harmonie am meisten entsprechen, zugleich auch diejenigen sind, die die größte Zweckhaftigkeit der Körper, Gegenstände und Hilfsmittel gewähren, und daß dieses Gesetz wie für das Reich der organischen Lebewesen so auch für das Reich und die Schöpfungen der Technik gilt.

Man braucht Kapp in dieser weitgehenden Verallgemeinerung der Wirksamkeit des Goldenen Schnittes nicht vollkommen zu folgen und kann dennoch diesem Prinzip auch eine gewisse technische Bedeutung zuschreiben. Die Paarung von zweckmäßigster Form und äußerem befriedigenden Eindruck des Werkes kann auch technisch betätigt werden. Das eben ist ja allgemein die tiefere Bedeutung des Goldenen Schnittes als Prinzip der Formgebung, daß er dort, wo er in Erscheinung tritt, sei es an den Erzeugnissen der Natur, sei es an den Werken und Einrichtungen von Menschenhand, ein Ausdruck für die zweckmäßigste und vorteilhafteste Form des Werkes wird. In unserem Wohlgefallen an der äußeren Form der Dinge, in unserem Empfinden von Schönheit und Harmonie, das diese in uns erwecken, bekundet sich nur unser Erkennen der inneren Zweckmäßigkeit der Dinge und ihrer Gestaltungen, die viel höher steht und auch für uns viel wichtiger einzuschätzen ist als das rein ästhetische Wohlgefallen. Der menschliche Körper ist in den Teilungsverhältnissen des Goldenen Schnittes zugleich am zweckmäßigsten gebaut, und wir empfinden die idealisierten Menschengestalten von Künstlerhand, wie den Apoxyomenos, den Doryphoros und die zahllosen anderen künstlerischen Schöpfungen, an denen wir das Formenprinzip des Goldenen Schnittes nachweisen können, deswegen als besonders schöne Menschengestaltungen, weil sie uns die Formen größter Zweckmäßigkeit, größter Kraft und Leistungsfähigkeit im Bau der Menschengestalt veranschaulichen. Zweckmäßigkeit ist Schönheit, und diese Paarung ist Grund und Sinn des Goldenen Schnittes, den wir schön finden, weil er zugleich die Form der größten Zweckmäßigkeit zum Ausdruck bringt.

Aber auch wenn wir unter den Dingen, Formen und Gestaltungen unserer selbstgeschaffenen Umwelt Umschau halten, tritt uns das Gesetz der Formgebung des Goldenen Schnittes in den mannigfachsten Erscheinungsweisen entgegen, und zwar überall dort, wo die Dinge und Werke außer ihrem reinen Nützlichkeitscharakter noch den Zweck eines gefälligen Aussehens oder einer bestimmten schönheitlichen Gestaltung zu erfüllen haben, durch den sie dazu beitragen sollen, uns Wohlgefallen und Freude an unserer Umgebung empfinden zu lassen. Hier äußert sich die Paarung von Zweck und Form nach der Regel des Goldenen Schnittes oftmals als der »gute Stil« in der Gestaltung unserer Umgebung.

Vor allem ist es das Haus, das bedeutsamste Werk zur Einrichtung unserer Umwelt und Umgebung, dann in erweitertem Sinne das Bauwerk überhaupt, das im guten Stil das Bildungsprinzip des Goldenen Schnittes erkennen läßt. Für die Baukunst ist die Lehre vom Goldenen Schnitt kaum minder bedeutungsvoll geworden wie für die reine Kunst selbst. Bewußt oder unbewußt befolgt der Baukünstler das Teilungsverhältnis des Goldenen Schnittes und erreicht damit die harmonische und ästhetische Wirkung, die wir als »Baustil« bezeichnen. Von ebensolcher Bedeutung ist jene Regel auch für die Formgebung und die Maßverhältnisse der wichtigsten Gegenstände unserer Wohnungseinrichtung, der Möbel. Gleichviel ob wir die Möbel der Antike, des Mittelalters oder der heutigen Zeit betrachten, immer finden wir als vorherrschendes Prinzip der Teilung und Formengebung die Proportionen des Goldenen Schnittes vorhanden, auch hier, ohne daß die Möbelbauer jemals eine bewußte Kenntnis jener Proportionen und ihrer ästhetischen und stilistischen Bedeutung gehabt hätten. Die Tischplatte, das Stuhlformat, Schrank und Truhe sind Beispiele für das Gesagte. Das Möbel befolgt diese Proportionen, weil es in diesen am besten den Gebrauchszweck erfüllt. Der Stuhl paßt sich in jenen Proportionen am meisten der Gestalt des Sitzenden an, Schrank, Truhe, Büfett und Tisch entsprechen in diesen Proportionen am meisten der Gestalt des an ihnen hantierenden Menschen, bieten ihm so die größte Bequemlichkeit und erfüllen damit ihren Gebrauchszweck in vollkommenster Weise. Ihrer Zweckmäßigkeit wegen finden wir die Proportionen des Goldenen Schnittes am Möbelstück schön, und so äußert sich auch hier wiederum nur die Paarung von Zweck und Form, die das eigentliche Wesen des Goldenen Schnittes ausmacht.

So bekundet sich in dem Goldenen Schnitt ein Naturgesetz der Formgebung, das wir in weitem Umfange an den Schöpfungen und Gestaltungen der Natur selbst nachweisen können und das durch seine Naturbedeutung zugleich auch das waltende Schönheitsgesetz für die Werke von Menschenhand ist, das aus dem Gestaltungstrieb des Künstlers wie des Kunstgewerblers, ohne ihm bewußt zu werden, gleichsam von innen als ein immanentes Gesetz des Schaffens herausfließt und wirksam wird. Es ist die Paarung von Zweck und Form, die durch die Regel vom Goldenen Schnitt verkörpert wird, und unser Schönheitsgefühl bevorzugt die Formen und Proportionen des Goldenen Schnittes, weil diese jene Paarung am vollkommensten verbürgen. Es dürfte ohne Zweifel sein, daß Kunst und Kunstgewerbe nur gewinnen können, wenn sie jenem Naturgesetz der Formgebung wieder mehr Aufmerksamkeit zuwenden und sich ihm als einem bewußt erkannten Richtsatz anvertrauen. Damit soll keinesfalls einer absoluten, mechanischen oder gar ausschließlichen Befolgung der Regel vom Goldenen Schnitt in allen Fällen und unter allen Umständen das Wort geredet werden. Künstler und Kunstgewerbler sollen frei schaffen und sich nicht abhängig machen von irgendwelchen Prinzipien oder Gesetzen, die leicht zur Erstarrung und damit zur Unterbindung der kraftvollen Lebensentwicklung der Kunst führen können. Aber sicher ist, daß die Regel vom Goldenen Schnitt bei kluger Beschränkung als ein wertvoller Wegweiser zu dienen bestimmt und geeignet ist, den schaffenden Künstler oder Kunstgewerbler vor Mißgriffen und Verirrungen zu bewahren, wie wir sie seit Jahrzehnten wieder und immer wieder erlebt haben. In der Regel vom Goldenen Schnitt erhebt die Natur selbst ihre Stimme, die die große Lehrmeisterin der Kunst ist und immer bleiben wird, so viele und merkwürdige Strömungen und Richtungen sich auch immer wieder breitmachen, die Kunst vom Wege der Natur abzudrängen und sie zum Spielball von Stil- und Modelaunen, oftmals aber auch von Stil- und Modenarrheiten zu machen.

Im Goldenen Schnitt spricht die Natur im Rhythmus der Zahl, wird die Zahl im Sinne der alten Philosophen und vielleicht in stärkerer Weise, als wir heute zu glauben geneigt sind, zum Wesen der Dinge, soweit sie die Gesetze des Schaffens und der Formgebung anbelangen.

Postskriptum

Kritik und Zustimmung – Kunst von einst und heute – Ein sonderbarer Besuch – Goldener Schnitt und Schicksalsdeutung

Das Erscheinen des vorstehenden Aufsatzes in einer Reihe von Zeitschriften hatte das Thema des Goldenen Schnittes, über das wohl seit Jahren kaum viel gesprochen worden war, doch wieder weiteren Kreisen in Erinnerung gebracht, und eine große Anzahl von Zuschriften, besonders aus Künstlerkreisen, ist dem Verfasser in der weiteren Folge zugegangen. Alte und neue Richtung der Kunst und der verschiedenen künstlerischen Gebiete kamen darin deutlich zum Ausdruck. Ein Teil der Einsender lehnte den Goldenen Schnitt als Formgesetz der bildenden Kunst ab, weil der Künstler frei schaffen müsse und keiner Bindung in der Formgebung unterliegen dürfe; nach diesen Äußerungen gehört der Goldene Schnitt der Vergangenheit an, denn »heute schafft sich der Künstler das Gesetz der Formgebung selber«, schrieb mir ein junger Maler. Ganz gegenteilig äußerten sich andere Einsender, die ihrer Befriedigung darüber Ausdruck gaben, daß wieder einmal die Aufmerksamkeit auf den Goldenen Schnitt als Gesetz der Formgebung gelenkt worden sei, denn der sei das Mittel, um weite Kreise, bei denen heute heillose Verwirrung und Willkür in Form und Stil herrsche, wieder zum Ausgang alles künstlerischen Schaffens, zur Natur und ihrem Formenschatz zurückzuführen.

Auch dieser Aufsatz führte zu einem sonderbaren Erlebnis, das allerdings mit Kunst und Ästhetik nichts zu tun hat. Besuchte mich einstmals ein Herr, der mir sagte, daß er in einem Café meinen Aufsatz über den Goldenen Schnitt gelesen habe. Der habe ihn im höchsten Maße gefesselt und ihn Tag und Nacht beschäftigt, habe ihn zu langen Versuchen und Untersuchungen veranlaßt und schließlich zu einer neuen Erkenntnis gebracht. Der Goldene Schnitt – diese Wahrheit habe sich ihm durch seine Forschungen als endliches Ergebnis aufgedrängt – habe noch eine andere und viel höhere Bedeutung als nur die des zahlenmäßig ausdrückbaren Formengesetzes für die Kunst; er sei vielmehr der eigentlichste und natürlichste Ausdruck für das innerste Wesen des Menschen selbst, und durch ihn seien Charakter und Zukunft jedes Menschen aufs genaueste zu erkennen. Das begründete mein Besucher, der Typus des unklaren Grüblers, in folgender Weise: Vollkommen sei der Goldene Schnitt nur an der menschlichen Idealgestalt. Solche Idealgestalten gibt es nicht, sondern die Proportionen des Menschen weichen immer mehr oder weniger vom Goldenen Schnitt ab. Diese Abweichungen seien das Wichtigste, denn aus ihnen und ihrer Art lasse sich der ganze Charakter des Menschen, seine Veranlagung und seine Fähigkeiten, auch die ihm selbst unbekannten, vor allem aber auch seine Zukunft feststellen, und das mit viel größerer Sicherheit als etwa durch Lesen von Karten und Handlinien oder durch die Astrologie, über welche Disziplinen sich mein Besucher höchst abfällig äußerte. Dadurch erst erweise sich der Goldene Schnitt als die sectio divina, der Göttliche Schnitt, wie ihn die Gelehrten des Mittelalters nannten, denn durch die Deutung, die der Goldene Schnitt für Leben und Schicksal der Menschen zulasse, bringe Gott selbst seinen Willen zum Ausdruck. Zulangen Ausführungen suchte mich der neue Prophet von der Wahrheit seiner Auffassung zu überzeugen, tat alle Einwände mit kraftvoller Handbewegung ab, und teilte mir auch mit, daß er schon bei allen seinen Familienmitgliedern, Freunden und Verwandten die Richtigkeit seiner Methode mit unfehlbarer Sicherheit festgestellt habe. Es habe immer gestimmt! Er bat mich um seine Unterstützung, um die neue Lehre der Welt bekanntzumachen, was am besten durch eine Reihe von Zeitungsaufsätzen geschehen könnte. Diese Zusage konnte ich meinem Besucher nun allerdings nicht geben, und als ich gewisse Zweifel an der Richtigkeit seiner Deduktionen und seiner Lehre äußerte, bat er, zum Beweis des Gegenteils seine Kunst an mir selbst demonstrieren zu dürfen. Was blieb mir übrig, als ihm seinen Willen zu tun! Hände und Kopf stellte ich ihm für seine mystische Kunst gutwillig zur Verfügung, und mit Meßstab und Tabelle – er hatte die Sache schon in eine komplette und vielgegliederte Methode gebracht – ging er an die Deutung meines inneren und zukünftigen Menschen. Manches, was er mir über mich selbst berichtete, war sehr richtig, anderes war mir neu und interessant, – man freut sich schließlich immer, sich auch einmal näher kennenzulernen. Über mein ferneres Schicksal, das er mir prophetischen Blickes ziemlich detailliert ankündigte, erlaubte ich mir allerdings andere Vermutungen zu haben. Als er schließlich, um seine Untersuchungen noch weiter und genauer ausdehnen zu können, um Entkleidung ersuchte, als ob er ein Oberstabsarzt wäre, da lehnte ich das denn doch ab, und gab auch meiner Skepsis über den Wert seiner Methode ziemlich deutlichen Ausdruck. Darauf verließ er mich, zwar merkbar herabgestimmt über meinen inneren Menschen, aber doch nicht, ohne mir einen wortreichen Dank abzustatten, daß ich ihm durch meine Aufsätze über den Goldenen Schnitt den Weg zur tieferen Erkennung und Wertung dieses göttlichen Gesetzes gewiesen habe. – Ich bin fest überzeugt, daß der gute Mann es zu einer Gemeinde bringen wird, was allerdings nicht die Absicht meines Aufsatzes gewesen war. Aber als Zeichen, wie heute neue Propheten entstehen, sei auch dieses Erlebnis mitgeteilt.

4. Der Stein der Weisen

Die Kunst, Gold zu machen – Die Alchemie im Altertum – Hermes Trismegistos – Die Araber – Geber – Christliche Alchemie – Der Stein der Weisen – Albertus Magnus – Roger Bacon – Villanovus – Raimundus Lullus – Basilius Valentinus – Gekrönte Alchemisten – Von der Alchemie zur Chemie – Auferstehung der Alchemie?

In der Geschichte des menschlichen Denkens und Forschens wird für immer jenes Problem, das unter dem Namen »der Stein der Weisen« bekannt und berühmt geworden ist, eins der eigenartigsten und reizvollsten, zugleich aber auch wichtigsten und folgenreichsten Kapitel sein. Eigenartig und reizvoll zunächst um des Zieles willen, das mit jenem Problem verfolgt wurde, und das darin bestand, eine geheimnisvolle Substanz, eben den Stein der Weisen, zu finden, die ihrem Besitzer ungeahnte Kräfte und Fähigkeiten zur Erlangung aller irdischen Macht und Glückseligkeit, vor allem aber auch die Fähigkeit, unedle Metalle in Gold zu verwandeln, verleihen sollte. An das Streben nach diesem Ziel, die Herstellung von Gold durch den Stein der Weisen, knüpft sich jene eigentümliche Wissenschaft, die wir als Alchemie bezeichnen und die etwa anderthalb Jahrtausende hindurch die Denk- und Forschungsweise der Gelehrten beherrscht hat. Die Geschichte des Problems des Steins der Weisen ist nahezu gleichbedeutend mit der Geschichte der Goldmacherkunst selbst. Wichtig und folgenreich aber wurde die Beschäftigung mit jenem merkwürdigen Problem deswegen, weil sie trotz des trügerischen und nie erreichten Zieles und trotz der Sonderbarkeiten ihrer Methoden schließlich doch der Weg wurde, auf dem die menschliche Forschung zu tieferer Einsicht in das Wesen der Dinge, insbesondere die Natur der Stoffe, und damit zur Erschließung eines der größten, wichtigsten und inhaltreichsten Gebiete der Naturerkenntnis überhaupt geführt wurde. Ähnlich wie aus der Astrologie die wissenschaftliche Astronomie, so ging aus den Irrwegen, auf denen sich das Denken im Streben nach dem Stein der Weisen und nach dem Geheimnis, Gold zu machen, bewegte, schließlich die Wissenschaft der Chemie hervor, und dieser Entwicklungsgang von mystischem Denken zu geläuterter Erkenntnis, der sich an das Streben nach der Lösung jenes merkwürdigen Problems knüpft, gibt diesem für immer einen hervorragenden Platz in der Geschichte des problematischen Denkens.

Wir sagten bereits, daß die Geschichte des Problems des Steins der Weisen nahezu gleichbedeutend mit der Geschichte der Goldmacherkunst selbst ist. Nahezu, aber nicht vollkommen. Die Idee, unedle Metalle in Gold zu verwandeln, hatte schon einige Jahrhunderte, bevor diese Denkweise sich zu dem Begriff des Steins der Weisen herauskristallisierte, Besitz von den Denkern und Forschern ergriffen. Das Problem, auf künstlichem Wege Gold zu machen, aber noch nicht mit jenem Begriff verquickt, beginnt vielmehr nahezu mit dem Zeitpunkt, in welchem das Gold in der Wertschätzung des Menschen überhaupt zu seiner folgenreichsten Bedeutung als Träger von Wert und Reichtum gelangte, um dessen Besitz gearbeitet, gestrebt und erbittert gekämpft wurde. Seitdem entstand auch das Bemühen, die natürliche Art der Goldgewinnung durch künstliche Mittel der Goldherstellung zu vermehren und zu erweitern und die Geheimnisse, an die vermeintlicherweise die Erreichung dieses Zieles gebunden war, aufzudecken. Schon Götterlehre und Sagenschatz der ältesten Kulturvölker verraten dieses Bemühen in mannigfachster Weise. Die Götter der Alten verstehen sich immer auf die Kunst, Gold zu schaffen oder gewöhnliche Dinge in Gold zu verwandeln, und ebenso vermögen sie auch gewöhnlichen Sterblichen diese schätzenswerte Fähigkeit zu verleihen. Der König Midas erbat sich von einem Gott die Gabe, daß alles, was er berührte, zu Gold werden sollte; der Gott erfüllte den törichten Wunsch, mit dem Erfolg, daß sich der ganze Palast des Midas, aber auch seine Nahrung und schließlich er selbst in Gold verwandelte. In anderen Fällen sind es Zauberer, die sich auf die Kunst der Goldverwandlung verstehen, und im Mittelalter wurde besonders dem Teufel diese Fähigkeit als eines seiner vielen Mittel zugeschrieben, um erfolgreich den Seelenfang zu betreiben. Aus allen den zahllosen Sagen, Erzählungen, Märchen usw. dieser Art spricht letzten Endes doch nur der Wunsch, durch göttliche oder zauberische Kräfte hinter das Geheimnis des Goldmachens zu kommen, zugleich aber auch die Auffassung, daß es durchaus möglich sei, das begehrte Edelmetall auf künstlichem Wege herzustellen, und daß es zu diesem Zweck eben nur besonderer Mittel und Kräfte bedürfe. Auch gewisse Stellen der Bibel sind – ob mit Recht oder Unrecht, sei dahingestellt – im alchemistischen Sinne ausgelegt worden. Schon die ältesten Alchemisten sahen in Moses ihren Ahnherrn, weil er nach dem Bericht der Bibel bitteres Wasser in süßes verwandelte, ebenso auch in Hiob, weil von ihm gesagt wird: »Du wirst Gold für Erde geben und goldene Bäche für Felsgestein.«

Der uralte Glaube an die Möglichkeit, gewöhnliche Stoffe, besonders unedle Metalle, in Gold zu verwandeln, hatte freilich eine sehr natürliche Wurzel. Die Art der Metallgewinnung selbst war es, die bei allen alten Völkern nahezu mit Notwendigkeit zu dieser Ansicht führen mußte. Die unedlen Metalle werden durch Ausschmelzen aus ihren Erzen gewonnen; in diesem Prozeß sah man aber weniger eine Scheidung des Metalls von den mineralischen Bestandteilen des Erzes als vielmehr eine Verwandlung des Erzes in Metall. Und wie die Erze sich nach dieser Auffassung in Blei, Zink, Zinn und andere unedle Metalle verwandeln ließen, so mußte es nach derselben Auffassung auch möglich sein, solche Erze oder die aus ihnen gewonnenen unedlen Metalle in Gold zu verwandeln. Durch die Ähnlichkeit vieler Metalle in Farbe und äußeren Eigenschaften wurde dieser Glaube noch bestärkt, ebenso auch durch gewisse Experimente, bei denen eine Verwandlung von Metallen stattzufinden schien, wie etwa ein Stück Eisen seine Farbe verändert, wenn es in eine Lösung von Kupfervitriol gelegt wird, eine Änderung, die als »Verwandlung« aufgefaßt wurde. Solche Erfahrungen kannte man schon in uralter Zeit, seitdem man sich überhaupt mit den Metallen zu beschäftigen begonnen hatte, aber der völlige Mangel tieferer metallurgischer oder chemischer Kenntnisse führte zu einer falschen Deutung solcher Vorgänge, die sich mit Vorliebe in der Richtung des heißersehnten Zieles der Goldverwandlung bewegte. Auch die Legierung der Metalle, durch welche diese ihre physikalischen Eigenschaften, Farbe, Härte, Schwere usw. wesentlich verändern, wurde ursprünglich sicher als Umwandlung im alchemistischen Sinne gedeutet und hat auch in der späteren Zeit in die Auffassungen und Methoden der Alchemisten hineingespielt; da aber durch Legierung der unedlen Metalle gerade die charakteristische Eigenschaft der Edelmetalle, ihre Beständigkeit und Unveränderlichkeit gegenüber Feuer, Luft und chemischen Substanzen, nicht zu erreichen war, so haben die Versuche, durch Legierung Gold zu machen, in den Rezepten der Alchemisten doch nur eine Nebenrolle gespielt.

In solcher wie der beschriebenen Weise wurde die Alchemie schon Hunderte von Jahren vor Beginn unserer Zeitrechnung bei den Phöniziern, dem Küstenvolke im alten Syrien, bei denen Metallgewinnung und Metallbearbeitung bereits zu hoher Blüte gelangt war, und ebenso auch bei den alten Ägyptern betrieben. Einer der Götter der Ägypter, der Mondgott Thoth oder Thouth, galt als der Schöpfer der Magie und ebenso auch der Alchemie. Die späteren Griechen sahen in dem sagenhaften Thoth jedoch mehr einen alten Weisen, den sie der vielen geheimnisvollen Eigenschaften wegen, die er besessen haben soll, als Hermes Trismegistos, d. h. der dreimal Größte, bezeichneten. Ihm wurde insbesondere auch die Kenntnis der Kunst des Goldmachens zugeschrieben, und er soll die geheime Vorschrift, die diesem Zwecke diente, auf eine Tafel von Smaragd niedergeschrieben haben. Diese » Tabula Smaragdina« ist das älteste schriftliche Dokument in der Geschichte der Goldmacherkunst und beginnt mit den Worten: »Es ist ohne Lüge, wahr und gewiß: was unten ist, ist wie das, was oben ist, und was oben, wie das, was unten ist, um die Wunder der Dinge zu durchdringen!« In dieser geheimnisvollen Weise geht es weiter, und es ist bis heute noch kein Mensch aus diesem ebenso alten wie dunklen Rezept zum Goldmachen klug geworden. Trotzdem aber stand Hermes Trismegistos bei den späteren Alchemisten in größtem Ansehen, und die Tabula Smaragdina galt, wenn sie auch nie einem Menschen dazu verholfen hat, Gold herzustellen, solange es überhaupt Alchemie gab, geradezu als die Bibel der Alchemisten. Hermes Trismegistos ist so die ganze Geschichte der Alchemie hindurch sozusagen der Schutzheilige und Inbegriff aller alchemistischen Tätigkeit und Weisheit geblieben; »hermetisch« war gleichbedeutend mit alchemistisch, und in der Bezeichnung »hermetischer Verschluß« dauert das Andenken an diesen ersten aller Alchemisten sogar noch heute fort. Ägyptischen Ursprungs ist übrigens auch die Bezeichnung »Alchemie« selbst; sie stammt von dem Namen des Landes, das in alter Sprache »Chemie« hieß, so daß Alchemie soviel wie ägyptische Wissenschaft bedeutet. Das Wort » chemie« hatte außerdem auch noch die Bedeutung »schwarz«, und daher wurde die Alchemie auch späterhin als »Schwarzkunst« bezeichnet, und diesen Namen hat sie die Jahrhunderte hindurch neben jenem anderen beibehalten.

In ähnlicher Weise wie bei den alten Ägyptern wurde die Alchemie wohl auch bei den alten Griechen ausgeübt, die ja viele Kenntnisse, Erfindungen und technische Errungenschaften erst von den alten Ägyptern übernommen haben. Auch bei den Griechen herrschte noch völliger Mangel tieferer chemischer Kenntnisse und daher ebenso wie bei jenen der naive Glaube an die Verwandelbarkeit der Stoffe und insbesondere der Metalle. Der große Naturforscher und Philosoph der Griechen Aristoteles lehrte, daß Feuer, Wasser, Luft und Erde die Grundstoffe seien, aus denen sich alle anderen Stoffe und überhaupt alle irdischen Dinge zusammensetzten; also mußte es doch wohl auch möglich sein, jene Grundstoffe zu Gold zusammenzufügen. Diese Auffassung des Aristoteles von der Natur der Stoffe hat noch viele Jahrhunderte, bis hoch ins Mittelalter hinein, nachgewirkt und war in Verbindung mit den Lehren des Hermes Trismegistos eine der Grundlagen und Hauptstützen für den Glauben an die Möglichkeit, unedle Metalle in Gold zu verwandeln.

Genauere Kenntnisse über die Goldmacherkunst haben wir dann erst aus den ersten Jahrhunderten der christlichen Zeitrechnung. Wir wissen, daß man sich auch um jene Zeit sowohl in Ägypten wie auch in Griechenland mit alchemistischen Versuchen befaßte und nicht nur Gold, sondern auch Silber auf künstliche Weise herzustellen suchte. Man war fest davon überzeugt, daß sich Kupfer oder Kupfererze in Gold umwandeln lassen müßten, und eifrig bemüht, die Mittel der Umwandlung zu finden. Aus dieser Zeit stammen auch verschiedene alchemistische Schriften, so eine solche des Bischofs Synesius aus dem fünften Jahrhundert, in der der Verfasser das Destillierverfahren, das bei allen alchemistischen und chemischen Versuchen und Prozessen eine große Rolle spielte, eingehend beschrieb, während der Ägypter Zosimos ein Werk über alchemistische und chemische Öfen und Apparate herausgab; Zosimos schreibt darin auch, daß die Götter oftmals irdischen Frauen ihre Geheimnisse verraten und sie auch in die Kunst, Gold und Silber künstlich herzustellen, einweihen sollten. Bemerkt sei noch, daß damals auch im fernen China die Alchemie betrieben wurde in der Weise, daß man zunächst Zinn in Silber, und dieses dann in Gold umzuwandeln suchte.

Abb. 50
Gerätschaften des Alchemisten Geber

Eine neue Epoche der Alchemie begann, als die Araber im siebenten Jahrhundert das alte Ägypten erobert und dadurch auch die alchemistischen Lehren und Kenntnisse, die seit des Hermes Trismegistos Zeiten dort gesammelt worden waren, kennengelernt hatten. Auf ihren weiteren Eroberungszügen verbreiteten sie die Schwarzkunst dann auch in Spanien und Italien, und von hier aus wurde jene Kunst dann auch nach den übrigen europäischen Ländern weitergetragen. Die Araber, ein tatkräftiges und geistig hochstehendes Kulturvolk, dem die europäische Wissenschaft und Technik auch auf anderen Gebieten viel zu verdanken hat, vertieften sich mit großem Eifer in die Kunst der Alchemie, und eine große Anzahl arabischer Gelehrter gehört zu den bedeutendsten Alchemisten aus der ganzen Geschichte dieser Geheimkunst. Bei den arabischen Alchemisten erweiterten sich aber die zusammenhanglosen und vielfach verworrenen und mißverstandenen metallurgischen und alchemistischen Erfahrungen ihrer Vorgänger zum ersten Male zu einigermaßen geordneten chemischen Kenntnissen, freilich immer mit dem Ziele, durch diese das große Geheimnis der Goldmacherkunst zu ergründen. Sie machten im Laufe der Zeiten eine große Anzahl neuer und wertvoller Entdeckungen und Erfindungen auf diesen Gebieten, gewannen nähere Einblicke in das Wesen des chemischen Prozesses und der chemischen Verbindungen und dadurch tiefere Einsichten in die Natur der Stoffe überhaupt als jemals ihre Vorgänger.

Der bedeutendste unter diesen arabischen Alchemisten war Abu-Mussa-Dschafar al Sofi, der in der Geschichte der Wissenschaften bekannter unter dem Namen Geber geworden ist. Er war ein für seine Zeit bedeutender Chemiker und verfügte besonders auf metallurgischem Gebiete über ein großes Wissen, das er durch zahlreiche neue Erfahrungen und Entdeckungen vermehrte. Er kannte und beschrieb eine große Anzahl neuer Metallverbindungen. Von ihm stammen die Verfahren des Sublimierens, Filtrierens und Kristallisierens, ferner auch die Anwendung des Wasserbades bei der Destillation, alles hochwichtige Prozesse bei der Tätigkeit des Chemikers. Er lehrte auch die Darstellung der Schwefelsäure und der Salpetersäure nach neuem und verbessertem Verfahren und entdeckte die Eigenschaften des Königswassers, das durch Mischung aus Schwefel- und Salpetersäure entsteht und die einzige Flüssigkeit ist, die Gold aufzulösen vermag. In seiner Auffassung von der Natur der Metalle wandte er sich entschieden von der Lehre des Aristoteles ab und gelangte auch hier zu einer immerhin schon höheren Ansicht. Nach dieser bestanden alle Metalle aus drei Stoffen, nämlich Quecksilber, Schwefel und Arsenik, und je nachdem man den einzelnen Metallen von diesen Grundstoffen mehr oder weniger zusetzte oder entzog, sollten sich diese ineinander verwandeln lassen. Dem Quecksilber besonders maß er eine besondere Bedeutung für die Alchemie bei; als einziges Metall, das schon bei gewöhnlicher Temperatur flüssig ist, sollte es auch besondere Eigenschaften für die Zwecke der Goldumwandlung haben und der wichtigste Grundstoff für die Herstellung des Edelmetalles sein. Diese Auffassung von der besonderen Wichtigkeit des Quecksilbers hat sich auch auf alle späteren Alchemisten übertragen, und das Quecksilber hat diese Rolle bis zum Ende der Alchemie gespielt. Freilich genügte nach Gebers Ansicht das Vorhandensein von Quecksilber, Schwefel und Arsenik allein noch nicht, um daraus Gold herzustellen; dazu war, wie er glaubte, außerdem noch die Anwendung gewisser Tinkturen und Medizinen notwendig, die durch die ihnen innewohnenden besonderen Kräfte erst die Umwandlung jener Grundstoffe in Gold bewirken sollten. Geber mag zu dieser Ansicht durch die Erfahrung gekommen sein, daß bei vielen chemischen Prozessen die zusammengebrachten Stoffe erst bei der Anwesenheit eines bestimmten anderen Stoffes aufeinander wirken und in Verbindung treten. Solche Stoffe, die erst die chemische Wirkung und Verbindung anderer Substanzen aufeinander auslösen, ohne selbst aber in die Verbindung jener miteinzutreten, nennt die Chemie bekanntlich Katalysatoren. Solcher Art mögen auch die geheimen Tinkturen und Medizinen gewesen sein, die nach der Ansicht Gebers erst die Umwandlung jener drei Grundstoffe in Gold bewirken oder auslösen sollten. Gerade diese Auffassung Gebers, in der sich also eine sehr richtige und wichtige Erfahrung widerspiegelt, ist für die Folgezeit von grundlegender Bedeutung für die ganze Alchemie geworden.

Abb. 51
Gerätschaften des Alchemisten Geber

Im 11. Jahrhundert hatte sich durch den Einfluß der Araber die Alchemie wohl in allen europäischen Kulturländern verbreitet als eine Art Geheimlehre, deren Jünger überall den Ruf besonderer Kenntnisse und Fähigkeiten genossen. Viel aufrichtiges Forschen und Streben, wenn auch auf dunklen und umständlichen Wegen, ist in der Tätigkeit der Alchemisten zu finden, aber bereits machte sich auch eine ausgesprochene Scharlatanerie breit seitens solcher Alchemisten, die sich nur den Anschein besonderer Fähigkeiten zu geben und diesen Nimbus zu unlauteren Zwecken zu benutzen verstanden, eine Mischung, wie sie für die ganze spätere Zeit der Alchemie so überaus charakteristisch ist. Der Glaube an die Möglichkeit, Gold zu machen, stand überall fest, und der Hunger nach dem kostbaren Metall schuf diesem Treiben überall einen günstigen Boden. Besonders an den Höfen der Fürsten nisteten sich bereits damals zahlreiche Alchemisten ein, die angaben, Kupfer in Gold verwandeln und dadurch dem ewigen Goldmangel der Herrschenden leicht abhelfen zu können. Die Hofalchemisten, die teuer bezahlt wurden und in ihren Laboratorien Jahre hindurch ihr geheimnisvolles Handwerk betrieben, ohne zum Ziele zu kommen, es aber immer von neuem verstanden, durch Versprechungen und geheimnisvolle Andeutungen ihre Auftraggeber hinzuhalten, wurden seitdem eine häufige Erscheinung. Als erster Alchemist auf deutschem Boden wird ein gewisser Paulus erwähnt, der im Jahre 1063 von dem Bischof Adalbert von Bremen in Dienst genommen wurde, um durch seine Kunst die erschöpften Kassen des Kirchenfürsten wiederaufzufüllen. Schon hieraus geht hervor, daß die Geistlichkeit, die sonst gegen alles, was nach Magie und Zauberei roch, unbarmherzig vorging, der Alchemie gegenüber ebenfalls eine sehr wohlwollende Stellung einnahm. Die Sehnsucht nach dem Golde erzog zur Toleranz.

Seit dem 12. Jahrhundert etwa wurde die Alchemie eine regelrechte und anerkannte Wissenschaft, die allerdings nicht auf den Universitäten gelehrt, sondern als Geheimkunst seitens zahlreicher Gelehrter aller Richtungen und Fakultäten betrieben wurde. Gerade im Bereich der christlichen Wissenschaft aber nahm die Alchemie in der Folgezeit eine sehr unwissenschaftliche Richtung an. Die frühere Alchemie, wie sie bei Ägyptern, Griechen und Arabern betrieben worden war, war bei aller Dunkelheit und Verworrenheit der Mittel und Wege doch eine Art wissenschaftlicher Tätigkeit gewesen, darauf gerichtet, durch Erfahrungen und Experimente das Wesen der Stoffe zu ergründen und auf diese Weise das sich daran knüpfende Problem der Umwandlung der Stoffe zu lösen. Denken und Forschen, Untersuchung und Experiment waren die Wege dieser Tätigkeit geradeso wie auf irgendeinem anderen Gebiet der Wissenschaft gewesen, und auf diesen Wegen war man zu Erfahrungen und Erkenntnissen, zu gewissen Erfolgen und freilich auch zu vielen Mißerfolgen gekommen, wie es in allen andern Wissenschaften auch der Fall war. Auf diesem Wege echter Forschungstätigkeit hoffte man schließlich auch bis an das erstrebte Ziel selbst zu gelangen. Anders aber betätigte sich die Alchemie des christlichen Mittelalters. Die Erfolglosigkeit aller alchemistischen Versuche während der vergangenen Jahrhunderte führte zu der Auffassung, das nur höhere als die gewöhnlichen menschlichen Kräfte zur Lösung des Problems führen könnten. Besonders waren es die schon von dem Araber Geber gemachten Andeutungen, daß zur Goldverwandlung gewisse katalytische Stoffe nötig seien, die diese Auffassung nährten, aber zugleich auch ins Mystische und Verworrene steigerten. Es bildete sich der Glaube heraus, daß es gewisse Stoffe gäbe, die durch die ihnen innewohnenden geheimnisvollen Kräfte die unedlen Metalle in Gold verwandeln sollten, wenn sie mit jenen nur in Berührung gebracht würden. Diesen geheimnisvollen Stoff zu finden, um auf solchem abgekürzten Wege das Problem der Goldmacherkunst lösen zu können, darauf richtete sich nunmehr das ganze Streben der Alchemisten.

Damit trat an die Stelle der früheren Forschung durch Verstand und Experiment eine unwissenschaftliche Geheimkunst, und diese blieb das Charakteristikum der Alchemie der späteren Jahrhunderte, wenn freilich auch bei dieser Art der Alchemie viel Scharfsinn aufgewandt wurde und man oftmals auch bei dieser Art des Forschens zu neuen und wertvollen Kenntnissen allgemeiner Natur gelangte. Das Suchen nach dem geheimnisvollen Stoff, der durch seine bloße Berührung Blei oder Quecksilber in Gold zu verwandeln imstande sei, beherrschte alles Denken und Arbeiten der Alchemisten. Bald sollte es eine Tinktur oder Medizin, bald ein fester Stoff sein, dem jene Wirkung zugesprochen und der bald als »Rote Tinktur« oder als »Roter Löwe« bezeichnet wurde. Besonders aber sollte es ein roter Stein sein, der, zu Pulver zerrieben, die höchste und vollkommenste Wirkung zur Umwandlung unedler Metalle in Gold zu entfalten imstande sei, nämlich der Stein der Weisen. Und noch mehr sollte dieser zauberische Stein vermögen: er sollte auch jegliche Krankheit zu beseitigen und ewige Jugendkraft und ewiges Leben zu verleihen imstande sein und so dem, der ihn fände, alle irdische Macht und Glückseligkeit gewähren. Was Wunder, wenn sich das ganze Streben der Alchemisten darauf richtete, diesen Zauberstoff zu finden oder zu erschaffen, und daß Jahrhunderte hindurch ein ungeheures Kapital von Scharfsinn und Arbeit darauf verwandt wurde, in den Besitz dieses Stoffes zu gelangen. Die Herstellung des Steins der Weisen, des lapis philosophorum, wie er gelehrt genannt wurde, galt als das größte und vollkommenste Meisterstück, das einem Alchemisten überhaupt je gelingen konnte, und wurde daher als das Große Magisterium bezeichnet.

Über die Beschaffenheit des geheimnisvollen Steins der Weisen und ebenso über die Art seiner Herstellung gingen die Meinungen freilich sehr auseinander, und jeder der berühmten Alchemisten hatte dafür sozusagen sein eigenes Rezept. Der Stoff, aus dem der Stein herzustellen sei, wurde als materia prima (Grundstoff) bezeichnet, und das sollten bald mineralische Substanzen, besonders Steine oder gar Edelsteine, bald seltene Pflanzen oder die Substanz bestimmter Tiere sein. Nach einer Vorschrift sollte aus der materia prima zunächst eine grüne Substanz, der Grüne Löwe oder Drache, auch der Merkur der Weisen genannt, entstehen; aus dieser entstand dann eine schwarze Substanz, Rabenhaupt genannt, die sich in einen weißen Stoff, den Weißen Schwan oder die Lilie, verwandelte, und aus dieser Substanz sollte durch Glühen in Feuer nach besonderen geheimen Vorschriften endlich der Rote Löwe oder der Stein der Weisen hervorgehen. Nur besonders Auserwählten sollte die Herstellung des lapis philosophorum gelingen; viele hielten göttlichen Beistand zum Gelingen des Großen Magisteriums für nötig, andere suchten durch Beschwörungen und Zauberformeln zum Ziele zu gelangen oder bändelten zu diesem Zweck auch mit dem Teufel an. Glaube und Aberglaube rankten sich in unübersehbarer Fülle um das Große Magisterium. Die Auserwählten, denen die Herstellung des geheimnisvollen Steines bereits gelungen sein sollte, wurden als Adepten bezeichnet, während Alchemisten diejenigen hießen, die noch nicht so weit, aber auf dem Wege zu diesem Ziel waren, und diejenigen, die noch Schüler in der hohen Kunst der Alchemie waren, wurden »Philosophen« genannt. Allgemein war man von der hohen Kraft des Steins der Weisen überzeugt. Schon eine Wenigkeit des Stoffes, auf geschmolzenes unedles Metall geworfen, sollte genügen, um das Zehn- oder Hundert-, ja Tausendfache seines Gewichtes in pures Gold zu verwandeln. Anderen, schwächeren Elixieren wurde nur die Kraft, Blei in Silber zu verwandeln, zugesprochen, aber im allgemeinen steigerten sich die vermeintlichen zauberischen Kräfte des Steins der Weisen in der weiteren Geschichte der Alchemie immer mehr. Bemerkt sei noch, daß man den Stein der Weisen auch mit anderen rätselhaften Problemen aus jener Zeit in Verbindung brachte, besonders mit der Quadratur des Kreises, die ja damals Gelehrten und Ungelehrten ebensoviel zu schaffen machte und allgemein als eines der tiefsten und schwersten Geheimnisse alles menschlichen Denkens überhaupt galt. Es bildete sich die Ansicht heraus, daß der, der die Quadratur des Kreises möglich machte, zugleich auch in den Besitz aller irdischen Weisheit überhaupt und damit auch in den Besitz des Steins der Weisen gelange samt allen Kräften und Fähigkeiten, die dieser zu verleihen imstande sei. Die Quadratur des Kreises ist nie möglich gemacht und der Stein der Weisen niemals gefunden oder geschaffen worden, aber jene seltsame Verknüpfung der beiden Probleme hat bis zum letzten Ende der Alchemie angehalten.

Abb. 52.
Alchemistisches Laboratorium aus dem 14. Jahrhundert

Die Blütezeit der Alchemie bei den christlichen Kulturvölkern beginnt im 13. Jahrhundert. Seit dieser Zeit etwa finden wir Jahrhunderte hindurch die berühmtesten Gelehrten aller Fakultäten und nahezu aller Nationen als Jünger der Alchemie tätig, damit beschäftigt, den Stein der Weisen zu finden oder zu erschaffen; der Glaube an diesen geheimnisvollen Stoff und seine zauberischen Kräfte beherrschte unterschiedslos selbst die hervorragendsten Geister, die auf anderen Gebieten viel kritischer und wissenschaftlicher dachten und zu Werke gingen. Gleich aus der Zeit des 13. Jahrhunderts tritt uns eine Anzahl hochberühmter Forscher und Gelehrter entgegen, die zugleich auch als Alchemisten tätig waren und als solche für die Geschichte der Goldmacherkunst, zugleich aber auch für die Entwicklung der Naturwissenschaften überhaupt, insbesondere der Chemie und der Metallkunde, von großer Bedeutung geworden sind.

An erster Stelle unter den berühmten Alchemisten aus jener Zeit ist der Bischof Albert von Bollstädt (1195-1280) zu nennen, der seiner großen Gelehrsamkeit wegen Albertus Magnus genannt wurde, einer der hervorragendsten Gelehrten seiner Zeit überhaupt und Lehrer des Thomas von Aquino. In naturwissenschaftlichen Dingen, die ja freilich damals noch völlig im Dunklen lagen, huldigte er noch vollkommen den Ansichten des Aristoteles und in chemischen Dingen denen der Araber, besonders des Geber. Er schrieb auch ein Werk über Alchemie und sprach darin mit aller Bestimmtheit aus, daß die Verwandlung unedler Metalle in Gold möglich sei. Doch verbesserte er das Rezept Gebers dahin, daß außer Quecksilber, Schwefel und Arsen auch noch Wasser zu dem Verwandlungsprozeß nötig sei und daß dieses überhaupt die besonderen Eigenschaften der Metalle mitbewirke. Er will selber die Verwandlung gewöhnlicher Stoffe in Gold festgestellt haben und behauptete, daß es am leichtesten sei, Gold aus Silber herzustellen, da letzteres dem Gold schon in vielen Eigenschaften ähnlich und es daher nur noch nötig sei, seine weiße Farbe in die rötlich-gelbe des Goldes umzuwandeln. Wenn nun seine Ergebnisse auf dem Gebiet der Goldmacherkunst ebenso zweifelhaft waren wie die aller seiner Vorgänger, so hat er doch auf allgemein-metallurgischem Gebiet manchen wichtigen Fortschritt erzielt. Er lehrte zuerst die Trennung von Gold und Silber vermittels Scheidewasser und ebenso auch die Scheidung unedler Metalle, gab das Verfahren der Sublimierung, der Gewinnung der Metalle aus den Erzen durch Quecksilber, an und ist durch diese Erfolge seiner alchemistischen Tätigkeit immerhin von Bedeutung geworden.

Ein Zeitgenosse des Albertus Magnus, und wie dieser ein berühmter Theologe und zugleich Alchemist, war auch der Engländer Roger Bacon (1214-1294), ebenfalls ein hochgelehrter und seiner Zeit in vielem vorausgeschrittener Mann, der zeit seines Lebens wegen seiner freimütigen Verurteilung des bei hoch und niedrig grassierenden Aberglaubens vielen Verfolgungen ausgesetzt war. Auch auf naturwissenschaftlichem Gebiete, besonders in Technik und Mechanik, hatte er für seine Zeit bedeutende Kenntnisse und hat da mancherlei Neues entdeckt und erfunden, ebenso wie er auch in der Chemie zu neuen und wertvollen Forschungsergebnissen gelangt ist. Er erkannte als erster, daß Alaun und Vitriol, die bis dahin für identisch gehalten worden waren, verschiedene Stoffe sind; er erfand die Methode zur Zersetzung des Schwefelarseniks durch Erhitzen mit Eisen, machte wichtige und aufschlußreiche Versuche über den damals noch sehr rätselhaften Vorgang der Verbrennung und soll auch bereits das Schießpulver gekannt, ja sogar dieses erfunden haben. In der Alchemie huldigte er freilich noch ganz den alten Anschauungen und war von der Möglichkeit der Umwandlung der Metalle in Gold vermittels des Steins der Weisen überzeugt. Auch er verfaßte ein Werk über die Goldmacherkunst, betitelt »Der Spiegel der Alchemie«, in welchem er den Nachweis zu führen suchte, daß alle Metalle Zusammensetzungen von Quecksilber und Schwefel seien und es daher auch möglich sein müsse, aus diesen beiden Stoffen Gold herzustellen. Trotz dieser verworrenen Auffassung ist auch die Tätigkeit dieses Alchemisten für die Weiterentwicklung der Metallkunde und der Chemie überhaupt von erheblichem Wert geworden.

Abb. 53
Alchemistische Geräte aus dem 14. Jahrhundert

Als ein weiterer berühmter Alchemist aus jener Zeit ist Arnold Bachuone oder, wie er sich nach dem Gebrauch vieler Gelehrter jener Zeit in latinisierter Form nannte, Arnoldus Villanovus zu nennen. Villanovus war ein viel weniger wissenschaftlicher Forscher als die Vorerwähnten; er war eben nur ein Alchemist, der sich völlig in jener unwissenschaftlichen Richtung bewegte, die durch dunkle und mystische Zauberkräfte an das Ziel, Gold zu machen, zu gelangen suchte. Er ging aus von den Lehren der Araber, seine eigene alchemistische Tätigkeit aber bestand hauptsächlich darin, den Stein der Weisen zu finden oder zu erzeugen, durch den er Quecksilber in Gold verwandeln zu können glaubte. Aber auch die Stellung der Himmelskörper sollte von Einfluß auf die Goldbereitung sein, weswegen er auch astrologische Studien trieb, und ebenso sollte das Gelingen des Prozesses von gewissen Gebet- und Zauberformeln abhängen, und die wahren und wirkungsvollen alchemistischen Formeln ausfindig zu machen, war sein eifriges Bestreben. Viele Jahre seines Lebens verbrachte er mit solchen Studien und Experimenten, behauptete auch, das große Geheimnis der Goldmacherkunst wirklich ergründet zu haben und Blei und Quecksilber in Edelmetall verwandeln zu können. Er stellte auch trinkbares Gold, eine Auflösung von Gold in Wasser oder Wein her und behauptete, daß dieser Goldtrank von den wunderbarsten Eigenschaften für Kraft und Leben des Menschen sei; dieses » aurum potabile« hat auch späterhin noch lange eine große Rolle als alchemistisches Heilmittel gespielt. Villanovus war der Typus des alchemistischen Scharlatans, dessen Tun und Treiben uns sogar nahezu schwindelhaft anmutet. Wie sehr er aber trotzdem als Alchemist geschätzt wurde, geht daraus hervor, daß ihn der aragonische König Friedrich II. in seine Dienste nahm, mit dem Auftrag, Gold zu machen. Gelang es ihm nun zwar auch nicht, Quecksilber in Gold zu verwandeln, so entdeckte er doch die Eigenschaften des Quecksilbers als Heilmittel. Er erfand die graue Quecksilbersalbe, die seitdem das wichtigste Heilmittel für die galante Krankheit geworden ist, ebenso auch noch eine ganze Anzahl anderer Arzneimittel. Auch die Methode der Herstellung des Weingeistes durch Destillation erfand er, und so ist denn schließlich auch aus der mystischen Tätigkeit dieses Alchemisten ein Erfolg hervorgegangen, der sein Ansehen bei seinen Zeitgenossen wie auch in der Geschichte der Schwarzkunst selber rechtfertigte.

Abb. 54
Alchemistisches Symbol

Der merkwürdigste und berühmteste Alchemist aus jener Zeit aber war der Spanier Raimundus Lullus, der von 1235 bis 1314 lebte. Er hatte die alchemistische Kunst von Roger Bacon und Villanovus kennengelernt und suchte das große Geheimnis durch Erzeugung des Steins der Weisen zu lösen. Noch mehr als seine Vorgänger glaubte er fest an die Wirksamkeit dieses geheimnisvollen Stoffes und nahm an, daß es möglich sei, mit diesem jede beliebige Menge Quecksilber in pures Gold zu verwandeln. Ein ganzes Meer von Quecksilber wollte er mit dem lapis philosophorum in Gold umwandeln, so vermaß er sich – und fand damit bei seinen Zeitgenossen Glauben. Er behauptete aber auch, den Stein der Weisen wirklich gefunden zu haben und gab folgende Vorschrift für dessen Anwendung: »Nimm von dem Stein der Weisen soviel wie eine Bohne, wirf es auf tausend Unzen Quecksilber, so wird dieses in rotes Pulver verwandelt sein; von diesem wirf abermals eine Unze auf tausend Unzen Quecksilber, so wird dieses zu einer Tinktur verwandelt, und wirfst du von dieser nochmals eine Unze auf tausend Unzen Quecksilber, so wird dieses ganz in Gold verwandelt, welches reiner ist als das Gold der Bergwerke!« – Aber nicht nur Gold, auch Edelsteine und Perlen behauptete er herstellen zu können, und zwar durch Umwandlung erdiger Flüssigkeiten vermittels Tinkturen und Härten. Sein Ruhm als Alchemist wuchs in dem Maße, wie er seine Verheißungen und Versprechungen steigerte und sich immer mehr und höhere Kräfte beilegte, ohne daß jedoch jemals ein Mensch das große Kunststück der Goldbereitung durch ihn erlebt hätte. Aber auch bei ihm trug die Beschäftigung mit der Alchemie Früchte auf anderem und reellerem Gebiete. Er entdeckte die Brennbarkeit des Alkohols und die Reinigung desselben durch Pottasche und erfand eine Anzahl neuer Operationsverfahren für chemische Zwecke. Am berühmtesten wurde er jedoch durch die Erfindung einer – Denkmaschine. Diese bestand aus sieben, um einen gemeinsamen Mittelpunkt drehbaren Kreisen, die mit Worten und Begriffssymbolen bedeckt waren. Durch Drehen der Kreise und die dadurch bewirkte Zusammenstellung der Worte und Begriffe sollte es möglich sein, auf rein mechanischem Wege zu allen überhaupt möglichen Erkenntnissen und zur Lösung aller Aufgaben und Probleme zu gelangen. Die »Lullische Kunst« wurde dieses Verfahren genannt, das in der ganzen damaligen Kulturwelt ungeheures Aufsehen erregte, und wenn die Denkmaschine auch ebensowenig wie die alchemistischen Künste ihres Urhebers zu wirklichen Erfolgen führte, so hat sie ihn doch zum berühmtesten Gelehrten, zum » Doctor illuminatissimus«, wie ihn seine Zeitgenossen nannten, gemacht.

In der Weise wie bei den genannten Alchemisten wurde die Goldmacherkunst auch in den folgenden Jahrhunderten betrieben. Die alchemistischen Gelehrten und ebenso die alchemistischen Scharlatane erschöpften sich in dem Streben nach dem Stein der Weisen, den zu finden oder zu erzeugen die höchste Aufgabe war. Keiner der zahllosen Alchemisten hat den geheimnisvollen Stoff jemals gesehen, aber nahezu jeder behauptete, ihn zu besitzen, und jeder fand immer neue Gläubige. Aber dennoch ging aus diesem alchemistischen Tun und Treiben im Laufe der Zeiten schließlich eine bedeutsame Mehrung der wirklichen und wertvollen Erfahrungen und Kenntnisse auf metallurgischem und allgemein-chemischem Gebiete hervor, ebenso wie auch andere Wissensgebiete hieraus Nutzen zogen, die Heilmittelkunde besonders, ebenso auch die technischen gewerblichen Zweige. Die Erfolge auf diesen Gebieten waren es auch, die wieder und immer wieder den Glauben an die Alchemie und die Erreichbarkeit ihres eigentlichen Hauptzieles, die Goldbereitung auf künstlichem Wege, stärkten und erneuerten, sooft die Gläubigen nach dieser Hinsicht auch enttäuscht wurden.

Abb. 55
Symbol des Alchemisten Basilius Valentinus

Dieses merkwürdige Nebeneinander von Alchemie und wirklicher Chemie setzte sich Jahrhunderte hindurch fort. Es kennzeichnete auch noch die Tätigkeit des bedeutendsten Alchemisten der späteren Zeit, des Basilius Valentinus, eines Benediktinermönches vom Oberrhein, der im 15. Jahrhundert lebte und seine Arbeiten und Studien im Peterskloster zu Erfurt betrieb. Basilius war zwar ebenfalls noch Alchemist im Sinne des Geber und Lullus, zugleich aber auch ein hervorragender Chemiker und vielleicht der erste, der diesen Namen mit Recht verdient. Auch für ihn galt der Stein der Weisen als das große Mysterium, das es zu ergründen galt, um die Kunst, Gold zu machen, vollkommen zu beherrschen. Nach ihm war eine bestimmte Menge vom Stein der Weisen imstande, das Zehn- bis Dreißigfache seines Gewichtes an unedlem Metall in Gold zu verwandeln, auch verfaßte er hierüber ein umfangreiches Werk, betitelt »Vom großen Stein der alten Weisen«, aus dem noch die ganze alchemistische Geheimniskrämerei der früheren Zeiten spricht. In anderen Werken aber befaßt er sich mit wirklicher Chemie, und auf diesem Gebiete war auch seine Tätigkeit am wichtigsten und erfolgreichsten. Er machte gründliche Forschungen über das Antimon und die Antimonpräparate, Stoffe, über die man damals noch sehr im unklaren war, und war damit grundlegend für Jahrhunderte; er fand auch die Herstellung der Salzsäure durch Erhitzen von Kochsalz und Eisenvitriol, entdeckte das Ammoniak, das Knallgold und den Bleizucker und lehrte neue Methoden der Quecksilbergewinnung. Zahlreiche andere Stoffe wurden von ihm teils entdeckt oder hergestellt, teils beschrieben; auch vermehrte er die chemischen Untersuchungs- und Arbeitsmethoden durch neue Verfahren und trug so mehr zur Bereicherung und Förderung der chemischen Wissenschaft bei als je ein Alchemist vor ihm.

In dem Maße, wie sich so die chemische Forschung immermehr entwickelte, ging es mit der Alchemie selbst immer mehr bergab. Bei den eigentlichen alchemistischen Gelehrten war in ihrer Beschäftigung doch immer das wahre wissenschaftliche Streben vorherrschend gewesen, das Streben, in die Geheimnisse der Stoffe und ihrer Kräfte einzudringen und dadurch zu höherer Erkenntnis überhaupt zu gelangen. In den Händen vieler, ja schließlich sogar der meisten anderen Alchemisten aber wurde diese Tätigkeit nur das nackte Streben, durch die Kunst des Goldmachens zu Macht und Reichtum zu gelangen, womit die Alchemie ihres wissenschaftlichen Charakters immer mehr entkleidet und zum Gewerbe von Gauklern und Scharlatanen wurde, die in trügerischer Weise Erfolge ihrer Kunst vorspiegelten, um sich dadurch Ansehen und Vorteil zu verschaffen. Dieses Treiben forderte allerdings auch Widerspruch und energische Kritik seitens einzelner Gelehrter heraus. Schon Leonardo da Vinci, der große italienische Künstler und Ingenieur, der sich auch mit den Problemen und Gesetzen der Physik und Chemie beschäftigte und auch auf diesem Gebiete erfolgreich tätig war, einer der genialsten und aufgeklärtesten Geister seiner Zeit überhaupt, nannte die Alchemisten samt und sonders »lügenhafte Interpreten der Natur« und verglich ihr Streben, aus Quecksilber Gold zu machen, mit dem nach der Herstellung des Perpetuum mobile, das ebenso unmöglich sei wie jenes. Auch der Humanist Erasmus von Rotterdam zog in Schrift und Wort energisch gegen den alchemistischen Unfug zu Felde, und auch der Reformator Melanchthon sprach gegen diesen manch kräftiges Wörtlein, weil er in dem mystischen Glauben an den Stein der Weisen nur einen Aberglauben sah. Aber solche und ähnliche warnende und anklagende Stimmen waren nur vereinzelt und vermochten nicht, den alchemistischen Wahn zu bannen, dem nicht nur die berufsmäßigen Alchemisten, sondern auch die Angehörigen fast aller anderen Kreise, wie Ärzte, Apotheker, Juristen, Philosophen, aber auch Offiziere, Mönche, Handwerker, Kaufleute usw., besonders auch viele hochgestellte Persönlichkeiten, Ritter und Fürsten, huldigten. Vereinzelt finden wir auch Frauen mit der Goldmacherkunst beschäftigt. Den eigentlichen, gelehrten Alchemisten ging diese Verallgemeinerung ihrer Kunst allerdings gegen den Strich, und einer von diesen, Franz Graßmann aus Passau, klagte in seinem Buche » Examen Alchemisticum« aus dem Jahre 1676 über dieses Treiben mit den Versen:

Es will fast jedermann ein Alchemiste heißen,
Der grobe Idiot, der Junge mit den Greisen,
Bartscherer, altes Weib, ein kurzweiliger Rat,
Der kahlgeschorne Mönch, der Priester und Soldat.

Ein besonderes Kapitel in der Geschichte der Alchemie sind die Hofalchemisten und ihre Tätigkeit im Dienste der Regierenden. Die Gunst der Fürsten war trotz aller kostspieligen Mißerfolge den Alchemisten durch die Jahrhunderte hindurch treu geblieben. Der Glaube an den Stein der Weisen und die Hoffnung, durch diesen die so oft verödeten Kassen mit Gold füllen zu können, ließ sie keine Opfer scheuen und verlieh ihnen immer wieder neues Vertrauen zu der zweifelhaften Kunst der Goldmacher. Seit dem 17. Jahrhundert gab es in Europa, besonders aber in Deutschland, kaum noch einen Hof, an dem nicht die Alchemie in großem Umfange betrieben wurde. Der Hofalchemist hatte eine gutbezahlte Stellung, wurde oft mit Geschenken und Ehren überhäuft und verstand es mit großem Geschick, die Hoffnungen auf Erfolge seiner Kunst immer wieder von neuem wach zu halten, so daß seine vermeintliche Kunst für ihn selbst auf alle Fälle goldene Früchte trug, wenn freilich auch nicht auf alchemistischem Wege. Viele Fürsten befaßten sich auch selbst mit der Alchemie, wodurch der wissenschaftliche Wert dieser Tätigkeit aber auch nicht gehoben wurde. Das war besonders an den zahlreichen großen und kleinen Fürstenhöfen in Deutschland der Fall. Kaiser Rudolf II. (1576-1612) war ein großer Gönner der Goldmacherkunst; er hatte nacheinander eine große Zahl von Alchemisten in seinen Diensten und beschäftigte sich auch selber sehr viel in einem eigens für ihn eingerichteten großen Laboratorium mit alchemistischen Versuchen. Dort sollen nach seinem Tode 84 Zentner Gold und 60 Zentner Silber, in Form von Ziegelsteinen gegossen, angeblich als Erfolg seiner alchemistischen Tätigkeit, gefunden worden sein. Auch die Kaiser Ferdinand III. und Leopold I. hatten viele Hofalchemisten und zeichneten sie durch Ehrenstellungen und sonstige Gnadenbeweise aus. Der Markgraf Johann von Brandenburg (1440-1464) befaßte sich selber so viel mit der Schwarzkunst, daß ihm der Beiname »der Alchemist« gegeben wurde. Der Historiker der Alchemie, Kopp, bemerkt dazu, daß von den andern deutschen Fürsten nur deswegen keiner weiter mit diesem Beinamen belegt wurde, weil es sonst zu viele dieses Namens geworden wären. Ein fruchtbares Feld für ihre zweifelhafte Tätigkeit fanden die Alchemisten auch am sächsischen Hofe. August von Sachsen beschäftigte sich ebenso wie seine Gattin Anna von Dänemark eifrig mit der Kunst, Gold zu machen, nahm aber auch eine ganze Anzahl fahrender Alchemisten in seinen Dienst und richtete in Dresden eine große alchemistische Werkstätte ein, die im Volksmunde das »Goldhaus« genannt wurde, und seine Nachfolger setzten diese kostspielige Liebhaberei mit demselben Mißerfolg unentwegt weiter fort. Überall war es das gleiche Bild: statt die Kassen ihrer Auftraggeber zu füllen, machten die Alchemisten diese nur noch leerer. Aber auch an anderen als deutschen Fürstenhöfen war das der Fall. König Karl VII. von Frankreich ernannte den Alchemisten Le Cor sogar zum Münzmeister und Finanzminister, und dieser kam dem Auftrag, Gold zu schaffen, in der Weise nach, daß er aus unedlem Metall, das eine goldähnliche Farbe hatte, Münzen schlagen, diese mit dem königlichen Münzstempel versehen und in Umlauf bringen ließ. Ähnlich machten es die Alchemisten am Hofe Heinrichs VI. von England, die Gold machen sollten, statt dessen aber das Land mit Falschgeld überschwemmten und so dessen Schuldenlast gewaltig vermehrten. Friedrich III. von Dänemark, auch einer der gekrönten Alchemisten, vergeudete durch diese Liebhaberei mehrere Millionen Taler.

Abb. 56
Probierofen aus dem 16. Jahrhundert

Allmählich artete das Treiben der Hofalchemisten völlig zum Betrug aus. Wurde dem Schwarzkünstler solcher nachgewiesen oder konnte er absolut keine vertrauenswerte Probe seiner Kunst liefern, so ging es ihm freilich zumeist schlecht, und Galgen oder Richtblock wurden die Todesstätte für so manchen dieser entlarvten Betrüger. Aber die meisten Hofalchemisten verstanden sich sehr wohl darauf, eine Probe ihrer angeblichen Fähigkeiten, sofern eine solche verlangt wurde, vorzutäuschen. Sie warfen bei dem Probeexperiment heimlich etwas Gold in den Tiegel und erklärten dieses dann hinterher triumphierend als Erzeugnis und Beweis ihrer Kunst, womit das erschütterte Vertrauen auch zumeist wiederhergestellt war. Als man ihnen aber schärfer auf die Finger sah, verwandten sie Schmelztiegel mit doppeltem Boden; bei diesen wurde etwas Gold zwischen den Böden verborgen, das dann beim Schmelzen in den Tiegel trat und dem Schwarzkünstler wiederum recht gab. Durch solche und ähnliche Betrugsmanöver gelang es dem Alchemisten, sich jahrelang in Amt und Gunst zu behaupten, und wurde ihm der Boden allmählich doch zu heiß, dann – verschwand er plötzlich und ward nie mehr gesehen. In dieser Weise wußte sich der Alchemist Leonhard Thurneysser aus Basel Jahre hindurch am Hofe des Kurfürsten Johann Georg von Brandenburg zu halten. Einen raffinierten Betrug setzte ein Alchemist, der sich Daniel von Siebenbürgen nannte, bei dem Fürsten Cosimo I. von Medici ins Werk. Er behauptete, aus unedlem Metall Gold machen zu können durch Besprengung mit einer Tinktur und erbot sich, gegen ein hohes Entgelt dem Fürsten Unterricht bis zum völligen Gelingen des Experimentes zu erteilen. Auch erklärte er sich zu jeder Probe bereit, und eine solche wurde denn auch angestellt, und zwar, weil man durch die zahlreichen alchemistischen Betrügereien gewitzigt war, mit größter Vorsicht. Die von Daniel bezeichnete Tinktur wurde aus einer Apotheke bezogen und dann das Experiment nach der Vorschrift Daniels vorgenommen, und zwar in dessen Abwesenheit, wodurch jede Möglichkeit eines Betruges ausgeschlossen schien. Und siehe da, das Experiment gelang; das geschmolzene Metall erwies sich nach der Besprengung mit der Tinktur als stark goldhaltig. Die Kunst Daniels galt als erwiesen, und nachdem die Experimente eine Zeitlang mit immer demselben günstigen Ergebnis fortgesetzt worden waren, wurde dem Alchemisten das vereinbarte Honorar von 20 000 Goldgulden ausgezahlt. Nachdem das geschehen war, verschwand Daniel, und seitdem wollte die Goldverwandlung nicht mehr gelingen. Als man der Sache auf den Grund ging, stellte es sich heraus, daß Daniel die Tinktur, die bei den ersten erfolgreichen Experimenten verwandt worden war, selbst an die Apotheke geliefert hatte, und zwar bestand diese Tinktur aus einer Goldlösung, durch die das geschmolzene unedle Metall goldhaltig geworden war. Der Alchemist Honauer hatte dem Herzog Friedrich von Württemberg zugesichert, ihm 25 Zentner Eisen in Gold umzuwandeln, und der Herzog opferte dem Alchemisten die Summe von 200 000 Talern zu dem genannten Zweck. Als sich aber Honauer außerstande erklärte, sein Versprechen zu erfüllen, ließ der Herzog aus jenen 25 Zentnern Eisen einen Galgen errichten, diesen mit Flittergold umkleiden und den entlarvten Betrüger an dem so zu »Gold« gewordenen Eisen aufhängen.

Abb. 57.
Goldgewinnung durch Sublimation im 16. Jahrhundert

Aber auch das Handwerk der Hofalchemisten führte in vereinzelten Fällen zu wertvollen Entdeckungen. So erfand der Alchemist Johann Friedrich Böttger, der von dem Kurfürsten von Sachsen gefangengesetzt worden war, um Gold zu machen, bei seinen diesbezüglichen Versuchen zwar nicht den Stein der Weisen, wohl aber das Porzellan, das sich in der Folge als eine viel ergiebigere Goldquelle als der Stein der Weisen erwies. Der Alchemist Brandt in Hamburg hingegen entdeckte bei seinen Arbeiten die Darstellung des Phosphors, und durch solche und ähnliche Erfolge ist auch diese Epoche der Alchemie schließlich nicht ganz erfolglos geblieben.

Seit der Zeit des Dreißigjährigen Krieges etwa schwand das Vertrauen zu der Kunst der Alchemisten doch allmählich dahin. Die ewigen und immer sehr kostspieligen Enttäuschungen, die diese Kunst noch jedem eingetragen hatte, der durch sie Gold und Reichtum zu schaffen gehofft hatte, die Tatsache vor allem, daß letzten Endes das Treiben eines jeden Alchemisten sich als Täuschung oder Betrug herausstellte, bahnte diese Wendung an. Der goldene Boden, den das Handwerk der Goldmacher für diese selbst so lange gehabt hatte, versiegte langsam, wenn auch immer wieder Rückfälle zu verzeichnen waren. Diese Wandlung der Dinge kam auch durch die gegen Ende des 17. Jahrhunderts erfolgte Gründung der Gesellschaft der Buccinatoren zum Ausdruck. Diese Gesellschaft, deren Sitz in Nürnberg war, forderte alle Adepten auf, sich zusammenzuschließen und ihre Geheimnisse zu offenbaren, um entweder das große Geheimnis der Alchemie, den Stein der Weisen, endlich zu ergründen oder aber, sofern das nicht innerhalb dreier Jahre gelingen sollte, die ganze alchemistische Kunst als Lüge und Betrug zu offenbaren und zur Warnung aller an den Pranger zu stellen. Letzten Endes mündete jedoch auch diese Gesellschaft wieder in das alchemistische Fahrwasser ein und hat sich mit dieser Betätigung bis über den Beginn des 18. Jahrhunderts hinaus erhalten.

Auch an den Fürstenhöfen wurde die Alchemie nur noch vereinzelt betrieben, am längsten erhielt sie sich an den kleinen deutschen Höfen, wo sie noch bis gegen Ende des 18. Jahrhunderts Gönner und Gläubige fand. Friedrich der Große spottete gern über die Alchemie und insbesondere auch über das Bemühen anderer Fürsten, auf diese Weise ihre Kassen auffüllen zu wollen. Immerhin ist er selbst einmal in jungen Jahren seiner Regierung einem alchemistischen Betrug zum Opfer gefallen, wenn er dabei auch nur geringen Schaden davontrug. Im Jahre 1751 stellte sich nämlich in Potsdam ein weiblicher Alchemist ein, eine Frau von Pfuel mit zwei sehr anmutigen Töchtern. Der Geheimrat Fredersdorf empfahl die Dame und ihre Kunst dem König; sie sollte imstande sein, dem Golde die Seele auszuziehen und mit der extrahierten Goldseele unedles Metall in Gold zu verwandeln. Zu dem Zweck mußte also zunächst einmal Gold in den Tiegel getan werden, und der König ließ sich veranlassen, zehntausend Taler in Goldgulden an das Experiment zu wenden. Unter genauer Kontrolle stellte die Dame das Experiment an; das Gold im Tiegel vermehrte sich jedoch nicht, im Gegenteil wurde nach Beendigung des Experimentes ein Verlust des Goldgewichtes im Werte von fünfzig Dukaten festgestellt, und mit dieser nicht allzu schmerzlichen Erfahrung mußte auch der aufgeklärte Preußenkönig die Kunst der Alchemisten bezahlen. Auch andere Alchemisten suchten sich an dem Hof des Königs einzunisten und eine Zeitlang gab es, wie ein Chronist bemerkt, in Potsdam bald keinen Fähnrich mehr, der nicht hoffte, durch die Kunst der Alchemisten seine Schulden bezahlen zu können. Doch der König beließ es bei dem einmaligen Versuch, und späterhin hatten die Alchemisten alle Ursache, den preußischen Hof zu meiden. Auch am Wiener Hof machte um dieselbe Zeit eine Alchemistin von sich reden, diesmal eine aus Regensburg; sie gab an, Silbergeld in Goldgeld verwandeln zu können und fand auch vertrauensselige Gemüter, denen sie ihr Geheimnis für den hübschen Preis von zwanzigtausend Gulden verkaufte. Bei vorgenommenen Probeexperimenten hatte sich wirklich das Gewicht des verwandten Goldes etwas vermehrt, hinterher stellte sich das Verfahren aber als ein sehr geschicktes Betrugsmanöver heraus.

Nach der Mitte des 18. Jahrhunderts gewann allmählich die Überzeugung von der Vergeblichkeit aller alchemistischen Bestrebungen die Oberhand, zunächst in wissenschaftlichen Kreisen, und von diesen ausgehend auch bei allen andern, die so lange die Alchemie als Quelle von Gold und Reichtum nutzen zu können gehofft hatten. Der Umschwung der Anschauungen ging von der Chemie aus, die sich um jene Zeit zur exakten Wissenschaft umzubilden begann. Lavoisier, der große französische Chemiker, hatte die Chemie auf wissenschaftlichen Boden gestellt, indem er als erster die Waage in das chemische Experiment eingeführt und zum exakten Instrument der chemischen Untersuchungsmethode erhoben hatte, mit dem die chemische Forschung viel tiefer in das Wesen der Stoffe einzudringen vermochte, als es jemals zuvor möglich gewesen war. Die Waage lehrte, daß alle chemischen Verbindungen und Wandlungen immer nur in den Umsetzungen der gleichen Mengen von Grundstoffen nach bestimmten und gleichbleibenden Gewichtsverhältnissen bestehen, bei denen nie ein größeres Gewicht von Stoff auftreten kann, als die verwandten Grundstoffe hatten. Als dann noch die Ausbildung der Atomtheorie erfolgte, welche die neu gewonnene Anschauung glänzend bestätigte und zugleich zeigte, daß alle Änderungen, die bei chemischen Vorgängen in Erscheinung treten, immer nur in der Bildung anderer Komplexe der kleinsten Massenteilchen der Stoffe, ihrer Atome, bestehen, da war mit der so gewonnenen Erkenntnis über die Natur der Stoffe und das Wesen der chemischen Verbindungen und Umwandlungen zugleich auch das Trügerische der Alchemie und ihrer Ziele mit aller Sicherheit erkannt, und der Stein der Weisen zerrann als ein wirrer Traum, der viele Jahrhunderte hindurch Gelehrte und Ungelehrte, hoch und niedrig, Fürsten und Untertanen geäfft hatte. Damit war das Grab der Alchemie gegraben. Doch ehe sie vollends erstarb, flackerte sie mit einem letzten Rest von Kraft noch einmal auf, in Deutschland wenigstens. Gegen Ende des 18. Jahrhunderts erfolgte in Hamburg noch einmal die Gründung einer alchemistischen Vereinigung, der sogenannten Hermetischen Gesellschaft, deren Leiter und geistiges Oberhaupt der Dichter Kortum war, der allerdings viel mehr als durch seine alchemistischen Neigungen durch seine originelle Schöpfung, das mit Recht vielbeliebte und vielgelesene komische Heldengedicht »Die Jobsiade« bekannt geworden ist. Er verfaßte aber auch eine Schrift zur »Verteidigung der Alchemie«, in der er mit Eifer und Wärme, freilich auch mit ebensoviel Unverstand, für jene fragwürdige Wissenschaft eintrat. Aber auch die Hermetische Gesellschaft und ihr dichterisches Oberhaupt konnten das völlige Sterben der Goldmacherkunst nicht aufhalten, und mit dem Ende der Hermetischen Gesellschaft, etwa um das Jahr 1820, ward zugleich auch die Alchemie zu Grabe getragen. Ein über zweitausend Jahre umfassender Traum der Menschheit war ausgeträumt, ein uraltes Problem durch den Nachweis seiner Nichtigkeit und Gegenstandslosigkeit zum Abschluß gebracht worden.

Hundert Jahre hat seitdem die Alchemie ihren Todesschlaf gehalten, da scheint sie wiederum zum Leben erwachen zu wollen. Wieder ist das Problem der Herstellung von Gold aus anderen Metallen ausgenommen worden, aber freilich nicht in der mystischen und verworrenen Form, in der sich die früheren Alchemisten die Lösung des Problems gedacht hatten, sondern seitens der exakten Wissenschaft selber. Wie einst die Erkenntnis von der atomistischen Struktur der Stoffe ein Hauptgrund für die Beseitigung der alten alchemistischen Anschauungsweise gewesen war, so gab eine abermalige Wandlung der wissenschaftlichen Auffassung über die Natur der Atome Anlaß, den Gedanken der Stoffverwandlung, auch den der Umwandlung von unedlem Metall in Gold, wieder aufzunehmen. Während man bis gegen Ende des vorigen Jahrhunderts in den Atomen, aus denen sich jeder Stoff zusammensetzt, kleinste unteilbare Massenteilchen sah, wird nach der heutigen Theorie jedes Atom als ein Komplex noch viel kleinerer Teilchen, der Elektronen, aufgefaßt. Hiernach besteht das einzelne Atom eines jeden Stoffes aus einem positiv geladenen Kernelektron, um das sich negative Elektronen ähnlich wie die Planeten um die Sonne herumbewegen. Der Unterschied der einzelnen Grundstoffe besteht im wesentlichen in der verschiedenen Zahl der negativen Elektronen im Bau der Atome. Nun gibt es Elemente, die sich im Bau ihrer Atome sehr ähneln. Das ist beispielsweise beim Gold und Quecksilber der Fall; das Atom des Goldes zählt 79, das Quecksilberatom dagegen 80 Elektronen. Gelingt es nun, dem Quecksilberatom ein Elektron zu entreißen, so muß es sich in ein Goldatom verwandeln, weil es dann denselben Bau wie ein solches, wenigstens was die Zahl der Elektronen anbetrifft, hat. Das ist in kurzer Andeutung die Auffassung der heutigen chemischen Wissenschaft von der Natur der Elemente und von der Beschaffenheit der Atome. Auf Grund dieser Theorie ging im Jahre 1922 ein angesehener deutscher Forscher, der Chemiker Adolf Miethe, daran, die Umwandlung von Quecksilber in Gold vorzunehmen. Durch Einwirkung hochgespannter elektrischer Ströme auf das hocherhitzte und in Dampfform übergeführte Metall nach besonderer Methode sollte das bewirkt, sollte den Atomen des Quecksilbers je ein Elektron entrissen werden. Merkwürdigerweise war also das Quecksilber, das schon den früheren Alchemisten bei ihren Versuchen als Grundstoff zur künstlichen Goldbereitung gedient hatte, auch bei diesem alchemistischen Versuche der exakten Wissenschaft der Ausgangsstoff der Goldmutation, frühere und modernste Zeit und Wissenschaft begegneten sich in demselben Element. Der Ausfall des Experimentes, das Miethe anstellte, schien die Möglichkeit der Umwandlung des Quecksilbers in Gold vollauf zu bestätigen. In dem behandelten Quecksilber wurde nach dem Experiment Gold gefunden, das vordem nicht darin vorhanden gewesen war, wenn freilich auch nur in allerwinzigsten, mikroskopisch kleinsten Spuren, die nur vermittels der schärfsten Untersuchungsmethoden festgestellt werden konnten. Es mußte also durch das Experiment eine wenn auch noch so geringe Menge Quecksilber in Gold verwandelt worden sein.

Das war damals eine große Überraschung, die die Welt der Gelehrten und ebenso auch das große Publikum lange Zeit hindurch in Aufregung erhielt. Der alte Traum der Alchemisten, die Verwandlung des Quecksilbers in Gold, schien, wenn auch in anderer Weise und ohne den sagenhaften Stein der Weisen, also nun doch in Erfüllung gehen zu wollen. Gleich auch meldeten sich einige Stimmen aus dem okkultistisch-alchemistischen Lager – denn vereinzelte Alchemisten der alten Schule gibt es auch heute noch, Querköpfe, die nicht alle werden und durch kein Ergebnis der Wissenschaft zu belehren sind –, die behaupteten, das, was Professor Miethe gelungen sei, sei nur eine Wiederholung dessen, was in früheren Jahrhunderten von einem Geber, Lullus oder Valentinus gemacht und erreicht worden sei, und die Mietheschen Versuche seien nur eine Bestätigung der Richtigkeit jener früheren alchemistischen Anschauungen und eine nachträgliche Ehrenrettung der alten Schwarz- und Goldmacherkünstler. Dann allerdings trat eine neue Wendung ein. Genaue Nachprüfungen des Experimentes ergaben, daß Miethe sich geirrt hatte; die winzigen Goldspuren waren dadurch in das Quecksilber gelangt, daß bei gelegentlicher Berührung der goldenen Uhrkette, des goldenen Fingerringes oder des Goldrandes der Brille seitens des Experimentators winzige Mengen dieses Goldes abgestreift worden und dann von der Hand des Forschers in das Quecksilber gelangt waren. Durch wiederholte Nachprüfung des Experimentes konnte dieses Ergebnis mit aller Sicherheit festgestellt werden.

So war also auch dieser neue Traum von der Kunst, Gold zu machen, so schnell wie er aufgetaucht war, wieder zerstört worden. Jene Stimmen aus dem okkultistisch-alchemistischen Lager, die so voreilig mit der Ehrenrettung der früheren Alchemisten bei der Hand gewesen waren, verstummten wieder, was aber natürlich nicht ausschließt, daß sie bei nächster sich bietender Gelegenheit sich wieder zum Worte melden. Professor Miethe ist übrigens bald, nachdem sein Irrtum und der negative Ausfall seines Experimentes festgestellt worden war, gestorben. Ob es auf dem Wege der heutigen Forschung und vermittels der Methoden der modernen Chemie doch noch einmal zur Herstellung von künstlichem Golde kommen wird? Nach der Theorie über den Bau der Elemente und der Atome müßte das durchaus möglich, ja vielleicht sogar wahrscheinlich sein. Kommt doch auch in der Natur, wie wir heute wissen, ständig die Umwandlung von Elementen zu anderen Elementen vor, wie es beispielsweise beim Zerfall der radioaktiven Elemente der Fall ist, und was die Natur vormacht, sucht der Forscher auf dem Wege des Experimentes nachzuahmen. Aber freilich, mit Sicherheit können wir heute auch über diese Möglichkeit nichts sagen, und ob die Theorie solchen weitgehenden Konsequenzen gegenüber in der Praxis des Experimentes standhält, ist fraglich. Bis jetzt hat jedenfalls auch die heutige Wissenschaft trotz aller Gewalt und allen Scharfsinnes ihrer Mittel und Methoden die Schranken der Natur nicht zu überwinden vermocht.

Noch liegt die Alchemie in dem Grabe, in das sie vor hundert Jahren versenkt worden ist, noch hat das merkwürdige Bild voller phantastischer Ideen und Spekulationen, voller Trug und Lug, aber auch voll echten Forschungs- und Erkenntnistriebes und unermüdlicher und zäher Arbeit, das ihr Leben war, keine Fortsetzung gefunden. Vielleicht ist das Bild für immer zum endgültigen Abschluß gebracht; vielleicht – wir wissen es heute noch nicht mit Sicherheit – wird es einmal eine Neubelebung durch die moderne Wissenschaft erfahren, die dann eine neue Ära und eine neue Geschichte der Goldmacherkunst einleiten würde, von der wir uns heute noch keinerlei Vorstellung zu machen vermögen.

Postskriptum

Nach altem Rezept – Ein Experiment zum Goldmachen – Die ganz modernen Alchemisten

Daß es auch in unserem aufgeklärten Zeitalter noch Alchemisten vom alten Schlage gibt, Leute, die auch heute noch auf okkultem Wege nach den Rezepten und Zauberformeln der mittelalterlichen Schwarzkünstler Gold machen wollen, dafür kann der Verfasser, der in jungen Jahren in einer Goldscheideanstalt tätig war, eigene Erfahrungen anführen. Da kamen oftmals Leute hin, die mit geheimnisvollen Mienen geheimnisvolle Rezepte vorwiesen, nach denen man unweigerlich Blei und Quecksilber in Gold verwandeln könnte. Aus den Rezepten ist niemals jemand klug geworden, ihre Besitzer sicher am allerwenigsten. Einmal aber wurde einem solchen Schwarzkünstler auf seine dringenden Bitten der Zutritt zum Schmelzofen gewährt, um sein Zauberexperiment ausführen zu können. Mit Mixturen, Pulvern und sonstigen geheimnisvollen Substanzen ging er ans Werk, und die Folge war, daß sich etwa nach einer Stunde Experimentierens ein penetranter Geruch entwickelte, der einfach alles in die Flucht schlug, die nähere und weitere Umgebung in unerträglicher Weise verpestete und schließlich die Polizei zum Einschreiten veranlaßte, um Herd und Urheber dieses groben Unfugs festzustellen. Ein nicht ganz kleines Strafmandat war der Abschluß des Experimentes, das im übrigen total negativ verlaufen ist, gottlob, denn sonst hätte die Erschütterung des Goldmarktes schon damals zu einer Inflation geführt, gegen welche die Geldverhältnisse der Nachkriegszeit das reine Kinderspiel gewesen wären. Daß ferner aber auch die Zunft jener Alchemisten noch nicht ausgestorben ist, die, wie einst ihre Vorgänger an den Fürstenhöfen, betrügerischerweise in ihren Mitmenschen den Glauben an ihre vermeintliche Fähigkeit, Gold zu machen, erwecken und diesen Glauben zum »Goldmachen« in ihrem Sinne auszunutzen verstehen, dafür hat erst die allerjüngste Vergangenheit ein drastisches Beispiel geliefert. Einem Klempnergesellen, der sich als Ingenieur bezeichnete, gelang es, unter dem Vorwande, Gold machen zu können, eine ganze Anzahl prominenter Persönlichkeiten zu prellen und damit mehrere Millionen Mark zu »verdienen«. Allerdings ist diesen modernen Schwarz- und Tausendkünstlern der Umstand zugute gekommen, daß sich die Wissenschaft sozusagen offiziell mit dem Problem des Goldmachens befaßt hat, wie es bei den erwähnten Versuchen des Professor Miethe der Fall gewesen ist. Das hat jenen ganz modernen Alchemisten die Möglichkeit gegeben, sich und ihr zweifelhaftes Metier mit einem wissenschaftlichen Mäntelchen zu verkleiden und damit erfolgreich nach Gläubigen zu angeln. Mehrfach sind seitdem Schwarzkünstler aufgetaucht, die vorgaben, daß das, was Professor Miethe nicht gelungen sei, von ihnen möglich gemacht werden könnte, und diese Berufung auf die Wissenschaft schafft ihnen immer wieder Vertrauen und Gewinn. Denn ganz so plump wie die früheren Alchemisten darf es der heutige Goldmacher doch nicht mehr anstellen, wenn er Erfolg haben will. Aber Erfolg findet er immer wieder und sorgt so dafür, daß die schwärzeste Seite im Buche der Schwarzkunst auch heute noch nicht ganz abgeschlossen ist.

VII.
Probleme des Physischen

1. Von der Erhaltung der Energie zur allgemeinen Relativität

Eine ärztliche Beobachtung und ihre Folgen – Wärme und Arbeit – Die Metamorphose der Wärme – Vom Wandel und von der Erhaltung der Energie – Fachmann und Laie – Das Wärmeäquivalent – Das Ende des Perpetuum mobile – Der erste Hauptsatz der Wärmetheorie – Erhaltung der Energie und Varianz der Masse – Energiegesetz und Relativitätstheorie – Relativität und Invarianz

Am 20. März 1878 starb in seiner Vaterstadt Heilbronn Robert Mayer, der Mann, an dessen Geistestat, die Entdeckung des Gesetzes von der Erhaltung der Energie, eine neue Ära der Naturerkenntnis und der Naturforschung anknüpft, eine Tat und eine Entdeckung, die ihre Wirkung in gleicher Weise auf das Gebiet der exakten Naturwissenschaften wie das der Technik ausstrahlen, ebenso aber auch der philosophischen und erkenntnistheoretischen Betrachtung des Universums grundlegende neue Gesichtspunkte erschlossen haben. Ein Pionier der Menschheit auf dem Wege zur Erkenntnis war Robert Mayer, ein Pionier sowohl durch die Bedeutung jener inhalt- und folgeschweren Entdeckung wie auch durch die Jahrzehnte hindurch währenden unendlichen Mühen, die er daransetzen mußte, um die Welt, insbesondere die Wissenschaftler selbst, von der Wahrheit der neuen Auffassungsweise zu überzeugen, die seine Zeitgenossen etwa ebenso fremdartig und grotesk anmutete, wie es in unseren Tagen in ähnlicher Weise bei der Aufstellung der Relativitätstheorie der Fall war.

Es war im Jahre 1840, als sich der junge Schiffsarzt Robert Mayer in Batavia aufhielt und hier eine ihn in höchstem Maße interessierende Beobachtung machte. Er hatte einigen Matrosen einen Aderlaß gemacht und dabei gefunden, daß das Venenblut eine ungewöhnlich helle Färbung aufwies. Andere Ärzte bestätigten ihm dann, daß allgemein im heißen Klima das Venenblut eine hellere Färbung zeige als in der kälteren Zone. Mayer ging der Ursache der Erscheinung nach und fand sie in dem Umstand, daß infolge der ständig hohen Temperatur in jenen Regionen der menschliche Körper dort zu seiner Erhaltung und Arbeitsleistung weniger Wärme durch Verbrennung zu erzeugen braucht, als es in kälterem Klima der Fall ist. Die geringere Verbrennung, insbesondere die geringere Menge der Verbrennungsprodukte, äußert sich in einer helleren Färbung des Venenblutes. Was Mayer hier erkannt hatte, war also zunächst eine rein physiologische Tatsache, die ihn jedoch zu weiteren Studien über das Verhältnis der Wärme zur Arbeitsleistung nicht nur im menschlichen Körper, sondern in der Natur allgemein anregte und so der Ausgangspunkt einer langen Kette von Folgerungen und Forschungen wurde, aus denen schließlich der neue umwälzende Gedanke, seine weltbewegende Entdeckung, geboren werden sollte. Sie gipfelte in der Erkenntnis: Wärme und mechanische Arbeit stehen in engem Zusammenhang und sind einander äquivalent! Das heißt: mit einem bestimmten Quantum Wärme kann immer nur ein ganz bestimmtes und gleichbleibendes Quantum Arbeit geleistet werden, und umgekehrt kann durch mechanische Arbeit Wärme erzeugt werden, und zwar durch ein bestimmtes Quantum mechanischer Arbeit immer nur ein bestimmtes und gleichbleibendes Quantum Wärme. Im menschlichen Körper wird durch die Verbrennung der aufgenommenen Nahrungsstoffe Wärme erzeugt, die die Quelle der Arbeit ist, die der Mensch tagsüber zu leisten hatte; deutlicher noch sehen wir den Vorgang der Verwandlung von Wärme in Arbeit bei einer Dampfmaschine. Hier wird durch die Verbrennung der Kohlen auf dem Rost die Wärme erzeugt, die das Wasser im Dampfkessel in Dampf von hohem Druck verwandelt. Dieser so erzeugte Dampf wird in den Zylinder der Maschine geleitet und setzt hier durch seinen Druck den Kolben und damit die ganze Maschine in arbeitende Bewegung. In diesem wie in jenem Falle hat sich eine Metamorphose der Wärme in mechanische Arbeit vollzogen.

Wieso kommt nun aber dieser Auffassungsweise eine so gewaltige Bedeutung zu, daß sie ihren Entdecker, der ja von Studium und Beruf nicht Physiker, sondern Mediziner war, dennoch in die Zahl der größten Physiker einreiht? Nun, sie erschloß der Naturerkenntnis einen vollkommen neuen Gesichtspunkt, indem sie einen engen naturgegebenen Zusammenhang zwischen Wärme und jeder Art mechanischer Arbeit, gleichviel auf welche Weise diese erzeugt oder vollzogen wird, erkennen ließ und die Verwandtschaft und Umwandelbarkeit der beiden äußerlich so vollkommen heterogenen Erscheinungen Wärme und Arbeit lehrte. Bis dahin hatte man eigentlich noch niemals Veranlassung genommen, sich um das Verhältnis zwischen Wärme und Arbeitsleistung theoretisch des näheren zu kümmern. Man nahm die Entstehung von Wärme, wie sie beispielsweise bei dem Kreisprozeß der Dampfmaschine stattfindet, als eine Tatsache hin, sah es weiter als Tatsache an, daß die Wärme verschwand und zugleich an einer anderen Stelle des Mechanismus Arbeit geleistet wurde, und ließ sich an diesen Tatsachen genügen. Die Wärme verschwindet, nachdem sie erzeugt worden ist, und es bleibt von ihr nichts übrig –, das war die wissenschaftliche Auffassung jener Vorgänge. Mayer hingegen lehrte, daß bei allen diesen Vorgängen die Wärme nicht verschwindet, sondern sich nur in eine andere Form, nämlich in mechanische Arbeit, verwandelt, im übrigen aber in vollem Umfange erhalten bleibt. Wärme und Arbeit sind nur verschiedene Formen eines und desselben Etwas, das Mayer mit der Ausdrucksweise seiner Zeit ›Kraft‹ nannte, während wir es heute als Energie bezeichnen. Und indem in diese Auffassung auch alle anderen Energien, auch die Energie bewegter Massen, ebenso aber auch die der Elektrizität und des Lichtes, auch die chemische Energie, die zwischen den Atomen der Körper wirkt, überhaupt alle Kraftäußerungen einbezogen wurden, indem auch für alle diese Energiearten ihre Verwandtschaft mit der Wärme und untereinander und ihre Umwandelbarkeit ineinander postuliert wurde, wurde mit einem Schlage alle Bewegung und überhaupt alles Geschehen in der Welt, gleichviel ob dieses im Kreislauf des Blutes der Organismen, ob in den Energiewirkungen einer Maschine oder eines Erdbebens, ob in den Eruptionsvorgängen oder der Licht- und Wärmesendung unserer Sonne oder in irgendwelchen anderen kosmischen Vorgängen in den fernsten Regionen des Weltalls besteht, in einen engen und großartigen Zusammenhang gebracht, der das ganze Universum umfaßt, einen Zusammenhang, dessen Erkenntnis die Naturforschung auf einen vollständig neuen Boden stellte. Energie kann ebensowenig vernichtet werden oder aus dem Nichts entstehen, wie Materie weder vernichtet noch aus dem Nichts erzeugt werden kann. Die Erhaltung der Energie (Mayer nannte es noch die Erhaltung der Kraft) – das war die große Idee, die dem jungen Schiffsarzt in einer genialen Stunde aufgeblitzt war und mit der er dem Streben der Menschheit nach Wissen und Erkennen, nach Erkennen dessen, ›was die Welt im Innersten zusammenhält‹, eine neue Grundlage schuf. Denn die Umwandelbarkeit der Energien im Qualitativen und die Erhaltung der Energie im Quantitativen sind Grundgesetze aus dem tiefsten Innern der Natur.

Uns mutet die durch Robert Mayer angeregte und heute unser gesamtes naturphilosophisches, naturwissenschaftliches und technologisches Denken beherrschende Auffassung, die sich an den Begriff der Erhaltung der Energie knüpft, als selbstverständlich, als schon beinahe banal geworden, an. Für die Zeitgenossen Mayers, gelehrte wie ungelehrte, aber war diese Auffassungsweise etwas absolut Fremdartiges und Abstruses, und Mayer stieß mit seinen Ideen zunächst auf völlige Verständnislosigkeit, ja geradezu Feindseligkeit bei den Wissenschaftlern. Seine erste Abhandlung über jene neuen Ideen, die er den »Annalen für Physik und Chemie«, dem von Poggendorff herausgegebenen führenden Organ der physikalischen Forschung, übersandt hatte, wurde von Poggendorff glatt abgelehnt, um so mehr als der Verfasser ja nicht einmal Physiker von Fach, sondern nur Arzt war. In veränderter Form schickte Mayer seine Arbeit dann unter dem Titel »Bemerkungen über die Kräfte der unbelebten Natur« an den großen Justus von Liebig, den berühmten Chemiker und Herausgeber der »Annalen für Chemie und Pharmazie«, der sich einsichtiger als Poggendorff erwies und Mayers Arbeit – einen Meilenstein von ewiger Bedeutung für die Geschichte der wissenschaftlichen Literatur – in seinem Organ zum Abdruck brachte. Der Gedanke, daß Wärme, mechanische Arbeit, Elektrizität, Licht, chemische Energie usw. im Grunde ihres Wesens eigentlich ein und dasselbe sind und jede dieser untereinander so heterogenen Energiearten in die andere umgewandelt werden kann, mußte freilich damals, weil noch jede geistige Vorbereitung für diesen Gedanken fehlte, geradeso seltsam anmuten wie ursprünglich in unseren Tagen die Grundgedanken der Relativitätstheorie. Erst als es gelang, die neue Betrachtungsweise mit dem Experiment und der Zahl zu verknüpfen, wich allmählich das Fremdartige der Auffassung. Mayer hatte die Theorie aufgestellt, daß in allen Fällen, wo durch Wärme Arbeit geleistet wird, mit einem bestimmten Quantum Wärme immer nur ein ganz bestimmtes Quantum Arbeit geleistet werden könne. Es galt, dieses Äquivalenzverhältnis zwischen Wärme und Arbeit zahlenmäßig zu bestimmen, also festzustellen, welches Quantum Wärme notwendig ist, um eine bestimmte Arbeitsleistung zu erzielen und umgekehrt. Diese Feststellung war eine der wichtigsten, zugleich aber auch eine der schwierigsten Untersuchungen, die die Physiker jener Zeit vorzunehmen hatten. Wir messen mechanische Arbeit bekanntlich in Meterkilogrammen. 1 Meterkilogramm ist die Arbeitsmenge, die geleistet wird, wenn 1 Kilogramm um 1 Meter gehoben wird; das Maß der Wärme hingegen ist die Kalorie, das heißt die Wärmemenge, die nötig ist, um die Temperatur von 1 Kilogramm Wasser um 1 Grad zu erhöhen. Es galt also festzustellen, welche Arbeitsmenge, ausgedrückt in Meterkilogrammen, durch 1 Kalorie erzielt bzw. geleistet werden kann. Mayer selbst suchte diese Größe durch das Experiment festzustellen, gelangte jedoch nur zu einem sehr ungenauen Resultat. Erst mehrere Jahre später konnte der englische Forscher Joule, der in ähnlicher Weise wie Mayer, jedoch unabhängig von diesem, die Beziehungen zwischen Wärme und Arbeit studiert hatte, durch geeignetere Versuche feststellen, daß 1 Kalorie einer Arbeitsmenge von 424 Meterkilogramm (Mayer hatte 365 Meterkilogramm gefunden) entspricht. Man sagt, daß 424 Meterkilogramm das mechanische Äquivalent der Wärme sind, weil eine Arbeit von 424 Meterkilogramm und 1 Kalorie als Energiemengen einander gleichwertig sind. Erst mit dieser rechnerisch ausdrückbaren Bezeichnung war der neue Gedanke Mayers dem allgemeineren Verständnis erschlossen.

Energie kann nicht vernichtet werden, kann aber auch niemals aus dem Nichts entstehen. Mit dieser Folgerung, die sich aus dem Gesetz von der Erhaltung der Energie ergibt, war zugleich einem alten Zauberspuk ein Ende gemacht, der nur auf dem Boden der früheren, unvollkommenen Auffassung vom Wesen der Arbeit entstehen und sich Jahrhunderte hindurch erhalten konnte, nämlich dem Perpetuum mobile. Ein solches soll bekanntlich eine Maschine sein, die, einmal in Bewegung gesetzt, diese ewig beibehält und so ewig mechanische Arbeit leisten kann, ohne einer neuen Zufuhr von Kraft bzw. Energie zu bedürfen. Auf Grund der neuen Betrachtungsweise fiel diese kuriose Idee, die Jahrhunderte hindurch ungezählte Köpfe – und nicht die schlechtesten – vergeblich beschäftigt hatte, endlich wie ein Luftschloß zusammen. Nach dem Gesetz von der Erhaltung der Energie kann mehr Arbeit, als in eine Maschine hineingesteckt worden ist, niemals aus dieser herausgeholt werden, ebensowenig wie es möglich ist, aus einem Portemonnaie mehr Geld herauszuholen, als man vordem hineingetan hat. Eine Maschine kann sogar niemals so viel Arbeit zurückgeben, als sie zuvor ausgenommen hat, denn ein erheblicher Teil der ihr zugeführten Energie setzt sich durch Reibung in Wärme um, die für den praktischen Zweck verlorengeht. Erst durch die neue Lehre von der Erhaltung der Energie war die Überwindung der Idee des Perpetuum mobile wissenschaftlich möglich geworden; der Grundgedanke der Lehre von der Erhaltung der Energie, der zugleich auch als erster Hauptsatz der Wärmetheorie bezeichnet wird, fällt geradezu zusammen mit der Folgerung von der Unmöglichkeit eines Perpetuum mobile.

Heute beherrscht das Gesetz von der Erhaltung der Energie unser gesamtes naturwissenschaftliches und technologisches Denken als eine ihrer gesichertsten und fruchtbarsten Grundlagen, und ebenso ist dieses Gesetz zu einem Grundgedanken und gesicherten Erkenntnisprinzip der naturphilosophischen Betrachtung geworden. Auch die Relativitätstheorie, die so viele Begriffe des naturwissenschaftlichen und insbesondere unseres physikalischen Denkens der Revision unterwerfen will, hat das Gesetz von der Erhaltung der Energie in vollem Umfange unangetastet stehengelassen. Im Gegenteil hat dieses Gesetz im Rahmen der Relativitätstheorie sogar noch erhöhte Bedeutung erlangt, denn es umfaßt jetzt auch das Gesetz von der Erhaltung der Masse. Die Masse ist nach der Relativitätstheorie nicht mehr als konstant zu betrachten, denn sie geht je nach ihrem Bewegungszustande in Energie über. Die Erhaltung der Energie aber ist auch für die Relativitätstheorie ein Grundpfeiler jeder exakten physikalischen Betrachtung und muß das sein.

Tatsächlich liegt die Relativitätstheorie vollkommen in der Denkrichtung, die durch die Entdeckung des Gesetzes von der Erhaltung der Energie eröffnet wurde. Mayers These von der Umwandlung der Energiearten, die bis dahin für völlig heterogen erachtet worden waren, war der stärkste relativistische Gedanke, der überhaupt möglich war; seine andere These von der Erhaltung der Energiemenge aber postuliert die Invarianz des Naturgesetzes bei allem Wechsel der Erscheinungen, geradeso wie die Relativitätstheorie bei aller Relativität des Geschehens nach Raum und Zeit die Invarianz der Naturgesetze begründet und zur Forderung erhebt. Zweifellos wäre es viel richtiger, statt die Relativitätstheorie mit der kopernikanischen Umgestaltung unseres Weltbildes in Parallele zu setzen, diese Theorie durch den Vergleich mit der Tat und der Theorie Robert Mayers zu werten. Dadurch würde die Bedeutung der Relativitätstheorie nicht gemindert, sondern sie wäre auf das richtige Maß zurückgeführt, was vielleicht auch zu einer objektiveren Würdigung dieser heute noch immer starkumstrittenen Theorie führen würde, deren Wurzeln jedenfalls viel mehr bei Robert Mayer als bei Kopernikus zu suchen sind.

2. Probleme des Falles

Ein Apfel fiel vom Baum – Das Gesetz der Gravitation – Fall und Fallstrecke – Rohrpost durch die Erde – 42 Zentner Körpergewicht – Der Springer auf dem Monde

Es wird berichtet, daß der große englische Physiker Isaak Newton im Garten seines Wohnhauses in seinem Geburtsort Woolsthorpe saß, als dicht vor ihm ein Apfel vom Baume fiel. Der unscheinbare Vorgang – er trug sich im Jahre 1666 zu – regte ihn zum Nachdenken an, zu der Frage: Warum fällt der Apfel vom Baum und welche Ursache oder Kraft ist es, die ihm jene Bewegung nach der Erde hin erteilt? Ungezählte Millionen von Menschen hatten schon das Fallen von Äpfeln beobachtet, ohne sich Gedanken darüber zu machen, gewohnt, solche Vorgänge als alltägliche Erscheinungen hinzunehmen, die ihren Grund in sich selber tragen und keiner weiteren Erklärung bedürfen; viele Male hatte sicher auch Newton einen solchen Vorgang verfolgt, bis er in der genialen Eingebung des Augenblicks das Rätselhafte und Geheimnisvolle in dem Fall des Apfels plötzlich herausfühlte, ein Problem erkannte und zum Nachforschen über dessen Lösung angespornt wurde.

Das ungeahnt inhaltsschwere Ergebnis dieses Forschens, das freilich Jahrzehnte bedurfte, ehe es fertig vorlag und der aufhorchenden Welt unterbreitet werden konnte, war die Entdeckung des Gesetzes der Gravitation. Es besagt, daß sich alle Körper im Weltenraume untereinander mit bestimmter Gesetzmäßigkeit anziehen. Die größten wie die kleinsten Körper im Weltraume unterliegen dieser geheimnisvollen Kraft; sie ist es, die sowohl den Apfel zur Erde fallen läßt wie auch den Lauf des Mondes um die Erde regelt; sie gibt dem Pfeil, der von der Sehne schwirrt, seinen Weg und bestimmt ebenso der Erde und allen übrigen Planeten ihre Bahnen um die Sonne. Sie wirkt auch noch über unser Sonnensystem hinaus in den unendlichen Tiefen des Weltraumes, so weit der forschende Menschengeist sich diese anschaulich oder begrifflich überhaupt vorzustellen vermag, alle Weltkörper auch in jenen unendlichen Weiten erfassend und ihre Bewegungen und Konstellationen in berechenbarer Weise regelnd.

Mit einem Schlage war so durch die Entdeckung jenes Gesetzes dem Menschengeiste die Fähigkeit verliehen, seine Forschung und Rechnung bis in die fernsten Weiten des Universums zu erstrecken, ein Fortschritt, der nächst der unsterblichen Tat des Kopernikus, der die Erde entthront und die Sonne als Mittelpunkt und Herrscherin des Planetensystems erkannt hatte, als die folgenreichste Tat der Naturerkenntnis bezeichnet werden muß. Und diese weltbewegende Entdeckung ging aus von dem Fall eines Apfels. Im Gegensatz zu vielen anderen Erzählungen, die sich anekdotisch an die Schöpfungsstunde großer Entdeckungen und Erfindungen knüpfen, darf der Bericht von jenem fallenden Apfel mit hoher Wahrscheinlichkeit als geschichtlich wahr bezeichnet werden. Schon in den Augen der Zeitgenossen Newtons erlangte der Baum, von dem einst dieser Apfel gefallen war, eine besondere Weihe als Baum der Erkenntnis, und als der Stamm im Jahre 1726, ein Jahr vor dem Tode Newtons, vom Sturm gefällt worden war, wurde aus seinem Holz ein Stuhl verfertigt, der noch heute im Museum zu Woolsthorpe als einzigartiges Erinnerungszeichen an das Zustandekommen eines der wichtigsten Ergebnisse der Naturerkenntnis aufbewahrt wird.

Nach dem von Newton entdeckten Gravitationsgesetz ist die Anziehung, die die Körper im Weltenraume aufeinander ausüben, um so größer, je größer ihre Massen sind. Angenommen zwei Körper A und B, die sich in einer bestimmten Entfernung voneinander im Weltenraume befinden, üben eine bestimmte Anziehungskraft aufeinander aus, so würde diese verdoppelt, wenn die Masse des einen der Körper plötzlich verdoppelt würde, und entsprechend verzehnfacht bei zehnfacher Massenvergrößerung jenes. Ferner ist die Anziehung der Körper aber auch noch abhängig von ihrer Entfernung; sie ist um so kleiner, je größer die Entfernung der sich anziehenden Körper ist, aber diese Beziehung ist nicht so einfacher Art wie die nach der Masse. Wenn unsere beiden Körper A und B bei gleichbleibender Masse in einer bestimmten Entfernung eine bestimmte Anziehung aufeinander ausüben, so würde diese, wenn die Entfernung plötzlich verdoppelt würde, nicht nur auf die Hälfte, sondern auf den vierten Teil der ursprünglichen Anziehung vermindert werden, bei dreifacher Entfernung auf den neunten, bei zehnfacher auf den hundertsten Teil usw. Die Körper im Weltraum ziehen sich also an mit einer Kraft, die im geraden Verhältnis ihrer Massen, aber im umgekehrt quadratischen Verhältnis ihrer Entfernungen steht. Das ist die genauere Formulierung des Gravitationsgesetzes, das sowohl den Fall eines Apfels wie den Lauf der Gestirne regelt und uns gestattet, die gesamte Mechanik des Universums der Rechnung zu unterwerfen.

Auf unserem Erdballe äußert sich die Gravitation als die Schwere der Körper, die also nur gleichsam ein Spezialfall jener allgemeinen Weltkraft ist. Die Erde zieht wie mit unsichtbaren langen Armen alle Körper in ihrem Bereich zu sich heran. Dieser Zug bekundet sich für unsere Wahrnehmung als der Druck, den jeder Körper auf seine Unterlage ausübt und den wir eben als Schwere oder auch als Gewicht des Körpers bezeichnen. Als Maß oder Einheit dient uns hierbei das Gewicht, das 1 Liter Wasser besitzt und das wir bekanntlich als Kilogramm bezeichnen. Wird ein Körper seiner Unterlage oder seines Haltes beraubt, wie etwa der Apfel, der sich vom Zweige loslöst, so strebt er, der Anziehung der Erde folgend, nach dieser hin, das heißt der Körper fällt. Die Fallbewegung und ihre Gesetze sind innerhalb unserer Erdenwelt die für uns wichtigsten Erscheinungen der Gravitation.

Die Erde wirkt nicht nur mit einem Teil ihrer Oberfläche, sondern mit allen und auch den entferntesten Teilen ihres Riesenleibes anziehend auf jeden einzelnen Körper ein. Diese Gesamtanziehung aller Teile der Erdkugel aber stellt sich so dar, als ob die gesamte Anziehungskraft der Erde in ihrem Mittelpunkte konzentriert wäre und die Erde nur von diesem Punkte aus ihre Anziehung ausübte. Von diesem Sitz des Anziehungszentrums sind also die Körper an der Oberfläche der Erde gerade um einen Halbmesser der Erdkugel, der rund 6380 Kilometer beträgt, entfernt. Bei einer solchen Entfernung des Anziehungszentrums übt also ein Körper von der Masse unserer Erde eine Anziehungskraft aus, durch die ein seiner Unterstützung beraubter Körper eine ganz bestimmte Beschleunigung in der Richtung nach dem Anziehungszentrum hin erfährt. Diese Beschleunigung beträgt pro Sekunde rund 10 Meter (genauer 9,802 Meter), das heißt, der seines Haltes beraubte Körper fällt mit zunehmender Geschwindigkeit und hat nach Verlauf der ersten Sekunde eine Geschwindigkeit von 10 Metern erlangt; während der zweiten Sekunde erhält er infolge der Anziehung der Erde einen ebensolchen Beschleunigungszuwachs, so daß seine Geschwindigkeit um abermals 10 Meter gesteigert wird und nach Ablauf der zweiten Sekunde 20 Meter beträgt; nach Ablauf der dritten Sekunde ist sie auf 30, nach der vierten Sekunde auf 40 Meter gesteigert usw., so daß sich also die Geschwindigkeit des fallenden Körpers nach jeder Sekunde leicht berechnen läßt.

Von der Beschleunigung und der durch diese erlangte Geschwindigkeit ist die Fallstrecke, die der Körper innerhalb eines gewissen Zeitraumes zurücklegt, abhängig. Sie ist aus jenen Faktoren leicht zu berechnen. In dem Moment, wo der Körper seines Haltes beraubt wurde, hatte er noch keine Geschwindigkeit; er fällt dann mit wachsender Geschwindigkeit, die nach Ablauf der ersten Sekunde auf 10 Meter gestiegen ist. Mithin können wir sagen, daß der Körper während der ersten Sekunde eine gleichmäßige mittlere Geschwindigkeit von 5 Metern (nämlich der Hälfte von 0 + 10) hatte, und da er mit dieser mittleren Geschwindigkeit gerade eine Sekunde lang gefallen ist, so muß er in dieser Zeit eine Fallstrecke von 1 × 5 = 5 Metern zurückgelegt haben. Die Fallstrecke eines Körpers muß also nach unserer Berechnung während jener ersten Sekunde 5 Meter (genauer 4,901 Meter) betragen, ein Ergebnis, das durch das praktische Experiment aufs genaueste bestätigt wird. Wie groß ist nun die Fallstrecke innerhalb der ersten zwei Sekunden? Der Körper hat am Beginn dieser Fallzeit wieder die Geschwindigkeit von 0 Metern, am Ende derselben aber wie berechnet eine solche von 20 Metern; wir können daher für diesen Fall unserer Rechnung eine gleichförmige mittlere Geschwindigkeit von 10 Metern (der Hälfte von 0 + 20) zugrunde legen, mit der sich der Körper während jener 2 Sekunden zur Erde bewegt hat, so daß also die Fallstrecke während dieser Zeit 2 × 10 = 20 Meter betragen muß. Der Körper, der in der ersten Sekunde seines Falles nur 5 Meter zurücklegte, legt also in 2 Sekunden nicht das Doppelte, sondern das Vierfache dieser Strecke zurück. Wir wollen auch noch die Fallstrecke während eines Zeitraumes von 3 Sekunden berechnen. Hier kommen wir auf eine mittlere Geschwindigkeit von 15 Metern (die Hälfte aus 0 + 30), und mithin auf eine Fallstrecke von 3 × 15 = 45 Metern, also das Neunfache der Fallstrecke in der ersten Sekunde. Rechnen wir in dieser Weise weiter, so finden wir, daß der Körper in 4 Sekunden eine Fallstrecke von 80 Metern, in 5 Sekunden eine solche von 125 Metern, in 10 Sekunden eine solche von 500 Metern zurücklegt. Die Fallstrecken wachsen also sehr schnell an.

Wir könnten die Fallstrecken in dieser Weise fortlaufend berechnen, können sie jedoch einfacher durch eine sehr einfache Formel angeben, die besagt, daß für jede Fallzeit die Fallstrecke = 5 × t ² Meter beträgt. In dieser Formel bedeutet t die Anzahl der Sekunden, während der der Fall stattfindet, t ² also das Quadrat dieser Größe (die Anzahl der Sekunden mit sich selbst multipliziert). Wie groß ist nun nach dieser Formel die Fallstrecke, die ein Körper in 20 Sekunden erreicht? Unsere Formel ergibt dafür 5 × 20 × 20 = 2000 Meter, und für die Fallzeit von 100 Sekunden finden wir 5 × 100 × 100 = 50 000 Meter oder 50 Kilometer. In der verhältnismäßig kurzen Zeit von 100 Sekunden würde also ein fallender Körper eine Strecke zurücklegen, für die ein Schnellzug etwa eine halbe Stunde Zeit benötigt.

Diese Rechnung stimmt allerdings nur unter der Voraussetzung, daß die Beschleunigung von rund 10 Metern pro Sekunde immer dieselbe bleibt. Das trifft jedoch nur bedingterweise zu, nur innerhalb des Bereiches der Erdoberfläche. Über und unterhalb der Erdoberfläche nimmt die Beschleunigung ab, entsprechend dem Newtonschen Anziehungsgesetz, in praktisch merkbarer Weise jedoch erst in erheblicher Entfernung von der Erdoberfläche. Für unsere abgerundete Rechnung können wir im Bereich von etwa 50 Kilometern über und unter der Erdoberfläche die Anziehungskraft bzw. die Beschleunigung als ungefähr gleichbleibend annehmen, so daß an der eben angestellten Rechnung über die Fallstrecken nicht viel zu ändern ist. Bei größeren Entfernungen von der Erdoberfläche müßten wir die Abnahme der Anziehung jedoch in Rechnung stellen. Im Mittelpunkt der Erde sind die anziehenden Kräfte ausgeglichen; ein hier befindlicher Körper wäre also gewichtslos, und ebenso ist die Beschleunigung hier mit Null anzunehmen.

An dieser Stelle wollen wir ein interessantes Gedankenexperiment machen. Wir wollen annehmen, es würde von einem Punkte der Erdoberfläche aus ein Schacht gegraben und in gerader Linie durch den Erdmittelpunkt hindurch bis zum anderen Ende der Erdkugel geführt werden. Wie würde sich dann ein Körper verhalten, den man an dem einen Ende des Schachtes in diesen hineinwirft? Das ist ein interessantes Problem, das auch von Laien gern und oft erörtert wird. Die Meinungen über das Verhalten des hineingeworfenen Körpers gehen dabei allerdings zumeist sehr weit auseinander. Die einen behaupten, daß der Körper mit abnehmender Geschwindigkeit bis zum Mittelpunkte der Erde falle und in diesem unweigerlich zur Ruhe komme, weil ja dort Anziehung und Beschleunigung gleich Null sei; andere hingegen sind der Meinung, daß der Körper nicht nur die ganze Strecke des Schachtes hindurchfallen, sondern, an dem anderen Ende angekommen, über dieses hinaus noch einmal eine ebenso lange Strecke, wie der Schacht selbst ist, in die Lüfte steigen müsse. Diese wie jene Ansicht ist aber falsch. Die Bewegung des hineingeworfenen Körpers stellt vielmehr einen Spezialfall der allgemeinen Fallbewegung dar und läßt sich aus den Fallgesetzen sehr genau berechnen, allerdings wegen der abnehmenden Wirkung der Kräfte nur vermittels Differentialrechnung. Wir wollen diese Rechnung nicht durchführen, was doch zu kompliziert sein würde, sondern uns auf die Angabe des interessanten Ergebnisses beschränken.

Ein solcher wie der erwähnte Schacht hätte, entsprechend dem Durchmesser unseres Globus, eine Länge von 12 760 Kilometern. Angenommen, der Schacht würde von Berlin aus beginnen, so würde er auf demselben Meridian wie unsere Reichshauptstadt im Stillen Ozean, auf einer der kleinen Inseln westlich von Neuseeland wieder zum Vorschein kommen. Wie würde sich also der Fall unseres Körpers in dieser hübschen Rohrpostanlage gestalten? Nun, innerhalb des Bereiches der Erdoberfläche und bei einer Beschleunigung von 10 Metern in der Sekunde würde der Körper zunächst mit der oben berechneten mittleren Geschwindigkeit für jede Sekunde fallen. Mit der wachsenden Annäherung an den Erdmittelpunkt ändern sich diese Verhältnisse allerdings in gewisser Weise. Die Beschleunigung, die der Körper in der Sekunde erhält, nimmt ab und wird im Mittelpunkt der Erde zu Null; die mittlere Sekundengeschwindigkeit wächst jedoch auch weiterhin, wenn auch in anderer Weise wie an der Erdoberfläche. Beschleunigung und Geschwindigkeit sind also sehr verschiedene Begriffe und dürfen nicht miteinander verwechselt werden, was bei der Erörterung unseres Problems oftmals der Fall ist. Alle die angeführten Faktoren würden nun bewirken, daß der – sagen wir in Berlin – in den Schacht hineingeworfene Körper mit gewaltig anwachsender Geschwindigkeit zunächst bis zum Mittelpunkt der Erde fallen und diesen mit einer Sekundengeschwindigkeit von rund 7900 Metern erreichen würde. Mit dieser ungeheuren Geschwindigkeit würde er über den Mittelpunkt der Erde hinaussausen und dann mit abnehmender Geschwindigkeit bis zum anderen Ende des Schachtes gelangen. Hier bis an die Oberfläche gekommen, wäre seine Geschwindigkeit zu Null geworden, der Körper würde wieder zurückfallen und die zurückgelegte Strecke jetzt in umgekehrter Richtung passieren, würde wieder mit wachsender Geschwindigkeit erst bis zum Mittelpunkt der Erde, in welchem er die bereits angegebene Höchstgeschwindigkeit erreicht, dann mit abnehmender Geschwindigkeit weiterfallen, bis er wieder in Berlin an der Oberfläche der Erde erscheint. Hier beginnt das Spiel von neuem, und so geht die Bewegung weiter.

Die ganze Bewegung ist zu vergleichen der Bewegung eines Pendels und ist, mathematisch betrachtet, sogar mit einer solchen identisch. Wie das Pendel zwischen zwei Höchstgeschwindigkeitspunkten hin und her schwingt, am Anfang und Ende der Schwingungsphase die Geschwindigkeit Null hat und im tiefsten Punkte eine Höchstgeschwindigkeit erreicht, so pendelt auch unser Körper erst mit wachsender, dann mit abnehmender Geschwindigkeit von einem Ende des Schachtes zum anderen und dann wieder dieselbe Strecke in derselben Weise zurück. Allerdings ist der Weg des schwingenden Pendels eine Bogenlinie, der unseres Körpers eine schnurgerade Strecke von einem bis zum anderen Ende des Schachtes, was jedoch für die Betrachtung des Bewegungsvorganges als solchen nicht in Betracht kommt. Unser Körper pendelt also in gerader Linie.

Noch in einem anderen Umstande verhält sich unser Körper wie ein physisches Pendel. Das Spiel der Hin- und Herschwingungen würde nicht ewig so wie beschrieben weitergehen. Wie beim Pendel die Ausschläge immer kürzer werden, weil Reibung und Luftwiderstand seine Bewegung verzögern und schließlich ganz aufheben, so daß es im tiefsten Punkte seiner Schwingungsphase zur Ruhe kommt, so ähnlich auch bei unserem Körper. Auch dieser hätte beim Durchfallen des Schachtes den Reibungswiderstand der Luft zu überwinden, der bei solchen wie den berechneten gewaltigen Geschwindigkeiten sehr bedeutend wäre; dadurch würden auch hier die Schwingungsphasen allmählich immer kürzer; der Körper bliebe bei seinen Pendelbewegungen immer mehr von den beiden Enden des Schachtes zurück und müßte schließlich im Mittelpunkte der Erde zur Ruhe kommen. Um den Körper in den Stand zu setzen, immer vollständig und ununterbrochen von einem Ende des Schachtes bis zum anderen zu gelangen, müßte er nach jeder Phase einen neuen Kraftimpuls erhalten, durch den der Kraftverlust auf der zurückgelegten Strecke infolge des Luftwiderstandes ausgeglichen würde, vergleichbar einem Uhrpendel, das ja ebenfalls nach jeder Schwingung durch die Kraft der Feder einen neuen Impuls erhält und dadurch seine Schwingungsbewegung unverändert und ununterbrochen auszuführen vermag. Bemerkt sei noch, daß der Körper für den vollständigen Fall von einem Ende des Schachtes bis zum anderen die Zeit von 42 Minuten und 12 Sekunden benötigte, während ein Schnellzug von 100 Kilometer Stundengeschwindigkeit für eine Strecke von solcher Länge etwa 4½ Tage brauchte. Unser Schacht würde also eine Art idealen Rohrpostbetriebes von aller nur wünschenswerten Einfachheit und Leistungsfähigkeit darstellen und die Beförderung unserer Postsendungen von einem Ende der Erde bis zum anderen in knapp drei Viertelstunden möglich machen.

Anders als auf der Erde sind die Schwereverhältnisse auf anderen Weltkörpern, weil ja dort Masse und Durchmesser, also jene Faktoren, von denen die Größe der Anziehung bzw. der Schwere abhängt, andere sind. Die Masse der Sonne ist beispielsweise an 320 000mal größer als die Erdmasse; dafür ist aber auch ihr Halbmesser 100mal größer als der der Erde, und diese Umstände bewirken, daß die Schwerkraft auf der Sonne etwa 28mal größer ist als auf der Erde. Das bedeutet, daß ein Körper, der auf der Erde 1 Kilogramm wiegt, auf der Sonne ein Gewicht von 28 Kilogramm hätte, oder daß ein Mann, der auf Erden mit dem Normalgewicht von 1½ Zentnern herumläuft, nach der Sonne versetzt sich mit dem stattlichen Körpergewicht von 42 Zentnern zu plagen hätte. Ebenso sind auch die Faktoren der Fallbewegung auf der Sonne 28mal größer als bei uns. Während auf Erden ein Körper in 1 Sekunde nur um 5 Meter fällt, würde er auf der Sonne in dieser Zeit schon volle 140 Meter, in 10 Sekunden schon die gewaltige Fallstrecke von 14 000 Metern zurücklegen. Gerade umgekehrt liegen die Verhältnisse beim Mond. Dessen Masse beträgt nur etwa den achtzigsten Teil der Masse unserer Erde, sein Halbmesser nur 1750 Kilometer, also etwas mehr als den vierten Teil des Erdhalbmessers. Hieraus läßt sich berechnen, daß die Schwerkraft auf dem Monde knapp den fünften Teil derjenigen der Erde beträgt, daß also ein Körper von 1 Kilogramm Erdgewicht dort knapp 200 Gramm wiegen und der bereits erwähnte irdische Normalmann auf dem Monde zu dem Kindergewicht von 30 Pfund zusammenschrumpfen würde. Auf dem Monde fällt ein Körper in einer Sekunde nur etwa 95 Zentimeter, die Körper schweben dort also mehr als sie fallen. Und weil die Schwere dort 5mal geringer ist als bei uns, kann ein Mondbewohner auch 5mal höher, als es bei uns möglich ist, springen; ein Turner auf dem Monde würde mit Leichtigkeit 5 bis 10 Meter hoch springen können.

Aber nicht nur auf der Oberfläche der Weltkörper wirkt die Gravitation als Fallbewegung, sondern auch von einem Weltkörper zum anderen, und sie hält dadurch die Körper in ihren vorgeschriebenen Bahnen fest. Der Mond beispielsweise hat das Bestreben, sich dauernd von der Erde zu entfernen; die Anziehungskraft, die die Erde auf ihn ausübt, bewirkt jedoch, daß er in jeder Sekunde um 1,36 Millimeter zur Erde fällt, und diese geringe Fallbewegung genügt, um unseren Erdtrabanten trotz seiner Neigung zur Fahnenflucht dauernd an die Erde zu fesseln und ihn zu seiner annähernd kreisförmigen Bahn um diese zu zwingen. Ebenso findet ständig eine gewisse Fallbewegung der Erde wie auch aller Planeten zur Sonne statt, und ebenso verhält es sich mit allen Weltkörpern überhaupt, die um einen Zentralkörper kreisen. Ohne diese regelnde Fallbewegung durch die Gravitation würden alle Weltkörper ziellos im Weltenraum herumvagabundieren, und statt der erhabenen Regelmäßigkeit und Harmonie des Kosmos würde ein ungeheures Chaos herrschen, das gleichbedeutend mit dem Untergang der Welt wäre.

3. Das Geheimnis der Schwerkraft

Die Frage nach dem Wesen der Gravitation – Die Äthertheorie – Die Erklärung der Relativitätstheorie – Der Fahrstuhl im Weltraum – Von träger und schwerer Masse – Das Äquivalenzprinzip – Vom gekrümmten Raum – Unvorstellbare Dinge – Gedankenspiel oder Wirklichkeit? – Ein ungelöstes Problem

Wir haben das Gesetz der Gravitation kennengelernt, jener Kraft, die die Lenkerin aller Bewegungen im Weltraum und dadurch die beherrschende Gewalt des gesamten Universums überhaupt ist. Isaak Newtons durchdringender Forscherblick hatte die Gesetzmäßigkeit im Wirken dieser Kraft erkannt und ihr gleichzeitig in der Formel den exakten Ausdruck gegeben, der es seitdem dem Menschengeiste gestattet, das kosmische Geschehen, soweit es durch die Gravitation bedingt ist, der Rechnung zu unterwerfen.

Aber was ist das Wesen dieser geheimnisvollen Kraft? Diese Frage ist in höchstem Maße berechtigt, denn das Gesetz, nach dem die Wirkung der Gravitation erfolgt, besagt ja noch nichts über die eigentliche Ursache und das Wesen dieser Naturerscheinung, ebensowenig wie die Regel, nach der der Uhrzeiger seine Umläufe macht, etwas über die Ursache dieser Drehbewegung besagt. Jene Frage beschäftigte daher die Naturforschung nahezu so lange, wie sie sich über den Begriff der Gravitation im Newtonschen Sinne klargeworden ist. Wie kommt es, daß die Sonne die Erde, die Erde den Mond an sich fesselt und die Erde den Apfel, der sich vom Zweige losgelöst hat, zu sich herabzieht? Wir bezeichnen diese Anziehung als eine »Kraft«, wobei uns der Vergleich mit der Muskelkraft und den Wirkungen, die wir durch diese ausüben, vorschwebt; wir stellen uns vor, daß die größeren Weltkörper die kleineren wie mit ungeheuer langen Armen zu sich heranziehen. Aber gerade dieser Vergleich enthüllt uns das Rätselhafte der Gravitation. Denn wo sind die Arme der Erde oder der Sonne oder der sonstigen Weltkörper? Wir sehen sie nirgends, die Wirkung der Gravitation erfolgt vielmehr unvermittelt, ohne Arme oder ein anderes sichtbares Medium, von einem Weltkörper zum anderen und über die unendlichen Entfernungen im Weltenraume.

Ferner drängte sich uns die Frage auf, ob die Wirkung der Gravitation mit momentaner Geschwindigkeit, etwa nach Art der Lichtgeschwindigkeit, erfolgt. Newton selbst hat sich an der Erkenntnis und formelmäßigen Bestimmung des Gravitationsgesetzes genügen lassen, die Frage nach dem Wesen dieser Kraft hat er nicht aufgeworfen. Nach der Galilei-Newtonschen Mechanik stellt sich die Gravitation dar als eine »Fernkraft«, die unvermittelt und mit unendlicher Geschwindigkeit durch das ganze Weltall wirkt. Die Gravitation ist in dieser als »klassische Mechanik« bezeichneten Auffassung eine unmittelbare physikalische Gegebenheit, die aber nichtsdestoweniger durch ihr Sein und die Art ihres gesetzmäßigen Wirkens ein Rätsel darstellt, dessen Lösung und Ergründung eine der reizvollsten Aufgaben der spekulativen Naturforschung ist.

Überaus zahlreich sind die Hypothesen, die aufgestellt wurden, um das Wesen der Gravitation zu erklären. Aber sie alle litten an dem Übelstand, daß sie das Wesen dieser Kraft mit Hilfe einer anderen Kraft zu erklären suchten, die dann wieder unerklärt blieb. So setzte man nur ein Rätsel an die Stelle eines anderen. Das gilt auch von der Äthertheorie, die ja lange Zeit hindurch die wissenschaftliche Spekulation zur Erklärung der Naturerscheinungen und der Naturkräfte beherrschte und zum Teil auch heute noch beherrscht. Der Äther, der als ein unendlich feiner und zugleich in höchstem Maße elastischer, das ganze Weltall erfüllender Stoff gedacht wird, sollte, obwohl selbst schwerelos, die Gravitationswirkung zwischen den Weltkörpern erzeugen und vermitteln, sei es durch den Druck, den er auf alle Körper ausübt, sei es durch eine Art Strahlung oder noch auf andere Weise. Letzte Klarheit und Wahrheit konnte auch diese Hypothese nicht geben, sie litt an ebensolchen Mängeln wie die vielen anderen Versuche zur Erklärung der Gravitation und ließ die Frage nach der Ursache der Kräfte, die den Äther zu solchen Wirkungen befähigen, ungelöst. Das Geheimnis der Gravitation schien unergründlich.

Aber in unseren Tagen ist ein hochbedeutsamer Schritt getan, der uns dem Wesen der Gravitation doch näher zu bringen scheint, und zwar durch die allgemeine Relativitätstheorie Albert Einsteins. Wir wollen versuchen, den Grundgedanken dieses Erklärungsversuches herauszuschälen, was bei dem komplizierten und abstrakten Gedankengebilde, als welches sich die Relativitätstheorie darstellt, allerdings seine Schwierigkeiten hat und auch nur zu einem andeutungsweisen Bilde führen kann.

Nach der Relativitätstheorie ist die Gravitation nur als ein Spezialfall der allgemeinen Relativität der Bewegung aufzufassen. Sie setzt die Gravitation in Beziehung zur Trägheit, jener Ureigenschaft aller stofflichen Dinge, die darin besteht, daß ein Körper den Bewegungszustand, in dem er sich befindet, nach Richtung und Geschwindigkeit beizubehalten sucht und ihn auch so lange beibehält, als nicht andere Kräfte auf ihn einwirken. Die Relativitätstheorie erklärt Gravitation und Trägheit für äquivalent, das heißt als für die Betrachtung gleichwertig, ja sogar im Grunde identisch, und es kommt nach ihr nur auf die Betrachtungsweise an, ob man Trägheitserscheinungen als Gravitation und ebenso Gravitationserscheinungen als Wirkungen der Trägheit auffassen will. Diese Wesensgleichheit von Gravitation und Trägheit kann durch das folgende Beispiel, das in den Darstellungen der Relativitätstheorie viel benutzt wird, veranschaulicht werden. Wir versetzen uns in Gedanken in den Weltraum, weitab von allen Weltkörpern, in einen geschlossenen Kasten, etwa nach Art eines Fahrstuhles. Da unser Kasten fern genug von allen anderen Weltkörpern ist, kann von diesen auch keine Gravitationswirkung auf ihn ausgeübt werden. In dem Kasten herrscht also keine Schwere. Daher würde ein Körper, den der Kastenbewohner aus der Hand läßt, nicht fallen, sondern unbewegt an derselben Stelle im Raume, unverändert in demselben Abstande vom Boden des Kastens, verharren. Wir wollen nunmehr annehmen, daß der Kasten durch irgendein Wesen nach oben gezogen werde, und zwar mit gleichmäßiger Beschleunigung. Was geschieht dann? Der Kasten und auch der auf dem Boden des Kastens stehende Experimentator werden gleichmäßig beschleunigt nach oben gezogen, der losgelassene Körper aber verharrt nach wie vor in derselben Stelle im Raume; daher nähert sich ihm der Boden des emporgehobenen Kastens mit gleichmäßiger Beschleunigung, das heißt die Entfernung zwischen jenem Körper und dem Boden des Kastens wird beschleunigt verringert. Der Kastenbewohner aber, der von dem Emporziehen des Kastens nichts weiß, wird den Eindruck haben: der losgelassene Körper fällt auf den Boden des Kastens. Denn der beobachtete Vorgang ist seiner Erscheinung nach tatsächlich genau derselbe wie beim freien Fall infolge der Gravitation. Derselbe Vorgang, nämlich beschleunigte Verringerung der Entfernung zwischen dem Körper und dem Kastenboden, würde auch eintreten, wenn der Kasten in Ruhe bliebe, statt dessen aber plötzlich unterhalb des Kastens eine große Masse hingezaubert würde, die eine Gravitationswirkung ausübt und daher jenen frei schwebenden Körper gemäß den Fallgesetzen zu sich heranzieht. Bleibt es dem Kastenbewohner im ungewissen, wodurch jene Bewegung verursacht wurde, ob durch Hochziehen des Kastens oder durch die Gravitationswirkung einer Masse unterhalb des Kastens, so kann er den beobachteten Vorgang sowohl als Trägheitswirkung des Körpers gegenüber der plötzlich erfolgten Beschleunigung des Kastens oder aber als Gravitationswirkung, also als Fall, auffassen. Die Relativitätstheorie schließt aus der Identität der Erscheinungen in den beiden Fällen auf die Identität der Vorgänge selbst und ebenso auf die Identität der Ursachen in beiden Fällen. Trägheit und Gravitation, die identische Erscheinungen bewirken, sind ihrem Wesen nach selbst identisch; die Gravitationserscheinungen werden als Trägheitswirkungen aufgefaßt.

Auf Grund des Äquivalenzprinzips, das also die Identität zwischen Trägheit und Gravitation oder, wie man sagt, zwischen träger und schwerer Masse postuliert, baut Einstein seine Gravitationstheorie auf. Nach dieser unterliegt ein Körper bei seiner Bewegung im Raume überhaupt keiner besonderen Kraft, sondern er befolgt dabei lediglich die Gesetze des Raumes. Die Bahn eines Körpers im Raume ist in allen Fällen eine sogenannte »geradeste« oder geodätische Linie, das heißt, allgemein gesagt, die Linie des geringsten Widerstandes im raumzeitlichen Kontinuum, das die Welt darstellt. Wenn ein Mensch auf dem Nordpol steht, und er will auf dem kürzesten Wege der Erdoberfläche nach irgendeinem Punkte des Äquators gelangen, so würde das der Viertelmeridian sein, der jenen Punkt des Äquators mit dem Nordpol verbindet; dieser Weg wäre für diesen Fall die geodätische Linie zwischen jenen beiden Punkten. Ähnlich verfolgen auch die Körper im »leeren« Welträume ihren Weg auf geodätischen Linien. Aber der Raum ist nach der Relativitätstheorie nicht ein unterschiedsloses Etwas, als das ihn die alte Physik und ebenso die eigentliche Wissenschaft vom Raume, die Geometrie, aufgefaßt hatten, sondern er ist »gekrümmt«, und zwar nach Maßgabe der den Raum erfüllenden trägen Massen. Jeder materielle Körper im Weltall, wie etwa die Sonne, erzeugt nach Maßgabe seiner trägen Masse eine Krümmung des Raumes um sich herum, und diese ist gleichbedeutend mit dem Gravitationsfeld des Körpers. Ein anderer Körper, der in dem Bereich der Sonne ist, also etwa die Erde, folgt der Raumkrümmung, die die Sonnenmasse bewirkt und die ihn um die Sonne herumführt. Die Erdbahn ist also die geodätische Linie der Erde im Krümmungsfelde der Sonne. Nur weitab von allen anderen Körpern und außerhalb der Krümmungssphäre solcher würde ein Körper sich geradlinig und mit gleichbleibender Geschwindigkeit fortbewegen, nur in einem solchen Falle erfolgen die Bewegungen der Körper nach dem Trägheitsgesetz der Galilei-Newtonschen Mechanik.

Die Relativitätstheorie scheidet also die Annahme einer besonderen Kraft für die Erklärung der Gravitation aus. Eine besondere anziehende Kraft gibt es überhaupt nicht, sondern die Bewegungen der Körper, die in der alten Physik als unter dem Einfluß der Gravitation erfolgend betrachtet wurden, erfolgen lediglich als die Bahnen ihrer geodätischen Linien im gekrümmten Raume; die Krümmung des Raumes und damit die Bewegungsbahnen der Weltkörper aber werden bewirkt durch die trägen Massen im Welträume. Für die Relativitätstheorie ist somit die Gravitation nur noch ein Raum- und Bewegungsproblem, ein Spezialfall der Relativität aller Bewegungen. In der Auffassung der heutigen Physik ist der Gravitation auch der Charakter der Fernkraft genommen; sie ist, wenn man das Bild der »Kraft« überhaupt noch beibehalten will, ebenso wie alle anderen Kräfte nur noch als Nahkraft aufzufassen, deren Ausbreitungsgeschwindigkeit ebenso wie die des Lichtes 300 000 Kilometer in der Sekunde beträgt.

Der große Wert dieser Auffassung der Gravitation besteht darin, daß sie überhaupt zum ersten Male eine logisch geschlossene Erklärung der Gravitation darbietet, ohne den Zirkelschluß früherer Hypothesen zu begehen, die immer eine Kraft durch eine andere erklärten und dadurch überhaupt zu keiner befriedigenden Erklärung kamen. Der große Reiz dieser Auffassung für den Naturforscher aber besteht in der Einfachheit und Einheitlichkeit des Erklärungsprinzips, des Prinzips der Äquivalenz zwischen träger und schwerer Masse, aus dem die Gravitation folgt. Dafür arbeitet freilich die Relativitätstheorie in ihrer Erklärungsweise mit Annahmen und Begriffen, die nicht nur in höchstem Maße abstrakt, sondern auch mit jeder menschlichen Vorstellung überhaupt unvereinbar sind. Der Begriff der »Krümmung des Raumes« insbesondere ist keiner Vorstellung fähig. Eine Linie, eine Ebene, ein Körper kann gekrümmt sein, ob es aber einen Sinn hat, den Raum selbst als gekrümmt zu bezeichnen, muß vorderhand dahingestellt bleiben, eine Vorstellung können wir jedenfalls mit dieser Annahme nicht verbinden. Die Relativitätstheoretiker allerdings machen sich über die Nichtvorstellbarkeit ihrer Annahmen und Begriffe keine Bedenken, sondern lassen sich an der mathematischen Darstellbarkeit ihrer Theorie genügen; die Gegner aber, die diese Theorie ablehnen, kommen zu ihrem ablehnenden Standpunkt nicht zum wenigsten durch die völlige Unvorstellbarkeit der Gebilde und Begriffe, mit denen jene Theorie arbeitet, und sind geneigt, die begrifflichen Operationen und Folgerungen dieser Theorie nur als einen Wettlauf mit der Schildkröte zu bewerten. Auch die Erklärung der Gravitation auf dem Boden der Relativitätstheorie steht und fällt mit dieser, und die Zukunft muß erweisen, ob die neue Gravitationshypothese, ebenso wie die Relativitätstheorie überhaupt, nur ein scharfsinniges Spiel mit Begriffen ist, oder ob sie Anspruch darauf erheben kann, als Wirklichkeitserklärung zu gelten.

Jener Apfel, der einst zur Erde fiel und einem genialen Denker zum ersten Male die Rätselhaftigkeit des Fallvorganges auf dämmern ließ, ist seines Geheimnisses auch heute noch keinesfalls völlig und widerspruchsfrei enthüllt. Dieser Vorgang, so unendlich einfach und so ungezählte millionenmal vordem und nachdem beobachtet, rührt an das Innerste der Natur und gibt unseren Forschern und Denkern nach wie vor eins der tiefsten Probleme der Naturerklärung auf.

4. Ist ein Perpetuum mobile möglich?

Tod und Auferstehung der Probleme – Vom alten Perpetuum mobile – Der erste Hauptsatz der Wärmetheorie – Die Logik des Naturgesetzes – Das Temperaturgefälle – Vom Perpetuum mobile zweiter Art – Der zweite Hauptsatz der Wärmetheorie – Ein Erfahrungssatz – Das Problem des Wärmetransformators – Das Leben ein Perpetuum mobile zweiter Art? – Eine Aufgabe für Erfinder

Die Ideen und Probleme haben in ihren Gräbern keine Ruhe! In ihrer alten Form von der Wissenschaft seziert und begraben, stehen sie in höherer und wissenschaftlicherer Form zu neuem Leben auf, um wiederum Mittelpunkte des Geisteskampfes der Wissenschaften zu werden. Das ist eine Erscheinung, die wir in der Geschichte der Forschung oftmals verfolgen können. Das Problem der Verwandlung der Elemente und insbesondere der Kunst, aus unedlen Metallen Gold zu machen, war in der mystisch-spekulativen Form, in der diese Idee von den mittelalterlichen Chemisten und Alchemisten verfolgt wurde, von der Wissenschaft als Traum und unwissenschaftliche Phantasie entlarvt und begraben worden; die heutige wissenschaftliche Chemie aber erkennt nicht nur die Möglichkeit der Verwandlung der Elemente an, sondern lehrt, daß solche Verwandlungen unaufhörlich in der Natur stattfinden, wenn freilich auch in ganz anderer Form, als sich die Alchemisten einst träumen ließen, und daß beispielsweise aus dem Zerfall des Radiums Blei entsteht. Bekanntlich hat auch der kürzlich verstorbene Professor Miethe den Traum der Alchemisten verwirklichen und Quecksilber in Gold verwandeln zu können geglaubt; wenn ihm das auch, wie sich schließlich herausgestellt hat, letzten Endes doch noch nicht gelungen ist, so geht aus den Versuchen des genannten hervorragenden Forschers jedenfalls klar hervor, daß die Wissenschaft von heute die künstliche Erzeugung von Gold durchaus in den Bereich der Möglichkeit gerückt hat.

Nicht ganz so, aber doch ähnlich verhält es sich auch mit dem uralten Problem, das als Perpetuum mobile bezeichnet wird. Die Lösung dieses Problems in der Form, wie sie jahrhundertelang in den Köpfen von Gelehrten und Ungelehrten herumgespukt hat und vereinzelt sogar noch heute herumspukt, war wissenschaftlich als unmöglich erkannt und damit diese Idee feierlich begraben worden; in einer neuen und andersartigen Form aber ist auch dieses Problem heute wieder aufgetaucht, nämlich als das sogenannte Perpetuum mobile zweiter Art, das sogar in den Mittelpunkt der Anschauungsweise der heutigen exakten Naturwissenschaften gerückt ist und wieder und immer wieder den Gegenstand wissenschaftlicher und Meinungskämpfe bildet. Dem großen Publikum, auch dem der Gebildeten, ist der Begriff des Perpetuum mobile zweiter Art – die Bezeichnung stammt von Wilhelm Ostwald, dem hervorragenden Chemo-Physiker – noch wenig bekannt, obwohl dieser Begriff nicht nur eins der wichtigsten, sondern zugleich auch interessantesten und reizvollsten Probleme der gegenwärtigen Naturforschung umfaßt, das nach Inhalt und Bedeutung auch dem Laien durchaus verständlich und geeignet ist, ihn in hohem Maße zu fesseln.

Wir werden zu dem Begriff des Perpetuum mobile zweiter Art am besten gelangen, wenn wir zuvor kurz auf das alte, erledigte und begrabene Perpetuum mobile eingehen. Beide Probleme stehen in engstem Zusammenhänge mit der sogenannten Wärmetheorie, die die Grundlage der gesamten heutigen exakten Naturforschung ist.

Perpetuum mobile heißt wörtlich: das dauernd Bewegliche, und wir verstehen unter diesem terminus technicus einen Apparat oder eine Maschine, die, wenn sie einmal in Bewegung gesetzt worden ist, diese Bewegung fortwährend beibehält, ohne eines weiteren Anstoßes oder weiterer Zufuhr von Energie zu bedürfen. Die zahllosen Erfinder, die sich um die Lösung jenes Problems bemühten, knüpften daran die weitere Erwartung, daß eine solche Maschine, einmal in Bewegung gesetzt, dann dauernd Arbeit leisten, dauernd zum Antrieb anderer Maschinen verwandt werden könnte. Daß eine Uhr kein Perpetuum mobile in diesem Sinne ist, sehen wir auf den ersten Blick, denn dieses kunstvolle Instrument bedarf der regelmäßigen Zufuhr von Energie, um seinen Betrieb fortsetzen zu können, und diese Zufuhr geschieht durch das »Aufziehen« der Uhr, wobei entweder eine Feder gespannt oder ein Gewicht gehoben wird; die Feder leistet dann durch ihre allmähliche Entspannung, das Gewicht durch sein langsames Herabsinken die Arbeit, die zum Betrieb der Uhr nötig ist. Ebensowenig ist auch eine sogenannte Kraftmaschine, etwa eine Dampfmaschine, ein Perpetuum mobile, denn eine solche Maschine bleibt nur so lange in Bewegung und vermag nur so lange Arbeit zu leisten, als ihr Wärme zugeführt wird, die selbst durch die Verbrennung von Kohlen erzeugt wird. Die so erzeugte Wärme von mehreren hundert Grad dehnt das Wasser im Dampfkessel der Maschine aus und verwandelt es in Dampf von hoher Spannung, der auf den Kolben im Zylinder der Maschine geleitet wird und diesen und damit die ganze Maschine in arbeitende Bewegung setzt. Nur solange ihr Wärme zugeführt wird, kann die Dampfmaschine diesen Bewegungs- und Arbeitsprozeß fortsetzen, und die Arbeit, die sie hierbei selbst zu leisten vermag, könnte im theoretisch günstigsten Falle höchstens dem Quantum Wärme entsprechen, das ihr selbst zugeführt worden ist. Die wissenschaftliche Wärmetheorie drückt das mit den Worten aus: Wärme und Arbeit sind äquivalent, das heißt: mit einem bestimmten Quantum Wärme kann immer nur ein ganz bestimmtes und gleichbleibendes Quantum Arbeit geleistet werden Des Zusammenhanges und der besseren Verständlichkeit wegen muß hier einiges, das bereits im vorigen Abschnitt behandelt worden ist, wiederholt werden..

Als die Maßeinheit der Wärme gilt bekanntlich die Kalorie, d. h. die Wärmemenge, die benötigt wird, um die Temperatur von 1 Kilogramm Wasser um 1 Grad zu erhöhen, als Einheit der Arbeit aber das Meterkilogramm, d. h. die Arbeitsmenge, die nötig ist, um ein Gewicht von 1 Kilogramm um 1 Meter zu heben. Eine Kalorie ist nun 424 Meterkilogramm gleichwertig, das heißt: mit der Wärmemenge von 1 Kalorie kann eine Arbeitsmenge von 424 Meterkilogramm geleistet, etwa ein Gewicht von 1 Kilogramm um 424 Meter oder ein Gewicht von 424 Kilogramm um 1 Meter gehoben werden. Diese durch genaue Experimente erkannte Äquivalenz von Wärme und Arbeit ist ein Fundamentalsatz der heutigen exakten Naturwissenschaft und wird als der erste Hauptsatz der Wärmetheorie bezeichnet. Wenn ich also einer Dampfmaschine eine Wärmemenge von 1000 Kalorien zuführe, so könnte sie theoretisch im günstigsten Falle höchstens eine Arbeit von 1000 × 424 = 424 000 Meterkilogramm leisten. In der Praxis allerdings setzt die Maschine nur etwa den zehnten Teil der ihr zugeführten Wärme in Nutzarbeit um, während die übrigen 90 Prozent durch Reibung, Ausstrahlung, Abwärme und sonstige technische Unvollkommenheiten der Maschine verlorengehen. Nehmen wir aber selbst eine ideale Dampfmaschine an, bei der absolut keine Wärmeverluste auftreten würden, so könnte doch auch aus einer solchen Maschine, wie nach dem Gesagten ohne weiteres einleuchtend ist, niemals mehr Arbeit herausgeholt werden, als ihr vordem in Gestalt von Wärme zugeführt worden ist.

Und wie bei der Dampfmaschine, so auch bei allen anderen Arbeitsmaschinen. Damit eine Maschine Arbeit leisten kann, muß ich ihr selbst vorher Arbeit, d. h. Energie, zuführen, sei es in Form von Wärme, Elektrizität, Bewegungsenergie des Wassers oder Windes, sei es in Form menschlicher oder tierischer Arbeitskraft. Niemals kann aus einer solchen Maschine mehr Arbeit herausgeholt werden, als ihr vordem zugeführt wurde, und eine Maschine, bei der das der Fall sein soll, die also mehr Arbeit leisten können soll, als ihr vordem zugeführt worden ist, ist gerade so unmöglich wie ein Portemonnaie, aus dem mehr Geld herausgenommen werden soll, als man vordem hineingetan hat. Dies wie jenes ist eine logische Unmöglichkeit, und an dieser ehernen Logik der Naturgesetze mußte das Problem des Perpetuum mobile in seiner alten Form scheitern, eine so ungeheure Summe von Scharfsinn und Arbeit auch von Gelehrten und Laien im Laufe der Jahrhunderte auf die Lösung dieses Problems verwandt worden ist, weil man jene in den Naturgesetzen selbst begründete logische Unmöglichkeit einer solchen Maschinerie erst verhältnismäßig spät, erst in der Mitte des vorigen Jahrhunderts, erkannte, nachdem nämlich der Arzt und Physiker Robert Mayer sein Gesetz von der Erhaltung der Energie aufgestellt hatte. Dieses Gesetz deckt sich seiner Bedeutung nach vollkommen mit dem obengenannten ersten Hauptsatz der Wärmetheorie, drückt diesen nur mit anderen Worten aus oder ist eine Betrachtung desselben Vorganges von einem anderen Gesichtspunkte aus.

Mit dieser in dem ersten Hauptsatz der Wärmetheorie niedergelegten Erkenntnis war das Perpetuum mobile der alten Art wissenschaftlich erledigt und begraben. Dieselbe Erkenntnis führte aber in ihrer weiteren Entwicklung dazu, jenes Problem in neuer Form, nämlich als Perpetuum mobile zweiter Art, zu neuem Leben erwachen zu lassen. Der Gedankengang, der hierzu führte, ging ebenfalls von der Wirkungsweise der Wärme als Naturkraft alles Geschehens aus und knüpfte an den Begriff des Temperaturgefälles an, mit dem wir uns kurz auseinandersetzen müssen.

Bei einer Dampf- oder sonstigen Wärmekraftmaschine erfolgt die Wirkungsweise der Wärme, indem sie von hoher Temperatur auf niedrigere herabfällt. Bei einer Dampfmaschine beispielsweise wird zunächst durch die Verbrennung der Kohlen Feuer, d. h. Wärme sehr hoher Temperatur, von über 1000 Grad, erzeugt. Diese Wärme erhitzt das Wasser im Dampfkessel, das bei dem Zustande, in welchem es sich in Dampf hoher Spannung verwandelt, aber nur noch eine Temperatur von etwa 200 Grad hat. Der Dampf leistet in der Maschine Arbeit, wobei er sich weiter erheblich abkühlt, um schließlich mit einer Temperatur von etwa 100 Grad die Maschine als sogenannter Abdampf zu verlassen. Die Wärme ist hierbei also von ihrer ursprünglichen Temperatur von über 1000 Grad auf eine solche von etwa 100 Grad gefallen, und den Zwischenraum von etwa 900 Grad nennt man das Temperaturgefälle, das die Wärme bei diesem Vorgang, von der Verbrennung der Kohlen bis zum Austritt des Abdampfes aus der Maschine, zu passieren hat. Soweit wir blicken können, findet die Wirkung der Wärme, sowohl beim Betrieb der Maschinen wie bei allen anderen Erscheinungen, immer nur statt, indem die Wärme ein Temperaturgefälle passiert und von höherer auf niedrigere Temperatur fällt, und wir kennen keinen Fall, in welchem es anders wäre.

Wenn nun auch alle Erfahrung gegen einen solchen Fall spricht, so können wir dennoch die Frage aufwerfen, ob die Wärme nicht auch in umgekehrter Temperaturrichtung wirken kann, also ob es möglich ist, daß Wärme von selbst von niedriger auf höhere Temperatur hinaufgehen, also statt eines Temperaturgefälles eine Temperatursteigung passieren kann. Eine solche Möglichkeit aber liefe in ihren Konsequenzen praktisch auf ein Perpetuum mobile hinaus, wie aus dem folgenden Beispiel ersichtlich ist. Nehmen wir an, ich habe 1 Liter kochenden Wassers, also Wasser von 100 Grad Temperatur. Wasser dieses Wärmezustandes entwickelt Dampf von 1 Atmosphäre Spannung, und ich könnte damit eine Zeitlang eine kleine Dampfmaschine treiben. Jetzt vermische ich das 1 Liter von 100 Grad mit 9 Litern eiskalten Wassers, also von 0 Grad, und erhalte dann im ganzen 10 Liter Wasser von 10 Grad Temperatur, also etwa Wasser von der Temperatur unseres Leitungswassers oder des Meerwassers, das wir nach dem Sprachgebrauch als »kalt« bezeichnen. In diesen 10 Litern Wasser ist noch die gesamte Wärmemenge des zuerst betrachteten Liters kochenden Wassers enthalten. Denn diese Wärmemenge ist durch das Umgießen nicht verlorengegangen, sondern nur auf eine niedrigere Temperatur gesunken, indem sie sich auf 10 Liter verteilte. Gelänge es mir nun, jene Wärmemenge aus den 10 Litern herauszuziehen und wieder auf 1 Liter Wasser zu konzentrieren, so würde dieses 1 Liter wieder die Temperatur von 100 Grad annehmen, und ich könnte damit meine kleine Dampfmaschine weiterbetreiben. Nun enthalten natürlich 10 Liter gewöhnlichen Meerwassers von 10 Grad Temperatur genau soviel Wärme wie jene zuerst betrachteten 10 Liter Wasser, die ich durch die Mischung von heißem und eiskaltem Wasser erhielt. Im Falle also das erwähnte Experiment bei jenen ersten 10 Liter Wasser gelingen würde, müßte es auch mit beliebigen anderen 10 Liter Wasser von 10 Grad Temperatur, die ich irgendwo aus dem Meere oder aus der Wasserleitung schöpfe, gelingen. Ich würde auch die Wärme dieser 10 Liter Meerwasser auf 1 Liter Wasser konzentrieren und dadurch Wasser von 100 Grad erhalten, mit dem ich meine Dampfmaschine wiederum betreiben könnte. Die Wärme hätte in diesem wie in jenem Falle eine Temperatursteigung vollbracht, und ich hätte aus dem »kalten« Wasser nutzbare Wärme von 100 Grad gezogen. Und was mit 10 Litern Meerwasser möglich ist, müßte dann natürlich mit den ganzen ungeheuren Wassermengen der Weltmeere ebenfalls möglich sein. Gelänge es also, die in jedem Wasser, also auch in dem »kalten« Meerwasser, enthaltenen unendlichen Wärmemengen zu veranlassen, sich vermittels einer geeigneten Vorrichtung von ihrem niedrigen Temperaturniveau von 10 Grad auf ein solches von 100 Grad oder noch höher, etwa bis zur Dampfkesseltemperatur, zu erheben, dann hätten wir in dem Apparat, der solches bewirken könnte, eine Maschine vor uns, die aus ihrer Umgebung immerwährend Wärme entnimmt, und diese Wärme könnten wir, ohne irgendwelcher Brennstoffe zu bedürfen, zum Betrieb unserer sämtlichen Kraftmaschinen verwenden. Eine solche Maschine wäre das Perpetuum mobile zweiter Art.

Es sind, das geht aus unserer Darstellung klar hervor, im »kalten« Meerwasser immer ganz ungeheure Wärmemengen enthalten, und jener interessante, vorderhand allerdings noch völlig hypothetische Apparat soll uns dazu verhelfen, jene unerschöpflichen Wärmemengen in unsere Hand zu geben. Wir müssen uns vergegenwärtigen, daß »kalt« lediglich ein sprachlicher Ausdruck für eine verhältnismäßig niedrige Temperatur ist, daß das aber keinesfalls bedeutet, daß ein »kalter« Körper überhaupt keine Wärme mehr enthalte. Jeder im üblichen Sinne »kalte« Körper, sogar jeder Eisblock, enthält immer noch Wärme. Um einen Körper absolut kalt zu machen, so daß er keine Spur Wärme mehr enthielte, müßte ich ihn bis auf -273 Grad, den sogenannten absoluten Nullpunkt, abkühlen, eine Temperatur, die bisher noch nicht erreicht worden ist, wenn man sich ihr auch schon sehr bedeutend genähert hat. Die Wärme beginnt also nicht erst bei der Temperatur von 0 Grad, sondern schon bei -273 Grad, und 1 Liter Wasser von 0 Grad enthält demnach immer noch 273 Kalorien, 1 Liter Wasser von Stubenlufttemperatur oder Meerwasser mit 10 Grad Temperatur sogar noch 283 Kalorien. 30 Liter Wasser von 10 Grad Celsius enthalten demnach eine Wärmemenge von 8490 Kalorien, das heißt mehr Wärme, als durch die Verbrennung von 1 Kilogramm bester Steinkohle gewonnen wird und ausreichend, um eine Dampfmaschine von 1 Pferdestärke etwa anderthalb Stunden lang in Betrieb zu halten. Wenn also schon 30 Liter Wasser eine so ansehnliche Wärmemenge enthalten, so können wir uns klarmachen, welche unendlich großen Wärmemengen in den Wassermassen der Meere vorhanden sein müssen, millionenmal mehr Wärme, als uns alle Steinkohlenlager der Erde liefern könnten. In Luft und Wasser, überall um uns herum ist Wärme in unerschöpflicher Menge vorhanden, aber – und das ist das Bedauerliche an der Sache – es ist nur Wärme niedriger Temperatur, die in dieser Form weder zum Betrieb von Maschinen noch für sonstige technische Zwecke nutzbar ist, weil diese immer Wärme hoher Temperatur verlangen.

Damit ist das Problem des Perpetuum mobile zweiter Art klar umschrieben. Es besteht in der Aufgabe, einen Apparat zu konstruieren, der imstande ist, Wärme niedriger Temperatur in Wärme hoher Temperatur umzuwandeln und damit in technisch nutzbare Form zu bringen. Das Perpetuum mobile zweiter Art hält sich also von dem logischen Widerspruch seines Vorgängers, durch den Arbeit aus nichts gewonnen werden sollte, vollkommen frei. Es stellt sich vollkommen auf den Boden der Äquivalenz von Wärme und Arbeit, verlangt für jedes Quantum Arbeit, die es leisten soll, das entsprechende Äquivalent Wärme, nur daß es diese nicht aus der Verbrennung von Heizstoffen, sondern aus der uns überall umgebenden Wärme niedriger Temperatur entnimmt. Mancher Leser wird hier an die vor einiger Zeit unternommenen und in der Presse vielbesprochenen Versuche französischer Forscher erinnert werden, die ebenfalls die Wärme der tropischen Meere für technische Zwecke nutzbar machen wollen. Es sei aber ausdrücklich betont, daß jene Versuche mit unserem Problem nichts zu tun haben. Denn jene Versuche laufen darauf hinaus, die Temperaturunterschiede zwischen den heißeren Wasserschichten an der Oberfläche und den tiefer gelegenen kühleren Schichten auszunutzen, also die Wärme in der normalen Weise durch ein vorhandenes Temperaturgefälle nutzbar zu machen. Diese Versuche also halten sich, so neu und eigenartig sie auch sein mögen, doch durchaus in den Bahnen der normalen Wärmewirkung.

Was sagt nun die Wissenschaft, die das alte Perpetuum mobile gerichtet und zu Grabe getragen hat, zu dem Perpetuum mobile zweiter Art? Nun, die Wissenschaft verhält sich dieser Idee gegenüber erheblich vorsichtiger. Sie bestreitet zwar auch die Möglichkeit eines Perpetuum mobile zweiter Art, aber nur deswegen, weil erfahrungsgemäß die Wärme nicht von einem niederen auf ein höheres Temperaturniveau übergeht, und diese Auffassung wird als der zweite Hauptsatz der Wärmetheorie formuliert. Also eine logische Unmöglichkeit des Perpetuum mobile zweiter Art kann auch die Wissenschaft nicht behaupten, nur auf Grund der Erfahrung hält sie es für ausgeschlossen. Aber unsere Erfahrungen sind keine so unerschütterlichen Wahrheiten wie die logischen Axiome, und daher hat es der offizielle Standpunkt der Wissenschaft zu diesem Problem nicht verhindern können, daß zahlreiche Naturforscher, Physiker und Technologen, ihren eigenen abweichenden Standpunkt vertreten und die Lösung jenes Problems in irgend welchen Formen für möglich erklären. Sie können sich dabei auf gute Gründe berufen, vor allem auf die Tatsache, daß ganz analoge Vorgänge, wie sie bei der Wärme in einem Perpetuum mobile zweiter Art stattfinden müßten und wie sie nach der Theorie unmöglich sein sollen, bei anderen Energiearten sehr leicht möglich sind und dauernd stattfinden. So ist es für den Elektrotechniker ein leichtes, einen elektrischen Strom niedriger Spannung, etwa von 100 Volt, auf einen solchen von viel höherer Spannung, 1000 oder 10 000 oder noch viel mehr Volt, zu bringen, und das Werkzeug, mit dem das bewirkt wird, ist der Transformator. Was aber beim elektrischen Strom die Spannung ist, das ist bei der Wärme die Temperatur, nämlich die Zustandsweise niedriger oder höherer Intensität. Es brauchte nur nach dem Vorbild der Elektrotechnik ein Wärmetransformator erfunden zu werden, und das Problem des Perpetuum mobile zweiter Art wäre in aller nur wünschenswerten Weise gelöst.

Auch sonst gibt es Erscheinungen, die dem offiziellen Standpunkt der Wissenschaft zu diesem Problem zu widersprechen scheinen. Es sei darauf hingewiesen, daß ein angesehener Physiker, Professor Auerbach in Jena, die überaus interessante Hypothese vertritt, daß jeder Lebensorganismus ein Perpetuum mobile zweiter Art darstelle und darin die bislang unerforschte und rätselhafte Eigenart der Lebenserscheinungen bestehe, ein schöner und tiefer Gedanke, der zum mindesten beweist, daß auch der auf der Höhe der Wissenschaft stehende Forscher gute Gründe dafür beibringen kann, daß auch naturgesetzlich ein solches Perpetuum mobile nicht unmöglich ist. Auf alle Fälle darf gesagt werden, daß die Wissenschaft mit solcher apodiktischen Sicherheit, mit der sie das Perpetuum mobile früherer Erfinderphantasie als unmöglich erwiesen hat, die Möglichkeit des Perpetuum mobile zweiter Art nicht zu erschüttern vermag. Also unseren Erfindern und Technikern, die an dem Perpetuum mobile vergangener Zeiten eine so böse Enttäuschung erlebt haben, winkt mit dem Perpetuum mobile zweiter Art eine neue Aufgabe, die – vielleicht – das Kopfzerbrechen eher lohnt.

Postskriptum

Permobilisten von heute – Lösungsversuche – Finanziers – Ein Beinah-Perpetuum mobile

Das Erscheinen des vorstehenden Aufsatzes in einer weitverbreiteten Zeitschrift hatte zur Folge, daß mir im Laufe der darauf folgenden Wochen nahezu hundert Projekte unterbreitet wurden von Leuten, die alle das Perpetuum mobile zweiter Art bereits fix und fertig zustande gebracht haben wollten. Mechaniker, Werkmeister, Lehrer, zwei Lokomotivführer, mehrere Uhrmacher und – ein Schneider waren unter diesen Permobilisten vertreten, aber auch eine ganze Reihe von Leuten, die sich als Ingenieure bezeichneten und auch ein Diplom-Ingenieur, seltsamer Weise auch ein Professor der Theologie einer ausländischen Universität (wenigstens nach seiner Angabe). Kennzeichnend für die Einstellung fast aller dieser »Permobilisten« war das Schreiben eines von ihnen. Er habe, so teilte dieser mit, sich Jahre hindurch mit dem Perpetuum mobile erster Art beschäftigt und schließlich das Vergebliche dieser Idee vollkommen erkannt. Wie ein Licht sei aber durch meinen Aufsatz die Idee des Perpetuum mobile zweiter Art in ihm aufgegangen, und da die Möglichkeit eines solchen ja von der Wissenschaft nicht mit ebensolcher Sicherheit und Entschiedenheit bestritten werde, so habe er sich an die Lösung dieses Problems gemacht, und nach zweiwöchentlicher angestrengter Tätigkeit sei es ihm gelungen, eine solche Konstruktion herzustellen. Sein Gedankengang knüpfte an die Verflüssigung der Gase an. Bei dieser wird den Gasen Wärme entzogen, und es sei theoretisch möglich, durch Verwertung dieser freiwerdenden Wärme die Gase mit einem Energieaufwand gleich Null zu verflüssigen und dann die Ausdehnungskraft der verflüssigten Gase als neue Kraft- bzw. Energiequelle zu verwenden; das sei ihm gelungen, und damit sei der Gedanke des Perpetuum mobile zweiter Art, die Wärme der Umgebung nutzbar zu machen, verwirklicht; seine Vorrichtung funktioniere in diesem Sinne völlig zur Zufriedenheit.

Diese Idee, also die Verflüssigung der Gase und die Ausnutzung der hierbei auftretenden Prozesse lag noch sehr vielen anderen der mitgeteilten Projekte zugrunde. Allen diesen Erfindern konnte ich nur antworten, daß es sich bei ihrer Idee nicht um das Perpetuum mobile zweiter Art, sondern ein solches der guten alten Art handele, denn die Gase geben bei diesem Verfahren keine Spur Wärme oder sonstiger Energie mehr ab, als man ihnen zuvor zugeführt hat, und die Idee, daß sich die Verflüssigung eines Gases »mit einem Kraftaufwand gleich Null« oder auch nur mit einer geringeren Energie bewirken ließe, als das Gas hinterher abgibt, ist eine ebenso frommer wie falscher Glaube der Permobilisten erster Art. Ein Maurermeister glaubte, daß die Idee des Perpetuum mobile zweiter Art, die Wärme des kalten Wassers auf höhere Temperatur zu bringen, verwirklicht werde, wenn man Kalk in Wasser löscht. Hierbei wird nun allerdings Wärme frei, aber diese wird nicht dem Wasser, in welches der Kalk getan wird, entzogen, sondern entsteht ganz nach Art der Verbrennung der Kohle durch die hierbei auftretende chemische Verbindung der Stoffe. Wenn genug Kalk für solche Zwecke zur Verfügung stände, könnte man vielleicht daran denken, die so entstehende Wärme nutzbar zu machen, aber ein Perpetuum mobile zweiter Art wäre das ebensowenig wie die Verbrennung der Kohle. So leicht ist das Perpetuum mobile zweiter Art, wenn man es vielleicht auch nicht mit absoluter Sicherheit für unmöglich erklären kann, denn doch nicht herzustellen, und es ist anzunehmen, daß diese Konstruktion doch wohl noch recht lange Problem bleiben dürfte.

Sehr ernst war es wohl einem meiner damaligen Korrespondenten, der mir ebenfalls die Idee eines Perpetuum mobile unterbreitete und mir zur Verwertung derselben die Gründung einer Gesellschaft vorschlug, für die er ein sehr ansehnliches Kapital zur Verfügung stellen wollte. Ich schrieb ihm, daß er sein Geld auf andere Weise ebensogut los werden könne. Ein anderer war ebenfalls bereit, seine Idee für eine Verwertungsgemeinschaft zur Verfügung zu stellen, verlangte aber das Betriebskapital, in der allerdings nicht gerade schwindelerregenden Höhe von 750 Mark von mir, das sich nach einer beigefügten Rentabilitätsberechnung binnen kurzem und mit absoluter Gewißheit in einem Millionengewinn verwandeln sollte. Ich habe auch diese glänzenden Gewinnchancen leichtsinnigerweise ausgeschlagen, denn ich hatte den schnöden Verdacht, daß es diesem Erfinder mehr um das begehrte Aktienkapital als um die Förderung der menschlichen Kultur zu tun sei.

Abb. 58 Abb. 59
Ein Beinah-Perpetuum mobile

Einer der übersandten Entwürfe, der sich durch einen sehr hübschen Gedanken auszeichnet, sei hier wiedergegeben. Er besteht, wie es Abbildung 58/59 veranschaulicht, aus einem Wasserbehälter, in den ein Schaufelrad einmontiert ist, und zwar derart, daß es sich zur Hälfte in dem Behälter, zur anderen Hälfte außerhalb desselben befindet, zu welchem Zwecke in der einen Wand des Behälters eine entsprechende Öffnung gelassen ist. Die Schaufeln des Rades sind abgeschlossene Hohlräume, und der außerhalb des Behälters befindliche Teil des Rades wird durch eine Haube wasserdicht, jedoch so, daß er die Drehung des Rades nicht behindert, abgeschlossen. Abbildung 59 zeigt den Apparat in Seitenansicht und mit abgenommener Haube. Wird nun der Behälter mit Wasser gefüllt, so erfolgt nach Meinung des Urhebers dieser Konstruktion folgendes: die Hohlschaufeln b, b … erhalten, da spezifisch leichter als Wasser, durch das Wasser im Behälter Auftrieb, das Rad dreht sich von rechts nach links. Gelangt hierbei eine Hohlschaufel mit ihrem Punkte d nach dem Punkt e des Behälters, so ist der Raum zwischen ihr und der vorhergehenden Hohlschaufel mit Wasser gefüllt, das von dem Wasser im Behälter getrennt ist, durch die Haube am Auslaufen verhindert wird und durch seine Schwerkraft nach unten drückt und so dem Rad einen abermaligen Impuls im Sinne der vorhandenen Rotation erteilt. So wirkt das Wasser im Behälter als auftreibende Kraft, innerhalb der Haube jedoch durch seine Schwerkraft. Auf beiden Seiten des Rades findet ein Antrieb in derselben Drehrichtung statt, also muß das Rad dauernd in Drehbewegung bleiben. Das Perpetuum mobile ist fertig!

Der Gedanke, Schaufel- oder Trommelräder mit teils leichteren, teils schweren Segmenten zu verwenden, ist nun allerdings eine uralte und immer vergeblich gewesene Idee der Permobilisten. Der geistige Vater der hier vorgeführten Konstruktion hat jedoch eine neue Idee hinzugefügt, und das ist die Haube. Durch diese wird tatsächlich, wie der Konstrukteur es sich gedacht hat, das Wasser in doppelter Weise als Kraftquelle benutzt. Die Wassermenge, die sich zwischen je zwei Hohlschaufeln befindet, wirkt innerhalb des Behälters nach oben, innerhalb des Haubenraumes nach unten. Die Idee ist sehr originell, und selbst der technisch Geschulte ist einen Augenblick lang verblüfft und sucht verzweifelt nach dem Fehler, den die Konstruktion doch haben muß. Der Urheber dieser hübschen Konstruktion ist selbst Techniker und war von der Richtigkeit seines Gedankens überzeugt. Aber dann findet sich gottlob auch hier der Denkfehler, wodurch der Umsturz der Naturgesetze verhütet wird. Er sitzt an dem Punkt f des Behälters, also an der Stelle, an der die nach unten strebenden Schaufeln wieder in den Behälter eintreten sollen. Hat eine Hohlschaufel mit ihrem Kreisbogen diesen Punkt gerade passiert, so will nun auch die zwischen ihr und der folgenden Hohlschaufel befindliche Wassermenge in den Behälter eintreten. Dem Eintritt dieser Wassermenge aber wird durch das Wasser in dem Behälter ein bestimmter Widerstand entgegengesetzt. Denn das Schaufelwasser muß das Wasser im Behälter, um in diesen eindringen zu können, verdrängen, also die Wassersäule überhalb f um eine gewisse Strecke heben, und der Widerstand, der hierbei zu überwinden, oder die Arbeit, die hierbei zu leisten ist, ist gerade so groß wie der Antrieb, den das Rad bis dahin erhalten hat. An dem kritischen Punkt f also kommt das Rad zum Stillstand, zeigt es sich, daß auch diese Konstruktion kein Perpetuum mobile, weder ein solches erster noch zweiter Art, sondern wie so viele andere Konstruktionen dieser Art nur eine Beinahe-Perpetuum mobile ist. Aber der Gedanke dieser Konstruktion ist neu und gibt dieser doch einen gewissen Reiz.

Ein Leser meines Aufsatzes endlich schrieb mir: Er begreife überhaupt nicht, wie man ein Perpetuum mobile für unmöglich halten könne; er habe ein solches fertiggestellt, das nach Abnehmen einer Bremse sofort zu laufen anfange, und er betreibe damit schon seit Jahren seine Nähmaschine. – Die Antwort: Es dürfte wohl gerade umgekehrt sein, Sie betreiben mit Ihrer Nähmaschine Ihr Perpetuum mobile!

5. Heureka

Ein merkwürdiger Vorfall – Die goldene Krone und die Wasserprobe – Die Entdeckung des archimedischen Prinzips – Vom spezifischen Gewicht – Metall, das schwimmt, und Holz, das sinkt – Der Schwimmer im Alkohol – Rätsel des Wassers – Vom Gewicht der Erde – Ein Stoff vom spezifischen Gewicht 53 000?

Wenn ein älterer Herr splitterfasernackt, dafür aber pudelnaß, durch die Straßen rennt, aufgeregt mit Händen und Füßen gestikuliert und in einem fort »Heureka!« – d. h. »ich hab's gefunden!« – ruft, so ist das ein Vorgang, der selbst für den blasierten Großstädter noch immer den Reiz der Neuheit haben dürfte. Das war denn auch der Fall, als sich vor rund 2200 Jahren ein genau solcher wie der beschriebene Vorfall in den Straßen von Syrakus, der damaligen Hauptstadt des sizilianischen Reiches, zutrug. Der ältere Herr, der in solcher Weise die Aufmerksamkeit seiner Mitbürger und vor allem das Hallo der sizilianischen Straßenjugend auf sich lenkte, aber war der große Gelehrte Archimedes, der bedeutendste und berühmteste Mathematiker und Physiker, sozusagen der Gauß und Einstein des Altertums in einer Person, und daß dieser hochgelehrte und berühmte Mann, der Stolz und die Zierde seiner Vaterstadt, so total aus dem Häuschen geraten war, das hatte seinen Grund in folgendem:

Damals herrschte in Syrakus der König Hiero, der eines Tages das Bedürfnis fühlte, sich für sein königliches Haupt eine neue Krone bauen zu lassen. Also ließ er aus seiner Schatzkammer wohlabgewogen 16 Pfund Gold und 4 Pfund Silber entnehmen und beauftragte seinen Hofgoldschmiedemeister, diese Metalle zusammenzuschmelzen und ihm aus der Legierung die gewünschte Kopfbekleidung anzufertigen. Nach geraumer Zeit lieferte der Goldschmied die fertiggestellte Krone ab. Die Nachprüfung ergab, daß sie genau 20 Pfund, also geradesoviel wie die gelieferten Metalle, wog. Sei es nun aber, daß König Hiero von Natur aus ein argwöhnischer Herr war und nur ein sehr bedingtes Vertrauen in die Ehrlichkeit seiner Untertanen im allgemeinen und der Hoflieferanten im besonderen setzte, sei es, daß ihm trotz des zutreffenden Gewichts etwas an der Krone nicht zu stimmen schien, kurz, er hegte den Verdacht, daß der Goldschmied eine kleine Schiebung bei der Verwendung der ihm gelieferten Metalle vorgenommen und ein gut Teil weniger Gold, als ihm geliefert worden war, in den Schmelztiegel getan und das fehlende Goldquantum durch das viel billigere Silber ersetzt habe. Aber wie die Wahrheit ermitteln? Der Hofjuwelier schwur hoch und teuer, daß er der ehrlichste aller Goldschmiede in der Welt und Umgegend sei und die Majestät in noch nie dagewesen reeller Weise bedient, auch kein Quentchen Gold weniger, als ihm geliefert worden sei, verwandt habe, und da ihm das Gegenteil nicht zu beweisen war, so schien es, daß König Hiero seinen Verdacht in der zottigen Männerbrust begraben müßte. Aber da erinnerte er sich des berühmten Professors Archimedes, dessen Scharfsinn sich in ähnlichen kniffligen Fällen schon oft glänzend bewährt hatte, und beauftragte ihn, die gelieferte Krone zu untersuchen und festzustellen, ob sie auch wirklich die gesamten 16 Pfund Gold enthalte.

Das war zunächst aber auch für den gelehrten Archimedes eine sehr schwierige Aufgabe; er konnte ebensowenig wie der König selbst dem Kronenmetall ansehen, wieviel Gold und Silber es enthielt, und physikalische oder chemische Methoden, die heute eine solche Untersuchung leicht möglich machen, waren damals noch nicht bekannt. Tagelang probierte und studierte er an der königlichen Krone herum, ohne zu der gewünschten Feststellung gelangen zu können, und war auch noch in Gedanken mit dem Problem beschäftigt, als er eines Tages ein Körper und Geist erfrischendes Bad nehmen wollte. Die Badewanne, die diesem Zweck dienen sollte, war bis an den Rand gefüllt, und als der Gelehrte einstieg und seinen Körper im Wasser ausstreckte, floß eine Menge Wasser über den Rand. Diese Erscheinung entzündete im Gehirn des Forschers einen Gedankenblitz. Er argumentierte: Es fließt so viel Wasser aus der Wanne, als der Rauminhalt meines Körpers beträgt; dann muß ein anderer Körper, der zwar ebensoviel wiegt wie ich, aber weniger Raum einnimmt, trotz des gleichen Gewichtes entsprechend weniger Wasser verdrängen. Ein Goldklumpen etwa von meinem Gewicht würde viel weniger Wasser zum Ausfließen bringen, und bei einem Klumpen Silber wäre es noch anders. Dann müßte sich also, wenn in ein mit Wasser gefülltes Gefäß Gold oder Silber hineingelegt wird, aus der Menge des verdrängten Wassers das Gewicht des Metalles bestimmen lassen, und damit wäre ja die Methode gefunden, um den Gehalt der königlichen Krone an Gold und Silber zu ermitteln. Als Archimedes bis zu diesem Punkt seiner Überlegung gelangt war, sah er die Lösung des Problems, das ihm soviel Kopfzerbrechen verursacht hatte, vor sich, und das brachte ihn so in Aufregung, daß er mit einem Satz aus der Badewanne sprang, auf die Straße lief und dort den beschriebenen groben Unfug verübte.

Dann aber machte er sich schleunigst daran, seine Entdeckung praktisch auszuprobieren. Er ermittelte, wieviel Wasser ein Pfund Gold, wieviel ein Pfund Silber und ferner eine Legierung von 16 Pfund Gold und 4 Pfund Silber verdrängt. Dann legte er die königliche Krone in Wasser und stellte fest, daß diese ein ganz bestimmtes Quantum mehr Wasser verdrängte, als es der Fall hätte sein dürfen, wenn sie wirklich aus einer solchen wie ausprobierten Legierung bestanden hätte. Aus der Differenz der in beiden Fällen verdrängten Wassermengen konnte er berechnen, daß die Krone rund 1½ Pfund weniger Gold enthielt, als jener Probelegierung entsprach, und dieses Fehlquantum durch Silber ersetzt worden war. Jetzt konnte der Goldschmied überführt werden. Was ihm für seine Mogelei blühte, ist nicht bekannt geworden; die Wissenschaft aber hätte Ursache, ihm dankbar zu sein, denn durch ihn wurde Archimedes zu dem Studium der Beziehungen zwischen Gewicht und Rauminhalt der Körper veranlaßt und dadurch zur Entdeckung eines hochwichtigen Naturgesetzes, des sogenannten hydrostatischen Gesetzes, das nach seinem Entdecker auch als das archimedische Prinzip bezeichnet wird, geführt. Die Entdeckung dieses Gesetzes eröffnete eine ganz neue Wissenschaft von größter Tragweite für unsere Naturerkenntnis.

Der Inhalt jenes Gesetzes besagt, daß ein Körper in Wasser um so viel an Gewicht verliert, als das Gewicht der von ihm verdrängten Wassermenge beträgt. Ein Klumpen Gold beispielsweise, der in Wasser gelegt wird, verliert in diesem den 19. Teil seines Gewichtes, was durch einen besonderen Wägeapparat, die sogenannte hydrostatische Waage, ermittelt werden kann. Das besagt aber zugleich, daß unser Goldklumpen 19mal (genauer 19,3mal) so schwer ist wie die verdrängte Wassermenge, bzw. daß ein Stück Gold 19mal soviel wiegt wie ein gleich großer Raum Wasser. Diese Beziehung zwischen Gewicht und Rauminhalt der Körper, die aus dem archimedischen Prinzip abgeleitet wird, ist es, die dieses Gesetz so wichtig und wertvoll macht. Sie wird als das spezifische Gewicht bezeichnet und drückt das Gewichtsverhältnis eines Stoffes zum Wasser aus. Weil unser Klumpen Gold 19mal so schwer ist wie ein gleich großer Raum Wasser, sagen wir, das spezifische Gewicht des Goldes beträgt 19. Wir können das noch anschaulicher ausführen. Als Einheit der Raummessung dient für praktische und technische Zwecke das Kubikdezimeter, d. h. ein Raumwürfel, dessen Höhe, Länge und Breite je 10 Zentimeter beträgt und den wir gemeinhin als Liter bezeichnen. Das Gewicht von 1 Liter Wasser nun wird als ein Kilogramm bezeichnet, und da Gold 19mal so schwer ist wie Wasser, so wiegt 1 Liter bzw. 1 Kubikdezimeter Gold 19 Kilogramm. In diesem Gewicht, das 1 Kubikdezimeter eines Stoffes aufweist, haben wir die anschaulichste Form des Begriffes vom spezifischen Gewicht vor uns. Das spezifische Gewicht ist also die Zahl, die angibt, wievielmal ein Körper oder Stoff schwerer ist als ein gleich großer Raum Wasser bzw. wieviel Kilogramm 1 Kubikdezimeter des Stoffes wiegt. In ähnlicher Weise wie beim Gold ist das spezifische Gewicht aller anderen irdischen Stoffe, sowohl der festen wie der flüssigen und gasförmigen, festgestellt worden, dann das spezifische Gewicht ist eine der wichtigsten Eigenschaften zur Untersuchung und Kennzeichnung der Stoffe, und eine große Anzahl von Naturerscheinungen beruht auf dieser Beziehung. Bei allen diesen Bestimmungen ist das spezifische Gewicht des Wassers = 1 gesetzt, denn das Gewicht eines Kubikdezimeters bzw. eines Liter Wasser wird ja als 1 Kilogramm bezeichnet. Das Gewicht des Wassers ist also die Einheit des spezifischen Gewichts für alle anderen Stoffe.

Von unseren irdischen Stoffen haben zunächst die Metalle das höchste spezifische Gewicht. Das Gold gehört mit dem spezifischen Gewicht von 19,3 mit zu den schwersten Stoffen unseres Erdballes überhaupt und wird nach dieser Hinsicht nur noch übertroffen von dem Metall Iridium (bekannt durch seine Verwendung für die Federspitzen der Füllfederhalter) mit 21,2, dem Platin mit 21,5 und dem Osmium mit 22,5 spezifischem Gewicht. Letzteres Metall, das heute für die Herstellung der Drähte unserer elektrischen Glühlampen eine große Rolle spielt, ist also der schwerste aller irdischen Stoffe. Von Laien wird oft das Blei für das schwerste Metall gehalten; die angeführten Zahlen zeigen, wie irrig diese Ansicht ist, denn das spezifische Gewicht des Bleis beträgt nur 11,4, also nur etwa halbmal soviel wie das des Osmiums. Das spezifische Gewicht des Quecksilbers, des einzigen bei gewöhnlicher Temperatur flüssigen Metalles, beträgt 13,5 (also ebenfalls mehr als das des Bleis), das des Silbers 10,6, des Nickels 8,9, des Zinns 7,3, des Zinks 7,1, während das spezifische Gewicht des Eisens, des wichtigsten und meistverarbeiteten unserer Metalle, je nach seiner Beschaffenheit als Gußeisen, reines Schmiedeeisen oder Stahl, zwischen 7,2 und 8 schwankt. Die Metalle mit einem spezifischen Gewicht von mehr als 5 bezeichnet man als Schwermetalle, die anderen als Leichtmetalle, darunter als das bekannteste und wichtigste das Aluminium, dessen spezifisches Gewicht nur 2,67 beträgt, und das dieses geringen Gewichts wegen für viele technische Zwecke ein unentbehrlicher Werkstoff geworden ist, besonders für den Bau von Luftschiffen und Flugzeugen, für die jene Eigenschaft des Metalls im Verein mit seiner Härte und Festigkeit geradezu Voraussetzung ist. Noch leichter ist das Metall Beryllium, dessen spezifisches Gewicht nur 2 beträgt. Von diesem Metall, das übrigens auch noch durch verschiedene andere technisch wertvolle Eigenschaften ausgezeichnet ist, das aber bisher nur sehr selten vorkam, sind in letzter Zeit bedeutende Fundstätten in Amerika entdeckt worden, die es vielleicht zur Folge haben können, daß dieses Metall in Zukunft in starken Wettbewerb mit dem Aluminium treten wird; schon heute wird seine Verwendung für Luftschiff- und Flugzeugbau geplant. Geringeres spezifisches Gewicht als Aluminium haben auch die Metalle Strontium mit 2,5, Magnesium mit 1,75 und Kalzium mit 1,56. Endlich aber gibt es auch noch einige Metalle, die sogar noch leichter als Wasser sind, so das Natrium mit einem spezifischen Gewicht von 0,97, das verwandte Metall Kalium mit 0,86 und endlich das silberweiße und viel für medizinische, aber nur wenig für technische Zwecke verwandte Metall Lithium mit einem spezifischen Gewicht von nur 0,59. Diese Metalle schwimmen also auf dem Wasser. Leichter als Wasser sind auch die heimischen Holzarten, deren spezifisches Gewicht zwischen 0,5 und 0,9 schwankt; am leichtesten aber sind gewisse exotische Korkhölzer mit einem solchen von nur 0,25. Wie es einige Metalle gibt, die auf dem Wasser schwimmen, so gibt es andererseits auch einige Holzarten von so hohem spezifischen Gewicht, daß sie im Wasser untergehen, so das außerordentlich schwere und harte Ebenholz, dessen spezifisches Gewicht etwa 1,2 beträgt, des weiteren die dem Ebenholz verwandten Arten von Eisenholz und endlich das Pockholz aus dem tropischen Amerika, das mit dem spezifischen Gewicht von 1,55 die schwerste und zugleich auch härteste aller Holzarten ist.

Das spezifische Gewicht des Menschen ist etwas größer als das des Wassers, weswegen der menschliche Körper im Wasser untergeht. Da der Unterschied jedoch nur ein sehr geringer ist, kann sich der Mensch durch Schwimmen auf dem Wasser halten. Nicht alle Flüssigkeiten verhalten sich jedoch in dieser Weise. In Alkohol etwa, dessen spezifisches Gewicht nur 0,8 beträgt, könnte sich selbst der beste Schwimmer nicht über Wasser halten, wogegen in dem flüssigen Quecksilber jeder Mensch schwimmen könnte, ohne es gelernt zu haben; das Untergehen in dieser Flüssigkeit wäre sogar ganz unmöglich, selbst wenn er so schwer wie Blei wäre. Ein höchst eigenartiges Verhalten hinsichtlich des spezifischen Gewichts weist übrigens das Wasser selbst auf. Dieses hat seine größte Dichte und daher sein höchstes spezifisches Gewicht, nämlich 1, nur bei der Temperatur von 4 Grad Celsius. Während nun alle anderen Körper beim Erkalten sich zusammenziehen und dadurch ein erhöhtes spezifisches Gewicht erlangen, ist es beim Wasser als einzigem Körper umgekehrt. Geht seine Temperatur unter 4 Grad Celsius herab, so dehnt es sich aus, wird also spezifisch leichter. So kommt es, daß Eis leichter ist als das flüssige Wasser und auf diesem schwimmt, während alle anderen Stoffe im festen Zustande spezifisch schwerer als im flüssigen sind. Dieses merkwürdige Verhalten des Wassers im flüssigen und festen Zustande ist für das Naturreich von größter Bedeutung. Denn dadurch, daß im Winter sich die Oberfläche unserer Seen und Flüsse mit Eis bedeckt, sinkt zugleich das spezifisch schwerere Wasser von höherer Temperatur nach unten und hält so unter dem Eise eine Temperatur von 4 Grad aufrecht, bei der die Wassertiere weiterexistieren können. Wäre es anders, so würden die Gewässer vom Grunde aus nach oben zufrieren, was dann gleichbedeutend mit der Vernichtung alles Lebens im Wasser wäre. Dieses Verhalten des Wassers, durch das die Natur das Leben im Wasser selbst zu schützen scheint, ist oft als ein Beweis eines besonderen in der Natur herrschenden Zweckmäßigkeitsstrebens ausgelegt worden. Unter bestimmten Verhältnissen kann es übrigens auch zur Bildung von Grund- oder Bodeneis kommen, das in den arktischen Regionen keine Seltenheit ist.

Das niedrigste spezifische Gewicht unter allen Stoffen haben die Gase. So beträgt das spezifische Gewicht der Luft nur etwas mehr als ¹/ ₁₀₉₀, d. h. erst etwa 1000 Liter oder 1 Kubikmeter Luft wiegen 1 Kilogramm; noch viel leichter ist der Wasserstoff, dessen spezifisches Gewicht ungefähr 14mal kleiner als das der Luft ist, so daß erst etwa 14 Kubikmeter dieses Gases 1 Kilogramm wiegen. Das durchschnittliche spezifische Gewicht endlich unseres ganzen Erdballes ist mit etwa 5 ermittelt worden. Das ist ein verhältnismäßig sehr hohes spezifisches Gewicht, wenn wir uns vergegenwärtigen, daß die weitaus meisten Stoffe, die wir an der Oberfläche der Erde antreffen, von viel geringerem spezifischen Gewicht sind, wie das Wasser, das allein zwei Drittel der Erdoberfläche bedeckt und nur das spezifische Gewicht 1 hat, ebenso auch die Gesteine, aus denen unsere Gebirge bestehen und von denen selbst die schwersten, wie etwa der Granit, nicht über das spezifische Gewicht 3 hinausgehen, ebenso auch die ungeheuren Kohlenlager, deren Substanz nur etwa das spezifische Gewicht 2 hat. Wenn also der Erdball trotzdem durchschnittlich ein so bedeutend höheres spezifisches Gewicht als die weitaus meisten an seiner Oberfläche vorkommenden Stoffe aufweist, so ist das nur dadurch zu erklären, daß in seinen tieferen Schichten gewaltige Mengen der spezifisch schwereren Stoffe, also der Metalle, vorkommen müssen. Das nimmt man daher auch an, und danach müssen sich im tiefen Innern unseres Erdkörpers ganz ungeheure Metallmassen befinden, von denen eben nur das wenigste an die Oberfläche gelangt ist, das meiste uns aber wohl für immer vorenthalten wird. Besonders die schweren Edelmetalle, Gold und Platin, müssen in Tiefen, die allerdings um Tausende von Kilometern unterhalb der Erdoberfläche liegen, in ungeheuren Mengen vorhanden sein, von denen das, was wir hier auf Erden an diesen Metallen fördern, nur ein verschwindend kleiner Prozentsatz ist. Das gilt in besonderem Maße von dem Gold, das, wie nicht jeder annehmen wird, nächst Eisen und Kupfer das verbreitetste aller Metalle in unserer Erde ist, sich aber infolge seines hohen spezifischen Gewichtes leider in unerreichbare Tiefen zurückgezogen hat.

Eine gewaltige Überraschung erlebte die Forschung über das spezifische Gewicht der Stoffe im Weltraum vor einigen Jahren. Auf unserer Erde ist das höchste bekannte spezifische Gewicht 22,5, wie es das Osmium aufzuweisen hat, alle übrigen Stoffe halten sich unterhalb dieser Gewichtsgrenze. Die Stoffe, aus denen die anderen Weltkörper zusammengesetzt sind, sind, wie die spektralanalytische Untersuchung ergeben hat, dieselben wie die unseres Erdballes. Daher hatte man bis vor kurzem angenommen, daß die spezifischen Gewichte unserer Erdenstoffe allgemein diejenigen der Stoffe im Weltenraum überhaupt seien. Diese Auffassung ist jedoch jetzt aufs schwerste erschüttert worden. Aus bestimmten Berechnungen und Folgerungen der Relativitätstheorie über die Ablenkung des Lichtes in der Nähe großer Massen, wie sie die Fixsterne darstellen, hat sich nämlich ergeben, daß ein bestimmter Fixstern, nämlich der Begleiter des Sirius, des hellsten und schönsten Gestirns am Fixsternhimmel, das unfaßbar hohe spezifische Gewicht von 53 000 aufzuweisen hat. Das bedeutet also, wenn jene Berechnung der Wirklichkeit entspricht, daß ein einziges Kubikdezimeter der Masse jenes Weltkörpers das Gewicht von 53 000 Kilogramm hätte. Ein einziges Literglas, mit jener Substanz gefüllt, würde 1000 Zentner wiegen und zu seiner Fortbewegung der Kraft von zwanzig schweren Pferden bedürfen. Man hat diese ungeheuerliche Abweichung jenes Weltkörpers von unseren gewohnten Begriffen über das spezifische Gewicht der Substanzen mit der Annahme zu erklären versucht, daß dort die Materie anders konstituiert sein müsse als auf Erden und dort die Atome und ihre Bestandteile in allen Stoffen viel enger zusammengedrängt sein müssen, als es in den irdischen Substanzen der Fall ist. Aber diese Auffassung ist doch so wenig befriedigend, daß man jenes absonderliche Rechenergebnis lieber mit einem Beobachtungsfehler zu erklären geneigt ist. Da aber andererseits ein solcher Fehler sich nicht hat nachweisen lassen, so neigen manche Forscher sogar der Ansicht zu, daß jenes rechnerische Resultat eine Erschütterung der Relativitätstheorie bedeutet und sich diese Theorie zum mindesten in jenen Punkten, die zu solchen wie den genannten Folgerungen führen, nicht aufrechterhalten läßt.

»Heureka – ich hab's gefunden!« rief vor über 2000 Jahren Archimedes, als er das Gesetz zwischen Gewicht und Raum der Stoffe entdeckt und damit die Lösung eines Problems des Naturreiches gefunden hatte; »heureka!« wird man einstmals wieder rufen können, wenn es gelungen ist, dieses neueste Rätsel zwischen Gewicht und Raum der Stoffe zu ergründen, das gegenwärtig die Forschung über die Konstitution der Materie und das spezifische Gewicht der Stoffe in ihrem Banne hält.

Postskriptum

Eine astronomische Entdeckung – Erschütterung der Relativitätstheorie?

In der Zwischenzeit ist die Frage, die sich an die beobachtete Lichtablenkung und Spektralverschiebung bei dem Begleiter des Sirius knüpft und die von der Relativitätstheorie mit der Annahme eines spezifischen Gewichtes dieses Weltkörpers von 53 000 beantwortet worden ist, in ein neues Stadium getreten. Astronomen und Astrophysiker hatten einer solchen Annahme, die mit allen sonstigen Erfahrungen innerhalb der beobachtbaren Welt in krassestem Widerspruch steht, von jeher Zweifel entgegengebracht. Schon vor einigen Jahren hatte ein deutscher Astronom, Anding in Gotha, darauf hingewiesen, daß sich jene Erscheinungen auch durch die Annahme erklären lassen, daß der Begleiter des Sirius selbst wieder einen Begleiter habe. Die beiden Weltkörper würden dann ein Doppelstern-System bilden und müßten durch ihre Gravitation und durch die Bewegung um den gemeinsamen Schwerpunkt einen ebensolchen wie den beobachteten Effekt der Lichtablenkung und Spektralverschiebung bewirken. Diese Hypothese ist damals seitens der Relativitätstheoretiker unbeachtet geblieben, vor allem wohl deswegen, weil jener Weltkörper lediglich hypothetischer Natur und noch niemals gesichtet worden war. Jetzt aber hat die Hypothese Anding eine überraschende Bestätigung gefunden. Von den Astronomen der Sternwarte Johannesburg in Südafrika ist, wie die Royal Astronomical Society in London kürzlich offiziell mitteilte, jener vermutete Begleiter des Siriusbegleiters tatsächlich entdeckt und als ein Stern 12. Größe festgestellt worden.

Sollte die Beobachtung der Johannesburger Sternwarte einwandfrei bestätigt werden, so wäre damit jene Annahme eines spezifischen Gewichtes von 53 000 ad absurdum geführt worden. Diese Entdeckung braucht noch keinesfalls eine Erschütterung der Relativitätstheorie zu bedeuten; eine Theorie braucht noch nicht falsch zu sein, weil sich herausstellt, daß gewisse Erscheinungen, für die sie eine Erklärung gegeben hat, sich auch auf andere und bessere Weise erklären lassen. Darüber hinaus aber würde jene Entdeckung doch wohl bedeuten, daß die Relativitätstheorie in ihrer gegenwärtigen Form selbst noch viel mehr Hypothese als gesicherte Theorie ist, daß sie in wesentlichen Punkten der Revision bedarf und zu ihren Voraussetzungen und Folgerungen noch keinesfalls mit apodiktischer Gewißheit »Heureka!« sagen kann.

VIII
Probleme der Erfindung

1. Die Fahrt in den Weltraum

Zu den Sternen – Das Problem – Die Gravitation und ihre Macht – Im gravitationsfreien Weltraum – Jules Vernes Mondrakete – Der Raketenmotor und das Raketenflugzeug – Das Raketenautomobil – Verfehlte Hoffnungen – Über die Äquivalenz von Wärme und Arbeit – Eine Folgerung – Kohle in der Tiefe – Ein Trugschluß – Tankstellen im Weltraum – Jetzt und einst – Ein Ausblick

Seit Jules Verne in dem bekanntesten seiner Romane den Einfall hatte, etliche Erdenbewohner eine Reise nach dem Monde unternehmen zu lassen, ist diese Idee nicht mehr zur Ruhe gekommen und die Frage, ob und auf welche Weise es dem Menschen jemals möglich sein wird, nach anderen Weltkörpern zu gelangen, ein viel und leidenschaftlich behandeltes Problem geworden. Aber man hat sich keinesfalls mit der platonischen Erörterung des Problems begnügt; man hat auch zahlreiche mehr oder weniger phantastische und mehr oder weniger wissenschaftlich durchdachte Projekte zur Verwirklichung jener Idee ausgearbeitet, hat in Zeichnungen, Berechnungen und Modellen »Weltraumschiffe« konstruiert, vermittels derer es gelingen soll, in den Weltraum vorzudringen und zunächst einmal unserem Erdtrabanten, unserem alten lieben Mond, dann aber auch sogar den Planeten, die ja immerhin noch einige hundertmal weiter als der Mond von unserer Erde entfernt sind, einen Besuch abzustatten. Insbesondere der Planet Mars, mit dem sich Forschung und Phantasie ja schon seit langem mit Vorliebe beschäftigen, weil man auf diesem Weltkörper Daseinsverhältnisse ähnlich denen unserer Erde und vielleicht sogar intelligente Lebewesen mit hoher Kultur annehmen zu können glaubt, spielt in den Projekten der Weltraumpioniere eine große Rolle als beliebtes Ziel des Ausflugs in die Sternenwelt. Heute bemühen sich zahlreiche Erfinder um die Lösung jenes grandiosen Problems, und sie versichern in Broschüren, Vorträgen und Aufsätzen der Tagespresse, daß man bereits unmittelbar vor der Verwirklichung jener Idee, die den höchsten und kühnsten Traum der Menschheit einschließt, stehe, daß das »Weltraumschiff« schon so gut wie betriebsfertig sei und es nur noch an dem nötigen Kapital fehle, um das Stadium der Theorie mit dem der Wirklichkeit zu vertauschen. Vereine und Zeitschriften sind bereits erstanden, die die Erreichung jenes Zieles auf ihre Fahnen geschrieben haben und mit viel Aufwand von Berechnungen und Beweisen darzutun suchen, daß die Menschheit, wenn sie nur wollte, bereits heute mit der Beherrschung des Weltraumes beginnen könnte.

So ist heute die Frage nach der Möglichkeit der Reise in den Weltraum mehr als jemals aktuell geworden, ist sie in gleicher Weise Gegenstand der ernsten wissenschaftlichen Betrachtung und Erörterung wie der ausschweifenden Phantasie geworden. Und eins ist auf alle Fälle wahr: die größte und gewaltigste technische Aufgabe, die der Menschheit jemals gestellt war, knüpft sich an jenes Problem, eine Aufgabe, der gegenüber alles, was bisher die technischen Wissenschaften erreicht haben, ein Kinderspiel ist, und die das kühnste Ziel einschließt, die dem ewig strebenden Menschengeiste jemals gestellt sein kann. Wahrlich Grund genug, um zu jenem Problem Stellung zu nehmen, und objektiv und ohne den himmelstürmenden Optimismus jener, die heute bereits die Zone bis zu den Planeten sozusagen als Vorort unseres Globus betrachten zu können vermeinen, zu erörtern, ob und wieweit dieser kühnste Menschheitstraum jemals Aussicht auf Verwirklichung hat.

Die Lösung unseres Problems ist gleichbedeutend mit dem Problem der Überwindung der Anziehungskraft der Erde. Unsere Mutter Erde hält vermöge ihrer anziehenden Gewalt, der Gravitation, jeden irdischen Körper ehern fest, gestattet ihm, wenn er hochgeworfen oder hochgeschossen oder auf sonstige Weise emporgetrieben wird, immer nur eine mehr oder weniger erhebliche Erhebung über die Erdoberfläche, will ihn aber niemals völlig aus ihrer Sphäre entlassen und zwingt ihn immer wieder zum Erdboden zurück. Es entsteht somit die Frage, ob uns technische Mittel oder Energien von solcher Kraft und Leistungsfähigkeit zur Verfügung stehen, um die Macht der Erdanziehung, die die größte Kraft ist, die auf unserem Erdballe überhaupt wirksam ist, völlig zu überwinden und einen irdischen Körper aus ihrer Sphäre zu entführen und bis in die gravitationsfreien Regionen des Weltraumes zu befördern. Damit wird die Idee der Fahrt in den Weltraum und das Projekt eines Weltraumschiffes in allererster Linie ein Problem der energetischen Leistung, gegenüber dem alle anderen Fragen, die sich an die Ausführbarkeit jener Idee knüpfen, zurücktreten. Von diesem Gesichtspunkte aus wollen wir die Frage nach der Lösung des Problems in erster Linie betrachten.

Wenn ich einen Stein senkrecht emporwerfe oder ein Geschoß hochschieße, so hat der entsandte Körper im Moment des Emporschleuderns seine größte Geschwindigkeit. Diese verringert sich jedoch mit jedem Augenblick und wird nach bestimmter Zeit und in bestimmter Höhe zu Null; von hier aus legt dann der Körper denselben Weg in umgekehrter Richtung zurück, er fällt, zunächst mit geringer Geschwindigkeit, die jedoch in jedem Augenblicke wächst, bis er mit derselben Geschwindigkeit, mit der er emporgeworfen wurde, wieder auf der Erde anlangt. Denn auf den entsandten Körper wirken zwei Kräfte: einerseits die Kraft des Triebmittels, die ihm seine Richtung und Geschwindigkeit nach oben erteilte, andererseits die Anziehungskraft der Erde, die seine Geschwindigkeit in jeder Sekunde um zehn Meter verringert, diese dadurch schließlich vollkommen vernichtet und dann den Körper mit wachsender Gewalt wieder zum Erdboden zurückzieht. Je größer die Kraft war, die dem Körper seinen Auftrieb erteilte, und je größer infolgedessen seine Anfangsgeschwindigkeit war, um so höher wird er sich über den Erdboden erheben und um so länger wird es dauern, bis er den Nullpunkt seiner Geschwindigkeit erreicht hat.

Die Erdanziehung ist jedoch keine konstante Größe. Sie wird, wenn in merklicher Größe freilich auch erst in sehr weiter Entfernung von der Erdoberfläche, allmählich geringer und in genügend großer Entfernung sogar zu Null. An dieser Stelle beginnt dann der gravitationsfreie Weltraum, in welchem die Erde keine Macht mehr über die Körper hat und einen solchen, wenn er so weit gelangt ist, auch nicht mehr auf ihren Boden zurückzwingen kann. Es kann daher die Frage aufgeworfen werden, ob es möglich ist, dem zu entsendenden Körper eine so große Anfangsgeschwindigkeit zu erteilen, daß er über die Grenze der Erdgravitation hinauszugelangen vermag. In einem solchen Falle würde der entsandte Körper nicht zu einem Nullpunkt seiner Geschwindigkeit kommen, sondern er würde mit einer gewissen Endgeschwindigkeit in die gravitationsfreie Sphäre des Weltraumes eintreten und in diesem dann seine Reise ungehindert fortsetzen können, bis er in die Gravitationssphäre eines anderen Weltkörpers gelangt und auf diesen niederfällt. Es läßt sich berechnen, daß ein emporgeworfener oder emporgeschossener Körper, der über die Gravitationssphäre der Erde hinausgelangen soll, eine Anfangsgeschwindigkeit von 11 180 Metern in der Sekunde haben müßte. Denn ein Körper, der, aus der Unendlichkeit des Weltraumes kommend, in den Anziehungsbereich der Erde gelangt und zu dieser herabstrebt, würde, sofern er keine Bremsung durch die Lufthülle erfährt, mit jener Geschwindigkeit von 11 180 Sekundenmetern auf die Erde niederfallen, und mindestens ebenso groß müßte daher die Abschußgeschwindigkeit eines irdischen Körpers sein, der über die Sphäre der Erdanziehung hinaus und in den gravitationsfreien Weltraum hineingelangen soll.

In dieser Weise dachte sich Jules Verne die Technik der Reise nach dem Monde. Er hat sich, wie das für einen phantasievollen Romandichter gut und zulässig ist, die Ausführung eines solchen ungewöhnlichen Unternehmens ziemlich einfach gemacht. In seinem Roman wird aus einem Riesengeschütz eine mit Menschen und Tieren bemannte Rakete nach dem Monde hin abgefeuert, die denn auch mitsamt Verne war nicht nur Dichter, sondern auch Wissenschaftler, und deswegen stattete er seine Mondrakete mit jener Anfangsgeschwindigkeit von 11 180 Metern in der Sekunde aus, denn sonst hätte er es weder mit seinem wissenschaftlichen noch mit seinem dichterischen Gewissen vereinbaren können, sein Fahrzeug bis zum Monde gelangen zu lassen. Was aber der Romandichter hier in so eleganter Weise zuwege bringt, ist leider der Technik bisher eine Unmöglichkeit gewesen. Mit keinem der uns heute zur Verfügung stehenden Triebmittel sind wir in der Lage, einem Körper jene Anfangsgeschwindigkeit von 11 180 Sekundenmetern zu erteilen. Selbst die brisantesten Explosivstoffe vermögen einem Geschoß nur eine Mündungsgeschwindigkeit von etwa 1000 Sekundenmetern zu geben, und mit einer solchen, ja selbst noch mit einer zehnmal größeren Geschwindigkeit würde der abgeschossene Körper niemals der Anziehungssphäre der Erde entfliehen können. Auf diese Weise wäre also die Lösung des Problems, rein energetisch betrachtet, für heute und für jede absehbare Zeit ausgeschlossen, und daher können wir von den anderen Faktoren und Hindernissen, die sich einer solchen Art der Weltraumreise überdies in den Weg stellen würden, vollständig absehen.

Eingedenk der Unzulänglichkeit des Jules Verneschen Verfahrens stellen die heutigen Pioniere zur Eroberung des Weltraumes ihre Projekte denn doch auf eine höhere technische Grundlage. Das Mittel, das ihnen zur Verwirklichung ihrer Projekte dienen soll, ist der Raketenmotor. Von der Kraft und Wirkungsweise dieses Mittels erhoffen sie die völlige Überwindung der Erdgravitation, erhoffen sie ferner aber auch die Erreichung bisher völlig ungeahnter Geschwindigkeiten, groß genug, um auch eine Reise nach dem Monde, ja selbst nach den Planeten in absehbarer Zeit zu Ende führen zu können. In den zahllosen Veröffentlichungen in Wort und Schrift der letzten Jahre, die sich mit dem Problem des Weltraumschiffes beschäftigten, war es immer der Raketenmotor, der diesem Projekt zur Verwirklichung verhelfen soll. Betrachten wir daher den Raketenmotor näher, um beurteilen zu können, ob und wieweit er jene hochgespannten Erwartungen zu erfüllen imstande sein wird.

Das Prinzip der Rakete findet in der modernen Technik, sowohl in der Ballistik wie auch in der Maschinentechnik, vielfache und wertvolle Anwendung. Es besteht in der Nutzbarmachung des Rücktriebes, der bei Gasen von hoher Strömungsgeschwindigkeit, insbesondere bei der Explosion von Stoffen, auftritt. Die Explosion von Pulver, Benzin, Gasen und sonstigen Explosivstoffen besteht immer in einer ungeheuer schnellen Verbrennung dieser Stoffe, bei der sich die entstehenden Verbrennungsgase mit entsprechend ebensolcher Geschwindigkeit ausdehnen. Und zwar findet diese Ausdehnung der Verbrennungsgase nicht nur nach einer Richtung, sondern vom Zentrum der Explosion aus radial nach allen Richtungen hin statt, wie wir es deutlich bei einem krepierenden Schrapnell oder einer Granate sehen, bei der die einzelnen Stücke des gesprengten Geschoßkörpers nach allen Richtungen hin fortgeschleudert werden. Ähnlich ist auch der Vorgang beim Abfeuern eines Geschützes. Auch hier haben die bei der Verbrennung bzw. der Explosion der Pulverladung auftretenden Verbrennungsgase an und für sich das Bestreben, sich nach allen Richtungen hin auszudehnen; aber durch den Lauf des Geschützes wird ihre Ausdehnung auf zwei Hauptrichtungen beschränkt, eine Vorwärtsbewegung zur Mündung des Geschützes hinaus, durch welche das Geschoß seine Richtung und Geschwindigkeit erhält, und eine dieser gerade entgegengesetzte Rückbewegung nach dem Boden des Geschützrohres hin, die den Rückstoß oder Rücklauf des Geschützes bewirkt und vom Erdboden aufgefangen wird. Auch beim Abschießen eines Gewehres findet ein solcher Rückstoß statt, wie jeder weiß, der einmal aus einem solchen einen Schuß abgegeben hat. Eine hochbedeutsame technische Anwendung findet das Prinzip des Rücktriebes bei der Dampfturbine, wo der mit ungeheurer Schnelligkeit aus den Düsen des Turbinenrades strömende hochgespannte Dampf durch seinen Rücktrieb das Turbinenrad in rotierende Bewegung versetzt, die immer entgegengesetzt der Richtung des strömenden Dampfes verläuft.

Der Rücktrieb explodierender Gase nun ist es auch, der die Triebkraft zur Beförderung des Weltraumschiffes liefern soll. Ein solches hat nach dem Projekt seiner Erfinder etwa die Form eines Luftschiffes starren Systems, ist aber an der Rückseite mit einem Raketenmotor versehen. Dieser stellt ein System düsenartiger, in der Längslinie des Fahrzeuges liegender Rohre dar, in denen ununterbrochen Pulverexplosionen stattfinden, die auf elektrischem Wege ausgelöst und reguliert werden können. Indem hierbei die Explosionsgase mit gewaltiger Geschwindigkeit und Kraft aus den Düsen austreten, erteilen sie durch ihren Rücktrieb dem Fahrzeug ununterbrochene Kraftimpulse nach der entgegengesetzten Richtung. Ist hierbei das Fahrzeug und mit ihm der Raketenmotor so eingestellt, daß die explodierenden Gase von oben nach unten strömen, so wird das Fahrzeug selbst in entgegengesetzter Richtung von unten nach oben, also vom Erdboden fort in die Höhe, getrieben und entfernt sich immer weiter von der Erde, durch die fortwährenden Explosionen gleichsam ununterbrochen immer weitergeschossen. Durch diese Wirkungsweise seines Motors erlangt das Raketenfahrzeug, ganz ebenso wie das Automobil auf fester Bahn, einen kontinuierlichen Antrieb im leeren Raum, durch den es in diesem immer weitergetrieben wird. Aber nicht nur das: nach der Theorie der Weltraumtechniker muß es möglich sein, durch diese Wirkungsweise des Raketenmotors dem Weltraumschiff auch jede beliebige Geschwindigkeit zu verleihen. Da das Raketenfahrzeug bei seiner Fahrt im leeren Raum keinen Reibungswiderstand durch Fahrbahn und Luft zu überwinden hat, wie es bei allen irdischen Fahrzeugen der Fall ist, so muß jeder neue Kraftimpuls auch jedesmals zu einer Erhöhung der Fahrtgeschwindigkeit führen und nach dem Gesetz der Relativität der Bewegungen die Geschwindigkeit des Fahrzeuges schließlich bis auf das Vielfache selbst der größten auf Erden technisch erreichbaren Geschwindigkeiten, bis auf Hunderte von Kilometern in der Sekunde, steigern. Damit wäre das Weltraumschiff dann in der Lage, selbst die kosmischen Entfernungen, die die anderen Weltkörper von der Erde trennen, in absehbarer Zeit zurückzulegen. Auch für die Navigation im leeren Weltraum ist gesorgt. Durch seitliche Düsen kann das Fahrzeug gesteuert, durch einen Gegenmotor an der Vorderseite gebremst werden, wodurch es auch vor dem vernichtenden Sturz bewahrt wird, der ihm sonst drohen würde, sobald es in die Anziehungssphäre des Weltkörpers, dem es zustrebt, gelangt. Langsam und allmählich wird es vermöge der motorischen Einrichtungen auf diesem landen, und ebenso gibt ihm der Raketenmotor die Möglichkeit, sich vom Boden des erreichten Weltkörpers wieder zu erheben und die Rückreise nach der Mutter Erde anzutreten.

Das wäre also Prinzip und Wirkungsweise des Raketenmotors, von dem die Pioniere der Weltraumfahrt die völlige Verwirklichung ihrer Ideen und Projekte erhoffen. Man sieht, noch ungleich kühner als in der Phantasie eines Jules Verne werden in den Berechnungen der Weltraumpioniere die Naturgesetze dem erstrebten Zwecke gefügig gemacht und alle Hindernisse von Raum und Zeit, an denen die wissenschaftliche Technik bisher machtlos zerschellte, spielend leicht überwunden. Die Phantasie kennt keine Schranken und macht sich die Naturgesetze selber.

Genährt und gesteigert wurden die Hoffnungen, die auf den Raketenmotor zur Lösung des Problems der Weltraumfahrt gefetzt werden, durch die seit dem Frühjahr 1928 unternommenen Versuchsfahrten mit Raketenautomobilen. Diese Versuchsfahrten hatten, rein technisch betrachtet, hervorragende Ergebnisse zu verzeichnen; es wurden Geschwindigkeiten bis zu 350 Kilometer die Stunde erreicht, und damit war die Verwendbarkeit des Raketenmotors als Antriebsmittel für Fahrzeuge auf fester Bahn festgestellt, ein Ergebnis, das zugleich auch zum mindesten die Verwendbarkeit dieses Motors für alle anderen Arten von Fahrzeugen innerhalb der Erdsphäre, auch für Flugzeug und Luftschiff, erwarten läßt und auch noch manche andere Ausblicke für neue beförderungstechnische Möglichkeiten eröffnet. Und nach den so bewiesenen Erfolgen glaubt man dem Raketenmotor auch die Kraft zutrauen zu dürfen, die zur Fahrt in den Weltraum, bis über die Sphäre der Erdgravitation hinaus, nötig ist, glaubt man in ihm die Maschine sehen zu dürfen, die über kurz oder lang das erste Weltraumschiff mindestens bis zum Monde befördern wird.

Hierzu ist aber zu bemerken, daß die Bedingungen und Anforderungen zu einer Fahrt über die Gravitationssphäre der Erde hinaus doch völlig andere sind als zu Raketenfahrten innerhalb der Erdsphäre, gleichviel ob auf fester Erdbahn, ob in der Luft oder selbst oberhalb der Lufthülle der Erde. Darüber scheint man sich bei der allgemeinen Begeisterung für die Raketenautomobile nicht genügend Rechenschaft gegeben zu haben. Mit Leichtigkeit kann nachgewiesen werden, daß den Anforderungen, die die Fahrt in den Weltraum stellt, auch der Raketenmotor selbst in seiner vollendetsten Form nicht auch nur im entferntesten gewachsen ist und er im Kampfe gegen die Gewalt der Erdanziehung versagen und zerschellen muß wie die Mücke im Kampfe gegen den Elefanten. Ist bei dem Jules-Verneschen Riesengeschoß die Unmöglichkeit, die notwendige Fluggeschwindigkeit zu erreichen, die Ursache der völligen Unmöglichkeit, auf diese Weise die Macht der Erdanziehung zu überwinden, so ist es beim Raketenfahrzeug nach dem Prinzip des Rücktriebes ein anderer physikalischer Faktor, der dieses Unternehmen genau so aussichtslos und unmöglich macht, ein Faktor, den wir leicht erkennen, wenn wir uns über die Wirkungsweise und Leistungsfähigkeit der Kraftmaschinen nach Art des Raketenmotors kurz Rechenschaft geben.

Unsere sämtlichen Kraftmaschinen sind Wärmekraftmaschinen, das heißt, sie entnehmen die Arbeit, die sie leisten, der Wärme, die durch die Verbrennung ihrer Heizstoffe erzeugt wird. Bei der Dampfmaschine dient die Kohle, beim Automobil Benzin oder Benzol als Brenn- und Betriebsstoff, beim Raketenmotor dagegen Pulver. Auch die Explosion von Pulver stellt nur eine Verbrennung dar, und die hierbei entstehende Wärme ist die alleinige Quelle der Energie zum Betrieb aller auf solche Weise betriebenen Maschinen. Durch die Verbrennungswärme des Pulvers wird das Geschoß aus der Kanone oder dem Gewehr getrieben, und ebenso liefert diese Verbrennungswärme die Energie zum Betrieb des Raketenmotors. Nun wissen wir, daß mit einem bestimmten Quantum Brennstoff immer nur ein bestimmtes Quantum Wärme erzeugt und mit einem bestimmten Quantum Wärme immer nur ein ganz bestimmtes Quantum mechanischer Arbeit geleistet werden kann. Mit einer Kalorie, das heißt der Wärmemenge, die zur Erhöhung der Temperatur eines Liters Wasser um 1 Grad nötig ist und die etwa bei der Verbrennung eines Streichholzes frei wird, kann theoretisch immer nur eine Arbeit von 424 Meterkilogramm geleistet werden, und alle Leistungen unserer Kraftmaschinen werden rechnerisch in dieser Weise auf die Einheiten von Wärme und Arbeit reduziert. Diese gegenseitige Bedingtheit ist das Naturgesetz der Äquivalenz von Wärme und Arbeit, das allem energetischen Geschehen auf Erden wie im ganzen Universum zugrunde liegt. Mit einem bestimmten Quantum Kohle kann eine Dampfmaschine immer nur ein ganz bestimmtes Quantum Arbeit leisten, mit einem bestimmten Quantum Benzin ein Automobil immer nur eine ganz bestimmte Strecke zurücklegen, und Entsprechendes gilt von allen Kraftmaschinen überhaupt. Bemerkt sei noch, daß unsere Kraftmaschinen übrigens keinesfalls den vollen theoretischen Höchstwert der durch Verbrennung ihrer Brennstoffe erzeugten Wärme in Arbeit umsetzen, sondern nur etwa 10 bis 15 Prozent derselben; der übrige große Rest geht durch Abwärme, Ausstrahlung und sonstige Unvollkommenheiten der Maschine verloren. Jener verhältnismäßig geringe Prozentsatz der in wirkliche Nutzarbeit umgesetzten Wärme heißt der thermische Wirkungsgrad der Maschine.

Wenden wir das Gesagte nun auf den Raketenmotor an, so ergibt sich für diesen und dessen Leistung eine ganz bestimmte Folgerung. Die Arbeit, die beim Raketenmotor, der zum Betrieb eines Weltraumschiffes bestimmt ist, aus der Verbrennung der mitgeführten Brennstoffe, also des Pulvers, geleistet werden soll, besteht in der Hebung des Fahrzeuges über die Erdoberfläche hinaus. Ein Teil dieser zu leistenden Hubarbeit entfällt dabei natürlich auf die Hebung des mitgeführten Brennstoffes selbst. Jedes Kilogramm des mitgeführten Brennstoffes, also des Pulvers, erfordert zu jedem Meter Höhenfahrt eine Arbeitsmenge von 1 Meterkilogramm, und die für diese Arbeit notwendige Wärme wird aus der Verbrennungswärme des Brennstoffes selbst entnommen. Nehmen wir nun einmal an, daß die Wärme, die 1 Kilogramm Pulver bei seiner Verbrennung erzeugt (etwa 4000 Kalorien), dazu dienen sollte, nur diese Masse selbst zu heben, so würde (unter Berücksichtigung des thermischen Wirkungsgrades des Antriebes) die so erzeugte Wärme ausreichen, dieses eine Kilogramm Pulver etwa 400 Kilometer über die Erdoberfläche zu heben, wie sich aus der Äquivalenz von Wärme und Arbeit leicht berechnen läßt. Dasselbe gilt natürlich auch für jedes andere Kilogramm Brennstoff, den das Raketenfahrzeug mitnimmt, das heißt, der gesamte Brennstoffvorrat könnte, wenn er lediglich zu seiner eigenen Hebung dienen sollte, niemals über 400 Kilometer Höhe hinausgelangen. Kann also der mitgenommene Brennstoff durch seine Verbrennungswärme sich selbst nicht über die genannte Höhe hinausheben, so selbstverständlich noch viel weniger das Gesamtgewicht des Fahrzeuges, das ja immer wesentlich höher als der mitgeführte Brennstoff ist. Jene 400 Kilometer Höhe wären also die theoretische Höchstgrenze, über die kein mit den uns heute zur Verfügung stehenden Brennstoffen betriebenes Raketenfahrzeug hinausgelangen kann; praktisch muß die erreichbare Höhe (unter Berücksichtigung des Gesamtgewichtes des Fahrzeuges) sogar noch erheblich unter dieser theoretischen Höchstgrenze bleiben, die durch die Äquivalenz von Wärme und Arbeit unüberschreitbar gesetzt ist.

Wir wollen das Gesagte noch an einem anderen Beispiel veranschaulichen. Angenommen, es sollte Kohle aus einer Tiefe von 400 Kilometern an die Erdoberfläche gefördert werden, so hätten wir (wiederum unter Berücksichtigung des thermischen Wirkungsgrades der Fördervorrichtung) in diesem Falle für die Förderung der Kohle selbst geradesoviel Wärme und Arbeit aufzuwenden, als uns die Kohle hinterher durch ihre Verbrennung leisten könnte; wir hätten also in einem solchen Falle von der Kohle nicht den geringsten Nutzeffekt zu erwarten. Oder angenommen, 1 Kilogramm Kohle in jener Tiefe sollte dazu verwandt werden, um durch seine Verbrennung die Wärme zu liefern, die für seine eigene Hebung bis an die Erdoberfläche benötigt wird, so würde es spätestens an der Erdoberfläche völlig verbrannt sein und könnte uns keinerlei Nutzarbeit mehr leisten. Entsprechend verhält es sich mit dem Brennstoff des über die Erde aufsteigenden Raketenfahrzeuges. Auch in diesem Falle hätte sich der mitgeführte Brennstoff spätestens in einer Höhe von 400 Kilometern selbst verzehrt, und es bliebe keine Spur mehr übrig, um das Fahrzeug selbst noch höher zu treiben. Allerdings spielen hier noch gewisse Faktoren hinein, wie die allmähliche Abnahme des Gewichtes des verbrennenden und zugleich emporsteigenden Brennstoffes, ferner auch die Abnahme der Gravitation über und unter der Erdoberfläche. Aber diese Faktoren sind verhältnismäßig unbedeutend und in unserer Rechnung bereits berücksichtigt. Beispielsweise hätte die Anziehungskraft der Erde, in deren Überwindung die von dem Raketenmotor bzw. die von seinem Brennstoff zu leistende Arbeit besteht, in jener Höhe von 400 Kilometern noch den weitaus größten Teil ihres Wertes wie unmittelbar auf der Erdoberfläche.

Auf einen Trugschluß sei noch hingewiesen, der hier leicht gemacht werden kann, nämlich auf den Einwand, daß das Raketenfahrzeug ja entsprechend mehr Brennstoff mitnehmen könnte, für jedes Kilogramm des Brennstoffes, der nötig ist, um die Höhe von 400 Kilometern zu erreichen, noch zehn oder hundert Kilogramm Brennstoff extra, und daß auf diese Weise das Fahrzeug zu entsprechend größeren Höhen gelangen könnte. Das wäre deswegen ein Trugschluß, weil das, was von einem Kilogramm des mitgeführten Brennstoffes gilt, auch für jedes andere Kilogramm gilt. Jedes einzelne Kilogramm des mitgeführten Brennstoffes verzehrt seine Energie zu seiner eigenen Hebung und hätte diese spätestens in 400 Kilometer Höhe erschöpft, und dasselbe gilt für den extra mitgenommenen Brennstoff. Jener Einwand liefe also auf eine Art raumfahrttechnischen Perpetuum mobile hinaus, das mehr Brennstoff mitnehmen will, als der Brennstoff selbst über jene Höchstgrenze hinaus zu heben vermag.

Unter Berücksichtigung dieser Verhältnisse kommt die Beurteilung des vorliegenden Problems auf eine sehr einfache Formel hinaus: das Raketenfahrzeug vermag für die Fahrt in den Weltraum niemals so viel Brennstoff mitzunehmen, wie für die Fahrstrecke über die Grenze der Erdgravitation hinaus, bis zum Monde oder gar zu den Planeten, erforderlich wäre. Es befindet sich in einer ganz ähnlichen Lage wie unsere irdischen Fahrzeuge. Ein Ozeandampfer kann für eine Reise um den Erdball niemals so viel Kohle mitnehmen, wie für diese Fahrstrecke benötigt wird, sondern muß unterwegs mehrfach an Kohlenstationen anlegen, um neuen Brennstoff aufzunehmen, und in entsprechender Weise muß das Automobil unterwegs tanken, weil ihm nach einer bestimmten Strecke seiner Fahrt der mitgenommene Brennstoff ausgegangen ist. Ebenso reicht der Brennstoff, den ein Raketenfahrzeug mitnehmen kann, günstigstenfalls immer nur bis zu jener theoretischen Höchstgrenze von 400 Kilometern Höhe. Ja, wenn, es für das Weltraumschiff unterwegs Brennstoffstationen oder Tankstellen gäbe, wo es sich mit neuem Brennstoff versorgen könnte, dann könnte es seine Fahrt fortsetzen und jede beliebige weitere Höhe erreichen. Aber solche Tankstellen im leeren Weltraum einzurichten, der noch weniger Balken als das Wasser hat, wird wohl selbst unseren verwegensten Weltraumpionieren als aussichtsloses Problem erscheinen.

Unser Mond ist an 360 000 Kilometer, der Mars in größter Erdnähe immer noch an 80 Millionen Kilometer von uns entfernt. Was wollen gegen solche Entfernungen jene 400 Kilometer Steigfähigkeit des »Weltraumschiffes« besagen? Aus dem ehernen Naturgesetz der Äquivalenz von Wärme und Arbeit folgt die unerschütterliche Tatsache, daß bei den uns heute zur Verfügung stehenden Energiequellen jede Fahrt über die Erde hinaus an jene Höchstgrenze gebunden ist, die noch unterhalb des tausendsten Teils der Entfernung des nächsten Weltkörpers, des Mondes, liegt. Damit sind alle Ideen, Projekte und papiernen Erfindungen der heute so zahlreichen Weltraumpropheten zum Scheitern verurteilt, erweisen sich alle daran geknüpften Berechnungen und Beweise als Trugschlüsse, was insbesondere auch von jener verwegenen Berechnung gilt, derzufolge es möglich sein soll, auf Grund der Relativität der Bewegungen, durch Schaffung von »Zusatzgeschwindigkeiten«, die Geschwindigkeit des Raketenfahrzeugs auf Hunderte von Kilometern in der Sekunde zu steigern. Die Erzeugung solcher Zusatzgeschwindigkeiten würde die Mitnahme der tausendfachen Brennstoffmenge erfordern, die nötig wäre, um nur jene Höchstgrenze von 400 Kilometern zu erreichen.

Gegenüber der energetischen Betrachtung des Problems und der sich hieraus ergebenden Tatsache, daß uns heute jede Möglichkeit fehlt, das Problem zunächst energetisch zu bewältigen, sind alle weiteren Faktoren, die sich der Fahrt in den Weltraum feindlich gegenüberstellen, wie das Moment des Luftwiderstandes, der mangelnden Widerstandsfähigkeit des Materials, der Navigation im Weltraume, ja selbst die vielfachen biologischen Momente, die zu berücksichtigen wären, nur von Nachgeordneter Bedeutung. Es hat keinen Zweck, über die Schwierigkeiten des Baues eines Hauses zu reden, solange noch die größte Schwierigkeit, nämlich der Mangel an Baugrund, besteht; und so lange uns für den Betrieb von Weltraumschiffen keine Energiequellen zur Verfügung stehen, die sich als stärker als die Anziehungskraft der Erde erweisen, so lange erübrigt es sich, über die zahlreichen anderen Schwierigkeiten und Hindernisse zu reden, mit denen die Fahrt in den Weltraum außerdem noch verknüpft sein müßte.

Also vorderhand und sicher für noch ganz unübersehbar lange Zeit bleibt die Fahrt in den Weltraum ein schöner Traum. Ob aber nicht später einmal, nach Jahrzehnten oder Jahrhunderten oder Jahrtausenden, dieser kühnste und gewaltigste Menschheitstraum und diese größte Sehnsucht des strebenden Menschengeistes Erfüllung finden kann? Dazu kann man nur sagen: Vielleicht! Völlig von der Hand zu weisen ist auch diese Idee nicht, und daß der Mensch ewig an die Erde gefesselt bleiben muß, daß es ihm und seinem unbezähmbaren Drange nach der Weite des Weltraumes niemals gelingen sollte, die Macht der Erdgravitation zu überwinden, kann mit apodiktischer Gewißheit keinesfalls behauptet werden. Aber zur Erreichung dieses Zieles müßten Kräfte und Energien mobil gemacht werden, von denen wir uns heute noch kaum Vorstellungen machen können. Wenn unsere wirkungsvollsten Triebmittel von heute nur eine Steigung von 400 Kilometern ermöglichen, von welcher Art und Kraft müssen dann die Energiequellen sein, die dereinst das Weltraumschiff auf das Tausendfache dieser Höhe führen sollen, um nur bis zu unserem Monde zu gelangen! Vielleicht daß uns einmal die Energie der radioaktiven Elemente, die ja ungeheuer viel größer ist als die unserer gewöhnlichen Brennstoffe, jenem Ziele näherführen kann, wenn wir gelernt haben, diese Energien, deren Erforschung heute noch in den Anfängen steckt, technisch nutzbar zu machen. Vielleicht auch, daß wir dieses nächste Ziel eher erreichen, als wir heute noch vermuten, und dann den ersten Aussicht bietenden großen Schritt zunächst zur energetischen Lösung des Problems der Fahrt in den Weltraum tun können.

Einst mag wohl auch der Tag kommen, an dem der Mensch imstande sein wird, dem Banne der Erde zu entfliehen und sein Wirken zu jenen fernen Welten zu tragen, die uns heute nur als Lichtpunkte am gestirnten Himmel gegeben sind, und dann mag die macht- und glanzvollste Epoche der Geistes- und Kulturentwicklung der Weltmenschheit beginnen. Aber die Art, wie heute phantasiereiche Köpfe mit gänzlich unzureichenden Mitteln jenes Ziel erreichen wollen, mutet an wie der Versuch eines Kindes, mit dem Suppenlöffel das Weltmeer auszuschöpfen.

Postskriptum

Ein vergessenes Argument – Erfinderphantasie – Die Reise nach dem Mars in 40 Stunden – 500 000 Meter Sekundengeschwindigkeit – Etwas von der »Zusatzgeschwindigkeit« – Eine Ansichtskarte aus dem Monde

Merkwürdigerweise ist in den umfangreichen Erörterungen für und gegen die Möglichkeit des Weltraumschiffes und die Fahrt in die Sternenwelt das Moment der Äquivalenz von Wärme und Arbeit bisher unberücksichtigt geblieben, obwohl es doch jene Frage in kürzester und eindeutigster Weise entscheidet. Sowohl den optimistischen Anhängern jener Idee, die heute schon den Fahrplan für die Reise nach Mond oder Mars ausarbeiten, wie auch den wissenschaftlichen Kreisen, die die Ausführbarkeit eines solchen Unternehmens nach dem heutigen Stande der Technik für eine Illusion erklären, scheint dieses Moment bisher entgangen zu sein. Die umfangreichen, schwierigen und oftmals recht komplizierten Berechnungen, mit denen die Projekte und »Beweise« der Weltraumpioniere von fachlicher Seite zurückgewiesen werden, könnten jedenfalls durch Verwendung jenes Momentes erheblich vereinfacht werden und zugleich an Überzeugungs- und Beweiskraft für diejenigen, für die sie bestimmt sind, gewinnen.

Wie weit sich die Phantasie der Weltraumpioniere versteigt, dafür legte ein Vortrag Zeugnis ab, den vor einiger Zeit in Wien ein Herr, Doktor und Erfinder, wie er sich nannte, vor dem dortigen Ingenieur-Verein hielt. Er suchte haarscharf nachzuweisen, daß er in der Lage sei, mit dem von ihm projektierten Weltraumschiff innerhalb vierzig Stunden nach dem Mars zu gelangen, ein Reiseweg, der selbst bei größter Erdnähe dieses Planeten an 80 Millionen Kilometer beträgt. Um diesen in der angegebenen Zeit zurückzulegen, bedürfte es also einer Geschwindigkeit des projektierten Weltraumschiffes von 500 Kilometern die Sekunde. Die von Skeptikern vorgebrachten Einwände bezeichnete der Herr als »unerheblich«, und das ist ungefähr das allgemeine Verfahren jener kühnen Projektemacher, die sachlichen Bedenken und Einwände derjenigen, die sich ihrem Optimismus nicht anschließen zu können glauben, abzutun. Zeitungsberichten zufolge glaubte auch dieser Erfinder, auf Grund der Relativität der Bewegungen, durch die Schaffung von »Zusatzgeschwindigkeiten« während der Fahrt, zu jener enormen Schnelligkeit seines Vehikels gelangen zu können. Wie man sich das denkt, sei kurz erläutert. Angenommen, eine Rakete steige mit einer Geschwindigkeit von 1000 Sekundenmetern empor; in gewisser Höhe entläßt sie aus ihrem Leibe eine Einsatzrakete, die durch die Explosion ihres Brennstoffes eine Zusatzgeschwindigkeit von 1000 Sekundenmetern relativ zur ersten Rakete, also eine Geschwindigkeit von 2000 Sekundenmetern relativ zur ruhend gedachten Erde, erlangt. Nach einer weiteren Strecke entsendet auch die Rakete Nr. 2 eine weitere Rakete Nr. 3, die abermals eine Zusatzgeschwindigkeit von 1000 Sekundenmetern relativ zu Rakete Nr. 2 und dadurch eine Gesamtgeschwindigkeit von 3000 Sekundenmetern relativ zur Erde, erlangt. So geht das Spiel in Infinitum weiter, bis eben die Geschwindigkeit von 500 000 Sekundenmetern erreicht worden ist, mit der man alle kosmischen Entfernungen innerhalb unseres Sonnensystems spielend leicht bewältigt. Quod erat demonstrandum!

Das ist eine sehr schöne Theorie, hat aber keinen anderen Wert als den eines Gedankenexperimentes, dessen Ausführung in praxi durch die Äquivalenz von Wärme und Arbeit unterbunden wird. Das gedachte Verfahren entspricht lediglich dem in unserem vorstehenden Aufsatz geschilderten Vorgang, bei welchem ein Kilogramm Kohle, das aus einer Tiefe von 400 Kilometern an die Erdoberfläche gefördert werden soll, durch seine Verbrennung die Wärme zu seiner eigenen Förderung liefern soll. In dem Maße, wie die Kohle verbrennt, nimmt sie an Gewicht ab, so daß nur ein immer geringer werdendes Gewicht zu heben ist, das an der Oberfläche der Erde sogar gleich Null werden muß. Diese Gewichtsabnahme ist aber in unserer Rechnung bereits berücksichtigt, denn wenn die ganze Masse der Kohle (wenn auch in verbrannten Zustande, etwa in Form von Rauch und Asche), nach oben befördert werden sollte, so würde die Verbrennungswärme der Kohle bereits nach 200 Kilometern Steighöhe aufgebraucht sein. Bei der Einsatzrakete verringert sich ähnlich das Ausgangsgewicht durch den allmählichen Fortfall der Mutterraketen. Aber eine größere Steighöhe als 400 Kilometer ist auf diese Weise doch nicht zu erreichen, denn bei der Berechnung der Steighöhe des Raketenfahrzeuges ist die allmähliche Verringerung des Gewichtes des verbrennenden Brennstoffes bereits miteingerechnet worden. Es wird hierdurch nichts an der Tatsache geändert, daß auch bei diesem Verfahren die Steighöhe des Fahrzeuges durch die Äquivalenz von Wärme und Arbeit bestimmt und an eine unüberschreitbare Höchstgrenze gebracht wird, und dasselbe gilt auch für die »Zusatzrakete«. Es kommt immer auf dasselbe hinaus: ob viel oder wenig Brennstoff, ob nur eine einzige Hauptrakete oder eine ganze Serie von Zusatzraketen ins Spiel kommen, die theoretische Höchstgrenze sind immer jene 400 Kilometer Höhe, und über diese kommt kein einziges Kilogramm hinaus. Damit wird auch der schöne Traum, durch »Zusatzgeschwindigkeiten« die Gesamtgeschwindigkeit eines Höhenfahrzeuges in infinitum steigern zu können, völlig zunichte, und jener kühne Erfinder, der in vierzig Stunden zum Mars gondeln will, wird, wenn er die Rechnung nachprüft, sich vielleicht doch veranlaßt sehen, das Fahrtempo bei seinem Gedankenexperiment recht erheblich herabzusetzen.

Nach einem vor einiger Zeit gehaltenen Rundfunkvortrage, in dem sich der Verfasser über das Problem der Fahrt in den Weltraum in dem hier dargelegten Sinne ausgesprochen hatte, erhielt er zahlreiche Zuschriften aus den Kreisen der überzeugten Weltraumpioniere, die der dargelegten Auffassung natürlich heftig opponierten. Eine dieser Zuschriften lautete: »Sie werden eines Tages, während Sie gerade an einem Aufsatz über die Unmöglichkeit der Reise nach dem Monde schreiben, eine Ansichtskarte erhalten, die Ihnen ein Mann, der kurz zuvor als erster mit seinem Raketenfahrzeug auf dem Monde landete, mit herzlichem Gruß zusendet. Dann werden Sie vielleicht einsehen, daß Sie über Ihren Unmöglichkeitstheorien Ihre Zeit verschlafen haben. Was Sie über die Unmöglichkeit der Fahrt in den Weltraum gesagt haben, haben die sogenannten Gelehrten und Fachleute bei neuen großen Erfindungen und Entdeckungen noch immer gesagt, nämlich: Unmöglich! So ist es Kolumbus und Stephenson ergangen und vielen anderen, die durch das, was sie geleistet haben, hinterher die Gelehrten blamierten!« – Dazu ist folgendes zu bemerken: Vor einer solchen Ansichtskarte aus dem Monde, wie sie mir jener Einsender so hübsch ausmalt, müßte man sich natürlich in Demut beugen, aber ich glaube nicht, daß ich sie in absehbarer Zeit erhalten werde. Aber auch zu jenem anderen Argument des Einsenders, seiner nicht gerade sehr achtungsvollen Einschätzung der Gelehrten und Fachleute als Rückschrittler und Unmöglichkeitsfanatiker, wollen wir Stellung nehmen, denn mit diesem Argument wird gerade seitens der Weltraumpioniere viel gearbeitet, und die Parallele mit Kolumbus und Stephenson gehört sozusagen zum eisernen Bestand ihrer Geisteswaffen gegen Andersmeinende. Aber ganz so verhält es sich doch nicht. Gewiß sind solche Fälle, wie sie jener Einsender mir schmähend vorhielt, zu verzeichnen, aber man darf sie nicht verallgemeinern. Solche Unmöglichkeitsfanatiker waren schließlich immer nur Vereinzelte gegenüber einer Mehrheit von zustimmenden und verständnisvollen Auffassungen. Jene spanischen Hofgelehrten, die mit so absonderlichen Gründen das Projekt des Kolumbus für unmöglich erklärten, müssen doch schließlich in der Minderheit geblieben sein, und die Mehrheit ihrer Kollegen muß sich für das Projekt ausgesprochen haben, denn sonst hätte sich die spanische Regierung doch wohl nicht zur Unterstützung des Unternehmens bereit finden lassen. Und wenn in jener Kommission von Fachleuten, die die englische Regierung einberufen hatte, um das Projekt Stephensons zu prüfen, die Nein- und Unmöglich-Sager in der Mehrheit gewesen wären, so wäre damals auch aus diesem Projekt nichts geworden. Also muß doch wohl in diesem wie in jenem Falle die Mehrheit der Fachleute das nötige Verständnis bewiesen haben. Gerade in diesen Blättern ist mehrfach betont, daß man gut tut, mit dem Wörtchen »unmöglich« äußerst sparsam umzugehen, und daß schon so manches möglich geworden ist, was so mancher für unmöglich erklärt hatte. Aber wenn sich die Wissenschaft und die Fachwelt so absolut einmütig über die Unmöglichkeit eines Projektes ausspricht, wie es angesichts der heutigen technischen Mittel und Möglichkeiten hinsichtlich des Problems des Weltraumschiffes und der Fahrt zu den Sternen der Fall ist, so dürfte es doch vielleicht mehr angebracht sein, wenn die Anhänger solcher Projekte ihrem Optimismus und ihrer Phantasie Zügel anlegen und danach streben würden, für die ablehnende Auffassung der Fachleute Verständnis zu gewinnen. Davon ist nun aber gerade bei den Problematikern des Weltraumschiffes wenig zu spüren. Unbeschwert von tieferer Sachkenntnis werden die Projekte entworfen, setzt man sich über alle Voraussetzungen und Bedingungen, an die die Lösung des Problems geknüpft ist, hinweg, und ist so auf dem besten Wege, das Problem des Weltraumschiffes zu dem Perpetuum mobile unserer Zeit zu machen, das mit aller Gewalt erfunden werden soll. Und es ist zu befürchten, daß dieses moderne Perpetuum mobile in der Geistesgeschichte eine ebenso berüchtigte Rolle spielen wird wie sein Vorgänger.

2. Das Problem der künstlichen Hand

Die Hand und das Problem – Kunsthände in alter Zeit – Die eiserne Hand des Götz von Berlichingen – Der »Schönheitsarm« – Passive und aktive Kunst-Hände – Die Ballif-Hand – Der Carnes-Arm – Der Arbeitsarm – Der Hoeftmann-Arm – Die Keller-Hand – Trost im Leid

Mit zu dem schwersten Leid, von dem der Mensch betroffen werden kann, gehört der Verlust der Hand. Körperliches und seelisches Leid bedeutet ein solcher Verlust in gleicher Weise. Der Körper büßt hierdurch mehr als durch den Verlust irgendeines anderen Organes an Arbeits- und Leistungsfähigkeit ein, und das Gemüt des Betroffenen fühlt sich infolge der schweren Beschränkung und Verminderung der persönlichen Selbständigkeit und Ungebundenheit, die eine solche körperliche Beschädigung in sich schließt, selbst in schwerster Weise herabgestimmt. Die Hand ist Ausdruck und Organ des individuellen Könnens des Menschen, ihr Verlust daher eine Minderung an individueller Fertigkeit und Lebenskraft, die Geist und Körper in gleicher Weise betrifft und in ihrer Wirksamkeit hindert. Die Wechselwirkung zwischen Geist und Körper, die das individuelle Gepräge des Menschen in seiner Erscheinung und seinem Auftreten, in seinem ganzen Tun und Lassen entscheidend bestimmt, tritt ja gerade an der Hand und in ihrer Funktionsweise in Erscheinung. Die Hand ist es, die alle und auch die feinsten Regungen des Geistes funktionell in Tat und Wirklichkeit umsetzt und dadurch das wichtigste und weitaus am meisten benötigte und verwandte Tätigkeitsorgan des Menschen ist, was vom Geistesarbeiter ebenso wie von dem eigentlichen Handarbeiter gilt. Die Hand ist in der Art und Fülle ihrer Lebenstätigkeit gleichsam die Seele von außen gesehen, wie man vielleicht im Sinne Schopenhauers sagen könnte, und gern und oft sprechen die Dichter von seelenvollen Händen.

Die tief eingreifende Schädigung, die der Verlust der Hand für Sein und Wirken des Menschen immer bedeutet, hat aber auch zugleich das Problem der künstlichen Hand gezeitigt, das Problem, Kunstglieder zu schaffen, die in Fällen solcher wie der genannten körperlichen Beschädigungen an die Stelle des abhanden gekommenen natürlichen Organs zu treten und wenigstens ein aushilfsweiser Ersatz für dieses zu werden geeignet sind. Dieses Problem ist uralt und hat schon vor Jahrhunderten, in vereinzelten Fällen sogar schon vor Jahrtausenden, zu Lösungsversuchen geführt, seine volle Bedeutung freilich erst in unserer Zeit erhalten. Denn der Mensch von heute ist der Gefahr körperlicher Beschädigung, insbesondere auch der des Verlustes des einen oder des anderen seiner Glieder, viel mehr ausgesetzt, als es für die Angehörigen früherer Zeitepochen der Fall war. Die technischen Hilfsmittel, mit denen wir die Naturkräfte in den Dienst unseres gesamten Wirtschafts- und Arbeitslebens zwingen, die aber auch in Haus und Familie zu unentbehrlichen Einrichtungen geworden sind, bedeuten bei allem Segen, den sie den Menschen stiften, doch zugleich eine erhebliche Gefährdung der persönlichen Sicherheit. Die Maschine, der willige und unermüdliche Diener und Helfer des Menschen, ohne den und dessen Gigantenkräfte die Entwicklung unseres Kulturlebens überhaupt nicht möglich geworden wäre, kann auch zum gefährlichsten Feinde des Menschen werden, indem sie ihre Riesenkräfte gegen ihn wendet, und eine ihrer verhängnisvollsten Tücken besteht in der Vermehrung der Unfälle und Unglücksfälle und der mehr oder weniger schweren körperlichen Verletzungen und Beschädigungen, denen der Arbeitende ausgesetzt ist. Entsprechendes gilt von den übrigen Hilfsmitteln und Erzeugnissen, die die hochentwickelte Technik für Werkstatt, Haus und Verkehr, für alles öffentliche und private Leben geschaffen hat. Die Technik bringt nicht nur Fortschritt und Vorteil, sie fordert auch ihre Opfer, Blutopfer, die, wie es scheint, ein unabwendbarer Tribut sind, den die Menschheit für die Leistungen und die Förderung, die sie jener verdankt, zu entrichten hat. Schädigungen oder Verlust von Hand und Arm sind daher auch im Friedensleben heute viel häufiger zu verzeichnen, als es bei den einfachen und ungleich gefahrloseren Einrichtungen und Hilfsmitteln früherer Zeiten der Fall war.

Und die Zahl dieser Opfer wird vermehrt durch die Opfer des Krieges. Die heutige Kriegführung und die heutigen Kriegsmittel haben auch die Zahl der Kriegsbeschädigten gegenüber früheren Zeiten vervielfacht, und der Weltkrieg hat allen Nationen, die an ihm beteiligt waren, eine erschreckende Ziffer solcher Beschädigten hinterlassen, die den Verlust von Hand oder Arm als schwerstes Leid durch ihr ganzes ferneres Leben zu tragen haben. Andererseits war aber auch gerade diese Folge des Krieges ein gewaltiger Ansporn, durch ärztliche und technische Kunst eine vollkommenere Lösung des Problems des Gliederersatzes, vor allem auch des Arm- oder Handersatzes, anzustreben, als bis dahin erreicht worden war. So ist es gekommen, daß schon während der Kriegsjahre das Problem der künstlichen Hand eine größere Förderung erfahren hat und feit dieser Zeit mehr und bessere Mittel und Formen, die jenem Zwecke zu dienen bestimmt und geeignet sind, als alle die Jahrhunderte vorher, und die Fortschritte, die seitdem auf diesem Gebiete erreicht worden sind, kommen heute auch denen zugute, die auf andere Weise, in friedlicher Arbeit und Wirtschaft, Beschädigung oder Verlust von Hand oder Arm erlitten haben. Das ist eine der wenigen guten Folgen, die selbst der blutige Krieg auf sein Konto schreiben darf.

So ist das Problem der künstlichen Hand eins der eigenartigsten technischen Probleme unserer Zeit überhaupt, um dessen Lösung sich Arzt und Techniker in gleicher Weise bemühen. Ärztliche Kunst bringt die schwere Wunde zum Heilen, die die Abnahme des natürlichen Organs zur Folge hatte, und sucht den Verletzten für seine fernere Lebens- und Arbeitsbetätigung so weit zu kräftigen, wie es nur möglich ist; dem Techniker hingegen fällt die Aufgabe zu, dem Verletzten für das verlorene natürliche Organ einen Ersatz in Form eines künstlichen Arbeitsgliedes zu schaffen, mit dem es dem der Hand Beraubten ermöglicht werden soll, sich trotzdem arbeitend zu betätigen, und das den erlittenen Verlust an persönlicher Funktions- und Leistungsfähigkeit so weit wie nur möglich ausgleichen soll. Das Eigenartige des Problems lag von jeher und liegt auch heute noch in der Schaffung dieses Ersatzes, eben in der Herstellung einer künstlichen Hand, die in derselben oder doch in ähnlicher Weise funktionieren soll wie das natürliche Organ, und diese Eigenart bedeutete zugleich auch die Schwierigkeit des Problems. Ungleich schwieriger war es von jeher, für die verlorene Hand einen Ersatz durch ein Kunstglied zu schaffen, als für den Verlust von Fuß oder Bein. Denn die Funktionen von Arm und Hand sind ungleich feiner und komplizierter als die jener. Für den Verlust des Beines ist schon das einfache Stelzbein ein brauchbarer Ersatz, der dem Verletzten die Funktionen des verlorengegangenen Gliedes zu einem erheblichen Teil ersetzt, und die heutigen Kunstbeine haben diesen Ersatz nahezu zu einem vollständigen gemacht. Das Problem der künstlichen Hand hingegen bedeutet immer die Schaffung eines komplizierten Bewegungsmechanismus, der die unendlich vielgestaltige Funktionsweise der Hand wenigstens zu einem Teil ausführen soll, und war daher zu allen Zeiten ein äußerst schwieriges Kunststück, das an den Erfindungsgeist die größten Anforderungen stellte.

Betrachten wir zunächst, wie man in früheren Zeiten das Problem der künstlichen Hand zu lösen versuchte. Daß schon in ältester Zeit die Herstellung von Kunstgliedern nicht unbekannt war, dürfen wir aus mancherlei Andeutungen in Sage und Geschichte der Alten entnehmen. Denn wenn Homer schildert, wie der kunstreiche Gott Hephästos sich für die Arbeit in seiner Werkstatt künstliche Gehilfen schuf, die, wenn auch aus Erz gebildet, doch Form und Glieder wirklicher Menschen hatten und wie solche sich zu bewegen und zu arbeiten verstanden, so dürfen wir auch annehmen, daß die Schaffung solcher künstlicher Glieder in Fällen, wo es not tat, ebenfalls schon in jener Homerischen Zeit versucht und mit mehr oder weniger Glück ausgeführt worden ist. Von Stelzbeinen wird mehrfach berichtet, und selbst schon verbesserte Formen künstlicher Beine scheinen bekannt und in Gebrauch gewesen zu sein, von einer künstlichen Hand wird dagegen nur ein einziges Mal erzählt. Plinius der Jüngere berichtet von einem Römer Namens Marcus Sergius, der um das Jahr 200 v. Chr. im Zweiten Punischen Kriege die rechte Hand verloren hatte und sich einer künstlichen Hand bediente, die er am Armstumpf befestigte und mit der er nach wie vor die Waffen führen konnte. Allerdings ist er selbst wohl kaum der Verfertiger des Stückes gewesen, vielmehr dürfte ihm ein geschickter Sklave das Kunstglied angefertigt haben. Über die technischen Einzelheiten dieser ältesten bekannten Ersatzhand weiß auch Plinius nichts zu berichten. Wenn das auch die einzige Erwähnung eines solchen Kunstgliedes aus dem Altertum ist, so ist doch nicht anzunehmen, daß das der einzige Fall dieser Art gewesen ist; mit mehr oder weniger Geschick und Erfolg mögen sich schon im Altertum auch andere Verletzte durch ein Kunstglied Ersatz für die verlorene Hand zu schaffen gesucht haben.

Dann sind erst wieder aus dem Mittelalter vereinzelte Fälle künstlicher Hände bekannt geworden. Von einer solchen berichtet eine Inschrift auf einem Grabstein aus dem Jahre 886, die besagt, daß der dort begrabene Falkner Odon sich für seinen in der Schlacht verlorenen Arm einen eisernen Arm anfertigen ließ, mit dem er ebenso wie mit einem natürlichen Glied gefochten habe. Erst nach einem Zeitraum von abermals mehreren Jahrhunderten hören wir dann wiederum von künstlichen Händen. Aus dem 16. Jahrhundert wird mehrfach über die Verfertigung derartiger Kunstglieder berichtet. Das bekannteste Beispiel dieser Art ist die eiserne Hand des Ritters Götz von Berlichingen, die kaum weniger als ihr Besitzer selbst eine historische Berühmtheit geworden ist und daher auch eingehendere Erwähnung finden soll.

Abb. 60
Die Eisenhand Götzens von Berlichingen

Abb. 61
Finger der eisernen Hand

Götz von Berlichingen, den Goethe mehr idealisiert als den Tatsachen entsprechend als ritterlichen Kämpen und Biedermann geschildert hat, der aber in Wirklichkeit ein ziemlich skrupelloser Raub- und Strauchritter war, hatte bei der Belagerung von Landshut im Jahre 1504 durch einen Schuß aus einer Feldschlange seine rechte Hand verloren. Seiner kriegerischen Laufbahn schien damit ein Ende gesetzt zu sein. Um jedoch dem geliebten Waffenhandwerk nicht ganz entsagen zu müssen, kam er auf den Gedanken, sich eine künstliche Hand aus Eisen anfertigen zu lassen. Er selbst dachte sich Konstruktion und Mechanismus eines für diesen Zweck geeigneten Kunstgliedes aus und ließ danach die Hand in Stahl von einem Waffenschmied bei Jagsthausen in Württemberg, dem Stammsitz der Berlichingen, verfertigen. Das Kunstwerk (Abb. 60), das bis auf den heutigen Tag erhalten geblieben und dessen Konstruktion daher sehr genau bekannt ist, bestand der äußeren Form nach aus einer Stulpe aus Stahlblech, die über den Armstumpf gezogen und an diesem angeschnallt wurde. Um die Stulpe möglichst leicht und bequem anlegen zu können, war sie mit einer Klappe versehen, die geöffnet und geschlossen werden konnte. Sie war der natürlichen Hand in Form und Bewegung genau nachgeahmt, und besonders Gliederung, Stellung und Beugung der Finger waren unmittelbar nach dem natürlichen Vorbild geschaffen. Die einzelnen Hand- und Fingerglieder (s. Abb. 61) waren durch Scharniere gelenkig und durch Federn beweglich und waren mit großer Kunstfertigkeit zusammengefügt. Der Mechanismus bestand aus einem System von Federn, Hebeln und Sperrrädern nach Art eines Gewehrschlosses. Die Beugung der gestreckten Finger wurde entweder mit der linken Hand ausgeführt oder durch Aufstützen der Finger auf eine ebene Unterlage, etwa die Tischplatte, bewirkt. Jeder einzelne Finger bestand, wie es unsere Abbildung veranschaulicht, aus drei Einzelgliedern mit Gelenken, konnte in jedem Gelenk gebeugt werden und behielt, nachdem er gebeugt war, diese Stellung unveränderlich bei. Um die gebeugten Finger wieder zu strecken, waren besondere Druckvorrichtungen vorhanden, nämlich je ein Druckknopf über dem Daumen und dem kleinen Finger in der Höhe der Handwurzel. Wurde auf den Knopf über dem kleinen Finger gedrückt, so sprangen die vier Finger gleichzeitig aus der gebeugten in die gestreckte Lage zurück; um auch die Streckung des Daumens zu bewirken, mußte auf einen über diesem Gliede befindlichen Knopf gedrückt werden. In ähnlicher Weise konnte auch die ganze Hand im Handgelenk entweder mit Hilfe der gesunden Hand oder durch Aufstützen gebeugt und durch Drücken auf einen Knopf auf dem Handrücken unterhalb des Gelenks wieder gestreckt werden. Unter Beugen und Strecken aller Finger konnte sich so die Hand schließen und öffnen und hielt in geschlossenem Zustande einen hineingesteckten Gegenstand, wie etwa den Schwertgriff, mit großer Kraft unbeweglich fest. Die genaue Nachahmung der Hand läßt darauf schließen, daß der Verfertiger dieses Kunstgliedes nach einem Skelett gearbeitet hat. Die fertige und vollständig aus Eisen bestehende Hand hatte ein Gewicht von 1,5 Kilogramm, war also durchaus nicht besonders schwer.

Dieses Kunstglied nun bewährte sich über alles Erwarten gut. Konnte die Hand zwar auch keine feineren Bewegungen ausführen, so war sie doch, was ihrem Besitzer die Hauptsache war, imstande, das Ritterschwert zu führen und hielt dieses so unverbrüchlich fest, wie nur je eine Hand ein Schwert gehalten hat, so daß sich Götz vollständig in den Stand gesetzt sah, seinem kriegerischen Tatendrange nach wie vor nachzugehen. Fünfundzwanzig Jahre war Götz von Berlichingen alt, als er sich die eiserne Hand anfertigen ließ, und nahezu sechzig Jahre focht er mit dieser in zahllosen Fehden und Schlachten, sich und seine Eisenfaust in ganz Europa berühmt machend. Noch heute wird die eiserne Hand Götzens von Berlichingen auf dem Stammschlosss zu Jagsthausen gezeigt.

Noch einige andere Fälle künstlicher Hände und Arme dieser Art sind aus jener Zeit bekannt. So wird von einem Seeräuber Barbarossa Horuk berichtet, der im Jahre 1517 durch das Geschoß einer Wurfmaschine seine rechte Hand verlor und sich eine eiserne machen ließ, die er am Ellbogen befestigte und mit der er noch lange und glücklich gekämpft haben soll. Einen hohen Ruf als Verfertiger solcher Kunstglieder hatte in der Mitte des 16. Jahrhunderts ein Schlosser in Paris, der der »kleine Lothringer« genannt wurde. Außer einer Anzahl von künstlichen Beinen stellte er auch eine eiserne Hand für einen Amputierten her, die aus Eisenblech gefertigt und wie ein Ritterhandschuh geformt war; auch hier wurde die Streckung durch eine Feder, durch eine andere die Beugung der Finger bewirkt, doch war das Handgelenk unbeweglich, und die Finger konnten nicht einzeln, sondern nur gleichzeitig bewegt werden. Diese Hand war also keinesfalls so kunstvoll gearbeitet und daher auch bei weitem nicht so gut verwendbar wie die Götzens von Berlichingen und hat auch lange nicht solche Berühmtheit erlangt. Eine andere Eisenhand dieser Art, die ebenfalls aus jener Zeit stammt, wurde in einem alten Flußbett bei Neuruppin gefunden; dort mag einst in einer Schlacht ein Rittersmann, der schon vordem die natürliche Hand verloren hatte, auch noch die künstliche eiserne eingebüßt haben. Noch mehrfach liegen Erwähnungen und zum Teil auch Beschreibungen künstlicher Hände aus dieser und der darauf folgenden Zeit vor. Sie waren mehr oder weniger alle nach der Art der eisernen Hand Götzens von Berlichingen konstruiert, wenn zumeist auch nicht so gut wie diese, und sie alle dienten ebenfalls wie diese nur dem einen Zweck, die Kampfwaffe festzuhalten und ihrem Besitzer die verlorengegangene Kampffähigkeit zurückzugeben. Diese spezielle Funktion der Hand hat sich, wie die angeführten Beispiele zeigen, verhältnismäßig gut auf künstlichem Wege erreichen lassen.

Die Eisenhände der Ritterzeit waren also hinsichtlich ihrer Funktions- und Verwendungsfähigkeit von einer ausgesprochenen Einseitigkeit. Sie dienten lediglich der Führung der Waffen und waren lediglich für diesen einzigen Zweck eingerichtet. Erst gegen Ende des 18. Jahrhunderts finden wir zum ersten Male Versuche vor, auch künstliche Hände von allgemeinerer Verwendungsfähigkeit herzustellen. Zu den ersten Versuchen dieser Art gehören wohl die künstlichen Hände und Arme, die der Engländer Wilson aus Edinburg um das Jahr 1790 herstellte. Diese waren nicht aus Eisen, sondern aus besonders präpariertem Leder verfertigt, und infolge der natürlichen Geschmeidigkeit dieses Materials waren die einzelnen Glieder auch ohne besondere Gelenkvorrichtung beweglich. Besondere Haltevorrichtungen dienten dazu, die Finger in der ihnen gegebenen Lage zu erhalten. Doch konnte ein festeres Halten auf diese Weise nicht erreicht werden. Die Finger konnten wohl um den Gegenstand, den sie halten sollten, herumgelegt werden, hielten ihn aber nicht eigentlich fest, doch war die Hand an der Innenfläche mit Federn und Schrauben versehen, an welchen kleinere Gegenstände, wie Messer und Gabel, zweckentsprechend befestigt werden konnten. Für solche und ähnliche leichtere Verwendungszwecke reichte die Hand aus, im übrigen aber war ihre praktische Gebrauchsfähigkeit nur beschränkt. Ihr Hauptwert lag wohl in der Beseitigung des störenden Eindrucks des verstümmelten Gliedes, und für diesen Zweck erlangte die Wilsonsche Kunsthand damals viel Anerkennung und Verwendung. Nach dem Muster dieses Kunstgliedes werden noch heute die sogenannten »Schönheitsarme« verfertigt, die einer eigentlichen Funktionsweise nicht dienen, sondern nur für einen solchen wie den genannten ästhetischen Zweck Verwendung finden.

Die Kunsthände der bisher beschriebenen Art haben nur eine passive Funktion. Sie dienen nur zum Halten oder Tragen, können aber keine selbständigen Bewegungen ausführen, sondern immer nur bewegt werden. Das Beugen und Strecken der Finger an der eisernen Hand Götzens von Berlichingen beispielsweise erfolgte nicht durch das Kunstglied selbst, sondern mußte durch die natürliche Hand oder durch Aufstützen des Kunstgliedes ausgeführt werden. Kunsthände dieser Art sind also nur passiv beweglich. Ein anderes und wesentlich höheres Prinzip verkörpern die aktiv beweglichen Kunsthände, die in der Lage sind, eigene selbständige Bewegungen nach Art des natürlichen Organs und ohne Zuhilfenahme der gesunden Hand auszuführen. Eine solche aktiv bewegliche Hand soll selbsttätig die Beuge- und Streckbewegungen der einzelnen Fingerglieder ausführen, die Finger selbsttätig öffnen und schließen, und nähert sich dadurch bedeutend mehr als die nur passiv beweglichen Kunstglieder der Funktionsweise der natürlichen Hand; sie läßt einen ungleich erweiterten und vielseitigeren Gebrauch als jene zu und ist für die selbsttätige Ausführung der verschiedenartigsten Funktionen bestimmt und eingerichtet. Ihrer Konstruktion wie Verwendungsweise nach stellen Kunstglieder dieser Art eine technisch viel höhere und kompliziertere Form von Bewegungsmechanismen dar, und sie sind in erster Linie dazu angetan, das Problem der künstlichen Hand, soweit als Gegenstand dieses Problems die universale Bewegungs- und Verwendungsfähigkeit der natürlichen selbsttätigen Hand verstanden wird, zu lösen. Auch hier ist man von Anfangsversuchen zu vollkommeneren und leistungsfähigeren Erzeugnissen fortgeschritten, die jenes Problem heute der Lösung ganz bedeutend nahe gebracht haben.

Abb. 62
Die Ballifsche Kunsthand

Abb. 63
Der Ballif-Arm

Die ersten Versuche aktiv beweglicher Kunstglieder gingen überwiegend von deutschen Erfindern aus. Hier sind zunächst die Arbeiten des Breslauer Mechanikers Klingert zu nennen, der im Jahre 1776 mit einer neuen Art von Kunsthänden an die Öffentlichkeit trat. An der Klingertschen Kunsthand waren die Finger mit Gelenken versehen; sie waren in den einzelnen Gliedern beweglich und in gewöhnlichem Zustande gestreckt. Das Schließen der Finger aber erfolgte in neuartiger Weise, nämlich durch Darmsaiten, die von den Spitzen der Finger aus durch das Innere derselben nach dem Handgelenk gingen und sich hier zu einem Strang vereinigten. Durch Zuziehen des Stranges schloß sich die Hand zur Faust, und damit war in den Mechanismus der Kunsthand ein neues und hochwichtiges Element hineingetragen, durch das Bewegungs- und Funktionsfähigkeit der Hand erheblich verbessert und erweitert wurde. Das Zuziehen des Stranges mußte freilich wieder mit der gesunden Hand ausgeführt werden, so daß auch bei diesem Kunstglied nur von einer teilweisen aktiven Beweglichkeit gesprochen werden konnte. Aber auf dem neuen Gedanken wurde weitergearbeitet, und der erste, der eine wirklich aktiv bewegliche Kunsthand herstellte und damit dieser eigenartigen Technik eine völlig neue Grundlage schuf, war der Berliner Chirurgietechniker Paul Ballif. Das vollständig neue Prinzip, das er für die Mechanik der künstlichen Hand zur Anwendung brachte, bestand darin, bestimmte Schulter- und Rumpfbewegungen auf die Kunsthand zu übertragen und dadurch die Bewegungen und Funktionen dieser und ihrer einzelnen Teile, Schließen, Öffnen, Halten, Greifen usw., selbsttätig zu bewirken. Das geschah, indem der Unterarm und die Finger des Ersatzgliedes vermittels Riemen und Saiten mit einem Brustgurt in Verbindung gesetzt wurden, wodurch die Bewegungen von Schulter und Rumpf auf jene übertragen werden konnten. Auf diese Weise bewirkte beispielsweise das Vor- und Rückwärtsbeugen der Schulter oder das Neigen des Rumpfes eine Bewegung des Ellbogens, Vorwärts- oder Seitwärtsheben des Rumpfes dagegen Streckung der gebeugten Finger, die nach Aufhören dieser Bewegung durch Federkraft von selbst wieder in ihre Beugestellung zurückgingen. Unsere Abbildungen 62 und 63 lassen den Mechanismus und die Befestigung der Ballifschen Kunsthand gut erkennen. Damit war zum ersten Male eine willkürlich bewegbare, also tatsächlich aktiv bewegliche, Kunsthand geschaffen, die sich ihrem Mechanismus wie ihrer Funktion nach in viel höherem Grade als die früheren Kunstglieder der Wirkungsweise der natürlichen Hand näherte, die ihre Bewegungen selbsttätig ausführte und die andere Hand nicht mehr oder doch nur aushilfsweise benötigte.

Diese Kunsthand erwies sich im Gebrauch als natürlicher und verwendungsfähiger als die früheren Ersatzglieder und verlieh ihrem Träger eine erheblich größere Selbständigkeit und Freiheit im Gebrauch. Mit jenem neuen Prinzip war die Grundlage einer neuen Technik der Kunst-Hand geschaffen, die in der Folgezeit von Ärzten und Technikern noch weiter ausgebaut wurde und die im wesentlichen noch heute für die Herstellung aktiv beweglicher Kunstglieder maßgebend ist, wenn seitdem in der technischen Anwendungsweise jenes Prinzips allerdings auch weitere bedeutende Verbesserungen erzielt worden sind. Die Konstruktion der heutigen verschiedenen Systeme aktiv beweglicher Kunsthände beruht durchweg auf dem Ballifschen Prinzip, die Bewegungen des erhaltenen Armstumpfes oder des Rumpfes und des Schulterblattes durch Zugschnüre auf die Kunsthand zu übertragen und dieser so bestimmte Bewegungen nach Art der natürlichen Hand zu erteilen. Jene Zugschnüre sind also den Beuge- und Strecksehnen des natürlichen Armes zu vergleichen; nur bei bestimmten Funktionen des Kunstgliedes muß die gesunde Hand noch helfend eingreifen, indem sie durch Drücken auf einen Knopf an der Kunsthand dieser eine bestimmte Einstellung gibt. Der Träger einer solchen Hand ist in der Lage, mit dieser eine große Zahl zweckdienlicher Funktionen auszuführen, die Hand zu schließen und zu öffnen, bestimmte Greifbewegungen zu betätigen und sich des Kunstgliedes annähernd wie eines natürlichen Organes zu bedienen. Auch kann er beim Gehen mit der geschlossenen Hand ein leichteres Paket tragen.

Abb. 64
Der Carnes-Arm

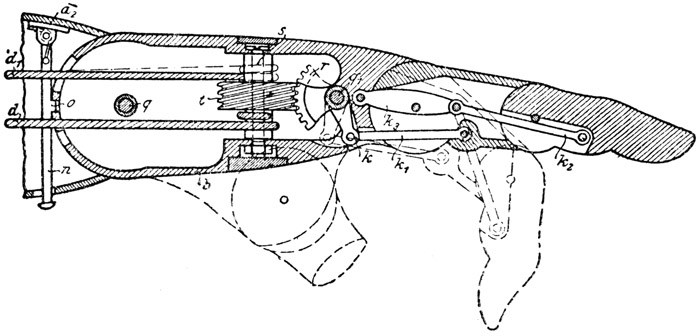
Abb. 65
Hand des Carnes-Armes

Die bisher beste und leistungsfähigste Form einer künstlichen Hand auf Grund des Ballifschen Prinzips dürfte wohl der sogenannte Carnes-Arm sein, der ein Erzeugnis amerikanischer Chirurgietechnik ist. Dieses Kunstglied ist in der äußeren Form dem menschlichen Arm genau nachgebildet und wird mit einem Geschirr von Gurten und Schnüren am Oberkörper des Verletzten befestigt. Die Schnüre führen zu dem gesunden Arm hinüber und werden von diesem durch Anziehen und Strecken betätigt, wodurch sie ihrerseits Finger, Hand und Arm des Kunstgliedes in bestimmte zweckdienliche Bewegungen versetzen. Unsere Abbildungen 64 und 65 lassen Konstruktion und Wirkungsweise des Carnes-Armes erkennen. Die obere Figur stellt den ganzen Unterarm, die untere die eigentliche Hand dar. An dem Arm ist a die Unterarmhülse, in welche der Armstumpf hineingesteckt wird; d, d ₁ und d ₂ sind die drei Zugschnüre, die längs der Wandung der Hülse, so daß sie den Armstumpf nicht berühren, zu der Hand führen, mit deren innerem Mechanismus sie in Verbindung stehen. Sobald die Zugschnüre von dem um die Schulter des Patienten gelegten Gurt angezogen werden, setzen sie ihrerseits den Handmechanismus in Bewegung. Aus der Abbildung 65 ist der Mechanismus der Hand und seine Betätigung durch die Zugschnüre genauer ersichtlich. Die Hand ist hier geöffnet; wird jetzt die Schnur d angezogen, so dreht sie das auf einer Achse sitzende Schraubenrad c, dessen Drehbewegung vermittels des Zahnradstückes r, der Kurbel k und der Pleuelstange k ₁ in eine Beugebewegung des Fingers umgewandelt wird, wie es durch die gestrichelte Linie, die den Finger in Beugestellung zeigt, angedeutet ist. Zwei Fingerglieder werden auf diese Weise gebeugt, das dritte, das Nagelglied, ist steif. Die vier Finger werden gleichzeitig gebeugt, der Daumen dagegen wird durch eine kräftige Feder gegen die Spitze des Zeigefingers gedrückt. Hierdurch hat die Hand jetzt die Einstellung erlangt, die zum Greifen, Halten und Bewegen eines Gegenstandes erforderlich ist. Diese hier vorgeführte Bewegung der Hand, also das Schließen der Finger zum Greifen, Halten usw., wird durch Anheben des gesunden Armes bzw. durch Übertragung dieser Bewegung auf den Ersatzarm bewirkt, beim Sinken des gesunden Armes öffnen sich die Finger wieder. Durch andere Bewegungen des gefunden Armes, des Rumpfes usw. können andere Schnüre gezogen und dementsprechend andere Bewegungen des Kunstgliedes bewirkt werden, und durch Kombination der Schnüre wird so eine große Mannigfaltigkeit der verschiedensten Funktionen, wie sie für den praktischen Gebrauch erforderlich ist, bewirkt, außer Öffnen und Schließen der Finger auch Beugung der Hand, Feststellen der Hand in gebeugter Lage, Drehung der Hand im Unterarm um 80 Grad, Feststellen und Entriegeln an verschiedenen Punkten der Drehung usw., ferner aber auch ganze Komplexe von Bewegungen, wie Auf- und Zuspannen eines Schirmes, Auf- und Zuknöpfen der Kleidung, Öffnen und Schließen der Tür durch Drücken auf die Klinke, Umblättern der Seiten eines Buches, Festhalten und Hochheben von Gegenständen aller Art, wobei das Gewicht des gehaltenen oder gehobenen Gegenstandes bis zu 50 Pfund betragen kann, Handhabung von Instrumenten usw. Nur in einem einzigen Falle bedarf das Kunstglied noch der Zuhilfenahme der gesunden Hand, wenn nämlich die Kunsthand in einer bestimmten Beugung festgestellt werden soll; zu diesem Zweck wird dann die Klinke n eingerückt, was vermittels der gesunden Hand geschieht. Alle anderen Bewegungen aber führt die Kunsthand selbst aus.

Der hohe Grad von Funktionsfähigkeit des Carnes-Armes umfaßt nahezu alle, zum mindesten die meisten und wichtigsten, Funktionen und Bewegungen im täglichen Leben des Gebrauchers. Sache der Übung und Intelligenz des Gebrauchers ist es, den höchsten Grad von Geschicklichkeit und Funktionsfähigkeit in der Anwendung des Kunstgliedes zu erzielen. In Amerika ist der Carnes-Arm schon seit langem bekannt, wobei erwähnt sein mag, daß die Carnes-Kompanie in Kansas, die dieses Kunstglied fabriziert, als Beweis für die hohe Funktions- und Verwendungsfähigkeit ihre Erzeugnisse diese zum größten Teil von – einarmigen Angestellten, die den Carnes-Arm selber tragen, herstellen läßt. In Deutschland wie auch in den anderen europäischen Ländern war der Carnes-Arm bis zum Kriege nur wenig bekannt; die Kriegsfolgen haben dazu geführt, die darauf erteilten Patente auch für Deutschland zu erwerben, und diejenigen Personen. die sich dieses Kunstgliedes bedienen, rühmen ebenfalls die ausgezeichnete Verwendungsfähigkeit desselben. Ein bekannter Berliner Spezialarzt und Leiter eines Krankenhauses, der schon vor Jahren seinen linken Arm verlor, trägt seitdem den Carnes-Arm und übt mit diesem alle Funktionen aus, die seine ärztliche Praxis von Hand und Arm der linken Seite verlangen. Er legt Verbände an, führt Operationen aus und hat überhaupt durch dieses Kunstglied nahezu die volle Selbständigkeit des gesunden Menschen erlangt, eine Tatsache von unleugbar höchster Beweiskraft für die Leistungsfähigkeit jener künstlichen Hand.

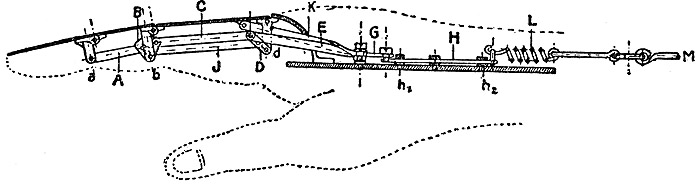
Abb. 66
Kunsthand aus der Werkstätte des Deutschen Museums

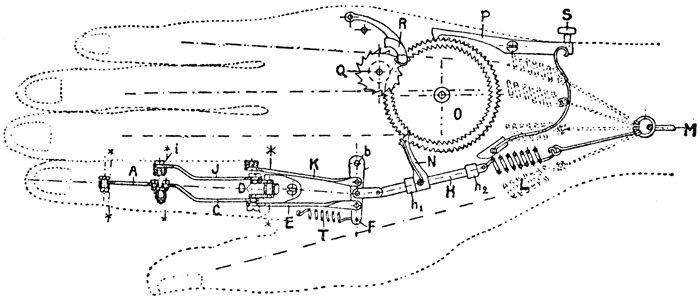
Abb. 67
Kunsthand aus der Werkstätte des Deutschen Museums

Aber noch in anderer Weise läßt sich das Problem der künstlichen Hand lösen, und unsere Abbildungen 66 und 67 zeigen das Modell einer künstlichen Hand, das aus den Werkstätten des Deutschen Museums stammt und die Carnes-Hand an Funktionsfähigkeit sogar noch übertrifft. In noch höherer Weise als bei dieser ist hier die Funktionsweise der natürlichen Hand zum Konstruktionsprinzip gemacht worden. Bei der Ausführung dieses Kunstgliedes wurde als Hauptbedingung erachtet, daß sich die Hand beim Greifen und Fassen selbsttätig wie die natürliche Hand jedem Gegenstand genau anpaßt, daß sie den ergriffenen Gegenstand beliebig lange festhält und der Griff nicht von einer Zwangslage abhängig ist, wie es auch noch beim Carnes-Arm der Fall ist. Greifen und Festhalten sollen vielmehr in jeder Armlage erfolgen können. Jeder Finger besteht aus drei Gliedern, die unter sich wie auch mit dem Handteller durch Scharniere verbunden sind. Die Hand weist dadurch einen noch höheren Grad der Gelenkigkeit und Beweglichkeit als der Carnes-Arm auf, bei dem immer nur zwei Fingerglieder gelenkig, das Nagelglied dagegen unbeweglich ist. Die Beugung der drei Fingerglieder wird durch einen Mechanismus von drei Hebeln, die parallel nebeneinanderliegen, bewirkt, von denen der erste A am Nagelglied, der zweite J am Mittelglied und der letzte K am dritten Glied angreift und die Beugung des entsprechenden Gliedes erzeugt. Alle drei Hebel endigen auf der Geradführung H, durch welche die Hebel zugleich bewegt und so alle drei Fingerglieder zugleich gebeugt werden. Die Fortsetzung der Geradführung bildet eine Feder L; an diese schließt sich ein Drahtzug M an, welcher kurz oberhalb des Ellbogens mit einer Manschette am Oberarm befestigt ist. Wird durch die Bewegung des Oberarms ein Zug auf M ausgeübt, so überträgt sich dieser auf die Feder L und damit auf die Hebelkonstruktion, der Finger bewegt sich und schließt sich um den zu erfassenden Gegenstand. Eine Sperrvorrichtung, die aus dem Sperrad O, dem Sperrkegel N und der Gegensperre P besteht, bewirkt die Fixierung des Griffes. Durch Drücken auf den Knopf S wird die Sperre aufgehoben, so daß der Hebelmechanismus in seine Anfangsstellung zurückkehrt und sich die Finger strecken. Infolge der Ankerhemmung QR erfolgt dieses Strecken der Finger nicht plötzlich, sondern langsam und allmählich in ähnlicher Weise, wie es bei der natürlichen Hand der Fall ist.

Die Anpassung an das natürliche Vorbild kommt bei diesem Kunstglied besonders bei der Gliederung und Funktionsweise der Finger zum Ausdruck. Die drei Hebel, die an jedem Finger die Beugung der drei Glieder bewirken, entsprechen den Fingersehnen der natürlichen Hand und bewirken dadurch eine ebensolche Funktionsweise wie bei dieser. Für jeden der fünf Finger ist ein besonderer Mechanismus mit Zughebeln, Geradführung und Sperrkegel vorgesehen, während Sperrad, Gegensperre und Ankerhemmung für alle fünf Finger gemeinsam sind. Der anpassende Griff der einzelnen Finger an den zu erfassenden Gegenstand wird durch die federnde Verbindung L zwischen der Geradführung H und dem Drahtzug M erreicht, da die Bewegung jedes einzelnen Fingers immer dann aufhört, wenn er auf einen Widerstand trifft, also den zu erfassenden Gegenstand berührt. Ein Zug von 20 bis 25 Millimeter genügt, um die gestreckte Hand in die Faustlage zu bringen; dabei kann der Zug durch ein geringes Strecken des Ellbogens oder, beim Fehlen des Unterarms, durch eine kleine Bewegung des Achselgelenks erfolgen. In der Ruhelage kann die geschlossene Hand in einer beliebig gewählten zwanglosen Stellung verbleiben. Das Lösen des Griffes geschieht in einfacher Weise durch Auflegen der Hand auf die Tischplatte oder durch Andrücken des Oberarms an den Körper. Um einen weichen und natürlichen Griff zu erzielen, ist die Innenfläche der Finger und der Hand mit einer elastischen Polsterung versehen.

Es darf gesagt werden, daß diese Konstruktion einen Grad von mechanischer Feinheit und Zweckdienlichkeit aufweist, der sie zu einer Höchstleistung als Ersatzglied stempelt. Scharfsinn und Kunstfertigkeit haben hier ein Erzeugnis zustande gebracht, das sich dem natürlichen Vorbild an Gliederung und Funktionsfähigkeit in hervorragendem Maße nähert und jedenfalls als die bisher vollkommenste Lösung des Problems der künstlichen Hand bezeichnet werden muß.

Solche wie die vorstehend beschriebenen Kunsthände sind im wesentlichen für die feineren und leichteren handlichen Tätigkeiten solcher Verletzter bestimmt, deren Tätigkeit im übrigen eine mehr geistige als körperliche ist oder doch keinen erheblichen Kraftaufwand erfordert, wie Beamte, kaufmännische Angestellte, wissenschaftlich und künstlerisch Berufstätige usw. Ganz andere Forderungen aber stellt das Problem, wo es sich um eigentliche Handarbeiten handelt, deren Tätigkeit in erster Linie physischer Art ist und von Arm und Hand eine ständige bedeutende Kraftaufwendung erfordert. Für Verletzte dieser Art, also für einarmige Handwerker, Fabrik- und Landarbeiter usw., sind jene Kunsthände kein geeigneter Ersatz, da der kunstvolle Mechanismus dieser Ersatzglieder weder einen solchen Kraftaufwand aufzubringen vermag, wie er für die Tätigkeit solcher Verletzter notwendig ist, noch der ständigen starken Kraftbeanspruchung bei einer solchen gewachsen ist. Hier bestand die Lösung des Problems vielmehr in der Schaffung eines sogenannten Arbeitsarmes, d. h. eines Kunstgliedes von der notwendigen Festigkeit, das zugleich dem ganz anders gearteten Arbeitsprozeß eines solchen Berufstätigen angepaßt ist. Hier muß von vornherein darauf verzichtet werden, eine mehr oder weniger kunstvolle Ersatzhand zur Anwendung zu bringen; vielmehr besteht das Ersatzglied hier im wesentlichen aus einer Hülse oder Stulpe, die an dem Armstumpf des Verletzten befestigt wird und als künstlicher Unterarm dient. An diesem ist ein kräftiges Ansatzstück von einer für den Arbeitszweck des Verletzten geeigneten Form angebracht, mit dem das Werkzeug gehalten und betätigt wird. Nach den sehr verschiedenen Arbeitsberufen, denen solche Arbeitsarme dienen sollen, ist dieses Ansatzstück, die Prothese, ebenfalls sehr verschieden gestaltet. Eine große Anzahl von Systemen solcher künstlicher Arbeitsglieder sucht das hier vorliegende Problem, das so wesentlich anderer Art ist und ganz andere Anforderungen und Bedingungen stellt als in den bisher erwähnten Fällen, in möglichster Zweckdienlichkeit zu lösen.

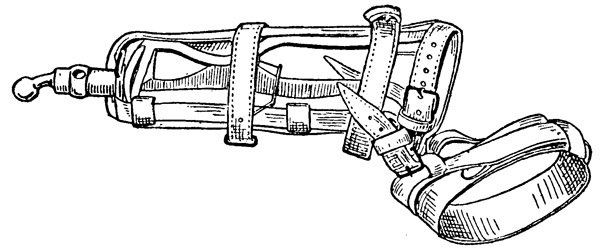
Abb. 68
Arbeitsarm von Hoeftmann

Als Typus dieser Art von Ersatzgliedern darf der Arbeitsarm des bald nach dem Kriege verstorbenen Professors Hoeftmann gelten, der auf diesem schwierigen Gebiete viel und segensreich gewirkt hat. Dieser Arbeitsarm besteht, wie unsere Abbildung 68 zeigt, aus einer Stulpe, die in der gewöhnlichen Weise dem Armstumpf des Verletzten angepaßt und an diesem angeschnallt wird. An der unteren Seite ist die Prothese, das Arbeitsstück, mit dem das zu handhabende Werkzeug gehalten und regiert werden soll, befestigt. Diese Prothese ist für einen Tischler bestimmt, den unsere Abbildung 69 in Tätigkeit zeigt. Die Prothese greift in den Hobel ein, der zu diesem Zweck mit einem entsprechenden Ansatzstück versehen ist, und verleiht dem Beschädigten die Fähigkeit, das Werkzeug wie mit einer natürlichen Hand zu betätigen. Er kann aber auch sägen, bohren, das Beil führen, mit dem Schneidemesser an der Drehbank arbeiten usw., muß sich dann allerdings jedesmal eine andere Prothese, die der Arbeit und dem Werkzeug in dem betreffenden Falle angepaßt ist, einsetzen. Abbildung 70 zeigt einen Landarbeiter mit einem ähnlichen Arbeitsarm und der Prothese zum Halten des landwirtschaftlichen Arbeitsgerätes. Dieser Mann ist seit Jahren bei einem Gutsbesitzer in Stellung, und zwar zur vollen Zufriedenheit seines Arbeitgebers. Er übt alle Tätigkeiten des landwirtschaftlichen Berufes aus, kann auch fahren und sogar ein Viergespann lenken, eine Leistung, die sehr hoch zu bewerten ist, da Lenken und Zügelführen bekanntlich eine erhebliche Beweglichkeit und Sicherheit der Hand erfordern. In der Herstellung und sachgemäßen Verwendung solcher Arbeitsglieder ist die Lösung des Problems, den handarbeitenden Einarmigen ihre Arbeitsfähigkeit zurückzugeben, in erster Linie zu suchen. Freilich erfordert es Zeit und Übung, ehe sich der Patient an die Anwendung des Ersatzgliedes gewöhnt und bis er die nötige Gewandtheit in dessen Gebrauch erlangt hat (was übrigens auch bei den Kunsthänden der Fall ist). Ist das aber geschehen, so entfaltet er oftmals eine überraschende Geschicklichkeit, die derjenigen seiner unverletzten Arbeitskollegen kaum etwas nachgibt.

Abb. 69
Tischler mit Kunstarm

Abb. 70
Landarbeiter mit Kunstarm

Die große Zahl von einarmigen Arbeitern, die der Weltkrieg im Gefolge hatte, gab Veranlassung, das bis dahin Erreichte nicht nur zu verbessern, sondern auch eine ganze Reihe neuer Systeme künstlicher Arbeitsarme zu schaffen, durch die auch dieses Problem, soweit es überhaupt in Menschenkräften stand, zur Lösung gebracht worden ist. Eine besondere Bedeutung unter diesen verschiedenen Systemen beansprucht noch der sogenannte Keller-Arm, der sowohl seiner Entstehung wie auch seiner Einrichtung und Verwendungweise nach Anspruch auf besondere Bedeutung erheben darf und eine besonders glückliche und erfolgreiche Lösung des Problems bedeutet.

Der Keller-Arm ist eine Erfindung des Landwirts Keller, der in jungen Jahren durch einen Unfall den rechten Unterarm verlor und nach vielen vergeblichen anderen Versuchen zu der Erfindung des nach ihm benannten Ersatzgliedes geführt wurde, das den Anforderungen, die an ein solches gestellt werden, in ganz hervorragender Weise entspricht. Der Keller-Arm, der in unserer Abbildung 71 wiedergegeben ist, besteht aus einem Eisengerippe mit drei Haken, die die Stelle der Finger vertreten, mit einer Öse an Stelle der Handwurzel und außer noch verschiedenen anderen Teilen aus einem Binderiemen, der zu einer Lederschlaufe an der inneren Handfläche geformt ist. Diese Lederschlaufe ist der vor allem wirksame Bestandteil der Hand. Im Verein mit den gekrümmten Eisenfingern und der eisernen Öse an der Handwurzel stellt sie eine vortreffliche Vorrichtung zum universalen Zufassen, Greifen und Festhalten und damit zur Anwendung nahezu aller Werkzeuge und Geräte dar. Mit dieser Schlaufe kann der Benutzer mit und ohne Zuhilfenahme der gesunden Hand Werkzeuge und Gegenstände der verschiedensten Art ergreifen. Die Schlaufe paßt sich dem ergriffenen Gegenstand an und hält ihn durch Klemmung und Reibung so fest, daß das Herausziehen selbst mit größter Kraftanwendung nicht möglich ist. Diese ebenso einfache wie sinnreiche und überaus dauerhafte Vorrichtung hat den großen Vorzug universaler Verwendungsmöglichkeit, die bei gleichbleibender Anwendungsweise diese Ersatzhand für den Gebrauch aller Werkzeuge geeignet macht und so das Einsetzen und Auswechseln verschiedener Ansatzstücke oder Prothesen, wie es bei den übrigen Arbeitsarm-Systemen immer erforderlich ist und das immer störende Pausen und Unterbrechungen mit sich bringt, erübrigt.

Abb. 71.
Die Keller-Hand

Abb. 72
Die Keller-Hand mit der Feile

Abb. 73
Die Keller-Hand an der Bohrmaschine

Abb. 74
Die Keller-Hand mit der Schaufel

Dieser Kunstarm mit seinen drei hakenförmig gekrümmten Fingern ist sowohl zum Tragen schwerer Lasten wie auch für die Ausführung leichterer Arbeiten geeignet, wie etwa zum Knüpfen von Schlingen, ebenso auch zum Schreiben, für welchen Zweck ein Halter von Kork, an dem das eigentliche Schreibgerät befestigt ist, zwischen zwei der eisernen Hakenfinger geklemmt wird. Unsere Abbildung 71 zeigt, in welcher Weise der Benutzer dieser Kunsthand ein Messer vermittels der Eisenfinger und der Eisenöse fest eingeklemmt hält. Das Messer hat hierbei einen festen Halt und kann dabei so leicht und sicher geführt werden, daß sowohl ganz leichte Arbeiten, wie Brotschneiden, Bleistiftspitzen, Kartoffelschälen u. dgl., wie auch schwere Schnitzarbeit ausgeführt werden kann. Selbstverständlich kann auf diese Weise auch jedes andere Werkzeug, das mit einem Griff versehen ist, festgehalten und angewandt werden, wie Feile, Hammer und alle anderen Griffwerkzeuge. Bei allen diesen verschiedenartigen und pausenlos ausgeführten Arbeiten arbeitet der Gebraucher eines solchen Kunstgliedes, wie Prüfungen und Erfahrungen zeigen, genau wie ein gesunder Arbeiter, so daß in Ausführung und Leistung kaum ein Unterschied gegen einen solchen wahrzunehmen ist. Endlich ist die Keller-Hand infolge ihrer ausgezeichneten Fähigkeit zum Greifen und Festhalten auch zum Gebrauch aller Werkzeuge in der mechanischen Werkstatt und ebenso auch zur Arbeit an den hier vorhandenen Maschinen geeignet. Sie vermag glatte eiserne Griffe an Maschinen jeder Art zu fassen, zu steuern und loszulassen. Unsere Abbildungen 72 bis 74 zeigen die Keller-Hand bei einer Anzahl verschiedener Arbeitsverfahren. Der Gebraucher der Keller-Hand arbeitet sicher und zuverlässig an der Bohrmaschine wie an der Drehbank, steuert die zylindrischen wie die birnenförmigen Griffe und läßt in seinen Bewegungen und Funktionen kaum einen Unterschied gegenüber der Arbeitsweise des gesunden Mannes erkennen.

Durch die Folgen des Krieges ist die Keller-Hand, die von ihrem Erfinder schon jahrelang vor dem Kriege mit bestem Erfolge bei seiner Tätigkeit als Landwirt gebraucht wurde, zu weit darüber hinausgehender allgemeiner Bedeutung gekommen. Der Prüfungsausschuß des Vereines deutscher Ingenieure hat mit dem Ersatzglied eingehende Versuche für die verschiedensten Arten der beruflichen Handarbeit angestellt und ist zu dem Ergebnis gekommen, daß die Keller-Hand ein ganz hervorragendes Ersatzglied von Universalcharakter für alle Hand- oder Unterarmamputierten darstellt, das sich sowohl für die landwirtschaftliche Tätigkeit wie auch für die Arbeiten in der mechanischen Werkstatt und alle hier vorkommenden technischen Verrichtungen in gleicher Weise als geeignet erweist. Heute leistet die Keller-Hand zahlreichen Kriegs- wie Friedensbeschädigten segensreiche Hilfe. Es liegt hier einer der in der Geschichte der Technik nicht vereinzelten Fälle vor, wo ein Laie, gedrängt durch eigene Not, zu einem wertvollen technischen oder Erfindungsgedanken geführt worden ist, der gleichzeitig einen bedeutsamen technischen Fortschritt in sich schließt. Auf diese Weise hat hier jedenfalls das Problem des künstlichen Arbeitsarmes, das heute von so ungeheurer Bedeutung geworden ist, eine seiner besten und glücklichsten Lösungen gefunden.

Es war einige Jahre vor dem Weltkrieg, da geriet in Wien ein Mann in eine Hochspannungsleitung und verbrannte sich dabei so schwer, daß ihm sämtliche Gliedmaßen abgenommen werden mußten. Ein Menschenleben schien damit von jeder ferneren werktätigen Arbeit ausgeschlossen und bis zu seinem Ende zu der schrecklichen Pein vollkommener Untätigkeit und Hilflosigkeit verdammt zu sein. Doch auch hier versagte menschlicher Erfindungsgeist nicht. Nachdem sich die Wunden des Verunglückten geschlossen hatten, bemühten sich Ärzte und Techniker in gleicher Weise, dem Unglücklichen einen Ersatz für seinen ungeheuren Verlust zu schaffen. Sobald sein Zustand es erlaubte, begann der Mann Übungen mit künstlichen Beinen und Armen, mit dem Erfolge, daß er schließlich wieder zu voller Arbeitsfähigkeit gelangte. Mit seinen künstlichen Händen verrichtete er nahezu alle Arbeiten eines gesunden Menschen, lernte sich selber an- und ausziehen, mit Messer und Gabel essen und seinen Beruf als Mechaniker in vollem Umfange wieder ausüben. Mit seinen künstlichen Beinen vermochte er täglich stundenlange Spaziergänge auszuführen, so tüchtig und ausdauernd wie nur irgendein gesunder Mensch. Es gibt keine Krüppel mehr! sagten damals die Ärzte, die dieses Hilfswerk zustande gebracht hatten. Das war freilich ein Optimismus, wenn auch ein verständlicher, geboren aus der Freude an dem in so hohem Maße gelungenen Werk, aber doch ein Optimismus, denn kein noch so vollkommenes Ersatzglied kann den Wunderbau und die Funktionsfähigkeit des natürlichen Organs vollkommen ersetzen, was in besonderem Maße von der Hand gilt. Aber jener Optimismus trifft wenigstens insoweit zu, als er allen denen, die das Unglück hatten, eins ihrer gesunden Glieder zu verlieren, die trostvolle Gewißheit gibt, daß sie trotzdem nicht zu Hilflosigkeit und Untätigkeit verurteilt sind, selbst in den schwersten derartigen Fällen nicht, und er ist insoweit berechtigt, als das, was menschlicher Scharfsinn und menschlicher Erfindungsgeist an technischen Hilfsmitteln für solche Fälle zu schaffen verstanden haben, eine zwar nicht vollkommene, aber doch weitgehende Lösung des Problem des Gliederersatzes, vor allem auch des ungeheuer schwierigen und heute mehr als jemals wichtigen Problems der künstlichen Hand, in sich schließt.

3. Erfinder-Schicksale

I

Die Problematik des Erfindens – Die Textilkunst als Erfindungsgebiet – Richard Arkwright und die Watermaschine – Vom Barbier zum Erfinder und Multimillionär – Crompton und die Mule-Maschine – Napoleon und die Flachsspinnmaschine – Philippe de Girard – Die Erfindung der Wollspinnmaschine – Josua Heilmann – Ernst Geßner

In der Geschichte der menschlichen Geistes- und Kulturentwicklung, die gleichbedeutend ist mit der Geschichte der Probleme des Menschengeistes, sind die Erfindungen Marksteine von besonderer Bedeutung. Jede Erfindung bedeutet die Lösung eines Problems in jenem Geistesgebiete, das wir als Technik bezeichnen. Verstehen wir unter »Technik« die Beherrschung von Kraft und Stoff durch Schaffung und Anwendung künstlicher Vorrichtungen, durch welche die Kräfte und Stoffe der Umwelt der menschlichen Werktätigkeit und Daseinsweise untertan und nutzbar gemacht werden, so bedeutet jede Erfindung die Lösung eines Problems, das darin bestand, bestimmte Formen zu finden, um bestimmte Kräfte und Stoffe einem bestimmten technischen Zweck in dem dargelegten Sinne dienstbar zu machen. Das Suchen solcher Formen ist die schöpferische Geistestat des Erfinders, das Finden derselben die Lösung des Problems.

Das Problematische der Erfindungstätigkeit tritt uns in der Geschichte und dem Werdegange jeder Erfindung und ebenso in dem Lebensschicksal nahezu jedes Erfinders deutlich entgegen. Einerseits in den oftmals verschlungenen und verwirrten Wegen und Umwegen, die verfolgt wurden, ehe es gelang, das gesteckte Ziel zu erreichen und das vorschwebende Problem zur befriedigenden Lösung zu bringen, Wegen und Umwegen, die den Werdegang so mancher Erfindung als echten, rechten Wettlauf mit der Schildkröte kennzeichnen; andererseits in der Tätigkeit des einzelnen Erfinders selbst, die immer ein Versenken in ein Problem und ein Ringen mit diesem um seine Lösung ist ganz von der Art, wie wir es aus der Geschichte der eigentlichen Geistesprobleme kennen. Das Problematische des Erfindens zeigt sich aber auch in der eigentümlichen Wertung, die Erfindungen und Erfinder so oft erfahren haben. Nicht immer haben die Erfinder den Dank für ihre Schöpfungen und Leistungen schon zu Lebzeiten erhalten. Im Gegenteil, in der Mehrzahl der Fälle wurde ihnen dieser Dank erst nach ihrem Tode durch die Anerkennung der Nachwelt gezollt, und auch hierin begegnen sie sich mit den Männern der geistigen Problematik.

An einer Reihe von Erfindungen wollen wir das Problematische des Erfindens näher darzustellen suchen, und aus der unübersehbaren Fülle der Erfindungen wählen wir zu diesem Zwecke die Geschichte der Erfindung der Textilmaschinen. Einerseits knüpft sich gerade an diese Erfindungen die Entwicklung eines der wichtigsten und größten Zweige der technisch-industriellen Werktätigkeit, andererseits zeigen die Lebensschicksale der Erfinder dieses Gebietes und die Art, wie sie zu ihren Erfindungen kamen, die Problematik des Erfindens wie auch die Eigenart und Tragik des Erfinderloses in besonders deutlicher und ergreifender Weise.

Die heutige Textilindustrie ist ihrer Technik nach im wesentlichen aus den Erfindungen der verschiedenartigen Spinn- und Webmaschinen hervorgegangen, die im Laufe des 18. und 19. Jahrhunderts gemacht wurden und dazu bestimmt waren, die früheren einfachen und wenig leistungsfähigen technischen Hilfsmittel der Textilkunst zu ersetzen. In erster Linie gilt das für die Erfindung der Spinnmaschine. Die Erfindung einer solchen Maschine, durch welche das mühevolle, langsame und wenig leistungsfähige Spinnen mit der Hand und ebenso das alte Spinnrad durch eine zweckmäßigere, schneller arbeitende und leistungsfähigere maschinelle Vorrichtung ersetzt werden sollte, war ein Problem, an dessen Lösung sich schon seit dem 16. Jahrhundert einzelne Erfinder versucht hatten. Schon der hochberühmte Leonardo da Vinci, Ingenieur, Architekt, Bildhauer und zugleich einer der genialsten und vielseitigsten Menschen aller Zeiten, hatte den Entwurf für eine solche Maschine hergestellt, der jedoch nicht zur Ausführung gelangte. In den ersten Jahrzehnten des 18. Jahrhunderts beschäftigte sich dann der Engländer John Wyatt mit der Erfindung einer solchen Maschine, die zum Spinnen von Baumwolle dienen sollte. Der wichtigste Teil seiner Maschine waren mehrere neben- und übereinanderliegende und mit gleicher Geschwindigkeit umlaufende geriefte Walzen, sog. Streckwalzen, durch welche die Baumwolle hindurchgeführt, dadurch gezogen und gestreckt und so zum mechanischen Verspinnen auf einer Spindel reif gemacht wurde. Als Spinnapparat dienten hierbei die sog. Flügelspindeln, die schon seit langem bekannt und in Anwendung waren. Diese Maschine, die im Jahre 1741 zum ersten Mal in Betrieb genommen wurde, darf als die erste Spinnmaschine überhaupt bezeichnet werden. Solche Flügelspinnmaschinen waren für 250 Spindeln eingerichtet, zwei Esel waren zum Antrieb der Maschine nötig und zehn Mädchen zur Bedienung derselben. In den Spinnereien von Birmingham wurden einige solcher Maschinen versuchsweise in Betrieb genommen, doch konnten diese befriedigende Erfolge nicht erzielen, und der Betrieb dieser Maschinen wurde daher schon sehr bald wieder eingestellt, womit das Schicksal dieser ersten Spinnmaschine besiegelt war.

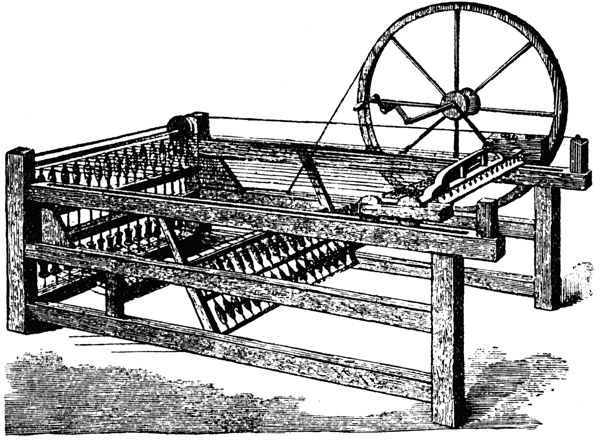
Abb. 75
Hargreaves Spinnmaschine

Eine wesentlich geeignetere und brauchbarere Vorrichtung für den erstrebten Zweck war dagegen die von James Hargreave erfundene Spinnmaschine. Hargreave, geboren in Standhill bei Blackburn und Weber von Beruf, beschäftigte sich ungefähr um dieselbe Zeit wie Wyatt mit der Erfindung einer Spinnmaschine. Seiner Maschine lag ein wesentlich anderer Erfindungsgedanke als der von Wyatt zugrunde. Statt der Streckwalzen waren bei ihr zwei horizontale zusammengepreßte Latten, die Presse, angebracht. Von dieser wurde der zu verspinnende Baumwollenbüschel, das Band, festgehalten. Die Spindeln, die ähnlich denen beim Spinnrad eingerichtet waren, standen vertikal auf einem beweglichen Wagen und bewirkten das Ausziehen und Drehen der Fasern und beim Rückwärtsfahren auch das Aufwickeln des gesponnenen Fadens. Nach seiner Tochter Jenny, die dem Erfinder bei seiner Tätigkeit fleißig half, nannte Hargreave diese Maschine Jenny-Maschine, welchen Namen diese Art der Spinnmaschine bekanntlich noch heute führt. Abbildung 75 stellt Hargreaves erste Spinnmaschine dar, die im Jahre 1767 fertiggestellt und mit acht Spindeln betrieben wurde. Bei einer weiteren und bereits verbesserten Maschine dieser Art konnten schon 100 Spindeln eingestellt werden, zu deren Bedienung nur ein Mädchen benötigt wurde.

Diese Maschine, deren Konstruktions- und Arbeitsweise bis auf den heutigen Tag in den Spinnmaschinen dieser Art erhalten ist, erwies sich als durchaus verwendbar und stellte gegen alle früheren Versuche und Konstruktionen einen sehr bedeutsamen Fortschritt dar. Aber ihr Erfinder hatte kein Glück mit ihr. Er stieß auf vollkommene Verständnislosigkeit der Fachkreise, und statt bei diesen Begeisterung für seine Erfindung zu wecken, wie er gehofft hatte, erweckte er nur die Befürchtung, daß die neue Maschine eine lebensgefährliche Konkurrenz für die Spinnereien werden müßte. Die zünftigen reichen Spinnereibesitzer blickten scheel auf den armen Weber, der mit seiner Erfindung ein reicher Mann werden wollte. Ihre Befürchtungen vor der Konkurrenz der Spinnmaschine übertrugen sie auch auf die Arbeiter in den Spinnereien. Diese wurden dadurch zu schroffer Feindseligkeit gegen den Erfinder veranlaßt, drangen in sein Haus ein und zerstörten seine Maschinen und Werkzeuge nahezu vollständig, ja drohten, ihn totzuschlagen, wenn er nochmals eine solche Maschine bauen würde. Diese Drohungen nötigten Hargreave, nach Nottingham zu flüchten.

In Nottingham setzte Hargreave seine Erfindungstätigkeit fort und stellte dort eine neue Maschine von abermals verbesserter Konstruktion her. Aber auch hier ereilte ihn die Mißgunst der zünftigen Spinner und der Unverstand der durch jene aufgehetzten Arbeiter. Auch diese Maschine wurde von einem eingedrungenen Haufen zerstört, wobei Hargreave selbst verwundet wurde. Damit war seine Kraft erschöpft. Aller Mittel entblößt, gebrochen an Geist und Körper, fand er eine letzte Zufluchtsstätte im Arbeitshause zu Nottingham, wo er auch gestorben ist, zu derselben Zeit, als schon Tausende von Spinnmaschinen seiner Erfindung in England, Frankreich und Deutschland arbeiteten. Selten ist einem hervorragenden Erfinder mit größerem Undanke von seinem Vaterlande gelohnt worden als Hargreave. Hat man ihm doch sogar die Anerkennung, daß er der Erfinder jener Maschine sei, bestritten, und nur ein bescheidener Dank ist ihm geworden, nämlich derjenige, daß, wie bereits gesagt, noch heute die Art von Spinnmaschinen, die nach dem von ihm herrührenden Prinzip gebaut werden, nach seiner Tochter als Jenny-Maschinen bezeichnet werden. Bemerkt sei noch, daß die Jenny-Maschine im Jahre 1772 durch den Engländer Wood eine Änderung in der Weise erfuhr, daß die Spindeln in den fahrbaren Wagen verlegt, die Presse aber festgelegt wurde, eine Konstruktion, die als »Billy-Maschine« bekannt geworden ist und bis gegen das Jahr 1830 in der Streichgarnspinnerei Anwendung gefunden hat.

Ein günstigeres Schicksal und ein großer Erfolg dagegen war dem Nachfolger Hargreaves in der Erfindungsgeschichte der Spinnmaschine Richard Arkwright beschieden, der den glänzendsten Namen als Erfinder in der Geschichte dieser Maschine aufweist und sich durch seine Leistungen für immer den Dank der Menschheit verdient hat. Sein Lebensgang und seine Laufbahn als Erfinder sind in mehrfacher Hinsicht interessant. Arkwright, geboren am 23. Dezember 1732 zu Preston in Lancashire, war ursprünglich Barbier und hat dieses Gewerbe auch Jahre hindurch ausgeübt, bevor er, einer angeborenen Neigung folgend, umsattelte und sich mit dem Uhrmacher Kay in Warrington zur Begründung einer mechanischen Werkstatt vereinigte. Seine erste Idee war freilich noch nicht diejenige der Spinnmaschine, sondern die Erfindung des – Perpetuum mobile. Glücklicherweise blieb er vor dem Schicksal so vieler anderer, die über der Lösung dieses Problems ihre Zeit, ihr Geld und schließlich auch ihren Verstand verloren, verschont, indem er schon bald das Verfehlte dieses Bemühens einsah und sich anderen Aufgaben zuwandte, wo ihm mehr Erfolg beschieden war. Er wandte sich der Erfindung der Spinnmaschine zu, die damals ein vielerörtertes Problem in England war. So wenig Erfolg bis dahin auch die Erfinder solcher Maschinen zu verzeichnen gehabt hatten, so arbeiteten damals doch zahlreiche mehr oder weniger genial veranlagte Köpfe an der Lösung dieses Problems. Arkwright soll durch das Bekanntwerden der Maschine von Hargreave angeregt worden sein, ebenfalls eine solche Maschine zu bauen. Mit finanzieller Unterstützung eines Freundes und unter dem Beistand seines Sozius Kay stellte er im Jahre 1768 seine erste Spinnmaschine fertig, auf die er im folgenden Jahre ein Patent nahm. Seine Maschine stellte eine Verbindung der Wyattschen Streckwalzen zum Strecken der Krempelbänder mit der Flügelspindel des altbekannten Spinnrades dar. Arkwrights Maschine war jedoch technisch bereits viel vollkommener und exakter ausgeführt und auch mit einer Reihe neuartiger Einrichtungen versehen; das Strecken wurde durch drei Paar Walzen bewirkt, das Aufwinden des Fadens durch Heben und Senken einer Spulenbank. Ausziehen, Drehen und Aufwickeln erfolgten, wie beim Spinnrade, gleichzeitig.

Diese erste Spinnmaschine Arkwrights wurde im Jahre 1768 fertiggestellt, aus welchem Jahre auch das Patent stammt. Zum Zweck der praktischen Verwertung der Maschine setzte sich Arkwright mit der berühmten Spinnerei von Strutt & Need in Nottingham in Verbindung. Die Besitzer der Firma, die den Wert der neuen Maschine sehr wohl zu würdigen wußten, schossen ihm die Mittel vor, um eine Spinnerei zu begründen, in der er seine Maschine zur praktischen Anwendung brachte. Von Anfang an hatte Arkwright die Maschine zum Betrieb mit Wasserkraft eingerichtet, und dieser Eigenschaften wegen wurden die nach seinen Konstruktionsprinzipien gebauten Maschinen Water-Maschinen, das von ihnen erzeugte Garn Watergarn oder Watertwist genannt, und diese Bezeichnungen sind bis heute beibehalten worden. Selbst als dann späterhin die Dampfmaschine zum Antrieb solcher Maschinen benutzt wurde, geschah das ursprünglich nur in der Weise, daß die Dampfmaschine vermittels einer Pumpe Wasser hob, welches dann auf das Wasserrad der Spinnmaschine geleitet wurde und diese in Bewegung setzte.

Abb. 76
Arkwrights Spinnmaschine

Die Arkwrightsche Maschine, die unsere Abbildung 76 wiedergibt, erwies sich von Anfang an als ein sehr geeignetes maschinelles Hilfsmittel für die Spinnerei und hatte bald bedeutende Erfolge zu verzeichnen. Damit beschwor aber Arkwright, in ganz ähnlicher Weise, wie es bei Hargreave der Fall gewesen war, die Mißgunst und den Unverstand der Kreise der berufsmäßigen Spinner, die sich durch seine Maschine bedroht glaubten, gegen sich. Auch er hatte Verfolgungen und Anfeindungen zu erleiden, auch seiner Maschine drohte mehr als einmal das Schicksal der Vernichtung. Doch hatte sich die neue Maschine verhältnismäßig bald und schnell auch in anderen Spinnereien eingeführt, so daß diese Vernichtungspläne nicht zu Ende geführt werden konnten. Späterhin aber wurde ihm von den Gebrauchern seiner Maschine das Erfindungsrecht bestritten und die Gültigkeit seines Patents angegriffen. Diese Angriffe stützten sich auf die Ähnlichkeit der Water-Maschine mit der Wyattschen Maschine sowie auf die Tätigkeit des früheren Mitarbeiters Arkwrights, Kays, der inzwischen verstorben war. Es wurde auch ein Modell Kays aus dem Jahre 1768 beigebracht, um an diesem die Ungültigkeit des Patents von Arkwright zu erweisen. Möglich, ja wahrscheinlich sogar, daß Arkwright von diesem Modell ausgegangen ist; dennoch vermochte er den Nachweis zu führen, daß seine Maschine so viel Neues aus seiner eigenen Erfindungstätigkeit enthielt, daß er seine Rechtsansprüche gegen seine Gegner in vollem Umfange durchzusetzen vermochte. Auch waren ja die Angriffe seiner Gegner viel weniger von dem Bestreben eingegeben, den früheren Erfindern zu ihrem Recht zu verhelfen, als vielmehr sich selbst ihrer Abgabepflicht an Arkwright zu entledigen, ein aus Krämergeist und Gewinnsucht in gleicher Weise gemischtes Verhalten, das gerade die englischen Industriellen hervorragenden Erfindern gegenüber in zahllosen Fällen an den Tag gelegt haben und das besonders auch die Erfinder auf dem Gebiete der Spinnerei- und Webereitechnik erfahren haben. Arkwright gewann seine Prozesse gegen die Besitzer seiner Patente, und aus den Gebühren, zu deren Zahlung jene verurteilt wurden, flossen ihm im Laufe der Jahre sehr bedeutende Mittel zu, ebenso wie sich auch seine eigene Spinnerei überaus günstig entwickelte. Diese Umstände machten ihn im Laufe der Jahre zu einem der reichsten Leute Englands. Auch an öffentlicher Anerkennung fehlte es ihm nicht; im Jahre 1786 wurde er zum Obersheriff von Derbyshire ernannt und bald darauf in den Adelstand erhoben. Als er am 3. August 1792 starb, hinterließ der ehemalige Barbier ein Vermögen von über 10 Millionen Mark.

Noch ein dritter Erfinder auf dem Gebiete der Spinnereimaschine sei hier erwähnt, Samuel Crompton (geb. 1753 zu Firwood in Lancashire, gest. 1827 ebendort), ein Mechaniker von Beruf. Dessen Maschine ging aus der Verbindung wesentlicher Bauelemente der Maschinen von Hargreave und Arkwright hervor. Crompton entlehnte aus der Jenny-Maschine den fahrbaren Wagen, aus der Water-Maschine hingegen das Walzenstreckwerk und schuf damit (während der Jahre 1774 bis 1779) einen neuartigen Typus der Spinnmaschine, der die Vorteile jener beiden Maschinen in sich vereinigte, ohne ihre Mängel zu haben, und damit berufen war, das bis auf den heutigen Tag vollkommenste System der Spinnmaschine zu werden. Da diese Maschine ihrer Bauart und Arbeitsweise nach gleichsam ein Bastard zwischen der Jenny-Maschine und der Water-Maschine war, nannte Crompton sie mit derbem englischen Humor Mule-Maschine (nach mule, Maultier, dem Bastard zwischen Stute und Eselhengst). Die Überlegenheit der Mule-Maschine bekundete sich von Anfang an darin, daß sie viel feineres Garn als die Jenny-Maschine und ebenso auch als die Water-Maschine erzeugte und das Spinnen auch des feinsten Garnes möglich machte, womit sie als die wichtigste Erfindung auf dem Gebiete der Spinnerei zu gelten hat.

Cromptons Maschine führte sich in den großen englischen Fabriken rasch ein, und um das Jahr 1800 wurden bereits in 300 Fabriken nahezu fünf Millionen Spindeln an Mule-Maschinen in Tätigkeit gesetzt, welche 70 000 Spinnern und 150 000 Webern Arbeit gaben. Crompton selbst hat freilich die Früchte seiner Erfindung nur in sehr bescheidenem Maße genossen. Zwar ist es ihm nicht so schlimm ergangen wie Hargreave, andererseits gestaltete sich sein Erfinderschicksal auch nicht im entferntesten so günstig wie das von Arkwright, obwohl seine Maschine einen wesentlich höheren und wertvolleren Typus der Spinnmaschine als die Arkwrights darstellte. Um sich nicht den Verfolgungen und Anfeindungen seitens der Manufakturisten und Arbeiter auszusetzen, hatte er von vornherein auf die Patentierung seiner Maschine verzichtet, in der Hoffnung, daß ihn die englische Regierung für seine Erfindertätigkeit, die, wie schon sehr bald ersichtlich wurde, von weittragendster Bedeutung für das gesamte industrielle und kommerzielle Leben des Landes werden mußte, in angemessener Weise entschädigen würde. Diese Hoffnung ist nur in sehr bedingter Weise in Erfüllung gegangen. Es wurde ihm auf sein Gesuch nur die Summe von ganzen 100 Pfund (= 2000 Mark) zuerkannt, im Jahre 1800 dann allerdings nochmals 500 Pfund und zehn Jahre später nochmals eine Belohnung von 5000 Pfund, gewiß ein bescheidenes Entgelt für eine Erfindung, die den Reichtum des Landes um Hunderte von Millionen Mark gemehrt hat. Diese Entschädigung von Staats wegen hat es denn auch nicht verhindern können, daß der Erfinder, der das Mehrfache jener Beträge auf seine Erfindung verwandt und dieser sein ganzes Vermögen geopfert hatte, in den dürftigsten Verhältnissen starb. Erst nach seinem Tode hat ihm sein Vaterland durch Aufstellung eines Kolossaldenkmals in Preston den Zoll der Dankbarkeit gewidmet.

Die bis zu dieser Stufe der technischen Entwicklung gelangten Spinnmaschinen dienten zunächst lediglich für das Verspinnen der Baumwolle, und Jahrzehnte hindurch blieb die Baumwollspinnerei die einzige Anwendungsweise jener Maschinen. In den ersten Jahrzehnten des vorigen Jahrhunderts machte sich dann auch das Bedürfnis nach einer geeigneten Maschine für das Verspinnen anderer Stoffe, vor allem des Flachses und der Wolle, geltend. Das erforderte jedoch eine Abänderung der Spinnmaschine für diese besonderen Zwecke, ja sogar eine konstruktive Neuerfindung in wesentlichen Teilen, die ein weiteres Kapitel in der Geschichte und Entwicklung der Spinnmaschine ist. Während die Baumwollspinnmaschinen von englischen Erfindern ausgebildet wurden, geschah die Erfindung der Flachsspinnmaschine durch einen Franzosen. Die Geschichte dieser Erfindung ist ein überaus interessantes Kapitel.

Dem Kaiser Napoleon gebührt das Verdienst, den Anstoß zur Erfindung der Flachsspinnmaschine gegeben und das erfinderische Genie, dem die Lösung dieses Problems gelingen sollte, ans Licht gezogen zu haben. Veranlaßt wurde das durch seinen Wirtschaftskampf gegen die englische Industrie, der seinen Höhepunkt in der Kontinentalsperre, der Abschließung des kontinentalen europäischen Handelsmarktes gegen die Einfuhr englischer Waren, erreichte. Aus diesen Bestrebungen des zielbewußten Korsen erwuchs auch der Plan, der infolge der Spinnmaschinen gewaltig aufgeblühten englischen Baumwollspinnerei, die ganz Europa mit ihren Erzeugnissen versorgte, einen Wettbewerb auf dem Kontinent zu schaffen. Da die Seemacht der Engländer ihn an der Einfuhr der Baumwolle nach dem Kontinent hinderte, kamen nur die heimischen Textilstoffe in Betracht, vor allem der Flachs. Eine aufblühende kontinentale Flachsspinnerei zu schaffen, durch welche der Kontinent von der englischen Baumwollindustrie unabhängig gemacht und so dem verhaßten England ein schwerer wirtschaftlicher Schlag beigebracht werden sollte, war der Plan, zu dem Napoleons weitblickende Politik führte. Die Ausführung dieses Planes aber setzte voraus, die Flachsspinnerei in ebenso großzügiger und rationeller Weise mit Maschinen zu betreiben, wie es die Engländer mit dem Verspinnen der Baumwolle tun konnten. Aus diesen Erwägungen heraus erließ Napoleon ein Dekret, datiert vom 12. Mai 1810, in welchem er einen Preis von einer Million Franken für den Erfinder einer Flachsspinnmaschine, gleichviel welcher Nation dieser angehören würde, aussetzte.

Ein französischer Erfinder, Philippe de Girard, war es, der die von dem französischen Kaiser gestellte Aufgabe in vollkommener Weise löste und sich dadurch für immer einen hervorragenden Platz in der Geschichte der Textiltechnik sicherte. Das Leben Girards war ein überaus eigenartiges Erfinderschicksal. Geboren 1755 zu Loumarin als Sohn eines begüterten Vaters, hatte er sich schon zeitig der Lösung wissenschaftlicher und technischer Probleme zugewandt. Die Erfindung eines achromatischen Fernrohrs und die einer hydrostatischen Lampe gelangen ihm schon in jungen Jahren. Das Dekret Napoleons regte den damals 35jährigen Girard mächtig an. Mit Feuereifer machte er sich an die Lösung der gestellten Aufgabe mit dem Erfolg, daß er bereits zwei Monate nach dem Erlaß jenes Dekrets ein Patent auf eine neue Flachsspinnmaschine anmelden konnte, das die Lösung des gestellten Problems enthielt.

Girard hatte die Aufgabe an der richtigen Seite angepackt. Er hatte die Flachsfaser eingehend untersucht und gefunden, daß deren ursprüngliche Länge und Härte dem Verspinnen auf der üblichen Baumwollspinnmaschine unüberwindliche Schwierigkeiten entgegensetzten, daß also eine Umwandlung im organischen Gefüge der Flachsfaser stattfinden müsse, um sie zum Verspinnen geeignet zu machen. Er fand, daß durch die Einwirkung von Wasser die ursprüngliche Flachsfaser in einzelne feine Fäserchen getrennt werden kann, die sich leicht und mühelos verspinnen lassen. Demgemäß baute er eine Maschine, bei der die Flachsfasern, bevor sie zur eigentlichen Verarbeitung gelangten, einen Trog mit heißem Wasser zu passieren haben, worauf durch Hechelkämme das Trennen der ursprünglichen Fasern in einzelne kleine Fäserchen und durch geeignete mechanische Vorrichtungen das Ausrichten der Faserbündel bewirkt wird. Das Verspinnen des so gewonnenen Materials feiner und geschmeidiger Fasern erfolgt dann ganz ähnlich wie bei der Baumwollspinnmaschine. »Die Million ist mein!«, rief der Erfinder beglückt aus, als er sein Patent angemeldet hatte. Darin aber sollte er sich sehr geirrt haben. Die von ihm erfundene Maschine wurde zwar von der französischen Regierung als vollkommene Lösung des Problems anerkannt, den ausgesetzten Preis hat der Erfinder jedoch nicht erhalten. Denn die Wirren der nächsten Jahre in Frankreich, der unglückliche Ausgang des Feldzuges Napoleons gegen Rußland und die weiter folgenden kriegerischen und politischen Ereignisse, die schließlich zum Sturz Napoleons und des Kaiserreiches führten, brachten die von Napoleon eingegangene Verpflichtung in Vergessenheit. Girard, der in der Hoffnung auf die Auszahlung des Preises bereits eine große Fabrik zum Bau von Flachsspinnmaschinen begründet hatte, geriet dadurch in schwere Bedrängnis. Da ihn die Gläubiger bedrängten, folgte er im Jahre 1815 einem Ruf nach Österreich, wo er in dem Orte Hirtenberg bei Wien eine Maschinenbauanstalt für Flachsspinnmaschinen und gleichzeitig eine Flachsspinnerei einrichtete, die er bis 1825 leitete.

Seine Erfindung hat dann sehr eigenartige Schicksale erfahren. Zwei Werkmeister der von ihm begründeten, dann aber wieder eingegangenen Fabrik gingen nach England und verkauften dort betrügerischerweise die Erfindung Girards als ihre eigene für 25 000 Pfund Sterling an englische Spinnereien, darunter auch an den Spinnereibesitzer Horace Fall, der, ebenso unehrlich wie jene, die Erfindung für England dann nochmals auf seinen Namen patentieren ließ. Damit war der Grund gelegt zu der englischen Flachsspinnerei, die in der Folge rasch und schnell emporblühte. So kam es, daß die Erfindung der Flachsspinnmaschine, die angeregt und gemacht worden war, um der englischen Textilindustrie einen vernichtenden Schlag zuzufügen, in der Folge englisches Besitztum und die Grundlage einer neuen Industrie Englands wurde. Von England kam die Flachsspinnmaschine dann wieder nach Frankreich zurück und galt dort zunächst für eine englische Erfindung, bis es Girard gelang, durch Veröffentlichung in französischen Zeitungen den Nachweis seiner Vaterschaft zu führen. Er hatte dabei mit dem heftigsten Widerstand der Regierung seines eigenen Vaterlandes zu kämpfen. Denn auf Veranlassung des französischen Handelsministeriums war die in England so erfolgreich eingeführte Flachsspinnmaschine auch nach Frankreich gebracht worden; das Ministerium fürchtete durch Anerkennung der Erfinderrechte Girards die Beziehungen zu England zu schädigen und stand daher den Ansprüchen und Veröffentlichungen Girards entschieden ablehnend gegenüber. Es bedurfte erst eines energischen Protestes seitens der französischen Gelehrten und Ingenieure, die aus nationalen Gründen die Sache Girards zu der ihrigen gemacht hatten, ehe das Ministerium seinen Widerstand aufgab. Auch sonst hat Girard keinen Dank von seinem Vaterlande geerntet. Durch die Unerbittlichkeit seiner Gläubiger blieb er verbannt, da damals in Frankreich noch die Institution der Schuldhaft bestand, und erst nach seinem siebzigsten Lebensjahre durfte er zurückkehren, ohne befürchten zu müssen, in den Schuldturm geworfen zu werden. Eine bescheidene Pension wurde dem Greis, der durch seine Erfindung der Welt eine neue und mächtige Industrie erschaffen hatte, verweigert, und die Mißgunst des Handelsministeriums ging so weit, dem Erfinder auch die für ihn vorgeschlagene öffentliche Ehrung durch den Orden der Ehrenlegion zu verwehren. So starb Girard in kümmerlichen Verhältnissen. Seine Erfindung aber trat von England aus einen Siegeszug um die ganze Welt an. Im Jahre 1830 wurde in Leeds in England bereits eine Flachsspinnerei von 20 000 Spindeln betrieben.

Noch länger dauerte es, bis auch die Wollspinnerei für die Anwendung der Spinnmaschine reif wurde. Wie für die Baumwollspinnerei, so war auch für die Wollspinnerei unbedingte Voraussetzung das Vorhandensein bzw. die Erfindung einer geeigneten Kämmaschine, durch welche aus dem Gemisch der sehr verschieden langen Wollfasern die kurzen Fasern ausgeschieden und so das Rohmaterial bis zu dem notwendigen Grade von Feinheit fertiggemacht werden konnte. So eifrig dieses Problem, von dessen Lösung die Möglichkeit der Wollspinnerei abhing, von den verschiedensten Seiten aus auch bearbeitet wurde, so dauerte es doch Jahrzehnte, ehe wirklich brauchbare Maschinen dieser Art erfunden wurden. Zwar hatte schon im Jahre 1790 Edmund Cartwright, der damals bereits als Erfinder des mechanischen Webstuhls berühmt geworden war, auch eine Maschine zum Wollkämmen gebaut, die sich jedoch darauf beschränkte, den Vorgang des Kämmens mit der Hand mechanisch nachzuahmen, also keinen neuartigen Erfindungsgedanken aufwies und auch keinen nennenswerten Erfolg zu verzeichnen hatte. Dennoch aber machten die gewerblichen Handkämmer gegen diese Maschine energisch Front, und sie setzten es durch, daß die von Cartwright im Jahre 1794 bei Ramsbottom bei Bradford errichtete und durch ein Göpelwerk betriebene Kämmaschine wieder stillgelegt wurde. Wieder einmal trugen Beschränkheit, Angst vor dem Neuen und handgreifliche Gewalt den Sieg über den Fortschritt der Technik davon. In den nächsten Jahrzehnten finden wir dann eine ganze Reihe von Erfindern, sowohl englischer wie auch französischer und deutscher Abstammung, an der Arbeit, eine brauchbare Kämmaschine zu bauen und dadurch auch die Wolle der mechanischen Verspinnung zugänglich zu machen. Angesichts der großen Bedeutung einer solchen Erfindung setzte die französische »Gesellschaft zur Aufmunterung der Nationalindustrie« in Paris, die eigens zu dem Zweck ins Leben gerufen war, den Erfindungsgeist des Landes durch Unterstützung und Belohnungen anzuregen, einen bedeutenden Preis auf die Lösung des Problems aus, der auch dem Erbauer einer solchen Maschine, Demaury mit Namen, im Jahre 1810 erteilt wurde. Doch konnte auch diese Maschine noch keinen dauernden Erfolg erzielen, ebenso wie eine vier Jahre später prämiierte andere Kämmaschine eines französischen Erfinders. Nach zahlreichen anderen Versuchen wurde dann in den dreißiger Jahren das erste brauchbare System einer Wollkämmaschine von dem Deutschen Heinrich Wieck aus Chemnitz erfunden, das dann in England weitere Verbesserung erfuhr und hier die Grundlage zum Bau solcher Maschinen wurde. Eine andere Wollkämmaschine stammte von Samuel Lister und dessen Landsmann Donnisthorpe her, die bereits seit 1835 getrennt an der Konstruktion von Kämmaschinen gearbeitet hatten, ohne Erfolg zu erzielen. Ein solcher wurde ihnen erst beschieden, als sie die Konstruktionsprinzipien ihrer beiden Maschinen zugleich mit Konstruktionselementen der Maschine von Wieck zu einem neuen System vereinigten, das seitdem unter dem Doppelnamen der beiden Genannten sich dauernd behauptet hat.

Die vollkommene Lösung erfuhr das Problem der Wollkämmaschine jedoch erst durch den Elsässer Josua Heilmann, einen genialen Kopf, dem die Textilindustrie noch zahlreiche andere und überaus wertvolle Neuerungen und Erfindungen verdankt und der in der Erfindungsgeschichte dieser Industrie für immer einen hervorragenden Platz einnimmt. Heilmann (geboren 1796 in Mülhausen) war ursprünglich für den Kaufmannsberuf bestimmt worden, dann jedoch durch den Plan seiner Verwandten, eine Baumwollspinnerei zu errichten, auf den Weg geleitet worden, der für sein ganzes Leben entscheidend werden sollte. Obwohl erst 22 Jahre alt, entwarf er alle Pläne für die neu zu errichtende Spinnerei, die er dann Jahre hindurch mit gutem Erfolge leitete. Eine Anzahl kleinerer Erfindungen zur Verbesserung der damals üblichen Spinn-, Webe- und Appreturmaschinen, die er als technischer Leiter jener Fabrik machte, stammt aus jener Zeit. Einige Jahre darauf machte er die hochbedeutende Erfindung der Stickmaschine, die seitdem grundlegend für den Bau solcher Maschinen geworden ist. In den dreißiger Jahren wandte er sich dann der Erfindung einer geeigneten Wollkämmaschine zu. Dieses Problem bereitete auch seinem erfinderischen Geist ungeahnte Schwierigkeiten. Sieben Jahre hindurch arbeitete er mit Mißerfolg an der Lösung der Aufgabe, der er sein ganzes Vermögen opferte. Auf die richtige Spur soll er dadurch geleitet sein, daß er zufällig beobachtete, wie sich seine Tochter, vor dem Spiegel stehend, das Haar kämmte, wodurch er die Idee der mechanischen Verrichtung des Wollkämmens faßte. Nach der ihm hierbei gekommenen neuen Idee baute er eine Wollkämmaschine, welche die vollständige Lösung des Problems bedeutete.

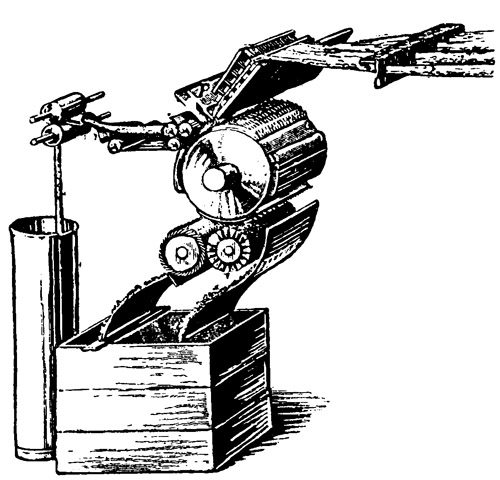
Abb. 77
Heilmanns Kämmaschine

Die Heilmannsche Methode beruht auf der Verwendung einer mit Zähnen besetzten Walze, der Kämmwalze, in Verbindung mit einem sich periodisch öffnenden und schließenden Apparat, dem Speiser, durch den das Garn der Walze in den notwendigen Abständen zugeführt wird. Unsere Abbildung 77 gibt eine Darstellung dieser beiden wichtigsten Teile der Heilmannschen Kämmaschine, die sich in der Folgezeit allen anderen Systemen solcher Maschinen als ganz bedeutend überlegen erwies und im wesentlichen die Grundlage für die dann erfolgte rasche Entwicklung der Wollkämmerei und Wollspinnerei geworden ist. Heilmann überlebte den Triumph seiner Erfindung nicht lange; die schweren geistigen und körperlichen Anstrengungen und die vielfachen Kämpfe, Leiden und Enttäuschungen seiner Erfinderlaufbahn hatten seine Gesundheit untergraben. Im Jahre 1848 starb der hochverdiente Mann, erst 52 Jahre alt. Die Nachwelt freilich zollte der Erfindung Heilmanns volle Anerkennung. Zwar erfuhr auch diese Erfindung das Schicksal so mancher andern, nämlich betrügerischerweise benutzt zu werden. Ein Engländer, der die Heilmannsche Kämmaschine auf der Ausstellung in Frankfurt a. M. gesehen hatte, baute die Maschine nach und ließ sie sich für England als eigene Erfindung patentieren. Als er jedoch sogar den Mut hatte, die Maschine auf einer Ausstellung in London im Jahre 1851 öffentlich zur Schau zu stellen, wurde der Betrug entdeckt und der Betrüger zur Rechenschaft gezogen. Die Leitung der Ausstellung stellte selbst die Priorität Heilmanns fest und ließ die Maschine des Betrügers bedecken. Von den Erben Heilmanns wurde dann das Patent der Maschine von einem englischen Konsortium für den Preis von zwei Millionen Mark angekauft, eine für die damalige Zeit ganz ungeheure Summe, die freilich dem Erfinder selbst nicht zugute kam.

Deutschen Ursprungs ist dann noch die Erfindung des Florteilers, einer Maschine, welche die Grundlage der Streichgarnspinnerei geworden ist. Der Erfinder war der sächsische Tuchmacher Ernst Geßner aus Lößnitz im Erzgebirge, der im Jahre 1861 seine Maschine an die Öffentlichkeit brachte. Diese Maschine machte es möglich, den vorgearbeiteten Faserstoff, der in Form eines breiten Florstreifens von der Abnahmewalze kommt und der Spinnmaschine zugeführt wird, in etwa 100 einzelne Fäden zu teilen, die sofort der Spinnmaschine zur weiteren Verarbeitung zugeführt werden können. Geßners Erfindung wurde einige Jahre später von dem Franzosen Cölestin Martin in Verviers nachgeahmt, und Martin ließ sich sogar ein eigenes Patent auf die Maschine geben, die er dann an französische und englische Fabrikanten verkaufte. Das ändert jedoch nichts an der Tatsache, daß Geßner der alleinige Erfinder dieser wichtigen und interessanten Maschine ist, welche die allergrößte Bedeutung für die Streichgarnspinnerei gewonnen hat. Geßner hat noch verschiedene andere wertvolle Erfindungen für die Textiltechnik gemacht, unter denen vor allem seine Universal-Rauhmaschine zu nennen ist, ohne jedoch große Reichtümer zu erwerben, während sein Nachahmer Martin mit der Verwertung der Geßnerschen Erfindung ein Vermögen erwarb.

II

Das Problem des Webstuhls – Der Bandwebstuhl und sein Erfinder – Liebe und Strickstrumpf – Die Erfindung der Strickmaschine – John Kay und seine Erfindungen – Der Kraftwebstuhl – Vorgänger – Edmund Cartwright, seine Erfindungen und sein Schicksal – Der Welt Lohn – James Jeffray

Die Spinnmaschine, wie sie in ihren verschiedenen Arten aus der Tätigkeit der bisher genannten Erfinder hervorgegangen ist, stellt nur die eine Seite der Textiltechnik dar; sie erzeugt aus dem Faserstoff das Garn. Die andere Seite der Textiltechnik und gleichsam die Ergänzung jener ist die Webemaschine, vermittels deren das Garn zum Tuch verarbeitet wird. Mit dem Erfindungsgange dieser Maschinen wollen wir uns nunmehr auch noch befassen. Auch hier tritt uns die Problematik des Erfindens in ihrer ganzen Eigenart entgegen, tritt uns eine Anzahl seltsamer Erfinderschicksale entgegen.

Die technische Entwicklung der Weberei war jahrhundertelang in nahezu unveränderter Form stehengeblieben, so wie sie von den Völkern des Altertums auf die des Mittelalters überkommen war. Die Weberei war ein Handwerk, dessen Zunftverfassung seiner technischen Entwicklung, der Erfindung und Anwendung neuer und vervollkommneter Hilfsmittel, vielfach hinderlich im Wege stand. Die zünftigen Weber des Mittelalters waren, wie die anderen Zünfte allerdings auch, recht futterneidische Gesellen, die ängstlich darüber wachten, daß der einzelne unter ihnen nicht mehr schaffen und verdienen konnte als ein anderer, und dementsprechend waren die Zunftgesetze fast überall abgefaßt. Aus diesen Gründen stand man auch allen Verbesserungen der Webereigeräte ziemlich ablehnend gegenüber, und wo solche dennoch gemacht wurden, konnten und durften sie nur zu Anwendung kommen, wenn der Erfinder seine Neuerung allen Berufsgenossen seines Ortes zugänglich machte, wobei er selbst besondere Vorteile oder Vorrechte aus seiner Erfindung nicht beanspruchen durfte. Damit war natürlich dem Erfindungsgeist von vornherein der stärkste Ansporn benommen. Gerade in den Webergilden war dieser beschränkte und futterneidische Geist heimisch, was zum großen Teil die Ursache gewesen sein mag, daß die technische Entwicklung dieses Gewerbes Jahrhunderte hindurch nahezu auf derselben Stelle blieb.

Die ersten Anfänge zur Vervollkommnung der Webereitechnik und der Verbesserung der für diese notwendigen Hilfsmittel gingen von der Seidenweberei aus. Als einer der ersten Erfinder auf diesem Gebiete tritt uns der Seidenbandweber Anton Moller aus Danzig, der Erfinder des verbesserten Seidenbandwebstuhles, auch Seidenmühle oder Bandmühle genannt, entgegen. Im Jahre 1586 (nach anderen 1600) stellte Moller einen solchen Apparat fertig, auf dem ein Arbeiter gleichzeitig 16 bis 20 Bänder auf einmal herstellen konnte, während auf dem alten Bandstuhl immer nur ein einziges Band gewebt werden konnte. Diese wichtige Erfindung sollte ihrem Urheber jedoch sehr verhängnisvoll werden. Die Danziger Bandweber sahen in der Neuerung eine schwere Bedrohung ihres Gewerbes, die nach ihrer Meinung zur Folge haben mußte, sie zum größten Teil arbeits- und brotlos zu machen. Sie rotteten sich zusammen, drangen in Mollers Haus ein und zerstörten seine Maschine vollkommen. Der Erfinder selbst wurde von der wütenden Menge gepackt und in die Weichsel geworfen, wo er seinen Tod fand. In verbesserter Form tauchte die Erfindung dann im Jahre 1623 in der Schweiz wieder auf, in Leiden dagegen im Jahre 1629, und im Lauf der folgenden Zeiten gewann der Bandwebstuhl langsam an Verbreitung, freilich immer nur unter heftigstem Widerstand der Bandweberzünfte, die sogar mehrfach behördliche Verbote der Benutzung der neuen Maschinen erwirkten. Ein solches Verbot wurde im Jahre 1685 in Deutschland erlassen, und Kaiser Karl VI. erneuerte noch im Jahre 1719 auf Drängen der Posamentierer und Bortenweber dieses Verbot für ganz Deutschland. In Hamburg soll sogar ein Bandwebstuhl auf Befehl des Magistrats öffentlich verbrannt worden sein.

Aus ungefähr derselben Zeit wie die Erfindung des Bandwebstuhles stammt übrigens auch die Erfindung einer anderen textiltechnischen Maschine, nämlich der Strickmaschine, durch den Engländer Lee. Es wird berichtet, daß Lee diese Maschine erfunden haben soll, um seiner Braut, die bei seinen Besuchen stets und ständig mit dem Strickstrumpf beschäftigt war und ihrem Verlobten infolgedessen nicht die Aufmerksamkeit zuwenden konnte, welche dieser wünschte, jene Arbeit zu erleichtern und ihr so mehr Muße zu schaffen, sich mit ihm zu beschäftigen. Demnach wäre also die Eifersucht auf den Strickstrumpf der Anlaß zu der Erfindung der Strickmaschine gewesen. Nach einer anderen Mitteilung dagegen soll Lee erst, als er bereits verheiratet und Prediger zu Calverton war, diese Erfindung gemacht haben, weil seine Frau durch Strümpfestricken einiges zum Unterhalt der Familie hinzuzuverdienen suchte. Wie dem auch sei, jedenfalls war es Lee, der den ersten Stuhl für die Strumpfstrickerei herstellte, und zwar gleich in solcher Vollkommenheit, daß noch die heutigen Maschinen dieser Art vollständig auf jener ersten Erfindungskonstruktion beruhen. Lees Maschine bestand aus 2000 Teilen und wurde zum ersten Male im Jahre 1589 von ihm zur Anwendung gebracht. Er suchte nunmehr die zünftigen Strumpfwirker für seine Maschine zu gewinnen, erfuhr jedoch dasselbe Schicksal wie die meisten Erfinder auf dem Gebiete der Textiltechnik. Die Maschine erweckte Argwohn und Befürchtungen bei den Zünftigen, und Lee wurde von diesen auf das heftigste angefeindet als Verderber der Zunft. Da sich auch die Regierung, an die er sich zwecks Verwertung seiner Erfindung gewandt hatte, seiner nicht annahm und ihm auch jede Unterstützung gegen die Anfeindungen der Zünfte versagte, wandte er sich nach Frankreich. Hier fand er mehr Verständnis für seine Erfindung als im eigenen Vaterlande, und die französische Regierung setzte ihm die Mittel zur Begründung einer mechanischen Strumpfwirkerei aus. In dieser stellte Lee auch die ersten auf einer Maschine gestrickten seidenen Strümpfe her, die Maria von Medici trug. Die politischen Ereignisse in Frankreich lenkten jedoch die Aufmerksamkeit von seiner Erfindung wieder ab, so daß letzten Endes auch dieser Erfinder um den Lohn seiner Arbeit kam. Nach seinem Tode wurde die Strickmaschine von einem Bruder Lees wieder nach England zurückgebracht. Diesmal fand sie hier mehr Verständnis. Eine Reihe von Fabrikanten sicherte sich die Benutzung und legte damit den Grund zu der alsbald kräftig emporblühenden mechanischen Strumpfwirkerei in England. Von dort aus gelangte die Maschine dann mit gleichem Erfolg auch nach den anderen europäischen Ländern. Ursprünglich nur für die Seidenstrickerei verwandt, wurde die Maschine in der Folgezeit auch zur Verarbeitung aller anderen Textilstoffe zur Anwendung gebracht.

Ein hervorragender Erfinder auf dem Gebiete der Webetechnik war dann der Engländer John Kay, durch dessen Tätigkeit die Verbesserung des alten Webstuhles zu einem vervollkommneteren und leistungsfähigeren Apparat überhaupt erst in die Wege geleitet wurde. Zwei Erfindungen Kays waren hierfür maßgebend. Die erste war die Verbesserung des Rietblattes, die von ihm im Jahre 1730 gemacht wurde. Bis dahin bestand das Rietblatt, auch Kamm genannt, also jenes Organ des Webstuhles, mit dem der Einschlag festgeschlagen wird, im wesentlichen aus einem Rahmen, der mit einer Reihe von Rohrstäben besetzt war. Diese Rohrstäbchen hatten den Nachteil, sich schnell abzunutzen und dadurch das Gewebe zu beschädigen, außerdem konnten nur grobe Gewebe mit ihnen gewebt werden. Um allen diesen Nachteilen zu begegnen, ersetzte Kay die Rohrstäbe durch Stäbe aus poliertem Metall, die sich als ungleich dauerhafter erwiesen, keinerlei schädigende oder reibende Wirkung auf das Garn ausübten und überdies viel dünner gehalten waren als die alten Rohrstäbe, so daß auch viel feinere Gewebe mit ihnen gewebt werden konnten. Diese Verbesserung gelangte bald und allgemein zur Anwendung.

Von wesentlich größerer Bedeutung jedoch war die andere Erfindung Kays, nämlich die des Schnellschützen, die aus dem Jahre 1736 stammt. Bei ausnahmslos allen Webstühlen war bis dahin das uralte Webschiffchen zur Einführung der Einschußfäden in die Kette in Gebrauch gewesen. Der Weber warf hierbei das Schiffchen mit der einen Hand durch die geöffnete Kette und fing es an der anderen Seite mit der anderen Hand wieder auf. So einfach, ja fast primitiv, diese Vorrichtung war, hatte sie sich doch die Jahrhunderte hindurch unverändert erhalten. Schmale oder mittelbreite Gewebe konnten hierbei von einem Arbeiter hergestellt werden, bei breiten Geweben jedoch, über die der Arm des Webers nicht hinwegreichte, war noch ein zweiter Arbeiter nötig, der das Schiffchen auf der anderen Seite auffing und wieder zurückwarf. John Kay war der erste, der eine bedeutsame Verbesserung anbrachte, indem er das Schiffchen mit Rollen versah und des weiteren die sogenannte Peitsche zur Anwendung brachte, einen Lederriemen, vermittels dessen das Schiffchen durch die Kette getrieben wurde. Durch diese Verbesserung wurde die Leistungsfähigkeit des Arbeiters reichlich verdoppelt, auch konnte er jetzt sehr breite Gewebe herstellen, ohne eines Hilfsarbeiters zu bedürfen. Damit begann die technische Entwicklung des Webstuhles, die dann von anderen fortgesetzt wurde. Von Kay stammt noch eine Anzahl weiterer Verbesserungen am Webegerät. Auch dieser Erfinder hat keinen Dank geerntet. Die Weber in Bury, dem Wohnort Kays, stürmten nach alter Tradition das Haus des Erfinders und zerstörten seine Maschinen, und als späterhin seine Verbesserungen dennoch zur Anwendung kamen, wurde ihm seitens der Benutzer seiner Patente jede Entschädigung verweigert. Wie Lee, so trieb auch ihn der Undank seiner Landsleute nach Frankreich, und als er sich von dort aus an das englische Parlament wandte und von Staats wegen um eine Entschädigung für seine Erfindung bat, welche zu dem großen Aufschwung der englischen Textilindustrie sehr bedeutend beigetragen hatte, erhielt er nicht einmal eine Antwort. Er starb im Elend, und heute weiß man nicht einmal, wo dieser geniale Erfinder begraben liegt, dem heute ungezählte Millionen seines Vaterlandes ihren Wohlstand verdanken. Sein Sohn Robert Kay betätigte sich ebenfalls als Erfinder auf dem Gebiete der Textiltechnik. Von ihm rührt die Wechsellade, auch Doppellade genannt, her, die das Einschießen verschiedenartiger Fäden möglich macht, indem der Weber abwechselnd mehrere Schützen mit verschiedenen Farben nach Belieben bewegt. Diese Vorrichtung wurde allerdings erst später so weit vervollkommnet, um ein wertvoller Bestandteil des Webstuhles zu werden.

Die stärkste und weitgehendste Umwälzung auf dem Gebiete der Webereitechnik erfolgte jedoch erst durch die Erfindung und Einführung des mechanischen Antriebs der Webstühle, also durch den Kraftwebstuhl, durch den die gesamte Webereiindustrie in der Folgezeit erst den Aufschwung nehmen konnte, der sie bis zu ihrer heutigen Höhe und Bedeutung führte.

Schon Leonardo da Vinci, dessen Entwurf einer Spinnmaschine wir bereits erwähnten, beschäftigte sich auch mit der Erfindung eines mechanischen Webstuhles, der jedoch ebenfalls wie jene im Entwurf steckengeblieben ist. Dann finden wir aus dem Jahre 1678 Mitteilungen über die Erfindung eines mechanischen Webstuhles vor, als deren Urheber der französische Seeoffizier de Game genannt wird. Doch ist auch dessen Idee nicht zur praktischen Anwendung gekommen, da er bei den Webern keinen Anklang für diese fand. Dann finden wir den berühmten französischen Erfinder Vaucanson, der in der Geschichte der Textiltechnik eine sehr bedeutsame Rolle spielt, auch mit der Konstruktion eines mechanischen Webstuhles beschäftigt, der mit Kurbelantrieb versehen war und mit Wasserkraft betrieben werden sollte. Ein Fabrikant in Manchester stellte auch einige solcher Stühle versuchsweise auf, konnte jedoch keinen dauernden Erfolg damit erzielen, so daß diese Erfindung Vaucansons wieder in Vergessenheit geriet. Als dann die Spinnmaschinen erfunden worden waren, durch welche die Garnproduktion gewaltig zunahm, war auch in verstärktem Maße der Antrieb zur Erfindung und Anwendung von Webmaschinen gegeben. Denn die neuen Spinnmaschinen erzeugten viel mehr Garn, als die alten Handwebstühle zu verarbeiten mochten, und die Erfindungen Hargreaves, Arkwrights, Cromptons usw. hätten ihren Zweck verfehlt, wenn es nicht gelang, auch Webemaschinen zu erfinden, vermittels deren die vermehrte Garnproduktion in entsprechendem Maße verarbeitet werden konnte. Das konnte nur durch einen Webstuhl mit mechanischem Antrieb erreicht werden, und damit war ein Problem von größter industrieller und technischer Wichtigkeit gegeben, an dessen Lösung sich viele erfinderische Köpfe versuchten.

Der Erfinder, dem es gelang, dieses Problem zu lösen, war Edmund Cartwright, geboren 1743 zu Marsham in Nottinghamshire und im Jahre 1786 Prediger in Doncaster, wo er seine Erfindertätigkeit begann, ein Mann von großem mechanischen und erfinderischen Talent. Durch eine Unterredung in einer Gesellschaft, in der die Arkwrightsche Spinnmaschine erörtert und darauf hingewiesen wurde, welche gewaltige industrielle Bedeutung es für das ganze Land haben müßte, wenn es gelänge, auch das Gegenstück zu dieser Maschine, nämlich die mechanisch betriebene Webemaschine, zu erfinden, wurde er zum Bau einer solchen Maschine angeregt. Ohne die Konstruktion des Webstuhles näher zu kennen oder einen solchen je arbeiten gesehen zu haben, machte er sich doch wagemutig an die Lösung jenes Problems nach einer ihm vorschwebenden Idee. Der Versuch fiel dementsprechend aus. Zwar ließ der auf solche Weise entstandene Webstuhl im Prinzip die Möglichkeit des mechanischen Antriebs erkennen, die Arbeitsweise war jedoch so unbeholfen und schwerfällig, daß an eine praktische Verwertung der Maschine nicht gedacht werden konnte. Bei dieser ersten Maschine Cartwrights war die Kette vertikal gerichtet, die Lade mit dem Rietblatt hatte ein Gewicht von über einem halben Zentner, und die Federn, mit denen das Schiffchen bewegt wurde, waren nach Cartwrights eigener humorvoller Schilderung so stark, daß sie ausgereicht hätten, eine Kanonenkugel fortzuschleudern. Zwei kräftige Männer waren nötig, um die Maschine in langsame Bewegung zu setzen, und konnten die schwere Arbeit dennoch nur kurze Zeit aushalten. Immerhin aber webte Cartwright auf diesem Ungetüm von Maschine ein Stück Tuch, was ihn so weit ermutigte, daß er sich ein Patent geben ließ. Als er dann jedoch die Weber bei der Arbeit kennengelernt hatte und fand, daß diese mit ihrem alten Webstuhl viel schneller und leichter zu weben vermochten, als es jemals mit seiner Maschine der Fall hätte sein können, baute er diese belehrt um und kam zu einer neuen und verbesserten Konstruktion, die sich als ein wirklich brauchbarer mechanischer Webstuhl erwies, und die er sich im Jahre 1789 patentieren ließ. Diese Maschine ließ Cartwright ursprünglich durch einen Ochsen treiben, späterhin richtete er sie für den Antrieb mit Wasserkraft ein und schließlich auch für den Dampfbetrieb.

Die Erfindung erregte in England das allergrößte Aufsehen. War doch eine seit Jahrtausenden lediglich durch Menschenkraft betriebene Maschine zum erstenmal mit mechanischem Antrieb versehen worden, ein Problem, das bis dahin von den meisten für unlösbar gehalten worden war, und dessen Lösung ganz unabsehbare Aussichten erschloß. Cartwright selbst gründete in Doncaster eine Weberei, in der er zwanzig mechanische Webstühle aufstellte. Mangels genügender geschäftlicher Gewandtheit rentierte sich die Fabrik jedoch nicht, so daß er sie nach wenigen Jahren wieder aufgeben mußte. Andere Fabrikanten brachten seine Erfindung mit besserem Erfolg als er selbst zur Anwendung. Da der in der Geschichte der Erfindungen, besonders der auf textiltechnischem Gebiet, so oft bekundete Krämergeist und Eigennutz der englischen Industriellen auch diesem Erfinder gegenüber in Erscheinung trat und die Benutzer seiner Patente ihm jegliche Entschädigung ablehnten, obwohl Cartwright sein gesamtes und viel fremdes Vermögen für seine Erfindung geopfert hatte, wurde er in eine Reihe schwieriger Prozesse verwickelt, die ihm sein letztes Geld kosteten und ihm das Leben verbitterten. Erst später gewährte ihm das englische Parlament aus Staatsmitteln eine Entschädigung von 10 000 Pfund Sterling. Cartwright, der das Dreifache dieser Summe auf seine Erfindung verwandt hatte, pflegte mit Galgenhumor zu sagen, das Parlament habe ein Drittel der Schuld Englands an ihn abgezahlt.

Gleichzeitig mit Cartwright hatte übrigens auch der schottische Arzt Dr. James Jeffray einen mechanischen Webstuhl gebaut, ohne von der Erfindung Cartwrights zu wissen. Er hatte in seiner Praxis die Tätigkeit der Kunstweber kennengelernt und war dadurch angeregt worden, eine Vorrichtung zur mechanischen Ausführung dieser Arbeit zu erfinden, was ihm auch durchaus gelang. Er erhielt auf den von ihm gebauten mechanischen Webstuhl ebenfalls ein Patent, mußte jedoch die Nutzbarmachung seiner Erfindung anderen überlassen. Noch ein anderer Schotte, der Instrumentenmacher Kinloch, wurde der Erfinder eines mechanischen Webstuhles, der im Jahre 1793 patentiert wurde. Die Tätigkeit dieser Erfinder bewirkte es, daß die Einführung des mechanischen Webstuhles in Schottland unabhängig von der in England selbst und früher als hier erfolgte.

III

Die Erfindung des Musterwebstuhls – Vorgänger: Falcon, Vaucanson – Charles-Marie Jacquard – Aus des Erfinders Jugendzeit – Napoleon und der Erfinder – Die große Tat – Kampf und Sieg – Einst und jetzt

Endlich sei auch noch der Erfindung des Musterwebstuhls gedacht, eines der wichtigsten und scharfsinnigsten technischen Hilfsmittel der modernen Textilkunst. Der Werdegang dieser genialen Erfindung ist eines der eigenartigsten und reizvollsten Kapitel nicht nur in der Geschichte der Textilkunst, sondern im großen Buche der Geschichte der Erfindungen überhaupt, und daher auch für unsere Betrachtung der Problematik des Erfindens von besonderer Bedeutung. Gerade diese Erfindung läßt das Problematische des Erfindens und des Erfinderschicksales mit besonderer Deutlichkeit hervortreten.

Während die Erfindung der anderen wichtigen Textilmaschinen, vor allem der Spinn- und Webmaschinen, fast vollständig auf englischem Boden erfolgte, ist die Schöpfung des Musterwebstuhls nahezu gänzlich den Köpfen französischer Erfinder entsprungen. Die Anregung für die Entstehung des Musterwebstuhls gab ein Spezialgebiet der Textilindustrie, nämlich die Seidenindustrie, die damals in Frankreich in höchster Blüte stand. Auf diesem Gebiete machte sich zuerst und mehr als in anderen Zweigen der Textilindustrie das Bedürfnis nach einer mechanischen Vorrichtung zur Ausführung der Gewebemuster geltend. Der Seidenwebstuhl war bis in das 18. Jahrhundert hinein von nahezu derselben einfachen Form wie die anderen Webstühle, die der Erzeugung von Woll-, Baumwoll- und Leinenstoffen dienten, und selbst die berühmtesten Seidenwebereien jener Zeit arbeiteten zur Herstellung der Muster in ihren Geweben mit dem sogenannten »Zug«, einer sehr einfachen Vorrichtung, bei der, um das Muster zu erzeugen, die Fäden der aufgespannten Kette von dem Weber einzeln in die Hand genommen werden mußten. Nach mancherlei anderen Versuchen wurde zuerst im Jahre 1728 von dem Franzosen Falcon eine sehr bedeutungsvolle Neuerung an diesem alten Webstuhl erfunden, die in der Anwendung von Zylindern und Karten bestand. Die Karten waren nach Maßgabe des herzustellenden Musters mit Löchern versehen. Indem die Kettenfäden automatisch durch diese Löcher geleitet wurden, fügten sie sich zu dem Webemuster zusammen. Damit war der erste Schritt zur mechanischen Ausführung der Gewebemuster getan, und die erste Form eines Musterwebstuhls geschaffen. Allerdings war diese Konstruktion noch sehr mangelhaft; die Zylinder mußten mit der Hand in Bewegung gesetzt werden, die Bewegungen waren auch noch sehr ungleichmäßig, und die Wirkung der Musterkarten erstreckte sich nur über einen kleinen Raum, so daß mit dieser Vorrichtung auch nur Muster kleinen Umfanges gewebt werden konnten. Größere Muster mußten nach wie vor mit dem Zuge gearbeitet werden. Infolge dieser Mängel konnte die neue Vorrichtung, wenn sie auch viel Aufmerksamkeit erweckte, doch keinen dauernden praktischen Erfolg erzielen und verschwand in der Folgezeit wieder vom Schauplatz.

Der größte Wert in der Erfindertätigkeit Falcons bestand darin, daß durch ihn ein anderer Erfinder, Jacques de Vaucanson, angeregt wurde, auf dem beschrittenen Wege weiterzuarbeiten und das Problem des mechanischen Webstuhls um ein bedeutendes Stück seiner Lösung näher zu bringen. Vaucanson war durch den Bau von Automaten eine Berühmtheit geworden; so konstruierte er einen durch ein Uhrwerk betriebenen Flötenspieler, einen Pfeifer und eine Ente, ferner auch einen durch Kurbelantrieb von dem Lenker in Bewegung gesetzten Wagen, den er dem König Ludwig XV. vorführte, und der als ein Vorläufer unserer selbstfahrenden Wagen zu gelten hat. Auch auf textiltechnischem Gebiet war er als erfolgreicher Erfinder tätig. Von ihm stammt eine Verbesserung zum Moirieren (Wässern) der Stoffe, ein Verfahren, bei dem der gummierte Stoff zwischen heißen Walzen in der Weise gepreßt wurde, daß ein wellenartiges Muster entstand. Auch eine sehr bedeutende Vervollkommnung des Seidenhaspels rührt von ihm her. Er versah diese Vorrichtung mit neuen Teilen und Bewegungen und erhöhte dadurch sowohl die Leistungen wie die Ausführung der Arbeit mit dem Apparat, der von erheblichem Einfluß für die französische Seidenindustrie wurde. Ein neuer Apparat für die Seidenappretur und eine Maschine zum Glätten von Brokatgeweben sind weitere Erzeugnisse seiner erfinderischen Tätigkeit, die ebenfalls von dauerndem Wert wurden.

Sein größtes Interesse wandte Vaucanson jedoch dem Musterwebstuhl zu. Er verbesserte Falcons Erfindung, indem er an einem für diesen Zweck besonders gebauten Webstuhl jeden Faden durch ein besonderes Loch führte und auch den Führungslöchern eine bessere Ausführung gab. Doch obwohl er sehr viel Zeit und Arbeit auf diese Maschine verwandte, hatte er damit viel weniger Erfolg als mit seinen anderen Erfindungen. Die Maschine verursachte viel Reibung und verlangte einen großen Kraftaufwand, und trotzdem arbeitete sie nur sehr langsam. Daher konnte auch Vaucansons Webstuhl, wenn er auch eine erhebliche Förderung des Problems bedeutete, noch keinen Erfolg erzielen. Vaucansons Webstuhl wurde späterhin im Konservatorium der Künste aufgestellt, wo er nach Jahrzehnten einem anderen Erfinder die Anregung zu einer vollkommeneren Ausführung und damit zur schließlichen Lösung geben sollte. Vaucanson selbst wurde in Anerkennung seiner vielfachen Verdienste um die Förderung der französischen Seidenindustrie zum Inspekteur der Seidenmanufaktur und später sogar zum Mitglied der Akademie der Wissenschaften ernannt. Sein Musterwebstuhl ist jedoch, gleich dem von Falcon, eine interessante Etappe in der Erfindungsgeschichte dieser Maschine geblieben; die französischen Seidenindustriellen konnten von Vaucansons Webstuhl noch keinen Gebrauch machen. Derjenige, dem es gelang, das von Falcon begonnene, von Vaucanson geförderte Problem des mechanischen Webstuhls zur vollständigen Lösung zu bringen und der durch diese Tat einer der bedeutendsten und erfolgreichsten Erfinder in der Geschichte der Textiltechnik wurde, war Charles-Marie Jacquard. Die überragende Bedeutung dieses Mannes und seines Werkes rechtfertigen ein näheres Eingehen auf beide.

Charles-Marie Jacquard wurde am 7. April 1752 in Lyon geboren, wo sein Vater Werkmeister in einer Seidenweberei war; auch seine Mutter war dort als Mustereinlegerin beschäftigt. Die Seidenindustrie Frankreichs bediente sich damals noch in ausgedehntem Maße der Kinderarbeit. Besonders für das sogenannte Latzenziehen wurden fast nur Kinder verwandt, und diese einförmige und anstrengende Arbeit, die den jugendlichen Arbeitern alle Jugendlust raubte und geradezu zur Verkümmerung ganzer Volksschichten führte, soll es gewesen sein, die dem jungen Jacquard schon als Knaben die Anregung gab, eine Erfindung zu machen, die das Latzenziehen mechanisch ausführte und so die gequälten Kinder von dieser unheilvollen Tätigkeit befreien sollte. Charles' Vater freilich hielt von solchen Ideen nicht viel; hatte er doch im Gegenteil seinen Sohn selbst zum Latzenzieher und Webergesellen bestimmt, und daher hielt er es sogar für überflüssig, dem Knaben Schulunterricht geben zu lassen. Nur hinter dem Rücken seines Vaters konnte Charles lesen und schreiben lernen. Die Abneigung gegen das Gewerbe seines Vaters war durch den Anblick der Kinderarbeit so stark in ihm geworden, daß er, als er alt genug war, um sich für einen Beruf zu entscheiden, lieber zu einem Buchbinder in die Lehre ging, nur um der Arbeit am Webstuhl zu entgehen, und eine Reihe von Jahren in diesem Beruf tätig war. Doch seine Ideen und Pläne zur Verbesserung des Webstuhls waren in ihm geblieben, und als er in seinem zwanzigsten Jahre seinen Vater verlor – seine Mutter war schon zehn Jahre vorher gestorben – und ihm als Erbe ein kleines Haus und ein Webstuhl zufielen, beschloß er, sich nunmehr doch der Weberei zuzuwenden, um seine Lieblingsidee verwirklichen zu können, und richtete sich eine Weberwerkstatt ein. In der Folge gestalteten sich die Verhältnisse für ihn jedoch recht trübe. Er hatte jung geheiratet; sein Schwiegervater galt zwar für reich, weigerte sich jedoch, ihm die versprochene Mitgift zu zahlen. Charles' Liebe zu seiner Gattin tat das zwar keinen Abbruch, wohl aber geriet er in Schulden und in so drückende Verhältnisse, daß er Haus und Webstuhl verkaufen und Arbeit in einem Gipsbruch nehmen mußte, während seine Frau durch Flechten von Strohhüten mitzuverdienen suchte. Dann kam die Französische Revolution, der er sich ebenfalls anschloß. Zusammen mit seinem siebzehnjährigen Sohn kämpfte er wacker in den Reihen seiner Landsleute auf den Schanzen von Lyon. Doch als sein Sohn von einer Kugel tödlich getroffen worden war, kam der hierdurch aufs schwerste erschütterte Vater um seine Entlassung ein, um sich wieder friedlicher Tätigkeit in Lyon zuzuwenden. Die Stadt hatte durch die Kämpfe der Revolution furchtbar gelitten. 40 000 Einwohner waren umgekommen, viele Tausende der besten Arbeiter der ehemals blühenden Lyoner Seidenindustrie waren geflüchtet, zum großen Teil ins Ausland; das industrielle Leben der Stadt war vernichtet. Es bedurfte erst eines besonderen Direktorialbeschlusses, um die geflohenen Arbeiter zur Rückkehr in ihre Vaterstadt zu veranlassen und so die Grundlage zum Wiederaufbau der dortigen Seidenindustrie zu schaffen.

Während dieses wechselvollen Lebens hatte Jacquard seine Idee zum Bau neuerer und zweckmäßigerer Webmaschinen niemals verlassen; im Gegenteil war diese Idee inzwischen in seinem Gehirn vollständig ausgereift, und in seine Vaterstadt zurückgekehrt, suchte er nunmehr zu verwirklichen, was schon seit Jahren vor seiner Seele stand. Es gelang ihm, mehrere Lyoner Seidenfabrikanten für den Plan zu interessieren und von ihnen die nötigen Mittel zum Bau seiner Maschine zu erhalten. Nahezu fünfzigjährig, stellte er im Jahre 1799 seine erste Maschine fertig, eine Latzenzugmaschine, die den Zug selbsttätig bewirkte und keiner Kinderarbeit mehr bedurfte. Die Aufgabe, die seit seinen Kindheitsjahren bis ins hohe Mannesalter ihn bewegt hatte, durch eine geeignete Erfindung die Kinder seiner Vaterstadt von der Fron am Webstuhl zu befreien, war gelöst. War auch diese Maschine noch verhältnismäßig umständlich, so brachte sie dennoch bedeutende Vorteile und gelangte in den Lyoner Seidenwebereien bald allgemein zur Anwendung. Auf der im Jahre 1801 in Paris stattgefundenen Industrieausstellung wurde Jacquard für seine Maschine die Bronzene Medaille zuerkannt, und im darauffolgenden Jahre wurde ihm ein Patent auf zehn Jahre erteilt. Auch räumte ihm die Stadt Lyon im Palast der Schönen Künste ein Arbeitslokal ein, woran nur die Bedingung geknüpft war, daß er junge Weber in der Handhabung der neuen Maschine unterrichtete.

Nach zweijähriger Wirksamkeit in Lyon traten Ereignisse ein, die seinem Leben eine andere Wendung gaben. Zur Aufmunterung des Gewerbefleißes hatte nämlich die Gesellschaft der Künste in Paris ein Preisausschreiben für die Erfindung einer Maschine zur Herstellung von Fangnetzen erlassen. Jacquard beschloß, sich an dem Preisausschreiben zu beteiligen und stellte ein dementsprechendes Modell her, das die gestellte Aufgabe löste. Diese Nachricht gelangte auch zu dem General Napoleon Bonaparte, welcher den Erfinder zu sich nach Paris beschied und ihn mit den Worten anfuhr: »Sie sind also derjenige, der behauptet, machen zu können, was Gott selbst nicht vermag, einen Knoten in eine gespannte Schnur?« Dann aber wünschte er dem Verblüfften Glück zu seiner Erfindung und versicherte ihn seiner Unterstützung für seine weiteren Arbeiten. Jacquard erhielt dann für seine Erfindung den ausgesetzten Preis von 3000 Franken sowie auch die Goldene Medaille. Außerdem aber wurde er im Konservatorium der Künste und Gewerbe angestellt, wo er einen seinen Neigungen und Wünschen äußerst entsprechenden Wirkungskreis und zugleich die Möglichkeit fand, seinen erfinderischen Plänen und Ideen in vollem Umfange nachzugehen. Hier war es auch, wo er den vor einem halben Jahrhundert aufgestellten Musterwebstuhl von Vaucanson vorfand. Die Zeichnung dazu war verlorengegangen, auch fehlten bereits Teile der Maschine, und kein Mensch wußte mehr, wie diese in Gang zu setzen sei. Jacquard untersuchte die Maschine eingehend, und es gelang ihm, sie in Gang zu bringen. Zugleich aber erkannte er auch klar die Mängel der Maschine, die deren praktische Anwendung verhindert hatten, erkannte, welche Änderungen und Verbesserungen nötig waren, um einen Musterwebstuhl zu bauen, der eine bessere und vollkommenere Lösung des Problems darstellen würde, und erhielt so die stärkste Anregung zu seiner späteren bedeutendsten Erfindung.

Einer Berufung der Stadt Lyon Folge leistend, kehrte Jacquard dann in seine Vaterstadt zurück, wo er sein früheres Amt wiederaufnahm. Gleichzeitig widmete er sich nunmehr auch mit größtem Eifer und unermüdlicher Arbeit der Erfindung des Musterwebstuhles, die, seit er die Maschine von Vaucanson kennengelernt hatte, die große Aufgabe seines Lebens geworden war. Die Elemente von Falcon und Vaucanson in geschickter Weise mit seinen eigenen Ideen verknüpfend, neue Teile und Organe erfindend und zu geschickter Anwendung bringend, schuf er so eine neue Maschine von bisher unbekannten Fähigkeiten, den wirklichen Musterwebstuhl, der durch eine selbständige Vorrichtung vermittels Platinen die Herstellung des Musters bewirkt, das über zahlreiche Ketten und Schußfäden gehen und die ganze Breite des Stuhles einnehmen kann. Im Jahre 1805 war die Maschine fertiggestellt. Durch eine Vorführung vor der Lyoner Handelskammer wurde sie den Fabrikanten und Fachkreisen bekanntgemacht.

Über das weitere Schicksal des Erfinders und seiner Maschine entschied dann ein Kaiserliches Dekret vom 27. Oktober 1806, durch das dem Magistrat von Lyon befohlen wurde, Jacquard eine lebenslängliche Rente von 3000 Franken zu zahlen, wofür Jacquard der Stadt alle seine Erfindungen und Maschinen als Eigentum überlassen mußte. Im Jahre 1808 erhielt er für seinen Webstuhl einen Preis von der Gesellschaft zur Aufmunterung des Gewerbefleißes. In einer an diese Preisverteilung anknüpfenden wissenschaftlichen Mitteilung wird der neue Webstuhl folgendermaßen beschrieben:

»Der Mechanismus, welchen Jacquard erfunden hat, ist zusammengesetzt aus Haken (Platinen), an welchen die Karden der Harnischlitzen befestigt sind, welche die Schnürung des Stuhles ausmachen, ebenso wie Vaucanson solche angewandt hat. Diese Litzenträgerhaken werden vermittels eines eisernen Messers (Leiste) in Bewegung gesetzt, welches an einem Gestell befestigt ist, das durch einen eisernen Fußtritt auf und nieder bewegt werden kann. Mehrere Streifen durchbohrter Pappe, nach dem Muster des Streifens zusammengesetzt, sind mit den Enden zu einer Kette verbunden, deren Länge dem auszuführenden Muster entspricht. Diese Karten sind über ein Prisma gegenüber den Nadeln in dem oberen Teil der Maschine aufgelegt. Ist die Maschine in Ruhe, so sind alle Litzenhaken geradestehend und ruhen dann auf dem Messer, welches sie zusammen oder einzeln aufhebt. Jedesmal, wenn der Arbeiter seinen Schemel niedertritt, setzt er die Karten in Bewegung, welche, da sie an einigen Stellen durchlöchert und an anderen voll sind, die Haken, welche die Litzen tragen, zurückstoßen oder an ihrem Platz lassen. So werden die Fäden der Kette, welche mit denjenigen Haken in Verbindung stehen, die nicht aus dem Bereiche des Messers zurückgedrängt worden sind, für den Durchgang des Schützen erhoben. Die große Zahl von Karten, welche man nacheinander auflegen, die Leichtigkeit, mit welcher man sie im Laufe der Arbeit wechseln kann, bieten ein leichtes und sicheres Mittel für so ausgedehnte Muster, als man es ohne Hilfe des Latzenziehers wünscht. Durch dieses Mittel kann jeder Arbeiter von gewöhnlicher Fähigkeit mit Leichtigkeit und Genauigkeit alle Arten Muster einlegen, so daß man in einer Stunde dieselbe Arbeit verrichten kann, welche bei dem alten Verfahren mehrere Tage erfordert.«

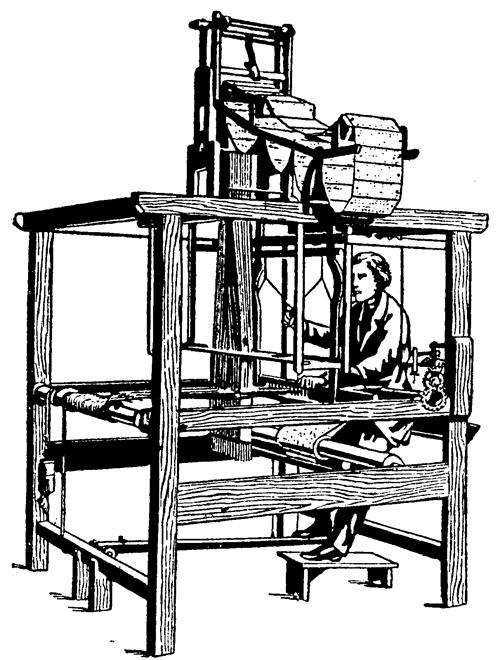
Abb. 78
Jacquards Musterwebstuhl

So weit jene Beschreibung der neuen Maschine, die sich an die Verleihung des Preises an den Erfinder knüpft. Sicher hat Jacquard durch den Webstuhl von Vaucanson erhebliche Anregungen für die Erfindung und Konstruktion seiner eigenen Maschine erhalten. Dennoch aber ist diese durch die völlig neuartige Ausführung der Grundgedanken jener Maschine sowie durch zahlreiche neue Teile und Anordnungen, die völlig der Erfindertätigkeit Jacquards angehören, unbedingt als Erfindung Jacquards zu bezeichnen, soweit überhaupt eine technische Neuerung als Erfindung eines einzelnen bezeichnet werden kann. Jacquard hat jedenfalls als erster eine verwendbare Musterwebmaschine geschaffen, und damit ist sein Verdienst als Erfinder dieser Maschine für immer sichergestellt.

Auch Jacquard ist nicht den schwersten Anfeindungen und Verfolgungen entgangen. Seine Maschinen wurden unberechtigterweise von anderen benutzt, und die Benutzer suchten sich ihren Verpflichtungen ihm gegenüber zu entziehen, indem sie sein Verdienst als Erfinder der Maschine bestritten und behaupteten, daß diese nur dem Vaucansonschen Webstuhl nachgebildet sei. Der Magistrat von Lyon ließ sich hierdurch sogar veranlassen, Jacquard die ihm zustehende gesetzliche Rente zu entziehen. Ebenso wandten sich, wie es fast alle Vorgänger in der Erfindungsgeschichte der Textilindustrie erfahren hatten, die Arbeiter auch gegen ihn. Die Lyoner Textilarbeiter befürchteten von der neuen Maschine eine Gefährdung ihrer Existenz, zertrümmerten daher die Maschinen und Modelle Jacquards und verbrannten die Trümmer öffentlich unter Verwünschungen gegen den Erfinder. Schließlich verklagten ihn sogar die Benutzer seiner Maschine auf Schadenersatz, weil die Maschine angeblich nicht das zu leisten imstande sei, was er versprochen habe, und der Magistrat verurteilte Jacquard dem Klageantrag gemäß. Nur auf dringende Bitten wurde ihm gewährt, einen Gegenbeweis zu seiner Rechtfertigung zu führen. Er tat es, indem er eine neue Maschine herstellte und auf dieser vor Klägern und Richtern auf einem öffentlichen Platz und in Gegenwart einer großen Menschenmenge ein hervorragendes Muster webte. Damit mußten sich seine Gegner als überwunden erklären, und nun trat ein allgemeiner Umschwung ein. Der Magistrat gab ihm seine Pension zurück und ließ auch sein Porträt in Seide weben, die Weber von Lyon aber stellten ihm eine Ehrenerklärung aus. Nunmehr bürgerte sich der neue Musterwebstuhl im In- und Auslande rasch ein; im Jahre 1825 waren allein in den Lyoner Webereien etwa 10 000 Jacquardmaschinen in Betrieb.

Als Jacquard im Jahre 1819 von der Regierung das Kreuz der Ehrenlegion erteilt wurde – eine Auszeichnung, die nie einem Würdigeren zuteil geworden ist –, zog er sich von der Öffentlichkeit auf ein kleines Landgut zurück. Seine mäßige Pension reichte für seine bescheidenen Verhältnisse und sicherte ihm einen freundlichen Lebensabend, der durch die allseitige Anerkennung seines Lebenswerkes in fast der ganzen Welt verschönert wurde. Am 7. August 1834 starb er im 83. Lebensjahre. Noch in demselben Jahre wurde von dem Gewerberat von Lyon mit der Sammlung zu einem Denkmal für den großen Erfinder begonnen, das im Jahre 1840 fertiggestellt und enthüllt wurde.

Der Musterwebstuhl, wie er von Jacquard erfunden und gebaut worden ist, ist seiner Konstruktion nach bis heute im wesentlichen unverändert geblieben, wenn auch die technische Ausführung seitdem sehr vervollkommnet worden ist. Die weiteren Verbesserungen der Maschine, die zur Zeit Jacquards nur für die Seidenweberei verwandt wurde, erstrebten vor allem die Nutzbarmachung des Webstuhles für möglichst alle Webearten, ein Ziel, das durch die Tätigkeit zahlreicher Erfinder aus beinahe allen Ländern mit entwickelter Textilindustrie und durch eine große Zahl mehr oder weniger bedeutungsvoller Verbesserungen und Änderungen im Laufe der Jahre vollkommen erreicht worden ist. Die von Jacquard erbaute Maschine war noch vollständig und in allen Teilen aus Holz gebaut; der Mechaniker und Seidenfabrikant Queva, der den Jacquardstuhl zuerst in Preußen (1816) einführte, war es, der solche Maschinen auch zuerst aus Eisen herstellte; nur Prisma, Nadelbrett, Federgehäuse und Platinenboden ließ er aus Holz, während er die Nadeln und Platinen aus englischem Federstahl anfertigte. Hierdurch wurde der Bau eiserner Musterwebstühle in die Wege geleitet. Der erste vollständig aus Eisen und Kupfer gebaute Jacquardstuhl ist von Boille in Paris im Jahre 1835 hergestellt worden.

Noch eine große Anzahl anderer Erfinder kennt die Geschichte der Textilindustrie, und die hier genannten Namen sind nur die hervorragendsten in der großen Reihe jener Männer, denen die heutige Textiltechnik ihre Entstehung und Entwicklung verdankt. Ein schweres und wechselvolles Geschick war allen diesen Erfindern beschieden, und selbst jene, die schon zu Lebzeiten zu Anerkennung und auch materiellem Erfolg gelangt sind, haben dennoch vordem alle Leiden des Erfinderloses erfahren.

Und Schaffen und Leben der Männer aus der Erfindungsgeschichte der Textilindustrie ist nahezu dasselbe wie das der Erfinder in allen anderen technischen Gebieten. In der Mehrzahl der Fälle sind auch diese undankbar gegen ihre großen Männer gewesen. Der Erfinder ist eine problematische Natur, seinem Schaffen wie seinem Lebensgange nach, und verhältnismäßig selten sind die Fälle, wo ein Erfinder sein Werk in ungestörter bürgerlicher Behäbigkeit zu Ende führen konnte. Heute allerdings hat sich das Los des Erfinders gegen früher wesentlich günstiger gestaltet. Unsere ausgebildete Gesetzgebung ermöglicht einen weitgehenden Schutz und eine unter Umständen sehr ausgiebige Nutzbarmachung selbst der kleinsten erfindungstechnischen Neuerung, und in den Gebieten der heutigen Technik und Industrie gibt es neben den zahllosen Neuerfindungen und Patenten, die sich nicht bewährt haben, doch auch zahlreiche solcher, die ihren Urhebern große Gewinne eingebracht haben. Erfinderische oder patenttechnische Kleinigkeiten, Neuerungen, die nichts grundlegend Neues gebracht haben, sondern nur in einer Änderung oder Verbesserung irgendeines kleinen Teils bestehen, sind die Quelle großer Reichtümer geworden, und für viele dieser Erfinder kann gesagt werden, daß der Gewinn, den sie gebracht haben, in umgekehrtem Verhältnis zu dem Aufwand an Geist und Können steht, den sie erforderten. Aber an den großen Erfindungsproblemen scheitert auch in unserer Zeit noch oftmals die Existenz des Erfinders, wie die Geschichte der Technik des letzten halben Jahrhunderts durch viele derartige Fälle bekunden kann. Nicht nur die Erfindung selbst ist ein Problem, auch die Kunst des Erfindens ist problematischer Natur, und nur wenigen der Problematiker in der Geschichte der Erfindungen ist es geglückt, gerade dieses Problem befriedigend zu lösen. Heute noch wie jemals zuvor stellen die Erfindungsprobleme durch ihre Bedeutung wie auch durch die Art, wie sie zur Lösung gebracht werden, ein Sondergebiet der Problematik des menschlichen Geistes dar, und der Kampf um den Erfolg ist auch hier in vielen Fällen vergleichbar dem Wettlauf mit der Schildkröte, an dem und an dessen Deutung die Kraft der Besten erlahmte.

4. Kinder als Erfinder

Eine neue Maschine und ein verspielter Junge – Eine wichtige Verbesserung – Der tiefe Sinn im kindlichen Spiel – Wie der Luftreifen erfunden wurde – Ein jugendliches Genie

Es war um das Jahr 1712 herum, da war in England zwei wackeren Handwerkern, dem Schmiede- und Schlossermeister Thomas Newcomen und dem Glaser John Cawley, beide aus dem Orte Darmouth in der Grafschaft Devonshire, die Herstellung einer neuartigen Maschine gelungen, die zu den merkwürdigsten Dingen gehörte, die es für jene Zeit überhaupt gab, nämlich einer Dampfmaschine. Was vielen Gelehrten und Ingenieuren nicht gelungen war, die Kraft des gespannten Dampfes für die Zwecke der menschlichen Arbeit vermittels geeigneter maschineller Vorrichtungen nutzbar zu machen, das hatten tatsächlich jene beiden einfachen Handwerker zustandegebracht.

Die von ihnen gebaute Maschine war die erste brauchbare Dampfmaschine und gelangte in dem Kohlenbergwerk des Grubenbesitzers Back in Wolverhampton zur Aufstellung, wo sie zum Auspumpen von Grubenwasser verwandt wurde. Freilich war die Newcomensche Dampfmaschine noch ein ziemlich roher und ungefüger Geselle und von der Vollendung, die ihr späterhin der große James Watt gegeben hat, noch recht weit entfernt. Sie stellte eine sogenannte atmosphärische Dampfmaschine dar, bei der Dampfdruck und Luftdruck gemeinsam wirkten, und war noch vieler Verbesserungen bedürftig.

Eine solche Verbesserung der Maschine nun kam auf sehr merkwürdige Weise zustande. An der Maschine befanden sich unter anderem auch zwei Hähne, durch die der Zustrom des Dampfes und des Kühlwassers nach dem Zylinder reguliert wurde, zu welchem Zweck die Hähne abwechselnd geöffnet und geschlossen werden mußten. Diese Funktionen automatisch auszuführen, so weit war die Dampfmaschine jener beiden Meister doch noch nicht vorgeschritten; das Öffnen und Schließen mußte vielmehr von einem Arbeiter mit der Hand ausgeführt werden, was eine zwar einfache, aber auch sehr langweilige und ermüdende Tätigkeit war.

Mit dieser Arbeit hatte Newcomen einen Knaben beauftragt, Humphry Potter hieß er, denn jene einfache Funktion bedurfte weder der Kraft noch der Intelligenz eines Erwachsenen. Der kleine Potter waltete für wenig Geld auch getreulich seines Amtes. Doch lieber freilich hätte er sich den Spielen seiner Altersgenossen gewidmet, die ihm viel interessanter dünkten als das ewige monotone Öffnen und Schließen der beiden vertrackten Hähne. Was also tun? Auf den Verdienst konnte er nicht verzichten, aber gespielt hätte er auch gern. Ja, wenn sich die beiden Hähne von selbst öffnen und schließen könnten, ebenso wie sich doch die Hebel und Stangen, Räder und Kolben der großen Maschine von selbst bewegten, dann, ja dann freilich …!

Dieser Gedanke durchzuckte das Gehirn des Jungen wie ein Blitz. Warum sollte er die Hähne nicht veranlassen können, sich ebenso automatisch zu bewegen wie alles andere, was an der Maschine geschah? Gedacht, getan. Durch Schnüre verband er die beiden Hähne derart mit dem auf- und abgehenden Balancier der Maschine, daß dieser die Schnüre abwechselnd nach oben und nach unten zog und dadurch die mit den Schnüren verbundenen Hähne abwechselnd öffnete und schloß. Hurra! der Versuch gelang über alles Erwarten gut, die Hähne und mit ihnen die gesamte Maschine funktionierten vermittels der Schnurvorrichtung ganz von selbst und ebensogut, ja sogar noch besser, weil regelmäßiger und exakter, als es durch ihre Betätigung mit der Hand geschehen war, und Humphry konnte sich, ohne seine Aufgabe zu vernachlässigen und ohne Einbuße an Verdienst befürchten zu müssen, mit seinen Spielkameraden vergnügen.

Freilich wurde die Untat bald entdeckt, und der Meister mag den verspielten Jungen, der einfach von der Arbeit fortlief, zunächst hart angelassen haben. Höchlichst erstaunt aber war er, als er konstatierte, daß Hähne und Maschine auch ohnedies zur vollen Zufriedenheit arbeiteten, und als er die Ursache dieser merkwürdigen Erscheinung und damit die von dem jungen Potter erfundene Vorrichtung wahrnahm, da ging auch ihm ein Licht auf. Es war ihm sofort klar, daß die von dem verspielten Jungen ausgeheckte Hilfsvorrichtung eine wertvolle Verbesserung der Maschine darstellte, die diese in einer wichtigen Funktion von der Hilfe der Menschenhand unabhängig machte und dadurch deren Zuverlässigkeit und Selbsttätigkeit bedeutend erhöhte. Schließlich wurden die Schnüre durch kleine Gestänge ersetzt, die jene automatischen Bewegungen noch besser ausführten. So hatte die Lust zum Spiel aus einem Jungen von zwölf Jahren einen Erfinder gemacht, der in der Entwicklungsgeschichte der Dampfmaschine nie vergessen werden wird.

Der hier geschilderte Vorfall zeigt, daß die erfinderische Fähigkeit schon im jungen Menschen, schon im Kinde ruht. Und das ist auch nicht weiter verwunderlich. Im Gegenteil, das Kind ist sogar der Erfinder schlechtweg, da es in seiner allmählichen geistigen Entwicklung, angeregt durch Spiel und Trieb und durch die mancherlei Notwendigkeiten seines jungen Daseins, die Erfindungen der Menschheit zum Teil wiederholt. Eins der wichtigsten und wertvollsten Ergebnisse der modernen biologischen Wissenschaft, das sogenannte phylogenetische Grundgesetz, besagt, daß das menschliche Individuum im Embryonalzustand alle die verschiedenen Formen und Entwicklungsphasen durchmacht, die der Mensch in seiner Artentwicklung, also in dem Aufstieg von den frühesten Formen seiner morphologischen Beschaffenheit bis zur heutigen Menschheitsstufe, im Lauf der Jahrmillionen zurückgelegt hat.

Und ebenso können wir zweifellos sagen, daß der Mensch als Kind und in seiner kindlichen Entwicklung, in der allmählichen Ausbildung seines Geistes, seiner Anschauungsweisen und Fähigkeiten, die ganze Kulturentwicklung der Menschheit in allen ihren Phasen und Stufen durchgeht und dabei auch die Erfindungsgeschichte der Menschheit zu einem großen Teil wiederholt. Das Kind, das zum erstenmal einen harten, schweren und widerstandsfähigen Körper, ein Stück Holz, eine Klapper, einen Löffel in die Hand bekommt und mit diesem voll Lust und Spiel auf den Tisch schlägt, hat damit die Wirkungsweise des Hammers erfahren und die Erfindung dieses wichtigsten aller Werkzeuge für seine kleine Person gemacht; das Kind, das zum erstenmal auf eine Fußbank gelangt und, sich auf dieser aufrichtend, plötzlich über den Tisch gucken kann, hat damit das Prinzip von Treppe und Leiter von neuem erfunden, und in zahllosen anderen Fällen schafft und findet es so selbst die für sein junges Dasein wertvollen und zweckmäßigen Formen heraus, erweist es sich ohne allen Anspruch auf Patentfähigkeit als Erfinder. Was der Mensch in den ur- und vorgeschichtlichen Entwicklungsstufen der Kultur in den bitteren Notwendigkeiten des Lebens und im Kampf ums Dasein vor ungezählten Zehntausenden von Jahren erfand, die ersten und primitivsten Werkzeuge und technischen Anwendungsweisen, das erfindet durch Spiel und Notwendigkeit das Kind von neuem. Vielleicht würde die Betrachtung und wissenschaftliche Erforschung dieser Seite der kindlichen Betätigung sehr wertvolle Aufschlüsse zur Psychologie des Kindes überhaupt liefern, würde vielleicht auch den Zusammenhang zwischen Spiel und Erfindungstrieb aufdecken und manchen Rückschluß auf die Psychologie des Urmenschen zulassen.

Also das Kind ist der Erfinder schlechtweg, und daher kann es uns auch nicht wundern, daß das kindliche Spiel auch zu Erfindungen im höheren technischen Sinne, sozusagen im Sinne der Patentfähigkeit, führt, wie wir es an der Erfindungstat des jungen Humphry Potter soeben sahen. Und diese ist keineswegs der einzige Fall, wo aus kindlichem Spiel eine bedeutsame Erfindung hervorgegangen ist. Auch eine der wichtigsten Erfindungen der modernen Verkehrstechnik, nämlich die Erfindung des Pneumatiks, ist auf ganz ähnliche Weise erfolgt. Das ging folgendermaßen zu: In den achtziger Jahren des vorigen Jahrhunderts war das Fahrrad, das »Veloziped«, wie man es damals noch nannte, aufgekommen, zumeist als Dreirad, erst späterhin als Zweirad in Form des Hochrades gebaut und zunächst noch mehr ein Kinderspielzeug, das seine spätere Bedeutung und Entwicklung als Sport- und praktisches Verkehrsmittel noch kaum ahnen ließ. Schon damals war die Bereifung des Vehikels ein Problem; man verwandte als solche eine Art Vollgummi, der seine Dienste denn auch recht und schlecht, zumeist allerdings mehr schlecht als recht, tat.

Ein solches Dreirad hatte auch der irische Tierarzt Dunlop aus Belfast seinem Sohn zum Geschenk gemacht, der mit dem neuen Fahrzeug alsbald fleißig auf den Straßen seiner Vaterstadt herumkutschierte. Das Vergnügen war nun allerdings mehr interessant als schön. Denn auf dem holperigen Pflaster Belfasts war der junge Radler einem dauernden Schütteln ausgesetzt, und der Vollgummireifen war nur wenig geeignet, dieses Übel zu mildern. Nannten doch die Engländer damals die neuartigen Fahrzeuge bezeichnenderweise noch » bone-shakers«, Knochenschüttler, und der junge Dunlop hatte die Berechtigung dieser Bezeichnung oftmals schmerzlich am eigenen Leibe zu spüren.

Zusammen mit seinem Vater suchte er dem Übel ein Ende zu machen, und die beiden kamen auf den Gedanken, daß sich dieser Zweck vielleicht erreichen ließe, wenn eine elastischere Bereifung als der Vollgummi um die Räder gelegt würde. Und als man den Blick suchend in der Runde schweifen ließ, da kamen sie auf den Gedanken, daß ein aufgepumpter Gasschlauch vielleicht eine solche gewünschte elastische Bereifung sein könne. Der Versuch wurde gemacht. Ein mit Hilfe einer Luftpumpe aufgeblasener und nur sehr primitiv verschlossener Gasschlauch statt des Vollgummireifens um das Rad gelegt, und – wie mit einem Schlage waren die unangenehmen Erschütterungen beim Fahren beseitigt oder doch wenigstens auf ein Minimum vermindert.

Der überraschende Erfolg ließ Dunlop die große praktische Bedeutung der Verbesserung erkennen und veranlaßte ihn, nachdem er sie noch etwas verbessert hatte, den Patentschutz dafür nachzusuchen. Das war die Erfindung des Pneumatiks, geboren aus kindlichem Spiel, um einem Übelstand beim Spielen abzuhelfen, aber dazu berufen, eine Grundlage moderner Verkehrstechnik zu werden, von der sowohl das Fahrrad wie das Automobil ihren Ausgangspunkt genommen haben, die beide niemals ohne den Pneumatik auch nur annähernd das hätten werden können, was sie in der verhältnismäßig kurzen Zeit seit jener Erfindungstat für alle Welt geworden sind.

Ein höchst berühmtes Beispiel der erfinderischen Fähigkeit eines kindlichen Geistes, das sogar in der selbständigen Auffindung einer wissenschaftlichen Erkenntnis bestand, hat uns der große Mathematiker Karl Friedrich Gauß hinterlassen. Als Neunjähriger besuchte der kleine Gauß die Volksschule seiner Vaterstadt Braunschweig, und in der Rechenstunde gab der Lehrer eines Tages den etwa hundert Schülern der Klasse die Aufgabe auf, die Summe aller Zahlen von 1 bis 100 auszurechnen. Er tat das allerdings weniger aus Unterrichtsgründen, als weil er selbst für eine schriftliche Arbeit, die er während der Unterrichtsstunde fertigstellen wollte, ungestört Zeit zu haben wünschte.

Natürlich glaubte er die Kinder für mindestens eine Stunde mit der gestellten Aufgabe beschäftigt und war daher aufs höchste verblüfft, als schon nach wenigen Minuten der kleine Gauß an das Katheder trat und ihm die Rechentafel mit dem fertigen Resultat und den klassischen Worten im Braunschweiger Dialekt: »Da ligget se!« auf den Tisch legte. Möglich, daß der gestrenge Präzeptor zunächst der Meinung war, daß der kleine Rechner in den wenigen Minuten wohl weiter nichts als irgendeinen blühenden Unsinn zusammengerechnet habe, da er sich sonst die Schnelligkeit des Verfahrens nicht erklären konnte; doch bei näherem Zusehen erlebte er ein Wunder. Das Resultat war richtig, aber freilich nicht in der Art errechnet, wie es der Lehrer vorausgesetzt hatte und wie es alle anderen Schüler der Klasse taten, also durch mühsames Addieren der aufgegebenen Zahlen, sondern nach eigener Methode, die viel schneller zum Ziel führte. Der kleine Gauß hatte, sowie die Aufgabe gestellt war, einen Zusammenhang gesehen und die Ausrechnung in der folgenden Weise vorgenommen:

1,	2,	3,	................	50
100,	99,	98,	................	51

101,	101,	101,		101

Er hatte also zunächst die Zahlen 1 bis 50 in einer Reihe hingeschrieben, dann in umgekehrter Reihenfolge darunter die Zahlen von 51 bis 100 und dadurch 50 Summen von je 101 erhalten. Das Gesamtresultat also mußte 50 × 101 = 5050 sein, was sich in einer Minute ausrechnen ließ, und damit war die ganze Aufgabe gelöst. Diesen Zusammenhang hatte der Neunjährige sofort herausgefunden und zur Anwendung gebracht. Natürlich hatte er damit nichts Neues gefunden, wenn seine Methode sicher auch dem Lehrer selbst unbekannt war. Wohl aber hatte er diese wissenschaftliche Methode für sich selbst gefunden und damit eine Probe erfinderischen Genies gegeben, wie sie in ihrer Art ganz einzig dasteht. Jener Lehrer, den der kleine Gauß durch die schnelle Lösung so sehr überraschte, nahm daraufhin Veranlassung, die Aufmerksamkeit Höhergestellter auf das junge Genie zu lenken und diesem die Wege zu ebnen, die Karl Friedrich Gauß schließlich zu der unbestrittenen Stellung des größten Mathematikers aller Zeiten oder, wie ihn seine Kollegen nannten, des Fürsten der Mathematiker führen sollten.

5. Unmöglichkeiten, die möglich wurden

Die unmögliche Erdkugel – Die unmögliche Eisenbahn – Der unmögliche Kraftwagen – Was selbst dem lieben Gott nicht möglich ist – Kleine und große »Unmöglichkeiten« – Das unmögliche Luftschiff – »Unmöglichkeiten« der Wissenschaft – Relative und absolute Unmöglichkeiten – Es gibt Unmöglichkeiten – Der Unmöglichkeitsbeweis – Der Wettlauf mit der Schildkröte

Im Jahre 1483 trug Christoph Kolumbus dem König Johann II: von Portugal seine Theorie vor, daß die Erde, die damals noch allgemein für eine runde, auf dem Weltmeere schwimmende Scheibe gehalten wurde, im Wahrheit eine Kugel sei und daß auf der entgegengesetzten Kugelhälfte das Land Indien liege; daher müsse es möglich sein, nach diesem Land, das bis dahin stets nur auf dem Ostwege erreicht werden konnte, auch von Westen her auf dem Seewege zu gelangen, und Kolumbus entwickelte seinen Plan, durch eine Umschiffung der Erdkugel dieses Gelobte Land zu erreichen. Der König berief eine Kommission von Gelehrten zur Prüfung jener Theorie und ebenso jenes wagehalsigen Unternehmens ein. Und die Hofgelehrten kamen nach langen und reiflichen Beratungen zu dem Ergebnis, daß es unmöglich sei, daß die Erde eine Kugel sein könnte, weil ja dann die Erdbewohner auf der entgegengesetzten Erdhälfte mit dem Kopf nach unten und den Beinen nach oben an der Erde hängen müßten wie die Fliegen an der Zimmerdecke, und daß es daher also auch unmöglich wäre, Indien auf einem anderen als dem gewohnten Ostwege zu erreichen. Kolumbus wurde urkundlich für einen Ignoranten, einen Schwätzer und Träumer erklärt und sein Projekt von dem portugiesischen Hofe abgewiesen. Neun Jahre später aber bewies er durch seine Entdeckerfahrten, daß die Kugelgestalt der Erde nicht nur möglich, sondern sogar Wirklichkeit sei, und gelangte er auch nicht nach Indien, so doch nach Amerika und erschloß so der Kulturwelt einen neuen Erdteil. Eine Unmöglichkeit war möglich geworden, und hätten jene portugiesischen Hofgelehrten damals nicht so schnell ihr Verdikt »unmöglich« abgegeben, so wären aller Wahrscheinlichkeit nach die Portugiesen und nicht die Spanier Herren der Neuen Welt geworden, und die Weltgeschichte hätte in vielem einen anderen Verlauf genommen.

Im Jahre 1828 hatte die englische Regierung eine Kommission von Gelehrten und Fachbeamten eingesetzt, die das Projekt einer Eisenbahn auf der Strecke Liverpool-Manchester prüfen sollte. Schienenbahnen wurden damals bereits mehrfach betrieben, aber nur mit Pferden oder stehenden Dampfmaschinen, die die Wagen an langen, über Trommeln laufenden Seilen vom Start zu Ziel wanden. Ganz vereinzelt wurden solche Bahnen auch mit den neuartigen Lokomotiven betrieben, die wie Pferde vor die Züge gespannt wurden. Aber dieser Betriebsweise brachte man damals allgemein noch das größte Mißtrauen entgegen, woran allerdings die Mangelhaftigkeit und geringe Leistungsfähigkeit jener ersten Lokomotiven, der »eisernen Pferde«, wie sie spöttisch genannt wurden, zum guten Teil Schuld haben mochten. Nur für die Schienenbahnen der Bergwerke, zum langsamen Kohlen- und Gütertransport derselben, waren bis dahin solche neumodischen Lokomotiven verwandt worden, für den Betrieb einer richtiggehenden Landbahn, die außer Güterwagen auch Wagen zur Personenbeförderung mit sich führen sollte, hielt man jene fauchenden, rauchenden und funkensprühenden Ungetüme weder für geeignet noch würdig. Für die projektierte Bahnstrecke Liverpool – Manchester nun war zum ersten Male die Verwendung von Lokomotiven erwogen worden, und zwar auf Betreiben des Maschinen- und Eisenbahnbauers George Stephenson, der schon mehrere Lokomotivbahnen für Bergwerke in Betrieb gesetzt hatte und nunmehr auch mit allem Eifer für die allgemeine Verwendung von Lokomotiven zum Bahnbetrieb eintrat, von der er der Mitwelt ungeahnte Vorteile, viel größere Schnelligkeit und Leistungsfähigkeit und erheblich mehr Ersparnis an Zeit und Geld als durch den Pferdebetrieb oder durch stehende Zugmaschinen versprach.

Diesen Versprechungen aber stand man sehr skeptisch gegenüber, und jene Kommission sollte prüfen, was von solchen Versprechungen zu halten wäre und ob sich die Verwendung von Lokomotiven für die geplante Bahnstrecke empfehle. Und die weisen und gelehrten Herren waren von der Unmöglichkeit des Projektes Stephensons viel mehr als von seinen Vorteilen überzeugt. »Glauben Sie wirklich, daß eine solche Lokomotive eine Geschwindigkeit von vier englischen Meilen (etwa sechs Kilometer) in der Stunde erreichen könnte?« fragte der Vorsitzende der Kommission Stephenson. »Gewiß«, meinte dieser. »Etwa auch acht Meilen?« fragte jener skeptisch und ironisch lächelnd weiter, und auch diese Frage bejahte Stephenson mit Entschiedenheit. »Angenommen nun aber den Fall,« fuhr der Vorsitzende fort, »Ihre Maschine käme mit einer Geschwindigkeit von acht Meilen dahergerast und eine Kuh hätte sich auf das Gleis verirrt, das könnte doch sehr böse Folgen haben.« »Gewiß, besonders für die Kuh!« antwortete ihm darauf Stephenson schlagfertig. Dann mischte sich ein anderes Mitglied der Prüfungskommission in die angeregte Auseinandersetzung und erklärte: Eine Geschwindigkeit von zehn englischen Meilen zu erreichen, wie sich Mr. Stephenson anheischig mache, sei unmöglich, denn bei einer solchen Geschwindigkeit müßte der entstehende Luftreibungswiderstand so groß werden, daß die Wagen in Brand gesetzt und vernichtet würden! Und ein weiteres Kommissionsmitglied berief sich zur Kennzeichnung des wahnsinnigen Projektes auf eine diesbezügliche Abhandlung von anerkannt fachmännischer Seite in der hochangesehenen Zeitschrift »Quarterly Review«; dort stand wörtlich zu lesen: »Was könnte wohl handgreiflicherer Unsinn, was alberner und lächerlicher sein als die Idee, Lokomotiven zu bauen, die die doppelte Geschwindigkeit der Postkutschen haben sollten? Ebensogut ließe sich annehmen, daß sich ein Mensch auf einer Kanonenkugel abfeuern ließe, wie daß er sich einer solchen Feuermaschine anvertrauen würde!« So urteilten Fachleute, die Gelehrten und Ungelehrten, über die Idee der Verwendung von Lokomotiven zum Bahnbetrieb. Unmöglich, unmöglich, unmöglich! schallte es Stephenson von allen Seiten her entgegen. Der hatte demgegenüber einen schweren Stand, aber schließlich wußte er die Kommission wenigstens so weit für sein Projekt zu gewinnen, daß ihm die Erlaubnis zur Anlage einer Versuchsbahn erteilt wurde. Die Bahn wurde gebaut, und am 7. Oktober 1829 fand auf der Strecke eine Wettfahrt von vier Lokomotiven mit Personen- und Güterwagen statt, bei der diejenige von Stephenson glänzend Sieger blieb und zugleich der staunenden Mitwelt ad oculos demonstriert wurde, daß das für absolut unmöglich Gehaltene dennoch möglich geworden war und die so mißgünstig beurteilte Lokomotive sich jeder anderen Art des Bahnbetriebes als ungeheuer überliegen erwies. Der Sieg über das vermeintlich Unmögliche bedeutete den Beginn einer neuen Ära in der Verkehrs-, Kultur- und Geistesgeschichte der Menschheit.

Stephenson, der so schwer und lange gegen die Unmöglichkeitstheoretiker anzukämpfen hatte, ehe es ihm gelang, diesen zum Trotz seine Ideen möglich zu machen, hat dann später freilich selbst einmal ein »Unmöglich« gesagt, und zwar auch ohne zureichenden Grund. Auch dabei handelte es sich um einen Verkehrsfortschritt und ein neuartiges Fahrzeug. Und das kam so: Nachdem sich die Eisenbahnen und Lokomotiven so erfolgreich bewährt hatten, wurden in England auch Versuche ausgenommen zum Bau von Dampffahrzeugen für den gewöhnlichen, ungeschienten Straßenweg nach Art der üblichen Pferdegespanne, mit einem Wort, von – Dampfautomobilen. Solche Versuche waren schon seit langem, sogar schon vor der Erfindung und Einführung der Eisenbahnen, unternommen worden, hatten jedoch niemals rechten Erfolg gehabt, weil der gewöhnliche Straßenweg jenen ältesten Dampfautomobilen bei der damaligen Art ihrer Konstruktion unüberwindliche Schwierigkeiten entgegensetzte. Die dauernden Erschütterungen, denen die auf gewöhnlichen, mit Eisenreifen beschlagenen Wagenrädern fahrenden Wagen auf solchen Wegen ausgesetzt waren, brachten dauernde Brüche, Pannen und sonstige Betriebsstörungen mit sich und verhinderten die zufriedenstellende Lösung des Problems. Das war schon mit den Dampfwagen vor der Eisenbahn der Fall gewesen, und das blieb auch so, als nach der Einführung der Eisenbahnen und, angespornt durch die großen Erfolge der auf Schienen laufenden Dampfwagen, jene Versuche mit verdoppeltem Eifer wiederaufgenommen wurden. Eine ganze Reihe von Erfindern bemühte sich um die Lösung des Problems. Verschiedene Typen von Straßenkraftfahrzeugen wurden gebaut und für kürzere oder längere Zeit in Verkehr gebracht, Lastwagen, Personenwagen und sogar auch schon Autobusse, und in den dreißiger Jahren des vorigen Jahrhunderts wurde eine Zeitlang in London schon eine Art Automobil- und Autobusverkehr unterhalten. Aber dauernden Erfolg hatten die Versuche auch damals nicht. Trotz aller Verbesserungen der Wagen erwiesen sich die Tücken und Schwierigkeiten des gewöhnlichen ungeschienten Straßenweges als stärker, und diese dauernden Mißerfolge veranlaßten selbst den weitblickenden Stephenson zu dem Ausspruch: Unmöglich sei es, daß Dampfwagen auf gewöhnlichen Straßenwegen jemals Aussicht auf Erfolg haben könnten, weil die Unebenheiten solcher Wege dem Dampfwagen bei der Eigenart seiner Konstruktion und Fortbewegung immer unüberwindliche Schwierigkeiten bereiten würde! – Jahrzehnte hindurch hat der große Dampfwagenbauer mit diesem pessimistischen Ausspruch über die Dampfautomobile freilich recht behalten, und erst weit über ein halbes Jahrhundert später wurde er Lügen gestraft, als nämlich der – Pneumatik erfunden und damit zugleich das so lange und heiß erstrebte Mittel gefunden worden war, mit dem die Kraftfahrzeuge auch die Schwierigkeiten und Unebenheiten des gewöhnlichen Straßenweges siegreich überwinden und zu erfolgreichen Verkehrsmitteln von ungeahnter Geschwindigkeit und Leistungsfähigkeit werden konnten. Wieder hatten, wenn allerdings auch erst nach langen Mühen und auf Umwegen, Ausdauer und Erfindungsgabe den Sieg über ein apodiktisches Unmöglich davongetragen.

Schon diese wenigen Beispiele zeigen, daß es eine eingewurzelte Neigung des menschlichen Geistes zu sein scheint, dem menschlichen Fortschritt vorschnell ein »Unmöglich!« entgegenzusetzen, sei es eingeborenen Theorien zuliebe, sei es angesichts ungewöhnlich großer und schwieriger Hindernisse, die die Resignation als der Weisheit besseres Teil erscheinen lassen, und daß selbst kluge und bedeutende Köpfe dieser Neigung unterliegen. Die Hemmnisse, mit denen wohl alle Pioniere der Menschheit auf dem Wege zum Fortschritt, alle Entdecker und Erfinder mehr oder weniger zu kämpfen hatten, wurzelten immer mit zum großen Teil in solchen Unmöglichkeitspostulaten der Zeitgenossen, und der Werdegang fast jeder neuen Idee ist ein Beweis für das Gesagte, insbesondere in der Geschichte der Technik und der Erfindung der maschinellen Hilfsmittel. Ein sehr charakteristisches Beispiel hierfür ist auch das folgende: Im Jahre 1801 hatte die »Gesellschaft der Künste« in Paris ein Preisausschreiben für die Erfindung einer Maschine zur Herstellung von Fischnetzen erlassen. Die maschinelle Nachahmung des Fadenknüpfens mit der Hand, wie es für die Verfertigung von Netzen seit Jahrtausenden ausgeführt wurde, wurde von klugen Leuten für eine pure Unmöglichkeit gehalten und jenem Preisausschreiben daher nur ein sehr fragwürdiger Erfolg prophezeit. Dennoch machten sich verschiedene Techniker an die Lösung der Aufgabe, und ein Erfinder aus dem Gebiete der Textil- und Seidenindustrie, der bereits verschiedene andere Erfindungen gemacht hatte, Charles-Marie Jacquard mit Namen, stellte ein Modell her, das die gestellte Aufgabe löste. Die Nachricht hiervon rief allerorts größtes Erstaunen hervor und gelangte auch zu dem damals allmächtigen General Napoleon Bonaparte, dem späteren Kaiser der Franzosen, der den Erfinder zu sich nach Paris berief und ihn, seiner Art gemäß, mit den Worten anfuhr: »Also Sie sind derjenige, der behauptet, möglich machen zu können, was selbst dem lieben Gott nicht möglich ist, einen Knoten in eine gespannte Schnur?« Dann allerdings wünschte er dem verblüfften Erfinder Glück und versicherte ihn seiner Unterstützung für seine weiteren Arbeiten. Die Worte des Gewaltigen sind charakteristisch für den Unmöglichkeitsglauben, mit dem man bis dahin die Lösung jenes Problems bedacht hatte. Jacquard hat dann später eine noch viel schwierigere und noch viel »unmöglichere« Aufgabe gelöst, nämlich die Erfindung des Musterwebstuhls, die die große Tat seines Lebens und der Ausgangspunkt einer ganz neuen Entwicklung der Seidenwebkunst geworden ist.

Noch eine andere Maschine, die ebenso wie die Maschine zum Netzestricken dazu bestimmt war, eine ausgesprochen handliche Tätigkeit maschinell auszuführen, nämlich die Nähmaschine, hatte in ihrem Werde- und Erfindungsstadium in den ersten Jahrzehnten des vorigen Jahrhunderts mit dem Unmöglichkeitsfanatismus zu kämpfen. Noch mehr als das Netzestricken wurde das Nähen als absolutes Reservat der menschlichen Hand erklärt, und die Versuche, diese feine und subtile Tätigkeit mit einer Maschine, mit grobem, ungelenkem Eisen auszuführen, als Tollheit, reif fürs Irrenhaus bezeichnet. Eine ganze Reihe von Erfindern war damals an der Arbeit, das Problem der Nähmaschine zu lösen; Thomas Saint in England, Joseph Madersperger in Österreich, Barthélemy Thimonnier in Frankreich, alle hatten sie mit dem Unmöglichkeitsglauben ihrer Zeitgenossen zu kämpfen. Allerdings tritt uns hier ein hochinteressantes Moment entgegen. Verschiedene Erfinder suchten das Problem in der Weise zu lösen, daß sie die Tätigkeit des Nähens, so wie diese von der menschlichen Hand ausgeführt wird, unmittelbar nachzuahmen versuchten. Alle diese Versuche hatten keinerlei Erfolg und konnten keinen haben, denn die Funktion der menschlichen Hand ist in ihrer Eigenart tatsächlich unnachahmbar mit einer Maschine. Die Lösung des Problems gelang erst, als man ein ganz neues Prinzip des Nähens ersann, und das war eben die Nähmaschine mit Schiffchen und Maschinennadel, die in ganz anderer Weise als die nähende Hand den Stoff mit dem Faden verknüpft und dadurch die Lösung des Problems brachte, was schließlich nach den ergebnislosen Versuchen vieler Vorgänger dem Amerikaner Elias Howe um das Jahr 1845 gelang. Wieder war ein Unmögliches möglich gemacht worden. Auch die Schreibmaschine war tatsächlich so lange eine Unmöglichkeit, als man die Lösung dieses Problems in der Weise versuchte, daß man die Tätigkeit der schreibenden Hand nachahmende Hände aus Stahl konstruierte; auch diese Unmöglichkeit wurde erst verwirklicht, als man ein neues Prinzip fand, daß die Schreibtätigkeit in ganz anderer Weise als die menschliche Hand ausführt und sich in bester Weise maschinell verwirklichen ließ, und das war die Schreibmaschine mit Tastenkorb und Wagen. In der Technik selbst hat lange Zeit die Lösung eines allerdings sehr komplizierten Problems, nämlich das der Geradführung, für unmöglich gegolten. Man hielt es für ein Problem ganz von der Art des Perpetuum mobile, hielt es für absolut unmöglich, daß die Bewegungen eines Mechanismus, dessen Teile sich rotierend in Achsgelenken bewegen, in eine geradlinige Bewegung übergeführt werden könnten, wie es für zahlreiche Mechanismen und maschinelle Funktionen notwendig ist. Eine Vorstufe dieser Vorrichtung war das Parallelogramm von James Watt, das bei den ältesten Dampfmaschinen zur Anwendung kam und die krummlinige Bewegung des Balanciers in eine geradlinige überführte; in aller nur wünschenswerten Vollkommenheit aber löste erst der Franzose Peaucellier das schwierige Problem und machte dadurch ein von den meisten und besten Technikern für tatsächlich unmöglich gehaltenes Ding möglich und wirklich.

Von der Unmöglichkeit, die dem Automobil nachgesagt wurde, sprachen wir schon, wobei noch zu bemerken wäre, daß Stephenson nicht etwa der einzige war, der dem Kraftwagen für den Straßenweg jede Möglichkeit absprach. Im Gegenteil, der jahrzehntelange Erfindungsweg des Autos war gepflastert mit ungezählten Unmöglichkeitseinwänden von berufener und unberufener Seite, ehe die unverdrossene Arbeit der Erfinder und Techniker zum Erfolg führte. Drastisch wurde der Unmöglichkeitsfanatismus noch bei einem anderen Erzeugnis der Automobiltechnik, dem Automobilschlitten, ad absurdum geführt. Ich entsinne mich, daß vor etwa zwanzig Jahren, als es schon lange Automobile gab, in einer führenden Automobilzeitschrift ein Artikel erschien, in dem ein Autoingenieur haarscharf und überzeugend ausführte, daß der Automobilschlitten eine Unmöglichkeit sei. Denn der eingebaute Motor eines Fahrzeuges, so deduzierte er, kann zwar auf Räder wirken, die sich um einen Zapfen drehen, nicht aber auf die starren und unbeweglichen Schlittenkufen. Damit hielt er die Möglichkeit, einen Schlitten von innen heraus anzutreiben, für ganz ausgeschlossen, und das war damals eine vielverbreitete Meinung. Kurz nach jenem Artikel aber erschien in demselben Autoblatt eine Abhandlung, die den inzwischen doch erfundenen Autoschlitten der Welt bekanntmachte. Das Unmögliche war möglich gemacht worden, indem der Schlitten mit einem Propeller versehen worden war, der, von dem inneren Motor angetrieben, die Fortbewegung des Kufenfahrzeuges in tadelloser Weise bewirkte und damit die vollkommene Lösung des Problems erbrachte.

Und wie war es mit Luftschiff und Flugzeug? Jahrzehntelang war es nachgerade eine stehende Phrase bei Fachleuten wie Laien geworden, alle Bemühungen der Erfinder auf diesem Gebiete mit einem achselzuckenden »Unmöglich!« abzutun, und manche Leute waren auch dann noch nicht von ihrem Unmöglichkeitsglauben zu bekehren, als schon die Gebrüder Wright und ebenso Zeppelin ihre ersten großen Erfolge erzielt und das Problem der Bezwingung der Luft so gut wie gelöst hatten. Stand doch bezeichnenderweise ein Mann von so hohem technischen und industriellen Weitblick wie der alte Emil Rathenau, der Begründer der Allgemeinen Elektricitäts-Gesellschaft, bis zuletzt und auch dann noch, als schon längst die ersten Zeppelinflüge Ereignis geworden waren, dem Projekt der Luftschiffahrt absolut skeptisch und ablehnend gegenüber. Die ersten Erfolge bewertete er nur als vorübergehende Erscheinungen, und das mehrfache Mißgeschick, das Zeppelin auch nach seinen ersten Erfolgen durch Vernichtung seiner Luftschiffe immer wieder betraf, betonte er immer wieder als Bestätigung seines Unmöglichkeitsglaubens.

Einige Jahrzehnte vordem hatte allerdings ein viel Größerer, sogar einer der Größten der exakten wissenschaftlichen Forschung unseres Zeitalters, Hermann Helmholtz, ein Unmöglichkeitsvotum über das Problem des Luftschiffes gefällt, jedoch mit bewußter Einschränkung. Helmholtz hatte gesagt und bewiesen, daß mit den zu seiner Zeit vorhandenen maschinellen Kräften und Hilfsmitteln die Idee des Luftschiffes unmöglich verwirklicht werden könnte. Und mit dieser Einschränkung hat er durchaus recht behalten. Damals gab es den Benzinmotor noch nicht, wenigstens nicht in einer für den erstrebten technischen Zweck brauchbaren Form, damals war noch die Dampfmaschine das nahezu einzige maschinelle Hilfsmittel der technischen und industriellen Arbeit. Niemals – das können wir auch heute noch mit aller Bestimmtheit sagen – wäre es möglich gewesen, mit der Dampfmaschine die Idee des Luftschiffes zu verwirklichen. Das wurde erst möglich, als in dem Benzinmotor eine viel konzentriertere motorische Kraft erfunden worden war, die den so ganz anders gestalteten Anforderungen der Luftfahrt in viel höherem Maße als jene entsprach und damit die Lösung des Problems brachte.

Aber auch in der reinen Wissenschaft ist schon manchmal ein Unmögliches möglich geworden. Das war beispielsweise der Fall, als im Jahre 1798 der junge Student Karl Friedrich Gauß die Welt mit der Entdeckung der 17-Teilung des Kreises überraschte und damit ein Problem gelöst hatte, das von vielen Mathematikern auf eine Stufe mit der Quadratur des Kreises gestellt und für ebensosehr oder ebensowenig unmöglich wie dieses erachtet worden war. Hatte man bis dahin auch keinen exakten Unmöglichkeitsbeweis gehabt, so hatte man doch wohl mit größter Wahrscheinlichkeit die Möglichkeit einer solchen Teilung mit Zirkel und Lineal für ausgeschlossen gehalten und erlebte nun zu allgemeiner Überraschung den Fall, daß in der Mathematik selbst die größte Wahrscheinlichkeit kein sicherer Beweis der Unmöglichkeit ist. Und in der Gegenwart hat die Chemie das Problem der Verwandlung der Elemente so gut wie gelöst und damit die Theorie einer ganz jungen Vergangenheit, derzufolge nichts so sicher war wie die elementare Natur der chemischen Grundstoffe und nichts so unmöglich wie die Umwandlung eines dieser Grundstoffe in einen anderen, einfach über den Haufen geworfen.

So scheint es, daß der Weg der Menschheit zu Fortschritt und Erkenntnis ständig und überall durch ein dichtes Gestrüpp von »Unmöglichkeiten« führt, die hinterher durchaus möglich werden. Fast scheint es, als ob das Wörtchen »unmöglich« überhaupt keine Existenzberechtigung im Sprachschatz der fortschreitenden Menschheit habe und nur dazu bestimmt sei, von der Entwicklung der Dinge stets und ständig desavouiert zu werden. Wie steht es dann aber mit den mancherlei Unmöglichkeiten, von denen in diesen Blättern die Rede war, wie etwa der Quadratur des Kreises, der Dreiteilung des Winkels, der Verdoppelung des Würfels, der 7-, 13- oder 19-Teilung des Kreises und ähnlichen Problemen, für die die Mathematiker mit aller Bestimmtheit das Verdikt »Unmöglich!« gesprochen haben? Sind das etwa auch nur »Unmöglichkeiten« in Anführungsstrichen, die ein besonders genial veranlagter Geist vielleicht doch möglich machen kann, so wie einst der junge Gauß die unmögliche 17-Teilung des Kreises möglich machte? So mancher Leser dieser Blätter, der sich mit jenen geometrischen Problemen beschäftigt hat, so mancher der zeitgenössischen Quadratoren oder Trisektoren wird geneigt sein, diese Frage entschieden und überzeugungsvoll zu bejahen, wird vielleicht glauben, jetzt den Verfasser, der ihn so oft und eindringlich der Unmöglichkeit der exakten Ausführung jener Konstruktionen versichert hat, mit den eigenen Waffen, nämlich mit der angeführten Blütenlese von Unmöglichkeiten, die in Wirklichkeit keine waren, schlagen zu können.

Aber diese Folgerung wäre mindestens ebenso voreilig und unlogisch, wie so viele jener Unmöglichkeitsprophezeiungen selbst. Es gibt auch Unmöglichkeiten von absoluter Sicherheit und Geltung, und wir haben glücklicherweise ein Kriterium, um die vermeintlichen von den wirklichen Unmöglichkeiten sicher und einwandfrei zu unterscheiden. Und dieses Kriterium heißt der Unmöglichkeitsbeweis! Bei allen jenen hier aufgezählten »Unmöglichkeiten«, die hinterher dennoch möglich wurden, handelte es sich um Dinge, die man mit mehr oder weniger Berechtigung und jedenfalls immer nur auf Grund subjektiver Auffassung für unmöglich hielt. Die Quadratur des Kreises und die anderen genannten geometrischen Konstruktionen, das Perpetuum mobile oder die Fahrt in den Weltraum mit den heute zur Verfügung stehenden Triebstoffen sind dagegen Dinge, die man nicht für unmöglich hält, sondern die bewiesenermaßen unmöglich sind. Der exakte Unmöglichkeitsbeweis erhebt diese Dinge über die Sphäre der persönlichen Ansichtssache und gibt hier der Behauptung der Unmöglichkeit die Bedeutung absoluter und unverbrüchlicher Wahrheiten, Wahrheiten so festbegründeter Art wie die, daß es unmöglich ist, daß 2 + 2 etwas anderes als 4 sein kann. Wo ein solcher Unmöglichkeitsbeweis besteht, da gibt es keinen Zweifel mehr, da wird jedes Bemühen, dem Problem eine Lösung abzugewinnen und das Unmögliche dennoch möglich zu machen, illusorisch. Für alle die in unserer Blütenlese angeführten vermeintlichen Unmöglichkeiten bestand ein Unmöglichkeitsbeweis nicht, und deswegen mußten es sich jene Unmöglichkeitspropheten gefallen lassen, daß sie hinterher durch den Gang der Entwicklung blamiert wurden. Aber der Unmöglichkeitsbeweis steht fest für die erwähnten mathematischen Probleme, er besteht für das Perpetuum mobile, er bestand im Sinne Helmholtz' und unter den technischen Bedingungen und Kräften seiner Zeit für das Luftschiff, und er besteht analog unter den heutigen technischen Bedingungen und Kräften auch für das Weltraumschiff, das das große technische Problem unserer Zeit geworden ist. Unter anderen technischen Bedingungen, das heißt, wenn uns einmal andere und wirkungsvollere technische Hilfsmittel und Kräfte als gegenwärtig noch zur Verfügung stehen werden, wird vielleicht auch dieses höchste und schwierigste technische Problem eine Möglichkeit und eine Lösung finden, gerade wie ja auch die Quadratur des Kreises und die anderen berühmten geometrischen Konstruktionen unter anderen als den von Plato vorgeschriebenen Bedingungen leicht und einfach möglich zu machen sind.

Also es gibt Unmöglichkeiten von absoluter Gewißheit, und wir haben das Kriterium, sie von den Unmöglichkeiten nur subjektiver oder relativer Bedeutung deutlich zu unterscheiden. Da könnte der hartgesottene Skeptiker allerdings noch die Frage aufwerfen, welches denn nun aber der Beweis für die Wahrheit und Richtigkeit der Unmöglichkeitsbeweise selber ist. Darauf ist zu antworten, daß die Unmöglichkeitsbeweise, so schwierig und kompliziert sie in ihrem Aufbau auch sein mögen, letzten Endes doch auf die letzten und einfachsten logischen oder arithmetischen Grundsätze zurückführen, an die sich für jeden Menschen überhaupt, den gelehrtesten wie den naivsten, das Wahrheitsbewußtsein knüpft, und die für diesen wie jenen eines weiteren Beweises weder fähig noch bedürftig sind.

Freilich, ehe die Probleme ihren Abschluß erreichen, sei es durch den Unmöglichkeitsbeweis, sei es auf andere Weise, gaukeln sie dem Menschengeiste, der mit ihnen ringt, gern das Spiel zwischen Möglichkeit und Unmöglichkeit vor. Jahrhunderte und Jahrtausende hindurch währt dieses Spiel, wie uns die Geschichte der Probleme zeigt, und es geht selbst dann noch weiter, wenn jener Abschluß erreicht worden ist, weil nur die wenigsten jenen Abschluß zu erkennen und zu beurteilen vermögen. So versuchen auch heute noch nur allzu viele, die bewiesenen Unmöglichkeiten dennoch möglich zu machen, während andererseits auch heute noch in vielen Fällen Möglichkeiten durch voreiliges Urteil zu Unmöglichkeiten gestempelt und an ihrer Verwirklichung verhindert werden.

Der Menschengeist jagt den Problemen nach. In den ewig schwankenden Begriffen von Möglichkeit und Unmöglichkeit, von Erreichbarkeit und Wirklichkeit ihrer Lösungen und Ziele, setzt sich der ewige Wettlauf mit der Schildkröte fort, der das merkwürdige Symbol des Geisteskampfes der Menschheit um die Probleme des Denkens geworden ist und zugleich für immer das romantische Schicksal des Menschengeistes zu sein bestimmt scheint.

Finis


Autoren	∞	Werke	∞	Neu	∞	Information	∞	Lesetips	∞	Textquelle

Dr. Th. Wolff

Der Wettlauf mit der Schildkröte

Gelöste und ungelöste Probleme

Vorbetrachtung

I. Probleme des Paradoxen

1. Der Wettlauf mit der Schildkröte Die Geschichte eines Widerspruches

2. Die Kunst des Lullus oder Eine Maschine, die den »Faust« dichten könnte

Postskriptum I Die Lullische Druckmaschine im Minimalformat

Postskriptum II Moderne Lullische Kunst

3. Der Streit um die Allmacht Eine höchst logische Geschichte

4. Heitere Logik

5. Trugschlüsse

II. Probleme der Linie

1. Mit Zirkel und Lineal

2. Die Quadratur des Kreises

Postskriptum

3. Der geheimnisvolle Würfel (Das Delische Problem)

4. Der widerspenstige Winkel (Das Trisektionsproblem)

Postskriptum

5. Das Problem der Kreisteilung

Postskriptum

III. Probleme der Zahl

1. Geheimnisse der Zahlenreihe

Postskriptum I

Postskriptum II

2. Das Gesetz der Primzahlen

3. Das Goldbachsche Problem

4. Das Fermatsche Problem

5. Vom Sinn und Unsinn der Zahlen

IV. Vom Humor der Zahl

3 + 3 = 11

2. Von Zinsen und Zinseszinsen

3. Rothschild und der Bettler

4. Heitere Rechenkunst

5. Lösungen und Löser der »Heiteren Rechenkunst«

6. Heitere Geometrie

7. Lösungen und Löser der »Heiteren Geometrie«

V. Das Problem der Dimensionen

1. Gibt es eine vierte Dimension?

2. Beweise und Gegenbeweise

3. Die Lösung des Problems

Postskriptum

VI. Probleme des Metaphysischen

1. Das Problem der Willensfreiheit

2. Sternenlauf und Menschenschicksal

Postskriptum

3. Der Goldene Schnitt

I

II

III

Postskriptum

4. Der Stein der Weisen

Postskriptum

VII. Probleme des Physischen

1. Von der Erhaltung der Energie zur allgemeinen Relativität

2. Probleme des Falles

3. Das Geheimnis der Schwerkraft

4. Ist ein Perpetuum mobile möglich?

Postskriptum

5. Heureka

Postskriptum

VIII Probleme der Erfindung

1. Die Fahrt in den Weltraum

Postskriptum

2. Das Problem der künstlichen Hand

3. Erfinder-Schicksale

I

II

III

4. Kinder als Erfinder

5. Unmöglichkeiten, die möglich wurden

I.
Probleme des Paradoxen

1. Der Wettlauf mit der Schildkröte
Die Geschichte eines Widerspruches

2. Die Kunst des Lullus
oder
Eine Maschine, die den »Faust« dichten könnte

Postskriptum I
Die Lullische Druckmaschine im Minimalformat

Postskriptum II
Moderne Lullische Kunst

3. Der Streit um die Allmacht
Eine höchst logische Geschichte

II.
Probleme der Linie

3. Der geheimnisvolle Würfel
(Das Delische Problem)

4. Der widerspenstige Winkel
(Das Trisektionsproblem)

III.
Probleme der Zahl

IV.
Vom Humor der Zahl

V.
Das Problem der Dimensionen

VI.
Probleme des Metaphysischen

VII.
Probleme des Physischen

VIII
Probleme der Erfindung