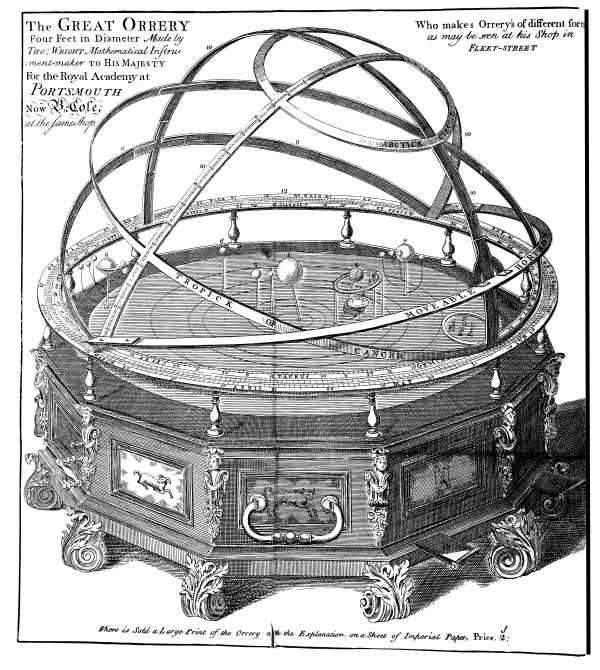
The Great Orrery Four Feet in Diameter Made by Tho:
Wright Mathematical Instrument-maker to His Majesty
For the Royal Academy at Portsmouth Now B. Cole, at the same
shop.
Who makes Orrery’s of different sorts as may be seen at his Shop in
Fleet Street
Where is Sold a Large Print of the Orrery with the Explanation on a
Sheet of Imperial Paper. Price 2s.
THE
Description and Use
OF
THE GLOBES,
AND
THE ORRERY.
To which is prefix’d,
By Way of Introduction,
A brief Account of the Solar System.
By JOSEPH HARRIS,
Teacher of the Mathematics.
The Eleventh Edition.
LONDON:
Printed for B. Cole,
at the Orrery, near the Globe Tavern, in Fleet street,
late the Shop of Mr. Thomas Wright,
Instrument-maker to his late Majesty; and
E. Cushee, near St. Dunstan’s Church,
Fleet Street.
MDCCLXXIII.
Advertisement.
The great encouragement
Mr. Wright has had for many years past
in making large Orreries, with the motions of all the Planets and
Satellites, and the true motion of Saturn’s Ring, has made him so
ready and perfect, that Gentlemen may depend on having them made
reasonable and sound, not liable to be out of Order.
As may be seen by one he made for Mr. Watt’s Academy in
Tower-street.
Another for his Majesty at Kensington.
Another for the New Royal Academy at Portsmouth.
Another for his Grace the Duke of Argyle (late Lord Ila.)
And several other large ones for Noblemen and Gentlemen.
The above, and all other Mathematical, Philosophical, and Optical
Instruments, are now made in the most complete manner, by B.
Cole, Servant to Mr. Wright, at the time of the above
being made, and successor to him in the same Trade and Business.
THE CONTENTS.
The Introduction:
Containing a brief Account of the Solar System, and of the Fixed
Stars.
Sect. I. |
Of
the Order and Periods of the Primary
Planets revolving about the Sun; and of
the Secondary Planets round their respective
Primaries. |
| ——— |
Of the Primary Planets |
1 |
| ——— |
Of the Secondary Planets |
5 |
| ——— |
Of the Annual and Diurnal Motion of the Planets |
7 |
| ——— |
That the Planets are Opaque and Globular |
9 |
| ——— |
That the Earth is placed betwixt the Orbits of Mars and Venus |
ibid. |
| ——— |
That the Planets turn round the Sun |
ibid. |
| ——— |
That the Earth also turns round the Sun |
15 |
| ——— |
How the Annual and Diurnal Motion of the Planets are computed |
ibid. |
| ——— |
How the relative Distance of the Planets from the Sun are determined |
18 |
| ——— |
How their absolute Distances from the Sun are computed |
23 |
| ——— |
How the Magnitudes of the Planets are determined |
26 |
| ——— |
Why the Moon appears bigger than any of the Planets |
27 |
| ——— |
A Table of the Distances, Magnitudes, Periodical, and Diurnal Revolutions of the Planets |
28 |
| ——— |
Of Comets |
29 |
| Sect. II. |
Of the Fixed Stars |
32 |
| ——— |
That the fixed Stars are luminous Bodies, at immense Distances from us |
ibid. |
| ——— |
Of Telescopical Stars |
35 |
| ——— |
The Stars digested into Constellations |
36 |
| ——— |
Of the Galaxy, or Milky Way |
38
[Pg iv] |

The Description
and Use of the Celestial
and Terrestrial Globes.
The Geometrical Definition of a Globe,
and of the principal Use of the Artificial Globes |
42 |
That there will be the same prospect of the Fixed Stars, whether the
Spectator be placed in the Sun, or on the Earth |
45 |
| Sect. I. |
An Explanation of the Circles of the Sphere,
and of some Astronomical Terms arising therefrom |
47 |
| ——— |
Of the Division of Time |
69 |
| ——— |
Of the Atmosphere |
81 |
| Sect. II. |
Geographical Definitions |
84 |
| ——— |
Of the Situation of Places upon the Earth |
ibid. |
| ——— |
Of Zones and Climates |
90 |
| ——— |
Of the Poetical Rising and Setting of the Stars |
96 |
| ——— |
Of the surface of the Earth, considered as it is composed of Land and Water |
ibid. |
| ——— |
Of the appurtenances of the Globes |
101 |
| Sect. III. |
The Use of the Globes |
104 |
| Problem I. |
To find the Latitude and Longitude of any given place upon the Globe; and
on the contrary, the Latitude and Longitude being given to find the Place |
ibid. |
| Prob. II. |
To find the Difference of Latitude betwixt any two given places |
106 |
| Prob. III. |
To find the Difference of Longitude betwixt any two given places |
ibid. |
| Prob. IV. |
Any Place being given; to find all those places that are in the same
Latitude with the said place |
107 |
| Prob. V. |
The Day of the Month being given; to find the Sun’s place in the Ecliptic,
and his Declination |
108 |
| Prob. VI. |
To rectify the Globe for the Latitude, Zenith, and Sun’s place |
109
[Pg v] |
| Prob. VII. |
To find the Distance between any two given Places upon the Globe,
and to find all those places upon the Globe that are at the same
Distance from a given place |
110 |
| Prob. VIII. |
To find the Angle of a Position of Places; or the angle formed by the
Meridian of one place, and a great circle passing through both the places |
111 |
| Prob. IX. |
To find the Antœci, Periœci, and Antipodes, to any given place |
113 |
| Prob. X. |
The Hour of the Day at one Place being given; to find the correspondent Hour
(or what o’Clock it is at that time) at any other place |
114 |
| Prob. XI. |
The Day of the Month being given; to find those places on the Globe
where the Sun will be Vertical, or in the Zenith, that Day |
115 |
| Prob. XII. |
A place being given in the Torrid Zone; to find those two
Days in which the Sun will be Vertical to the same |
116 |
| Prob. XIII. |
To find where the Sun is Vertical at any given time assigned; or,
the Day of the Month and the Hour at any place (suppose London)
being given, to find in what place the Sun is Vertical at that very time |
ibid. |
| Prob. XIV. |
The Day, and the Hour of the Day at one place, being given; to find
all those places upon the Earth where the Sun is then Rising, Setting,
Culminating (or on the Meridian); also where it is Day-light, Twilight,
Dark Night, Midnight; where the Twilight then begins, and where it
ends; the Height of the Sun in any part of the illuminated Hemisphere;
also his Depression in the obscure Hemisphere |
117 |
| Prob. XV. |
The Day of the Month being given, to show, at one View, the Length
of Days and Nights in all Places upon the Earth, at that time; and to
explain how the Vicissitudes of Day and Night are really made by the
motion of the Earth round her Axis, in 24 Hours, the Sun standing still |
119 |
| Prob. XVI. |
To Explain in general the Alteration of Seasons, or Length of the
Days and Nights, made in all places of the World, by the Sun’s, or the
Earth’s Annual motion in the Ecliptic |
121 |
| Prob. XVII. |
To shew by the Globe, at one View, the Length of the Days and Nights,
at any particular place, at all times of the Year
[Pg vi] |
128 |
| Prob. XVIII. |
The Latitude of any place, not exceeding 69½ Degrees, and the Day
of the Month being given; to the time of Sun-rising and Setting, and
the length of the Day and Night |
136 |
| Prob. XIX. |
To find the length of the longest and shortest Day and Night
in any given place, not exceeding 66½ Degrees of Latitude |
137 |
| Prob. XX. |
To find in what Latitude the longest Day is, of any given length less than 24 Hours |
139 |
| Prob. XXI. |
A Place being given in one of the Frigid Zones (suppose the
Northern) to find what number of Days (of 24 Hours each) the Sun doth
constantly shine upon the same, how long he is absent, and also the
first and last day of his appearance |
140 |
| Prob. XXII. |
To find in what Latitude the longest Day is, of any given length,
less than 182 natural Days |
141 |
| Prob. XXIII. |
The Day of the Month being given; to find when the Morning and Evening
Twilight begins and ends, in any place upon the Globe |
142 |
| Prob. XXIV. |
To find the time when total Darkness ceases, or when the Twilight
continues from Sun-setting to Sun-rising, in any given place |
144 |
| Prob. XXV. |
The Day of the Month being given; to find those places of the
Frigid Zones, where the Sun begins to shine constantly without setting;
and also those places where he begins to be totally absent |
146 |
| Prob. XXVI. |
The Latitude, the Sun’s Place, and his Altitude being given; to
find the Hour of the Day, and Sun’s Azimuth from the Meridian |
149 |
| Prob. XXVII. |
The Latitude, Hour of the Day, and the Sun’s Place being given;
to find the Sun’s Altitude |
150 |
| Prob. XXVIII. |
The Latitude of the Place, and the Day of the Month being given; to
find the depression of the Sun below the Horizon, and his Azimuth, at
any Hour of the Night |
151 |
| Prob. XXIX. |
The Latitude of the Sun’s Place, and his Azimuth being given;
to find his Altitude, and the Hour |
152 |
| Prob. XXX. |
The Latitude, the Sun’s Altitude, and his Azimuth being given;
to find his Place on the Ecliptic, and the Hour |
ibid.
[Pg vii] |
| Prob. XXXI. |
The Declination, and Meridian Altitude of the Sun, or of any
Star being given; to find the Latitude of the Place |
153 |
| Prob. XXXII. |
The Day and Hour of a Lunar Eclipse being known; to find all those
Places upon the Globe in which the same will be visible |
154 |
| Prob. XXXIII. |
The Day of the Month, and Hour of the Day, according to our way of
reckoning in England, being given; to find thereby the Babylonish,
Italic, and Jewish, or Judaical Hour |
155 |
| Prob. XXXIV. |
To find the Right Ascension and Declination of the Sun, or any Fixed Star |
156 |
| Prob. XXXV. |
To find the Longitude and Latitude of a given Star |
158 |
| Prob. XXXVI. |
The Latitude of the Place, the Day of the Month, and the Hour being
given; to find what Stars are then rising and setting, what Stars are
culminating, or on the Meridian, and the Altitude and Azimuth of any
Star above the Horizon; and also how to distinguish the Stars in the
Heavens one from the other, and to know them by their proper Names |
159 |
| Prob. XXXVII. |
The Latitude of the Place being given; to find the Amplitude,
Oblique Ascension, and Descension, Ascensional Difference, Semi-diurnal
Arch, and the time of Continuance above the Horizon, of any given Point
in the Heavens |
162 |
| Prob. XXXVIII. |
The Latitude and the Day of the Month being given; to find the
Hour when any known Star will be on the Meridian, and also the time
of its Rising and Setting |
165 |
| Prob. XXXIX. |
To find at what time of the Year a given Star will be
upon the Meridian, at a given Hour of the Night |
166 |
| Prob. XL. |
The Day of the Month and the Azimuth, of any known Star being given;
to find the Hour of the Night |
167 |
| Prob. XLI. |
Two known Stars, having the same Azimuth, or the same Height,
being given; to find the Hour of the Night |
168 |
| Prob. XLII. |
The Latitude, Day of the Month, and the Altitude of any known Star
being given; to find the Hour of the Night |
169
[Pg viii] |
| Prob. XLIII. |
Having the Latitude of the Place, to find the Degree of the Ecliptic,
which rises or sets with a given Star; and from thence to determine the
time of its Cosmical and Achronical Rising and Setting |
171 |
| Prob. XLIV. |
Having the Latitude of the Place; to find the time when a Star
rises and sets Heliacally |
172 |
| Prob. XLV. |
To find the Place of any Planet upon the Globe, so by that Means to
find its Place in the Heavens; also to find at what Hour any Planet
will rise or set, or be on the Meridian, at any Day in the Year |
173 |
| Prob. XLVI. |
To find all that space upon the Earth where an Eclipse of one of
the Satellites of Jupiter will be visible |
175 |
| |
| |
The Description
of the ORRERY |
177 |
| |
| |
Of the Motions of the Planets in general |
183 |
| |
Of the Stations and Retrogadations of the Planets |
186 |
| |
Of the Annual and Diurnal Motion of the Earth |
194 |
| |
Of the Phases of the Moon, and of her Motion in her Orbit |
201 |
| |
Of the Eclipses of the Sun and Moon |
208 |
| |
Of the Eclipses of Jupiter’s Satellites |
212 |
[Pg 1]
THE
INTRODUCTION,
CONTAINING
A Brief Account of the Solar System,
and of the Fixed Stars.
SECT. I.
Of the Order and Periods of the Primary Planets
revolving about the Sun; and of the Secondary Planets round their
respective Primaries.
Planets.
The Sun is
placed in the midst of an immense space, wherein six opaque
spherical bodies revolve about him as their center. These wandering
globes are called the Planets, who, at different distances, and
[Pg 2]
in different periods, perform their revolutions from West to East, in
the following order:
1. ☿ Mercury is nearest to the Sun of all the
planets, and performs its course in about three months. 2. ♀ Venus in
about seven months and a half. 3. ♁ The Earth in a year. 4. ♂ Mars
in about two years. 5. ♃ Jupiter in twelve. And lastly, ♄ Saturn,
whose[1]
Orbit includes all the rest, spends almost 30 years in one revolution
round the Sun. The distances of the Planets from the Sun are nearly
in the same proportion as they are represented in Plate 1.
viz. Supposing the distance of the Earth from the Sun to be divided into
10 equal parts; that of Mercury will be about 4 of these parts; of
Venus 7; of Mars 15; of Jupiter 52; and that of Saturn 95.
The Characters placed before the
names of the Planets, are for brevity’s sake commonly made use of
by Astronomers, instead of the words at length, as ♀, for Venus,
&c.
Plate 1.

[Pg 3]
Nodes.
The orbits of the Planets are not all in the same plane, but variously
inclined to one another; so that supposing one of them to coincide with
the above scheme, the others will have one half above, and the other
half below it; intersecting one another in a line passing through the
Sun. The plane of the Earth’s orbit is called the Ecliptic; and this
the astronomers make the standard to which the planes of the other
orbits are judged to incline. The right line passing thro’ the Sun, and
the common intersection of the plane of the orbit of any planet and the
Ecliptic, is called the Line of the Nodes of that planet; and the
points themselves, wherein the orbit cuts the Ecliptic are called the
Nodes.
Excentricity.
The inclinations of the orbits of the Planets to the plane of the
ecliptic, are as follows, viz. the orbit of Mercury makes an
angle with it of almost 7 degrees; that of Venus something above
3⅓ degrees; of Mars a little less than 2 degrees; of Jupiter, 1⅓
degree; and of Saturn, about 2½ degrees. The orbits of the Planets
are not circles, but ellipses or ovals. What an ellipsis is, may be
[Pg 4]
easily understood from the following description. Imagine two small
pegs fixed upright on any plane, and suppose them tied with the ends
of a thread somewhat longer than their distance from one another: Now
if a pin be placed in the double of the thread and turned quite round
(always stretching the thread with the same force) the curved described
by this motion is an Ellipsis. The two points where the pegs stood,
(about which the thread was turned) are called the foci of that
ellipsis; and if, without changing the length of the thread, we alter
the position of the pegs, we shall then have an ellipsis of a different
kind from the former; and the nearer the focus’s are together, the
nearer will the curve described be to a circle; until at last, the two
focus’s coincide, and then the pin in the doubling of the thread
will describe a perfect circle. The orbits of all the Planets have the
Sun in one of their focus’s, and half the distance between the two
focus’s is called the Excentricity of the orbits. This excentricity
is different in all the planets, but in most of them so small, that in
little schemes or instruments, made to represent the planetary orbits,
it need not be considered.
[Pg 5]
Primary Planets.
Secondary Planets.
The six Planets above-mentioned, are called Primaries, or Primary
Planets; but besides these, there are ten other lesser Planets, which
are called Secondaries, Moons, or Satellites. These moons always
accompany their respective primaries, and perform their Revolutions
round them, whilst both together are also carried round the Sun. Of the
six Primary Planets, there are but three, as far as observation can
assure us, that have these attendants, viz. the Earth, Jupiter,
and Saturn.
The Earth is attended by the Moon, who performs her revolution in
about 27⅓ Days, at the distance of about 30 Diameters of the Earth from
it; and once a Year is carried round the Sun along with the Earth.
Jupiter’s four Moons.
Jupiter has four Moons, or Satellites; the first, or
innermost, performs its revolution in about one Day, and 18½ Hours, at the
distance of 5⅔ Semidiameters of Jupiter, from his Center; the
second revolves about Jupiter in 3 Days, 13 Hours, at the distance
of 9 of his Semidiameters; the third in 7 Days, and 4 Hours, at the
[Pg 6]
distance of 14⅓ Semidiameters; the fourth, and outermost, performs
its course in the space of 16 Days, 17 Hours; and is distant from
Jupiter’s center, 25⅓ of his Semidiameters.
Saturn has five Moons.
Saturn has no less than five Satellites; the first, or
innermost, revolves about him in 1 Day, and 21 Hours, at the distance of 4⅜
Semidiameters of ♄, from his center; the second compleats
his period in 2¾ Days, at the distance of 5³/₅ of his Semidiameters;
the third, in about 4½ Days, at the distance of 8 Semidiameters;
the fourth performs its course in about 16 Days, at the distance
of 18 Semidiameters; the fifth, and outermost, takes 79⅓ Days, to
finish his course, and is 54 Semidiameters of Saturn distant from
his center. The Satellites, as well as their primaries, perform their
revolutions from West to East: The planes of the Orbits of the
Satellites of the same Planet are variously inclined to one another,
and consequently are inclined to the plane of the Orbit of their
primary.
Saturn’s Ring.
Besides these attendants, Saturn is encompassed with a thin plain
Ring, that does no where touch his body; The diameter of this Ring is
[Pg 7]
to the diameter of Saturn, as 9 to 4; and the void space between
the Ring and the body of Saturn is equal to the breadth of the Ring
itself; so that in some situations the Heavens may be seen between the
Ring and his body. This surprizing phænomenon of Saturn’s Ring, is a
modern discovery; neither were the Satellites of Jupiter and Saturn
known to the ancients. The Jovial Planets were first discovered by
the famous Italian philosopher Galilæus, by a telescope which he
first invented; and the celebrated Cassini, the French king’s
astronomer, was the first that saw all the Satellites of Saturn;
which by reason of their great distances from the Sun, and the
smallness of their own bodies, cannot be seen by us, but by the help of
very good glasses.
Annual Motion.
Diurnal Motion.
The motion of the primary Planets round the Sun (as also of the
Satellites round their respective primaries) is called their Annual
Motion; because they have one Year, or alteration of Seasons compleat,
in one of these revolutions. Besides this annual motion, four of the
Planets, viz. Venus, the Earth, Mars, and Jupiter revolve
about their own Axis, from West to East; and this is called their
[Pg 8]
Diurnal Motion. For by this rotation, each point of their surfaces is
carried successively towards or from the Sun, who always illuminates
the hemisphere which is next to him, the other remaining obscure; and
while any place is in the hemisphere, illuminated by the Sun, it is
Day, but when it is carried to the obscure hemisphere, it becomes
Night; and so continues, until by this rotation the said place is
again enlightened by the Sun.
Diurnal Motion of the ♁, ♀, ♂ and ♃.
☉ and ☽ likewise turn round their Axis.
The Earth performs its revolution round its axis in 23 Hours, 56
Minutes;[2]
Venus, in 24 Days, 8 Hours; Mars, in 24 Hours, and
40 Minutes; and Jupiter moves round his own axis in 9 Hours, and
56 Minutes. The Sun also is found to turn round his axis from West
to East, in 27 Days: And the Moon, which is nearest to us of all the
Planets, revolves about her axis in a Month, or in the same space of
time that she turns round the Earth; so that the Lunarians have but 1
Day throughout the Year.
[Pg 9]
The Planets are Opaque and Globular.
I. The Planets are all Opaque bodies, having no light but what they
borrow from the Sun; for that side of them which is next towards the
Sun, has always been observed to be illuminated, in what position
soever they be; but the opposite side, which the Solar rays do not
reach, remains dark and obscure; whence it is evident that they have
no light but what proceeds from the Sun; for if they had, all parts of
them would be lucid, without any darkness or shadow. The Planets are
likewise proved to be Globular; because let what part soever of them
be turned towards the Sun, its boundary, or the line separating that
part from the opposite, always appears to be circular; which could not
happen, if they were not globular.
The Planets turn round the Sun.
[Pg 10]
II. That the Earth is placed betwixt the Orbs of Mars and Venus,
and that ☿, ♀, ♂, ♃ and ♄, do all turn round the Sun, is proved from
observations as follow:
1. Whenever Venus is in conjunction with the Sun, that is, when she
is in the same direction from the Earth, or towards the same part of
the Heavens the Sun is in; she either appears with a bright and round
face, like a Full Moon, or else disappears: Or, if she is visible, she
appears horned, like a new Moon; which phænomena could never happen
if ♀ did not turn round the Sun, and was not betwixt him and the
Earth: For since all the Planets borrow their light from the Sun, it
is necessary that ♀’s lucid face should be towards the Sun; and when
she appears fully illuminated, she shews the same face to the Sun and
Earth; and at that time she must be above or beyond the Sun; for in
no other position could her illuminated face be seen from the Earth.
Farther, when she disappears, or if visible, appears horned; that face
of her’s which is towards the Sun is either wholly turned from the
Earth, or only a small part of it can be seen by the Earth; and in this
case she must of necessity be betwixt us and the Sun. Let S be the
Sun, T the Earth, and V Venus, having the same face presented
both towards the Sun and Earth; here it is plain that the Sun is
betwixt us and Venus and therefore we must either place Venus in an
[Pg 11]
Orbit round the Sun, and likewise betwixt him and us, as in Fig. 1.
or else we must make the Sun to move round the Earth in an Orbit within
that of Venus, as in Fig. 2.
Again, after Venus disappears, or becomes horned, at
her[3]
☌ with the ☉, she then must be betwixt us and the Sun, and must move
either in an Orbit round the Sun and betwixt us and him, as in Fig. 1.
or else round the Earth, and betwixt us and the Sun, as in Fig. 2.
But Venus cannot move sometimes within the Sun’s Orbit, and
sometimes without it, as we must suppose if she moves round the Earth;
therefore it is plain that her motion is round the Sun.
Why Venus is always either our Morning or Evening Star.
Besides the forgoing, there is another argument to prove that Venus
turns round the Sun in an Orbit that is within the Earth’s, because she
is always observed to keep near the Sun, and in the same quarter of the
Heavens that he is in, never receding from him more than about ⅛ of a
whole circle; and therefore she can never come in opposition to him;
which would necessarily happen, did she perform her course round the
Earth either in a longer or shorter time than a Year. And this is the
[Pg 12]
reason why Venus is never to be seen near midnight, but always either
in the Morning or Evening, and at most not above three or four Hours
before Sun-rising or after Sun-setting. From the time of ♀’s superior
conjunction (or when she is above the Sun) she is more Easterly than
the Sun, and therefore sets later, and is seen after Sun-setting; and
then she is commonly called the Evening Star. But from the time of
her inferior conjunction, ’till she comes again to the superior, she
then appears more Westerly than the Sun, and is only to be seen in the
morning before Sun-rising, and is then called the Morning Star.
After the same manner we prove that Mercury turns round the Sun, for
he always keeps in the Sun’s neighbourhood, and never recedes from him
so far as Venus does; and therefore the Orbit of ☿ must lie within
that of ♀; and on the account of his nearness to the Sun, he can seldom
be seen without a Telescope.
The Orbit of Mars includes the Earth’s.
Mars is observed to come in opposition, and likewise to have all
[Pg 13]
other aspects with the Sun; he always preserves a round, full, and
bright face, except when he is near his quadrate aspect, when he
appears somewhat gibbous, like the Moon three or four Days before or
after the full: Therefore the Orbit of ♂ must include the Earth within
it, and also the Sun; for if he was betwixt the Sun and us at the
time of his inferior conjunction, he would either quite disappear, or
appear horned, as Venus and the Moon do in that position. Let S be
the Sun, T the Earth, and A P Mars, both in his conjunction
and opposition to the Sun, and in both positions full; and B C Mars at
his quadratures, when he appears somewhat gibbous from the Earth at
T. ’Tis plain hence, that the Orbit of Mars does include the Earth,
otherwise he could not come in opposition to the Sun; and that it
likewise includes the Sun, else he could appear full at his conjunction.
Mars when he is in opposition to the Sun, looks almost seven times
larger in diameter than when he is in conjunction with him, and
therefore must needs be almost seven times nearer to us in one position
[Pg 14]
than in the other; for the apparent magnitudes of far distant objects
increase or decrease in proportion to their distances from us: But
Mars keeps always nearly at the same distance from the Sun; therefore
it is plain that it is not the Earth, but the Sun, that is the center
of his motion.
It is proved in the same way, that Jupiter and Saturn have both
the Sun and the Earth within their Orbits, and that the Sun, and not
the Earth, is the center of their motions; altho’ the disproportion of
the distances from the Earth is not so great in Jupiter, as it is in
Mars, nor so great in Saturn, as it is in Jupiter, by reason
that they are at a much greater distance from the Sun.
Inferior and Superior Planets.
We have now shewn that all the Planets turn round the Sun, and that
Mercury and Venus are included between him and the Earth, whence
they are called the Inferior Planets, and that the Earth is placed
between the Orbits of Mars and Venus, and therefore included within
the Orbits of Mars, Jupiter, and Saturn, whence they are called
the Superior Planets: And since the Earth is in the middle of these
[Pg 15]
moveable bodies, and is of the same nature with them, we may conclude
that she has the same sort of motions; but that she turns round the Sun
is proved thus:
The Earth does not stand still, but turns round the Sun.
All the Planets seen from the Earth appear to move very unequally,
as sometimes to go faster, at other times slower; sometimes to go
backwards, and sometimes to be stationary, or not to move at all; which
could not happen if the Earth stood still. Let S be the Sun, T the
Earth, the great circle A B C D the Orbit of Mars, and the numbers 1,
2, 3, &c. its equable motion round the Sun; the correspondent numbers
1, 2, 3, &c. in the circle a, b, c, d, the
motion of Mars, as it would be seen from the Earth. It is plain from this
Figure, that if the Earth stood still, the motion of Mars, will be always
progressive, (tho’ sometimes very unequal;) but since observations
prove the contrary, it necessarily follows, that the Earth turns round
the Sun.
The Annual and Diurnal Motions of the Planets, how computed.
The annual periods of the Planets round the Sun are determined by
carefully observing the length of time since their departure from a
certain point in the Heavens, (or from a fix’d Star) until they arrive
[Pg 16]
to the same again. By these sort of observations the ancients
determined the periodical revolutions of the Planets round the
Sun, and were so exact in their computations, as to be capable of
predicting Eclipses of the Sun and Moon. But since the invention of
telescopes, astronomical observations are made with greater accuracy;
and of consequence, our tables are far more perfect than those of
the ancients. And in order to be as exact as possible, astronomers
compare observations made at a great distance of time from one another,
including several periods; by which means, the error that might be in
the whole, is in each period subdivided into such little parts as to be
inconsiderable. Thus the mean length of a Solar Year is known, even to
Seconds.
The Diurnal rotation of the Planets round their axis, was discovered by
certain spots which appear on the surfaces. These spots appear first in
the margin of the Planet’s disk, (or the edge of their surfaces) and
seem by degrees to creep toward their middle, and so on, going still
forward, ’till they come to the opposite side or edge of the disk,
[Pg 17]
where they set or disappear; and after they have been hid for the
same space of time, that they were visible, they again appear to rise
in or near the same place, as they did at first, then to creep on
progressively, taking the same course as they did before. These spots
have been observed on the surfaces of the Sun, Venus, Mars,
and Jupiter; by which means it has been found that these bodies
turn round their own axis, in the times before-mentioned. It is very
probable that Mercury and Saturn have likewise a motion round
their axis, that all the parts of their surface may alternately enjoy the
light and heat of the Sun, and receive such changes as are proper and
convenient for their nature. But by reason of the nearness of ☿ to the
Sun, and ♄’s immense distance from him, no observations have hitherto
been made whereby their spots (if they have any) could be discovered,
and therefore their Diurnal motions could not be determined. The
Diurnal motion of the Earth is computed from the apparent revolution of
the Heavens, and of all the Stars round it, in the space of a natural
Day. The Solar spots do not always remain the same, but sometimes old
[Pg 18]
ones vanish, and afterwards others succeed in their room; sometimes
several small ones gather together and make one large spot, and
sometimes a large spot is seen to be divided into many small ones. But,
notwithstanding these changes, they all turn round with the Sun in the
same time.
How the relative distances of the Planets from the Sun are
determined.
The relative distances of the Planets from the Sun, and likewise
from each other, are determined by the following methods: First, the
distance of the two inferior Planets ☿ and ♀ from the Sun, in respect
of the Earth’s distance from him, is had by observing their greatest
Elongation from the Sun as they are seen from the Earth.
The greatest Elongation of Venus is found by observation to be
about 48 degrees, which is the angle S T ♀; whence, by the known rules
of Trigonometry, the proportion of S ♀, the mean distance of Venus
from the Sun to ST, the mean distance of the Earth from him may be
easily found. After the same manner, in the right-angled triangle S
T ☿, may be found the distance S ☿ of Mercury from the Sun. And if
the mean distance of the Earth from the Sun S T be made 1000, the mean
[Pg 19]
distance of Venus S ♀ from the Sun will be 723; and of Mercury S
☿ 387: And if the Planets moved round the Sun in circles, having him
for their center, the distances here found would be always their true
distances: But as they move in Ellipses, their distances from the Sun
will be sometimes greater, and sometimes less. Their Excentricities
are computed to be as follows, viz.
| |
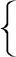 |
Mercury |
80 |
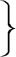 |
of the parts |
| Excent. of |
Venus |
5 |
above-mentioned. |
| |
Earth |
169 |
|
Heliocentric and Geocentric Place, what.
The distances of the superior Planets, viz. ♂, ♃, and ♄, are found
by comparing their true places, as they are seen from the Sun, with
their apparent places, as they are seen from the Earth. Let S be the
Sun, the circle ABC the Earth’s orbit, AG a line touching the Earth’s
orbit, in which we’ll suppose the superior Planets are seen from the
Earth in the points of their orbits ♂, ♃, ♄; and let DEFGH be a portion
of a great circle in the Heavens, at an infinite distance: Then the
place of Mars seen from the Sun is D, which is called his true, or
Heliocentric Place; but from the Earth, he will be seen in G, which
[Pg 20]
is called his apparent, or Geocentric Place. So likewise Jupiter
and Saturn will be seen from the Sun in the points E and F, their
Heliocentric places; but a spectator from the Earth will see them in
the point of the Heavens G, which is their Geocentric place. The arches
DG, EG, FG, the differences between the true and apparent places of the
Superior Planets, are called the Parallaxes of the Earth’s annual
Orb, as seen from these Planets. If thro’ the Sun we draw SH parallel
to AG, the angles A ♂ S, A ♃ S, A ♄ S, will be respectively equal to
the angles D S H, E S H, and F S H; and the angle A G S is equal to
the angle GSH, whose measure is the arch GH; which therefore will be
the measure of the angle AGS, the angle under which the semidiameter
A S of the Earth’s orbit, is seen from the Starry Heavens. But this
semidiameter is nothing in respect of the immense distance of the
Heavens or Fixed Stars; for from thence it would appear under no
sensible angle, but look like a point. And therefore in the Heavens,
the angle G S H, or the arch G H vanishes; and the Points G and H
coincide; and the arches D H, E H, F H, may be considered as being of
[Pg 21]
the same bigness with the arches D G, E G, and F G, which are the
measures of the angles A ♂ S, A ♃ S, A ♄ S; which angles are nearly
the greatest elongation of the Earth from the Sun, if the Earth be
observed from the respective Planets, when the line G ♄ ♃ ♂ A, touches
the Earth’s orbit in A. The nearer any of the superior Planets is to
the Sun, the greater is the Parallax of the annual Orb, or the angle
under which the semidiameter of the Earth’s orbit is seen from that
Planet. In Mars the angle ♂ S, (which is the visible elongation of
the Earth seen from Mars, or the Parallax of the annual Orb seen from
that Planet) is about 42 degrees, and therefore the Earth is always to
the inhabitants of Mars either their Morning or Evening Star, and
is never seen by them so far distant from the Sun as we see Venus.
The greatest elongation of the Earth seen from Jupiter, being nearly
equal to the angle A ♃ S, is about 11 degrees. In Saturn the angle A
♄ S is but 6 degrees, which is not much above ¼ part of the greatest
elongation we observe in Mercury. And since Mercury is so rarely
seen by us, probably the astronomers of Saturn (except they have
[Pg 22]
better Optics than we have) have not yet discovered that there is such
a body as our Earth in the Universe.
The Parallax of the annual Orb, or the greatest elongation
of the Earth’s orbit seen from any of the superior Planets, being given;
the distance of that Planet from the Sun, in respect of the Earth’s
distance from him, may be found by the same methods as the distances of
the inferior Planets were. Thus, to find the distance of Mars from
the Sun, it will be as the Sine of the angle S ♂ A is to the Radius,
so is the distance AS (the distance of the Earth from the Sun) to S
♂, the distance from the Sun to Mars. After the same manner the
distances of Jupiter and Saturn are also found. The mean distance
of the Earth from the Sun being made 1000, the mean distances of the
superior Planets from the Sun are, viz. the mean distance from the
Sun of
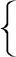 |
♂ |
1524 |
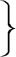 |
|
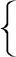 |
141 |
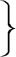 |
| ♃ |
5201 |
and the Excentricity |
250 |
| ♄ |
9538 |
|
547 |
To which, if you add or subtract their mean distances, we shall have
the greatest or least distances of those Planets from the Sun.
[Pg 23]
There are other methods by which the relative distances of the
Planets might be found; but that which hath been here illustrated, is
sufficient to evince the certainty of that Problem.
How the absolute distances of the Planets from the Sun are
computed.
Parallax of the Earth’s Semidiameter.
Hitherto we have only considered the distances of the Planets in
relation to one another, without determining them by any known measure;
but in order to find their absolute distances in some determinate
measure, there must be something given, whose measure is known. Now
the circumference of the Earth is divided into 360 degrees, and
each of these degrees into 60 Geographical miles, so that the whole
circumference contains 21600; and by the known proportion for finding
the diameter of a circle from its circumference, the Earth’s diameter
will be found to be 6872 miles, and its semidiameter 3436 miles. The
Parallax of the Earth’s semidiameter, or the angle under which it is
seen from a certain Planet, may be found by comparing the true place of
the Planet, as it would be seen from the center of the Earth (which is
known by computation) with its apparent place, as it is seen from some
[Pg 24]
point on the Earth’s surface. Let CZA be the Earth, ZC its
semidiameter, ♁ some Planet, and BHT arch of a great circle in the
Heavens, at an infinite distance. Now the Planet ♁ will appear from the
Earth’s center C, in the point of the Heavens H; but a spectator from
the point Z upon the Earth’s surface, will see the same object ♁ in the
point of the Heavens B; and the arch BH the difference, is equal to the
angle B ♁ H = Z ♁ C, the Parallax; which being known, the side C ♁
the distance of the Planet from the center of the Earth, at that time,
may be easily found. Now if this distance of the Planet from the Earth
be determined, when the centers of the Sun, the said Planet, and of the
Earth, are in the same right line, we have the absolute distance of the
Planet’s orbit from the Earth’s in known measure; then it will be, as
the relative distance betwixt the Earth’s orbit and that of the Planet
is to the relative distance of the said Planet from the Sun; so is the
distance of the Planet’s orbit from the Earth’s in known measure to the
distance of the said Planet from the Sun in the same measure: Which
being known, the distance of all the other Planets from the Sun may be
found. For it will be, as the relative distance of any Planet from the
[Pg 25]
Sun, is to its distance from him in a known measure; so is the relative
distance of any other Planet from him to its distance in the same
measure. This may be done by finding the distance of the Planet Mars,
when he is in opposition to the Sun, after the same manner as we find
the distance of a tree, or the like, by two stations.
Let ♂ be Mars, D the point on the Earth’s superficies, where Mars
is vertical when he is in opposition to the Sun, which may be found
exactly enough by calculation, at which time let an observer, at the
point Z (whose situation from D must be known) take the altitude of
Mars, whose complement will be the angle ♂ ZR; then in the triangle
♂ ZC will be given the angle Z ♂ C, the angle C (whose measure is the
arch DZ) and consequently the angle Z ♂ C the Parallax, and also the
side Z C the semidiameter of the Earth; by which we may find C ♂ the
distance of Mars from the Earth. The extreme nicety required in this
observation, makes it very difficult to determine the exact distances
of the Planets from the Sun; but the celebrated Dr. Halley has, in
[Pg 26]
the Philosophical Transactions, shewed us a more certain method for
finding the distances of the Planets; which is by observing the Transit
of Venus over the Sun.
How the Magnitudes of the Planets are determined.
The eye judgeth of the magnitudes of far distant objects, according
to the quantities of the angles under which they are seen (which are
called their apparent magnitudes;) and these angles appear greater
or less in a certain proportion to their distances. Wherefore the
distances of the Planets from the Earth, and their apparent diameters
being given, their true diameters (and from thence their magnitudes)
may be found. How the distances of the Planets may be found has been
already shewn; their apparent diameters are found by a telescope,
having a machine fix’d to it for measuring of angles, called a
Micrometer. Let BD, or the angle BAD be the apparent diameter of any
Planet, and AB, or AD, (which by reason of the great distance of the
Planets in respect of their magnitudes) may be considered as being the
distance of the said Planet from the observer. Now in the triangle ABD,
having the sides AB, AD, given, and the angle, A, we have also the
other angles B and D, (because the Side AB, AD, are equal) whence the
[Pg 27]
side BD the diameter of the Planet may be easily found by Trigonometry.
Why the Moon appears bigger than any of the Planets.
From hence it appears, that the same body at different distances, will
seem to have very different magnitudes. Thus the diameter BD will
appear from the point E, to be twice as large as from the point A. It
also follows, that a small body, when at no great distance from us,
may appear to be equal, or even to exceed another at a great distance,
tho’ immensely bigger. Thus b d appears under the same angle, and
consequently of the same bigness from the point A, that the line B D
doth, tho’ one vastly exceeds the other. And this is the reason, why
the Moon, which is much less than any of the Planets, appears to us
vastly bigger than either of them, and even to equal the Sun himself,
which is many thousand times greater in magnitude.
The distances of the Planets, and periods round the Sun, their
diameters and velocities round their own axis, according to modern
computations, are as follows:
[Pg 28]
| |
Revolves about
the Sun in the
space of
Y. D. H. |
Distance
in Miles |
| Saturn |
29:167:22 |
777.000.000 |
| Jupiter |
11:314:12 |
424.000.000 |
| Mars |
1:321:23 |
123.000.000 |
| Earth |
0:365: 6 |
81.000.000 |
| Venus |
0:224:16 |
59.060.000 |
| Mercury |
0: 87:23 |
32.000.000 |
| |
| |
Round the
Earth.
D. H. M. |
|
| Moon |
27: 7:43 |
240.000 |
| |
Periods round
their own axis
D. H. M. |
Diameters
in Miles. |
| Sun |
25 : |
6 : |
0 |
763.000 |
| Saturn |
: |
: |
|
61.000 |
| Jupiter |
0 : |
9 : |
56 |
81.000 |
| Mars |
1 : |
0 : |
40 |
4.440 |
| Earth |
0 : |
23 : |
56 |
7.970 |
| Venus |
24 : |
8 : |
0 |
7.900 |
| Mercury |
: |
: |
|
4.240 |
| Moon |
27 : |
7 : |
43 |
2.170 |
The cause of Eclipses and Phases of the
Moon, and some other phænomena not here explained, shall be shewed when
we come to give a Description of the Orrery.
Plate 2.

Besides the Planets already mentioned, there are other great bodies
that sometimes visit our system, which are a sort of temporary Planets;
for they come and abide with us for a while, and afterwards withdraw
from us, for a certain space of time, after which they again return.
These wandering bodies are called Comets.
Of Comets.
The motion of Comets in the Heavens, according to the best observations
hitherto made, seem to be regulated by the same immutable law that
rules the Planets; for their orbits are elliptical, like those of
the Planets, but vastly narrower, or more excentric. Yet they have
not all the same direction with the Planets, who move from West to
East, for some of the Comets move from East to West; and their orbits
have different inclinations to the Earth’s orbit; some inclining
Northwardly, others Southwardly, much more than any of the Planetary
orbits do.
Altho’ both the Comets and the Planets move in elliptic orbits, yet
their motions seem to be vastly different: For the excentricities of
the Planet’s orbits are so small, that they differ but little from
[Pg 29]
circles; but the excentricities of the Comets are so very great, that
the motions of some of them seem to be almost in right lines, tending
directly towards the Sun.
Now, since the orbits of the Comets are so extremely excentric, their
motions, when they are in their Perihelia, or nearest distance from
the sun, must be much swifter than when they are in their Aphelia,
or farthest distance from him; which is the reason why the Comets make
so short a stay in our system; and when they disappear, are so long in
returning.
The figures of the Comets are observed to be very different; some of
them send forth small beams, like hair, every way round them; others
are seen with a long fiery tail, which is always opposite to the Sun.
Their magnitudes are also very different, but in what proportion they
exceed each other, it is as yet uncertain. Nor is it probable, that
their numbers are yet known, for they have not been observed with due
care, nor their theories discovered, but of late years. The ancients
[Pg 30]
were divided in their opinions concerning them; some imagined that they
were only a kind of Meteors kindled in our atmosphere, and were there
again dissipated; others took them to be some ominous prodigies: But
modern discoveries prove, that they are Worlds subject to the same laws
of motion as the Planets are; and they must be very hard and durable
bodies, else they could not bear the vast heat that some of them, when
they are in their Perihelia, receive from the Sun, without being
utterly consumed. The great Comet which appeared in the year 1680, was
within ¹/₆ part of the Sun’s diameter from his surface; and therefore
its heat must be prodigiously intense beyond imagination. And when it
is at its greatest distance from the Sun, the cold must be as rigid.
[Pg 31]

SECT. II.
Of the Fixed Stars.
The fixed Stars are at immense distance from us.
The fixed Stars are
those bright and shining bodies, which in a clear night appear to us
every where dispersed through the boundless regions of space. They
are term’d fix’d, because they are found to keep the same immutable
distance one from another in all ages, without having any of the
motions observed in the Planets. The fixed Stars are all placed at such
immense distances from us, that the best of telescopes represent them
no bigger than points, without having any apparent diameters.
The fixed Stars are luminous bodies like the Sun.
It is evident from hence, that all the Stars are luminous bodies, and
shine with their own proper and native light, else they could not be
seen at such a great distance. For the Satellites of Jupiter and
Saturn, tho’ they appear under considerable angles through good
[Pg 32]
telescopes, yet are altogether invisible to the naked eye.
The distance from us to the Sun is nothing in comparison of
the vast distance of the fixed Stars.
Although the distance betwixt us and the Sun is vastly large, when
compared to the diameter of the Earth, yet it is nothing when compared
with the prodigious distance of the fixed Stars; for the whole diameter
of the Earth’s annual orbit, appears from the nearest fixed Star no
bigger than a point, and the fixed Stars are at least 100,000 times
farther from us than we are from the Sun; as may be demonstrated from
the observation of those who have endeavoured to find the Parallax of
the Earth’s annual Orb, or the angle under which the Earth’s orbit
appears from the fixed Stars.
As to appearance, the Earth may be consider’d as being the
center of the Heavens.
Hence it follows, that tho’ we approach nearer to some fixed Stars at
one time of the year than we do at the opposite, and that by the whole
length of the diameter of the Earth’s orbit; yet this distance being
so small in comparison with the distance of the fixed Stars, their
magnitudes or positions cannot thereby be sensibly altered; therefore
we may always, without error, suppose ourselves to be in the same center
[Pg 33]
of the Heavens, since we always have the same visible prospect of the
Stars without any alteration.
The fixed Stars are Suns.
If a spectator was placed as near to any fixed Star, as we are to the
Sun, he would there observe a body as big, and every way like, as the
Sun appears to us: and our Sun would appear to him no bigger than a
fixed Star: and undoubtedly he would reckon the Sun as one of them in
numbering the Stars. Wherefore since the Sun differeth nothing from a
fixed Star, the fixed Stars may be reckoned so many Suns.
The fixed Stars are at vast distance from each other.
It is not reasonable to suppose that all the fixed Stars are placed at
the same distance from us; but it is more probable that they are every
where interspersed thro’ the vast indefinite space of the universe; and
that there may be as great a distance betwixt any two of them, as there
is betwixt our Sun and the nearest fixed Star. Hence it follows, why
they appear to us of different magnitudes, not because they really are
so, but because they are at different distances from us; those that are
nearest excelling in brightness and lustre those that are most remote,
who give a fainter light, and appear smaller to the eye.
[Pg 35]
The distribution of the Stars into 6 classes.
Of Telescopical Stars.
The astronomers distribute the Stars into several orders or classes;
those that are nearest to us, and appear brightest to the eye, are
called Stars of the first magnitude; those that are nearest to them
in brightness and lustre, are called Stars of the second magnitude;
those of the third class, are stiled Stars of the third magnitude;
and so on, until we come to the Stars of the sixth magnitude, which
are the smallest that can be discerned by the naked eye. There are
infinite numbers of smaller Stars, that can be seen through telescopes;
but these are not reduced to any of the six orders, and are only
called Telescopical Stars. It may be here observed, that tho’ the
astronomers have reduced all the Stars that are visible to the naked
eye, into some one or other of these classes, yet we are not to
conclude from thence that all the Stars answer exactly to some or other
of these orders; but there may be in reality as many orders of the
Stars, as they are in number, few of them appearing exactly of the same
bigness and lustre.
[Pg 36]
The Stars digested into constellations
The ancient astronomers, that they might distinguish the Stars, in
regard to their situation and position to each other, divided the
whole starry firmament into Several Asterisms, or systems of Stars,
consisting of those that are near to one another. These Asterisms
are called Constellations, and are digested into the forms of some
animals; as Men, Lyons, Bears, Serpents, &c. or to the images of some
known things; as, of a Crown, a Harp, a Triangle, &c.
Zodiac.
The starry firmament was divided by the ancients into 48 images,
or constellations; twelve of which they placed in that part of the
Heavens wherein are the planes of the Planetary orbits; which part is
called the Zodiac, because most of the constellations placed therein
resemble some living creature. The two regions of the Heavens that are
on each side of the Zodiac, are called the North and South parts of
the Heavens.
Constellations within the Zodiac.
The constellations within the Zodiac are, 1. Aries, the Ram;
2. Taurus, the Bull; 3. Gemini, the Twins; 4. Cancer, the
Crab; 5. Leo, the Lion; 6. Virgo, the Virgin; 7. Libra,
the[Pg 37]
Balance; 8. Scorpio, the Scorpion; 9. Sagittarius,
the Archer; 10. Capricornus, the Goat; 11. Aquarius, the
Water-Bearer; and, 12. Pisces, the Fishes.
Northern constellations.
The constellations on the North side of the Zodiac are Twenty-one,
viz. the Little Bear; the Great Bear; the Dragon; Cepheus, a
king of Ethiopia; Bootes, the keeper of the Bear; the Northern
Crown; Hercules with his Club, watching the Dragon; the Harp;
the Swan; Cassiopeia; Persius; Andromeda; the Triangle;
Auriga; Pegasus, or the Flying Horse; Equuleus; the Dolphin;
the Arrow; the Eagle; Serpentarius; and the Serpent.
Southern constellations.
The constellations noted by the ancients on the South side of the
Zodiac, were fifteen, viz. the Whale; the river Eridanus;
the Hare; Orion; the Great Dog; Little Dog; the Ship Argo;
Hydra; the Centaur; the Cup; the Crow; the Wolf; the
Altar; the Southern Crown; and the Southern Fish. To these have
been lately added the following, viz. The Phœnix; the Crane;
the Peacock; the Indian; the Bird of Paradise; the Southern
Triangle; the Fly; Cameleon; the Flying Fish; Toucan, or
the[Pg 38]
American Goose; the Water Serpent, and the Sword Fish. The
ancients placed those particular constellations or figures in the
Heavens, either to commemorate the deeds of some great man, or some
notable exploit or action; or else took them from the fables of their
religion, &c. And the modern astronomers do still retain them, to
avoid the confusion that would arise by making new ones, when they
compare the modern observations with the old ones.
Unformed Stars.
Some of the principal Stars have particular names given them, as
Syrius, Arcturus, &c. There are also several Stars that are not
reduced into constellations, and these are called Unformed Stars.
The Galaxy, or Milky Way.
Besides the Stars visible to the naked eye, there is a very remarkable
space in the Heavens, called the Galaxy, or Milky Way. This is a
broad circle of a whitish hue, like milk, going quite round the whole
Heavens, and consisting of an infinite number of small Stars, visible
thro’ a telescope, tho’ not discernable by the naked eye, by reason
of their exceeding faintness; yet with their light they combine to
[Pg 39]
illustrate that part of the Heavens where they are, and to cause that
shining whiteness.
The places of the fixed Stars, or their relative situations one from
another, have been carefully observed by astronomers, and digested into
catalogues. The first among the Greeks, who reduced the Stars into
a catalogue, was Hypparchus, who, from his own observations, and of
those who lived before him, inserted 1022 Stars into his catalogue,
about 120 years before the Christian Æra: This catalogue has been
since enlarged and improved by several learned men, to the number of
3000, of which there are a great many telescopical, and not to be
discerned by the naked eye; and these are all ranked in the catalogue
as the Stars of the seventh magnitude.
It may seem strange to some, that there are no more than this number
of Stars visible to the naked eye; for sometimes in a clear night
they seem to be innumerable: but this is only a deception of our
sight, arising from their vehement sparkling, while we look upon them
confusedly, without reducing them into any order; for there can seldom
[Pg 40]
be seen above 1000 Stars in the whole Heavens with the naked eye at the
same time; and if we should distinctly view them, we shall not find
many but what are inserted upon a good Celestial Globe.
Altho’ the number of Stars that can be discerned by the naked eye
are so few, yet it is probable there are many more which are beyond
the reach of our optics, for through telescopes they appear in vast
multitudes, every where dispersed throughout the whole Heaven; and
the better our glasses are, the more of them we still discover. The
ingenious Dr. Hook has observed 78 Stars in the Pleiades, of
which the naked eye is never able to discern above 7; and in Orion,
which has but 80 Stars in the British catalogue (and some of them
telescopical) there has been numbered 2000 Stars.
An idea of the Universe.
Those who think that all these glorious bodies were created for no
other purpose than to give us a little dim light, must entertain a very
slender idea of the Divine Wisdom; for we receive more light from the
Moon itself, than from all the Stars put together. And since the
Planets are subject to the same laws of motion with our Earth, and
[Pg 41]
some of them not only equal, but vastly exceed it in magnitude, it
is not unreasonable to suppose, that they are all habitable Worlds.
And since the Fixed Stars are no ways behind our Sun, either in
bigness or lustre, is it not probable, that each of them have a system
of Planetary Worlds turning round them, as we do round our Sun? And
if we ascend as far as the smallest Star we can see, shall we not then
discover innumerable more of these glorious bodies, which now are
altogether invisible to us? And so ad infinitum, thro’ the boundless
space of the universe. What a magnificient idea must this raise in us
of the Divine Being! Who is every where, and at all times present,
displaying his Divine Power, Wisdom and Goodness, amongst all his Creatures!
[Pg 42]

The DESCRIPTION and USE of the
Celestial and Terrestrial Globes.
Globe or Sphere.
A Globe or Sphere is a round solid body, having every part of its
surface equally distant from a point within it, called its Center;
and it may be conceived to be formed by the revolution of a semicircle
round its diameter.
Great Circle.
Hemispheres.
Any circle passing through the center of the sphere, thereby dividing
into two equal parts or segments, is called a Great Circle; and the
segments of the sphere so divided, are called Hemispheres.
Every great circle has its Poles and Axis.
Poles.
The Poles of a great circle are two points on the surface of the
[Pg 43]
sphere, diametrically opposite to one another, and every where equally
distant from the said circle.
Axis.
The Axis of a circle is a right line passing through the center of
the sphere, and through the Poles of the said circle, and is therefore
perpendicular to the Plane: Therefore
Secundaries.
All circles passing through the Poles of any great circle, intersect
it in two places diametrically opposite, and also at right angles;
and with respect to the said great circle, they may be called its
Secundaries.
Parallel or lesser Circles.
All circles dividing the sphere into two unequal parts, are called
lesser or parallel Circles, and are usually denominated by that
great circle to which they are parallel.
Terrestrial Globe.
The Earth being globular, its outward parts, as the several
Countries, Seas, &c. are best, and most naturally represented
upon the surfaces of a Globe; and when such a body has the outward
parts of the Earth and Sea delineated upon its surface, and placed in
their natural order and situation, it is called a Terrestrial Globe.
[Pg 44]
Celestial Globe.
The Celestial Bodies appear to us as if they were all placed in the
same concave sphere, therefore astronomers place the Stars according to
their respective situations and magnitudes, and also the images of the
constellations, upon the external surface of a Globe; for it answers
the same purposes as if they were placed within a concave sphere, if we
suppose the Globe to be transparent, and the eye placed in the center.
A Globe having the Stars placed upon its surface, as above described,
is called a Celestial Globe. These Globes are both placed in frames,
with other appurtenances, as shall be described in a proper place.
The principal use of the Globes.
The principal uses of the Globes (besides their serving as Maps, to
distinguish the outward parts of the Earth, and the situations of the
fixed Stars) is to explain and resolve the phænomena arising from the
diurnal motion of the Earth round its Axis.
There will be the same prospect of the fixed Stars whether
the spectator be placed on the Earth, or in the Sun.
It has been shewed in the Introduction, that the distance of the Earth
from the Sun, is no more than a point, when compared with the immense
[Pg 45]
distance of the fixed Stars; therefore let the Earth be in what point
soever of her orbit, there will be the same prospect of the Heavens,
as a spectator would observe did he reside in the Sun: And if several
circles be imagined to pass thro’ the center of the Earth, and others,
parallel to them, be conceived to pass thro’ the center of the Sun,
these circles in the Heavens will seem to coincide, and to pass exactly
thro’ the same Stars. Wherefore as to the appearances of the fixed
Stars, it is indifferent whether the Earth or the Sun be made the
center of the Universe. But because it is from the Earth that we always
observe the celestial bodies, and their apparent motions seem to us to
be really made in the Heavens, it is more natural in explaining the
phænomena arising from these motions, to place the Earth in the center.
And again, because the semidiameter of the Earth, when compared to her
distance from the Sun, is of no sensible magnitude, any point, upon the
Earth’s surface, let her be in what part soever of the orbit, may be
considered as being the center of the Universe. Upon these principles,
the different phænomena arising from the diurnal motion of the Earth,
[Pg 46]
and the different situation of a spectator upon its surface, are very
naturally illustrated and explained by the Globes.
As to the alterations of seasons, &c. arising from the annual motion
of the Earth round the Sun, it is indifferent which we suppose to move,
the Earth or the Sun, for in both cases the effect will be the same.
Wherefore because it is the Sun that appears to us to move, we say the
Sun is in such a part of the ecliptic, without attributing any motion
to the Earth, any more than if she had actually been at rest. For the
same reason we say the Sun rises, or the Sun sets; by which we mean
that he begins to appear or disappear, without considering in the least
how these effects are produced. These things are here mentioned, to
obviate the objections that might be made by beginners, after they have
been told that the Sun stands still.
[Pg 47]
SECT. I.
An Explanation of the Circles of the Sphere,
and of some Astronomical Terms arising therefrom.
The Circles of the Sphere.
In order to determine
the relative situations of places upon the Earth, as well as the
positions of the fixed Stars, and other Celestial phænomena, the Globe
of the Earth is supposed to be environed by several imaginary circles,
and these are called the Circles of the Sphere. These imaginary
circles are either fixed, and always obtain the same position in the
Heavens, or moveable, according to the position of the observer.
Those circles that are fixed, owe their origin to the two-fold motion
of the Earth, and are the Equator, and the Ecliptic, with their
[Pg 48]
Secundaries and Parallels. These fixed circles are usually
delineated upon the surface of the Globes.
The moveable circles are only the Horizon, its Secundaries and
Parallels: These are represented by the wooden frame, and the brass
ring, wherein the Globe is hung, and a thin plate of brass to be
screwed in a proper place, upon the said ring, as occasion requires.
I. Of the Equinoctial.
The Equator, or Equinoctial.
1. The Equator, or the Equinoctial, is that great circle in the
Heavens, in whose plane the Earth performs her diurnal motion round her
axis; or it is that great circle, parallel to which the whole Heavens
seem to turn round the Earth from East to West in 24 Hours.
Note, The Equator and the Equinoctial are generally synonymous terms;
but sometimes the Equator particularly signifies that great circle upon
the surface of the Earth, which coincides with the Equinoctial in the
Heavens. This circle is also by Mariners commonly called the Line.
[Pg 49]
Northern and Southern Hemispheres.
The Axis of the World.
Poles of the World, or of the Equator.
The equinoctial divides the globe of the Earth, and also the whole
Heavens into two equal parts, North and South, which are called the
Northern and Southern Hemispheres. The axis of this circle, is
called the Axis of the World, or the Earth’s Axis, because the
Earth revolves about it (from West to East) in 24 hours. The extreme of
this axis are called the Poles of the World, whereof that which lies
in the Northern Hemisphere, is called the North Pole, and the other
is called the South Pole. The equinoctial circle is always delineated
upon the surface of each globe, with its name at length expressed; the
axis of this circle, or the Earth’s axis, is only an imaginary line in
the Heavens, but on the globes it is expressed by the wires about which
they really turn. The Poles of the world, are the two points upon the
surface of the globe through which these wires pass; the North Pole is
that which hath the little brass circle, with a moveable index placed
round it; and the other opposite to it is the South Pole. The Northern
Hemisphere is that wherein the North Pole is placed, and the opposite
one is the Southern Hemisphere.
[Pg 50]
The astronomers divide all circles into 360 equal parts, called
Degrees, each degree into 60 equal parts, called Minutes, each
minute into 60 Seconds, &c. But besides this division into degrees,
the equinoctial is also divided into 24 equal parts, or Hours, each
hour into 60 Minutes, each minute into 60 Seconds, &c. so that
one hour is equal to 15 degrees, each minute of time is equal to 15 minutes
of a degree, &c.
Hour Circles or Circles of Ascension,
also called Meridians.
2. All circles conceived to pass through the Poles of the world,
intersecting the equinoctial at right angles, are, with respect to
any point in the Heavens, called Hour Circles; and the Circles
of Ascension, because the ascension of the Heavenly bodies, from a
certain point, are by them determined.
These circles are also, with regard to places upon Earth, called
Meridians.
The Brass Meridian.
The Meridians are commonly drawn upon the Terrestrial Globe thro’
every 15 degrees of the equinoctial, thereby making an Hour difference
betwixt the places through which they pass. On the Celestial Globe
there are commonly drawn but two of these Meridians, crossing the
[Pg 51]
equinoctial in four points equidistant from one another, thereby
dividing it into four quadrants; but the intermediate ones are here
supplied, and also upon the Terrestrial Globe, by the brass circle on
which they are hung, which, is therefore called the Brass Meridian,
and sometimes only the Meridian, it serving for this purpose to all
the points upon either Globe.
The Hour Circle.
There is also a little brass circle fixed upon this meridian, divided
into 24 Hours, having an index moveable round the axis of the globe, to
be turned to any particular Hour. The use of this circle is to shew the
difference of time betwixt any two meridians, and is therefore called
the Hour Circle.
Parallels of Declination.
3. All circles parallel to the equinoctial are, with respect to any
point in the Heavens, called Parallels of Declination. So that,
Declination North and South.
4. The Declination of any Point in the Heavens (as of the Sun, a
fixed Star, or the like) is an arch of the meridian passing through
that point, and intercepted betwixt it and the equator; and if the said
[Pg 52]
point be to the (Northward/Southward) of the equator, it is called
(North/South) Declination.
Tropics and Polar Circles.
Of the parallels of declination, four are eminently distinguished by
particular names, viz. The two Tropics, and the two Polar Circles.
Tropic of Cancer; of Capricorn.
The tropics are on different sides of the equator each 23 degrees and
29 minutes distant from it; that which lies in the Northern Hemisphere,
is called the Tropic of Cancer, and the Southern one, the Tropic of
Capricorn.
These circles are the limits of the Sun’s greatest declination, and are
called tropics, because whenever the Sun arrives to them, he seems to
return back again towards the equator.
Arctic Circle.
Arctic Pole.
Antarctic Circle.
Antarctic Pole.
6. The Polar Circles are each of them
at the same distance from the Poles of the world, that the tropics are
from the equator, viz. 23° 29′. That which lies near the North Pole,
is called the Arctic Circle, from Arctos, a constellation situated
[Pg 53]
in the Heavens near that Place; whence also this Pole is sometimes
called the Arctic Pole. The other Polar circle, which is situated
near the South Pole; is called the Antarctic Circle, because its
position is contrary to the other; and the South Pole is sometimes
called the Antarctic Pole.
The tropics and the Polar circles have each their names expressed upon
the Globes.
II. Of the Ecliptic.
Ecliptic.
Equinoctial.
Solstitial Points.
Colures.
Equinoctial Colure.
Solstitial Colure.
7. The Ecliptic is that great circle in whose plane the Earth
performs its annual motion round the Sun; or, in which the Sun seems
to move round the Earth, once in a year. This circle makes an angle
with the equinoctial of 23 degrees 29 minutes, and intersects it in
two opposite points, which are called the Equinoctial Points; and
the two points in the ecliptic that are at the greatest distance from
the equinoctial points, are called the Solstitial Points. The two
meridians passing through those points, are, by way of eminence, called
Colures; whereof that which passeth thro’ the equinoctial points, is
called the Equinoctial Colure; and that which is at right angles to
[Pg 54]
it, passing through the Solstitial Points, is called the Solstitial
Colure.
The Ecliptic divided into signs.
The ecliptic is divided into 12 equal parts, called Signs, each sign
being 30 degrees, beginning from one of the equinoctial points, and
numbered from West to East; the names and characters of the twelve
signs are as follows, viz.
| Aries, |
Taurus, |
Gemini, |
Cancer, |
Leo, |
Virgo, |
| 1. ♈ |
2. ♉ |
3. ♊ |
4. ♋ |
5. ♌ |
6. ♍ |
| Libra, |
Scorpio, |
Sagittarius, |
Capricornus, |
Aquaries, |
Pisces. |
| 7. ♎ |
8. ♏ |
9. ♐ |
10. ♑ |
11. ♒ |
12. ♓ |
Northern Signs.
The first six of these are called the Northern Signs, and possess
that half of the ecliptic which is to the Northward of the equator;
beginning with the first point of ♈, and ending with the last point of
♍.
Southern Signs.
The latter six are called the Southern Signs, because they possess
the Southern half of the ecliptic; beginning at the first point of ♎,
and ending with the last point of ♓.
The division of the ecliptic into signs, and the names of the colures,
are particularly expressed upon the globes.
[Pg 55]
The signs of the ecliptic took their names from 12 constellations
mentioned in the Introduction to be situated in the Heavens near those
places. It is to be observed, that the signs are not to be confounded
with the constellations of the same name: For the Sign of Aries, is
not the same with the Constellation Aries; the latter is a system of
Stars digested into the figure of a Ram, but the sign of Aries is
only 30 degrees of the ecliptic, counted from the equinoctial point ♈,
(which is reckoned the first point in the ecliptic) to the beginning
of Taurus: Or, it is sometimes taken for all that space upon the
Celestial Globe contained between the two circles passing through the
first points of ♈ and ♉. What has been here said of Aries, is to be
noted of all the rest of the signs.
The constellations above-mentioned were formerly situated within
the signs which now bear their names; but by a slow motion of the
equinoctial points, being one degree in 72 years, the constellation
Aries has now got into the sign ♉, and so of the rest. So that
Pisces is now got into the Sign of ♈; this slow motion in the Heavens
is called the Precession of the Equinoctial Points.
[Pg 56]
Poles of the Ecliptic.
The Poles of the Ecliptic are both situated in the Solstitial Colure,
at 23 degrees, 29 minutes distance from the Pole of the world; and they
take their denomination from the Hemisphere wherein they are placed,
viz. that which lies in the (Northern/Southern) Hemisphere, is called
the (North/South) Pole of the ecliptic. The arctic and antarctic
circles, are described by the Poles of the ecliptic in the diurnal
motion of the Earth round its axis, whence it seems these two circles
are called Polar.
Circles of Longitude.
8. All great circles passing through the Poles of the ecliptic, and
consequently intersecting it at right angles, are called Circles of
Longitude: So that,
Longitude of any Point in the Heavens.
Place of a Star.
[Pg 57]
9. The Longitude of any Point in the Heavens (as a Star or
Planet, &c.) is an arch of the ecliptic contained between the
circle of longitude passing thro’ that point, and the equinoctial
point ♈. And that degree of any sign which lies under the circle of
longitude, passing thro’ any Star or Planet, is called the Place of
that Star or Planet.
Note, The Sun never goes out of the ecliptic, and it is not usual
to say the Sun’s longitude, but we commonly express it the Sun’s
Place, which is that sign, degree, minute, &c., of the ecliptic,
which he at any time passes.
10. All circles conceived to be drawn parallel to the ecliptic, are
called Parallels of Latitude: So that,
Latitude of a Star, &c.
11. The Latitude of any point in the Heavens, (as a fixed Star,
&c.) is an arch of the circle of longitude, in passing thro’ that
point, and intercepted betwixt it, and the ecliptic; or, the latitude
is the distance from the ecliptic; and if the said point be to the
Northward of the ecliptic, it is called North Latitude; but if it be to
the Southward, is called South Latitude.
Upon the Terrestrial Globe, none of the circles of longitude are
described; and upon the Celestial, they are commonly drawn thro’
the beginning of every Sign; but they are all supplied upon both
Globes, by fastening a thin plate of brass over one of the Poles of the
ecliptic, and so as to be moved to any degree thereof at pleasure. The
[Pg 58]
parallels of latitude are also supplied by the graduations upon the
said plate, as shall be shewn in a proper place.
We have now done with all those circles that are fixed, and such as
are drawn upon the Globes themselves; we next proceed to the moveable
circles.
III. Of the Horizon.
Horizon.
12. The Horizon is that great circle which divides the upper, or
visible Hemisphere of the world, from the lower, or invisible: This
circle is distinguished into two sorts, the Sensible, and the
Rational.
Sensible Horizon.
The Sensible, or Apparent Horizon, is that circle which limits or
determinates our prospect, whether we are at land or sea, reaching as
far as we can see, or it is that circle where the Sky and the Earth, or
Water, seem to meet. When we are on Terra Firma, this circle commonly
seems rugged and irregular, occasioned by the unevenness of the ground
terminating our prospect; but at sea there are no such irregularities;
the semidiameter of this circle varieth according to the height of the
[Pg 59]
eye of the observer; if a man of six feet high stood upon a large
plain, or the surface of the sea, he could not see above three miles
round.
This circle determines the rising and setting of the Heavenly bodies,
and distinguishes Day and Night.
Rational Horizon.
The Rational, or true Horizon, is a great circle passing thro’
the center of the Earth, parallel to the sensible Horizon, being distant
from it by the Earth’s semidiameter, which is about 3980 miles: This
distance is nothing in comparison of the immense distance of the Sun
and the fixed Stars, therefore astronomers make no distinction between
these two circles, but consider the apparent Horizon, or that wherein
the Sun appears to rise and set, as passing thro’ the center of the
Earth.
Cardinal Points of the Horizon.
This circle is divided by astronomers into four quadrants, and each of
the quadrants into 90 degrees, &c. The four points quartering this
circle are called the Cardinal Points, and are termed the East,
West, North, and South. The East is that point of the Horizon
[Pg 60]
where the Sun rises when he is in the equinoctial, or on that day when
he ascends above the Horizon exactly at six o’clock; and the West
is that point of the Horizon which is directly opposite to the East,
or where the Sun Sets when he is in the Equinoctial. The South is
90 degrees distant from the East and West, and is toward that part of
the Heavens wherein the Sun always appears to us in Great-Britain at
Noon; and the North is that part of the Heavens which is directly
opposite to the South: Or, the North and South points of the Heavens
may be found by turning yourself either directly towards the East or
the West: If you look towards the (East/West) the (South/North) will be
to the right Hand, and the (North/South) to the left.
Points of the Compass.
Besides the aforementioned divisions of the Horizon into degrees.
Mariners divide it into 32 equal parts, which they call the Points
of the Compass; to each of which points they give a particular name,
compounded of the four Cardinals, according to what quarter of the
Compass is intended.
[Pg 61]
Zenith.
Nadir.
The center of the Horizon is the place of observation, and the Poles of
it are one exactly over our heads, called the Zenith; and the other
exactly under our feet, called the Nadir.
Vertical Circles.
Meridian.
Azimuth.
13. All circles conceived to pass thro’ the Zenith and Nadir, are
called Vertical Circles, or Azimuths. Of these circles, that which
passeth thro’ the North and South points of the Horizon, is called the
Meridian; so that when any object is upon the Meridian, it then bears
either due South, or due North from us; and the Azimuth of any object
is an arch of the Horizon intercepted between the vertical circle
passing through it, and either the North or South part of the Meridian;
which part is commonly specified.
The meridian passes thro’ the Poles of the world, as well as through
the Zenith and Nadir, and therefore is a secundary both of the
equinoctial and the horizon: This circle divides the globe into the
Eastern and Western Hemispheres, and the Poles of it are the East
and West points of the Horizon. All the heavenly objects are,
during one half of their continuance above the horizon, in the Eastern
[Pg 62]
Hemisphere, and for the other half in the Western; so that whenever the
Sun arrives upon the upper part of the meridian, it is then Noon, or
Mid-day, which is the reason why this circle is called the meridian;
and when he comes to the lower part, it is then Midnight.
Prime Vertical.
The vertical circle passing thro’ the East and West points of the
horizon, is called the Prime Vertical, or Circle of East and
West, so that when any object is upon this circle in the Eastern
hemisphere, it appears due East; and if it be in the Western
hemisphere, it appears due West.
Amplitude.
That degree in the horizon wherein any object rises or sets from the
East or West points, is called the Amplitude; which for rising is
called Amplitude Ortive, and Occasive for setting; which must be
also denominated whether it be Northerly or Southerly.
It may be observed, that the Amplitude and Azimuth are much the
same; the amplitude shewing the bearing of any object when he rises or
sets, from the East or West points of the horizon; and the azimuth, the
[Pg 63]
bearing of any object when it is above the horizon, either from the
North or South point thereof. As for example, if an object rises or
sets within 10 degrees of the East or West, suppose towards the South,
we accordingly say, its Amplitude is 10 degrees Southerly; but if
an object, that is of any height above the horizon, should be in the
vertical circle, passing thro’ the before-mentioned point, we then say,
its Azimuth is 80 degrees from the South, or 100 degrees from the
North, both which expressions signify the same.
Almacanthers.
Altitudes.
Meridian Altitude.
Zenith Distance.
14. All circles drawn parallel to the horizon, in the upper hemisphere,
are called Almacanthers, or Parallels of Altitude: So that the
Altitude of any point in the Heavens is an arch of the vertical
circle passing thro’ that point, and intercepted betwixt it and the
horizon; and if the object be upon the meridian, it is commonly called
the Meridian Altitude. The complement of the altitude, or what it
wants of 90 degrees, is called the Zenith Distance.
The horizon (by which we mean the rational) is represented by the upper
[Pg 64]
surface of the Wooden frame, wherein the globes are placed; upon this
horizon are described several concentric circles, the innermost of
which is divided into degrees, which ought to be numbered both ways
from the East and the West, until they end at 90 degrees in the North
and South points. The use of these divisions is to shew the amplitudes
of the Sun and Stars, at their rising and setting: Also in some
convenient place upon this horizon, there is commonly noted the points
of the Compass. Without the before-mentioned circle there is drawn the
ecliptic with its divisions, into signs, and degrees, and a circle of
months and days: The use of these two circles is to serve as a kalendar
to shew the Sun’s place at any time of the year, and by that means to
find his place in the Ecliptic, drawn upon the globe itself.
The Vertical Circles, and the Parallels of Altitude, are supplied
by a thin plate of brass, having a nut and screw at one end to fasten
it to the brass meridian in the Zenith point; which being done, the
lower end of it may be put between the globe it self, and the inner
edge of the horizon, and so turned round about to any point required.
[Pg 65]
Quadrant of Altitude.
The fiducial edge thereof representing the Vertical Circles, and the
Degrees upon it, describing the Parallels of Altitude. This thin
plate is called the Quadrant of Altitude.
The center of the horizon being the place of observation, it is
evident that this circle, and all the others belonging to it, are
continually changed, which way soever we move; wherefore we may suppose
the horizon, with its secundaries and parallels, to invest the globe
like a rete or net; and to be moveable every way round it. This is
very naturally illustrated by the globes; if we move directly North,
or directly South, the change made in the horizon, is represented
by moving the brass meridian (keeping the globe from turning about
its axis) in the notches made in the wooden horizon, just so much
as we travelled. If our course should be due East, or due West,
the alterations made thereby are represented by turning the globe
accordingly about its axis, the brass meridian being kept fixed; and
if we steer betwixt the meridian and the East or West points, then
we are to turn the brass meridian, and also the globe about its axis
[Pg 66]
accordingly; the sum of which is, let the spectator be at what point
soever of the Earth’s surface, he’ll there gravitate, or tend exactly
towards its center, and imagine himself to be on the highest part
thereof, (the unevenness of the ground not being here considered)
wherefore if we turn the globe in such a manner as to bring the several
progressive steps of a traveller successively to the Zenith, we shall
then have the successive alterations made in the horizon, in every part
of his journey. This explication being well considered, will be of help
to young beginners, to conceive how the Earth is every where habitable;
and how passengers can travel quite round it; for since every thing
tends toward the center of the Earth, we are to conceive that point as
being the lowest, and not to carry our idea of downwards any farther.
Those that are diametrically opposite to us being as much upon the
upper part of the Earth as we are, there being no such thing in nature
as one place being higher than another, but as it is at a greater
distance from the center of the Earth, let it be in what country soever.
We have now done with all the circles of the sphere, and it may be
[Pg 67]
observed, that the Equinoctial, the Ecliptic, and the Horizon,
with their Secundaries and parallels, are all alike; and altering their
position, may be made to serve for one another. Thus, if the Poles of
the World be brought into the Zenith and Nadir, the Equinoctial
will coincide with the Horizon, the Meridians will be the same
with the Vertical Circles, and the parallels of Declination will
be the parallels of Altitude. After the same manner, if shifting
the position, we bring the Ecliptic to coincide with the Horizon,
the circles of Longitude will be the Vertical Circles, and the
parallels of Latitude and Altitude will coincide.
The horizon and the equator may be either parallel, perpendicular, or
oblique to each other.
Parallel Sphere.
15. A Parallel Sphere is that position where the equator coincides
with the horizon, and consequently the poles of the world are in the
Zenith and Nadir: The inhabitants of this sphere (if there be any) are
those who live under the poles of the world.
Right Sphere.
16. A Right or Direct Sphere is that position where the equator is
[Pg 68]
perpendicular to the horizon, the inhabitants whereof are those who
live under the equinoctial.
Oblique Sphere.
17. An Oblique Sphere is when the equinoctial and the horizon make
oblique angles with each other, which every where happens but under the
equator and the poles.
Diurnal and Nocturnal Arch.
The arch of any parallel or declination, which stands above the horizon
is called the Diurnal Arch; and the remaining part of it, which is
below the horizon, is called the Nocturnal Arch.
That point of the equinoctial which comes to the (Eastern/Western)
part of the horizon with any point of the Heavens, is called the
(Ascension/Descension) of that point, counted from the beginning of ♈;
and if it be in a right sphere, the ascension or descension is called
right; but if it be an oblique sphere it is called an oblique ascension
or descension. So that,
Right Ascension.
18. The Right Ascension of the Sun, Moon, or any Star, &c. is
[Pg 69]
an arch of the equator contained betwixt the beginning of ♈, and that
point of the equinoctial which rises with them in a Right Sphere, or
which comes to the meridian with them in an oblique sphere.
Oblique Ascension.
19. Oblique Ascension, or Descension, is an arch of the equinoctial
intercepted between the beginning of ♈, and that Point of the
Equator which rises or sets with any point in the Heavens in an
oblique sphere.
Ascensional Difference.
20. Ascensional Difference, is the difference betwixt the right and
oblique ascension or descension, and shews how long the Sun rises or
sets before or after the hour of six.
IV. Of the Division of Time.
The parts that time is distinguished into, are Days, Hours,
Weeks, Months, and Years.
A Day is either natural or artificial.
Natural and Artificial Day.
A Natural Day is the space of time elapsed while the Sun goes from
any meridian or horary circle, ’till he arrives to the same again; or,
[Pg 70]
it is the time contained from noon, or any particular hour, to the next
noon, or the same hour again: An Artificial Day is the time betwixt
the Sun’s rising and setting; to which is opposed the Night, that is,
the time the Sun is hid under the horizon.
Hours, &c.
Equinoxes.
Vernal and Autumnal Equinox.
Solstices.
Summer and Winter Solstices.
The Natural Day is divided into 24 Hours, each hour into 60
Minutes, each minute into 60 Seconds, &c. The Artificial Days are
always unequal to all the inhabitants that are not under the equator,
except when the Sun is in the equinoctial points ♈ and ♋, which happens
(according to our way of reckoning) about the 21st of March, and
the 23d of September; at those times the Sun rises at six and sets
at six to all the inhabitants of the Earth. These days are called the
Equinoxes, or Equinoctial Days; the first of which, or when the Sun
is in the first point of Aries, is called the Vernal Equinox, and
the latter is called the Autumnal Equinox. In all places where the
Sun descends below the horizon, excepting under the equator, the days
continually lengthen or shorten, and that faster or slower, according
as the Sun is nearer to, or further from the equinoctial, until he
arrives to either of the Solstitial Points ♋ or ♑. At those times
[Pg 71]
the Sun seems to stand still for a few days, and then begins to return
with a slow motion towards the equinoctial, still hastening his pace
as he comes nearer to it: The Sun enters the tropics of ♋ and ♑, about
the 21st of June, and the 22d of December, which days are sometimes
called the Solstices; the first of which we call the Summer
Solstice, and the latter the Winter Solstice.
The different beginning of the day.
All nations do not begin their day, and reckon their hours alike. In
Great-Britain. France, and Spain, and in most places in Europe,
the days is reckoned to begin at midnight, from whence is counted
twelve hours ’till noon, then twelve hours more ’till next midnight,
which makes a compleat day; yet the Astronomers (in these countries)
commonly begin their day at noon, and so reckon 24 hours ’till next
noon, and not twice twelve, according to the vulgar computation.
Babylonish Hours.
Italian Hours.
The Babylonians began their day at Sun-rising, and reckoned 24 hours
’till he rose again! This way of computation we call the Babylonish
Hours. In several parts of Germany they count their hours from
[Pg 72]
Sun-setting, calling the first hour after the Sun has set, the first
hour, &c. ’till he sets the next day, which they call the 24th hour:
These are commonly called the Italian Hours. According to both these
ways of computation, their hours are commonly either a little greater
or less than the ¹/₂₄ part of a natural day, in proportion as the
Sun rises or sets sooner or later in the succeeding days. They have
also this inconvenience, that their mid-day and midnight happen on
different hours, according to the seasons of the year.
Jewish Hours.
Planetary Hours.
The Jews and the Romans formerly divided the artificial days and
nights each into 12 equal parts; these are termed the Jewish Hours,
and are of different lengths, according to the seasons of the year;
a Jewish Hour in summer being longer than one in winter, and a
night-hour shorter. This method of computation is now in use among the
Turks, and the hours are stiled the first hour, second hour, &c.
of the day or night; so that Mid-day always falls on the sixth hour
of the day. These hours are also called Planetary Hours, because in
every hour one of the seven Planets were suppose to preside over the
[Pg 73]
World, and so take it by turns. The first hour after Sun-rising on
Sunday was allotted to the Sun; the next to Venus, the third to
Mercury; and the rest in order to the Moon, Saturn, Jupiter,
and Mars. By this means on the first hour of the next day, the Moon
presided, and so gave the name to that day; and so seven days by this
method had names given them from the Planets that were supposed to
govern on the first hour.
A Week.
A Week is a system of seven days, in which each day is distinguished
by a different name. In most countries these days are called after the
names of the seven Planets, as above noted. All nations that have any
notion of religion, lay apart one day in seven for public worship; the
day solemnized by Christians is Sunday, or the first day of the
week, being that on which our saviour rose from the grave, on which
the apostles afterwards used more particularly to assemble together
to perform divine worship. The Jews observed Saturday, or the
seventh day of the week, for their sabbath, or day of rest, being that
appointed in the fourth commandment under the Law. The Turks perform
their religious ceremonies on Friday.
[Pg 74]
A Month.
Periodical and Synodical Month.
A Month is properly a certain space of time measured by the Moon
in his course round the Earth. A Lunar Month is either Periodical
or Synodical. A Periodical Month is that space of time the Moon
takes to perform her course from one point in the ecliptic ’till she
arrives to the same again, which is 27 days, and some odd hours; and
a Synodical Month is the time betwixt one new Moon, and the next
new Moon, which is commonly about 29½ days. But a Civil Month, is
different from these, and consists of a certain number of days, fewer
or more, according to the laws and customs of the country where they
are observed.
A Year Sydereal and Tropical.
The compleatest period of time is a Year, in which all the variety
of seasons return, and afterwards begin anew. A Year is either
Astronomical or Civil. An Astronomical Year is either a
Sydereal wherein the Sun departing from a fixed Star, returns to
it again; or Tropical, which is the space of time the Sun takes to
perform his course from any point of the ecliptic, ’till he returns to it again.
[Pg 75]
A Tropical Year consists of 365 days, 5 hours, and 49 minutes; this
is the time in which all the seasons compleatly returns, which is a
small matter less than a Sydereal Year.
Egyptian Year.
The Civil Year is the same with the Political established with the
laws of a country; and is either moveable or immoveable. The moveable
year consists of 365 days, being less than the tropical year by almost
six hours, and is called the Egyptian Year, because observed in that
Country.
The Romans divided the year into 12 kalendar months, to which they
gave particular names, and are still retained by most of the European
nations, viz. January, February, March, April, May, June,
July, August, September, October, November, and December.
The number of days in each month may be known by the following verses:
Thirty Days hath September,
April, June, and November;
February hath Twenty-eight alone,
And all the rest have Thirty-one.
[Pg 76]
The year is also divided into four quarters or seasons, viz.
Spring, Summer, Autumn, and Winter. These quarters are properly
made when the Sun enters into the equinoctial and solstitial points
of the ecliptic; but in civil uses they are differently reckoned,
according to the customs of several countries. In England, we
commonly reckon the first day of January to be the first in the
year, which is therefore vulgarly called New-Year’s-Day; but in
political and ecclesiastical affairs, the year is reckoned to commence
on Lady-day which is the 25th of March; and from thence to
Midsummer-day, which is the 24th of June, is reckoned the first
quarter; from Midsummer-day to Michaelmas-day, which is the 29th of
September, is the second quarter; the third quarter is reckoned from
Michaelmas-day to Christmas-day, which is the 25th of December;
and from Christmas-day to Lady-day, is reckoned the last quarter
in the year. In common affairs, a quarter is reckoned from a certain
day to the same in the fourth month following. Sometimes a month is
reckoned four weeks, or 28 days, and so a quarter 12 weeks. To all the
[Pg 77]
inhabitants in the (Northern/Southern) Hemisphere, their Midsummer is
properly when the Sun is in the tropic of (Cancer,/Capricorn,) and
their Midwinter at the opposite time of the year; but those who live
under the equinoctial have two winters, &c. when the Sun is in either
tropic; tho’ indeed properly, there is no season that may be called
winter in those parts of the world.
Bissextile, or Leap-Year.
The Egyptian year of 365 days being less than the true solar year,
by almost six hours, it follows, that four such years are less than
four solar years by a whole day; and therefore in 365 times four years,
that is, in 1460 years, the beginning of the years move through all
the seasons. To remedy this inconveniency, Julius Cæsar (considering
that the six hours, which remain at the end of every year, will in four
years make a natural day) ordered that every fourth year should have an
intercalary day, which therefore consists of 366 days; the day added
was put in the month of February, by postponing St. Matthias’s day,
[Pg 78]
which in common years fall on the 24th, to the 25th of the said
month, all the fixed feasts in the year from thenceforwards falling
a week-day later than otherwise they would. According to the Roman
way of reckoning, the 24th of February was the sixth of the kalends
of March, and it was ordered that for this year there should be two
sixths, or that the sixth of the kalends of March should be twice
repeated; upon which account the year was called Bissextile, which we
now call the Leap-Year.
To find whether the year of our Lord be leap-year, or the first,
second, or third after; divide it by four, and the remainder, if there
be any, shews how many years it is after leap-year; but if there be no
remainder, then that year is leap-year: Or, you may omit the hundreds
and scores, and divide the residue by 4, Examp. 1757, omitting the
hundreds and the twenties, I divide the residue 17, by 4, and the
remainder 1, shews it to be the first after leap-year.
Julian Account or the Old Style.
This method of reckoning the year, viz. making the common year to
consist of 365 days, and every fourth year to have 366 days, is now
[Pg 79]
used in Great-Britain and Ireland, and some of the Northern parts
of Europe, and is called the Julian Account, or the Old Style.
But the time appointed by Julius Cæsar for the length of a solar year
is too much; for the Sun finishes his course in the ecliptic, in 365
days, 5 hours, and 49 minutes, which is 11 minutes less than the civil
year; and therefore he again begins his circuit 11 minutes before the
civil year is ended; and so much being gained every year, amounts in
131 years, to a whole day. So that if the Sun in any year entered the
equinox upon the 20th of March at noon, after the space of 131 years,
he’ll enter the same point on the same hour, on the 19th of March.
And therefore the exquinoxes will not always fall on the same day of
the month, but by degrees will move towards the beginning of the year.
Gregorian Account, or New Style.
At the time of the Council of Nice, when the terms were settled for
observing of Easter, the Vernal Equinox fell upon the 21st of
March; but by its falling backwards 11 minutes every year, it was
found that in Anno 1582, when the kalendar was corrected, the Sun
[Pg 80]
entered the equinoctial circle on the 11th of March, having departed
ten whole days from its former place in the year: and therefore Pope
Gregory the XIIIth, designing to place the equinoxes in their
situation with respect to the year, took these ten days out of the
kalendar, and ordered that the 11th of March should be reckoned as
the twenty-first: And to prevent the seasons of the year from going
backwards for the future, he ordered every hundredth year, which in
Julian form was to be a Bissextile, should be a common year, and
consist only of 365 days; but that being too much, every fourth hundred
was to remain Bissextile. This form of reckoning being established
by the authority of Pope Gregory XIII. is called the Gregorian
Account, or the New Style; and is observed in all the countries
where the authority of the Pope is acknowledged, and likewise by
several nations of the reformed religion. There being now above an
hundred years past, since the reformation was made in the kalendar, the
Gregorian account has accordingly got before the Julian one day
more than it was in the time of its institution, the difference between
these two accounts being now eleven days; so that the first day of any
[Pg 81]
month, according to that way of reckoning, is the 12th of the same
month, according to the New Style.
I shall conclude this section with a brief account of the Atmosphere.
Atmosphere.
The Atmosphere is that thin body of air which surrounds the Earth,
in which the clouds hover, and by which in their descent they are
broke into drops of rain; which sometimes, according to the warmth or
coldness of air, are froze into Snow, or Hailstones. Thunder
and Lightning are also made in the Atmosphere, and wind is nothing
else but a percussion of the air, occasioned by its different density
in different places. The benefits we receive from the atmosphere are
innumerable; without air no earthly creature could live, as is plainly
proved by experiments made by the Air-Pump; and the wholsomeness
of a climate chiefly depends upon that of its air: If there was no
atmosphere to reflect the rays of the Sun, no part of the heavens would
be lucid and bright, but that wherein the Sun was placed; and if a
spectator should turn his back towards the Sun, he would immediately
[Pg 82]
perceive it to be quite dark, and the least Stars would be seen shining
as they do in the clearest night; and the Sun immediately before his
setting would shine as brisk as at noon, but in a moment, as soon as
he got below the horizon, the whole hemisphere of the Earth would be
involved in as great a darkness as if it were midnight.
But by means of the atmosphere it happens, that while the Sun is above
the horizon, the whole face of the heavens is strongly illuminated by
its rays, so as to obscure the faint light of the Stars, and render
them invisible; and after Sun-setting, though we receive no direct
light from him, yet we enjoy its reflected light for some time: For
the atmosphere being higher than we are, is a longer time before it is
withdrawn from the Sun (as if a man was to run to the top of a steeple,
he might see the Sun after it had been set to those at the bottom.) The
rays which the atmosphere receives from the Sun, after he is withdrawn
from our sight, are by refraction faintly transmitted to us; until
the Sun having got about 18 degrees below the horizon, he no longer
enlightens our atmosphere, and then all that part thereof which is over
[Pg 83]
us becomes dark. After the same manner in the morning, when the Sun
comes within 18 degrees of our horizon, he again begins to enlighten
the atmosphere, and so more and more by degrees, until he rises and
makes full day.
Twilight, or Crepusculum.
This small illumination of the atmosphere, and the state of the Heavens
between day and night, is called the Twilight, or the Crepusculum.
The duration of twilight is different in different climates, and in
the same place at different times of the year. The beginning or ending
of twilight being accurately given, we may from thence easily find the
height of the atmosphere, which is not always the same. The mean height
of the atmosphere is computed to be about 40 miles; but it is probable,
the air may extend itself a great deal further, there being properly no
other limits to it, as we can conceive, but as it continually decreases
in density the farther remote it is from the Earth, in a certain ratio;
which at last, as to our conception, must in a manner terminate.
[Pg 84]
SECT. II.
Geographical Definitions.
Of the Situations of Places upon the Earth; of
the different Situations of its Inhabitants; of Zones and Climates.
The situations of places upon
the Earth, are determined by their Latitude and Longitude.
Latitude.
1. The Latitude of any place (upon the Earth) is its nearest
distance, either North or South from the Equator; and if the place
be in the (Northern/Southern) hemisphere, it is accordingly called
(North/South) Latitude; and is measured by an arch of the
meridian intercepted betwixt the zenith of the said place, and the
equator. And all places that lie on the same side, and at the same
[Pg 85]
distance from the equator, are said to be in the same parallel of
latitude: the parallels in Geography, being the same with the
parallels of declination in Astronomy.
From this definition arise the following Corollaries.
(1.) That no place can have above 90 degrees of latitude, either
North or South.
(2.) Those places that lie under the equinoctial (or thro’ which
the equator passes) have no latitude, it being from thence that the
calculation of latitudes is counted; and those places that lie under
the Poles have the greatest latitude, those points being at the
greatest distance from the equator.
(3.) The latitude of any place is always equal to the elevation of
the Pole in the same place above the horizon; and is therefore often
expressed by the Pole’s height, or elevation of the Pole; the reason
of which is, because from the equator to the Pole there is always the
distance of 90 degrees, and from the zenith to the horizon the same
number of degrees, each of these including the distance from the
[Pg 86]
zenith to the Pole: That distance therefore being taken away from both,
will leave the distance from the zenith to the equator, (which is the
latitude) equal to the distance of the Pole to the horizon.
(4.) The elevation of the equator in any place is always equal to
the complement of the latitude of the same place.
(5.) A ship sailed directly (towards/from) the equator
(lessens/augments) her latitude, (or (depresses/raises) the Pole) just
so much as is her distance sailed.
Difference of Latitude.
2. Difference of latitude is the nearest distance betwixt any two
parallels of latitude, shewing how far the one is to the Northward or
Southward of the other, which can never exceed 180 degrees. And when
the two places are in the same hemisphere (or on the same side of the
equator) the lesser latitude subtracted from the greater, and when they
are on different sides of the equator, the two latitudes added, gives
the difference of latitude.
[Pg 87]
Longitude.
3. The Longitude of any place (upon the Earth) is an arch of the
equator, contained betwixt the meridian of the given place, and some
fixed or known meridian; or, it is equal to the angle formed by the two
meridians, which properly can never exceed 180 degrees, tho’ sometimes
the Longitude is counted Easterly quite round the globe.
Since the meridians are all moveable, and not one that can be fixed
in the heavens, (as the equinoctial circle is fixed, from whence the
latitudes of all places are determined to be so much either North or
South) the longitudes of places cannot so well be fixed from any other
meridian, but every Geographer is at his liberty to make which he
pleases his first meridian, from whence to calculate the longitudes
of other places. Hence it is that geographers of different nations
reckon their longitudes from different meridians, commonly choosing the
meridian passing through the metropolis of their own country for their
first: Thus, the English geographers generally make the meridian
of London to be their first, the French that of Paris, and the
[Pg 88]
Dutch that of Amsterdam, &c. and mariners generally reckon the
longitude from the last known land they saw. This arbitrary way of
reckoning the longitude from different places, makes it necessary,
whenever we express the longitude of any place, that the place from
whence it is counted be also expressed.
From the preceding definitions arise the following corollaries:
1. If a body should steer directly North, or directly South, quite
round the globe, he’ll continually change his latitude; and pass
through the two Poles of the world, without deviating the least from
the meridian of the place he departed from; and consequently on his
return will not differ in his account of time from the people residing
in the said place.
2. If a body should steer round the globe either due East, or
due West, he’ll continually change his longitude, but will go quite
round without altering his latitude; and if his course should be due
East, he’ll gain a day compleatly in his reckoning, or reckon one day
more than the inhabitants of the place from whence he departed; or if
his course had been West, he would have lost one day, or reckon one less.
[Pg 89]
The reason of which is evident; for admitting our traveller steers due
East; so many miles in one day as to make his difference of longitude
equivalent to a quarter of an hour of time, it is evident that the
next day the Sun will rise to him a quarter of an hour sooner than to
the inhabitants of the place from whence he departed; and so daily,
in proportion to the rate he travels, which in going quite round,
will make up one natural day. In like manner, if he steers due West
after the same rate, he’ll lengthen each day a quarter of an hour,
and consequently the Sun will rise to him so much later every day; by
which means, in going quite round, he’ll lose one day compleat in his
reckoning. From whence it follows,
3. If two bodies should set out from the same place, one steering
East, and the other West, and so continue their courses quite round,
until they arrive at the place from whence they set out, they’ll differ
two days in their reckoning at the time of their return.
4. If a body should steer upon an oblique course (or
[Pg 90]
any where betwixt the meridian and the East or West points) he’ll
continually change both latitude and longitude, and that more or less,
according to the course he steers; and if he should go quite round the
globe, he’ll differ in his account of time, as by the second Corol.
5. The people residing in the Easternmost of any two places, will
reckon their time so much the sooner than those who live in the other
place, according to the difference of longitude betwixt the two places,
allowing one hour for every 15 degrees, &c. and the contrary.
II. Of Zones and Climates, &c.
Zones, Torrid, Temperate, and Frigid.
4. Zones are large tracts of the surface of the Earth, distinguished
by the tropics and polar circles, being five in number; viz. one
Torrid, two Temperate and two Frigid.
The Torrid, or Burning Zone, is all the space comprehended between
the two tropics; the ancients imagined this tract of the Earth to be
uninhabitable, because of the excessive heat, it being so near the Sun.
All the inhabitants of the torrid zone have the Sun in their zenith, or
exactly over their heads twice in every year; excepting those who live
[Pg 91]
exactly under the two tropics, where the Sun comes to their zenith only
once in a year.
The two Temperate Zones lie on either side of the globe, between the
tropics and the polar circles.
The two Frigid Zones are those spaces upon the globe that are
included between the two polar circles.
Amphiscians.
Ascians.
The inhabitants of the Earth are also distinguished by the diversity
of their Shadows. Those who live in the torrid zone, are called
Amphiscians, because their noon-shadow is cast different ways,
according as the Sun is to the northward or southward of their zenith;
but when the Sun is in their zenith, they are called Ascians.
Heteroscians.
Ascians Heteroscians.
Periscians.
The inhabitants of the temperate zones, are called Heteroscians,
because their noon-shadow is always cast the same way: But those who
live under the tropics are called Ascians Heteroscians; those who
live in the frigid zones are called Periscians, because sometimes
their shadow is cast round about them.
[Pg 92]
These hard names are only Greek words, importing how the Sun casts
the shadow of the several inhabitants of the Earth; which would be a
too trifling distinction to be made here, was it not for the sake of
complying with custom.
The inhabitants of the Earth are also distinguished into three sorts,
in respect to their relative situation to one another, and these are
called the Periœci, Antœci, and Antipodes.
Periœci.
5. The Periœci are those who live under opposite points of the same
parallel of latitude. They have their seasons of the year at the same
time, and their days and nights always of the same length with one
another, but the one’s Noon is the other’s Midnight; and when the
Sun is in the equinoctial, he rises with the one, when he sets with the
other. Those who live under the Poles have no Periœci.
Antœci.
6. The Antœci live under the same meridian, and in the same latitude,
but on different sides of the equator; their Seasons of the year are
[Pg 93]
contrary, and the days of the one are equal to the nights of the other,
but the hour of the day and night is the same with both; and when the
Sun is in the equinoctial, he rises and sets to both exactly at the
same time. Those who live under the equator have no Antœci.
Antipodes.
7. The Antipodes are those who live diametrically opposite to one
another, standing, as it were, exactly feet to feet: Their days and
nights, summer and winter, are at direct contrary times.
The surface of the Earth is by some distinguished into Climates.
Climates.
8. A Climate is a tract of the surface of the Earth, included between
two such parallels of latitude, that the length of the longest day in
the one exceeds that in the other by half an hour.
The whole surface of the Earth is considered, as being divided into
60 climates, viz. from the equator to each of the polar circles 24,
arising from the difference of ½ hour in the length of their longest
days; and from the polar circles to the Poles themselves, are six,
[Pg 94]
arising from the difference of an entire month, the Sun being seen
in the first of these a whole month without setting; in the second
two; and in the third, three months, &c. These climates continually
decrease in breadth, the farther they are from the equator. How they
are framed, viz. the parallel of latitude in which they end (that
being likewise the beginning of the next) with the respective breadth
of each of them, is shewed in the following table:
[Pg 95]
A TABLE of the Climates.
Climates between the Equator and the Polar Circles.
| |
| Climates |
Longest |
Latitude. |
Breadth |
| Day. |
D. |
M. |
D. |
M. |
| 1 |
12½ |
8 |
25 |
8 |
25 |
| 2 |
13 |
16 |
25 |
8 |
00 |
| 3 |
13½ |
23 |
50 |
7 |
25 |
| 4 |
14 |
30 |
25 |
6 |
30 |
| 5 |
14½ |
36 |
28 |
6 |
8 |
| 6 |
15 |
41 |
22 |
4 |
54 |
| 7 |
15½ |
45 |
29 |
4 |
7 |
| 8 |
16 |
49 |
1 |
3 |
32 |
| 9 |
16½ |
51 |
58 |
2 |
57 |
| 10 |
17 |
54 |
27 |
2 |
29 |
| 11 |
17½ |
56 |
37 |
2 |
10 |
| 12 |
18 |
58 |
29 |
1 |
52 |
| 13 |
18½ |
59 |
58 |
1 |
29 |
| 14 |
19 |
61 |
18 |
1 |
20 |
| 15 |
19½ |
62 |
25 |
1 |
7 |
| 16 |
20 |
63 |
22 |
0 |
57 |
| 17 |
20½ |
64 |
6 |
0 |
44 |
| 18 |
21 |
64 |
49 |
0 |
43 |
| 19 |
21½ |
65 |
21 |
0 |
32 |
| 20 |
22 |
65 |
47 |
0 |
26 |
| 21 |
22½ |
66 |
6 |
0 |
19 |
| 22 |
23 |
66 |
20 |
0 |
14 |
| 23 |
23½ |
66 |
28 |
0 |
8 |
| 24 |
24 |
66 |
31 |
0 |
3 |
| |
Climates between the Polar Circles and the Poles.
| |
| Length of Days. |
Latitude. |
| Months. |
D. |
M. |
| 1 |
67 |
21 |
| 2 |
69 |
48 |
| 3 |
73 |
37 |
| 4 |
78 |
30 |
| 5 |
84 |
5 |
| 6 |
00 |
00 |
| |
[Pg 96]
III. Of the Poetical rising and setting of the Stars.
Cosmical, Acronical, and Heliacal rising and
setting.
The ancient Poets make frequent mention of the Stars rising and
setting, either Cosmically, Acronically, or Heliacally; whence
these distinctions are called Poetical.
A Star is said to rise or set Cosmically, when it rises or sets at
Sun-rising; and when it rises or sets at Sun-setting, it is said
to rise or set Acronically. A Star rises Heliacally, when first it
becomes visible, after it had been so near the Sun as to be hid by the
splendor of his rays: And a Star is said to set Heliacally, when it
is first immersed, or hid by the Sun’s rays.
The Fixed Stars, and the three superior Planets, Mars, Jupiter,
and Saturn, rise Heliacally in the morning; but the Moon rises
Heliacally in the evening, because the Sun is swifter than the
superior Planets, and slower than the Moon.
IV. Of the surface of the Earth, considered as it is composed of Land
and Water.
The Earth consists naturally of two parts, Land and Water, and therefore
[Pg 97]
it is called the Terraqueous Globe. Each of these elements is
subdivided into various forms and parts, which accordingly are
distinguished by different names.
I. Of the Land.
The land is distinguished into Continents, Islands, Peninsula’s,
Isthmus’s, Promontories, Mountains, or Coasts.
Continent.
Main Land.
9. A Continent is a large quantity of land, in which many great
countries are joined together, without being separated from each other
by the sea: such are Europe, Asia, Africa, and the vast continent
of America; which four are the principal divisions of the Earth. A
continent is sometimes called the Main Land.
Island.
10. An Island is a country, or portion of land, environed round with
water: such are Great-Britain and Ireland; Sardinia, Sicily,
&c. in the Mediterranean Sea; the Isles of Wight, Anglesey, &c.
near England. Also a small part of dry land, in the midst of a river,
is called an island, when compared to a lesser, is called the continent;
[Pg 98]
as if we compare the Isle of Wight to England, the latter may be
properly called the continent.
Peninsula.
11. A Peninsula is a part of land almost environed with water, save
one narrow neck adjoining it to the continent; or which is almost
an island: such is Denmark joining to Germany; also Africa is
properly a large peninsula joining to Asia.
Isthmus.
12. An Isthmus is a narrow neck of land joining a peninsula to the
continent; as the Isthmus of Sues, which joins Africa to Asia,
that of Panama, joining North and South America, &c.
Promontory.
Mountain.
13. A Promontory is a high part of land stretching out into the sea,
and is often called a Cape or Headland: such is the Cape of
Good Hope in the South of Africa; Cape Finistre on the West of
Spain; also the Lizard Point, and the Land’s End, are two Capes
or Headlands on the West of England. A Mountain is a high part of
land in the midst of a country, over topping the adjacent parts.
[Pg 99]
A Coast or Shore.
Inland.
14. A Coast or Shore is that part of land which borders upon the
sea, whether it be in islands or a continent: And that part of the land
which is far distant from the sea, is called the Inland Country.
These are the usual distinctions of the land.
The Water is distinguished into Oceans, Seas, Lakes, Gulfs,
Straits, and Rivers.
The Ocean, or Main Sea.
15. The Ocean, or Main Sea, is a vast spreading collection of
water, not divided or separated by lands running between; such is the
Atlantic or Western Ocean; between Europe and America; the
Pacific Ocean, or South Sea, &c.
Note, Those parts of the ocean which border upon the land, are called
by various names, according to those of the adjacent countries; as, the
British Sea, the Irish Sea, the French and Spanish Sea.
A Lake.
16. A Lake is a collection of deep standing water, inclosed all round
with land, and not having any visible and open communication with the
[Pg 100]
sea: But when this lake is very large, it is commonly called a sea; as
the Caspian Sea in Asia, &c.
A Gulf.
Creek or Haven.
17. A Gulf is a part of the sea almost encompassed with land, or that
which runs up a great way into the land; as, the Gulf of Venice,
&c. But if it be very large, ’tis rather called an Inland Sea;
as the Baltic Sea, the Mediterranean Sea, the Red Sea, or the
Arabian Gulf, &c. And a small part of sea thus environed with land is
usually called a Bay. If it be but a very small Part, or, as it were,
a small arm of the sea, that runs but a few miles between the land, it
is called a Creek or Haven.
A Strait.
18. A Strait is a narrow passage lying between two shores, whereby
two seas are joined together; as, the Straits of Dover, between the
British Channel and the German Sea; the Straits of Gibralter,
between the Atlantic and the Mediterranean Sea. The Mediterranean
itself is also sometimes called the Straits.
These are all the necessary terms commonly used in Geography.
The names of the several countries and seas, and all the principal
[Pg 101]
divisions of the Earth, the reader will find expressed upon the
Terrestrial Globes. To give a tolerable account of the produce of each
country, the genius of the people, their political institutions, &c.
is properly a particular subject of itself, and quite foreign to our
design. We shall next proceed to the use of the Globes; but first it
may not be amiss to take a short review of their appurtenances.
Those circles of the sphere that are fixed, are (as has been already
said) drawn upon the Globes themselves; those that are moveable,
are supplied by the Brass Meridian, the Wooden Horizon, and the
Quadrant of Altitude.
Brass Meridian.
1. That side of the Brazen Meridian, which is divided into degrees,
represents the true Meridian; this side is commonly turned towards
the East, and ’tis usual to place the globe so before you, that the
North be to the right hand, and the South to the left. The meridian
is divided into 4 quadrants, each being 90 degrees, two of which are
numbered from that part of the equinoctial, which is above the horizon,
towards each of the Poles; the other two quadrants are numbered from
[Pg 102]
the Poles towards the equator. The reason why two quadrants of the
meridian are numbered from the equator, and the other two from the
Poles, is because the former of these two serve to shew the distance of
any point on the globe from the equator, and the other to elevate the
globe to the latitude of the place.
Wooden Horizon.
2. The upper side of the wooden frame called the Wooden Horizon;
represents the true horizon; the circles drawn upon this plane have
been already described; we may observe, that the first point of ♈ is
the East, and the opposite being the first point of ♎ is the West, the
meridian passing through the North and South points.
Quadrant of Altitude.
3. The Quadrant of Altitude is a flexible plate of thin brass, having
a nut and screw at one end, to be fastened to the meridian of either
globe, as occasion requires. The edge of this quadrant which has the
graduations upon it, called the fiducial edge, is that which is always
meant whenever we make mention of the quadrant of altitude.
Hour Circle.
4. The Horary or Hour Circle, is divided into twice twelve hours,
[Pg 103]
the two XII’s coinciding with the meridian; the uppermost XII is that
at Noon, and the lowermost towards the horizon is XII at Night.
The hours on the East side of the meridian are the Morning Hours,
and those on the West side the Hours after Noon. The axis of
the globe carries round the Hand or Index which points the hour, and
passes through the center of the hour circle.
The things above described are common to both globes; but there are
some others which are peculiar or proper to one sort of globe. The two
Colures, and the Circles of Latitude from the ecliptic, belong
only to the Celestial Globes; also the ecliptic itself does properly
belong only to this globe, tho’ it is always drawn on the Terrestrial,
for the sake of those that might not have the other globe by them. The
equinoctial on the celestial globe is always numbered into 360 degrees,
beginning at the equinoctial point ♈; but on the terrestrial, it is
arbitrary, where these numbers commence, according to the meridian of
what place you intend for your first; and the degrees may be counted
either quite round to 360, or both ways, ’till they meet in the
opposite part of the meridian, at 180.
[Pg 104]
SECT. III.
The USE of the Globes.
Problem I. To find
the Latitude and Longitude of any given Place upon the Globe; and on
the contrary, the Latitude and Longitude being given, to find the Place.
1.
Turn the globe round its axis,
’till the given place lies exactly under the (Eastern side of the
brass) meridian, then that degree upon the meridian, which is directly
over it, is the Latitude; which is accordingly North or South, as it
lies in the Northern or Southern hemisphere, the globe remaining in the
same position.
That degree upon the equator which is cut by the brazen meridian, is
the Longitude required from the first meridian upon the globe. If the
[Pg 105]
longitude is counted both ways from the first meridian upon the globe,
then we are to consider, whether the given place lies Easterly or
Westerly from the first meridian, and the longitude must be expressed
accordingly.
The Latitudes of the following places: and upon a globe where the
longitude is reckoned both ways from the meridian of London, their
longitudes will be found as follow:
| |
Latitude.
Deg. |
Longitude.
Deg. |
| Rome |
41¾ |
North. |
13 |
East. |
| Paris |
48¾ |
N. |
2½ |
E. |
| Mexico |
20 |
N. |
102 |
W. |
| Cape Horn |
58 |
S. |
80 |
W. |
2. The Latitude and Longitude being given to find the Place.
Seek for the given longitude in the equator, and bring that point to
the meridian; then count from the equator on the meridian the degree of
latitude given, towards the arctic and antarctic Pole, according as the
latitude is Northerly or Southerly, and under that degree of latitude
lies the Place required.
[Pg 106]
Prob. II. To find the Difference
of Latitude betwixt any two given Places.
Bring each of the places proposed successively to the meridian, and
observe where they intersect it, then the number of degrees upon
the meridian, contained between the two intersections, will be the
Difference of Latitude required. Or, if the places proposed are on
the same side of the equator, having first found their latitudes,
subtract the lesser from the greater; but if they are on contrary sides
of the equator, add them both together, and the difference in the first
case, and the sum in the latter, will be the difference of latitude required.
Thus the difference of latitude betwixt London and Rome will be
found to be 9¾ degrees; betwixt Paris and Cape Bona Esperance 83 degrees.
Prob. III. To find the Difference
of Longitude betwixt any two given Places.
Bring each of the given places successively to the meridian, and see
where the meridian cuts the equator each time; the number of degrees
[Pg 107]
contained betwixt those two points, if it be less than 180 degrees,
otherwise the remainder to 360 degrees, will be the difference of
longitude required. Or,
Having brought one of the given places to the meridian, bring the
index of the hour circle to 12 o’clock; then having brought the other
place to the meridian, the number of hours contained between the place
the index was first set at, and the place where it now points, is the
difference of longitude in time betwixt the two places.
Thus the difference of longitude betwixt Rome and Constantinople
will be found to be 19 degrees, or 1 hour and a quarter; betwixt
Mexico and Pekin in China, 240 degrees, or 9⅓ hours.
Prob. IV. Any Place
being given to find all those Places that are in the same Latitude with
the same Place.
The latitude of any given place being marked upon the meridian, turn
the globe round its axis, and all those places that pass under the same
mark are in the same latitude with the given place, and have their days
[Pg 108]
and nights of equal lengths. And when any place is brought to the
meridian, all the inhabitants that lie under the upper semicircle of
it, have their Noon or mid-day at the same point of absolute time exactly.
Prob. V. The day of
the Month being given; to find the Sun’s Place in the Ecliptic, and his
Declination.
1. To find the Sun’s Place: Look for the day of the month given in
the kalendar of months upon the horizon, and right against it you’ll
find that sign and degree of the ecliptic which the Sun is in. The
Sun’s place being thus found, look for the same in the ecliptic line
which is drawn upon the globe, and bring that point to the meridian,
then that degree of the meridian, which is directly over the Sun’s
place, is the Declination required; which is accordingly either North
or South, as the Sun is in the Northern or Southern signs. Thus,
| |
Sun’s Place. |
Declination. |
| |
Deg. |
Min. |
Deg. |
Min. |
| April 23 |
♉ |
3 |
00 |
12 |
32 N. |
| July 31 |
♌ |
7 |
51 |
18 |
20 N. |
| October 26 |
♏ |
2 |
49 |
12 |
28 S. |
| January 20 |
♒ |
0 |
49 |
20 |
07 S. |
[Pg 109]
Prob. VI. To rectify the
Globe for the Latitude, Zenith, and the Sun’s Place.
1. For the Latitude: If the place be in the Northern hemisphere,
raise the arctic Pole above the horizon; but for the South latitude you
must raise the antarctic; then move the meridian up and down in the
notches, until the degrees of the latitude counted upon the meridian
below the Pole, cuts the horizon, and the globe is adjusted to the
latitude.
2. To rectify the Globe for the Zenith: Having elevated the globe
according to the latitude, count the degrees thereof upon the meridian
from the equator, towards the elevated Pole, and that point will be the
zenith or the vertex of the place; to this point of the meridian fasten
the quadrant of altitude, so that the graduated edge thereof may be
joined to the said point.
3. Bring the Sun’s place in the ecliptic to the meridian, and then set
the hour index to XII at Noon, and the globe will be rectified to the
Sun’s Place. If you have a little mariner’s compass, the meridian of
the globe may be easily set to the meridian of the place.
[Pg 110]
Prob. VII. To find
the Distance between any two given places upon the Globe, and to find
all those places upon the globe that are at the same distance from a
given place.
Lay the quadrant of altitude over both the places, and the number of
degrees intercepted between them being reduced into miles, will be the
distance required: Or, you may take the distance betwixt the two places
with a pair of compasses, and applying that extent to the equator,
you’ll have the degrees of distance as before.
Note, A geographical mile is the ¹/₆₀th part of a degree; whereof
if you multiply the number of degrees by 60, the product will be the
number of geographical miles of distance sought; but to reduce the
same into English miles, you must multiply by 70, because about 70
English miles make a degree of a great circle upon the superficies of
the Earth.
Thus, the distance betwixt London and Rome will be found to be
about 13 degrees, which is 780 geographical miles.
[Pg 111]
If you rectify the globe for the latitude and zenith of any given
place, and bring the said place to the meridian; then turning the
quadrant of altitude about, all those places that are cut by the same
point of it, are at the same distance from the given place.
Prob. VIII. To find
the angle of position of Places, or the angle formed by the meridian of
one Place, and a great circle passing through both the Places.
Having rectified the globe for the latitude and zenith of one of the
given places, bring the said place to the meridian, then turn the
quadrant of altitude about, until the fiducial edge thereof cuts the
other place, and the number of degrees upon the horizon, contained
between the said edge and the meridian, will be the angle of position
sought.
Thus, the angle of position at the Lizard, between the meridian of
the Lizard and the great circle, passing from thence to Barbadoes
is 69 degrees South-Westerly; but the angle of position between the
same places at Barbadoes, is but 38 degrees North-Easterly.
[Pg 112]
SCHOLIUM
The angle of position between two places is a different thing from
what is meant by the bearings of places; the Bearings of two places
is determined by a sort of spiral line, called a Rhumb Line, passing
between them in such a manner, as to make the same or equal angles
with all the meridians through which it passeth; but the angle or
position is the very same thing with what we call the azimuth in
astronomy, both being formed by the meridian and a great circle passing
thro’ the zenith of a given place in the heavens, then called the
azimuth, or upon the Earth, then called the angle of position.
From hence may be shewed the error of that geographical paradox, viz.
If a place A bears from another B due West, B shall not bear from A
due East. I find this paradox vindicated by an author, who at the same
time gives a true definition of a rhumb line: But his arguments are
ungeometrical; for if it be admitted that the East and West lines make
the same angles with all the meridians through which they pass, it will
[Pg 113]
follow that these lines are the parallels of latitude: For any parallel
of latitude is the continuation of the surface of a Cone, whose
sides are the radii of the sphere, and circumference of its base the
said parallel; and it is evident, that all the meridians cut the said
surface at right (and therefore at equal) angles; whence it follows,
that the rhumbs of East and West are the parallels of latitude, though
the case may seem different, when we draw inclining lines (like
meridians) upon paper, without carrying our ideas any farther.
Prob. IX. To find the Antœci,
Periœci, and Antipodes to any given place.
Bring the given place to the meridian; and having found its latitude,
count the same number of degrees on the meridian from the equator
towards the contrary Pole, and that will give the place of the
Antœci. The globe being still in the same position, set the hour
index to XII at noon, then turn the globe about ’till the index points
to the lower XII; the place which then lies under the meridian, having
the same latitude with the given place, is the Periœci required. As
[Pg 114]
the globe now stands, the Antipodes of the given place are under
the same point of the meridian, that its Antœci stood before: Or,
if you reckon 180 degrees upon the meridian from the given place,
that point will be the Antipodes. Let the given place be London,
in the latitude of 51½ degrees North, that place which lies under the
same meridian and the latitude 51½ degrees South, is the Antœci;
that which lies in the same parallel with London, and 180 degrees of
longitude from it, is the Periœci, and the Antipodes is the place
whose longitude from London is 180 degrees, and latitude 51½ degrees South.
Prob. X. The Hour
of the Day at one place being given; to find the correspondent Hour (or
what o’Clock it is at that time) in any other place.
The difference of time betwixt two places is the same with their
difference of longitude; wherefore having found their difference
of longitude, reduced into time (by allowing one hour for every 15
degrees, &c.) and if the place where the hour is required lies
[Pg 115]
(Easterly/Westerly) from the place where the hour is given,
(add/subtract) the difference of longitude reduced into time (to/from)
the hour given; and the sum or remainder will accordingly be the hour
required. Or,
Having brought the place at which the hour is given to the meridian,
set the hour index to the given hour; then turn the globe about until
the place where the hour is required comes to the meridian, and the
index will point out the hour at the said place.
Thus when it is Noon at London, it is
| |
H. |
M. |
|
| At |
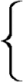 |
Rome |
0 |
52 |
P. M. |
| Constantinople |
2 |
07 |
P. M. |
| Vera-Cruz |
5 |
30 |
A. M. |
| Pekin in China |
7 |
50 |
P. M. |
Prob. XI. The Day
of the Month being given, to find those places on the globe where the
Sun will be Vertical, or in the Zenith, that day.
Having found the Sun’s place in the ecliptic, bring the same to the
[Pg 116]
meridian, and note the degree over it; then turning the globe round,
all places that pass under that degree will have the Sun vertical that day.
Prob. XII. A place
being given in the Torrid Zone, to find those two Days in which the Sun
shall be Vertical to the same.
Bring the given place to the meridian, and mark what degree of latitude
is exactly over it; then turning the globe about its axis, those two
points of the ecliptic, which pass exactly under the said mark, are the
Sun’s place; against which, upon the wooden horizon, you’ll have the
days required.
Prob. XIII. To find
where the Sun is Vertical at any given time assigned; or the Day of the
Month and the Hour at any Place (suppose London) being given,
to find in what place the Sun is Vertical at that very time.
Having found the Sun’s declination, and brought the first place
(London) to the meridian, set the index to the given hour, then turn
the globe about until the index points to XII at noon; which being
[Pg 117]
done, that place upon the globe which stands under the point of the Sun’s
declination upon the meridian, has the Sun that moment in the Zenith.
Prob. XIV. The
Day, and the Hour of the Day at one place, being given; to find all
those places upon the Earth, where the Sun is then Rising, Setting,
Culminating (or on the meridian) also where it is Day-light, Twilight,
Dark Night, Midnight; where the Twilight then begins, and where it
ends; the height of the Sun in any part of the illuminated hemisphere;
also his depression in the obscure hemisphere.
Having found the place where the Sun is vertical at the given hour,
rectify the globe for that latitude, and bring the said place to the
meridian.
Then all those places that are in the Western semicircle of the
horizon, have the Sun rising at that time.
Those in the Eastern semicircle have it setting.
To those who live under the upper semicircle of the meridian, it is 12
[Pg 118]
o’clock at noon. And,
Those who live under the lower semicircle of the meridian, have it at
midnight.
All those places that are above the horizon, have the Sun above them,
just so much as the places themselves are distant from the horizon;
which height may be known by fixing the quadrant of altitude in the
zenith, and laying it over any particular place.
In all those places that are 18 degrees below the Western side of the
horizon, the twilight is just beginning in the morning, or the day
breaks. And in all those places that are 18 degrees below the Eastern
side of the horizon, the twilight is ending, and the total darkness
beginning.
The twilight is in all those places whose depression below the horizon
does not exceed 18 degrees. And,
All those places that are lower than 18 degrees, have dark night.
The depression of any place below the horizon is equal to the altitude
of its Antipodes, which may be easily found by the quadrant of altitude.
[Pg 119]
Prob. XV. The Day
of the Month being given; to show, at one view, the length of Days and
Nights in all places upon the Earth at that time; and to explain how
the vicissitudes of Day and Night are really made by the motion of the
Earth round her axis in 24 hours, the Sun standing still.
The Sun always illuminates one half of the globe, or that hemisphere
which is next towards him, while the other remains in darkness: And if
(as by the last problem) we elevate the globe according
to the Sun’s place in the ecliptic, it is evident, that the Sun (he being at an
immense distance from the Earth) illuminates all that hemisphere, which
is above the horizon; the wooden horizon itself, will be the circle
terminating light and darkness; and all those places that are below it,
are wholly deprived of the solar light.
The globe standing in this position, those arches of the parallels of
latitude which stand above the horizon, are the Diurnal Arches, or
the length of the day in all those latitudes at that time of the year;
and the remaining parts of those parallels, which are below the horizon,
[Pg 120]
are the Nocturnal Arches, or the length of the night in those places.
The length of the diurnal arches may be found by counting how many
hours are contained between the two meridians, cutting any parallel of
latitude, in the Eastern and Western parts of the horizon.
In all those places that are in the Western semicircle of the horizon,
the Sun appears rising: For the Sun, standing still in the vertex (or
above the brass meridian) appears Easterly, and 90 degrees distant from
all those places that are in the Western semicircle of the horizon; and
therefore in those places he is then rising. Now, if we pitch upon any
particular place upon the globe, and bring it to the meridian, and then
bring the hour index to the lower 12, which in this case, we’ll suppose
to be 12 at noon; (because otherwise the numbers upon the hour circle
will not answer our purpose) and afterwards turn the globe about, until
the aforesaid place be brought to the Western side of the horizon; the
index will then shew the time of the Sun rising in that place. Then
turn the globe gradually about from West to East, and minding the hour
[Pg 121]
index, we shall see the progress made in the day every hour, in all
latitudes upon the globe, by the real motion of the Earth round its
axis; until, by their continual approach to the brass meridian (over
which the Sun stands still all the while) they at last have noon day,
and the Sun appears at the highest; and then by degrees, as they move
Easterly the Sun seems to decline Westward, until, as the places
successively arrive in the Eastern part of the horizon, the Sun appears
to set in the Western: For the places that are in the horizon, are 90
degrees distant from the Sun. We may observe, that all places upon the
Earth, that differ in latitude, have their days of different length
(except when the Sun is in the equinoctial) being longer or shorter,
in proportion to what part of the parallels stands above the horizon.
Those that are in the same latitude, have their days of the same
length; but have them commence sooner or later, according as the places
differ in longitude.
Prob. XVI. To
explain in general the alteration of Seasons, or length of the Days and
Nights made in all places of the World, by the Sun’s (or the Earth’s)
annual motion in the Ecliptic.
[Pg 122]
It has been shewed in the last problem, how to place
the globe in such a position as to exhibit the length of the diurnal and
nocturnal arches in all places of the Earth, at a particular time:
If the globe be continually rectified, according as the Sun alters
his declination, (which may be known by bringing each degree of the
ecliptic successively to the meridian) you’ll see the gradual increase
or decrease made in the days, in all places of the World, according as
a greater or lesser portion of the parallels of latitude, stands above
the horizon. We shall illustrate this problem by examples taken at
different times of the year.
1. Let the Sun be in the first point of ♋ (which happens on the 21st
of June) that point being brought to the meridian, will shew the
Sun’s declination to be 23½ degrees North; then the globe
must be rectified to the latitude of 23½ degrees; and for the better
illustration of the problem, let the first meridian upon the globe be
brought under the brass meridian. The globe being in this position,
you’ll see at one view the length of the days in all latitudes, by
[Pg 123]
counting the number of hours contained between the two extreme
meridians, cutting any particular parallel you pitch upon, in the
Eastern and Western part of the horizon. And you may observe that
the lower part of the arctic circle just touches the horizon, and
consequently all the people who live in that latitude have the Sun
above their horizon for the space of 24 hours, without setting; only
when he is in the lower part of the meridian (which they would call 12
at night) he just touches the horizon.
To all those who live between the arctic circle and the Pole, the Sun
does not set, and its height above the horizon, when he is in the
lower part of the meridian, is equal to their distance from the arctic
circle: For example, Those who live in the 83d parallel have the Sun
when he is lowest at this time 13½ degrees high.
If we cast our eye Southward, towards the equator, we shall find, that
the diurnal arches, or the length of days in the several latitudes,
gradually lessen: The diurnal arch of the parallel of London at this
[Pg 124]
time is 16½ hours; that of the Equator (is always) 12 hours; and so
continually less, ’till we come to the Antarctic Circle, the upper
part of which just touches the horizon; just those who live in this
latitude have just one sight of the Sun, peeping as it were in the
horizon: And all that space between the antarctic circle and the South
Pole, lies in total darkness.
If from this position we gradually move the meridian of the globe
according to the progressive alterations made in the Sun’s declination,
by his motion in the ecliptic, we shall find the diurnal arches of
all those parallels, that are on the Northern side of the equator,
continually decrease; and those on the Southern side continually
increase, in the same manner as the days in those places shorten and
lengthen. Let us again observe the globe when the Sun has got within
10 degrees of the equinoctial; now the lower part of the 80th parallel
of North latitude just touches the horizon, and all the space betwixt
this and the pole, falls in the illuminated hemisphere: but all those
parallels that lie betwixt this and the arctic circle, which before
were wholly above the horizon, do now intersect it, and the Sun appears
[Pg 125]
to them to rise and set. From hence to the equator, we shall find that
the days have gradually shortened; and from the equator Southward, they
have gradually lengthened, until we come to the 80th parallel of the
South latitude; the upper part of which just touches the horizon; and
all places betwixt this and the South Pole are in total darkness; but
those parallels betwixt this and the antarctic circle, which before
were wholly upon the horizon, are now partly above it; the length
of their days being exactly equal to that of the nights in the same
latitude in the contrary hemisphere. This also holds universally, that
the length of one day in one latitude North, is exactly equal to the
length of the night in the same latitude South; and vice versa.
Let us again follow the motion of the Sun, until he has got into the
equinoctial, and take a view of the globe while it is in this position.
Now all the parallels of latitude are cut into two equal parts by the
horizon, and consequently the days and nights are of equal lengths,
viz. 12 hours each, in all places of the world; the Sun rising and
setting at six o’clock, excepting under the two Poles, which now lie
[Pg 126]
exactly in the horizon: Here the Sun seems to stand still in the same
point of the heavens for some time, until by degrees, by his motion in
the ecliptic, he ascends higher to one and disappears to the other,
there being properly no days and nights under the Poles; for there the
motion of the Earth round its axis cannot be observed.
If we follow the motion of the Sun towards the Southern tropic, we
shall see the diurnal arches of the Northern parallels continually
decrease, and the Southern ones increase in the same proportion,
according to their respective latitudes; the North Pole continually
descending, and the South Pole ascending, above the horizon, until the
Sun arrives into ♑, at which time all the space within the antarctic
circle is above the horizon; while the space between the arctic circle,
and its neighbouring Pole, is in total darkness. And we shall now find
all other circumstances quite reverse to what they were when the Sun
was in ♋; the nights now all over the world being of the same length
that the days were of before.
[Pg 127]
We have now got to the extremity of the Sun’s declination; and if
we follow him through the other half of the ecliptic, and rectify the
globe accordingly, we shall find the seasons return in their order,
until at length we bring the globe into its first position.
The two foregoing problems were not, as I know of, published in any
book on this subject before; and I have dwelt the longer upon them,
because they very well illustrate how the vicissitudes of days and
nights are made all over the world, by the motion of the Earth round
her axis; the horizon of the globe being made the circle, separating
light and darkness, and so the Sun to stand still in the vertex. And
if we really could move the meridian, according to the change of the
Sun’s declination, we should see at one view, the continual change made
in the length of days and nights, in all places on the Earth; but as
globes are fitted up, this cannot be done; neither are they adapted for
the common purposes, in places near the equator, or any where in the
Southern hemisphere. But this inconvenience is now remedied (at a small
[Pg 128]
additional expence) by the hour circle being made to shift to either
Pole; and some globes are now made with an hour circle fixed to the
globe at each Pole between the globe and meridian, so as to have none
without side to interrupt the meridian from moving quite round the
wooden horizon.
Prob. XVII. To shew
by the globe, at one view, the longest of the Days and Nights in any
particular places, at all times of the Year.
Because the Sun, by his motion in the ecliptic, alters his declination
a small matter every day; if we suppose all the torrid zone to be
filled up with a spiral line, having so many turnings; or a screw
having so many threads, as the Sun is days in going from one tropic
to the other: And these threads at the same distance from one another
in all places, as the Sun alters his declination in one day in all
those places respectively: This spiral line or screw will represent
the apparent paths described by the Sun round the Earth every day; and
by following the thread from one tropic to the other, and back again,
we shall have the path the Sun seems to describe round the Earth in a
[Pg 129]
year. But because the inclinations of these threads to one another are
but small, we may suppose each diurnal path to be one of the parallels
of latitude, drawn, or supposed to be drawn upon the globe. Thus much
being premised, we shall explain this Problem, by placing the globe
according to some of the most remarkable positions of it, as before we
did for the most remarkable seasons of the year.
In the preceding problem, the globe being rectified
according to the Sun’s declination, the upper parts of the parallels of latitude,
represented the Diurnal Arches, or the length of the days all over
the world, at that particular time: Here we are to rectify the globe
according to the latitude of the place, and then the upper parts of the
parallels of declination are the diurnal arches; and the length of the
days at all times of the year, may be here determined by finding the
number of hours contained between the two extreme meridians, which cut
any parallel of declination in the Eastern and Western points of the
horizon; after the same manner, as before we found the length of the
day in the several latitudes at a particular time of the year.
[Pg 130]
1. Let the place proposed be under the equinoctial, and let the globe
be accordingly rectified for 00 degrees of latitude, which is called
a direct position of the sphere. Here all the parallels of latitude,
which in this case we will call the parallels of declination, are cut
by the horizon into two equal parts; and consequently those who live
under the equinoctial, have the days and nights of the same length at
all times of the year; and also in this part of the Earth, all the
Stars rise and set, and their continuance above the horizon, is equal
to their stay below it, viz. 12 hours.
If from this position we gradually move the globe according to
the several alterations of latitudes, which we will suppose to be
Northerly; the lengths of the Diurnal Arches will continually
increase, until we come to a parallel of declination, as far distant
from the equinoctial, as the place itself is from the Pole. This
parallel will just touch the horizon, and all the heavenly bodies that
are betwixt it and the Pole never descend below the horizon. In the
mean time, while we are moving the globe, the lengths of the diurnal
[Pg 131]
arches of the Southern parallels of declination, continually diminish
in the same proportion that the Northern ones increased; until we
come to that parallel of declination which is so far distant from the
equinoctial Southerly, as the place itself is from the North Pole. The
upper part of this Parallel just touches the horizon, and all the
Stars that are betwixt it and the South Pole never appear above the
horizon. And all the nocturnal arches of the Southern parallels of
declination, are exactly of the same length with the diurnal arches of
the correspondent parallels of North declination.
2. Let us take a view of the globe when it is rectified for the
latitude of London, or 51½ degrees North. When the Sun is in the
tropic of ♋, the day is about 16½ hours; as he recedes from this
tropic, the days proportionably shorten, until, he arrives into ♑, and
then the days are at the shortest, being now of the same length with
the night, when the Sun was in ♋, viz. 7½ hours. The lower part of
that parallel of declination, which is 38½ degrees from the equinoctial
Northerly, just touches the horizon; and the Stars that are betwixt
this parallel and the North Pole, never set to us at London. In like
[Pg 132]
manner the upper part of the Southern parallel of 38½ degrees just
touches the horizon, and the Stars that lie betwixt this parallel and
the Southern Pole, are never visible in this latitude.
Again, let us rectify the globe for the latitude of the Arctic
Circle, we shall then find, that when the Sun is in ♋, he touches the
horizon on that day without setting, being 24 hours compleat above the
horizon; and when he is in Capricorn, he once appears in the horizon,
but does not rise in the space of 24 hours: When he is in any other
point of the ecliptic, the days are longer or shorter, according to his
distance from the tropics. All the Stars that lie between the tropic
of Cancer, and the North Pole, never set in this latitude; and those
that are between the tropic of Capricorn, and the South Pole, are
always hid below the horizon.
If we elevate the globe still higher, the circle of perpetual
Apparition will be nearer the equator, as will that of perpetual
Occultation on the other side. For example, Let us rectify the globe
for the latitude of 80 degrees North: when the Sun’s declination is 10
[Pg 133]
degrees North; he begins to turn above the horizon without setting;
and all the while he is making his progress from this point to the
tropic of ♋, and back again, he never sets. After the same manner, when
his declination is 10 degrees South, he is just seen at noon in the
horizon; and all the while he is going Southward, and back again, he
disappears, being hid just so long as before, at the opposite time of
the year he appeared visible.
Let us now bring the North Pole into the Zenith, then will the
equinoctial coincide with the horizon; and consequently all the
Northern parallels are above the horizon, and all the Southern ones
below it. Here is but one day and one night throughout the year, it
being day all the while the Sun is to the Northward of the equinoctial,
and night for the other half year. All the Stars that have North
declination, always appear above the horizon, and at the same height;
and all those that are on the other side, are never seen.
What has been here said of rectifying the globe to North latitude,
[Pg 134]
holds for the same latitude South; only that before the longest days
were, when the Sun was in ♋, the same happening now when the Sun is
in ♑; and so of the rest of the parallels, the seasons being directly
opposite to those who live in different hemispheres.
I shall again explain some things delivered above in general terms, by
particular problems.
But from what has been already said, we may first make the following
observations:
1. All places of the Earth do equally enjoy the benefit of the Sun, in
respect of time, and are equally deprived of it, the Days at one time
of the Year, being exactly equal to the Nights at the opposite season.
2. In all places of the Earth, save exactly under the Poles, the Days
and Nights are of equal length (viz. 12 hours each) when the Sun is
in the equinoctial.
3. Those who live under the equinoctial, have the days and nights of
equal lengths at all times of the year.
[Pg 135]
4. In all places between the equinoctial and the Poles, the days and
nights are never equal, but when the Sun is in the equinoctial points
♈ and ♎.
5. The nearer any place is to the equator, the less is the difference
between the length of the artificial days and nights in the said place;
and the more remote the greater.
6. To all the inhabitants lying under the same parallel of latitudes
the days and nights are of equal lengths, and that at all times of the
year.
7. The Sun is vertical twice a year to all places between the tropics;
to those under the tropics, once a year; but never any where else.
8. In all places between the Polar Circles, and the Poles, the Sun
appears some number of days without setting; and at the opposite time
of the year he is for the same length of time without rising; and the
nearer unto, or further remote from the Pole, those places are, the
longer or shorter is the Sun’s continued presence or absence from the
Pole.
[Pg 136]
9. In all places lying exactly under the Polar Circles, the Sun, when
he is in the nearest tropic, appears 24 hours without setting; and
when he is in the contrary tropic, he is for the same length of time,
without rising; but at all other times of the year, he rises and sets
there, as in other places.
10. In all places lying in the (Northern/Southern) hemisphere,
the longest day and shortest night, is when the Sun is in the
(Northern/Southern) tropic, and on the contrary.
Prob. XVIII. The Latitude
of any place, not exceeding 66½ degrees, and the day of the Month being given;
to find the time of Sun-rising and setting, and the length of the Day and Night.
Having rectified the globe according to the latitude, bring the Sun’s
place to the meridian, and put the hour index to 12 at noon; then bring
the Sun’s place the Eastern part of the horizon, and the index will
shew the time when the Sun rises. Again, turn the globe until the Sun’s
place be brought to the Western side of the horizon, and the index will
shew the time of Sun-setting.
[Pg 137]
The hour of Sun-setting doubled, gives the length of the day; and the
hour of Sun-rising doubled, gives the length of the night.
Let it be required to find when the Sun rises and sets at London on
the 20th of April. Rectify the globe for the latitude of London,
and having found the Sun’s place corresponding to May the 1st, viz.
♉ 10¾ degrees, bring ♉ to 10¾ degrees to the meridian, and set the
index to 12 at noon; then turn the globe about ’till ♉ 10¾ degrees be
brought to the Eastern part of the horizon, and you’ll find the index
point 4¾ hours, this being doubled, gives the length of the night 9½
hours. Again, bring the Sun’s place to the Western part of the horizon,
and the index will point 7¼ hours, which is the time of Sun-setting;
this being doubled, gives the length of the day 14½ hours.
Prob. XIX. To find
the length of the longest and shortest Day and Night in any given
place, not exceeding 66½ degrees of Latitude.
Note, The longest day at all places on the (North/South)
[Pg 138]
side of the equator, is when the Sun is in the first point of
(Cancer/Capricorn) Wherefore having rectified the globe for
the latitude, find the time of Sun-rising and setting, and thence the
length of the day and night, as in the last problem,
according to the place of the Sun: Or, having rectified the globe for the latitude,
bring the solstitial point of that hemisphere, to the East part of
the horizon, and set the index to 12 at noon; then turning the globe
about ’till the said solstitial point touches the Western side of the
horizon, the number of hours from noon to the place where the index
points (being counted according to the motion of the index) is the
length of the longest day; the complement whereof to 24 hours, is the
length of the shortest night, and the reverse gives the shortest day
and the longest night.
| |
Longest Day. |
Shor. N. |
| |
Deg. |
Hours. |
Hours. |
| Thus in Lat. |
 |
45 |
15½ |
8½ |
| 51½ |
16½ |
7½ |
| 60 |
18½ |
5½ |
If from the length of the longest day, you subtract 12 hours, the
[Pg 139]
number of half hours remaining, will be the Climate: Thus that place
where the longest day is 16½ hours, lies in the 9th Climate. And by
the reverse, having the Climate, you have thereby the length of the
longest day.
Prob. XX. To find
in what Latitude the longest Day is, of any given length, less than 24
hours.
Bring the solstitial point to the meridian, and set the index to 12 at
noon; then turn the globe Westward, ’till the index points at half the
number of hours given; which being done, keep the globe from turning
round its axis, and slide the meridian up or down in the notches, ’till
the solstitial point comes to the horizon, then that elevation of the
Pole will be the latitude.
If the hours given be 16, the latitude is 49 degrees; if 20 hours, the
latitude is 63¼ degrees.
[Pg 140]
Prob. XXI. A place
being given in one of the Frigid Zones (suppose the Northern) to
find what number of Days (of 24 hours each) the Sun doth constantly
shine upon the same, how long he is absent, and also the first and last
Day of his appearance.
Having rectified the globe according to the latitude, turn it about
until some point in the first quadrant of the ecliptic (because the
latitude is North) intersects the meridian in the North point of the
horizon; and right against that point of the ecliptic on the horizon,
stands the day of the month when the longest day begins.
And if the globe be turned about ’till some point in the second
quadrant of the ecliptic cuts the meridian in the same point of the
horizon, it will shew the Sun’s place when the longest day ends,
whence the day of the month may be found, as before: Then the number
of natural days contained between the times the longest day begins and
ends is the length of the longest day required.
[Pg 141]
Again, turn the globe about, until some point in the third quadrant of
the ecliptic cuts the meridian in the South part of the horizon; that
point of the ecliptic will give the time when the longest night begins.
Lastly, turn the globe about, until some point in the fourth quadrant
of the ecliptic cuts the meridian in the South point of the horizon;
and that point of the ecliptic will be the place of the Sun when the
longest night ends.
Or, the time when the longest day or night begins, being known, their
end may be found by counting the number of days from that time to the
succeeding solstice; then counting the same number of days from the
solstitial day, will give the time when it ends.
Prob. XXII. To find
in what Latitude the longest Day is, of any given length less than 182
Natural Days.
Find a point in the ecliptic half so many degrees distant from the
solstitial point, as there are days given, and bring that point to the
[Pg 142]
meridian; then keep the globe from turning round its axis, and move the
meridian up or down until the aforesaid point of the ecliptic comes to
the horizon; that elevation of the Pole will be the latitude required.
If the days given were 78, the latitude is 71½ degrees.
This method is not accurate, because the degrees in the ecliptic do not
correspond to natural days; and also because the Sun does not always
move in the ecliptic at the same rate; however, such problems as these
may serve for amusements.
Prob. XXIII. The
day of the Month being given, to find when the Morning and Evening
Twilight begins and ends, in any place upon the Globe.
In the foregoing problem, by the length of the day,
we mean the time from Sun-rising to Sun-set; and the night we reckoned from Sun-set,
’till he rose next morning. But it is found by experience, that Total
Darkness does not commence in the evening, ’till the Sun has got 18
degrees below the horizon; and when he comes within the same distance
[Pg 143]
of the horizon next morning, we have the first Dawn of Day. This
faint light which we have in the morning and evening, before and after
the Sun’s rising and setting, is what we call the Twilight.
[4]
Having rectified the globe for the latitude, the zenith, and the
Sun’s place, turn the globe and the quadrant of altitude until the
Sun’s place cuts 18 degrees below the horizon (if the quadrant reaches
so far) then the index upon the hour circle will shew the beginning or
ending of twilight after the same manner as before we found the time
of the Sun-rising and setting, in Prob. 18. But by
reason of the thickness of the wooden horizon, we can’t conveniently see, or compute
when the Sun’s place is brought to the point aforesaid. Wherefore the
globe being rectified as above directed, turn the globe, and also the
quadrant of altitude, Westward, until that point in the ecliptic, which
is opposite to the Sun’s place, cuts the quadrant in the 18th degree
above the horizon; then the hour index will shew the time when day
breaks in the morning. And if you turn the globe and the quadrant of
[Pg 144]
altitude, until the point opposite to the Sun’s place cuts the quadrant
in the Eastern hemisphere, the hour hand will shew when twilight ends
in the evening. Or, having found the time from midnight when the
morning twilight begins, if you reckon so many hours before midnight,
it will give the time when the evening twilight ends. Having found the
time when twilight begins in the morning, find the time of Sun-rising,
by Prob. 18, and the difference will
be the duration of twilight.
Thus at London on the 12th of May twilight begins at three quarters
past one o’clock: The Sun rises at about half an hour past four: Whence
the duration of twilight now is 2¾ hours, both in the morning and
evening. On the 12th of November, the twilight begins at half an hour
past six, being somewhat above an hour before Sun-rising.
Prob. XXIV. To find
the time when total Darkness ceases, or when the Twilight continues
from Sun-setting to Sun-setting, in any given place.
Let the place be in the Northern hemisphere; then if the complement of
[Pg 145]
the latitude be greater than (the depression) 18 degrees, subtract 18
degrees from it, and the remainder will be the Sun’s declination North,
when total darkness ceases. But if the complement of the latitude is
less than 18 degrees, their difference will be the Sun’s declination
South, when the twilight begins to continue all night. If the latitude
is South, the only difference will be, that the Sun’s declination will
be on the contrary side.
Thus at London, when the Sun’s declination North is greater than
20½ degrees, there is no total darkness, but constant twilight, which
happens from the 26th of May to the 18th of July, being near two
months. Under the North Pole the twilight ceases, when the Sun’s
declination is greater than 18 degrees South, which is from the 13th
of November, ’till the 29th of January: So that notwithstanding
the Sun is absent in this part of the world for half a year together,
yet total darkness does not continue above 11 weeks; and besides,
the Moon is above the horizon for a whole fortnight of every month
throughout the year.
[Pg 146]
Prob. XXV. The day
of the Month be given; to find those places of the Frigid Zones, where
the Sun begins to shine continually without setting; and also those
places where he begins to be totally absent.
Bring the Sun’s place to the meridian, and mark the number of degrees
contained betwixt that point and the equator; then count the same
number of degrees from the nearest Pole (viz. the North Pole, if the
Sun’s declination is Northerly, otherwise the South Pole) towards the
equator, and note that point upon the meridian; then turn the globe
about, and all the places which pass under the said point, are those
where the Sun begins to shine constantly, without setting on the given
day. If you lay the same distance from the opposite Pole towards the
equator, and turn the globe about, all the places which pass under that
point, will be those where the longest night begins.
The Latitude of the place being given, to find the
hour of the day when the Sun shines.
[Pg 147]
If it be in the summer, elevate the Pole according to the latitude,
and set the meridian due North and South; then the shadow of the axis
will cut the hour on the Dial plate: For the globe being rectified in
this manner, the hour circle is a true Equinoctial Dial; the axis of
the globe being the Gnomon. This holds true in Theory, but it
might not be very accurate in practice, because of the difficulty in placing
the horizon of the globe truly horizontal, and its meridian due North
and South.
If it be in the winter half year, elevate the South Pole according
to the latitude North, and let the North part of the horizon be in
the South part of the meridian; then the shade of the axis will show
the hour of the day as before: But this cannot be so conveniently
performed, tho’ the reason is the same as in the former case.
To find the Sun’s altitude, when it shines, by the Globe.
Having set the frame of the globe truly horizontal or level, turn the
North Pole towards the Sun, and move the meridian up or down in the
[Pg 148]
notches, until the axis casts no shadow; then the arch of the meridian,
contained betwixt the Pole and the horizon, is the Sun’s altitude.
Note, The best way to find the Sun’s altitude, is by
a little quadrant graduated into degrees, and having sights and a plummet to it:
Thus, hold the quadrant in your hand, so as the rays of the Sun may
pass through both the sights, the plummet then hanging freely by the
side of the instrument, will cut in the limb the altitude required.
These quadrants are to be had at the instrument-makers, with lines
drawn upon them, for finding the hour of the day, and the azimuth; with
several other pretty conclusions, very entertaining for beginners.
The Latitude and the Day of the Month being given,
to find the hour of the day when the Sun shines.
Having placed the wooden frame upon a level, and the meridian due
North and South, rectify the globe for the latitude, and fix a needle
perpendicularly over the Sun’s place: The Sun’s place being brought to
[Pg 149]
the meridian, set the hour index at 12 at noon, then turn the globe
about until the needle points exactly to the Sun, and casts no shadow,
and then the index will shew the hour of the day.
Prob. XXVI. The
Latitude, the Sun’s Place, and his Altitude, being given; to find the
hour of the Day, and the Sun’s Azimuth from the Meridian.
Having rectified the globe for the latitude, the zenith, and the Sun’s
place, turn the globe and the quadrant of altitude, so that the Sun’s
place may cut the given degree of altitude: then the index will show
the hour, and the quadrant will cut the azimuth in the horizon. Thus,
if at London, on the 21st of August, the Suns altitude, be 36
degrees in the forenoon, the hour of the day will be IX, and the Sun’s
azimuth about 58 degrees from the South part of the meridian.
The Sun’s Azimuth being given, to place the
Meridian of the Globe due North and South, or to find a Meridian Line
when the Sun shines.
[Pg 150]
Let the Sun’s azimuth be 30 degrees South-Easterly, set the horizon of
the globe upon a level, and bring the North Pole into the zenith; then
turn the horizon about until the shade of the axis cuts as many hours
as is equivalent to the azimuth (allowing 15 degrees to an hour) in
the North-West part of the hour circle, viz. X at night, which being
done, the meridian of the globe stands in the true meridian of the
place. The globe standing in this position, if you hang two plummets
at the North and South points of the wooden horizon, and draw a line
betwixt them, you will have a meridian line; which if it be on a fixed
plane (as a floor or window) it will be a guide for placing the globe
due North and South, at any other time.
Prob. XXVII. The
Latitude, Hour of the Day, and the Sun’s place being given, to find the
Sun’s Altitude and Azimuth.
Rectify the globe for the latitude, the zenith, and the Sun’s place,
then the number of degrees contained betwixt the Sun’s place and the
[Pg 151]
vertex, is the Sun’s meridional zenith distance; the complement of
which to 90 degrees, is the Sun’s meridian altitude. If you turn the
globe about until the index points to any other given hour, then
bringing the quadrant of altitude to cut the Sun’s place, you will
have the Sun’s altitude at that hour; and where the quadrant cuts the
horizon, is the Sun’s azimuth at the same time. Thus May the 1st at
London, the Sun’s meridian altitude will be 61½ degrees; and at 10
o’clock in the morning, the Sun’s altitude will be 52 degrees, and his
azimuth about 50 degrees from the South part of the meridian.
Prob. XXVIII. The
Latitude of the place, and the day of the Month being given; to find
the depression of the Sun below the Horizon, and the Azimuth at any
Hour of the Night.
Having rectified the globe for the latitude, the zenith, and the Sun’s
place, take a point in the ecliptic exactly opposite to the Sun’s
place, and find the Sun’s altitude and azimuth, as by the last problem,
and these will be the depression and the altitude required. Thus, if
the time given be the 1st of December, at 10 o’clock at night, the
[Pg 152]
depression and azimuth will be the same as was found in the last problem.
Prob. XXIX. The
Latitude, the Sun’s Place, and his Azimuth being given, to find his
Altitude, and the Hour.
Rectify the globe for the latitude, the zenith, and the Sun’s place,
then put the quadrant of altitude to the Sun’s azimuth in the horizon,
and turn the globe ’till the Sun’s place meet the edge of the quadrant,
then the said edge will shew the altitude, and the index point to
the hour. Thus, May the 21st at London when the Sun is due East,
his altitude will be about 24 degrees, and the hour about VII in
the morning; and when his azimuth is 60 degrees South-Westerly, the
altitude will be about 44½ degrees, and the hour about 2¾ in the
afternoon.
Thus, the latitude and the day being known, and having besides either
the altitude, the azimuth, or the hour; the other two may be easily found.
Prob. XXX. The
Latitude, the Sun’s Altitude, and his Azimuth being given; to find his
Place in the Ecliptic and the Hour.
[Pg 153]
Rectify the globe for the latitude and zenith, and set the edge of the
quadrant to the given azimuth; then turning the globe about, that point
of the ecliptic which cuts the altitude, will be the Sun’s place. Keep
the quadrant of the altitude in the same position, and having brought
the Sun’s place to the meridian, and the hour index to 12 at noon, turn
the globe about ’till the Sun’s place cuts the quadrant of altitude,
and then the index will point the hour of the day.
Prob. XXXI. The
Declination and Meridian Altitude of the Sun, or of any Star being
given; to find the Latitude of the Place.
Mark the point of declination upon the meridian, according as it is
either North or South from the equator; then slide the meridian up or
down in the notches, ’till the point of declination be so far distant
from the horizon, as is the given meridian altitude; that elevation of
the Pole will be the latitude.
Thus, if the Sun’s, or any Star’s meridian altitude be 50 degrees, and
[Pg 154]
its declination 11½ degrees North, the latitude will be 51½ degrees North.
Prob. XXXII. The Day
and Hour of a Lunar Eclipse being known; to find all those Places upon
the Globe where the same will be visible.
[5]
Find where the Sun is vertical at the given hour, and bring that
point to the zenith; then the Eclipse will be visible in all those
places that are under the horizon; Or, if you bring the Antipodes to
the place where the Sun is vertical, into the zenith, you will have the
places where the Eclipse will be visible above the horizon.
Note, Because Lunar eclipses continue
sometimes for a long while together, they may be seen in more places
than one hemisphere of the Earth; for by the Earth’s motion round its
axis, during the time of the eclipse, the Moon will rise in several
places after the eclipse began.
Note, When an eclipse of the Sun is central,
if you bring the place where the Sun is vertical at that time, into
the zenith, some part of [Pg 155] the eclipse will be visible in most
places within the upper hemisphere; but by reason of the short duration
of Solar eclipses, and the latitude which the Moon commonly has at that
time (tho’ but small) there is no certainty in determining the places
where those eclipses will be visible by the globe; but recourse must be
had to calculations.
Prob. XXXIII.
The Day of the Month, and Hour of the Day, according to our way of
reckoning in England, being given; to find thereby the Babylonic,
Italic, and the Jewish, or Judaical Hour.
1. To find the Babylonic Hour (which is the number of hours from
Sun-rising.) Having found the time of Sun-rising in the given place,
the difference betwixt this and the hour given, is the Babylonic Hour.
2. To find the Italic Hour (which is the number of hours from
Sun-setting.) Subtract the hour of Sun-setting from the given hour, and
the remainder will be the Italic Hour required.
3. To find the Jewish Hour (which is ¹/₁₂ part of an Artificial Day.)
[Pg 156]
Find how many hours the day consists of; then say, as the number
of hours the day consists of is to 12 hours, so is the hour since
Sun-rising to the Judaical hour required.
Thus, if the Sun rises at 4 o’clock (consequently sets at 8) and the
hour given be 5 in the evening, the Babylonish hour will be the 13th,
the Italic the 21st and the Jewish hour will be nine and three
quarters.
The converse being given, the hour of the day, according to our way of
reckoning in England, may be easily found.
The following Problems are peculiar to the Celestial Globe.
Prob. XXXIV. To
find the Right Ascension and Declination of the Sun, or any Fixed Star.
Bring the Sun’s place in the ecliptic to the meridian; then that degree
of the equator, which is cut by the meridian, will be the Sun’s Right
Ascension; and that degree of the meridian, which is exactly over the
Sun’s place, is the Sun’s Declination.
[Pg 157]
After the same manner, bring the place of any Fixed Star to the
meridian, and you will find its Right Ascension in the equinoctial, and
Declination of the meridian.
Thus, the right ascension and declination is found, after the same manner
as the longitude and latitude of a place upon the Terrestrial Globe.
Note, The right ascension and declination of the Sun vary
every day; but the right ascension, &c. of the Fixed Stars is the same
throughout the year[6].
| The Sun’s Right Ascension. |
Declin. |
| |
Deg. |
Deg. |
| Thus on |
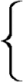 |
January 31 |
314 |
17⅓ S. |
| April 5 |
14¼ |
6 N. |
| July 21 |
120¼ |
20½ N. |
| November 26 |
242¼ |
21 S. |
| |
| R. |
Asc. |
Dcl. |
| |
Deg. |
Deg. |
| Aldebaran |
65 |
16 N. |
| Spica Virginis |
197¾ |
9¾ S. |
| Capella |
74 |
45⅔ |
| Syrius, or the Dog-Star |
98¼ |
16⅓ |
[Pg 158]
Note, The declination of the Sun may be found after the
same manner by the Terrestrial Globe, and also his right ascension, when the
equinoctial is numbered into 360 degrees, commencing at the equinoctial
point ♈: But as the equinoctial is not always numbered so, and this being
properly a Problem in Astronomy, we choose rather to place it here.
By the converse of this problem, having the right ascension and
declination of any point given, that point itself may be easily found
upon the globe.
Prob. XXXV. To find
the Longitude and Latitude of a given Star.
Having brought the solstitial colure to the meridian, fix the quadrant
of altitude over the proper Pole of the ecliptic, whether it be North
or South; then turn the quadrant over the given Star, and the arch
contained betwixt the Star and the ecliptic, will be the latitude, and
the degree cut on the ecliptic will be the Star’s longitude.
Thus the latitude of Arcturus will be found to be 31 degrees North,
[Pg 159]
and the longitude 200 degrees from ♈, or 20 degrees from ♎: The
latitude of Fomalhaut in the Southern Fish, 21 degrees South, and
longitude 299½ degrees, or ♑ 29½ degrees. By the converse of this
method, having the latitude and longitude of a Star given, it will be
easy to find the Star upon the globe.
The distance betwixt two Stars, or the number of degrees contained
betwixt them, may be found by laying the quadrant of altitude over each
of them, and counting the number of degrees intercepted; after the same
manner as we found the distance betwixt two places on the Terrestrial
Globe, in Prob. VII.
Prob. XXXVI. The Latitude
of the Place, the Day of the Month, and the Hour being given; to find
what Stars are then rising or setting, what Stars are culminating, or
on the meridian, and the Altitude and Azimuth of any Star above the
Horizon; and also how to distinguish the Stars in the Heavens one from
the other, and to know them by their proper Names.
[Pg 160]
Having rectified the globe for the latitude, the zenith, and the Sun’s
place, turn the globe about until the index points to the given hour,
the globe being kept in this position.
All those Stars that are in (Eastern/Western) side of the horizon,
are then (Rising/Setting).
All those Stars that are under the meridian, are then culminating. And
if the quadrant of altitude be laid over the center of any particular
Star, it will show that Star’s altitude at that time; and where it cuts
the horizon, will be the Star’s azimuth from the North or South part of
the meridian.
The globe being kept in the same elevation, and from turning round its
axis, move the wooden frame about until the North and South points of
the horizon lie exactly in the meridian; then right lines imagined to
pass from the center thro’ each Star upon the surface of the globe,
will point out the real Star in the heavens, which those on the globe
are made to represent. And if you are by the side of some wall whose
[Pg 161]
bearing you know, lay the quadrant of altitude to that bearing in the
horizon, and it will cut all those Stars which at that very time are
to be seen in the same direction, or close by the side of the said
wall. Thus knowing some of the remarkable Stars in any part of the
heavens, the neighbouring Stars may be distinguished by observing their
situations with respect to those that are already known, and comparing
them with the Stars drawn upon the globe.
Thus, if you turn your face towards the North, you will find the North
Pole of the globe points to the Pole Star; then you may observe two
Stars somewhat less bright than the Pole Star, almost in a right line
with it, and four more which form a sort of quadrangle; these seven
Stars make the constellation called the Little Bear; the Pole-Star
being in the tip of the tail. In this neighbourhood you will observe
seven bright Stars, which are commonly called Charles’s Wane; these
are the bright Stars in the Great Bear, and form much such another
figure with those before-mentioned in the little Bear: The two
foremost of the square lie almost in a right line with the Pole Star,
[Pg 162]
and are called the Pointers, so that knowing the Pointers, you
may easily find the Pole Star. Thus the rest of the Stars in this
constellation, and all the Stars in the neighbouring constellations
may be easily found, by observing how the unknown Stars lie either in
quadrangles, triangles, or strait lines from those that
are already known upon the globe.
After the same manner the globe being rectified, you may distinguish
those Stars that are to the Southward of you, and be soon acquainted
with all the Stars that are visible in our hemisphere.
SCHOLIUM.
The globe being rectified to the latitude of any
place, if you turn it round its axis, all those Stars that do not go
below the horizon during a whole revolution of the globe, never set in
that place; and those that do not come above the horizon never rise.
Prob. XXXVII. The
latitude of the place being given; to find the Amplitude, Oblique
Ascension and Descension, Ascensional Difference, Semi-diurnal Arch,
and the time of continuance above the horizon, of any given point in
the heavens.
[Pg 163]
Having rectified the globe for the latitude, and brought the given
point to the meridian, set the index to the hour of 12; then turn the
globe until the given point be brought to the Eastern side of the
horizon, and that degree of the equinoctial which is cut by the horizon
at that time, will be the Oblique Ascension; and where the given
point cuts the horizon, is the Amplitude Ortive: If the globe be
turned about until the given point be brought to the Western side of
the horizon, it will there show the Amplitude Occasive; and where the
horizon cuts the equinoctial at that time, is the Oblique Descension.
The time between the index at either of these two positions, and the
hour of 6; or half the difference between the oblique ascension and
descension is the Ascensional Difference.
If the place be in North latitude and the declination of the given
point be (North/South) the ascensional difference reduced into time,
and (added to/subtracted from) 6 o’Clock, gives the Semi-diurnal Arch;
[Pg 164]
the complement whereof to a semicircle, is the Semi-nocturnal
Arch. If the place be in South latitude, then the contrary is to be
observed with respect to the declination.
The semi-(diurnal/nocturnal) arch being doubled, gives the time of
continuance (above/below) the horizon. Or the time of continuance above
the horizon, may be found by counting the number of hours contained in
the upper part of the horary circle, betwixt the place where the index
pointed when the given point was in the Eastern or Western parts of
the horizon. If the given point was the Sun’s place, the index pointed
the time of his rising and setting, when the said place was in the
Eastern and Western parts of the horizon, as in Prob. 18.
Or the time of Sun-rising may be found by adding or subtracting his ascensional
difference, to or from the hour of six, according as the latitude and
declination are either contrary or the same way.
Thus, at London, on the 31st of May, the Sun’s
[Pg 165]
- Amplitude is 24 degrees Northerly.
- Oblique Ascension, 20.
- Oblique Descension, 58.
- Ascensional Difference, 19.
- Semi-diurnal Arch, 109.
- His continuance above the horizon, 14½ hours.
- Sun rises at three quarters past four.
- Sun sets a quarter past seven.
These things for the Sun vary every day; but for a Fixed Star the day
of the month need not be given, for they are the same all the year round.
- In the latitude of 51½ North,
- Syrus’s Amplitude is about 28 degrees Southerly.
- Oblique Ascension, 121.
- Oblique Descension, 75.
- Ascensional Difference, 23.
- Semi-diurnal Arch, 67.
- Continuance above the horizon, 9 hours.
Prob. XXXVIII. The
Latitude and the Day of the Month being given; to find the Hour when
any known Star will be upon the meridian, and also the time of its
rising and setting.
Having rectified the globe for the latitude of the Sun’s place, bring
[Pg 166]
the given Star to the meridian, and also to the East or West side
of the horizon, and the index will shew accordingly when the Star
culminates, or the time of the rising or setting.
Thus at London, on the 21st of January, Syrius will be
upon the meridian, at a quarter past ten in the evening; rises at 5¼
hours, and sets at three quarters past two in the morning.
By the converse of this problem, knowing the time when any Star is upon
the meridian, you may easily find the Sun’s place. Thus, bring the
given Star to the meridian, and set the index to the given hour; then
turn the globe ’till the index points to 12 at noon, and the meridian
will cut the Sun’s place in the ecliptic. Thus when Syrius comes to
the meridian at 10½ hours after noon, the Sun’s place will be ≈ ¼ deg.
Prob. XXXIX. To
find at what time of the Year a given Star will be upon the Meridian,
at a given Hour of the Night.
Bring the Star to the meridian, and set the index to the given hour,
[Pg 167]
then turn he globe ’till the index points to 12 at noon, and the
meridian will cut the ecliptic in the Sun’s place; whence the day of
the month may be easily found in the kalendar upon the horizon.
Prob. XL. The Day
of the Month, and the Azimuth of any known Star being given; to find
the Hour of the Night.
Having rectified the globe for the latitude and the Sun’s place, if
the given Star be due North or South, bring it to the meridian, and
the index will show the hour of the night. If the Star be in any other
direction, fix the quadrant of altitude in the zenith, and set it to
the Star’s azimuth in the horizon; then turn the globe about until the
quadrant cuts the center of the Star, and the index will shew the hour
of the night.
The bearing of any point in the heavens may be found by the following
methods.
Having a meridian line drawn in two windows, that are opposite to
one another, you may cross it at right angles with another line
representing the East and West; from the point of the intersection
[Pg 168]
describe a circle, and divide each quadrant into 90 degrees; then get
a smooth board, of about 2 feet long, and ¾ foot broad (more or less,
as you judge convenient) and on the back part of it fix another small
board crossways, so that it may serve as a foot to support the biggest
board upright, when it is set upon a level, or an horizontal plane. The
board being thus prepared, set the lower edge of the smooth, or fore
side of it, close to the center of the circle, then turn it about to
the meridian, or to any azimuth point required (keeping the edge of it
always close to the center) and casting your eye along the flat side of
it, you will easily perceive what Stars are upon the meridian, or any
other bearing that the board is set to.
Prob. XLI. Two
known Stars having the same Azimuth, or the same Height, being given;
to find the Hour of the Night.
Rectify the globe for the latitude, the zenith, and the Sun’s place.
1. When the two Stars are in the same azimuth, turn the globe, and also
the quadrant about, until both Stars coincide with the edge thereof;
[Pg 169]
then will the index shew the hour of the night; and where the quadrant
cuts the horizon, is the common azimuth of both Stars.
2. If the two Stars are of the same altitude, move the globe so that
the same degree on the quadrant will cut both Stars, then the index
will shew the hour.
This problem is useful when the quantity of the azimuth of the two
Stars in the first case, or of their altitude in the latter case, is
not known.
If two Stars were given, one on the meridian,
and the other in the East or West part of the horizon; to find the Latitude.
Bring that Star which was observed on the meridian, to the meridian of
the globe, and keep the globe from turning round its axis; then slide
the meridian up or down in the notches, ’till the other Star is brought
to the East or West part of the horizon, and that elevation of the Pole
will be the Latitude sought.
Prob. XLII. The Latitude,
Day of the Month, and the Altitude of any known Star being given; to
find the Hour of the Night.
[Pg 170]
Rectify the globe for the latitude, zenith, and Sun’s place: Turn the
globe, and the quadrant of altitude, backward or forward, ’till the
center of that Star meets the quadrant in the degree of altitude given;
then the index will point the true hour of the night; and also where
the quadrant cuts the horizon, will be the azimuth of the Star at that time.
If the Latitude, the Sun’s Altitude, and his
Declination (instead of his Place in the Ecliptic) are given; to find
the Hour of the Day and Azimuth.
Rectify the globe for the latitude and zenith, and having brought
the equinoctial colure to the meridian, set the index to 12 at
noon; which being done, turn the globe and the quadrant, until the
given declination in the equinoctial colure, cuts the altitude on the
quadrant; then the index will shew the Hour of the day, and the
quadrant cut the Azimuth in the horizon.
If the Altitude of two Stars on the same Azimuth
were given; to find the Latitude of the Place.
[Pg 171]
Set the quadrant over both Stars at the observed degrees of altitude,
and keep it fast upon the globe with your fingers; then slide the
meridian up or down in the notches, ’till the quadrant cuts the given
azimuth in the horizon; that elevation of the Pole will be the latitude
required.
Prob. XLIII. Having
the Latitude of the place, to find the degree of the Ecliptic, which
rises or sets with a given Star; and from thence to determine the time
of its Cosmical and Achronical rising and setting.
Having rectified the globe for the latitude, bring the given Star to
the Eastern side of the horizon, and mark what degree of the ecliptic
rises with it: Look for that degree in the wooden horizon, and right
against it, in the kalendar, you will find the month and day when the
Star rises Cosmically. If you bring the Star to the Western side of
the horizon, that degree of the ecliptic which rises at that time, will
give the day of the month when the said Star sets Cosmically. So
likewise against the degree which sets with the Star, you will find the
[Pg 172]
day of the month of the Achronical setting; and if you bring it to
the Eastern part of the horizon, that degree which sets at that time
will be the Sun’s place when the Star rises Achronically.
Thus, in the latitude of London, Syrius, or the Dog-Star, rises
Cosmically the 10th of August, and sets Cosmically the 10th of
October. Aldebaran, or the Bull’s Eye, rises Achronically on
the 22d of May, and sets Achronically on the 19th of December.
Prob. XLIV. Having the
Latitude of the place, to find the time when a Star rises and sets Heliacally.
Having rectified the globe for the latitude, bring the Star to the
Eastern side of the horizon, and turn the quadrant round to the Western
side, ’till it cuts the ecliptic in 12 degrees of altitude above the
horizon, if the Star be of the first magnitude; then that point of the
ecliptic which is cut by the quadrant, is 12 degrees high above the
Western part of the horizon, when the Star rises; but at the same time
the opposite point in the ecliptic is 12 degrees below the Eastern
part of the horizon, which is the depression of a Star of the
[Pg 173]
first magnitude, when she rises Heliacally; or has got so far
from the Sun’s beams, that she may be seen in the morning before Sun-rising.
Wherefore look for the said point of the ecliptic on the horizon, and
right against it will be the day of the month when the Star rises
Heliacally. To find the Heliacal setting, bring the Star to the
West side of the horizon, and turn the quadrant about to the Eastern side,
’till the 12th degree of it above the horizon, cuts the ecliptic; then
that degree of the ecliptic which is opposite to this point, is the
Sun’s place when the Star sets Heliacally.
Thus you will find that Arcturus rises Heliacally the 28th of
September, and sets Heliacally December the 2d.
Prob. XLV. To find
the place of any Planet upon the globe; and so by that means, to find
its place in the Heavens: Also to find at what Hour any Planet will
rise or set, or be on the meridian at any one Day in the Year.
You must first seek in an Ephemeris (White’s Ephemeris will do well
enough) for the place of the Planet proposed on that day; then mark
[Pg 174]
that point of the ecliptic, either with chalk, or by sticking on
a little black patch; and then for that night you may perform any
problem, as before, by a Fixed Star.
Let it be required to find the situation of Jupiter among the Fixed
Stars in the heavens, and also what time he rises and sets, and comes
to the meridian on the 19th of May, 1757, N. S. at London.
Looking for the 19th of May, 1757, in White’s Ephemeris, I find
that Jupiter’s place at that time is in about 12 degrees of ♏;
latitude about 1¼ degree North. Then looking for that point upon the
Celestial globe, I find that ♃ is then nearly in conjunction with the
bright Star in the Southern Balance, and about 1 degree North of it.
To find when he rises and sets, and comes to the meridian: Having put
a little black patch on the place of Jupiter, elevate the globe
according to the latitude, and having brought the Sun’s place to the
meridian, set the hour index to 12 at noon; then turn the mark which
was made for Jupiter, to the Eastern part of the horizon, I find ♃
will rise somewhat more than half an hour after three in the afternoon;
[Pg 175]
and turning the globe about, I find it comes to the meridian a little
before eleven at night; and sets almost a quarter past six next morning.
This example being understood, it will be easy to find when either of
the other two superior Planets, viz. Mars and Saturn, rise, set,
and come to the meridian.
I shall conclude this subject about the Globes with the following
problems.
Prob. XLVI. To
find all that space upon the Earth, where an Eclipse of one of the
Satellites of Jupiter will be visible.
Having found that place upon the Earth, in which the Sun is vertical at
the time of the eclipse, by Prob. 13, elevate the
globe according to the latitude of the said place; then bring the place to the meridian,
and set the hour index to 12 at noon. If Jupiter be in consequence of
the Sun, draw a line with black lead, or the like, along the Eastern
side of the horizon, which line, will pass over all those places where
the Sun is setting at that time; then count the difference betwixt the
right ascension of the Sun, and that of Jupiter, and turn the globe
[Pg 176]
Westward, ’till the hour index points to this difference; then keep the
globe from turning round its axis, and elevate the meridian, according
to the declination of Jupiter. The globe being in this position, draw
a line along the Eastern side of the horizon; then the space between
this line, and the line before drawn, will comprehend all those places
of the Earth where Jupiter will be visible, from the setting of the
Sun, to the setting of Jupiter.
But if Jupiter be in antecedence of the Sun (i. e. rises before
him) having brought the place where the Sun is vertical, to the zenith,
and put the hour index to 12 at noon, draw a line on the Western side
of the horizon; then elevate the globe according to the declination of
Jupiter, and turn it about Eastward, until the index points to so
many hours distant from noon, as is the difference of right ascension
of the Sun and Jupiter. The globe being in this position, draw a line
along the Western side of the horizon; then the space contained between
this line, and the other last drawn, will comprehend all those places
upon the Earth where the Eclipse is visible, between the rising of the
Sun, and that of Jupiter.
[Pg 177]
The DESCRIPTION of the Great Orrery,
lately made by Mr. Thomas Wright, Mathematical
Instrument-Maker to his late Majesty, and now by
Benjamin Cole, his Successor.
The Orrery is
an Astronomical Machine, made to represent the motions of the Planets.
These machines are made of various sizes, some having more Planets than
others; but I shall here confine myself to the description of that
above-mentioned.
In the Introduction we gave a short account of the Order, Periods,
Distances, and Magnitudes of the Primary Planets; and of the
Distances and Periodical Resolutions of the Secondary Planets
round their respective Primaries. We shall here explain their
[Pg 178]
Stations, Regradations, Eclipses, Phases, &c.
but first let us take a general view of the Orrery.
The Description of the Orrery.
The frame which contains the wheel-work, &c. that regulates the whole
Machine, is made of fine ebony, and is near four feet in diameter;
the outside thereof is adorned with twelve pilasters, curiously wrought
and gilt: Between these pilasters the twelve Signs of the Zodiac are
neatly painted, with gilded frames. Above the frame is a broad ring,
supported with twelve pillars: This ring represents the Plane of the
Ecliptic, upon which there are two scales of degrees, and between
those the names and characters of the twelve Signs. Near the outside is
a scale of months and days, exactly corresponding to the Sun’s place at
noon, each day throughout the year.
Above the ecliptic stands some of the principal circles of the sphere,
according to their respective situations in the heavens, viz. N°
10, are the two Colures, divided into degrees, and half degrees;
N° 11, is one half of the Equinoctial Circle, making an angle with
the ecliptic of 23½ degrees. The Tropic of Cancer, and the
[Pg 179]
Arctic Circle, are each fixed parallel, and at their proper distance from
the equinoctial. On the Northern half of the ecliptic is a brass
semicircle, moveable upon two points fixed in ♈ and ♎: This semicircle
serves as a moveable horizon, to be put to any degree of latitude upon
the North part of the meridian. The whole machine is also so contrived,
as to be set to any latitude, without in the least affecting any of
the inside motions: For this purpose there are two strong hinges (N°
13,) fixed to the bottom frame, upon which the instrument moves, and a
strong brass arch, having holes at every degree, thro’ which a strong
pin is to be put, according to the elevation. This arch and the two
hinges, support the whole machine, when it is lifted up according to
any latitude; and the arch at other times lies conveniently under the
bottom frame.
When the machine is set to any latitude (which is easily done by two
men, each taking hold of two handles, conveniently fixed for that
purpose) set the moveable horizon to the same degree upon the meridian,
and you may form an idea of the respective altitude, or depressions of
[Pg 180]
the Planets, above or below the horizon, according to their respective
positions, with regard to the meridian.
Within the ecliptic, and nearly in the same place thereof, stands the
Sun, and all the Planets, both Primary and Secondary. The Sun (Nº
1.) stands in the middle of the whole system, upon a wire, making an
angle with the plane of the ecliptic, of about 82 degrees; which is
the inclination of the Sun’s axis, to the axis of the ecliptic. Next
to the Sun is a Small ball (Nº 2.) representing Mercury: Next to
Mercury is Venus (Nº 3.) represented by a larger ball (and both
these stand upon wires,) so that the balls themselves may be more
visibly perceived by the eye. The Earth is represented (Nº 4.) by an
ivory ball, having some of the principal meridians and parallels, and a
little sketch of a map described upon it. The wire which supports the
Earth, makes an angle with the plane of the ecliptic 66½ degrees, which
is the inclination of the Earth’s axis to that of the ecliptic. Near
the bottom of the Earth’s axis is a Dial Plate (Nº 9.) having an index
pointing to the hours of the day, as the Earth turns round its axis.
[Pg 181]
Round the Earth is a ring, supported by two small pillars, which ring
represents the Orbit of the Moon, and the division upon it answers to
the Moon’s latitude; the motion of this ring represents the motion of
the Moon’s Orbit, according to that of the Nodes. Within this ring
is the Moon (Nº 5.) having a black cap or case, which by its motion,
represents the Phases of the Moon according to her age. Without the
Orbits of the Earth and Moon is Mars (Nº 6.) The next in order to
Mars is Jupiter, and his four Moons (Nº 7); each of these moons is
supported by a crooked wire fixed in a socket, which turns about the
pillar that supports Jupiter. These satellites may be turned by the
hand to any position; and yet when the machine is put in motion, they
will all move in their proper times. The outermost of all is Saturn,
and his five Moons (Nº 8.) These moons are supported and contrived
after the same manner with those of Jupiter. The whole machine is put
into motion by turning a small winch (like the key of a clock, Nº 14.)
and all the inside work is so truly wrought, that it requires but very
small strength to put the whole motion.
[Pg 182]
Above the handle there is a cylindrical pin, which may be drawn a
little out, or pushed in, at pleasure: when it is pushed in, all the
Planets, both primary and Secondary, will move according to their
respective periods, by turning the handle: When it is drawn out, the
motions of the Satellites of Jupiter and Saturn will be stopped,
while all the rest move without interruption. This is a very good
contrivance to preserve the instrument from being clogged by the
swift motions of the wheels belonging to the Satellites of Jupiter
and Saturn, when the motions of the rest of the Planets are only
considered.
There is also a brass lamp having two convex glasses, to be put in the
room of the Sun; and also a smaller Earth and Moon, made somewhat in
proportion to their distance from each other, which may be put on at
pleasure.
The lamp turns round in the same time with the Earth, and by means of
the glasses cast a strong light upon her; and when the smaller Earth
and Moon are placed on, it will be easy to shew when either of them may
be eclipsed.
[Pg 183]
Having thus given a brief description of the outward part of this
machine, I shall next give an account of the phænomena explained by it,
when it is put into motion.
Of the Motions of the Planets in general.
Having put on the handle, push in the pin which is just above it, and
place a small black patch (or bit of wafer) upon the middle of the Sun
(for instance) right against the first degree of ♈; you may also place
patches upon Venus, Mars, and Jupiter, right against some
noted point in the ecliptic. If you lay a thread from the Sun to the first
degree of ♈, you may set a mark where it intersects the orbit of each
Planet, and that will be a help to note the time of their revolutions.
One entire turn of the handle answers to the diurnal motion of the
Earth round her axis, as may be seen by the motion of the hour index,
which is placed at the foot of the wire on which the terella is fixed.
When the index has moved the space of ten hours, you may observe that
[Pg 184]
Jupiter has made one revolution compleat round its axis; the handle
being turned until the hour index has passed over 24 days, 8 hours,
will bring the patch upon Venus to its former situation with respect
to the ecliptic, which shews that ♀ has made one entire revolution
round her axis. Mars makes one compleat revolution round its axis
in 24 hours and about 40 minutes. When the handle is turned 25½ times
round, the spot upon the Sun will point to the same degree of the
ecliptic, as it did when the instrument was first put into motion. By
observing the motions of the spots upon the surface of the Sun, and
of the Planets in the heavens, their diurnal motion was discovered;
after the same manner as we do here observe the motions of their
representatives, by that of the marks placed upon them.
If while you turn the handle you observe the Planets, you will see them
perform their motions in the same relative times as they really do
in the heavens, each making its period in the times mentioned in the
Tables, Page, 28, 27¼ turns of the handle will bring the Moon round
[Pg 185]
the Earth, which is called a Periodic Month; and all the while she
keeps the same face towards the Earth; for the Moon’s annual and
diurnal motion are performed both in the same time nearly, so that we
always see the same face or side of the Moon.
If before the instrument is put into motion, the satellites of
Jupiter and Saturn be brought into the same right line from their
respective primaries, you will see them, as you turn the handle,
immediately dispersed from one another, according to their different
celerities. Thus one turn of the handle will bring the first of
Jupiter’s Moons about ⁴/₇ part round Jupiter, while the second has
described but ²/₇ part, the third but above ¹/₇, and the fourth not
quite ¹/₁₆ part, each of its respective orbits. If you turn the handle
until the hour index has moved 18½ hours more, the first satellite will
then be brought into its former position, and so has made one entire
revolution; the second at the same time will be almost diametrically
opposite to the first, and so has made a little more than half of one
revolution; the others will be in different aspects, according to the
length of their periods, as will be plainly exhibited by the instrument.
[Pg 186]
The same observations may be made with respect to the satellites of
Saturn.
The machine is so contrived, that the handle may be turned either way;
and, if before you put it into motion, you observe the aspect (or
situation with respect to each other) of the Planets, and then turn the
handle round any number of times; the same number of revolutions being
made backwards, will bring all the Planets to their former situations.
I shall next proceed to particulars.
Of the Stations and Retrogradations of the Planets.
Retrograde Motion of the Planets.
The primary Planets, as they all turn round the Sun, at different
distances, and in different times, appear to us from the Earth to have
different motions; as sometimes they appear to move from West to East,
according to the order of the signs, which is called their Direct
Motion; then by degrees they slacken their pace, until at last they
lose all their motion, and become Stationary, or not to move at all;
[Pg 187]
that is, they appear in the same place with respect to the fixed Stars
for some time together; after which they again begin to move, but with
a contrary direction, as from East to West, which is called their
Retrograde Motion; then again they become stationary, and afterwards
reassume their direct motion. The reason of all these appearances is
very evidently shewn by the Orrery.
Of the Stations, &c. of the Inferior Planets.
We shall instance in the Planet Mercury, because his motion round the
Sun differs more from the Earth’s than that of Venus does.
When Mercury is in his superior conjunction (or when he is in a
direct line from the Earth beyond the Sun) fasten a string about the
axis of the Earth, and extend it over Mercury to the ecliptic; then
turning the handle, keep the thread all the while extended over ☿,
and you will find it move with a direct motion in the ecliptic, but
continually slower, until Mercury has the greatest elongation from
[Pg 188]
the Earth. Near this position, the thread for some time will lay over
Mercury without being moved in the ecliptic, tho’ the Earth and
Mercury both continue their progressive motion in their respective
orbits. When Mercury has got a little past this place, you will find
the thread must be moved backward in the ecliptic, beginning first
with a slow motion, and then faster by degrees, until Mercury is in
his inferior conjunction, or directly between the Earth and the Sun.
Next this position of ☿, his retrograde motion will be the swiftest;
but he still moves the same way, tho’ continually slower, ’till he has
again come to his greatest elongation, where he will appear the second
time to be stationary; after which he begins to move forward, and that
faster by degrees, until he is come to the same position with respect
to the Earth, that he was in at first. The same observations may be
made relating to the motions of Venus. In like manner the different
motions observed in the superior Planets may be also explained by the
Orrery. If you extend the thread over Jupiter, and proceed after
the same manner as before we did in regard to Mercury, you will find
that from the time Jupiter is in conjunction with the Sun, his motion
[Pg 189]
is direct, but continually slower, until the Earth is nearly in a
quadrate aspect with Jupiter, near which position Jupiter seems
to be stationary: After which he begins to move, and continually mends
his pace, until he comes in opposition to the Sun, at which time his
retrograde motion is swiftest. He still seems to go backward, but with
a slower pace, ’till the Earth and he are again in a quadrate aspect,
where Jupiter seems to have lost all his motion; after which he again
resumes his direct motion, and so proceeds faster by degrees, ’till the
Earth and he are again in opposition to each another.
These different motions observed in the Planets, are easily
illustrated, as followeth: The lesser circle round the Sun is the
orbit of Mercury, in which he performs his revolution round the
Sun, in about three months, or while the Earth is going thro’ ¼ part
of her orbit, or from A to N. The numbers 1, 2, 3, &c. in the orbit
of Mercury, show the spaces he describes in a week nearly, and the
distance AB, BC, DC, &c. in the Earth’s orbit, do likewise show her
motion in the same time. The letters A, B, C, &c. in the great orb,
are the motions of Mercury in the Heavens, as they appear from the
[Pg 190]
Earth. Now if the Earth be supposed in A, and Mercury in 12, near his
superior conjunction with the Sun; a spectator on the Earth will see ☿,
as if he were in the point of the Heavens A, and while ☿ is moving from
12 to 1, and from 1 to 2, &c. the Earth in the same time also moves
from A to B, and from B to C, &c. All which time ☿ appears in the
Heavens to move in a direct motion from A to B, and from B to C, &c.
but gradually slower, until he arrives near the point G; near this
place he appears stationary, or to stand still; and afterwards (tho’ he
still continues to move uniformly in his own orbit, with a progressive
motion) yet in the sphere of the fixed Stars he will appear to be
retrograde, or to go backwards, as from G to H, from H to I, &c.
until he has arrived near the point L, where again he will appear to be
stationary; and afterwards to move in a direct motion from L to M, and
from M to N, &c.
What has been here shewed concerning the motions of Mercury, is
also to be understood of the motions of Venus; but the conjunctions
of Venus with the Sun do not happen so often as in Mercury; for
[Pg 191]
Venus moving in a larger orbit, and much slower than Mercury, does
not so often overtake the Earth. But the retrogradations are much
greater in Venus than they are in Mercury, for the same reasons.
The innermost circle represents the Earth’s orbit, divided into 12
parts, answering to her monthly motion; the greatest circle is in the
orbit of Jupiter, which he describes in about 12 years; and therefore
the ¹/₁₂ thereof, from A to N, defines his motion, in one of our years
nearly; and the intermediate divisions, A, B, C, &c. his monthly
motion. Let us suppose the Earth to be in the point of her orbit 12,
and Jupiter in A, in his conjunction with the Sun; it is evident
that from the Earth Jupiter will be seen in the great orb, or in the
point of the Heavens A, and while the Earth is moving from 12 to 1, 2,
&c. ♃ also moves from A to B, &c. all which time he appears in
the Heavens to move with a direct motion from A to B, C, &c., until he
comes in opposition to the Earth near the point of the Heavens E, where
he appears to be stationary; after which ♃ again begins to move
[Pg 192]’
(tho’ at first with a slow pace) from E through F, H, I to K, where again he
appears to stand still, but afterwards he reassumes his direct motion
from I thro’ K, to M, &c.
From the construction of the preceding figure it appears, that when
the superior Planets are in conjunction with the Sun, their direct
motion is much quicker than at other times; and that because they
really move from West to East, while the Earth in the opposite part
of the Heavens is carried the same way, and round the same center.
This motion afterwards continually slackens until the Planet comes
almost in opposition to the Sun, when the line joining the Earth and
Planet, will continue for some time nearly parallel to itself, and so
the Planet seems from the Earth to stand still; after which, it begins
to move with a slow motion backward, until it comes into a quartile
aspect with the Sun, when again it will appear to be stationary, for
the above reasons; after that it will resume its direct motion, until
it comes into a conjunction with the Sun, then it will proceed as above
explained. Hence it also appears, that the retrogradations of the
superior Planets are much slower than their direct motions, and their
[Pg 193]
continuance much shorter; for the Planet, from its last quarter, until
it comes in opposition to the Sun, appears to move the same way with
the Earth, by whom it is then overtaken: After which it begins to go
backwards, but with a slow motion, because the Earth being in the same
part of the Heavens, and moving the same way that the Planet really
does, the apparent motion of the Planet backwards, must thereby be
lessened.
What has been here said concerning the motions of Jupiter, is also
to be understood of Mars and Saturn. But the retrogradations
of Saturn do oftener happen than those of Jupiter, because the
Earth oftener overtakes Saturn; and for the same reason, the
regressions of Jupiter do oftener happen than those of Mars. But
the retrogradations of Mars are much greater than those of Jupiter,
whose are also much greater than those of Saturn.
In either of the satellites of Jupiter or Saturn, these different
appearances in the neighbouring Worlds are much oftener seen than they
are by us in the primary Planets.
[Pg 194]
We never observe these different motions in the Moon, because she turns
round the Earth as her center; neither do we observe them in the Sun,
because he is the center of the Earth’s motion; whence the apparent
motion of the Sun always appears the same way round the Earth.
Of the Annual and Diurnal Motion of the Earth, and of
the increase and decrease of Days and Nights.
The Earth in her annual motion round the Sun, has her axis always in
the same direction, or parallel to itself; that is, if a line be drawn
parallel to the axis, while the Earth is in any point of her orbit, the
axis in all other positions of the Earth will be parallel to the said
line. This parallelism of the axis, and the simple motion of the Earth
in the ecliptic, solves all the phænomena of different seasons. These
things are very well illustrated by the Orrery.
Plate 3.
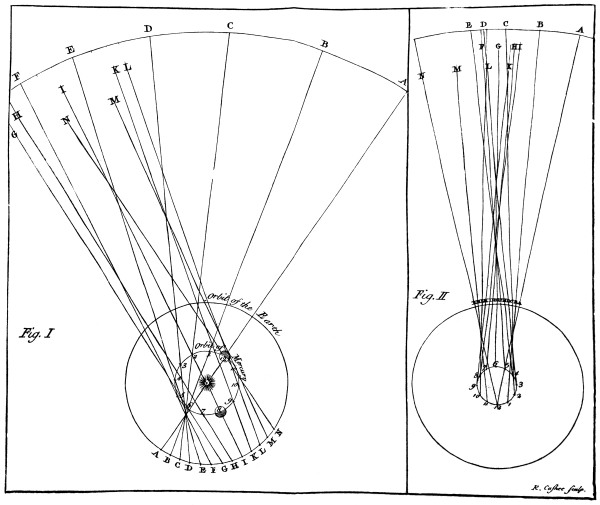
[Pg 195]
If you put on the lamp in the place of the Sun, you will see how one
half of our globe is always illuminated by the Sun, while the other
hemisphere remains in darkness; how Day and Night are formed by the
revolution of the Earth round her axis; for as she turns from West to
East, the Sun appears to move from East to West. And while the Earth
turns in her orbit, you may observe that her axis always points the
same way, and the several seasons of the year continually change.
To make these things plainer, we will take a view of the Earth in
different parts of her orbit.
When the Earth is in the first point of Libra (which is found
by extending a thread from the Sun, and over the Earth, to the ecliptic)
we have the Vernal Equinox, and the Sun at that time appears in the
first point of ♈. In this position of the Earth, two Poles of the world
are in the line separating light and darkness; and as the Earth turns
round her axis, just one half of the equator, and all its parallels,
will be in the light, and the other half in the dark; and therefore the
days and nights must be every where equal.
As the Earth moves along in her orbit, you will perceive the North Pole
[Pg 196]
advances by degrees into the illuminated hemisphere, and at the same
time the South Pole recedes into darkness; and in all places to the
Northward of the equator, the days continually lengthen, while the
contrary happens in the Southern parts, until at length the Earth is
arrived in Capricorn. In this position of the Earth all the space
included within the arctic circle falls wholly within the light, and
all the opposite part lying within the antarctic circle, is quite
involved in darkness. In all places between the equator and the arctic
circle, the days are now at the longest, and are gradually longer, as
the place are more remote from the equator. In the Southern hemisphere
there is a contrary effect. All the while the Earth is travelling from
Capricorn towards Aries, the North Pole gradually recedes from
the light, and the South Pole approaches nearer to it; the days in the
Northern hemisphere gradually decrease, and in the Southern hemisphere
they increase in the same proportion, until the Earth be arrived in
♈; then the two Poles of the world lie exactly in the line separating
light and darkness, and the days are equal to the nights in all places
of the world. As the Earth advances towards Cancer, the North Pole
[Pg 197]
gradually recedes from the light, while the Southern one advances into
it, at the same rate. In the Northern hemisphere the days decrease,
and in the Southern one they gradually lengthen, until the Earth being
arrived in Cancer, the North frigid Zone is all involved in darkness,
and the South frigid Zone falls intirely within the light; the days
every where in the Northern hemisphere are now at the shortest, and to
the Southward they are at the longest. As the Earth moves from hence
towards Libra, the North Pole gradually approaches the light, and
the other recedes from it; and in all places to the Northward of the
equator, the days now lengthen, while in the opposite hemisphere they
gradually shorten, until the Earth has gotten into ♎; in which position
the days and nights will again be of equal length in all parts of the world.
You might have observed that in all positions of the Earth, one half of
the equator was in the light, and the other half in darkness; whence
under the equator, the days and nights are always of the same length:
And all the while the Earth was going from ♎ towards ♈, the North Pole
[Pg 198]
was constantly illuminated, and the South Pole all the while in
darkness; and for the other half year, the contrary. Sometimes there
is a semicircle exactly facing the Sun, fixed over the middle of the
Earth, which may be called the horizon of the disk: This will do
instead of the lamp, if that half of the Earth which is next the Sun be
considered, as being the illuminated hemisphere, and the other half, to
be that which lies in darkness.
The great circle ♈, ♉, ♊ &c. represent the Earth’s annual orbit;
and the four lesser circles ESQC, the ecliptic, upon the surface of the
Earth, coinciding with the great ecliptic in the Heavens. These four
lesser figures represent the Earth in the four cardinal points of the
ecliptic, P being the North Pole of the equator, and p the North Pole
of the ecliptic; SPC, the solstitial colure which is always parallel to
the great solstitial colure ♋ ☉ ♑ in the Heavens; EPQ the equinoctial
colure. The other circles passing thro’ P, are meridians at two hours
distance from one another; the semicircle EÆQ is the Northern half of
the equator; the parallel circle touching the ecliptic in S, is the
tropic of Cancer; the dotted circle, the parallel of London,
[Pg 199]
and the small circle, touching the Pole of the ecliptic, is the Arctic
Circle. The shaded part, which is always opposite to the Sun, is the
obscure hemisphere, or that which lies in darkness; and that which is
next the Sun, is the illuminated hemisphere.
If we suppose the Earth in ♎, she will then see the Sun in ♈ (which
makes our vernal equinox) and in this position the circle bounding
light and darkness, which here is SC, passes thro’ the Poles of the
World, and bisects all the parallels of the equator; and therefore the
diurnal and nocturnal arches, or the length of the days and nights, are
equal in all places of the world.
But while the Earth in her annual course, moves through ♏, ♐, to ♑, the
line SC, keeping still parallel to itself, or to the place where it was
at first, the Pole P will, by this motion, gradually advance into the
illuminated hemisphere; and also the diurnal arches of the parallels
gradually increase, and consequently the nocturnal ones decrease in the
same proportion, until the Earth has arrived into ♑; in which position
[Pg 200]
the Pole P, and all the space within the arctic circle, fall wholly
within the illuminated hemisphere, and the diurnal arches of all the
parallels that are without this circle, will exceed the nocturnal
arches more or less, as the places are nearer to, or farther off from
it, until the distance from the Pole is as far as the equator, where
both these arches are always equal.
Again, while the Earth is moving from ♑ through ♒, ♓, to ♈, the Pole P
begins to incline to the line, distinguishing light and darkness, in
the same proportion that before it receded from it; and consequently
the diurnal arches gradually lessen, until the Earth has arrived into
♈ where the Pole P will again fall on the horizon, and so cause the
days and nights to be every where equal. But when the Earth has passed
♈, while she is going thro’ ♉, and ♊, &c. the Pole P will begin
to fall in the obscure hemisphere, and so recede gradually from the light,
until the Earth is arrived in ♋; in which position not only the Pole,
but all the space within the arctic circle, are involved in darkness,
and the diurnal arches of all the parallels, without the arctic circle,
are equal to the nocturnal arches of the same parallels, when the
Earth was in the opposite point ♑; and it is evident that the days are
now at the shortest, and the nights the longest. But when the Earth
has past this point, while she is going through ♌ and ♏, the Pole P
will again gradually approach the light, and so the diurnal arches of
the parallels gradually lengthen, until the Earth is arrived in ♎; at
which time the days and nights will again be equal in all places of the
World, and the Pole itself just see the Sun.
Plate 4.
[Pg 201]
Here we only considered the phænomena belonging to the Northern
parallels; but if the Pole P be made the South Pole, then all the
parallels of latitude will be parallels of South latitude, and the
days, every where, in any position of the Earth, will be equal to the
nights of those who lived in the opposite hemisphere, under the same
parallels.
Of the Phases of the Moon, and of her Motion in her Orbit.
Nodes.
Dragon’s Head.
Dragon’s Tail.
Retrograde Motion of the Nodes.
The orbit of the Moon makes an angle with the plane of the ecliptic, of
above 5¼ degrees, and cuts it into two points, diametrically opposite
[Pg 202]
(after the same manner as the equator and the ecliptic cut each other
upon the globe, in ♈ and ♎) which points are called the Nodes; and
a right line joining these points, and passing through the center of
the Earth, is called the Line of the Nodes. That node where the
Moon begins to ascend Northward above the plane of the ecliptic, is
called the Ascending Node, and the Head of the Dragon, and is thus
commonly marked [Symbol]. The other node from whence the Moon, descends
to the Southward of the ecliptic, is called the Descending Node, and
the Dragon’s Tail, and is thus marked [Symbol]. The line of nodes
continually shifts itself from East to West, contrary to the order of
the signs; and with this retrograde motion, makes one revolution
round the Earth, in the space of about 19 years.
Periodical Month.
Synodical Month.
The Moon describes its orbit round the Earth in the Space of 27 days
and 7 hours, which space of time is called a Periodical Month; yet
from one conjunction to the next, the Moon spends 29 days and a half,
which is called a Synodical Month; because while the Moon in her
proper Orbit finishes her course, the Earth advances near a whole sign
[Pg 203]
in the ecliptic; which space the Moon has still to describe, before she
will be seen in conjunction with the Sun.
When the Moon is in conjunction with the Sun, note her place in the
ecliptic; then turning the handle, you will find that 27 days and 7
hours will bring the Moon to the same place; and after you have made
2¼ revolutions more, the Moon will be exactly betwixt the Sun and the
Earth.
Phases of the Moon.
The Moon all the while keeps in her orbit, and so the wire that
Supports her continually rises or falls in a socket, as she changes her
latitude; the black cap shifts itself, and so shews the phases of the
Moon, according to her age, or how much of her enlightened part is seen
from the Earth. In one synodical month, the line of the nodes moves
about 1½ degree from West to East, and so makes one entire revolution
in 19 years.
Let AB be an arch of the Earth’s orbit, and when the Earth is in T, let
the Moon be in N, in conjunction with the Sun in S, while the Moon is
[Pg 204]
describing her orbit NAFD, the Earth will describe the arch of
her orbit T t; and when the Earth has got into the point t,
the Moon will be in the point of her orbit n, having made one
compleat revolution round the Earth. But the Moon, before she comes
in conjunction with the Sun, must again describe the arch n o;
which arch is similar to T t, because the lines FN, f n, are
parallel; and because, while the Moon describes the arch n o, the
Earth advances forward in the ecliptic; the arch described by the
Moon, after she has finished her periodical month, before she makes a
synodical month, must be somewhat greater than n o. To determine the
mean length of a synodical month, find the diurnal motion of the Moon
(or the space she describes round the Earth in one day) and likewise
the diurnal motion of the Earth; then the difference betwixt the two
motions, is the apparent motion of the Moon round the Earth in one day;
then it will be, as this differential arch is to a whole circle; so is
one day to that space of time wherein the Moon appears to describe a
compleat circle round the Earth, which is about 29½ days. But this is
not always a true Lunation, for the motion of the Moon is sometimes
[Pg 205]
faster, and sometimes slower, according to the position of the Earth in
her orbit.
In one synodical month the Moon has all manner of aspects with the
Sun and Earth, and because she is opaque, that face of hers will only
appear bright which is towards the Sun, while the opposite remains in
darkness. But the inhabitants of the Earth can only see that face of
the Moon which is turned towards the Earth; and therefore, according to
the various positions of the Moon, in respect of the Sun and Earth, we
observe different portions of her illuminated face, and so a continual
change in her[7]
Phases.
Let S be the Sun, RTV an arch of the Earth’s orbit, T the Earth, and
the circle ABCD, &c. the Moon’s orbit, in which she turns round the
Earth in the space of a month; and let A, B, C, &c. be the centers of
the Moon in different parts of her orbit.
Now if with the lines S A, S B, &c. we join the centers of the Sun and
[Pg 206]
Moon, and at right angles to these draw the lines H O; the said lines
H O will be the circles that separate the illuminated part of the Moon
from the dark and obscure. Again, if we conceive another line I L to
be drawn at right angles to the lines TA, TB, &c. passing from the
center of the Earth to the Moon, the said line I L will divide the
visible hemisphere of the Moon, or that which is turned towards us,
from the invisible, or that which is turned from us; and this circle
may be called the Circle of Vision.
Full Moon.
Half Moon.
New Moon.
Now it is manifest, that whenever the Moon is in the position A, or in
that point of her orbit which is opposite to the Sun, the circle of
vision, and the circle bounding light and darkness, do coincide, and
all the illuminated face of the Moon is turned towards the Earth, and
is visible to us; and in this position the Moon is said to be full.
But when the Moon arrives to B, all her illuminated face is then not
towards the Earth, there being a part of it, HBI, not to be seen by us;
and then her visible face is deficient from a circle, and appears of a
gibbous form, as in B. Fig. 3.
Again when she arrives to C, the two
[Pg 207]
forementioned circles cut each other at right angles, and then we
observe a half Moon, as in C, Fig. 3. And again
the illuminated face of the Moon is more and more turned from the Earth, until she
comes to the Point E, where the circle of vision, and that bounding
light and darkness, do again coincide. Here the Moon disappears, the
illuminated part being wholly turned from the Earth; and she is now
said to be in Conjunction with the Sun, because she is in the
same direction from the Earth that the Sun is in, which position we
call a New Moon. When the Moon is arrived to F, she again assumes
a horned figure, but her horns (which before the change were turned
Westward) have now changed their position, and look Eastward. When she
has arrived to a quadrate aspect at G, she will appear bissected, like
a half Moon, afterwards she will still grow bigger, until at last she
comes to A, where again she will appear in her full splendor.
The same appearances which we observe in the Moon are likewise observed
by the Lunarians in the Earth, our Earth seeing a Moon to them, as
their Moon is to us; and we are observed by them to be carried round in
[Pg 208]
the space of time that they are really carried round the Earth. But
the same phases of the Earth and Moon happen when they are in contrary
position; for when the Moon is in conjunction to us, the Earth is then
in opposition to the Moon, and the Lunarians have then a full Earth,
as we in a similar position have a full Moon. When the Moon comes in
opposition to the Sun, the Earth, seen from the Moon, will appear in
conjunction with her, and in that position the Earth will disappear;
afterwards she will assume a horned figure, and so shew the same phases
to the inhabitants of the Moon as she does to us.
Of the Eclipses of the Sun and Moon.
Eclipse.
An Eclipse is that deprivation of light in a Planet, when another
is interposed betwixt it and the Sun. Thus, an eclipse of the Sun is made
by the interposition of the Moon at her conjunction, and an eclipse
of the Moon is occasioned by the shadow of the Earth falling upon the
Moon, when she is in opposition to the Sun.
[Pg 209]
Lunar Eclipse.
Let S be the Sun, T the Earth, and ABC its shadow; now if the Moon,
when she is in opposition to the Sun, should come into the conical
space ABC, she will then be deprived of the solar light, and so undergo
an eclipse.
Solar Eclipse.
In the same manner, when the shadow of the Moon falls upon the Earth
(which can never happen but when the Moon is in conjunction with
the Sun) that part upon which the shadow falls will be involved in
darkness, and the Sun eclipsed. But because the Moon is much less than
the Earth, the shadow of the ☽ cannot cover the whole Earth, but only a
part of it. Let S be the Sun, T the Earth, ABC the Moon’s orbit, and L
the Moon in conjunction with the Sun: Here the shadow of the Moon falls
only upon the part DE of the Earth’s surface, and there only the Sun
is intirely hid: but there are other parts EF, DG, on each side of the
shadow, where the inhabitants are deprived of part of the Solar rays,
and that more or less, according to their distance from the shadow.
Those who live at H and I will see half of the Sun eclipsed, but in the
spaces FM, GN, all the Sun’s body will be visible, without any eclipse.
From the preceding figure it appears, that an eclipse of the Sun does
[Pg 210]
not reach a great way upon the superficies of the Earth; but the whole
body of the Moon may sometimes be involved in the Earth’s shadow.
Although the Moon seen from the Earth, and the Earth seen from the
Moon, are each alternately, once a month, in conjunction with the Sun;
yet, by reason of the inclination of the Moon’s orbit to the ecliptic,
the Sun is not eclipsed every new Moon, nor the Moon at every full.
Let T be the Earth, DTE an arch of the ecliptic, ALBF, the Moon’s
orbit, having the Earth T, in its center; and let AGBG be another
circle coinciding with the ecliptic, and A, B, the nodes, or the two
points where the Moon’s orbit and the ecliptic cut each other. A the
ascending node, and B the descending node. The angle GAL equal to GBL
is the inclination of the Moon’s orbit to the ecliptic, being about 5¼
degrees. Now a spectator from the Earth at T, will observe the Sun to
move in the circle AGBC, and the Moon in her orbit ALBF; whence it is
evident, that the Sun and Moon can never be seen in a direct line, from
the center of the Earth, but when the Moon is in one of the nodes A or
[Pg 211]
B; and then only will the Sun appear centrally eclipsed. But if the
conjunction of the Moon happens when she is any where within the
distance A c of the nodes, either North or South, the Sun will then
be eclipsed, more or less, according to the distance from the node A,
or B. If the conjunction happens when the Moon is in b, the Sun will
be then one half eclipsed; and if it happens when she is in c, the
Moon’s limb will just touch the Sun’s disk, without hiding any part of it.
The shadow of the Earth at the place where the Moon’s orbit intersects
it, is three times as large as the Moon’s diameter, as in Fig. 4.
and therefore it often happens that eclipses of the Moon are total, when
they are not central: And for the same reason the Moon may sometimes be
totally eclipsed for three hours together; whereas total eclipses of
the Sun can scarcely ever exceed four minutes.
The eclipses of the Sun and Moon are very well explained by the
Orrery: Thus having put the lamp in the place of the Sun, and the
[Pg 212]
little Earth and the little Moon in their proper places, instead of the
larger ones, let the room wherein the instrument stands be darkened;
then turning the handle about, you will see when the conjunction of the
Moon happens. When she is in or near one of the nodes, her shadow will
fall upon the Earth, and so deprive that part upon which it falls of
the light of the Sun: If the conjunction happens when the Moon is not
near one of the nodes, the light of the lamp will fall upon the Earth,
either above or below the Moon, according to her latitude at that time.
In like manner, when the full Moon happens near one of the nodes,
the shadow of the Earth will fall upon the Moon; and if the Moon’s
latitude be but small, her whole face will be involved in darkness. At
other times, when the full Moon happens when she is not near one of
her nodes, the shadow of the Earth will pass either above or below the
Moon, and so by that means the Moon will escape being eclipsed.
Of the Eclipses of the Satellites of Jupiter.
The apparent diameters of the inferior Planets are so small, that when
[Pg 213]
they pass betwixt us and the Sun, they only appear like small spots
upon the Sun’s surface, without depriving us of any sensible quantity
of his light. The shadow of the Earth likewise terminates before it
reaches any of the superior Planets, so that they are never eclipsed by
us; and the Earth when she is in conjunction with the Sun, only appears
like a black spot upon his surface.
But Jupiter and his Moons mutually eclipse each other, as our Earth
and Moon do; as also doth Saturn and his Moons. The satellites of
Jupiter become twice hid from us, in one circulation round ♃; viz.
once behind the body of Jupiter, i. e. when they are in the right
line joining the centers of the Earth and ♃; and again they become
invisible when they enter the shadow of Jupiter, which happens when
they are at their Full, as seen from ♃, at which times they also suffer
eclipses; which eclipses happen to them after the same manner as they
do to our Moon, by the interposition of the Earth betwixt her and the
Sun.
Let S be the Sun, ABT the Earth’s orbit; and C ♃ D, an arch of
[Pg 214]
Jupiter’s orbit, in which let Jupiter be in the point ♃; and let
CFDH be the orbit of one of Jupiter’s satellites, which we will here
suppose to be the farthest from him. These satellites, while they move
thro’ the inferior parts of their orbs, viz. from D thro’ H, I, to
C, seem from the Earth and the Sun to have a retrograde motion; but
when they are in the superior part of their orbit, they are then seen
to move from West to East, according to their true motion. Now while
they describe the superior part of their orbits, they will be twice hid
from the Earth, once in the shadow of ♃, and once behind his body. If
Jupiter be more Westerly than the Sun, that is, when the Earth is in
A, they will be first hid in the shadow F, and afterwards behind the
body of ♃ in G: But when the Earth is in B, then they are first hid
behind ♃’s body in E, and afterwards fall into the shadow F. While the
satellites describe the inferior parts of their orbit, they only once
disappear, which may be either in I or H, according to the position of
the Earth, in which places they cannot be distinguished from the body
of Jupiter.
Plate 5.

[Pg 215]
When the satellites seen from ♃ are in conjunction with the Sun, their
shadows will then fall upon ♃, and some part of his body be involved in
darkness, to which part the Sun will be totally eclipsed.
By observing the eclipses of Jupiter’s satellites, it was first
discovered that light is not propogated instantaneously, though it
moves with an incredible swiftness: For if light came to us in an
instant, an observer in T will see an eclipse of one of the satellites,
at the same time that another in K would. But it has been found by
observations, that when the Earth is in K, at her nearest distance from
Jupiter, these eclipses happen much sooner than when she is in T.
Now having the difference of time betwixt these appearances in K and
T, we may find the length of time the light takes in passing from K to
T, which space is equal to the diameter of the Earth’s annual orb. By
these kinds of observations it has been found, that light reaches from
the Sun to us in the space of eleven minutes of time, which is at least
at the rate of 100,000 miles in a second.
FINIS.
[Pg 216]
AN INDEX OF THE
Astronomical Terms
Made Use of in this BOOK.
Acronical Rising and Setting of the Stars |
Page 96 |
| Almacanthers |
63 |
| Altitudes |
ib. |
| ——— Meridian Altitude |
63 |
| Amplitude |
62 |
| Amphiscians |
91 |
| Annual Motion |
7 |
| Antœci |
92 |
| Antarctic Circle |
53 |
| ——— Pole |
ib. |
| Antipodes |
93
[Pg 217] |
| Arctic Circle |
52 |
| Arctic Pole |
53 |
| Ascension |
68 |
| ——— Right |
ib. |
| ——— Oblique |
69 |
| Ascensional Difference |
ib. |
| Ascians |
91 |
| ——— Heteroscians |
ib. |
| Asterisms |
36 |
| Atmosphere |
81 |
| Axis |
43 |
| ——— of the World |
49 |
| Azimuth |
61 |
| Babylonish Hours |
71 |
| Bissextile |
78 |
| Circle |
42 |
| ——— Great Circles |
ib. |
| ——— Parallel, or lesser Circles |
43 |
| ——— Secondary Circles |
ib. |
| Circles of the Sphere |
47 |
| Climates |
93 |
| Colures |
53 |
| ——— Equinoctial Colure |
ib. |
| ——— Solstitial Colure |
54 |
| Comets |
29 |
| Conjunction |
11, 207 |
| Constellations |
36 |
| Cosmical rising and setting of the Stars |
96 |
| Crepusculum |
83 |
| Day, Natural and Artificial |
69 |
| Declination |
52 |
| Diurnal Motion |
7
[Pg 218] |
| Diurnal Arch |
68 |
| Eclipses |
208 |
| ——— Solar |
ib. |
| ——— Lunar |
ib. |
| Eclipses of Jupiter’s Satellites |
212 |
| Ecliptic |
53 |
| Egyptian Year |
75 |
| Elongation |
18 |
| Equator, or Equinoctial |
48 |
| Equinoctial Points |
53 |
| ——— Precession of |
55 |
| ——— Vernal and Autumnal |
70 |
| Excentricity |
4 |
| Galaxy, or Milky Way |
38 |
| Geocentric Place |
19 |
| Globe |
42 |
| ——— Terrestrial |
43 |
| ——— Celestial |
44 |
| Gregorian Account |
80 |
| Heliacal rising and setting of the Stars |
96 |
| Heliocentric Place |
19 |
| Hemisphere |
42 |
| ——— Northern and Southern |
49 |
| Heteroscians |
91 |
| Horizon |
58 |
| ——— Sensible |
ib. |
| ——— Rational |
59 |
| Hour Circles |
50 |
| Italian Hours |
72 |
| Jewish Hours |
ib. |
| Julian Account |
79
[Pg 219] |
| Latitude, in Astronomy |
56 |
| ——— in Geography |
84 |
| Longitude in Astronomy |
56 |
| ——— in Geography |
87 |
| Meridian |
50, 61 |
| Nadir |
61 |
| Nodes |
3, 202 |
| Nocturnal Arch |
68 |
| Orbit |
3 |
| Parallel of the Earth’s Semidiameter |
23 |
| ——— of the Earth’s Annual Orb |
20 |
| Periœci |
92 |
| Periscians |
91 |
| Periodical Month |
74, 202 |
| Phases of the Moon |
201 |
| Planets |
1 |
| ——— Inferior and Superior |
14 |
| Planetary Hours |
72 |
| Poles |
42 |
| ——— of the World |
49 |
| ——— of the Ecliptic |
56 |
| Polar Circles |
52 |
| Points of the Compass |
60 |
| ——— Cardinal Points |
59 |
| Primary Planets |
5 |
| Retrograde Motion of the Planets |
187 |
| ——— of the Nodes |
202 |
| Secondary Planets |
5 |
| Sidereal Year |
74 |
| Signs of the Zodiac |
54
[Pg 220] |
| ——— Northern and Southern |
ib. |
| Solstices |
71 |
| ——— Summer and Winter Solstices |
ib. |
| Solstitial Points |
53 |
| Sphere |
42 |
| ——— Parallel and Right |
67 |
| ——— Oblique |
68 |
| Stationary |
186 |
| Style Old |
79 |
| ——— New Style |
80 |
| Synodical Month |
74, 202 |
| Tropics (of Cancer and Capricorn) |
52 |
| Twilights |
83 |
| Vertical Circles |
61 |
| ——— Prime Vertical |
62 |
| Zenith |
61 |
| Zenith Distance |
63 |
| Zones, Torrid, Temperate, and Frigid |
90 |
THE END
Directions to the Binder.
| The great Orrery to face the Title. |
| Plate I. |
Page 2 |
| Plate II. |
28 |
| The Globes |
35 |
| Plate III. |
194 |
| Plate IV. |
200 |
| Plate V. |
214 |
A CATALOGUE
Of Mathematical, Philosophical,
and Optical Instruments,
MADE and SOLD by
BENJAMIN COLE,
At his Shop, the Sign of the Orrery, No. 136,
in Fleet street, London.
| |
l. |
s. |
d. |
Variety of pocket
cases of Drawing Instruments, in Silver, |
from 3l. 3s. to |
20 |
0 |
0 |
| Ditto, in Brass, |
from 5s. to |
5 |
5 |
0 |
| Magazine Cases, in Silver, |
from 12l. to |
150 |
0 |
0 |
| Ditto, in Brass, |
from 5l. to |
50 |
0 |
0 |
| Circular Compasses to describe a Circle as small as a pin’s head, |
from 3s. to |
0 |
7 |
6 |
| Long Hand Drawing-pens, |
from 1s. to |
0 |
5 |
0 |
| Compasses in Brass, with shifting points, as the Ink and Black Lead points, |
from 2s. 6d. to |
1 |
1 |
0 |
| Plain Compasses, |
from 6d. to |
0 |
5 |
0 |
| Beam Compasses, for drawing large circles, |
from 12. to |
3 |
0 |
0 |
| Proportionable Compasses, |
from 1l. 1s. to |
5 |
5 |
0 |
| Triangular Compasses, |
from 14s. to |
0 |
18 |
0 |
| Elliptical Compasses, for Ovals, |
from 1l. 11s. 6d. to |
5 |
5 |
0 |
| Hair Compasses |
|
0 |
7 |
6 |
| Bows for drawing curved lines, |
from 4s. to |
0 |
10 |
6 |
| Sets of Feather-edge Scales, in Brass, Ivory, or Wood, |
from 12s. to |
1 |
16 |
0 |
| Plain ditto, or Plotting ditto, in ditto, |
from 8d. to |
0 |
18 |
0 |
| Gunter’s 2 feet, and 1 foot Scales, in Brass or Wood, |
from 2s. to |
2 |
2 |
0 |
| Protractors of all sorts, |
from 1s. 6d. to |
1 |
16 |
0 |
| Parallel Rules, from 6 to 36 inches, |
from 2s. 6d. to |
1 |
16 |
0 |
| Cross-bar ditto, in Brass, Ivory, or Wood, from 4½ inches, to 3 feet, |
from 10s. 6d. to |
3 |
0 |
0 |
| Sectors, in ditto, |
from 2s. 6d. to |
4 |
14 |
6 |
| Theodolites, |
from 3l. 3s. to |
6 |
6 |
0 |
| Ditto, with Vertical arch, Spirit Levels, Telescope, &c. |
from 10l. 10s. to |
21 |
0 |
0 |
| Plain Tables, |
from 3l. 3s. to |
5 |
5 |
0 |
| Circumferentors, the principal Instrument for Surveying in the West-Indies, |
from 1l. 16s. to |
3 |
13 |
6 |
| Gunter’s four pole chains, |
from 6s. to |
0 |
12 |
0 |
| Spirit Levels of all sorts, |
from 5s. to |
12 |
12 |
0 |
| Pentographia, for the ready and exact reduction or copying of |
|
|
|
|
| Schemes, Drawings, Prints, &c. |
|
4 |
14 |
6 |
| Measuring Wheels for Surveying, |
from 4l. 14s. 6d. to |
6 |
6 |
0 |
| Hadley’s Quadrants, with Diagonal Divisions |
|
1 |
14 |
0 |
| Ditto, with a Nonius, |
from 2l. 2s. to |
3 |
13 |
6 |
| Ditto, all in Brass, |
from 3l. 13s. 6d. to |
6 |
6 |
0 |
| Davies’s Quadrant, |
from 12s. to |
1 |
1 |
0 |
| Cole’s ditto, |
from 18s. to |
1 |
5 |
0 |
| Sutton’s ditto |
|
0 |
6 |
0 |
| Gunter’s ditto, |
from 3s. 6d. to |
1 |
1 |
0 |
| Horizontal Sun Dials, for all Latitudes, |
from 5s. to |
10 |
0 |
0 |
| Ring Dials, |
from 10s. 6d. to |
21 |
0 |
0 |
| Azimuth Compasses, |
from 5l. 5s. to |
10 |
0 |
0 |
| Amplitude ditto, |
from 1l. 7s. to |
5 |
5 |
0 |
| Mariner’s Compasses, either for the Cabin, or Binacle, |
from 7s. 6d. to |
3 |
13 |
0 |
| Pocket Compasses, |
from 1s. to |
1 |
11 |
6 |
| Large Orreries, |
from 50l. to |
250 |
0 |
0 |
| Armillary Spheres, |
from 12l. to |
50 |
0 |
0 |
| Seventeen inch Globes |
|
6 |
6 |
0 |
| Fifteen inch ditto |
|
5 |
5 |
0 |
| Twelve inch ditto |
|
3 |
3 |
0 |
| Nine inch ditto |
|
2 |
2 |
0 |
| Six inch ditto |
|
1 |
16 |
0 |
| Three inch ditto, in a case, |
from 8s. to |
0 |
10 |
0 |
| Large double Barrell’d standing air pumps |
|
25 |
0 |
0 |
| Apparatus to ditto, |
from 3l. 3s. to |
12 |
12 |
0 |
| Double Barrell’d table air pumps, with their apparatus, |
from 5l. 15s. 6d. to |
20 |
0 |
0 |
| Single Barrell’d ditto |
|
2 |
12 |
6 |
| Apparatus to ditto |
|
2 |
2 |
0 |
| Electrical Machines, in Brass, with apparatus, box, &c. |
from 5l. 5s. to |
13 |
13 |
0 |
| Barometers, |
from 1l. 1s. to |
1 |
16 |
0 |
| Ditto & Thermometer, in one frame, |
from 1. 11s. 6d. to |
2 |
12 |
6 |
| Barometer, Thermometer, and Hydrometer, all in one frame, |
from 2l 12s. 6d. to |
3 |
13 |
6 |
| Farenheit’s Thermometers, in mahogany cases, |
from 1l. 5s. to |
1 |
11 |
6 |
| Pocket ditto, in black cases, |
from 12s. to |
1 |
1 |
0 |
| Spirit Thermometers, on box scales, for hot-houses |
|
0 |
10 |
6 |
| Hydrometers, in Ivory, |
from 4s. to |
0 |
5 |
6 |
| Ditto, in copper, with weights, &c. for proving Spirits, |
from 1l. 1s. to |
1 |
5 |
0 |
| Hydrostatic Balance, with apparatus, &c. |
|
1 |
15 |
0 |
| Speaking Trumpets, |
from 10s. to |
1 |
11 |
6 |
| Hearing ditto, |
from 7s. 6d. to |
1 |
1 |
0 |
| Reflecting Telescopes, |
from 1l. 16s. to |
50 |
0 |
0 |
| Refracting ditto, of various lengths, with four or six glasses, |
from 7s. 6d. to |
6 |
6 |
0 |
| Double reflecting Microscopes, |
from 3l. 13s. 6d. to |
7 |
7 |
0 |
| Solar ditto, in Brass, |
from 4l. 4s. to |
6 |
6 |
0 |
| Wilson’s pocket ditto, |
from 1l. 5s. to |
2 |
12 |
6 |
| Opake ditto, |
from 2l. 12s. 6d. to |
3 |
13 |
6 |
| Cloth ditto, |
from 3s. 6d. to |
0 |
7 |
6 |
| Flower ditto, |
from 3s. 6d. to |
0 |
5 |
0 |
| Diagonal Machines for viewing prints, |
from 16s. to |
1 |
11 |
6 |
| Large Book Camera Obscura, |
from 4l. 4s. to |
5 |
5 |
0 |
| Box Camera Obscura, |
from 10s. 6d. to |
2 |
2 |
0 |
| Scioptric Ball and Socket, in Wood |
|
0 |
7 |
6 |
| Opera Glasses, |
from 5s. to |
2 |
12 |
6 |
| Prospect ditto, |
from 8d. to |
0 |
10 |
6 |
| Magic Lanthorn, without objects, |
from 1l. 1s. to |
1 |
7 |
0 |
| Magic Lanthorn sliders, with objects, |
from 5s. to |
0 |
10 |
6 |
| Mirrors, convex or concave, of all sizes, in black frames, |
from 10s. 6d. to |
16 |
16 |
0 |
| Prisms, |
from 6s. to |
1 |
1 |
0 |
| Reading Glasses set in a variety of curious frames, |
from 2s. 6d. to |
2 |
12 |
6 |
| Watchmaker’s Glasses, in frames, |
from 1s. to |
0 |
10 |
6 |
| Concave ditto, for short sighted persons, |
from 1s.6d. to |
2 |
2 |
0 |
| Spectacles ground on brass tools, and set in silver, tortoise shell, horn, &c. |
from 1s. to |
1 |
7 |
0 |
| Achromatic, Opera, and Prospect glasses, |
from 1l. 1s. to |
1 |
16 |
0 |
| Achromatic Telescopes of any length, at 1l. 1s. each foot. |
| Gauging Rules, Carpenter’s Rules, and all other kind of Rules, |
| at the usual Prices. |
| |
| The Eleventh Edition of Harris on the Globes, with the |
| Description and Use of the Orrery, 3s. 6d. |
| The Use of the Sector and plain Scale explained, 1s. |
| The Use of Hadley’s Quadrant explained, 6d. |
| A fine Print of the Orrery, on imperial paper, 2s. |
| A smaller ditto, 6d. |
Variety of other Instruments too tedious
to mention, are made and sold at the above place: Where any Gentleman,
by Letter, or other Directions, may depend on being as faithfully
served as if present. And as I have been long in the Wholesale part of
the Business, Merchants, &c. may be sure of being supplied on
the Best Terms. As also by M. Allison, at
Falmouth.
Transcriber’s Notes:
The cover image was created by the transcriber, and is in the public domain.
Illustrations were moved so as not to break up paragraphs.
Antiquated spellings were not corrected.
Typographical errors have been silently corrected.














