
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Populäre Vorlesung gehalten i. J. 1864 zu Graz.
Wir besprechen heute ein Thema, vielleicht von etwas allgemeinerem Interesse: die Erklärung der Harmonie der Töne. Die ersten und einfachsten Erfahrungen über die Harmonie sind uralt. Nicht so die Erklärung der Gesetze. Diese wurde erst von der neuesten Zeit geliefert. Erlauben Sie mir einen historischen Rückblick.
Schon Pythagoras (540–500 v. Chr.) wußte daß der Ton einer Saite von bestimmter Spannung in die Oktave umschlägt, wenn man die Saitenlänge auf die Hälfte, in die Quinte, wenn man sie auf zwei Dritteile verkürzt, und daß dann der erstere Grundton mit den beiden anderen konsoniert. Er wußte überhaupt, daß dieselbe Saite bei gleicher Spannung konsonierende Töne gibt, wenn man ihr nach und nach Längen erteilt, welche in sehr einfachen Zahlenverhältnissen stehen, sich etwa wie 1:2, 2:3, 3:4, 4:5, u. s. w. verhalten.
Den Grund dieser Erscheinung vermochte Pythagoras nicht zu finden. Was haben die konsonierenden Töne mit den einfachen Zahlen zu tun? So würden wir heute fragen. Pythagoras aber muß dieser Umstand weniger befremdlich als unerklärlich vorgekommen sein. Er suchte in der Naivetät der damaligen Forschung den Grund der Harmonie in dem geheimen wunderbaren Wesen der Zahlen. Dies hat wesentlich zur Entwickelung einer Zahlenmystik beigetragen, deren Spuren sich auch heute noch in den Traumbüchern finden und bei solchen Gelehrten, welche das Wunderbare der Klarheit vorziehen.
Euklides (300 v. Chr.) gab bereits eine Definition der Konsonanz und Dissonanz, wie wir sie den Worten nach heute kaum besser hinstellen könnten. Die Konsonanz zweier Töne, sagt er, sei die Mischung derselben, die Dissonanz hingegen die Unfähigkeit sich zu mischen, wodurch sie für das Gehör rauh werden. Wer die heutige Erklärung der Erscheinung kennt, hört sie sozusagen aus Euklides Worten wiederklingen. Dennoch kannte er die wahre Erklärung der Harmonie nicht. Er war der Wahrheit unbewußt sehr nahe gekommen, ohne sie jedoch wirklich zu erfassen.
Leibniz (1646–1716 n. Chr.) nahm die von seinen Vorgängern ungelöst zurückgelassene Frage wieder auf. Er wußte wohl, daß die Töne durch Schwingungen erregt werden, daß der Oktave doppelt so viele Schwingungen entsprechen als dem Grundtone. Ein leidenschaftlicher Liebhaber der Mathematik, wie er war, suchte er die Erklärung der Harmonie in dem geheimen Zählen und Vergleichen der einfachen Schwingungszahlen und in der geheimen Freude der Seele an dieser Beschäftigung. Ja, wie denn aber – werden Sie sagen – wenn jemand gar nicht ahnt, daß die Töne Schwingungen sind, dann wird wohl das Zählen und auch die Freude am Zählen so geheim sein müssen, daß kein Mensch darum weiß! Was doch die Philosophen treiben! Die langweiligste Beschäftigung, das Zählen, zum Prinzip der Ästhetik zu machen! Sie haben mit diesen Gedanken so unrecht nicht, und doch hat auch Leibniz gewiß nicht ganz Unsinniges gedacht, wenn gleich sich schwer klar machen läßt, was er unter seinem geheimen Zählen verstanden wissen wollte.
Ähnlich wie Leibniz suchte der große Euler (1707–1783) die Quelle der Harmonie in der von der Seele mit Vergnügen wahrgenommenen Ordnung unter den Schwingungszahlen.
Rameau und d' Alembert (1717 – 17S3) rückten der Wahrheit näher. Sie wußten, daß jeder musikalisch brauchbare Klang neben seinem Grundtone noch die Duodecime und die nächst höhere Terz hören lasse, daß ferner die Ähnlichkeit zwischen Grundton und Oktave allgemein auffalle. Hiernach mußte ihnen das Hinzufügen der Oktave, Quinte, Terz u. s. w. zum Grundtone als »natürlich« erscheinen. Allerdings hatten sie den richtigen Gesichtspunkt, allein mit der bloßen Natürlichkeit einer Erscheinung kann sich der Forscher nicht begnügen; denn gerade das Natürliche ist es, dessen Erklärung er sucht.
Rameaus Bemerkung schleppte sich nun durch die ganze neuere Zeit fort, ohne jedoch zur vollständigen Auffindung der Wahrheit zu führen. Marx stellt sie an die Spitze seiner Kompositionslehre, ohne eine weitere Anwendung von derselben zu machen. Auch Goethe und Zelter in ihrem Briefwechsel streifen sozusagen die Wahrheit. Letzterem ist Rameaus Ansicht bekannt. Sie werden nun gewiß erschrecken vor der Schwierigkeit dieses Problems, wenn ich Ihnen noch sage, daß bis auf die neueste Zeit selbst die Professoren der Physik keine Auskunft zu geben wußten, wenn sie um die Erklärung der Harmonie befragt wurden.
Erst kürzlich hat Helmholtz die Lösung der Frage gefunden. Um Ihnen diese aber klar zu machen, muß ich einige Erfahrungssätze der Physik und Psychologie erwähnen.
1. Bei jedem Wahrnehmungsprozeß, bei jeder Beobachtung, spielt die Aufmerksamkeit eine bedeutende Rolle. Nach Belegen hierfür brauchen wir nicht lange zu suchen. Sie erhalten ein Schreiben mit sehr schlechter Schrift; es will Ihnen nicht gelingen, dasselbe zu entziffern. Sie fassen bald diese, bald jene Linie zusammen, ohne daß sich daraus ein Buchstabe gestalten will. Erst wenn Sie Ihre Aufmerksamkeit auf Gruppen von Linien leiten, die wirklich zusammen gehören, ist das Lesen möglich. Schriften, die aus kleineren Figuren und Verzierungen bestehen, sind nur aus größerer Entfernung zu lesen, wenn die Aufmerksamkeit nicht mehr von den Gesamtkonturen auf die Einzelheiten abgelenkt wird. Ein schönes hierher gehöriges Beispiel geben die bekannten Bilderscherze von Giuseppe Arcimboldo im Erdgeschosse der Belvedere-Gallerie zu Wien. Es sind dies symbolische Darstellungen des Wassers, Feuers u. s. w., menschliche Köpfe, zusammengesetzt aus Wassertieren und Feuermaterial. Man sieht aus geringer Entfernung nur die Einzelheiten, welche die Aufmerksamkeit auf sich ziehen, aus größerer Entfernung hingegen nur die Gesamtfigur. Doch erwählt man leicht eine Distanz, bei der es keine Schwierigkeit hat, durch bloße willkürliche Leitung der Aufmerksamkeit bald die ganze Figur zu sehen, bald die kleineren Gestalten, aus welchen sie sich zusammensetzt. Häufig findet man ein Bild, das Grab Napoleons vorstellend. Das Grab ist von dunklen Bäumen umgeben, zwischen welchen der helle Himmel als Grund durchblickt. Man kann dieses Bild lange betrachten, ohne etwas anderes zu bemerken als eben die Bäume. Plötzlich aber erblickt man die Gestalt Napoleons zwischen den Bäumen, wenn man nämlich unwillkürlich dem hellen Grunde die Aufmerksamkeit zuwendet. An diesem Falle sieht man am deutlichsten, welche wichtige Rolle die Aufmerksamkeit spielt. Dasselbe sinnliche Objekt kann durch ihr Zutun allein zu ganz verschiedenen Wahrnehmungen Veranlassung geben.
Schlage ich irgend eine Harmonie am Piano an, so können Sie durch die bloße Aufmerksamkeit jeden Ton derselben fixieren. Sie hören dann am deutlichsten diesen fixierten Ton und alle übrigen erscheinen als bloße Zugabe, welche nur die Klangfarbe des ersteren verändert. Der Eindruck derselben Harmonie verändert sich wesentlich, wenn wir andern und andern Tönen unsere Aufmerksamkeit zuwenden.
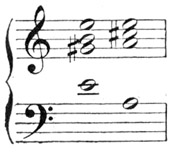
Fig. 9.
Versuchen Sie eine beliebige Harmoniefolge, z. B. und fixieren Sie einmal die Oberstimme e, dann den Bass e – a, so hören Sie dieselbe Harmoniefolge in beiden Fällen ganz verschieden. Im ersten Falle erhalten Sie den Eindruck, als ob der fixierte Ton sich gleich bliebe und bloß seine Klangfarbe veränderte, im zweiten Falle hingegen scheint die ganze Klangmasse in die Tiefe zu steigen. Es gibt eine Kunst des Komponisten, die Aufmerksamkeit des Hörers zu leiten. Es gibt aber ebensowohl eine Kunst des Hörens, die auch nicht jedermanns Sache ist.
Der Klavierspieler kennt die merkwürdigen Effekte, welche man erzielt, wenn man von einer angeschlagenen Harmonie irgend eine Taste losläßt.

Fig. 10.
Der Satz 1 auf dem Piano gespielt klingt fast wie 2. Der Ton, welcher der losgelassenen Taste zunächst liegt, erklingt nach dem Loslassen der letzteren wie neu angeschlagen. Die Aufmerksamkeit, von der Oberstimme nicht mehr in Anspruch genommen, wird eben auf denselben hinüber geleitet.
Die Auflösung einer beliebigen Harmonie in die einzelnen Tonbestandteile vermag schon ein mäßig geübtes musikalisches Ohr auszuführen. Bei fortschreitender Übung gelangt man noch weiter. Dann zerfällt der bisher für einfach gehaltene musikalische Klang in eine Reihe von Tönen. Schlägt man z. B. auf dem Piano 1 an, so hört man – bei nötiger Anspannung der Aufmerksamkeit neben diesem starken Grundtone noch die schwächeren höheren Obertöne 2 .... 7, also die Oktave, die Duodecime, die Doppeloktave, Terz, Quint und kleine Septime der Doppeloktave.

Fig. 11.
Ganz dasselbe bemerkt man an jedem musikalisch verwendbaren Klange. Jeder läßt neben seinem Grundtone, freilich mehr oder weniger stark, noch die Oktave, Duodecime, Doppeloktave u. s. f. hören. Namentlich ist dies leicht an den offenen und gedeckten Labialpfeifen der Orgel zu beobachten. Je nachdem nun gewisse Obertöne in einem Klange mehr oder weniger stark hervortreten, verändert sich die Klangfarbe, jene Eigentümlichkeit des Klanges, durch welche. wir den Klang des Klaviers von jenem der Violine, der Klarinette u. s. w. unterscheiden.
Am Piano lassen sich diese. Obertöne sehr leicht auffallend hörbar machen. Schlage ich z. B. nach der letzten Notenangabe 1 kurz an, während ich nach ein-, ander die Tasten 1, 2, 3, .... 7 bloß halte, so klingen nach dem Anschlag von 1 die Töne 2, 3, ..... 7 fort, indem die vom Dämpfer befreiten Saiten ins Mitschwingen geraten.
Wie Sie wissen, ist dieses Mitschwingen der gleichgestimmten Saiten mit den Obertönen nicht als Sympathie, sondern vielmehr als dürre mechanische Notwendigkeit aufzufassen. Man hat sich also das Mitschwingen nicht so zu denken, wie es ein geistreicher Feuilletonist sich vorgestellt hat, der von Beethovens F-moll-Sonate Op. 2 eine schauerliche Geschichte erzählt, welche ich Ihnen nicht vorenthalten will. »Auf der letzten Londoner Industrieausstellung spielten neunzehn Virtuosen die F-moll-Sonate auf demselben Piano. Als nun der zwanzigste Virtuose hintrat, um zur Abwechslung die F-moll-Sonate zu spielen, da begann das Klavier selbst, zum Schrecken aller Anwesenden, die Sonate von sich zu geben. Der eben anwesende Erzbischof von Canterbury mußte ans Werk und den F-moll-Teufel austreiben.«
Obgleich nun die besprochenen Obertöne bloß bei besonderer Aufmerksamkeit gehört werden, spielen sie doch die wichtigste Rolle bei Bildung der Klangfarbe sowohl, als auch bei der Konsonanz und Dissonanz der Klänge. Dies erscheint ihnen vielleicht befremdlich. Wie soll das, was nur unter besonderen Umständen gehört wird, doch für das Hören überhaupt von solcher Bedeutung sein?
Ziehen Sie doch Ihre tägliche Erfahrung zu Rate. Wie viele Dinge gibt es, die Sie gar nicht bemerken, die Ihnen erst dann auffallen, wenn sie nicht mehr da sind. Ein Freund tritt zu Ihnen herein; Sie wissen nicht, welche Veränderung mit ihm vorgegangen. Erst nach längerer Musterung finden Sie, daß sein Haar geschoren sei. Es ist nicht schwer, den Verlag eines Werkes nach dem bloßen Druck zu erkennen, und doch vermag kaum jemand genau anzugeben, wodurch sich diese Typen von jenen so auffallend unterscheiden. Oft erkannte ich ein gesuchtes Buch an einem Stückchen unbedruckten weißen Papiers, das unter dem Gewühle der übrigen Bücher hervorsah, und doch habe ich das Papier nie genau gemustert, wüßte auch nicht anzugeben, wodurch es von anderen Papieren so sehr verschieden ist.
Wir wollen also festhalten, daß jeder musikalisch verwendbare Klang neben seinem Grundtone noch die Oktave, Duodecime, Doppeloktave u. s. w. als Obertöne hören läßt, und daß diese für das Zusammenwirken mehrerer Klänge von Wichtigkeit sind.
2. Es handelt sich nun noch um eine zweite Tatsache. Betrachten Sie eine Stimmgabel. Dieselbe gibt angeschlagen einen ganz glatten Ton. Schlagen Sie aber zu dieser Gabel eine zweite etwas höhere oder tiefere an, welche für sich allein ebenfalls einen ganz glatten Ton gibt; so hören Sie, sobald Sie beide Gabeln zusammen auf den Tisch stemmen oder beide vor das Ohr halten, keinen gleichmäßigen Ton mehr, sondern eine Anzahl von Tonstößen. Diese Tonstöße werden rascher, wenn der Unterschied der Tonhöhen größer wird. Man nennt diese Tonstöße, welche für das Ohr sehr unangenehm werden, wenn sie etwa 33 mal in der Sekunde stattfinden, Schwebungen.
Immer, wenn von zwei gleichen Tönen einer gegen den anderen verstimmt wird, entstehen Schwebungen. Ihre Zahl wächst mit der Verstimmung und sie werden gleichzeitig unangenehmer. Diese Rauhigkeit erreicht ihr Maximum bei etwa 33 Schwebungen in der Sekunde. Bei weiterer Verstimmung und noch größerer Zahl der Schwebungen nimmt dies Unangenehme wieder ab, so zwar, daß Töne, welche in ihrer Höhe bedeutend verschieden sind, keine beleidigenden Schwebungen mehr geben.
Um sich das Zustandekommen der Schwebungen einigermaßen klar zu machen, nehmen Sie zwei Metronome zur Hand und stellen dieselben nahezu gleich ein. Sie können geradezu beide gleich einstellen. Sie brauchen deshalb nicht zu fürchten, daß sie auch wirklich gleich schlagen. Die im Handel vorkommenden Metronome sind schlecht genug, um bei Einstellung auf gleiche Skalenteile merklich ungleiche Schläge zu geben. Setzen Sie nun diese etwas ungleich schlagenden Metronome in Gang, so bemerken Sie leicht, daß ihre Schläge abwechselnd bald aufeinander, bald zwischeneinander fallen. Die Abwechslung ist desto rascher, je verschiedener der Takt beider Metronome. In Ermangelung von Metronomen führen Sie das Experiment mit zwei Taschenuhren aus.
Auf ähnliche Weise entstehen die Schwebungen. Die taktmäßigen Stöße zweier tönender Körper fallen bei ungleichen Tonhöhen bald aufeinander, bald zwischeneinander, wobei sie sich abwechselnd verstärken und schwächen. Daher das stoßweise unangenehme Anschwellen des Tones.
Nachdem wir nun die Obertöne und die Schwebungen kennen gelernt, gehen wir zur Beantwortung unserer Hauptfrage über. Warum bewirken gewisse Tonhöhenverhältnisse einen angenehmen Zusammenklang, eine Konsonanz, andere einen unangenehmen, eine Dissonanz? Es scheint, daß alles Unangenehme des Zusammenkingens von den entstehenden Schwebungen herrührt. Die Schwebungen sind nach Helmholtz die einzige Sünde, das einzige Böse in der harmonischen Musik. Konsonanz ist Zusammenklang ohne merkliche Schwebungen.
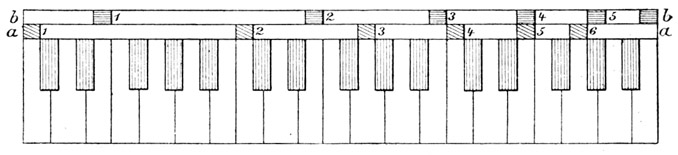
Fig. 12.
Um Ihnen dies recht anschaulich darzustellen, habe ich ein Modell konstruiert. Sie sehen in Fig. 12 eine Klaviatur. Oben an derselben befindet sich eine verschiebbare Leiste aa mit den Marken 1, 2 .... 6. Bringe ich diese Leiste in irgend eine Stellung, etwa so, daß die Marke 1 auf den Ton c der Klaviatur fällt, so bezeichnen, wie Sie sehen, die Marken 2, 3 ... 6 die Obertöne von c. Dasselbe gilt, wenn die Leiste in eine andere Stellung gebracht wird. Eine zweite ganz gleiche Leiste bb zeigt dieselbe Eigenschaft. Beide Leisten in irgend zwei Stellungen bezeichnen nun durch ihre Marken alle Töne, welche bei dem Zusammenwirken der durch die Marke 1 bezeichneten Klänge ins Spiel kommen.
Beide Leisten auf denselben Grundton eingestellt, lassen erkennen, daß auch sämtliche Obertöne zusammenfallen. Es wird der eine Klang durch den anderen eben nur verstärkt. Die einzelnen Obertöne eines Klanges liegen zu weit voneinander, um miteinander merkliche Schwebungen zu geben. Der zweite Klang fügt nichts Neues hinzu, demnach auch keine neuen Schwebungen. Der Einklang ist die vollkommenste Konsonanz.
Verschieben wir eine Leiste gegen die andere, so bedeutet dies eine Verstimmung des einen Klanges. Alle Obertöne des einen Klanges fallen nun neben jene des anderen, es treten sofort Schwebungen auf, der Zusammenklang wird unangenehm, wir erhalten eine Dissonanz. Wenn wir mit der Verschiebung der einen Leiste fortfahren, so finden wir, daß im allgemeinen die Obertöne immer nebeneinander fallen, immer Schwebungen und Dissonanzen veranlassen. Nur in ganz bestimmten Stellungen fallen die Obertöne beider Klänge zum Teil zusammen. Solche Stellungen bezeichnen eben einen höheren Grad des Wohlklanges, die konsonanten Intervalle.
Man kann diese konsonanten Intervalle leicht versuchsweise auffinden, wenn man Fig. 12 aus Papier ausschneidet und bb gegen aa verschiebt. Die vollkommensten Konsonanzen sind die Oktave und die Duodecime, weil bei diesen die Obertöne des einen Klanges ganz auf die des anderen fallen. Bei der Oktave z. B. fällt 1 b auf 2 a, 2 b auf 4 a, 3 b auf 6 a. Es können also keine Schwebungen entstehen. Konsonanzen sind also solche Zusammenklänge, welche nicht von unangenehmen Schwebungen begleitet sind.
Nur solche Klänge konsonieren, welche einen Teil ihrer Partialtöne gemeinsam haben. Natürlich wird man an solchen. Klängen, auch wenn' sie nacheinander angegeben werden, eine gewisse Verwandtschaft erkennen; Denn der folgende erregt eben, der gemeinsamen Obertöne wegen, zum Teil dieselbe Empfindung wie der vorhergehende. Am auffallendsten ist dies bei der Oktave. Wenn die Skale bei der Oktave anlangt, glaubt man in der Tat den Grundton wieder zu hören. Die Grundlagen der Harmonie sind also auch jene der Melodie.
Konsonanz ist Zusammenklang ohne merkliche Schwebungen! Dieser Grundsatz genügt, um in die Lehren des Generalbasses eine wunderbare Ordnung und Konsequenz zu bringen. Die Kompendien der Harmonielehre, welche bisher an Feinheit der Logik – Gott sei's geklagt – den Kochbüchern wenig nachgaben, werden ungemein klar und einfach. Noch mehr! Viel von dem, was geniale Musiker wie Palestrina, Mozart, Beethoven unbewußt richtig getroffen, worüber bisher kein Lehrbuch Rechenschaft zu geben vermochte, erfährt durch obigen Satz seine Begründung.
Und das Beste an dieser Theorie ist, daß sie den Stempel ihrer Wahrheit an sich trägt. Sie ist kein Hirngespinst. Jeder Musiker kann die Schwebungen selbst hören, welche die Obertöne der Klänge miteinander geben. Jeder Musiker kann sich überzeugen, daß man die Schwebungen ihrer Zahl und Rauhigkeit nach für einen beliebigen Fall voraus berechnen kann, und daß sie in dem Maße eintreten, als die Theorie es bestimmt.
Dies ist die von Helmholtz gegebene Beantwortung der von Pythagoras aufgeworfenen Frage, so weit sie sich nämlich mit jenen Mitteln darstellen läßt, die ich anwenden durfte. Ein langer Zeitraum liegt zwischen der Aufstellung der Frage und der Lösung. Mehr als einmal waren bedeutende Forscher näher an dieser Beantwortung, als sie selbst ahnten.
Der Forscher sucht die Wahrheit. Ich weiß nicht, ob die Wahrheit auch den Forscher sucht. Wäre dem aber so, dann würde die Geschichte der Wissenschaft lebhaft an das von Malern und Dichtern oft verewigte bekannte Stelldichein erinnern. Eine hohe Gartenmauer, rechts der Jüngling, links das Mädchen. Der Jüngling seufzt, das Mädchen seufzt! Beide warten. Beide ahnen nicht, wie nahe sie sich sind.
In der Tat, die Analogie gefällt mir. Die Wahrheit läßt sich zwar den Hof machen, allein sie verhält sich passiv. Sie führt wohl gar den Forscher an der Nase herum. Sie will verdient sein und verachtet den, der sie zu rasch erlangen will. Und wenn sich der eine den Kopf zerbricht, was schadet's – es kommt ein anderer – und die Wahrheit bleibt ja immer jung. Zwar scheint es mitunter, als ob sie ihrem Verehrer gewogen wäre, aber das eingestehn – niemals! Nur wenn die Wahrheit besonders gut aufgeräumt ist, wirft sie dem Verehrer einen Sonnenblick zu. Denn wenn ich gar nichts tue, denkt die Wahrheit – zuletzt erforscht mich der Kerl gar nicht mehr.
Dies eine Stückchen Wahrheit haben wir nun. Die kommt uns nicht mehr los! Wenn ich aber bedenke, was sie gekostet, wie viel Arbeit, wie viele Denkerleben, wie sich durch Jahrhunderte ein halber Gedanke fortgequält, bis er zum ganzen geworden, wenn ich bedenke, daß es die Mühe von mehr als zwei Jahrtausenden ist, welche aus meinem unscheinbaren Modell spricht, dann – ohne zu heucheln – gereut mich fast mein Scherz.
Und auch uns fehlt ja noch so viel. Wenn man einst nach einem Jahrtausend Stiefel, Cylinderhüte und Krinolinen, Klaviere und Baßgeigen aus dem Schoß der Erde graben wird, aus dem jüngsten Alluvium, als Leitmuscheln des neunzehnten Jahrhunderts, wenn man über diese wunderlichen Gebilde und unsere moderne Ringstraße Studien machen wird, wie heute über Steinaxt und Pfahlbau – dann wird man wohl nicht begreifen, wie wir an mancher großen Wahrheit so nahe sein konnten, ohne sie wirklich zu erfassen. Und so ist es ewig die ungelöste Dissonanz, ewig die trübende Septime, die uns überall entgegentönt; wir ahnen zwar, sie wird sich lösen, aber den reinen Dreiklang erleben wir nicht und – auch unsere Urenkel nicht.
Meine Damen! Wenn es Ihre reizende Lebensaufgabe ist, konfus zu machen, so ist es die meinige, klar zu sein. Und da muß ich Ihnen denn eine kleine Sünde eingestehen, deren ich mich der Klarheit wegen schuldig gemacht. Ich habe Sie nämlich ein wenig belogen. Sie werden mir diese Lüge verzeihen, wenn ich sie sofort wieder reuig verbessere. Das Modell (Fig. 12) spricht nicht die volle Wahrheit, denn es ist für die sogenannte temperierte Stimmung berechnet. Die Obertöne der Klänge aber sind nicht temperiert, sondern rein gestimmt Durch diese kleine Unrichtigkeit fällt nun das Modell bedeutend einfacher aus. Dabei genügt es für die gewöhnlichen Zwecke vollständig, und wer an demselben seine Studien macht, darf keinen merklichen Irrtum befürchten.
Wenn Sie nun aber von mir die volle Wahrheit fordern würden, so könnte ich Ihnen diese nur in einer mathematischen Formel darstellen. Ich müßte die Kreide zur Hand nehmen und – pfui! – in Ihrer Gegenwart rechnen. Das könnten Sie mir übel nehmen. Es soll auch nicht geschehen. Ich habe mir vorgenommen heute nicht mehr zu rechnen. Ich rechne heute auf gar nichts mehr, als auf Ihre Nachsicht, und diese werden Sie mir nicht versagen, wenn Sie bedenken, daß ich von meinem Rechte, Sie zu langweilen, doch einen beschränkten Gebrauch gemacht habe. Ich könnte ja noch länger sprechen, und bin demnach berechtigt, mit Lessings Epigramm zu schließen:
Wenn Du von allem dem, was diese Blätter füllt,
Mein Leser, nichts des Dankes wert gefunden;
So sei mir wenigstens für das verbunden,
Was ich zurück behielt.