
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Vortrag gehalten zu Graz i. J. 1866.
Wenn der Kriminalrichter einen recht feinen Schurken vor sich hat, der es wohl versteht, sich durchzulügen, so ist es seine Hauptaufgabe, ihm durch einige geschickte Fragen ein Geständnis abzupressen. In einem ähnlichen Falle fast scheint sich der Naturforscher der Natur gegenüber zu befinden. Zwar dürfte er sich hier nicht sowohl als Richter, wie vielmehr als Spion fühlen, aber das Ziel bleibt ziemlich dasselbe. Die geheimen Motive und Gesetze des Wirkens sind es, welche die Natur gestehen soll. Von der Schlauheit des Forschers hängt es ab, ob er etwas erfährt. Nicht ohne Grund hat also Baco von Verulam die experimentelle Methode ein Befragen der Natur genannt. Die Kunst besteht darin, die Fragen so zu stellen, daß sie ohne Verletzung der Etikette nicht unbeantwortet bleiben können.
Betrachten Sie nun noch die zahlreichen Instrumente, Werkzeuge und Quälapparate, mit welchen man der Natur forschend zu Leibe geht, und die des Dichterwortes spotten »was sie Dir nicht offenbaren mag, zwingst Du ihr nicht ab mit Hebeln und mit Schrauben« – betrachten Sie diese Apparate, und die Analogie mit der Tortur liegt nahe.
Die Auffassung der Natur, als der absichtlich verhüllten, die man nur mit Zwangsmitteln oder auf unredliche Weise entschleiern könne, lag manchem älteren Denker näher als uns. Ein griechischer Philosoph äußerte sich über die Naturforschung seiner Zeit und meinte, es könnte den Göttern nur unangenehm sein, wenn die Menschen das zu erspüren suchten, was jene ihnen nicht offenbaren wollten. Xenophon, Memorabil. IV, 7 läßt den Sokrates sagen: – οὔτε γὰρ εὑρετὰ ἀνθρώποις αὐτὰ ἐνόμιζεν εἶναι οὔτε χαρίζεσθαι θεοῖς ἂν ἡγεῖτο τὸν ζητοῦντα ἃ ἐκεῖνοι σαφηνίσαι οὐκ ἐβουλήθησαν. Freilich waren hiemit bei weitem nicht alle Zeitgenossen einverstanden. Spuren dieser Anschauung finden sich auch heute noch. Im ganzen jedoch sind wir nicht mehr so engherzig. Wir glauben nicht mehr, daß die Natur sich absichtlich verbirgt. Wir wissen jetzt aus der Geschichte der Wissenschaft, daß unsere Fragen zuweilen unsinnig gestellt sind, und daß deshalb keine Antwort erfolgen kann. Bald werden wir vielmehr sehen, wie der Mensch selbst mit seinem ganzen Denken und Forschen nichts ist als ein Stück Naturleben.
Mögen Sie nun die Instrumente des Physikers als Quäl- oder als Liebkosungsapparate auffassen, was Ihnen mehr zusagt, jedenfalls wird Sie ein Stückchen Geschichte dieser Werkzeuge interessieren, jedenfalls wird es Ihnen nicht unangenehm sein, zu erfahren, welche eigentümlichen Schwierigkeiten zu so sonderbaren Formen der Apparate geführt haben.
Galilei (geb. 1564 zu Pisa – gest. 1642 zu Arcetri) war der erste, welcher sich die Frage vorlegte, wie groß wohl die Geschwindigkeit des Lichtes, d. h. wie viel Zeit nötig sei, damit ein irgendwo aufleuchtendes Licht in einer bestimmten Entfernung sichtbar werde. Galilei, Discorsi e dimostrazione matematiche Leyden 1638. Dialogo primo.
Die Methode, welche Galilei ersann, war ebenso einfach, als natürlich. Zwei mit verdeckten Laternen versehene und geübte Beobachter sollten zur Nachtzeit in bedeutender Entfernung aufgestellt werden, der eine in A, der andere in B. A hatte den Auftrag, zu einer bestimmten Zeit seine Laterne abzudecken. Sobald dies B bemerkte, mußte er das Gleiche tun. Nun ist klar, daß die Zeit, welche A zählt von der Abdeckung der eigenen Laterne bis zum Sichtbarwerden der Laterne von B, diejenige ist, die das Licht benötigt, um von A nach B und von B nach A wieder zurück zu kommen. Der Versuch wurde nie ausgeführt und konnte, wie Galilei selbst einsah, gar nicht gelingen.
Fig. 13.
Wie wir heute wissen, geht nämlich das Licht viel zu rasch, um so beobachtet zu werden. Die Zeit zwischen der Ankunft des Lichtes in B und der Wahrnehmung desselben durch den Beobachter, die Zeit zwischen dem Entschluß und der Tat der Abdeckung der Laterne ist, wie wir heute wissen, unvergleichlich größer, als die Zeit, welche das Licht auf irdischen Strecken verweilt. Die Größe der Geschwindigkeit wird sofort ersichtlich, wenn man beachtet, daß ein Blitz in dunkler Nacht eine weit ausgedehnte Landschaft auf einmal sichtbar macht, während die einzelnen an verschiedenen Orten reflektierten Donnerschläge in beträchtlichen Zwischenzeiten das Ohr des Beobachters treffen.
Galileis Bemühungen um die Ermittelung der Lichtgeschwindigkeit blieben also bei seinen Lebzeiten erfolglos. Dennoch ist die spätere Geschichte der Messung der Lichtgeschwindigkeit eng verknüpft mit seinem Namen, denn er entdeckte mit dem von ihm konstruierten Fernrohr die vier Jupiterstrabanten, und diese wurden das Mittel zur Bestimmung der Lichtgeschwindigkeit.
Die irdischen Räume waren zu klein für Galileis Versuch. Die Bestimmung gelang erst, als man die Räume des Planetensystems zu Hilfe nahm. Olof Römer (geb. 1644 zu Aarhuus – gest. 1710 zu Kopenhagen) war es, dem dies (1675-1676) gelang. Er beobachtete mit Cassini auf der Pariser Sternwarte die Umläufe der Jupitersmonde.
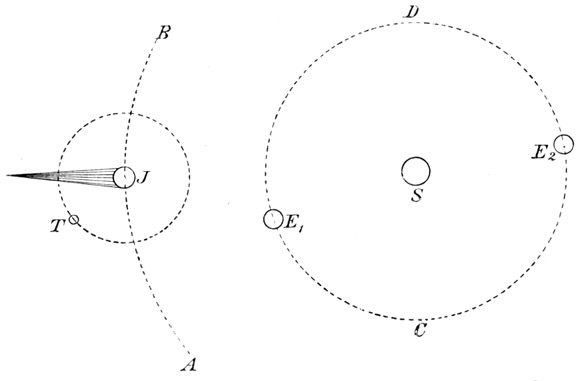
Fig. 14.
AB sei die Jupitersbahn. Es bedeute S die Sonne, E die Erde, J, den Jupiter und T den ersten Trabanten. Wenn die Erde in E 1 steht, sieht man den Trabanten regelmäßig in den Schatten des Jupiter eintreten und kann aus dieser periodischen Verfinsterung die Umlaufszeit berechnen. Römer fand für dieselbe 42 Stunden 27 Minuten 33 Sekunden. Wenn nun die Erde in ihrer Bahn fortschreitend über C bis E 2 kommt, so scheinen dabei die Umläufe des Trabanten langsamer zu werden, die Verfinsterungen treten etwas später ein. Die Verspätung der Verfinsterung, wenn die Erde in E 2 ist, beträgt 16 Minuten 26 Sekunden. Wenn die Erde wieder über D nach E 1sich zurückbewegt, werden die Umläufe scheinbar wieder rascher, und sie erfolgen ebenso schnell wie früher, sobald die Erde in E 1 angelangt ist. Zu bemerken ist, daß der Jupiter bei einem Bahnumlauf der Erde seine Stelle nur wenig ändert. Römer erriet sofort, daß diese periodischen Veränderungen der Umlaufszeit nicht wirkliche, sondern bloß scheinbare sein können, welche mit der Lichtgeschwindigkeit zusammenhängen.
Machen wir uns die Erscheinung durch ein Bild klar. Wir erfahren durch die regelmäßige Post von dem Stande der politischen Ereignisse in einer Stadt. Soweit wir auch von der Stadt entfernt sind, wir hören zwar von jedem Vorgange später, aber von allen gleich spät. Die Vorgänge erscheinen uns so rasch, als sie wirklich sind. Wenn wir nun aber reisen und uns dabei von der genannten Stadt entfernen, so hat jede folgende Nachricht einen längern Weg zu uns zurückzulegen, und die Vorgänge erscheinen uns langsamer, als sie wirklich sind. Das Umgekehrte würde stattfinden, wenn wir uns nähern.
Ein Musikstück hört man in jeder Entfernung, solange man in Ruhe ist, in demselben Tempo. Das Tempo muß scheinbar rascher werden, wenn wir der Musikbande rasch entgegen fahren, langsamer, wenn wir schnell fortfahren.
Denken Sie sich ein gleichförmig um seinen Mittelpunkt gedrehtes Kreuz, z. B. Windmühlflügel. Das Kreuz erscheint Ihnen offenbar langsamer gedreht, wenn Sie sich sehr rasch von demselben entfernen. Denn die Lichtpost, welche Ihnen die Nachricht von den Stellungen des Kreuzes bringt, hat in jedem folgenden Moment einen längern Weg zu Ihnen zurückzulegen.
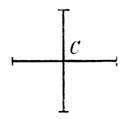
Fig. 15.
Ähnlich muß es sich nun bei der Drehung (dem Umlauf) des Jupiterstrabanten verhalten. Die größte Verspätung der Verfinsterung, während die Erde von E 1 nach E 2 geht, sich also um den Erdbahndurchmesser von Jupiter entfernt, entspricht offenbar der Zeit, welche das Licht zum Durchlaufen des Erdbahndurchmessers braucht. Der Erdbahndurchmesser ist bekannt, die Verspätung auch. Hieraus berechnet sich die Lichtgeschwindigkeit, d. i. der vom Licht in einer Sekunde zurückgelegte Weg zu 42,000 geographischen Meilen, oder 300,000 Kilometern.
Die Methode ist ähnlich jener Galileis. Nur sind die Mittel besser gewählt. Statt der kleinen Distanz verwenden wir den Erdbahndurchmesser (41 Millionen Meilen), die Stelle der ab- und zugedeckten Laterne vertritt der abwechselnd verfinsterte und aufleuchtende Jupitermond. Galilei konnte also seine Messung nicht ausführen, aber die Laterne hat er gefunden, mit der sie ausgeführt wurde.
Diese schöne Entdeckung wollte den Physikern bald nicht mehr genügen. Man suchte nach bequemeren Mitteln, die Lichtgeschwindigkeit auf der Erde zu messen. Man konnte dies tun, nachdem die Schwierigkeiten offen dalagen. Fizeau (geb. 1819 zu Paris) führte 1849 eine solche Messung aus.

Fig. 16.
Ich will es versuchen, Ihnen das Wesen des Fizeauschen Apparates klar zu machen. S sei eine am Rande mit Löchern versehene um ihren Mittelpunkt drehbare Scheibe. L sei eine Lichtquelle, welche ihr Licht auf die gegen die Axe der Scheibe um 45° geneigte unbelegte Glasplatte A sendet. Dieses wird dort reflektiert, geht durch ein Loch der Scheibe hindurch senkrecht auf den Spiegel B, der etwa eine deutsche Meile weit von S aufgestellt ist. Vom Spiegel B wird das Licht abermals in sich zurückgeworfen, geht wieder durch das Loch in S, dann durch die Glasplatte in das Auge O des Beobachters. O sieht also das Spiegelbild der Lichtflamme L durch die Glasplatte und das Loch der Scheibe hindurch im Spiegel B.
Wenn nun die Scheibe in Drehung versetzt wird, so werden an die Stellen der Löcher abwechselnd die Zwischenräume treten, und das Auge O wird jetzt nur in Unterbrechungen das Lichtbild in B sehen. Bei rascherer Drehung werden jedoch diese Unterbrechungen für das Auge wieder unmerklich, und es sieht den Spiegel B gleichförmig erleuchtet.
Alles dies gilt jedoch nur für nicht sehr große Geschwindigkeiten der Scheibe, wenn nämlich das Licht, welches durch ein Loch in S nach B gegangen ist, bei seiner Rückkehr das Loch fast noch an derselben Stelle trifft und zum zweitenmale hindurchkommt. Denken Sie sich nun die Geschwindigkeit so weit gesteigert, daß das Licht bei seiner Rückkehr an der Stelle des Loches einen Zwischenraum vorfindet, so kann es nicht mehr zum Auge O hindurch. Man sieht dann den Spiegel B nur, wenn er kein Licht aussendet, sondern eben welches zu ihm hingeht; derselbe ist hingegen verdeckt, wenn Licht von ihm kommt. Der Spiegel wird also immer dunkel erscheinen.
Würde nun die Drehungsgeschwindigkeit noch weiter gesteigert, so könnte das durch ein Loch hindurchgegangene Licht bei seiner Rückkehr wohl nicht mehr dasselbe, dafür aber etwa das nächstfolgende Loch antreffen und wieder zum Auge gelangen.
Es muß also bei fortwährend gesteigerter Rotationsgeschwindigkeit der Spiegel B abwechselnd hell und dunkel erscheinen. Offenbar kann man nun, wenn die Löcherzahl der Scheibe, die Umdrehungszahl in der Sekunde und der Weg SB bekannt ist, die Lichtgeschwindigkeit berechnen. Das Ergebnis stimmt mit dem Römerschen.
Die Sache ist übrigens nicht ganz so einfach, wie ich sie dargestellt habe. Es muß dafür gesorgt werden, daß das Licht den meilenlangen Weg SB und zurück BS unzerstreut zurücklegt. Dies geschieht mit Hilfe von Fernrohren.
Sehen wir den Fizeauschen Apparat etwas näher an, so finden wir in ihm einen alten Bekannten, die Disposition des Galileischen Versuches. L ist die Laterne, A, die rotierende durchlöcherte Scheibe, besorgt das regelmäßige Ab- und Zudecken derselben. Statt des ungeschickten Beobachters B finden wir den Spiegel B, der nun gewiß in dem Momente aufleuchtet, in welchem das Licht von S ankommt. Die Scheibe S, indem sie das rückkehrende Licht bald durchläßt, bald nicht, unterstützt nun den Beobachter O. Der Galileische Versuch wird hier sozusagen unzählige Male in einer Sekunde ausgeführt, und das Gesamtergebnis läßt sich nun wirklich beobachten. Dürfte ich die Darwinsche Theorie in diesem Gebiete anwenden, so würde ich sagen, der Fizeausche Apparat stammt von der Galileischen Laterne ab.
Eine noch feinere Methode zur Messung der Lichtgeschwindigkeit hat Foucault angewandt, doch würde uns die Beschreibung derselben hier zu weit führen.
Die Messung der Schallgeschwindigkeit gelingt nach der Galileischen Methode. Man hatte es also nicht nötig, sich weiter den Kopf zu zerbrechen. Der Gedanke aber, welcher durch die Not hervorgebracht war, der griff nun Platz auch in diesem Gebiete.
König in Paris verfertigt einen Apparat zur Messung der Schallgeschwindigkeit, welcher an die Fizeausche Methode erinnert. Die Vorrichtung ist sehr einfach. Sie besteht aus zwei elektrischen Schlagwerken, welche vollkommen gleichzeitig etwa Zehnteile von Sekunden schlagen. Stellt man beide Werke unmittelbar nebeneinander auf, so hört man überall, wo man auch stehen mag, die Schläge gleichzeitig. Stellt man sich aber neben dem einen Werke auf, und bringt das andere in größere Entfernung, so findet im allgemeinen kein Zusammenfallen der Schläge mehr statt. Die entsprechenden Schläge des ferneren Werkes kommen durch den Schall später an. Es fällt z. B. der erste Schlag des ferneren Werkes unmittelbar nach dem ersten des nahen u. s. f. Bei Vergrößerung der Distanz kann man es dahin bringen, daß wieder ein Zusammenfallen eintritt. Es fällt z. B. der erste Schlag des ferneren Werkes auf den zweiten des näheren, der zweite des ferneren auf den dritten des näheren u. s. f. Schlagen nun die Werke Zehnteile von Sekunden, und man entfernt sie so lange, bis das erste Zusammenfallen der Schläge eintritt, so wird ihre Entfernung vom Schall offenbar in einem Zehnteil einer Sekunde zurückgelegt.
Oft begegnen wir derselben Erscheinung wie hier, daß ein Gedanke Jahrhunderte braucht, um sich mühsam zu entwickeln; ist er aber einmal da, dann wuchert er sozusagen. Er macht sich's überall bequem, auch in solchen Köpfen, in welchen er niemals hätte wachsen können. Er ist einfach nicht mehr umzubringen.
Die Bestimmung der Lichtgeschwindigkeit ist nicht der einzige Fall, in welchem die unmittelbare Auffassung unserer Sinne zu langsam und schwerfällig wird. Das gewöhnliche Mittel, für die unmittelbare Beobachtung zu rasche Vorgänge zu studieren, besteht darin, daß man mit den zu untersuchenden Vorgängen andere bereits bekannte, ihrer Geschwindigkeit nach mit ihnen vergleichbare in Wechselwirkung setzt. Das Ergebnis ist meist sehr augenfällig und läßt auf die Art des noch unbekannten Vorganges schließen.
Die Fortpflanzungsgeschwindigkeit der Elektrizität läßt sich durch unmittelbares Beobachten nicht finden. Wheatstone hat sie aber zu ermitteln versucht, indem er den elektrischen Funken in einem enorm rasch rotierenden Spiegel (von bekannter Geschwindigkeit) betrachtete.
Wenn man einen Stab irgendwie willkürlich hin- und herbewegt, so läßt die bloße Betrachtung nicht erkennen, wie schnell er sich in jedem Punkte seiner Bahn bewegt. Betrachten wir aber den Stab durch die Randlöcher einer rasch rotierenden Scheibe. Wir sehen dann den bewegten Stab nur in bestimmten Stellungen, wenn eben ein Loch vor dem Auge vorbeigeht.
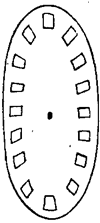
Fig. 17.
Die einzelnen Stabbilder verbleiben dem Auge einige Zeit. Wir meinen mehrere Stäbe zu sehen, etwa wie die unten folgende Zeichnung, Fig. 18, dies andeutet. Wenn nun die Löcher der Scheibe gleich weit abstehen und dieselbe gleichmäßig gedreht wurde, so sehen wir daraus deutlich, daß sich der Stab von a bis b langsam, schneller von b bis c, schneller von c bis d, am schnellsten von d bis e bewegt hat.
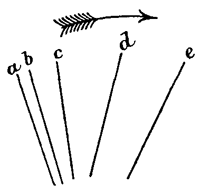
Fig. 18.
Ein Wasserstrahl, der aus einem Gefäß ausfließt, erscheint ganz ruhig und gleichmäßig. Beleuchtet man ihn jedoch im Dunkeln nur momentan mit dem elektrischen Funken, so sieht man, daß der Strahl aus einzelnen Tropfen besteht. Indem diese Tropfen rasch fallen, verwischen sich ihre Bilder, und der Strahl erscheint gleichmäßig. Betrachten wir den Strahl durch die rotierende Scheibe. Die Scheibe würde so rasch gedreht, daß, während das zweite Loch an die Stelle des ersten tritt, auch der Tropfen 1 bis an die Stelle von 2, 2 an die Stelle von 3 u. s. f. fällt. Dann sieht man immer an denselben Stellen Tropfen. Der Strahl scheint Fig. 19. in Ruhe zu sein. Drehen wir nun die Scheibe etwas langsamer, so wird, während das zweite Loch an die Stelle des ersten getreten ist, der Tropfen etwas unter 2, 2 etwas unter 3 gefallen sein u. s. f. Wir werden durch jedes folgende Loch Tropfen an etwas tieferen Stellen sehen. Der Strahl erscheint langsam abwärts fließend.
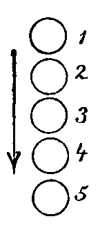
Fig. 19.
Drehen wir nun aber die Scheibe schneller. Dann kann, während das zweite Loch an die Stelle des ersten tritt, der Tropfen 1 nicht ganz an die Stelle von 2 gelangen, sondern wir finden ihn etwas ober 2, 2 etwas ober 3 u. s. f. Wir sehen durch jedes folgende Loch Tropfen an etwas höheren Stellen. Es hat nun den Anschein, als ob der Strahl nach oben flösse, als ob die Tropfen aus dem unteren Gefäß in das obere aufsteigen würden. Vgl. Artikel X Sie merken, die Physik wird nach und nach furchtbar. Bald wird es der Physiker in seiner Macht haben, die Rolle des Krebses im Mohriner See zu spielen, die Kopisch im folgenden Gedicht so schauerlich beschreibt.
Der große Krebs im Mohriner See
von
Kopisch.
Die Stadt Mohrin hat immer acht,
Guckt in den See bei Tag und Nacht:
Kein gutes Christenkind erlebt's,
Daß los sich reißt der große Krebs!
Er ist im See mit Ketten geschlossen unten an,
Weil er dem ganzen Lande Verderben bringen kann!
Man sagt: er ist viel Meilen groß
Und wend't sich oft, und kommt er los,
So währt's nicht lang, er kommt ans Land,
Ihm leistet keiner Widerstand:
Und weil das Rückwärtsgehen bei Krebsen alter Brauch,
So muß dann alles mit ihm zurücke gehen auch.
Das wird ein Rückwärtsgehen sein!
Steckt einer was ins Maul hinein,
So kehrt der Bissen, vor dem Kopf,
Zurück zum Teller und zum Topf!
Das Brot wird wieder zu Mehle, das Mehl wird wieder zu Korn –
Und alles hat beim Gehen den Rücken dann von vorn.
Der Balken löst sich aus dem Haus
Und rauscht als Baum zum Wald hinaus;
Der Baum kriecht wieder in den Keim,
Der Ziegelstein wird wieder Leim,
Der Ochse wird zum Kalbe, das Kalb geht nach der Kuh,
Die Kuh wird auch zum Kalbe, so geht es immer zu!
Zur Blume kehrt zurück das Wachs,
Das Hemd am Leibe wird zu Flachs,
Der Flachs wird wieder blauer Lein
Und kriecht dann in den Acker ein.
Man sagt, beim Bürgermeister zuerst die Not beginnt,
Der wird vor allen Leuten zuerst ein Päppelkind.
Dann muß der edle Rat daran,
Der wohlgewitzte Schreiber dann;
Die erbgesess'ne Bürgerschaft
Verliert gemach die Bürgerkraft.
Der Rektor in der Schule wird wie ein Schülerlein,
Kurz eines nach dem andern wird Kind und dumm und klein.
Und alles kehrt im Erdenschoß
Zurück zu Adams Erdenkloß.
Am längsten hält, was Flügel hat;
Doch wird zuletzt auch dieses matt:
Die Henne wird zum Küchlein, das Küchlein kriecht ins Ei,
Das schlägt der große Krebs dann mit seinem Schwanz entzwei!
Zum Glücke kommt's wohl nie so weit!
Noch blüht die Welt in Fröhlichkeit:
Die Obrigkeit hat wacker acht,
Daß sich der Krebs nicht locker macht;
Auch für dies arme Liedchen war' das ein schlechtes Glück:
Es lief vom Mund der Leute ins Tintenfaß zurück.
Erlauben Sie mir nun einige allgemeine Betrachtungen. Sie haben schon bemerkt, daß einer ganzen Reihe von Apparaten zu verschiedenen Zwecken oft dasselbe Prinzip zu Grunde liegt. Häufig ist es eine ganz unscheinbare Idee, welche sehr fruchtbar wirkt und in die physikalische Technik überall umgestaltend eingreift. Es ist hier eben nicht anders als im gewöhnlichen praktischen Leben
Das Rad am Wagen erscheint uns ganz einfach und unbedeutend. Aber der Erfinder desselben war sicher ein Genie. Zufällig mochte vielleicht ein runder Baumstamm zu der Bemerkung geführt haben, wie leicht sich eine Last auf einer Walze fortbewegen läßt. Da scheint nun der Schritt von der einfach untergelegten Walze zur befestigten Walze, zum Rade, ein sehr bequemer. Uns freilich, da wir von Kindheit an das Rad kennen, scheint dies sehr leicht. Denken wir uns aber lebhaft in die Lage eines Menschen, der nie ein Rad gesehen hat, der erst das Rad erfinden soll, so werden wir anfangen, die Schwierigkeiten zu fühlen. Ja, es muß uns sogar zweifelhaft werden, ob ein Mensch dies zu stände gebracht, ob nicht vielmehr Jahrhunderte nötig waren, um aus der Walze das erste Rad zu bilden.
Die Fortschrittsmänner, welche das erste Rad gebaut, nennt keine Geschichte, sie liegen weit hinaus über die historische Zeit. Keine Akademie hat sie gekrönt, kein Ingenieurverein zum Ehrenmitglied erwählt. Sie leben nur fort in den großartigen Wirkungen, die sie hervorgerufen. Nehmen Sie uns das Rad – und wenig wird von der Technik und Industrie der Neuzeit übrig bleiben. Es verschwindet alles. Vom Spinnrade bis zur Spinnfabrik, von der Drehbank bis zum Walzwerke, vom Schiebkarren bis zum Eisenbahnzuge, alles ist weg!
Dieselbe Bedeutung hat das Rad in der Wissenschaft. Die Drehapparate, als das einfachste Mittel, rasche Bewegungen ohne bedeutende Ortsveränderung zu erzielen, spielen in allen Zweigen der Physik eine Rolle. Sie kennen Wheatstones rotierenden Spiegel, Fizeaus gezahntes Rad, Plateaus durchlöcherte rotierende Scheiben u. s. w. – Allen diesen Apparaten liegt dasselbe Prinzip zu Grunde. Sie unterscheiden sich von einander nicht mehr, als sich das Taschenmesser vom Messer des Anatomen, vom Messer des Winzers seinem Zweck nach unterscheiden muß. Fast dasselbe ließe sich über die Schraube sagen.
Es wird Ihnen wohl schon klar geworden sein, daß neue Gedanken nicht plötzlich entstehen. Die Gedanken bedürfen ihrer Zeit, zu keimen und zu wachsen, sich zu entwickeln wie jedes Naturwesen; denn der Mensch mit seinem Denken ist eben auch ein Stück Natur.
Langsam, allmählich und mühsam bildet sich ein Gedanke in den andern um, wie es wahrscheinlich ist, daß eine Tierart allmählich in neue Arten übergeht. Viele Ideen erscheinen gleichzeitig. Sie kämpfen den Kampf ums Dasein nicht anders wie der Ichthyosaurus, der Brahmane und das Pferd. Vgl. Artikel XIV.
Wenige bleiben übrig, um sich rasch über alle Gebiete des Wissens auszubreiten, um sich abermals zu entwickeln, zu teilen und den Kampf von neuem zu beginnen. Wie manche längst überwundene, einer vergangenen Zeit angehörige Tierart noch fortlebt in abgelegenen Gegenden, wo sie von ihren Feinden nicht aufgestöbert werden konnte, so finden wir auch längst überwundene Ideen noch fortlebend in manchen Köpfen. Wer sich genau beobachtet, muß gestehen, daß sich die Gedanken so hartnäckig um ihr Dasein wehren wie die Tiere. Wer möchte leugnen, daß manche überwundene Anschauungsweise noch lange in abseitigen Winkeln des Gehirnes fortspukt, die sich in die klaren Gedankenreihen nicht mehr hinauswagt? Welcher Forscher weiß nicht, daß er bei Umwandlung seiner Ideen den härtesten Kampf mit sich selbst zu bestehen hat?
Ähnliche Erscheinungen begegnen dem Naturforscher auf allen Wegen, in den unbedeutendsten Dingen. Was so ein rechter Naturforscher ist, der forscht überall, auch auf der Promenade, auch auf der Ringstraße. Wenn er nun nicht zu gelehrt ist, so bemerkt er, daß gewisse Dinge, wie etwa die Damenhüte, der Veränderung unterliegen. Ich habe über diesen Gegenstand keine besonderen Forschungen angestellt, aber eines ist mir erinnerlich, daß eine Form allmählich in die andere übergegangen. Man trug Hüte mit weit vorstehendem Rand. Tief darin, kaum mit einem Fernrohr erreichbar, lag das Antlitz der Schönen verborgen. Der Rand wurde immer kürzer, das Hütchen schrumpfte zur Ironie eines Hutes zusammen. Nun fängt oben ein mächtiges Dach an hervorzuwachsen und die Götter wissen, wie groß es noch werden soll. Es ist nicht anders bei den Damenhüten wie bei den Schmetterlingen, deren Formmannigfaltigkeit oft nur darauf beruht, daß ein kleiner Auswuchs am Flügel bei einer verwandten Art sich zu einem mächtigen Lappen entwickelt. Auch die Natur hat ihre Moden, sie währen aber Jahrtausende. Ich könnte dies noch an manchem Beispiel, etwa an der Entstehung des Fracks, erläutern, wenn ich nicht fürchten müßte, daß meine Causerie zu ungemütlich wird.
Wir haben nun ein Stückchen Geschichte der Wissenschaft durchwandert! Was haben wir gelernt? Eine kleine, ich möchte sagen, unbedeutende Aufgabe, die Messung der Lichtgeschwindigkeit – und mehr als zwei Jahrhunderte haben an der Lösung derselben gearbeitet! – Drei der bedeutendsten Naturforscher, Galilei ein Italiener, Römer ein Däne und Fizeau ein Franzose, haben redlich die Mühe geteilt. Und so geht es bei unzähligen andern Fragen. Wenn wir so die vielen Gedankenblüten betrachten, die alle welkend fallen müssen, bevor eine reift, dann lernen wir's erst recht verstehen, das ernste, aber wenig tröstliche Wort:
Viele sind berufen, aber wenige sind auserwählt.
So spricht jedes Blatt der Geschichte! Aber ist die Geschichte auch gerecht? Sind wirklich nur jene auserwählt, welche sie nennt? Haben die umsonst gelebt und gekämpft, die keinen Preis errungen?
Fast möcht' ich das bezweifeln. Jeder wird es bezweifeln, welcher die Gedankenqual der schlaflosen Nächte kennt, die, oft lange ohne Erfolg, endlich doch zum Ziele führt. Kein Gedanke wurde da umsonst gedacht, jeder, auch der unbedeutendste, der falsche sogar, der scheinbar unfruchtbarste diente dazu, den folgenden fruchtbaren vorzubereiten. Wie im Denken des Einzelnen nichts umsonst, so auch in jenem der Menschheit!
Galilei wollte die Lichtgeschwindigkeit messen. Er *mußte die Augen schließen, ohne daß es ihm gelungen war. Aber er hat wenigstens die Laterne gefunden, mit der es sein Nachfolger vermochte. Und so darf ich denn behaupten, daß wir alle, sofern wir nur wollen, an der künftigen Kultur arbeiten. Wenn wir nur alle das Rechte anstreben, alle sind wir dann berufen und alle sind wir auserwählt!