Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

Oswald Spengler

Der Untergang des Abendlandes – Erster Band

9

Während die antike Seele durch Pythagoras um 540 zur Entdeckung ihrer, der apollinischen Zahl als einer meßbaren Größe gelangt war, fand die Seele des Abendlandes durch Descartes und seine Generation (Pascal, Fermat, Desargues) im genau entsprechenden Zeitpunkte die Idee einer Zahl, die aus dem leidenschaftlichen faustischen Hang zum Unendlichen geboren wurde. Die Zahl als reine Größe, die sich an die körperliche Gegenwart des Einzeldinges heftet, findet ihr Gegenstück in der Zahl als reine Beziehung.Das entspricht genau dem Verhältnis von Geldmünze und doppelter Buchführung im Gelddenken der beiden Kulturen, vgl. Bd. II, S. 1168ff.. Darf die antike Welt, der Kosmos, aus jenem tiefen Bedürfnis nach sichtbarer Begrenztheit als abzählbare Summe von stofflichen Dingen definiert werden, so hat sich unser Weltgefühl im Bild eines unendlichen Raumes verwirklicht, in dem alles Sichtbare, als etwas Bedingtes dem Unbedingten gegenüber, beinahe als eine Wirklichkeit zweiten Ranges empfunden wird. Sein Symbol ist der entscheidende, in keiner andern Kultur angedeutete Begriff der Funktion. Die Funktion ist nichts weniger als die Erweiterung irgend eines vorhandenen Zahlbegriffs; sie ist dessen völlige Überwindung. Nicht nur die euklidische und damit auch die »allgemein menschliche«, auf alltäglicher Erfahrung beruhende Geometrie der Kinder und Ungelehrten, sondern auch die archimedische Sphäre des elementaren Rechnens, die Arithmetik, hört damit auf, für die wirklich bedeutende Mathematik Westeuropas Wert zu haben. Es gibt nur noch eine abstrakte Analysis. Für den antiken Menschen waren Geometrie und Arithmetik in sich geschlossene und vollständige Wissenschaften von höchstem Range, beide anschaulich, beide mit Größen zeichnerisch oder rechnerisch verfahrend; für uns sind sie nur noch praktische Hilfsmittel des alltäglichen Lebens. Addition und Multiplikation, die beiden antiken Methoden der Größenrechnung und Schwestern der zeichnerischen Konstruktion, verschwinden völlig in der Unendlichkeit funktionaler Prozesse. Gerade die Potenz, die zunächst nur ein Zahlzeichen für eine bestimmte Gruppe von Multiplikationen (für Produkte gleicher Größen) ist, wird durch das neue Symbol des Exponenten (Logarithmus) und seine Anwendung in komplexen, negativen, gebrochenen Formen vom Größenbegriff gänzlich abgelöst und in eine transzendente Beziehungswelt überführt, die den Griechen, welche nur zwei positive, ganzzahlige Potenzen als Repräsentanten von Fläche und Körper kannten, unzugänglich bleiben mußte, man denke an Ausdrücke wie

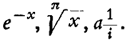
Jede der tiefsinnigen Schöpfungen, welche von der Renaissance an rasch aufeinander folgen, die der imaginären und komplexen Zahlen, welche Cardanus schon 1550 einführt, die der unendlichen Reihen, welche durch Newtons große Entdeckung des Binominalsatzes 1666 theoretisch sicher begründet werden, die der Logarithmen um 1610, der Differentialgeometrie, des bestimmten Integrals durch Leibniz, der Menge als neuer Zahleneinheit, von Descartes schon angedeutet, die neuen Prozesse wie die unbestimmte Integration, die Entwicklung der Funktionen in Reihen, sogar in unendliche Reihen andrer Funktionen, sind ebensoviel Siege über das populär-sinnliche Zahlengefühl in uns, das aus dem Geiste der neuen Mathematik heraus, die ein neues Weltgefühl zu verwirklichen hatte, überwunden werden mußte. Es gab bisher keine zweite Kultur, welche den Leistungen einer andern, längst erloschenen, so viel Verehrung entgegentrug und wissenschaftlich so viel Einfluß gestattete, wie die abendländische gerade der antiken. Es dauerte lange, bevor wir den Mut fanden, unser eignes Denken zu denken. Auf dem Grunde lag der beständige Wunsch, es der Antike gleichzutun. Trotzdem war jeder Schritt in diesem Sinne eine tatsächliche Entfernung von dem erstrebten Ideal. Deshalb ist die Geschichte des abendländischen Wissens die einer fortschreitenden Emanzipation vom antiken Denken, einer Befreiung, die nicht einmal gewollt, die in den Tiefen des Unbewußten erzwungen wurde. So gestaltete sich die Entwicklung der neuen Mathematik zu einem heimlichen, langen, endlich siegreichen Kampf gegen den Größenbegriff.Dasselbe gilt vom römischen Recht, vgl. Bd. II, S. 652ff., und der Geldmünze, vgl. Bd. II, S. 1175 f.